Using Explainable Artificial Intelligence (XAI) to Predict the Influence of Weather on the Thermal Soaring Capabilities of Sailplanes for Smart City Applications
Abstract
1. Introduction
2. Literature Review
2.1. Soaring Gliders and Unmanned Aerial Vehicles
2.2. Contribution
3. Methods
3.1. Dataset
3.1.1. Flights Used in Regression Dataset
3.1.2. Flights Used in Classification Dataset
3.1.3. Weather Data Used for Both Datasets
3.2. Regression
3.3. Classification
3.4. Explainable Artificial Intelligence
3.5. Limitations
4. Results
4.1. Regression (Prediction of Flight Duration)
4.1.1. Random Forest
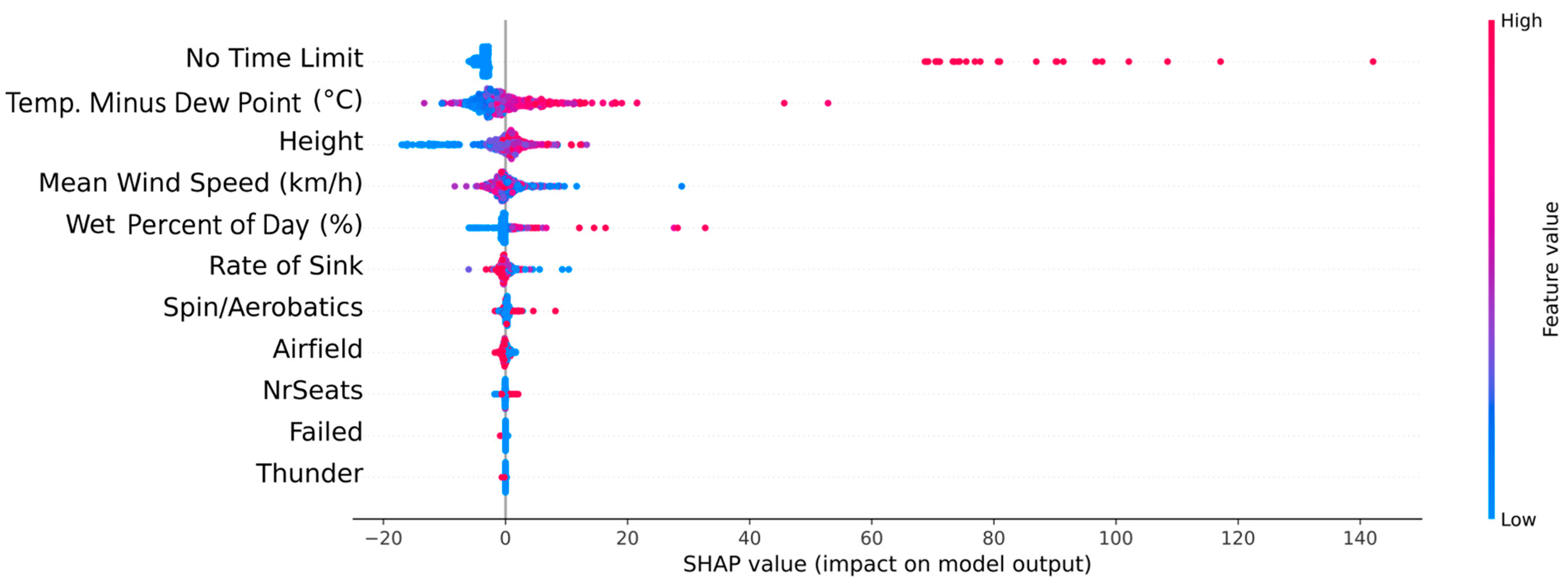
4.1.2. Explainable Artificial Intelligence (SHapley Additive exPlanations; SHAP)
4.2. Classification Task
4.2.1. Classification Task
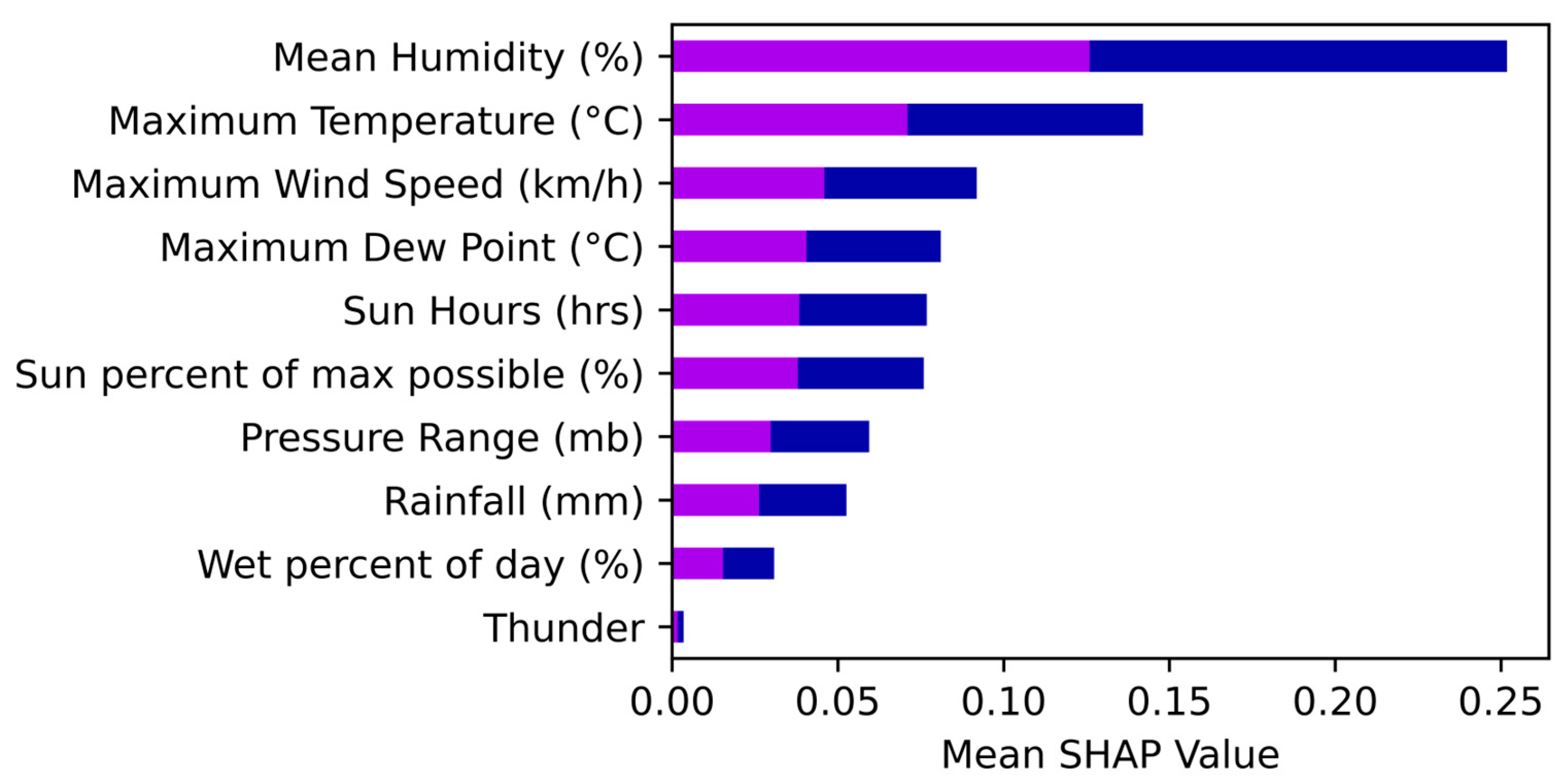
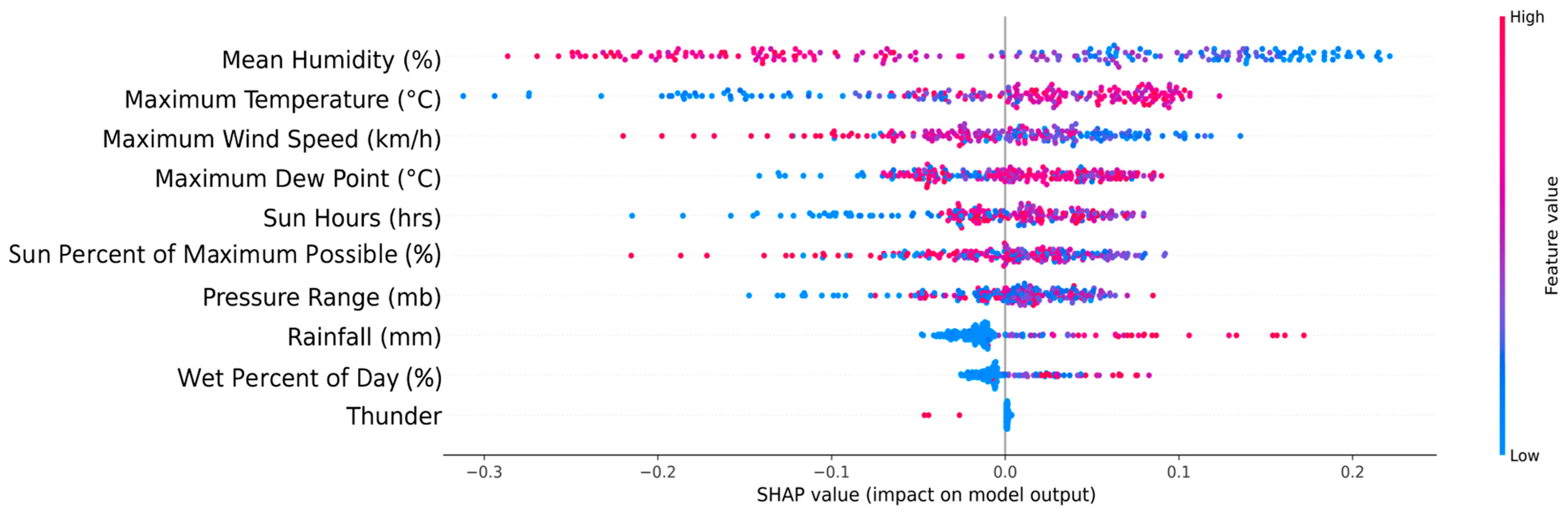
4.2.2. Explainable Artificial Intelligence (SHapley Additive exPlanations; SHAP)
5. Discussion
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lawrance, N.R.J.; Sukkarieh, S. A guidance and control strategy for dynamic soaring with a gliding UAV. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; IEEE: Piscataway, NJ, USA, 2009. [Google Scholar]
- Gao, X.-Z.; Hou, Z.-X.; Guo, Z.; Fan, R.-F.; Chen, X.-Q. Analysis and design of guidance-strategy for dynamic soaring with UAVs. Control Eng. Pract. 2014, 32, 218–226. [Google Scholar] [CrossRef]
- White, C.; Lim, E.; Watkins, S.; Mohamed, A.; Thompson, M. A feasibility study of micro air vehicles soaring tall buildings. J. Wind Eng. Ind. Aerodyn. 2012, 103, 41–49. [Google Scholar] [CrossRef]
- Kim, S.-H.; Lee, J.; Jung, S.; Lee, H.; Kim, Y. Deep neural network-based feedback control for dynamic soaring of unpowered aircraft. IFAC-PapersOnLine 2019, 52, 117–121. [Google Scholar] [CrossRef]
- Chudej, K.; Klingler, A.-L.; Britzelmeier, A. Flight path optimization of a hang-glider in a thermal updraft. IFAC-PapersOnLine 2015, 48, 808–812. [Google Scholar] [CrossRef]
- Schermann, E.; Omran, H.; Durand, S.; Kiefer, R. Stochastic trajectory optimization for autonomous soaring of UAV. IFAC-PapersOnLine 2019, 52, 562–567. [Google Scholar] [CrossRef]
- Rejeb, A.; Abdollahi, A.; Rejeb, K.; Treiblmaier, H. Drones in agriculture: A review and bibliometric analysis. Comput. Electron. Agric. 2022, 198, 107017. [Google Scholar] [CrossRef]
- Edulakanti, S.R.; Ganguly, S. Review article: The emerging drone technology and the advancement of the Indian drone business industry. J. High Technol. Manag. Res. 2023, 34, 100464. [Google Scholar] [CrossRef]
- de Villiers, C.; Munghemezulu, C.; Mashaba-Munghemezulu, Z.; Chirima, G.J.; Tesfamichael, S.G. Weed Detection in Rainfed Maize Crops Using UAV and PlanetScope Imagery. Sustainability 2023, 15, 13416. [Google Scholar] [CrossRef]
- Mndela, Y.; Ndou, N.; Nyamugama, A. Irrigation Scheduling for Small-Scale Crops Based on Crop Water Content Patterns Derived from UAV Multispectral Imagery. Sustainability 2023, 15, 12034. [Google Scholar] [CrossRef]
- Hafeez, A.; Husain, M.A.; Singh, S.; Chauhan, A.; Khan, M.T.; Kumar, N.; Chauhan, A.; Soni, S. Implementation of drone technology for farm monitoring & pesticide spraying: A review. Inf. Process. Agric. 2023, 10, 192–203. [Google Scholar] [CrossRef]
- Hart, L.; Quendler, E.; Umstaetter, C. Sociotechnological Sustainability in Pasture Management: Labor Input and Optimization Potential of Smart Tools to Measure Herbage Mass and Quality. Sustainability 2022, 14, 7490. [Google Scholar] [CrossRef]
- Coutinho, W.P.; Fliege, J.; Battarra, M. Glider Routing and Trajectory Optimisation in disaster assessment. Eur. J. Oper. Res. 2019, 274, 1138–1154. [Google Scholar] [CrossRef]
- Maqbool, A.; Mirza, A.; Afzal, F.; Shah, T.; Khan, W.Z.; Bin Zikria, Y.; Kim, S.W. System-Level Performance Analysis of Cooperative Multiple Unmanned Aerial Vehicles for Wildfire Surveillance Using Agent-Based Modeling. Sustainability 2022, 14, 5927. [Google Scholar] [CrossRef]
- Josipovic, N.; Viergutz, K. Smart Solutions for Municipal Flood Management: Overview of Literature, Trends, and Applications in German Cities. Smart Cities 2023, 6, 944–964. [Google Scholar] [CrossRef]
- Munawar, H.S.; Ullah, F.; Qayyum, S.; Heravi, A. Application of deep learning on uav-based aerial images for flood detection. Smart Cities 2021, 4, 1220–1242. [Google Scholar] [CrossRef]
- Runnström, M.C.; Ólafsdóttir, R.; Blanke, J.; Berlin, B. Image analysis to monitor experimental trampling and vegetation recovery in icelandic plant communities. Environments 2019, 6, 99. [Google Scholar] [CrossRef]
- Cagnazzo, C.; Potente, E.; Regnauld, H.; Rosato, S.; Mastronuzzi, G. Autumnal beach litter identification by mean of using ground-based ir thermography. Environments 2021, 8, 37. [Google Scholar] [CrossRef]
- Rachmawati, T.S.N.; Kim, S. Unmanned Aerial Vehicles (UAV) Integration with Digital Technologies toward Construction 4.0: A Systematic Literature Review. Sustainability 2022, 14, 5708. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Huang, C. Smart data-driven policy on unmanned aircraft systems (UAS): Analysis of drone users in U.S. cities. Smart Cities 2021, 4, 78–92. [Google Scholar] [CrossRef]
- Kharchenko, V.; Kliushnikov, I.; Rucinski, A.; Fesenko, H.; Illiashenko, O. UAV Fleet as a Dependable Service for Smart Cities: Model-Based Assessment and Application. Smart Cities 2022, 5, 1151–1178. [Google Scholar] [CrossRef]
- Karakikes, I.; Nathanail, E. Using the delphi method to evaluate the appropriateness of urban freight transport solutions. Smart Cities 2020, 3, 1428–1447. [Google Scholar] [CrossRef]
- Wang, Y.; Kumar, L.; Raja, V.; Al-Bonsrulah, H.A.Z.; Kulandaiyappan, N.K.; Tharmendra, A.A.; Marimuthu, N.; Al-Bahrani, M. Design and Innovative Integrated Engineering Approaches Based Investigation of Hybrid Renewable Energized Drone for Long Endurance Applications. Sustainability 2022, 14, 16173. [Google Scholar] [CrossRef]
- Lee, D.; Longo, S.; Kerrigan, E.C. Predictive control for soaring of unpowered autonomous UAVs. IFAC Proc. Vol. 2012, 45, 194–199. [Google Scholar] [CrossRef]
- Camacho, N.; Dobrokhodov, V.N.; Jones, K.D. Cooperative Autonomy of Multiple Solar-Powered Thermaling Gliders⋆. In Proceedings of the 19th World Congress the International Federation of Automatic Control, Cape Town, South Africa, 24–29 August 2014. [Google Scholar]
- Teodoro, A.; Santos, P.; Marques, J.E.; Ribeiro, J.; Mansilha, C.; Melo, A.; Duarte, L.; de Almeida, C.R.; Flores, D. An integrated multi-approach to environmental monitoring of a self-burning coal waste pile: The são pedro da cova mine (porto, portugal) study case. Environments 2021, 8, 48. [Google Scholar] [CrossRef]
- Dickmanns, E. Collocated Hermite Approximation Applied to Time Optimal Crosscountry Soaring. IFAC Proc. Vol. 1983, 16, 137–145. [Google Scholar] [CrossRef]
- Cui, Y.; Yan, D.; Wan, Z. Study on the Glider Soaring Strategy in Random Location Thermal Updraft via Reinforcement Learning. Aerospace 2023, 10, 834. [Google Scholar] [CrossRef]
- Harzer, J.; De Schutter, J.; Diehl, M.; Meyers, J. Dynamic soaring in wind turbine wakes. Eur. J. Control. 2023, 74, 100842. [Google Scholar] [CrossRef]
- Thakker, D.; Mishra, B.K.; Abdullatif, A.; Mazumdar, S.; Simpson, S. Explainable artificial intelligence for developing smart cities solutions. Smart Cities 2020, 3, 1353–1382. [Google Scholar] [CrossRef]
- Englund, C.; Aksoy, E.; Alonso-Fernandez, F.; Cooney, M.; Pashami, S.; Åstrand, B. AI perspectives in smart cities and communities to enable road vehicle automation and smart traffic control. Smart Cities 2021, 4, 783–802. [Google Scholar] [CrossRef]
- You, J.; van der Klein, S.A.; Lou, E.; Zuidhof, M.J. Application of random forest classification to predict daily oviposition events in broiler breeders fed by precision feeding system. Comput. Electron. Agric. 2020, 175, 105526. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. Available online: www.tensorflow.org (accessed on 2 July 2023).
- Gulli, A.; Pal, S. Deep Learning with Keras. Available online: https://keras.io (accessed on 2 July 2023).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. 2011. Available online: http://scikit-learn.sourceforge.net (accessed on 2 July 2023).
- O’Malley, T.; Bursztein, E.; Long, L.; Chollet, F.; Jin, H.; Invernizzi, L. KerasTuner. Available online: https://github.com/keras-team/keras-tuner (accessed on 2 July 2023).
- Waskom, M.; Botvinnik, O.; Hobson, P.; Cole, J.B.; Halchenko, Y.; Hoyer, S.; Miles, A.; Augspurger, T.; Yarkoni, T.; Megies, T.; et al. Seaborn: v0.5.0 (November 2014). Available online: https://zenodo.org/records/12710 (accessed on 2 July 2023).
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010. [Google Scholar]
- Rosenberg, G.; Brubaker, J.K.; Schuetz, M.J.A.; Salton, G.; Zhu, Z.; Zhu, E.Y.; Kadıoğlu, S.; Borujeni, S.E.; Katzgraber, H.G. Explainable Artificial Intelligence Using Expressive Boolean Formulas. Mach. Learn. Knowl. Extr. 2023, 5, 1760–1795. [Google Scholar] [CrossRef]
- Cabitza, F.; Campagner, A.; Natali, C.; Parimbelli, E.; Ronzio, L.; Cameli, M. Painting the Black Box White: Experimental Findings from Applying XAI to an ECG Reading Setting. Mach. Learn. Knowl. Extr. 2023, 5, 269–286. [Google Scholar] [CrossRef]
- Kim, M.-Y.; Atakishiyev, S.; Babiker, H.K.B.; Farruque, N.; Goebel, R.; Zaïane, O.R.; Motallebi, M.-H.; Rabelo, J.; Syed, T.; Yao, H.; et al. A Multi-Component Framework for the Analysis and Design of Explainable Artificial Intelligence. Mach. Learn. Knowl. Extr. 2021, 3, 900–921. [Google Scholar] [CrossRef]
- Buhrmester, V.; Münch, D.; Arens, M. Analysis of Explainers of Black Box Deep Neural Networks for Computer Vision: A Survey. Mach. Learn. Knowl. Extr. 2021, 3, 966–989. [Google Scholar] [CrossRef]
- Trebbien, J.; Gorjão, L.R.; Praktiknjo, A.; Schäfer, B.; Witthaut, D. Understanding electricity prices beyond the merit order principle using explainable AI. Energy AI 2023, 13, 100250. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Allen, P.G.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. Available online: https://github.com/slundberg/shap (accessed on 2 July 2023).
- Utama, C.; Meske, C.; Schneider, J.; Schlatmann, R.; Ulbrich, C. Explainable artificial intelligence for photovoltaic fault detection: A comparison of instruments. Sol. Energy 2023, 249, 139–151. [Google Scholar] [CrossRef]
- Thrun, M.C.; Ultsch, A.; Breuer, L. Explainable AI Framework for Multivariate Hydrochemical Time Series. Mach. Learn. Knowl. Extr. 2021, 3, 170–204. [Google Scholar] [CrossRef]
- Lohaj, O.; Paralič, J.; Bednár, P.; Paraličová, Z.; Huba, M. Unraveling COVID-19 Dynamics via Machine Learning and XAI: Investigating Variant Influence and Prognostic Classification. Mach. Learn. Knowl. Extr. 2023, 5, 1266–1281. [Google Scholar] [CrossRef]
- Hawkins, C. How to Estimate Cloud Bases and Heights. Available online: https://www.flymac.co.uk/how-to-estimate-cloud-bases-and-heights/ (accessed on 11 October 2023).

| MAE in Minutes | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Features * | 5.74 | 5.76 | 5.76 | 5.76 | 5.77 | 5.79 | 5.79 | 5.80 | 5.80 | 5.81 |
| Mean Wind Speed | X | X | ||||||||
| Maximum Gust | X | X | X | X | X | X | X | X | ||
| Temperature Minus Dew Point | X | X | X | X | X | X | X | X | X | X |
| Maximum Dew Point | X | X | ||||||||
| Mean Temperature | X | |||||||||
| Maximum Temperature | X | X | X | X | X | X | X | X | ||
| Thunder | X | X | X | X | X | X | ||||
| Rainfall | X | |||||||||
| Wet percent of day | X | X | X | X | X | X | X | X | X | X |
| Mean Pressure | X | X | X | X | ||||||
| Pressure Range | X | X | X | |||||||
| Accuracy | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Features | 0.812 * | 0.812 | 0.812 | 0.812 | 0.797 | 0.797 | 0.797 | 0.797 | 0.797 | 0.797 |
| Mean Wind Speed | X | |||||||||
| Maximum Wind Speed | X | X | X | X | X | X | X | X | X | X |
| Temperature Minus Dew Point | X | X | ||||||||
| Minimum Dew Point | X | |||||||||
| Mean Dew Point | X | X | X | X | X | |||||
| Maximum Dew Point | X | X | ||||||||
| Maximum Temperature | X | |||||||||
| Minimum Temperature | X | X | X | |||||||
| Mean Humidity | X | X | X | X | X | X | X | X | X | X |
| Sun Percent of Max Possible | X | X | X | X | X | X | X | X | ||
| Sun Hours | X | X | X | X | X | X | X | |||
| Thunder | X | X | X | X | ||||||
| Wet Percent of Day | X | X | X | X | X | X | ||||
| Rainfall | X | X | X | X | X | X | X | X | ||
| Mean Pressure | X | X | X | X | X | X | ||||
| Pressure Range | X | X | X | X | X | X | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schnieder, M. Using Explainable Artificial Intelligence (XAI) to Predict the Influence of Weather on the Thermal Soaring Capabilities of Sailplanes for Smart City Applications. Smart Cities 2024, 7, 163-178. https://doi.org/10.3390/smartcities7010007
Schnieder M. Using Explainable Artificial Intelligence (XAI) to Predict the Influence of Weather on the Thermal Soaring Capabilities of Sailplanes for Smart City Applications. Smart Cities. 2024; 7(1):163-178. https://doi.org/10.3390/smartcities7010007
Chicago/Turabian StyleSchnieder, Maren. 2024. "Using Explainable Artificial Intelligence (XAI) to Predict the Influence of Weather on the Thermal Soaring Capabilities of Sailplanes for Smart City Applications" Smart Cities 7, no. 1: 163-178. https://doi.org/10.3390/smartcities7010007
APA StyleSchnieder, M. (2024). Using Explainable Artificial Intelligence (XAI) to Predict the Influence of Weather on the Thermal Soaring Capabilities of Sailplanes for Smart City Applications. Smart Cities, 7(1), 163-178. https://doi.org/10.3390/smartcities7010007





