Robust-Adaptive Controllers Designed for Grid-Forming Converters Ensuring Various Low-Inertia Microgrid Conditions
Abstract
:1. Introduction
1.1. Significance and Problem
1.2. Related Publications
- As future MGs transition towards lower inertia levels due to the increased penetration of DERs, grid-forming technologies are gaining increasing popularity. Nevertheless, there remains a limited amount of research dedicated to the design of controllers for grid-forming converters;
- The consequences of reducing MG’s inertia often go overlooked during the design of robust or adaptive controllers. This oversight can have significant implications for the stability and performance of MGs, necessitating increased attention in controller development and system design processes;
- The design process typically overlooks the dynamics of DERs. Previous literature commonly treats DERs as a collective or aggregate model, which may not align with the practical complexities of actual MGs.
1.3. Summary of Key Contributions
- This paper presents the development of robust-adaptive controllers specifically designed for GFM converters in MGs. The GFM converters are modeled as distributed VSCs. This contribution addresses the critical need for stable and reliable operation of MGs as renewable energy sources and distributed generation are integrated. These controllers are designed to handle the intricate control challenges posed by the inherent low inertia of MGs.
- The proposed adaptive-robust control framework is specifically developed to address the diverse challenges encountered in low-inertia MGs. It incorporates a novel adaptive law that dynamically adjusts the control parameters of the robust controller, enhancing the adaptability of the controller in MGs characterized by high levels of uncertainty such as intermittent power outputs from such resources, etc. To clarify further, our proposed framework aims to substantially enhance both the frequency and voltage regulation in low-inertia MGs, especially during critical operating conditions.
- The efficacy of the recently introduced adaptive-robust controllers has been substantiated in a low-inertia MG characterized by a significant integration of converter-interfaced resources. This validation aims at comprehensive testing of the proposed controllers under a wide range of MG operational scenarios and conditions. The testing results mainly focus on probabilistic analysis, probabilistic small-signal stability analysis, and time-domain simulations.
1.4. Paper Organization
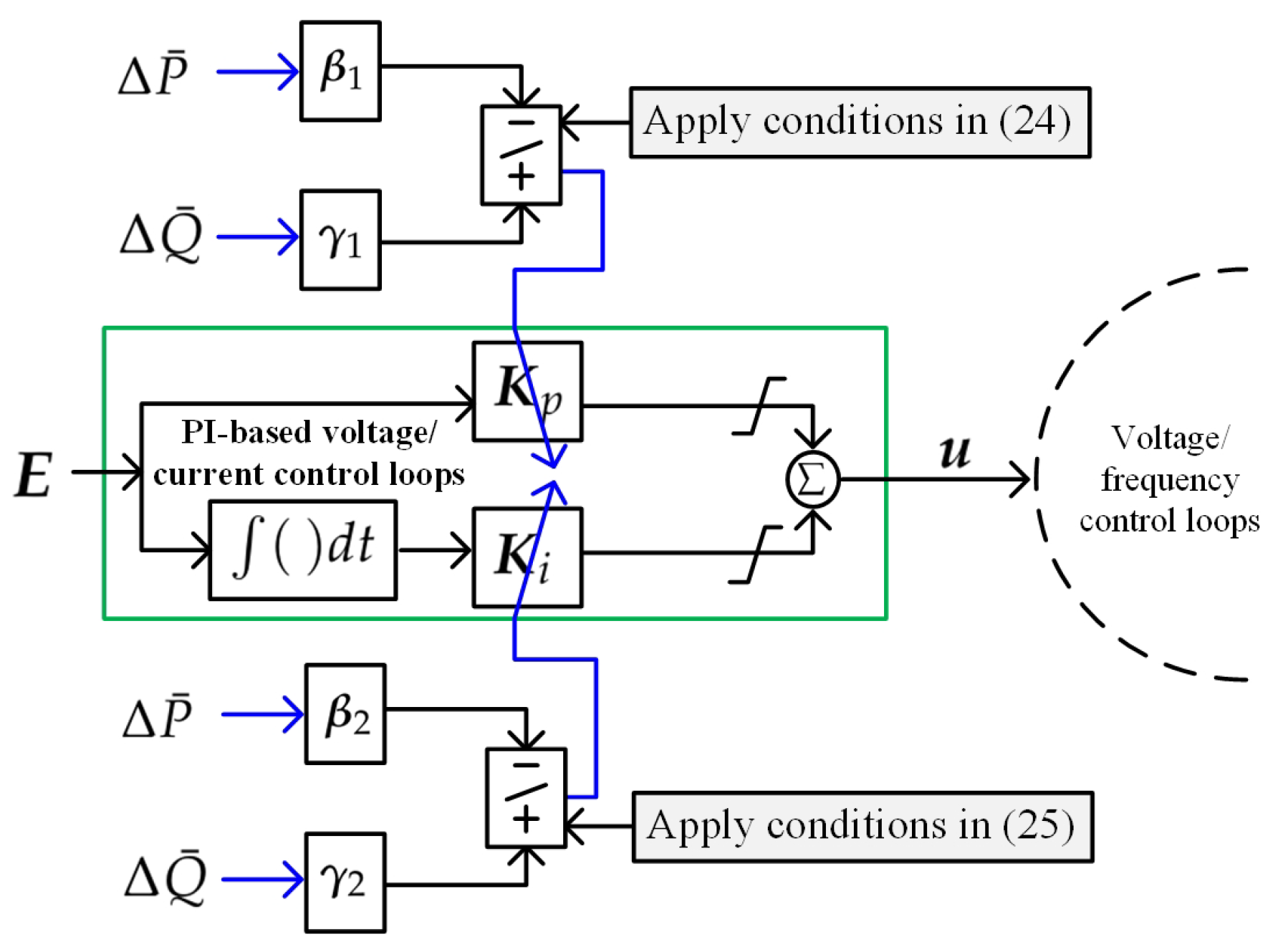
2. Overview of Robust-Adaptive Framework
2.1. Proposed Grid-Forming Converter Control
2.2. Structure of Robust-Adaptive Controller
3. Proposed Robust-Adaptive Control Design
4. Simulation Results and Discussions
4.1. Modified Islanding MG with DERs
4.2. Benchmark
4.3. Numerical Results and Discussion
5. Key Insights and Concluding Remarks
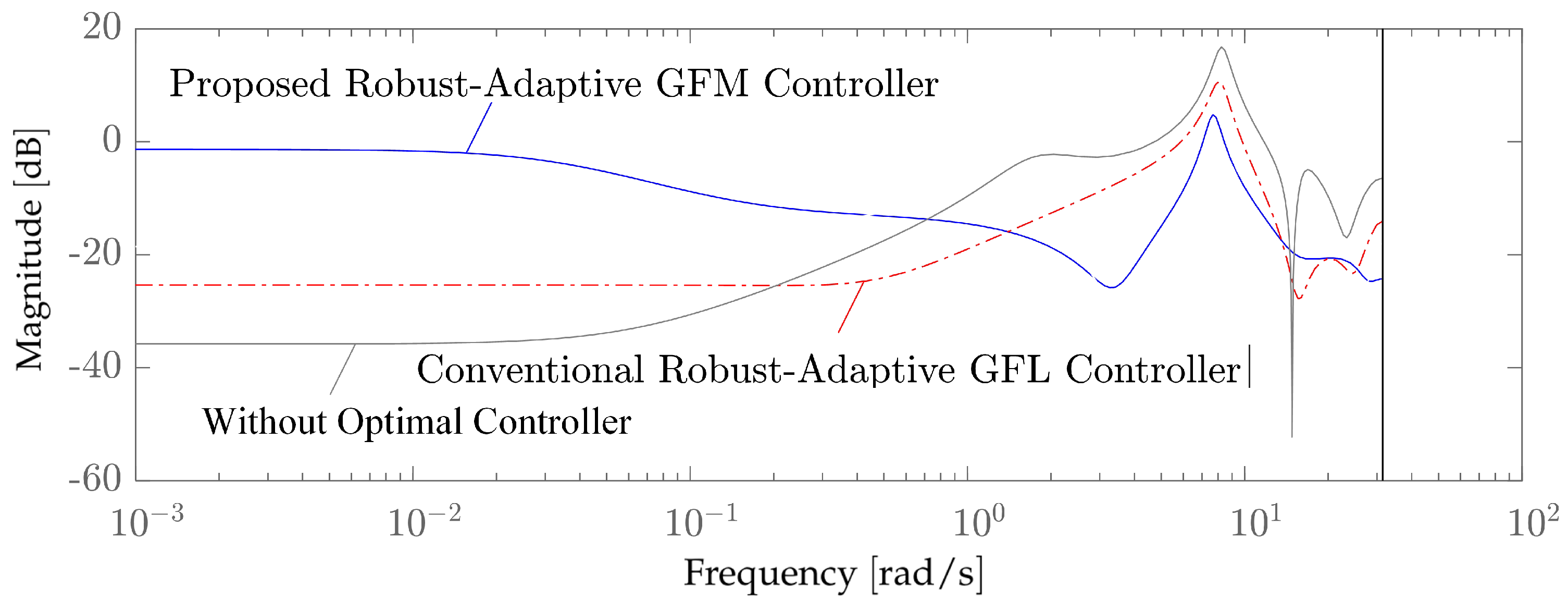
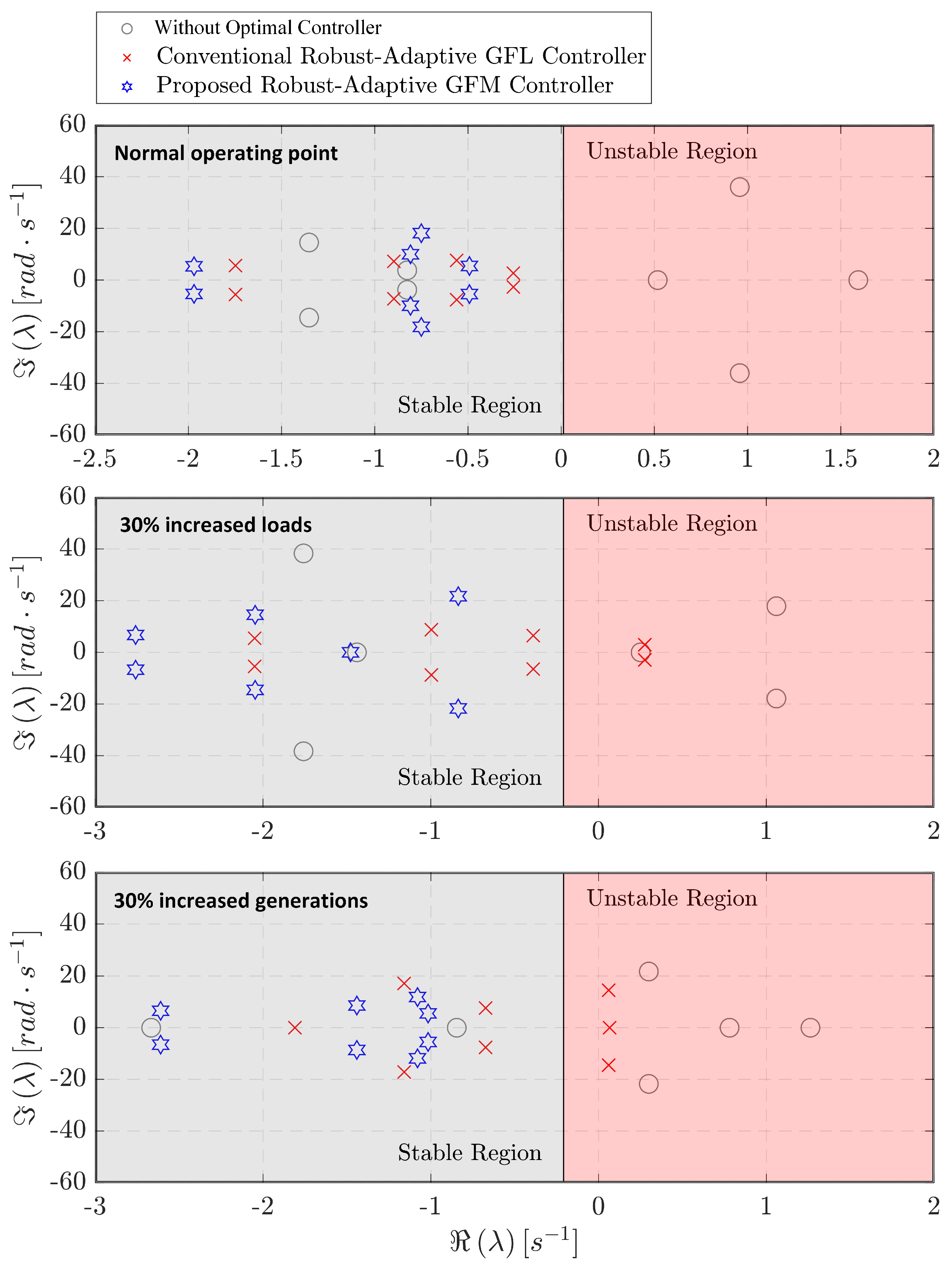
- The Proposed Robust-Adaptive Controller consistently outperforms other controllers in terms of damping ratios, providing enhanced stability and performance across various operating conditions;
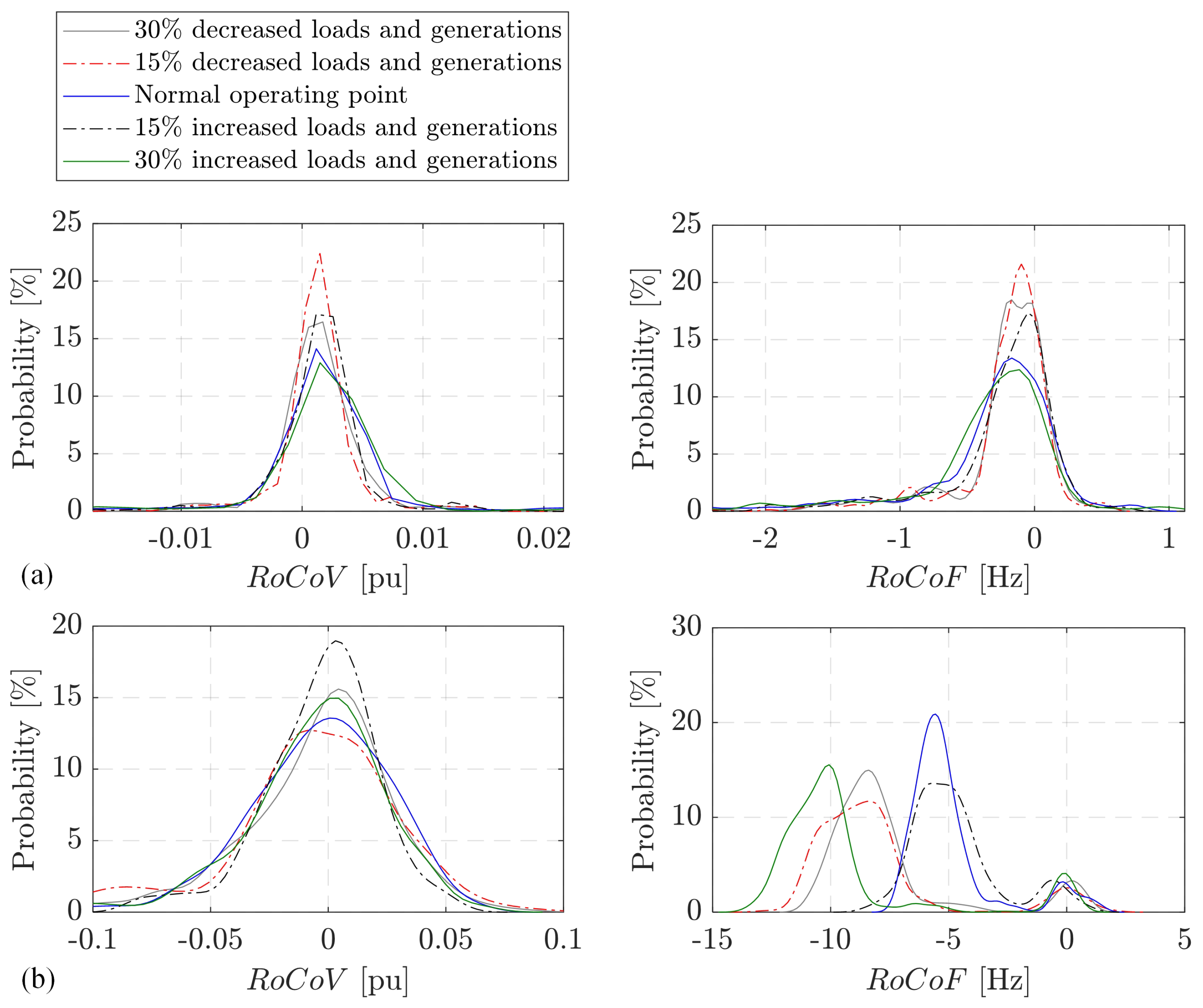
- Through extensive time-domain simulations, it is evident that the Proposed Controller maintains superior performance when dealing with fluctuations in load, generation, voltage, and frequency, even in low-inertia scenarios;
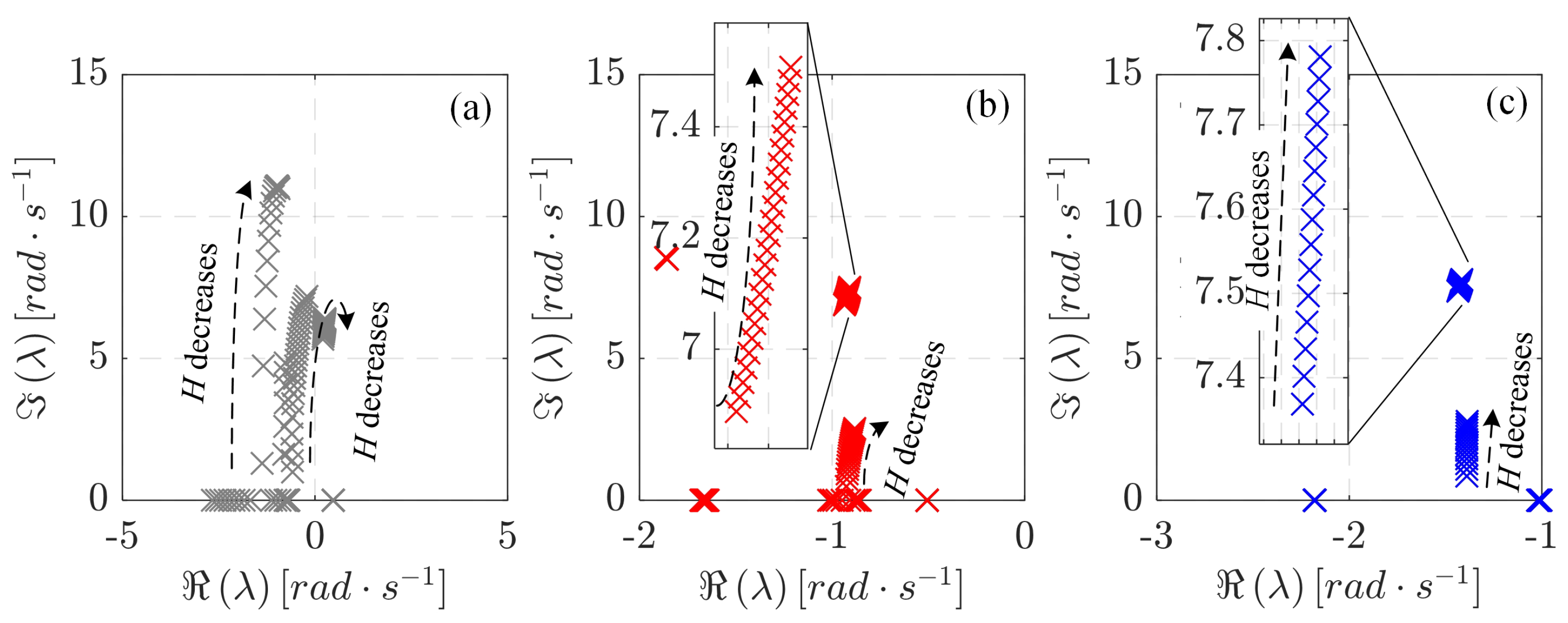
- When compared to the Conventional Robust-Adaptive GFL Controller, the Proposed Robust-Adaptive GFM Controller demonstrates significantly reduced rate of changes in voltage () and frequency (), indicating its superiority in ensuring stable MG operation;
- The probability analysis further corroborates the robustness and reliability of the Proposed Controller, emphasizing its suitability for MG applications under a wide range of scenarios.
- Building upon the favorable outcomes observed in our simulations, we will strive to further enhance the performance of the Proposed Robust-Adaptive GFM Controller. This includes fine-tuning its parameters and algorithms to optimize damping ratios and response times;
- We recognize the importance of exploring the controller’s adaptability to even more diverse and complex MG scenarios. Our aim is to ensure that it can effectively handle a broader range of disturbances and uncertainties;
- To validate the practical applicability of our controller, we plan to conduct real-world experiments and field tests within actual MG systems using a real-time simulation with hardware-in-the-loop (known as HIL). This will help bridge the gap between simulation findings and real-world implementation;
- We will continue to emphasize the robustness and reliability of the proposed controller, making it a viable and trustworthy choice for MG applications, even in challenging operational conditions;
- We will explore the implementation of a central master controller to oversee the regulation of the GFM converter system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BESS | Battery energy storage system |
| DER | Distributed energy resource |
| DG | Distributed Generation |
| MG | Microgrid |
| GFM | Grid-forming converter |
| GFL | Grid-following converter |
| PV | Photovoltaic |
| RES | Renewable energy resource |
| Rate of changes of frequency | |
| Rate of changes of voltage | |
| SG | Synchronous generator |
| VSC | Voltage source converter |
References
- Aboelezz, A.M.; Sedhom, B.E.; El-Saadawi, M.M.; Eladl, A.A.; Siano, P. State-of-the-art review on shipboard microgrids: Architecture, control, management, protection, and future perspectives. Smart Cities 2023, 6, 1435–1484. [Google Scholar] [CrossRef]
- Saeed, M.H.; Fangzong, W.; Kalwar, B.A.; Iqbal, S. A review on microgrids’ challenges & perspectives. IEEE Access 2021, 9, 166502–166517. [Google Scholar]
- Joshal, K.S.; Gupta, N. Microgrids with model predictive control: A critical review. Energies 2023, 16, 4851. [Google Scholar] [CrossRef]
- Ratnam, K.S.; Palanisamy, K.; Yang, G. Future low-inertia power systems: Requirements, issues, and solutions-A review. Renew. Sustain. Energy Rev. 2020, 124, 109773. [Google Scholar] [CrossRef]
- Sørensen, D.A.; Pombo, D.V.; Iglesias, E.T. Energy storage sizing for virtual inertia contribution based on ROCOF and local frequency dynamics. Energy Strategy Rev. 2023, 47, 101094. [Google Scholar] [CrossRef]
- Pinthurat, W.; Hredzak, B. Distributed control strategy of single-phase battery systems for compensation of unbalanced active powers in a three-phase four-wire microgrid. Energies 2021, 14, 8287. [Google Scholar] [CrossRef]
- Pinthurat, W.; Hredzak, B.; Konstantinou, G.; Fletcher, J. Techniques for compensation of unbalanced conditions in LV distribution networks with integrated renewable generation: An overview. Electr. Power Syst. Res. 2023, 214, 108932. [Google Scholar] [CrossRef]
- Shahzad, S.; Abbasi, M.A.; Ali, H.; Iqbal, M.; Munir, R.; Kilic, H. Possibilities, challenges, and future opportunities of microgrids: A review. Sustainability 2023, 15, 6366. [Google Scholar] [CrossRef]
- Shi, J.; Ma, L.; Li, C.; Liu, N.; Zhang, J. A comprehensive review of standards for distributed energy resource grid-integration and microgrid. Renew. Sustain. Energy Rev. 2022, 170, 112957. [Google Scholar] [CrossRef]
- Musca, R.; Vasile, A.; Zizzo, G. Grid-forming converters: A critical review of pilot projects and demonstrators. Renew. Sustain. Energy Rev. 2022, 165, 112551. [Google Scholar] [CrossRef]
- Teng, Y.; Deng, W.; Pei, W.; Li, Y.; Dingv, L.; Ye, H. Review on grid-forming converter control methods in high-proportion renewable energy power systems. Glob. Energy Interconnect. 2022, 5, 328–342. [Google Scholar] [CrossRef]
- Araujo, L.S.; Brandao, D.I. Self-adaptive control for grid-forming converter with smooth transition between microgrid operating modes. Int. J. Electr. Power Energy Syst. 2022, 135, 107479. [Google Scholar] [CrossRef]
- Qoria, T.; Gruson, F.; Colas, F.; Guillaud, X.; Debry, M.S.; Prevost, T. Tuning of cascaded controllers for robust grid-forming voltage source converter. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–7. [Google Scholar]
- Rathnayake, D.B.; Akrami, M.; Phurailatpam, C.; Me, S.P.; Hadavi, S.; Jayasinghe, G.; Zabihi, S.; Bahrani, B. Grid forming inverter modeling, control, and applications. IEEE Access 2021, 9, 114781–114807. [Google Scholar] [CrossRef]
- Narula, A.; Bongiorno, M.; Beza, M.; Chen, P.; Karlsson, D. Coordinated control of grid-forming converters and hydro generators to enhance frequency quality of future power system. Electr. Power Syst. Res. 2022, 212, 108456. [Google Scholar] [CrossRef]
- Zuo, Y.; Yuan, Z.; Sossan, F.; Zecchino, A.; Cherkaoui, R.; Paolone, M. Performance assessment of grid-forming and grid-following converter-interfaced battery energy storage systems on frequency regulation in low-inertia power grids. Sustain. Energy Grids Netw. 2021, 27, 100496. [Google Scholar] [CrossRef]
- Li, Z.; Zang, C.; Zeng, P.; Yu, H.; Li, S.; Bian, J. Control of a grid-forming inverter based on sliding-mode and mixed H2/Hinf control. IEEE Trans. Ind. Electron. 2016, 64, 3862–3872. [Google Scholar] [CrossRef]
- Alcaide-Godinez, I.; Bai, F. Frequency support from multiple utility-scale grid-forming battery energy storage systems. In Proceedings of the 2022 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Chongqing, China, 7–9 July 2022; pp. 1271–1276. [Google Scholar]
- Lin, T.; Das, M.; Gole, A.; Isaacs, A. Adaptive fault ride through control of VSM Grid-forming converters. Electr. Power Syst. Res. 2023, 223, 109606. [Google Scholar] [CrossRef]
- Yu, J.; Liu, W.; Sun, J.; Zhang, F.; Yang, Y. An improved grid impedance estimator for grid-forming converters in consideration of controller dynamics. Int. J. Electr. Power Energy Syst. 2023, 154, 109424. [Google Scholar] [CrossRef]
- Liu, X.K.; Wang, Y.W.; Liu, Z.W.; Huang, Y. On the stability of distributed secondary control for DC microgrids with grid-forming and grid-feeding converters. Automatica 2023, 155, 111164. [Google Scholar] [CrossRef]
- Ngamroo, I.; Surinkaew, T. Control of distributed converter-based resources in a zero-inertia microgrid using robust deep learning neural network. IEEE Trans. Smart Grid 2023. [Google Scholar] [CrossRef]
- Surinkaew, T.; Emami, K.; Shah, R.; Islam, M.R.; Islam, S. Forced oscillation management in a microgrid with distributed converter-based resources using hierarchical deep-learning neural network. Electr. Power Syst. Res. 2023, 222, 109479. [Google Scholar] [CrossRef]
- Pal, B.; Chaudhuri, B. Robust Control in Power Systems; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Ahn, S.J.; Park, J.W.; Chung, I.Y.; Moon, S.I.; Kang, S.H.; Nam, S.R. Power-sharing method of multiple distributed generators considering control modes and configurations of a microgrid. IEEE Trans. Power Deliv. 2010, 25, 2007–2016. [Google Scholar] [CrossRef]
- Awal, M.; Husain, I. Unified virtual oscillator control for grid-forming and grid-following converters. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 4573–4586. [Google Scholar] [CrossRef]

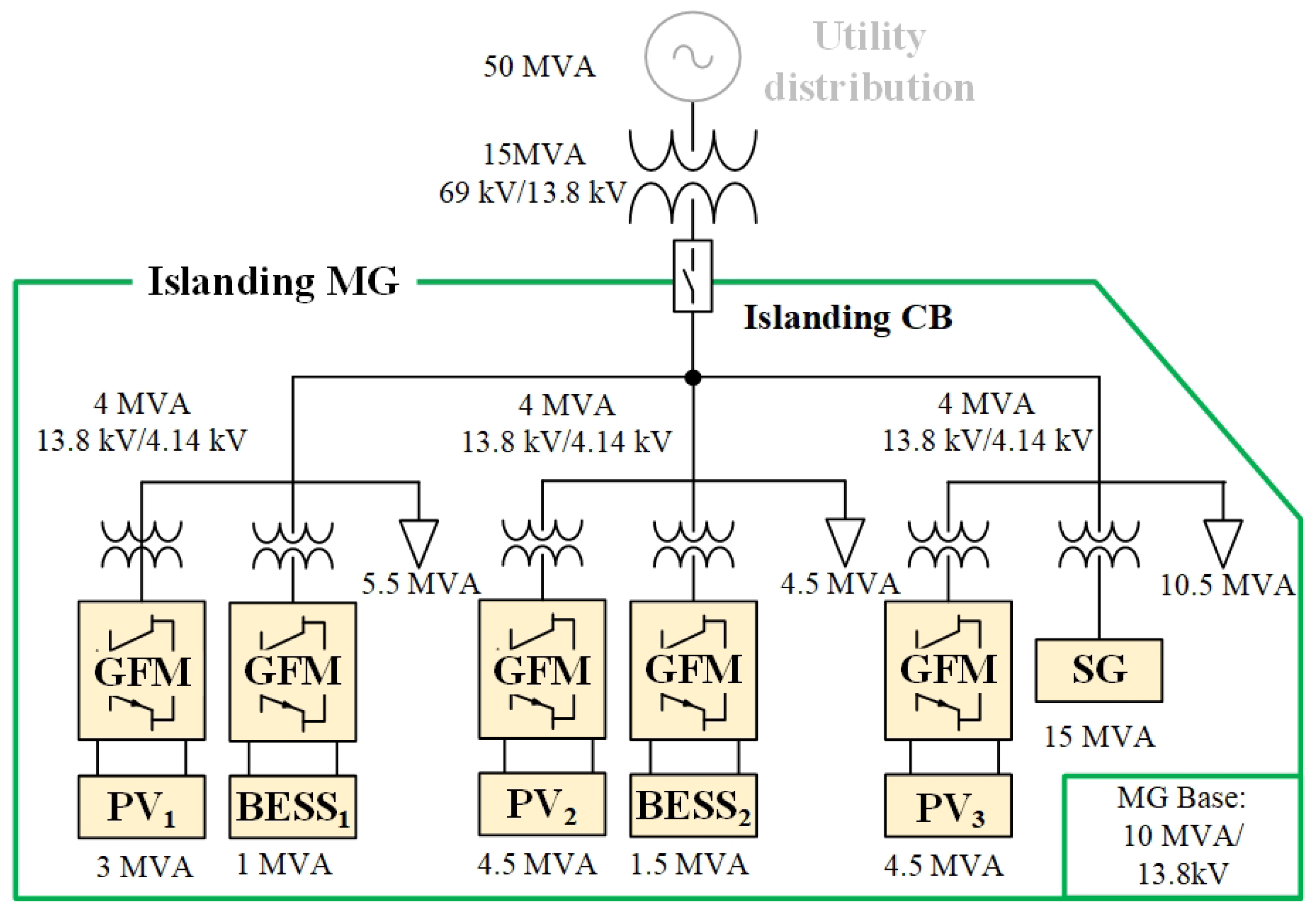


| Parameters | GFM of PV1 | GFM of BESS1 | GFM of PV2 | GFM of BESS2 | GFM of PV3 | |
|---|---|---|---|---|---|---|
| Voltage control loop | 0.33515329 | 0.094445386 | 0.271325736 | 0.147474377 | 0.385127392 | |
| 0.026304523 | 0.058286678 | 0.052011219 | 0.036870451 | 0.051688293 | ||
| 0.662944737 | 0.525397363 | 0.626471849 | 0.555699644 | 0.691501367 | ||
| 0.27337439 | 1.152883643 | 0.980308516 | 0.563937411 | 0.971428063 | ||
| 7.418055244 | 7.590513661 | 7.416084176 | 4.576922387 | 7.711214672 | ||
| 2.767837589 | 8.183050979 | 3.783900159 | 2.84628543 | 4.8782461 | ||
| Current control loop | 0.367027178 | 0.36968155 | 0.084139142 | 0.241408532 | 0.387710987 | |
| 0.058823711 | 0.039415026 | 0.025675454 | 0.056629421 | 0.058379697 | ||
| 0.681158387 | 0.682675171 | 0.519508081 | 0.609376304 | 0.692977707 | ||
| 1.16765206 | 0.633913214 | 0.256074972 | 1.107309078 | 1.155441669 | ||
| 8.868469794 | 8.073493511 | 7.79534566 | 3.228488359 | 9.626665366 | ||
| 9.504949358 | 5.441702647 | 2.738746348 | 8.675933712 | 2.758345604 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinthurat, W.; Kongsuk, P.; Marungsri, B. Robust-Adaptive Controllers Designed for Grid-Forming Converters Ensuring Various Low-Inertia Microgrid Conditions. Smart Cities 2023, 6, 2944-2959. https://doi.org/10.3390/smartcities6050132
Pinthurat W, Kongsuk P, Marungsri B. Robust-Adaptive Controllers Designed for Grid-Forming Converters Ensuring Various Low-Inertia Microgrid Conditions. Smart Cities. 2023; 6(5):2944-2959. https://doi.org/10.3390/smartcities6050132
Chicago/Turabian StylePinthurat, Watcharakorn, Prayad Kongsuk, and Boonruang Marungsri. 2023. "Robust-Adaptive Controllers Designed for Grid-Forming Converters Ensuring Various Low-Inertia Microgrid Conditions" Smart Cities 6, no. 5: 2944-2959. https://doi.org/10.3390/smartcities6050132
APA StylePinthurat, W., Kongsuk, P., & Marungsri, B. (2023). Robust-Adaptive Controllers Designed for Grid-Forming Converters Ensuring Various Low-Inertia Microgrid Conditions. Smart Cities, 6(5), 2944-2959. https://doi.org/10.3390/smartcities6050132







