Optimization Approaches for Demand-Side Management in the Smart Grid: A Systematic Mapping Study
Abstract
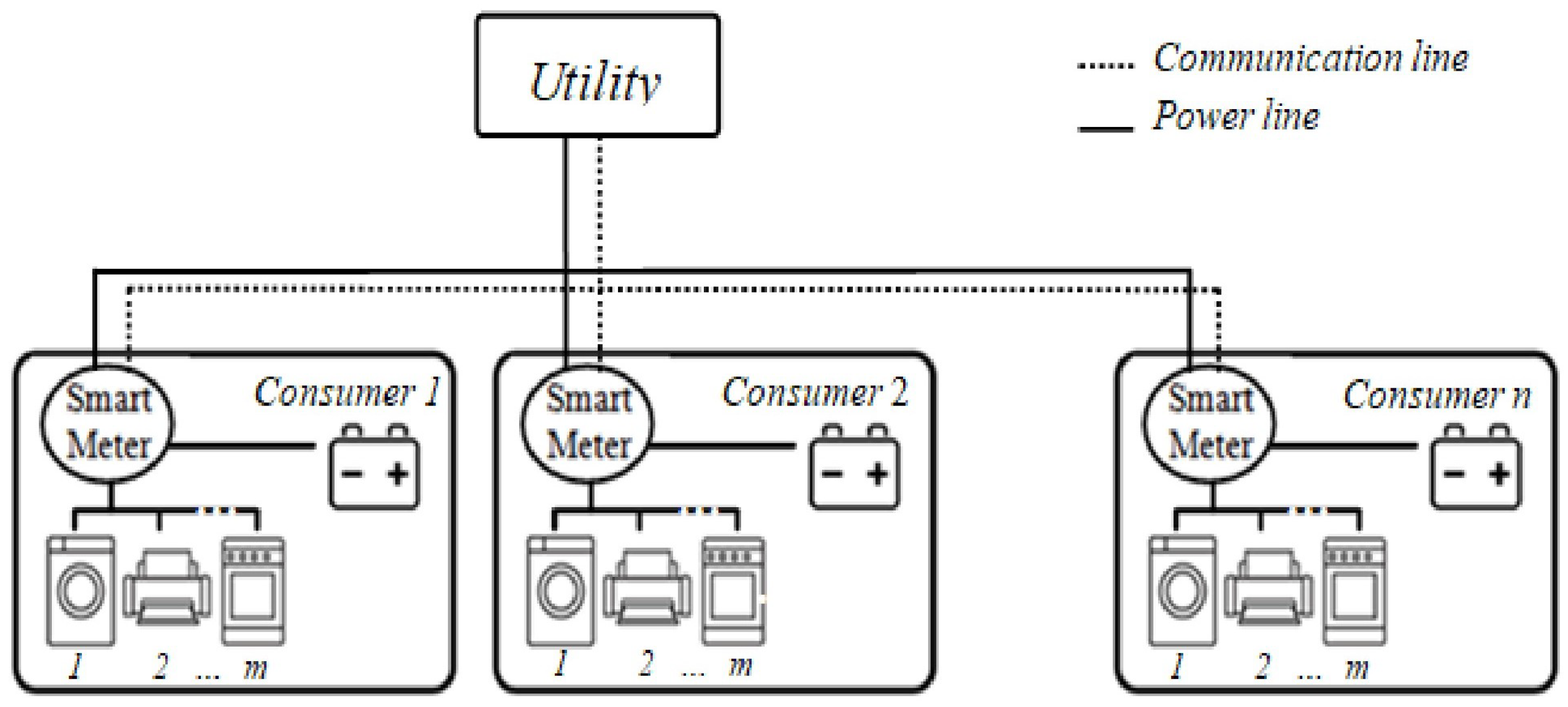
1. Introduction
2. Background
- Essential devices. They are interactive with minimal scheduling freedom, fixed power and operational periods. These devices require a steady power supply (e.g., lamps).
- Shiftable devices. They have specific energy consumption profiles and elastic delays. Their operation period can be shifted (e.g., washing machines).
- Throttleable devices. They have a fixed operating period but can accept adjustments in their power consumption, within a certain range (e.g., electrical vehicles).
2.1. Load Demand Description
2.2. Peak-to-Average Ratio
2.3. Electricity Pricing System
2.4. Energy Cost Model
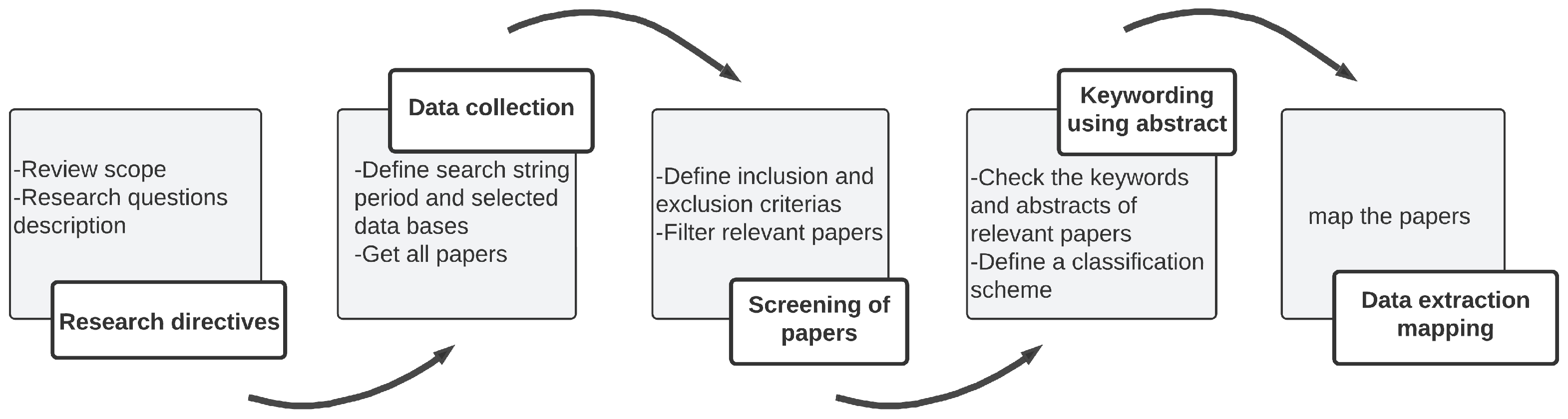
3. Systematic Mapping Study
- Research directives define the study protocol and identify the dimensions to be analyzed, as well as the research questions that need to be answered.
- Data collection identifies primary studies by using search strings on several selected scientific databases.
- Screening of the papers brings together the articles related to the inclusion and exclusion criteria defined in the protocol.
- Key-wording using the abstract identifies and combines keywords to seek high-level understanding about the nature and contribution of the research, thereby generating an organized classification.
- Data extraction mapping maps the existing literature according to the defined criteria and answers the research questions.
3.1. Research Directives
- RQ1.
- What are the most used algorithms and techniques for peak and cost reduction?
- RQ2.
- What type of energy source has been chosen (e.g., utility grid, renewable or storage)?
- RQ3.
- What type of building has been treated (e.g., residential, commercial, industrial)?
- RQ4.
- What are the optimization objectives of the algorithms cited?
- RQ5.
- What type of energy pricing has been chosen ?
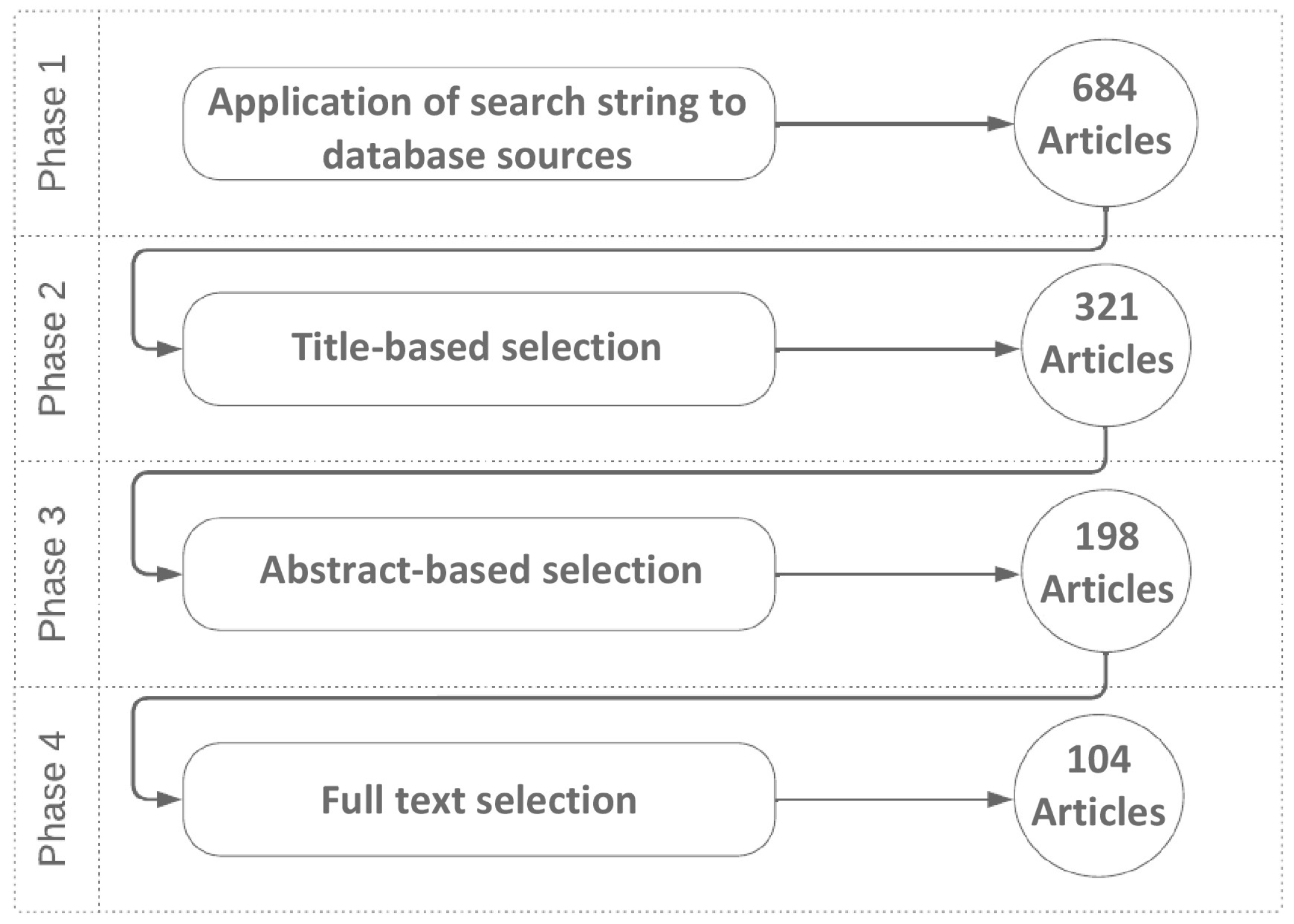
3.2. Data Collection
- MDPI data bases (https://www.mdpi.com/, accessed on 31 December 2022);
- Elsevier ScienceDirect (www.sciencedirect.com, accessed on 31 December 2022);
- SpringerLink (https://link.springer.com, accessed on 31 December 2022);
- IEEExplore (http://ieeexplore.ieee.org, accessed on 31 December 2022).
3.3. Screening of Papers for Inclusion and Exclusion
3.3.1. Inclusion Criteria
- Articles focusing on DSM in SGs.
- Articles proposing algorithms and control systems for optimizing PAR and reducing cost.
- Articles published between 1 January 2013 and 31 December 2022.
- Articles dealing with cost optimization and PAR reduction.
3.3.2. Exclusion Criteria
- Reviews and surveys. Only first-hand research work is considered.
- Articles not related to the research.
- Non-peer-reviewed articles.
3.4. Keywording and Selection Strategy

3.5. Data Extraction and Classification
- Ref: the paper reference;
- Year: the year of publication;
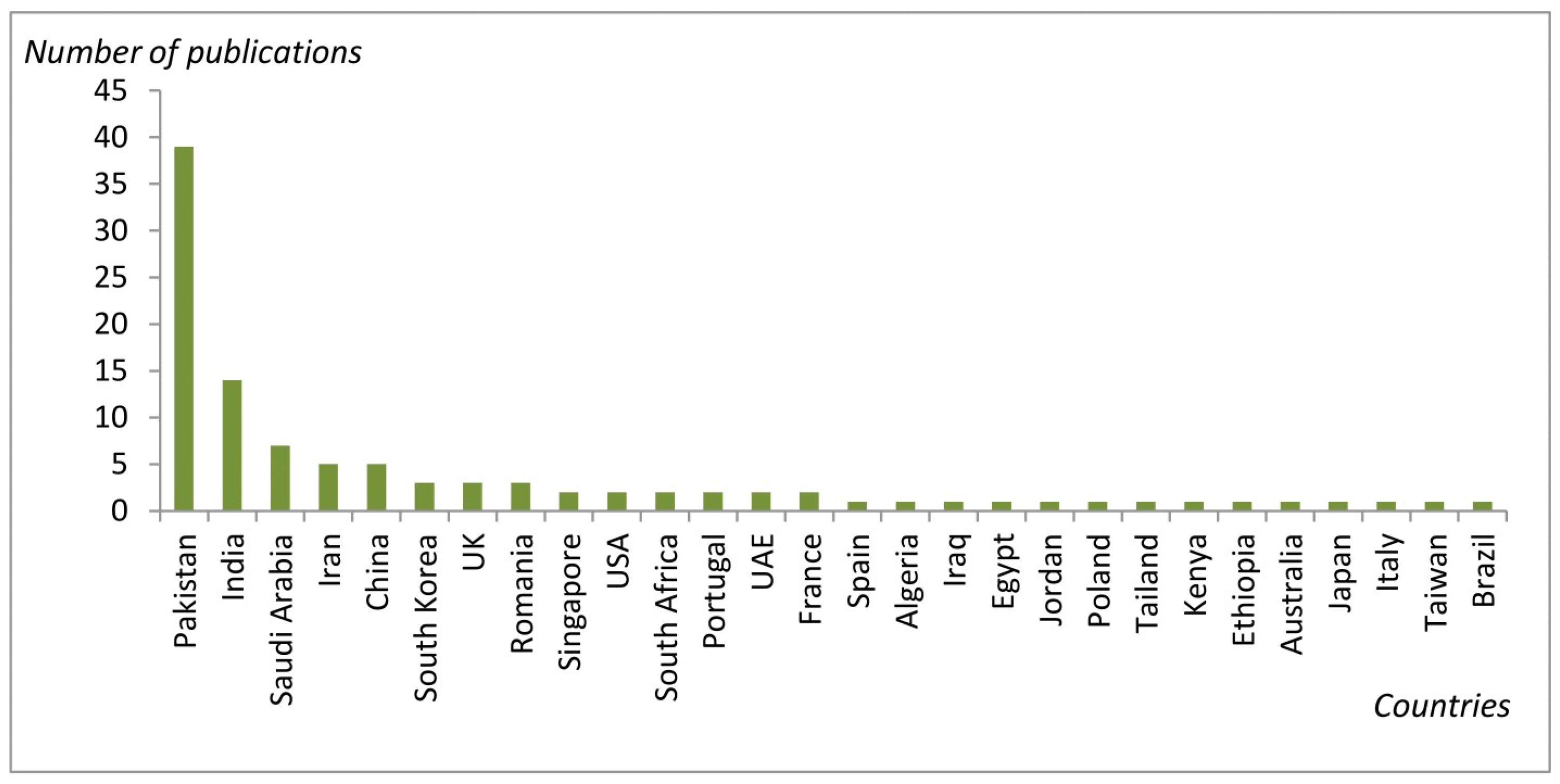
- Country: the country of the study;
- Journal/Conference: the publication venue;
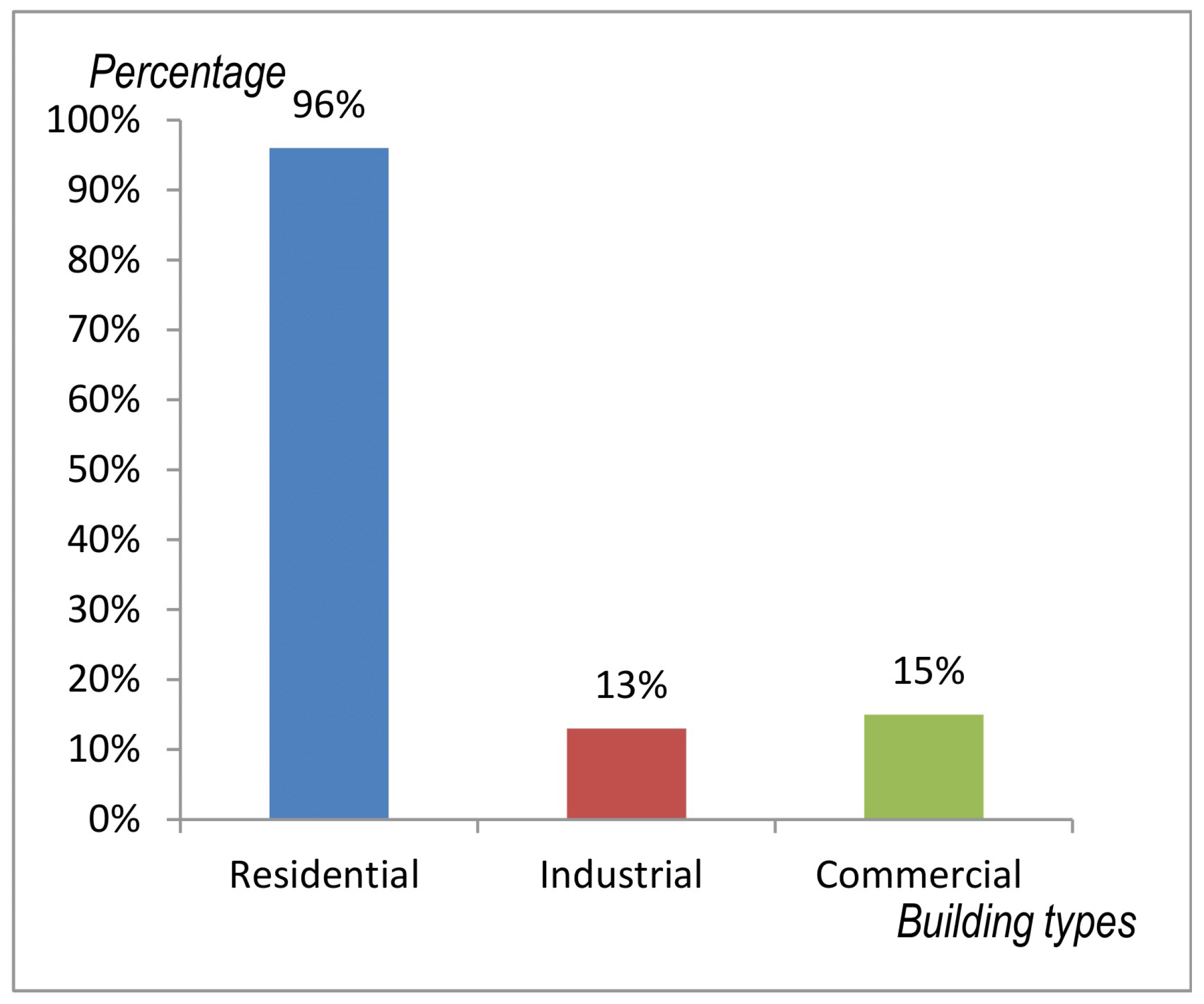
- Building sector: residential, commercial or industrial;
- Energy source: utility, renewable, or energy storage;
- Control Schemes: the general type of control scheme (e.g., heuristic, exact method, hybrid);
- Algorithm/method: the algorithm/method name used by authors;
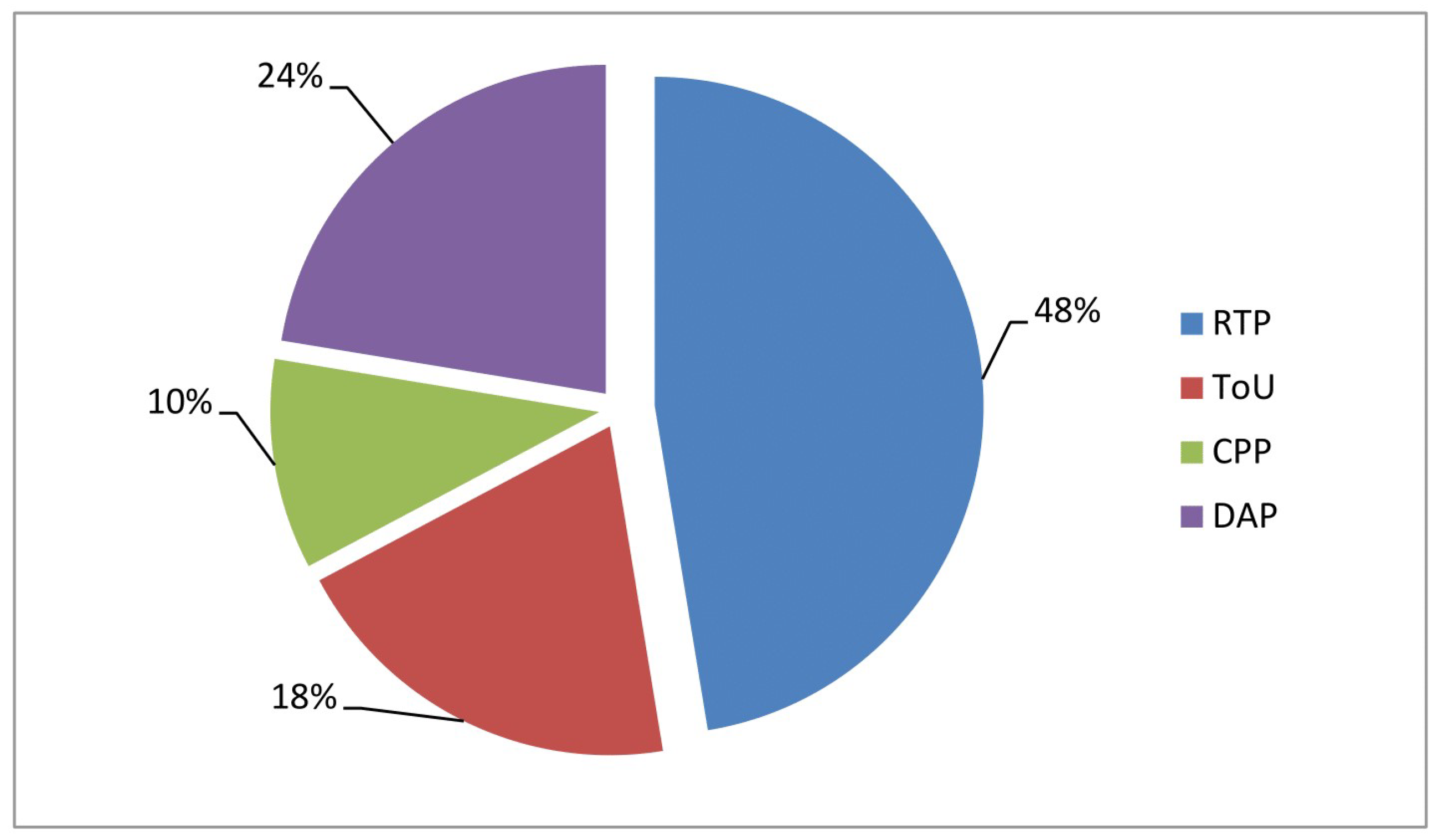
- Pricing scheme: the pricing scheme hypothesis (e.g., time of use, real time, day-ahead pricing);
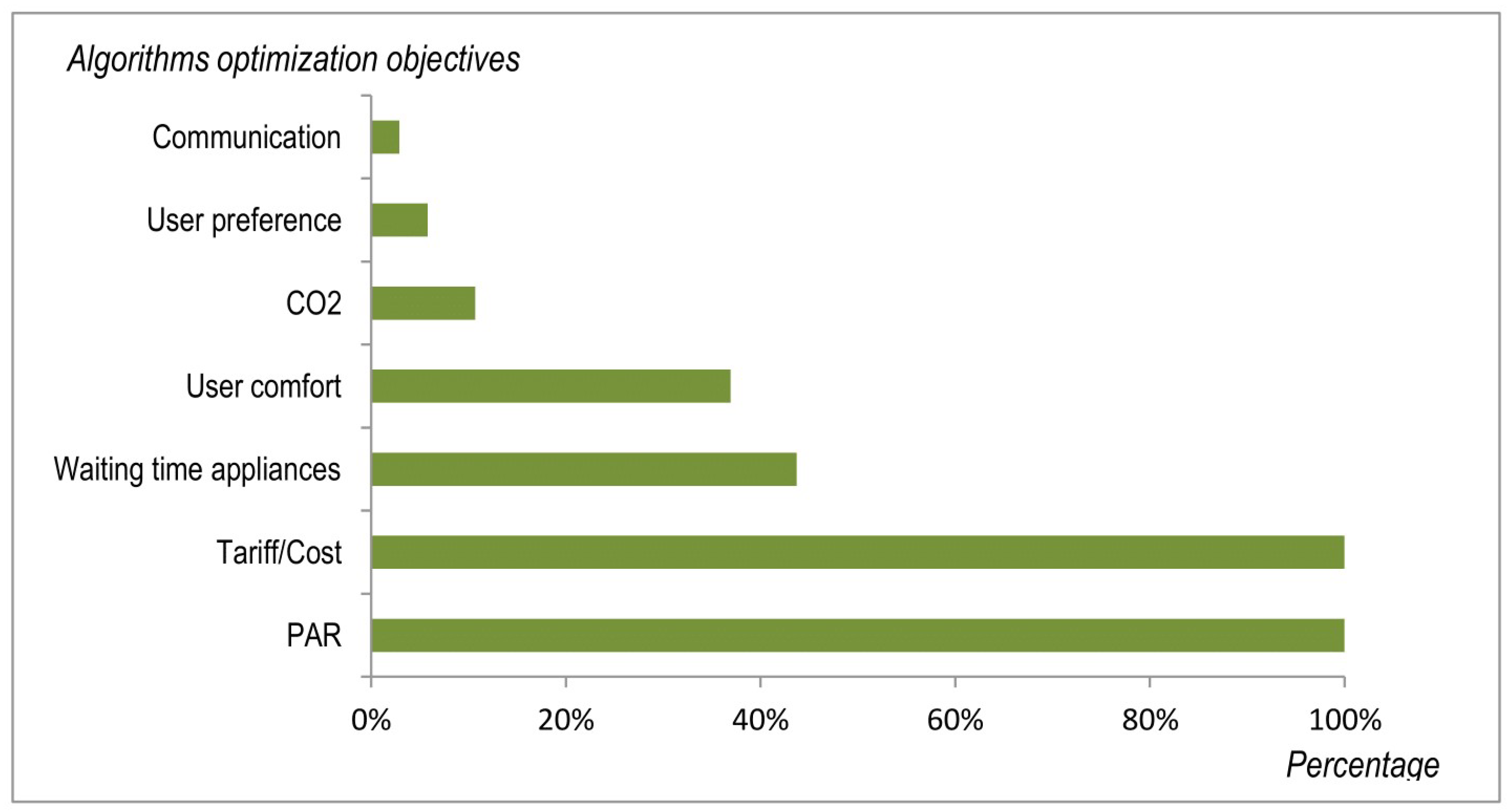
- The optimization objectives: (e.g., PAR, cost, communications, appliances waiting time);
- User comfort: is user comfort taken into account in the optimization?
- User preferences: are user preferences taken into account in the optimization?
- Simulation tool: is there a simulation tool involved in the optimization?
| Ref. | Year | Country | Journal/Conference | Building Sector | Energy Source | Control Schemes | Algorithm/Method | Pricing Scheme | Optimization Objective(s) | User Comfort | User Preferences | Simulation Tool | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PAR | Cost | CO2 Emission | Communication | Average Waiting Time | ||||||||||||
| [22] | 2022 | Saudi Arabia | Processes | Residential | Utility ESS RES | Meta-heuristic technique | Ant colony optimization (ACO) | Fixed price | √ | √ | √ | – | – | – | – | MATLAB 2018b |
| [23] | 2022 | Pakistan | IEEE Access | Residential | Utility RES | Meta-heuristic technique | Artificial bee colony | RTP ToU DAP CPP | √ | √ | √ | – | √ | √ | – | MATLAB |
| [24] | 2022 | Romania | Computers and Industrial Engineering | Residential | Utility | Meta-heuristic technique | Signaling game model for optimization | RTP ToU | √ | √ | – | – | √ | – | – | – |
| [25] | 2022 | France | Applied Energy | Residential | Utility ESS RES | Hybrid technique | Particle swarm optimization and binary particle swarm optimization | ToU | √ | √ | – | – | √ | √ | – | – |
| [26] | 2022 | India | Journal of The Institution of Engineers (India): Series B volume | Residential | Utility | Meta-heuristic technique | Particle swarm optimization | RTP | √ | √ | – | – | – | – | – | MATLAB |
| [27] | 2022 | Pakistan | Energy Systems | Industrial | Utility RES | Meta-heuristic technique | Genetic algorithm | ToU | √ | √ | – | – | – | – | – | – |
| [28] | 2022 | UAE | Cluster Computing | Residential | Utility | Meta-heuristic technique | Grey wolf optimizer | RTP | √ | √ | – | – | √ | √ | – | – |
| [29] | 2022 | Portugal | Energy | Residential | UtilityRES | Meta-heuristic technique | Genetic algorithm | RTP | √ | √ | – | – | – | √ | √ | Python |
| [30] | 2022 | China | Computers and Electrical Engineering | Residential | Utility RES ESS | Meta-heuristic technique | Grey wolf optimization | RTP | √ | √ | – | – | – | – | – | – |
| [31] | 2022 | India | Measurement: Sensors | Residential | Utility | Meta-heuristic technique | Eagle hard optimization | ToU | √ | √ | – | – | – | – | – | – |
| [32] | 2022 | Pakistan | Sustainable Energy Technologies and Assessments | Industrial | Utility RES ESS | Meta-heuristic technique | Lion’s algorithm | DAP | √ | √ | – | – | √ | √ | – | MATLAB |
| [33] | 2022 | Iran | Knowledge-Based Systems | Residential | Utility RES ESS | Meta-heuristic technique | Multi-objective arithmetic optimization algorithm | CPP RTP | √ | √ | – | – | √ | √ | – | – |
| [34] | 2022 | Iran | Journal of Building Engineering | Residential Commercial Industrial | Utility | Hybrid technique | Simplex and improved grey wolf optimization | ToU | √ | √ | – | – | – | – | – | MATLAB and CPLEX |
| [35] | 2022 | Pakistan | Energies | Residential | Utility | Hybrid technique | Earth worm algorithm and harmony search algorithms | RTP | √ | √ | – | – | √ | √ | – | MATLAB |
| Ref. | Year | Country | Journal/Conference | Building Sector | Energy Source | Control Schemes | Algorithm/Method | Pricing Scheme | Optimization Objective(s) | User Comfort | User Preferences | Simulation Tool | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PAR | Cost | CO2 Emission | Communication | Average Waiting Time | ||||||||||||
| [36] | 2022 | Saudi Arabia and Pakistan | IEEE Access | Residential | Utility RES ESS | Hybrid technique | Ant colony optimization and teaching–learning-based optimization | RTP | √ | √ | √ | – | √ | √ | √ | MATLAB |
| [37] | 2022 | Saudi Arabia | Sustainability | Residential | Utility RES ESS | Hybrid technique | Enhanced differential evolution and genetic algorithm | RTP | √ | √ | √ | – | √ | √ | – | MATLAB R2018b |
| [38] | 2022 | Iraq | Inventions | Residential | Utility ESS RES | Meta-heuristic technique | Bald eagle search optimization algorithm | RTP | √ | √ | – | – | – | – | – | MATLAB and ThingSpeak |
| [39] | 2022 | India | Energies | Residential | Utility | Meta-heuristic technique | Remodeled sperm swarm optimization | RTP | √ | √ | – | – | – | – | – | PythonGUROBI |
| [40] | 2022 | Pakistan | Sustainability | Residential | Utility ESS RES | Meta-heuristic technique | Cuckoo search algorithm and mixed-integer linear programming | RTP | √ | √ | – | – | – | – | – | – |
| [41] | 2022 | Taiwan | Sustainability | Residential | Utility | Meta-heuristic technique | Non-dominated sorting genetic algorithm | RTP | √ | √ | – | – | √ | √ | √ | – |
| [42] | 2022 | india | 2022 International Virtual Conference on Power Engineering Computing and Control | Residential | Utility | Meta-heuristic technique | Sine–cosine algorithm | RTP | √ | √ | – | – | √ | √ | – | MATLAB |
| [43] | 2022 | India | International Conference on Power Electronics and Renewable Energy Systems | Residential | Utility | Hybrid technique | Antlion optimization | RTP | √ | √ | – | – | – | – | – | – |
| [36] | 2022 | Saudi Arabia and Pakistan | IEEE Access | Residential | Utility RES ESS | Hybrid technique | Ant colony optimization and teaching–learning-based optimization | RTP | √ | √ | √ | – | √ | √ | √ | MATLAB |
| [37] | 2022 | Saudi Arabia | Sustainability | Residential | Utility RES ESS | Hybrid technique | Enhanced differential evolution and genetic algorithm | RTP | √ | √ | √ | – | √ | √ | – | MATLAB R2018b |
| [44] | 2021 | Brazil | Journal of Cleaner Production | Residential | Utility ESS RES | Meta-heuristic technique | Nonlinear programming, genetic algorithms, ant colony systems and particle swarm optimization | RTP | √ | √ | – | – | – | – | √ | |
| [45] | 2021 | India | Journal of Building Engineering | Residential | Utility RES | Meta-heuristic technique | Least slack time-based scheduling | RTP ToU CPP | √ | √ | – | – | – | √ | – | – |
| [46] | 2021 | Saudi Arabia | 2021 IEEE 4th International Conference on Renewable Energy and Power Engineering | Residential | Utility | Meta-heuristic technique | Genetic algorithm | RTP | √ | √ | – | √ | – | – | – | – |
| Ref. | Year | Country | Journal/Conference | Building Sector | Energy Source | Control Schemes | Algorithm/Method | Pricing Scheme | Optimization Objective(s) | User Comfort | User Preferences | Simulation Tool | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PAR | Cost | CO2 Emission | Communication | Average Waiting Time | ||||||||||||
| [47] | 2021 | Pakistan | IEEE Access | Residential Commercial | Utility ESS RES | Hybrid technique | Genetic algorithm, wind-driven optimization and particle swarm optimization | DAP | √ | √ | √ | – | √ | √ | – | MATLAB |
| [48] | 2021 | Pakistan | Energies | Residential | Utility ESS RES | Hybrid technique | Genetic algorithm and ant colony optimization | RTP | √ | √ | √ | – | √ | √ | – | MATLAB R2013b |
| [49] | 2021 | Saudi Arabia | Mathematics | Residential Commercial Industrial | Utility ESS RES | Meta-heuristic technique | Particle swarm optimization and the strawberry optimization | RTP ToU | √ | √ | – | – | √ | – | – | – |
| [50] | 2021 | Pakistan | Energies | Residential | Utility ESS RES | Hybrid technique | Firefly algorithm and lion algorithm | DAP | √ | √ | – | – | √ | √ | – | MATLAB |
| [51] | 2021 | Jordan | Multimedia Tools and Applications(s) | Residential | Utility | Hybrid technique | Grasshopper optimization algorithm and differential evolution | ToU and CPP | √ | √ | – | – | √ | √ | – | MATLAB |
| [52] | 2021 | India | Sadhana | Residential | Utility RES | Hybrid technique | Genetic algorithm and particle swarm optimization | DAP | √ | √ | – | – | – | – | – | NI LabVIEW.2015 |
| [53] | 2021 | Romania | Journal of Optimization Theory and Applications | Residential | Utility | Hybrid technique | Stackelberg game | ToU | √ | √ | – | – | – | – | – | – |
| [54] | 2021 | Egypt | Energy Reports | Residential commercial | Utility RES | Meta-heuristic | Cuckoo optimization algorithm | ToU | √ | √ | – | – | – | – | – | MATLAB |
| [55] | 2021 | Pakistan | IEEE Access | Residential | Utility ESS RES | Hybrid technique | Hybrid genetic ant colony | RTP | √ | √ | √ | – | √ | √ | – | MATLAB R2018a |
| [56] | 2021 | Pakistan | International Journal of Energy Research | Residential | Utility ESS RES | Hybrid technique | Hybrid genetic ant colony optimization | RTP | √ | √ | √ | – | √ | √ | – | MATLAB R2013b |
| [57] | 2021 | Pakistan | International Conference on Emerging Technologies | Residential | Utility | Meta-heuristic technique | Jaya algorithm | ToUand CPP | √ | √ | – | – | √ | √ | – | MATLAB 2014a |
| [58] | 2020 | China and Pakistan | IEEE Access | Residential Commercial Industrial | Utility | Hybrid technique | Hybrid bacterial foraging and particle swarm optimization | DAP CPP ToU | √ | √ | √ | – | √ | √ | – | – |
| [20] | 2020 | Pakistan | Multidisciplinary IEEE Access | Residential | Utility | Hybrid technique | Grey-wolf-modified enhanced differential evolution algorithm | DAP | √ | √ | – | – | √ | √ | – | – |
| Ref. | Year | Country | Journal/Conference | Building Sector | Energy Source | Control Schemes | Algorithm/Method | Pricing Scheme | Optimization Objective(s) | User Comfort | User Preferences | Simulation Tool | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PAR | Cost | CO2 Emission | Communication | Average Waiting Time | ||||||||||||
| [59] | 2020 | South Korea | IEEE Transaction on Smart Grid | Residential | Utility ESS | Heuristic technique | Game theory | RTP | √ | √ | – | – | – | – | – | – |
| [60] | 2020 | Pakistan | IEEE Access | Residential | Utility ESS RES | Hybrid technique | Hybrid genetic particle swarm optimization | RTP | √ | √ | √ | – | √ | √ | – | MATLAB |
| [61] | 2020 | Spain | EEEICand ICPS Europe | Industrial | Utility | Heuristic technique | Linear programming | DAP | √ | √ | – | – | – | – | – | – |
| [62] | 2020 | South Korea | IEEE Access | Residential | Utility ESS RES | Hybrid technique | Particle swarm optimization (PSO) and binary particle swarm optimization | DAP | √ | √ | – | – | – | – | – | Cplex/ Dicopt |
| [63] | 2020 | India | Peer-to-Peer Networking and Applications | Residential | Utility ESS RES | Hybrid technique | Adaptive neuro-fuzzy inference system | RTP | √ | √ | – | – | √ | – | – | MATLAB |
| [64] | 2020 | Singapore | Applied Energy | Residential | Utility ESS RES | Meta-heuristic technique | Game theory and genetic algorithm | RTP | √ | √ | – | – | – | – | – | – |
| [65] | 2020 | Pakistan | Applied Science | Residential | Utility | Meta-heuristic technique | Multi-verse optimization sine–cosine algorithm | DAP | √ | √ | – | – | √ | – | – | – |
| [66] | 2020 | Poland | IET Smart Grid | Residential | Utility ESS RES | Heuristic technique | Fuzzy logic | RTP | √ | √ | – | – | – | – | – | C++ with OOP |
| [67] | 2020 | Algeria | Optimization and Engineering | Residential | Utility | Meta-heuristic technique | Harris hawks optimization | RTPand CPP | √ | √ | – | – | – | – | – | MATLAB |
| [68] | 2020 | Pakistan | Electronics | Residential Commercial Industrial | Utility | Meta-heuristic technique | Dragonfly algorithm | DAP | √ | √ | – | – | √ | – | – | – |
| [69] | 2020 | Pakistan | Electronics | Industrial | Utility | Meta-heuristic technique | Grasshopper optimization algorithm and cuckoo search optimization algorithm | DAP | √ | √ | – | – | √ | √ | – | MATLAB |
| [70] | 2020 | Pakistan | Electronics | Residential Commercial Industrial | Utility | Meta-heuristic technique | Dragonfly algorithm | DAP | √ | √ | – | – | √ | – | – | – |
| [71] | 2020 | Pakistan | Advanced Information Networking and Applications | Residential | Utility | Meta-heuristic technique | Flower pollination algorithm and Jaya optimization algorithm | CPP | √ | √ | – | – | √ | √ | – | MATLAB 2017a |
| Ref. | Year | Country | Journal/Conference | Building Sector | Energy Source | Control Schemes | Algorithm/Method | Pricing Scheme | Optimization Objective(s) | User Comfort | User Preferences | Simulation Tool | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PAR | Cost | CO2 Emission | Communication | Average Waiting Time | ||||||||||||
| [72] | 2019 | Pakistan | Sustainability | Residential | Utility ESS RES | Trajectory search family | Dijkstra algorithm | DAP | √ | √ | – | – | √ | √ | – | MATLAB 2014a |
| [73] | 2019 | South Africa | Energy | Residential | Utility ESS RES | Evolutionary algorithms | Improved differential evolution algorithm | DAP | √ | √ | – | – | √ | √ | – | – |
| [74] | 2019 | Pakistan | Web, Artificial Intelligence and Network Applications | Residential | Utility | Meta-heuristic technique | Runner updation optimization algorithm | CPPRTP | √ | √ | – | – | – | – | – | MATLAB |
| [75] | 2019 | Ethiopia | IEEE CSEE | Residential | Utility RES | Meta-heuristic technique | Grey wolf optimizer | ToU | √ | √ | – | – | – | – | – | – |
| [76] | 2019 | Korea | Future Generation Computer System | Residential | Utility | Meta-heuristic technique | Mutation ant colony optimization | ToU | √ | √ | – | – | √ | – | – | MATLAB Visual C# on Visual Studio 2010 compatible with. NET framework 4.0 |
| [77] | 2019 | Pakistan | Process MDPI | Residential Commercial | Utility | Meta-heuristic technique | Grasshopper optimization algorithm and bacterial foraging optimization | DAP | √ | √ | – | – | – | – | – | MATLAB |
| [78] | 2019 | Pakistan | Artificial Intelligence and Network Applications | Residential | Utility | Meta-heuristic technique | Strawberry algorithm and earthworm optimization algorithm | RTP CPP | √ | √ | – | – | √ | – | – | – |
| [79] | 2019 | Taiwan | IEEE International Conference on Systems, Man and Cybernetics | Residential | Utility | Meta-heuristic technique | Search economics for home appliances scheduling | DAP | √ | √ | – | – | – | – | – | C++Clang++ |
| [80] | 2019 | India | Microprocessors and Microsystems | Residential | Utility ESS RES | Hybrid technique | Glow-worm swarm optimization and support vector machine | DAP | √ | √ | – | – | – | – | – | MATLAB 2018 a |
| [5] | 2019 | China | Energies | Residential | Utility ESS RES | Heuristic technique | Game theory | DAP | √ | √ | – | √ | – | – | √ | MATLAB 2013a -YALMIP -ILOG’s CPLEX v.12 CPLEX |
| [81] | 2019 | UAE | Ambient Intell Human Comput Springer | Residential | Utility | Hybrid technique | Harmony search algorithm and enhanced differential evolution | RTP | √ | √ | – | – | √ | √ | – | MATLAB |
| [82] | 2018 | Pakistan | Energies | Residential | Utility | Heuristic technique | Genetic harmony search algorithm | RTP andCPP | √ | √ | – | – | √ | √ | – | MATLAB 2014b |
| [83] | 2018 | Kenya | Power and Energy Engineering | Residential | ESS RES | Hybrid technique | Bayesian game theory | RTP | √ | √ | – | – | – | – | – | – |
| [84] | 2018 | USA | IEEE Trans. Smart Grid | Residential | Utility | Stochastic technique | Game theory | RTP | √ | √ | – | √ | – | – | – | IBM ILOG CPLEX |
| Ref. | Year | Country | Journal/Conference | Building Sector | Energy Source | Control Schemes | Algorithm/Method | Pricing Scheme | Optimization Objective(s) | User Comfort | User Preferences | Simulation Tool | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PAR | Cost | CO2 Emission | Communication | Average Waiting Time | ||||||||||||
| [85] | 2018 | USA | IEEE Green Technologies Conference | Residential Commercial | UtilityESS | Heuristic technique | PSO | ToU | √ | √ | – | – | – | – | – | – |
| [86] | 2018 | Thailand | IEEE Transaction on Smart Grid | Residential | UtilityESS RES | Heuristic technique | Fuzzy low-cost operation | ToU | √ | √ | – | – | – | – | – | – |
| [87] | 2018 | Iran | IEEE Smart Grid Conference | Residential | Utility ESS Conventional-Units | Hybrid technique | Unnamed scheduling and fuzzy logic | DAP and ToU | √ | √ | √ | – | – | – | – | GAMS -MILP and CPLEX |
| [88] | 2018 | Pakistan | IEEE International Conference on Advanced Information Networking and Applications | Residential | Utility | Hybrid technique | Enhanced differential harmony binary particle swarm optimization | RTP | √ | √ | – | – | – | √ | – | MATLAB |
| [89] | 2018 | Romania | Computers and Industrial Engineering Elsevier | Residential | Utility | Evolutionary optimization technique | Shifting optimization algorithm | ToU | √ | √ | – | – | – | – | – | MATLAB 2016a |
| [3] | 2018 | Pakistan | IEEE International Conference on Advanced Information Networking and Applications | Residential | Utility | Hybrid technique | Enhanced differential harmony binary particle swarm optimization | RTP | √ | √ | – | – | – | √ | – | MATLAB |
| [90] | 2018 | Pakistan | IEEE International Conference on Advanced Information Networking and Applications | Residential | Utility | Hybrid technique | Bacterial foraging tabu search | RTP | √ | √ | – | – | √ | √ | – | MATLAB |
| [4] | 2018 | China | Neural Comput and Applic | Residential Industrial | Utility ESS RES | Heuristic technique | Game theory | Equilibrium market | √ | √ | – | – | – | – | – | Cplex DECIS OSL-SE |
| [91] | 2018 | Brazil | Springer International Conference, PAAMS | Residential | Utility | Meta-heuristic technique | Gravitational search algorithm | RTP | √ | √ | – | – | – | – | – | LPG |
| [92] | 2017 | Pakistan | Advances in Network-Based Information Systems | Residential | Utility | Meta-heuristic technique | Bacterial foraging optimization and strawberry algorithm | RTP | √ | √ | – | – | √ | √ | – | MATLAB |
| [93] | 2017 | India | IEEE International Conference on Electrical, Instrumentation and Communication Engineering | Residential | Utility | Evolutionary optimization technique | Unnamed scheduling | DAP | √ | √ | – | – | – | – | – | MATLAB |
| [94] | 2017 | India | IEEE International Conference on Power Systems | Residential Commercial Industrial | Utility | Meta-heuristic technique | Multi-objective particle swarm optimization | DAP | √ | √ | – | – | – | – | – | MATLAB |
| [95] | 2017 | UK | IEEE Trans. Ind. Inf | Residential | RES | – | Artificial immune algorithm | DAP | √ | √ | – | – | – | – | – | – |
| [96] | 2017 | Pakistan | Advances in Network-Based Information Systems | Residential | Utility | Meta-heuristic technique | Enhanced differential evolution | ToU | √ | √ | – | – | √ | – | – | – |
| Ref. | Year | Country | Journal/Conference | Building Sector | Energy Source | Control Schemes | Algorithm/Method | Pricing Scheme | Optimization Objective(s) | User Comfort | User Preferences | Simulation Tool | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PAR | Cost | CO2 Emission | Communication | Average Waiting Time | ||||||||||||
| [97] | 2017 | India | Sustainable Cities and Society | Residential | Utility | Linear programming | Mixed-integer linear programming | ToU | √ | √ | – | – | – | – | – | GAMS/ CPLEX |
| [98] | 2017 | Pakistan | Advances on P2P, Parallel, Grid, Cloud and Internet Computing | Residential | Utility | Meta-heuristic technique | Crow search algorithm | RTP | √ | √ | – | – | √ | √ | – | MATLAB |
| [99] | 2017 | Pakistan | IEEE International Renewable and Sustainable Energy Conference | Residential | Utility RES ESS | Heuristic technique | Knapsack algorithm | RTP | √ | √ | – | – | – | – | – | – |
| [100] | 2017 | Pakistan | Advances in Intelligent Networking and Collaborative Systems | Residential | Utility | Meta-heuristic technique | Enhanced differential evolution & Strawberry Algorithm | RTP | √ | √ | – | – | √ | √ | – | MATLAB |
| [101] | 2017 | UK | IEEE International Conference on Smart Energy Grid Engineering | Residential | Utility | Unnamed technique | Unnamed scheduling | RTP | √ | √ | – | – | – | – | – | – |
| [102] | 2017 | Pakistan | Advances on P2P, Parallel, Grid, Cloud and Internet Computing | Residential | Utility | Meta-heuristic technique | Flower pollination algorithm | RTP | √ | √ | – | – | √ | – | – | MATLAB |
| [103] | 2016 | India | IEEE National Power Systems Conference | Residential Commercial Industrial | Utility | Meta-heuristic technique | Particle swarm optimization | DAP | √ | √ | – | – | – | – | – | – |
| [104] | 2016 | Australia | Applied Energy Elsevie | Residential | Utility | Unnamed technique | Unnamed scheduling | RTP | √ | √ | – | – | – | – | – | – |
| [105] | 2016 | Pakistan | Applied Sciences | Residential | Utility | Heuristic technique | Knapsack optimization | ToU | √ | √ | – | – | – | √ | – | MATLAB |
| [106] | 2015 | Singapore | IEEE Innovative Smart Grid Technologies | Residential Commercial Industrial | Utility | Meta-heuristic technique | Particle swarm optimization | DAP | √ | √ | – | – | – | – | – | MATLAB |
| [107] | 2015 | India | IEEE Power, Communication and Information Technology Conference | Residential | RES | Meta-heuristic technique | 2D particle swarm optimization | DAP | √ | √ | – | – | – | – | – | MATLAB |
| [108] | 2015 | Pakistan | IEEE International Conference on Network-Based Information Systems | Residential Commercial Industrial | Utility | Meta-heuristic technique | Genetic algorithm | RTP | √ | √ | – | – | – | – | – | – |
| [109] | 2015 | South Africa | IEEE Innovative Smart Grid Technologies | Residential | Utility | Evolutionary technique | Daily maximum energy scheduling | ToU | √ | √ | – | – | – | – | – | MILP CPLEX |
| Ref. | Year | Country | Journal/Conference | Building Sector | Energy Source | Control Schemes | Algorithm/Method | Pricing Scheme | Optimization Objective(s) | User Comfort | User Preferences | Simulation Tool | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PAR | Cost | CO2 Emission | Communication | Average Waiting Time | ||||||||||||
| [110] | 2015 | Pakistan | Energy Research | Residential | Utility | Meta-heuristic technique | Genetic algorithm | RTP | √ | √ | – | – | √ | – | – | – |
| [111] | 2015 | Italy-France | Computer Communications | Residential | Utility | Heuristic technique | Game theory | RTP | √ | √ | – | – | – | – | – | – |
| [112] | 2014 | Japan | 2014 International Conference on Electronics, Information and Communications | Residential | Utility ESS | Convex optimization technique | Unnamed scheduling | RTP | √ | √ | – | – | – | – | – | – |
| [113] | 2014 | China | IEEE International Joint Conference on Neural Networks | Residential | Utility | Meta-heuristic technique | Stackelberg game and genetic algorithm | RTP | √ | √ | – | – | – | – | – | IBM CPLEX |
| [9] | 2014 | Singapore | IEEE Journal of Selected Topics in Signal Processing | Residential | Utility | Distributed schemes | Distributed algorithm | RTP | √ | √ | – | – | – | – | – | – |
| [114] | 2013 | UK | Soft Computing | Residential | Utility | Meta-heuristic technique | Stackelberg game and genetic algorithms | RTP | √ | √ | – | – | – | – | – | – |
| [115] | 2013 | Iran | 2013 13th international conference on environment and electrical engineering | Residential | Utility | Meta-heuristic technique | Genetic algorithm | RTP | √ | √ | – | – | – | – | – | MATLAB |
| [116] | 2013 | China | 2013 IEEE international conference on communications workshops | Residential | Utility | Heuristic technique | Linear programming | RTP | √ | √ | – | – | – | – | – | – |
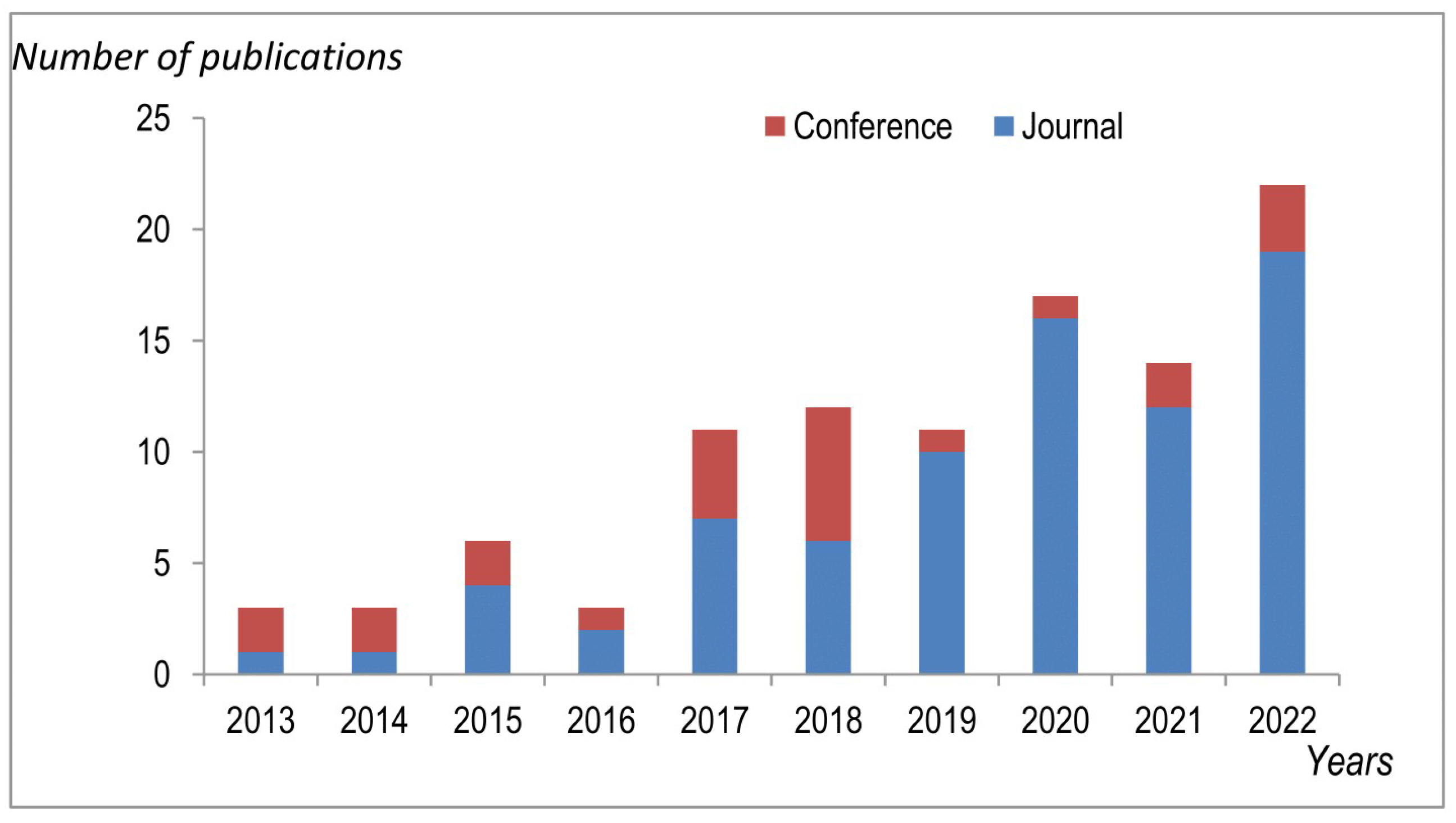
4. Mapping Questions Results and Analysis
- Long-range consumers are able to shift their consumption over a wide range of time following changes in prices;
- Real-world postponing consumers have a perception depending only on current and future prices;
- Real-world advancing customers have a perception depending only on current and past periods;
- Real-world mixed consumers are a mix of postponing and advancing consumers, taking into account the past, present and future;
- Short-range consumers do not optimize their load and are only concerned and worried about the power price at the current time.
5. Discussion
5.1. Algorithmic Hybridization
5.2. Interactive and Real-Time User Preference Consideration
5.3. Accurate Renewable Energy and Storage Systems Integration
5.4. Broadening the Scope of PAR Optimization
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| i | essential appliances |
| s | shiftable appliance |
| r | throttleable appliance |
| n | consumer |
| time interval [s] | |
| T | total number of time intervals in a day |
| essential energy consumed by user n during time interval t [] | |
| shiftable energy consumed by user n during time interval t [] | |
| throttleable energy consumed by user n during time interval t [] | |
| total consumed energy by user n during time interval t [] | |
| total daily energy demand of consumer n [] | |
| battery level at the beginning of the day for consumer n [] | |
| battery capacity of user n [Wh] | |
| maximum rates of battery charge/discharge of user n [] | |
| battery charging/discharging schedule for user n during time interval t | |
| load demand to be purchased by user n from the utility during time interval t [] | |
| operating time slot of consumer n | |
| peak load of the smart grid network [] | |
| average load of the smart grid network [] | |
| cost function |
References
- Popik, T.S. Preserving Ukraine’s Electric Grid During the Russian Invasion. JCIP J. Crit. Infrastruct. Policy 2022, 3, 15. [Google Scholar] [CrossRef]
- Kockel, C.; Nolting, L.; Pacco, K.; Schmitt, C.; Moser, A.; Praktiknjo, A. How dependent are european electricity systems and economies on natural gas? In Proceedings of the 17th IAEE European Conference—Future of Global Energy Systems, Athens, Greece, 21–24 September 2022.
- Qureshi, T.N.; Javaid, N.; Naz, A.; Ahmad, W.; Imran, M.; Khan, Z.A. A Novel Meta-Heuristic Hybrid Enhanced Differential Harmony Wind Driven (EDHWDO) Optimization Technique for Demand Side Management in Smart Grid. In Proceedings of the 2018 32nd International Conference on Advanced Information Networking and Applications Workshops (WAINA), Krakow, Poland, 16–18 May 2018; pp. 454–461. [Google Scholar] [CrossRef]
- Qin, H.; Wu, Z.; Wang, M. Demand-Side Management for Smart Grid Networks Using Stochastic Linear Programming Game. Neural Comput. Appl. 2018, 32, 139–149. [Google Scholar] [CrossRef]
- He, M.f.; Zhang, F.x.; Huang, Y.; Chen, J.; Wang, J.; Wang, R. A Distributed Demand Side Energy Management Algorithm for Smart Grid. Energies 2019, 12, 426. [Google Scholar] [CrossRef]
- Gellings, C. The Concept of Demand-Side Management for Electric Utilities. Proc. IEEE 1985, 73, 1468–1470. [Google Scholar] [CrossRef]
- Rahim, S.; Javaid, N.; Ahmad, A.; Khan, S.A.; Khan, Z.A.; Alrajeh, N.; Qasim, U. Exploiting Heuristic Algorithms to Efficiently Utilize Energy Management Controllers with Renewable Energy Sources. Energy Build. 2016, 129, 452–470. [Google Scholar] [CrossRef]
- Mann, Z.Á. The top eight misconceptions about NP-hardness. Computer 2017, 50, 72–79. [Google Scholar] [CrossRef]
- Liu, Y.; Yuen, C.; Huang, S.; Ul Hassan, N.; Wang, X.; Xie, S. Peak-to-Average Ratio Constrained Demand-Side Management With Consumer’s Preference in Residential Smart Grid. IEEE J. Sel. Top. Signal Process. 2014, 8, 1084–1097. [Google Scholar] [CrossRef]
- Manasseh, E.; Ohno, S.; Kalegele, K.; Tariq, R. Demand Side Management to Minimize Peak-to-Average Ratio in Smart Grid. In Proceedings of the ISCIE International Symposium on Stochastic Systems Theory and its Applications, Honolulu, HI, USA, 5–8 December 2015; Volume 2015, pp. 102–107. [Google Scholar] [CrossRef]
- Aghaei, J.; Alizadeh, M.I. Demand Response in Smart Electricity Grids Equipped with Renewable Energy Sources: A Review. Renew. Sustain. Energy Rev. 2013, 18, 64–72. [Google Scholar] [CrossRef]
- Shao, S.; Zhang, T.; Pipattanasomporn, M.; Rahman, S. Impact of TOU Rates on Distribution Load Shapes in a Smart Grid with PHEV Penetration. In Proceedings of the IEEE PES T&D 2010, New Orleans, LA, USA, 19–22 April 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Vardakas, J.S.; Zorba, N.; Verikoukis, C.V. A Survey on Demand Response Programs in Smart Grids: Pricing Methods and Optimization Algorithms. IEEE Commun. Surv. Tutorials 2015, 17, 152–178. [Google Scholar] [CrossRef]
- Zhou, Q.; Guan, W.; Sun, W. Impact of Demand Response Contracts on Load Forecasting in a Smart Grid Environment. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Herter, K. Residential Implementation of Critical-Peak Pricing of Electricity. Energy Policy 2007, 35, 2121–2130. [Google Scholar] [CrossRef]
- Faruqui, A.; George, S.S. The Value of Dynamic Pricing in Mass Markets. Electr. J. 2002, 15, 45–55. [Google Scholar] [CrossRef]
- Chen, C.; Kishore, S.; Snyder, L.V. An Innovative RTP-Based Residential Power Scheduling Scheme for Smart Grids. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 5956–5959. [Google Scholar] [CrossRef]
- Webber, G.; Warrington, J.; Mariethoz, S.; Morari, M. Communication Limitations in Iterative Real Time Pricing for Power Systems. In Proceedings of the 2011 IEEE International Conference on Smart Grid Communications (SmartGridComm), Brussels, Belgium, 17–20 October 2011; pp. 445–450. [Google Scholar] [CrossRef]
- Joe-Wong, C.; Sen, S.; Ha, S.; Chiang, M. Optimized Day-Ahead Pricing for Smart Grids with Device-Specific Scheduling Flexibility. IEEE J. Sel. Areas Commun. 2012, 30, 1075–1085. [Google Scholar] [CrossRef]
- Soliman, H.M.; Leon-Garcia, A. Game-Theoretic Demand-Side Management With Storage Devices for the Future Smart Grid. IEEE Trans. Smart Grid 2014, 5, 1475–1485. [Google Scholar] [CrossRef]
- Petersen, K.; Vakkalanka, S.; Kuzniarz, L. Guidelines for conducting systematic mapping studies in software engineering: An update. Inf. Softw. Technol. 2015, 64, 1–18. [Google Scholar] [CrossRef]
- Albogamy, F.R.; Ashfaq, Y.; Hafeez, G.; Murawwat, S.; Khan, S.; Ali, F.; Aslam Khan, F.; Rehman, K. Optimal Demand-Side Management Using Flat Pricing Scheme in Smart Grid. Processes 2022, 10, 1214. [Google Scholar] [CrossRef]
- Habib, H.U.R.; Waqar, A.; Junejo, A.K.; Ismail, M.M.; Hossen, M.; Jahangiri, M.; Kabir, A.; Khan, S.; Kim, Y.S. Optimal Planning of Residential Microgrids Based on Multiple Demand Response Programs Using ABC Algorithm. IEEE Access 2022, 10, 116564–116626. [Google Scholar] [CrossRef]
- Oprea, S.V.; Bâra, A. A signaling game-optimization algorithm for residential energy communities implemented at the edge-computing side. Comput. Ind. Eng. 2022, 169, 108272. [Google Scholar] [CrossRef]
- Chreim, B.; Esseghir, M.; Merghem-Boulahia, L. LOSISH—LOad Scheduling In Smart Homes based on demand response: Application to smart grids. Appl. Energy 2022, 323, 119606. [Google Scholar] [CrossRef]
- Bhongade, S.; Dawar, R.; Sisodiya, S. Demand-Side Management in an Indian Village. J. Inst. Eng. (India) Ser. B 2021, 103, 63–71. [Google Scholar] [CrossRef]
- Sardar, A.; Khan, S.U.; Hassan, M.A.; Qureshi, I.M. A demand side management scheme for optimal power scheduling of industrial loads. Energy Syst. 2022, 14, 335–356. [Google Scholar] [CrossRef]
- Makhadmeh, S.N.; Abasi, A.K.; Al-Betar, M.A.; Awadallah, M.A.; Doush, I.A.; Alyasseri, Z.A.A.; Alomari, O.A. A novel link-based multi-objective grey wolf optimizer for appliances energy scheduling problem. Clust. Comput. 2022, 25, 4355–4382. [Google Scholar] [CrossRef]
- Mota, B.; Faria, P.; Vale, Z. Residential load shifting in demand response events for bill reduction using a genetic algorithm. Energy 2022, 260, 124978. [Google Scholar] [CrossRef]
- Wang, Z.; Zhai, C. Evolutionary Approach for Optimal Bidding Strategies in Electricity Markets. Comput. Electr. Eng. 2022, 100, 107877. [Google Scholar] [CrossRef]
- Roopa, Y.M.; SatheshKumar, T.; Mohammed, T.K.; Turukmane, A.V.; Krishna, M.S.R.; Krishnaiah, N. Power allocation model for residential homes using AI-based IoT. Meas. Sens. 2022, 24, 100461. [Google Scholar] [CrossRef]
- Hussain, I.; Ullah, I.; Ali, W.; Muhammad, G.; Ali, Z. Exploiting lion optimization algorithm for sustainable energy management system in industrial applications. Sustain. Energy Technol. Assess. 2022, 52, 102237. [Google Scholar] [CrossRef]
- Bahmanyar, D.; Razmjooy, N.; Mirjalili, S. Multi-objective scheduling of IoT-enabled smart homes for energy management based on Arithmetic Optimization Algorithm: A Node-RED and NodeMCU module-based technique. Knowl.-Based Syst. 2022, 247, 108762. [Google Scholar] [CrossRef]
- Ebrahimi, J.; Abedini, M. A two-stage framework for demand-side management and energy savings of various buildings in multi smart grid using robust optimization algorithms. J. Build. Eng. 2022, 53, 104486. [Google Scholar] [CrossRef]
- Hassan, C.A.u.; Iqbal, J.; Ayub, N.; Hussain, S.; Alroobaea, R.; Ullah, S.S. Smart Grid Energy Optimization and Scheduling Appliances Priority for Residential Buildings through Meta-Heuristic Hybrid Approaches. Energies 2022, 15, 1752. [Google Scholar] [CrossRef]
- Ali, S.; Rehman, A.U.; Wadud, Z.; Khan, I.; Murawwat, S.; Hafeez, G.; Albogamy, F.R.; Khan, S.; Samuel, O. Demand Response Program for Efficient Demand-side Management in Smart Grid Considering Renewable Energy Sources. IEEE Access 2022, 10, 53832–53853. [Google Scholar] [CrossRef]
- Albogamy, F.R.; Khan, S.A.; Hafeez, G.; Murawwat, S.; Khan, S.; Haider, S.I.; Basit, A.; Thoben, K.D. Real-Time Energy Management and Load Scheduling with Renewable Energy Integration in Smart Grid. Sustainability 2022, 14, 1792. [Google Scholar] [CrossRef]
- Alhasnawi, B.N.; Jasim, B.H.; Siano, P.; Alhelou, H.H.; Al-Hinai, A. A Novel Solution for Day-Ahead Scheduling Problems Using the IoT-Based Bald Eagle Search Optimization Algorithm. Inventions 2022, 7, 48. [Google Scholar] [CrossRef]
- Ramalingam, S.P.; Shanmugam, P.K. Hardware Implementation of a Home Energy Management System Using Remodeled Sperm Swarm Optimization (RMSSO) Algorithm. Energies 2022, 15, 5008. [Google Scholar] [CrossRef]
- Asghar, F.; Zahid, A.; Hussain, M.I.; Asghar, F.; Amjad, W.; Kim, J.T. A Novel Solution for Optimized Energy Management Systems Comprising an AC/DC Hybrid Microgrid System for Industries. Sustainability 2022, 14, 8788. [Google Scholar] [CrossRef]
- Chang, C.Y.; Tsai, P.F. Multiobjective Decision-Making Model for Power Scheduling Problem in Smart Homes. Sustainability 2022, 14, 11867. [Google Scholar] [CrossRef]
- Hussain, I.; Ullah, I.; Ramalakshmi, R.; Ashfaq, M.; Nayab, D.e. Smart Energy Management System for University Campus using Sine-Cosine Optimization Algorithm. In Proceedings of the IEEE 2022 International Virtual Conference on Power Engineering Computing and Control: Developments in Electric Vehicles and Energy Sector for Sustainable Future (PECCON), Online, 5–6 May 2022; pp. 1–6. [Google Scholar]
- Venkatesh, B.; Padmini, S. Managing the smart grid with demand side management using Antlion Optimization. In Proceedings of the International Conference on Power Electronics and Renewable Energy Systems, Kedah, Malaysia, 5–6 December 2022; pp. 313–322. [Google Scholar]
- Almeida, V.A.; de AL Rabelo, R.; Carvalho, A.; Rodrigues, J.J.; Solic, P. Aligning the interests of prosumers and utilities through a two-step demand-response approach. J. Clean. Prod. 2021, 323, 128993. [Google Scholar] [CrossRef]
- Sharda, S.; Sharma, K.; Singh, M. A real-time automated scheduling algorithm with PV integration for smart home prosumers. J. Build. Eng. 2021, 44, 102828. [Google Scholar] [CrossRef]
- Al-Duais, A.; Osman, M.; Shullar, M.H.; Abido, M.A. Optimal Real-Time Pricing-Based Scheduling in Home Energy Management System Using Genetic Algorithms. In Proceedings of the 2021 IEEE 4th International Conference on Renewable Energy and Power Engineering (REPE), Online, 9–11 October 2021; pp. 243–248. [Google Scholar]
- Rehman, A.U.; Hafeez, G.; Albogamy, F.R.; Wadud, Z.; Ali, F.; Khan, I.; Rukh, G.; Khan, S. An Efficient Energy Management in Smart Grid Considering Demand Response Program and Renewable Energy Sources. IEEE Access 2021, 9, 148821–148844. [Google Scholar] [CrossRef]
- Ali, S.; Khan, I.; Jan, S.; Hafeez, G. An optimization based power usage scheduling strategy using photovoltaic-battery system for demand-side management in smart grid. Energies 2021, 14, 2201. [Google Scholar] [CrossRef]
- Ahmed, E.M.; Rathinam, R.; Dayalan, S.; Fernandez, G.S.; Ali, Z.M.; Abdel Aleem, S.H.; Omar, A.I. A comprehensive analysis of demand response pricing strategies in a smart grid environment using particle swarm optimization and the strawberry optimization algorithm. Mathematics 2021, 9, 2338. [Google Scholar] [CrossRef]
- Ullah, H.; Khan, M.; Hussain, I.; Ullah, I.; Uthansakul, P.; Khan, N. An Optimal Energy Management System for University Campus Using the Hybrid Firefly Lion Algorithm (FLA). Energies 2021, 14, 6028. [Google Scholar] [CrossRef]
- Ziadeh, A.; Abualigah, L.; Elaziz, M.A.; Şahin, C.B.; Almazroi, A.A.; Omari, M. Augmented grasshopper optimization algorithm by differential evolution: A power scheduling application in smart homes. Multimed. Tools Appl. 2021, 80, 31569–31597. [Google Scholar] [CrossRef]
- Roy, C.; Das, D.K. A hybrid genetic algorithm (GA)–particle swarm optimization (PSO) algorithm for demand side management in smart grid considering wind power for cost optimization. Sādhanā 2021, 46, 1–12. [Google Scholar] [CrossRef]
- Oprea, S.V.; Bâra, A.; Ifrim, G.A. Optimizing the electricity consumption with a high degree of flexibility using a dynamic tariff and stackelberg game. J. Optim. Theory Appl. 2021, 190, 151–182. [Google Scholar] [CrossRef]
- Shaban, A.; Maher, H.; Elbayoumi, M.; Abdelhady, S. A cuckoo load scheduling optimization approach for smart energy management. Energy Rep. 2021, 7, 4705–4721. [Google Scholar] [CrossRef]
- Wasim Khan, H.; Usman, M.; Hafeez, G.; Albogamy, F.R.; Khan, I.; Shafiq, Z.; Usman Ali Khan, M.; Alkhammash, H.I. Intelligent Optimization Framework for Efficient Demand-Side Management in Renewable Energy Integrated Smart Grid. IEEE Access 2021, 9, 124235–124252. [Google Scholar] [CrossRef]
- Sarker, E.; Halder, P.; Seyedmahmoudian, M.; Jamei, E.; Horan, B.; Mekhilef, S.; Stojcevski, A. Progress on the demand side management in smart grid and optimization approaches. Int. J. Energy Res. 2021, 45, 36–64. [Google Scholar] [CrossRef]
- Sadiq, F.; Sajjad, I.A.; Sadiq, Z. Appliance Scheduling in Smart Homes using JAYA Based Optimization Algorithm. In Proceedings of the IEEE 2021 16th International Conference on Emerging Technologies (ICET), Online, 22–23 December 2021; pp. 1–6. [Google Scholar]
- Nawaz, A.; Hafeez, G.; Khan, I.; Jan, K.U.; Li, H.; Khan, S.A.; Wadud, Z. An intelligent integrated approach for efficient demand side management with forecaster and advanced metering infrastructure frameworks in smart grid. IEEE Access 2020, 8, 132551–132581. [Google Scholar] [CrossRef]
- Mohsenian-Rad, A.H.; Wong, V.W.; Jatskevich, J.; Schober, R.; Leon-Garcia, A. Autonomous Demand-Side Management Based on Game-Theoretic Energy Consumption Scheduling for the Future Smart Grid; IEEE: New York, NY, USA, 2010; Volume 1, pp. 320–331. [Google Scholar]
- Imran, A.; Hafeez, G.; Khan, I.; Usman, M.; Shafiq, Z.; Qazi, A.B.; Khalid, A.; Thoben, K.D. Heuristic-Based Programable Controller for Efficient Energy Management Under Renewable Energy Sources and Energy Storage System in Smart Grid. IEEE Access 2020, 8, 139587–139608. [Google Scholar] [CrossRef]
- Lok, J.J.; Tan, W.N.; Yip, S.C.; Gan, M.T. Optimizing Industrial Process Flow for Energy Cost Reduction through Demand-Side Management. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Hafeez, G.; Alimgeer, K.S.; Wadud, Z.; Khan, I.; Usman, M.; Qazi, A.B.; Khan, F.A. An Innovative Optimization Strategy for Efficient Energy Management With Day-Ahead Demand Response Signal and Energy Consumption Forecasting in Smart Grid Using Artificial Neural Network. IEEE Access 2020, 8, 84415–84433. [Google Scholar] [CrossRef]
- Gk, J.S. MANFIS Based SMART Home Energy Management System to Support SMART Grid. Peer-to-Peer Netw. Appl. 2020, 13, 2177–2188. [Google Scholar] [CrossRef]
- Dinh, H.T.; Yun, J.; Kim, D.M.; Lee, K.H.; Kim, D. A Home Energy Management System With Renewable Energy and Energy Storage Utilizing Main Grid and Electricity Selling. IEEE Access 2020, 8, 49436–49450. [Google Scholar] [CrossRef]
- Ullah, I.; Hussain, I.; Uthansakul, P.; Riaz, M.; Khan, M.N.; Lloret, J. Exploiting Multi-Verse Optimization and Sine-Cosine Algorithms for Energy Management in Smart Cities. Appl. Sci. 2020, 10, 2095. [Google Scholar] [CrossRef]
- Lim, K.Z.; Lim, K.H.; Wee, X.B.; Li, Y.; Wang, X. Optimal Allocation of Energy Storage and Solar Photovoltaic Systems with Residential Demand Scheduling. Appl. Energy 2020, 269, 115116. [Google Scholar] [CrossRef]
- Mouassa, S.; Bouktir, T.; Jurado, F. Scheduling of smart home appliances for optimal energy management in smart grid using Harris-hawks optimization algorithm. Optim. Eng. 2021, 22, 1625–1652. [Google Scholar] [CrossRef]
- Chojecki, A.; Rodak, M.; Ambroziak, A.; Borkowski, P. Energy Management System for Residential Buildings Based on Fuzzy Logic: Design and Implementation in Smart-Meter. IET Smart Grid 2020, 3, 254–266. [Google Scholar] [CrossRef]
- Ullah, I.; Hussain, I.; Singh, M. Exploiting Grasshopper and Cuckoo Search Bio-Inspired Optimization Algorithms for Industrial Energy Management System: Smart Industries. Electronics 2020, 9, 105. [Google Scholar] [CrossRef]
- Hussain, I.; Ullah, M.; Ullah, I.; Bibi, A.; Naeem, M.; Singh, M.; Singh, D. Optimizing Energy Consumption in the Home Energy Management System via a Bio-Inspired Dragonfly Algorithm and the Genetic Algorithm. Electronics 2020, 9, 406. [Google Scholar] [CrossRef]
- Khan, S.; Khan, Z.A.; Javaid, N.; Ahmad, W.; Abbasi, R.A.; Faisal, H.M. On Maximizing User Comfort Using a Novel Meta-Heuristic Technique in Smart Home. In Advanced Information Networking and Applications; Barolli, L., Takizawa, M., Xhafa, F., Enokido, T., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 926, pp. 26–38. [Google Scholar] [CrossRef]
- Ullah, I.; Rasheed, M.B.; Alquthami, T.; Tayyaba, S. A Residential Load Scheduling with the Integration of On-Site PV and Energy Storage Systems in Micro-Grid. Sustainability 2019, 12, 184. [Google Scholar] [CrossRef]
- Essiet, I.O.; Sun, Y.; Wang, Z. Optimized Energy Consumption Model for Smart Home Using Improved Differential Evolution Algorithm. Energy 2019, 172, 354–365. [Google Scholar] [CrossRef]
- Shuja, S.M.; Javaid, N.; Khan, S.; Akmal, H.; Hanif, M.; Fazalullah, Q.; Khan, Z.A. Efficient Scheduling of Smart Home Appliances for Energy Management by Cost and PAR Optimization Algorithm in Smart Grid. In Web, Artificial Intelligence and Network Applications; Barolli, L., Takizawa, M., Xhafa, F., Enokido, T., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 927, pp. 398–411. [Google Scholar] [CrossRef]
- Molla, T.; Khan, B.; Moges, B.; Alhelou, H.H.; Zamani, R. Integrated Energy Optimization of Smart Home Appliances with Cost-Effective Energy Management System. CSEE J. Power Energy Syst. 2019, 5, 249–258. [Google Scholar] [CrossRef]
- Silva, B.N.; Han, K. Mutation Operator Integrated Ant Colony Optimization Based Domestic Appliance Scheduling for Lucrative Demand Side Management. Future Gener. Comput. Syst. 2019, 100, 557–568. [Google Scholar] [CrossRef]
- Ullah, I.; Khitab, Z.; Khan, M.; Hussain, S. An Efficient Energy Management in Office Using Bio-Inspired Energy Optimization Algorithms. Processes 2019, 7, 142. [Google Scholar] [CrossRef]
- Abbasi, R.A.; Javaid, N.; Khan, S.; ur Rehman, S.; Amanullah; Asif, R.M.; Ahmad, W. Minimizing Daily Cost and Maximizing User Comfort Using a New Metaheuristic Technique. In Web, Artificial Intelligence and Network Applications; Barolli, L., Takizawa, M., Xhafa, F., Enokido, T., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 927, pp. 80–92. [Google Scholar] [CrossRef]
- Fan, C.H.; Chen, H.; Tsai, C.W. SEHAS: A Novel Metaheuristic Algorithm for Home Appliances Scheduling in Smart Grid. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 786–791. [Google Scholar] [CrossRef]
- Puttamadappa, C.; Parameshachari, B.D. Demand Side Management of Small Scale Loads in a Smart Grid Using Glow-Worm Swarm Optimization Technique. Microprocess. Microsyst. 2019, 71, 102886. [Google Scholar] [CrossRef]
- Khan, Z.A.; Zafar, A.; Javaid, S.; Aslam, S.; Rahim, M.H.; Javaid, N. Hybrid Meta-Heuristic Optimization Based Home Energy Management System in Smart Grid. J. Ambient. Intell. Humaniz. Comput. 2019, 10, 4837–4853. [Google Scholar] [CrossRef]
- Hussain, H.; Javaid, N.; Iqbal, S.; Hasan, Q.; Aurangzeb, K.; Alhussein, M. An Efficient Demand Side Management System with a New Optimized Home Energy Management Controller in Smart Grid. Energies 2018, 11, 190. [Google Scholar] [CrossRef]
- Ininahazwe, H.; Muriithi, C.M.; Kamau, S. Optimal Demand-Side Management for Smart Micro Grid with Storage. J. Power Energy Eng. 2018, 6, 38–58. [Google Scholar] [CrossRef]
- Parizy, E.S.; Bahrami, H.R.; Choi, S. A Low Complexity and Secure Demand Response Technique for Peak Load Reduction. IEEE Trans. Smart Grid 2019, 10, 3259–3268. [Google Scholar] [CrossRef]
- Sun, M.; Chang, C.L.; Zhang, J.; Mehmani, A.; Culligan, P. Break-Even Analysis of Battery Energy Storage in Buildings Considering Time-of-Use Rates. In Proceedings of the 2018 IEEE Green Technologies Conference (GreenTech), Austin, TX, USA, 4–6 April 2018; pp. 95–99. [Google Scholar] [CrossRef]
- Mansiri, K.; Sukchai, S.; Sirisamphanwong, C. Fuzzy Control Algorithm for Battery Storage and Demand Side Power Management for Economic Operation of the Smart Grid System at Naresuan University, Thailand. IEEE Access 2018, 6, 32440–32449. [Google Scholar] [CrossRef]
- Chamandoust, H.; Hashemi, A.; Derakhshan, G.; Hakimi, M. Scheduling of Smart Micro Grid Considering Reserve and Demand Side Management. In Proceedings of the 2018 Smart Grid Conference (SGC), Sanandaj, Iran, 28–29 November 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Naz, A.; Javaid, N.; Qureshi, T.N.; Imran, M.; Ali, M.; Khan, Z.A. EDHBPSO: Enhanced Differential Harmony Binary Particle Swarm Optimization for Demand Side Management in Smart Grid. In Proceedings of the 2018 32nd International Conference on Advanced Information Networking and Applications Workshops (WAINA), Krakow, Poland, 16–18 May 2018; pp. 218–225. [Google Scholar] [CrossRef]
- Oprea, S.V.; Bâra, A.; Ifrim, G. Flattening the Electricity Consumption Peak and Reducing the Electricity Payment for Residential Consumers in the Context of Smart Grid by Means of Shifting Optimization Algorithm. Comput. Ind. Eng. 2018, 122, 125–139. [Google Scholar] [CrossRef]
- Khan, A.J.; Javaid, N.; Iqbal, Z.; Anwar, N.; Saboor, A.; ul-Haq, I.; Qasim, U. A Hybrid Bacterial Foraging Tabu Search Heuristic Optimization for Demand Side Management in Smart Grid. In Proceedings of the 2018 32nd International Conference on Advanced Information Networking and Applications Workshops (WAINA), Krakow, Poland, 16–18 May 2018; pp. 550–558. [Google Scholar] [CrossRef]
- Spavieri, G.; Fernandes, R.A.S.; Vale, Z. Gravitational Search Algorithm Applied for Residential Demand Response Using Real-Time Pricing. In Trends in Cyber-Physical Multi-Agent Systems. The PAAMS Collection—15th International Conference, PAAMS 2017; De la Prieta, F., Vale, Z., Antunes, L., Pinto, T., Campbell, A.T., Julián, V., Neves, A.J., Moreno, M.N., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 619, pp. 101–111. [Google Scholar] [CrossRef]
- Khan, H.N.; Iftikhar, H.; Asif, S.; Maroof, R.; Ambreen, K.; Javaid, N. Demand Side Management Using Strawberry Algorithm and Bacterial Foraging Optimization Algorithm in Smart Grid. In Advances in Network-Based Information Systems; Barolli, L., Enokido, T., Takizawa, M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 7, pp. 191–202. [Google Scholar] [CrossRef]
- Balakumar, P.; Sathiya, S. Demand Side Management in Smart Grid Using Load Shifting Technique. In Proceedings of the 2017 IEEE International Conference on Electrical, Instrumentation and Communication Engineering (ICEICE), Karur, India, 27–28 April 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Lokeshgupta, B.; Sadhukhan, A.; Sivasubramani, S. Multi-Objective Optimization for Demand Side Management in a Smart Grid Environment. In Proceedings of the 2017 7th International Conference on Power Systems (ICPS), Pune, India, 21–23 December 2017; pp. 200–205. [Google Scholar] [CrossRef]
- Li, D.; Chiu, W.Y.; Sun, H.; Poor, H.V. Multiobjective Optimization for Demand Side Management Program in Smart Grid. IEEE Trans. Ind. Informatics 2018, 14, 1482–1490. [Google Scholar] [CrossRef]
- Ansar, S.; Ansar, W.; Ansar, K.; Mehmood, M.H.; Raja, M.Z.U.; Javaid, N. Demand Side Management Using Meta-Heuristic Techniques and ToU in Smart Grid. In Advances in Network-Based Information System; Barolli, L., Enokido, T., Takizawa, M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 7, pp. 203–217. [Google Scholar] [CrossRef]
- Shakouri G., H.; Kazemi, A. Multi-Objective Cost-Load Optimization for Demand Side Management of a Residential Area in Smart Grids. Sustain. Cities Soc. 2017, 32, 171–180. [Google Scholar] [CrossRef]
- Khan, M.; Khalid, R.; Zaheer, B.; Tariq, M.; ul Abideen, Z.; Malik, H.; Javaid, N. Residential Demand Side Management in Smart Grid Using Meta-Heuristic Techniques. In Advances on P2P, Parallel, Grid, Cloud and Internet Computing; Xhafa, F., Caballé, S., Barolli, L., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 13, pp. 76–88. [Google Scholar] [CrossRef]
- Anzar, M.; Iqra, R.; Kousar, A.; Ejaz, S.; Alvarez-Alvarado, M.S.; Zafar, A.K. Optimization of Home Energy Management System in Smart Grid for Effective Demand Side Management. In Proceedings of the 2017 International Renewable and Sustainable Energy Conference (IRSEC), Tangier, Tangier, Morocco, 4–7 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Khan, M.S.; Anwar ul Hassan, C.H.; Sadiq, H.A.; Ali, I.; Rauf, A.; Javaid, N. A New Meta-Heuristic Optimization Algorithm Inspired from Strawberry Plant for Demand Side Management in Smart Grid. In Advances in Intelligent Networking and Collaborative Systems; Barolli, L., Woungang, I., Hussain, O.K., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 8, pp. 143–154. [Google Scholar] [CrossRef]
- Yaseen, Y.; Ghita, B. Peak-to-Average Reduction by Community-Based DSM. In Proceedings of the 2017 IEEE International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 21–24 August 2017; pp. 194–199. [Google Scholar] [CrossRef]
- Abbasi, B.Z.; Javaid, S.; Bibi, S.; Khan, M.; Malik, M.N.; Butt, A.A.; Javaid, N. Demand Side Management in Smart Grid by Using Flower Pollination Algorithm and Genetic Algorithm. In Advances on P2P, Parallel, Grid, Cloud and Internet Computing; Xhafa, F., Caballé, S., Barolli, L., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 13, pp. 424–436. [Google Scholar] [CrossRef]
- Gupta, I.; Anandini, G.; Gupta, M. An Hour Wise Device Scheduling Approach for Demand Side Management in Smart Grid Using Particle Swarm Optimization. In Proceedings of the 2016 National Power Systems Conference (NPSC), Bhubaneswar, India, 19–21 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Anees, A.; Chen, Y.P.P. True Real Time Pricing and Combined Power Scheduling of Electric Appliances in Residential Energy Management System. Appl. Energy 2016, 165, 592–600. [Google Scholar] [CrossRef]
- Rasheed, M.; Javaid, N.; Ahmad, A.; Khan, Z.; Qasim, U.; Alrajeh, N. An Efficient Power Scheduling Scheme for Residential Load Management in Smart Homes. Appl. Sci. 2015, 5, 1134–1163. [Google Scholar] [CrossRef]
- Logenthiran, T.; Srinivasan, D.; Phyu, E. Particle Swarm Optimization for Demand Side Management in Smart Grid. In Proceedings of the 2015 IEEE Innovative Smart Grid Technologies—Asia (ISGT ASIA), Bangkok, Thailand, 3–6 November 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Nayak, S.K.; Sahoo, N.C.; Panda, G. Demand Side Management of Residential Loads in a Smart Grid Using 2D Particle Swarm Optimization Technique. In Proceedings of the 2015 IEEE Power, Communication and Information Technology Conference (PCITC), Bhubaneswar, India, 15–17 October 2015; pp. 201–206. [Google Scholar] [CrossRef]
- Awais, M.; Javaid, N.; Shaheen, N.; Iqbal, Z.; Rehman, G.; Muhammad, K.; Ahmad, I. An Efficient Genetic Algorithm Based Demand Side Management Scheme for Smart Grid. In Proceedings of the 2015 18th International Conference on Network-Based Information Systems, Taipei, Taiwan, 2–4 September 2015; pp. 351–356. [Google Scholar] [CrossRef]
- Longe, O.M.; Ouahada, K.; Rimer, S.; Ferreira, H.C. Optimization of Energy Expenditure in Smart Homes under Time-of-Use Pricing. In Proceedings of the 2015 IEEE Innovative Smart Grid Technologies—Asia (ISGT ASIA), Bangkok, Thailand, 3–6 November 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Khan, M.A.; Javaid, N.; Mahmood, A.; Khan, Z.A.; Alrajeh, N. A Generic Demand-Side Management Model for Smart Grid: A Generic Demand-Side Management Model for Smart Grid. Int. J. Energy Res. 2015, 39, 954–964. [Google Scholar] [CrossRef]
- Barbato, A.; Capone, A.; Chen, L.; Martignon, F.; Paris, S. A Distributed Demand-Side Management Framework for the Smart Grid. Comput. Commun. 2015, 57, 13–24. [Google Scholar] [CrossRef]
- Manasseh, E.; Ohno, S.; Yamamoto, T.; Mvuma, A. Autonomous demand-side optimization with load uncertainty. In Proceedings of the IEEE 2014 International Conference on Electronics, Information and Communications (ICEIC), Sabah, Malaysia, 15–18 January 2014; pp. 1–2. [Google Scholar]
- Meng, F.L.; Zeng, X.J. An Optimal Real-Time Pricing for Demand-Side Management: A Stackelberg Game and Genetic Algorithm Approach. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 1703–1710. [Google Scholar] [CrossRef]
- Meng, F.L.; Zeng, X.J. A Stackelberg game-theoretic approach to optimal real-time pricing for the smart grid. Soft Comput. 2013, 17, 2365–2380. [Google Scholar] [CrossRef]
- Khomami, H.P.; Javidi, M.H. An efficient home energy management system for automated residential demand response. In Proceedings of the IEEE 2013 13th International Conference on Environment and Electrical Engineering (EEEIC), Wroclaw, Poland, 1–3 November 2013; pp. 307–312. [Google Scholar]
- Zhao, G.; Li, L.; Zhang, J.; Letaief, K.B. Residential demand response with power adjustable and unadjustable appliances in smart grid. In Proceedings of the 2013 IEEE international conference on communications workshops (ICC), Budapest, Hungary, 9–13 June 2013; pp. 386–390. [Google Scholar]
- Muhammad, B. Energy consumption, CO2 emissions and economic growth in developed, emerging and Middle East and North Africa countries. Energy 2019, 179, 232–245. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Talbi, E.G. Metaheuristics: From Design to Implementation; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Khan, B.; Singh, P. Selecting a Meta-Heuristic Technique for Smart Micro-Grid Optimization Problem: A Comprehensive Analysis. IEEE Access 2017, 5, 13951–13977. [Google Scholar] [CrossRef]
- Bharathi, C.; Rekha, D.; Vijayakumar, V. Genetic Algorithm Based Demand Side Management for Smart Grid. Wirel. Pers. Commun. 2017, 93, 481–502. [Google Scholar] [CrossRef]
- Owen, G. Game Theory; Emerald Group Publishing: Bingley, UK, 2013. [Google Scholar]
- Gao, B.; Liu, X.; Wu, C.; Tang, Y. Game-theoretic energy management with storage capacity optimization in the smart grids. J. Mod. Power Syst. Clean Energy 2018, 6, 656–667. [Google Scholar] [CrossRef]
- Sheikhi, A.; Rayati, M.; Bahrami, S.; Ranjbar, A.M.; Sattari, S. A Cloud Computing Framework on Demand Side Management Game in Smart Energy Hubs. Int. J. Electr. Power Energy Syst. 2015, 64, 1007–1016. [Google Scholar] [CrossRef]
- Hájek, P. Metamathematics of Fuzzy Logic; Springer Science & Business Media: Dordrecht, The Netherlands, 2013; Volume 4. [Google Scholar]
- Asif, A.A.; Singh, R. Further cost reduction of battery manufacturing. Batteries 2017, 3, 17. [Google Scholar] [CrossRef]
- Vineetha, C.P.; Babu, C.A. Smart Grid Challenges, Issues and Solutions. In Proceedings of the 2014 International Conference on Intelligent Green Building and Smart Grid (IGBSG), Taipei, Taiwan, 23–25 April 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Tan, X.; Li, Q.; Wang, H. Advances and Trends of Energy Storage Technology in Microgrid. Int. J. Electr. Power Energy Syst. 2013, 44, 179–191. [Google Scholar] [CrossRef]
- Pacheco, R.; Ordóñez, J.; Martínez, G. Energy efficient design of building: A review. Renew. Sustain. Energy Rev. 2012, 16, 3559–3573. [Google Scholar] [CrossRef]
- Venkatesan, N.; Solanki, J.; Solanki, S.K. Residential Demand Response Model and Impact on Voltage Profile and Losses of an Electric Distribution Network. Appl. Energy 2012, 96, 84–91. [Google Scholar] [CrossRef]
- Shoreh, M.H.; Siano, P.; Shafie-khah, M.; Loia, V.; Catalão, J.P. A Survey of Industrial Applications of Demand Response. Electr. Power Syst. Res. 2016, 141, 31–49. [Google Scholar] [CrossRef]
- Lofthouse, T. The Taguchi loss function. Work Study 1999, 48, 218–223. [Google Scholar] [CrossRef]
- Mavromatidis, L.E. A Review on Hybrid Optimization Algorithms to Coalesce Computational Morphogenesis with Interactive Energy Consumption Forecasting. Energy Build. 2015, 106, 192–202. [Google Scholar] [CrossRef]
- Salehizadeh, S.M.A.; Yadmellat, P.; Menhaj, M.B. Local optima avoidable particle swarm optimization. In Proceedings of the 2009 IEEE Swarm Intelligence Symposium, Nashville, TN, USA, 30 March–2 April 2009; pp. 16–21. [Google Scholar]
- Houssein, E.H.; Gad, A.G.; Hussain, K.; Suganthan, P.N. Major advances in particle swarm optimization: Theory, analysis, and application. Swarm Evol. Comput. 2021, 63, 100868. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Heitkoetter, W.; Medjroubi, W.; Vogt, T.; Agert, C. Regionalised heat demand and power-to-heat capacities in Germany–An open dataset for assessing renewable energy integration. Appl. Energy 2020, 259, 114161. [Google Scholar] [CrossRef]
- Liserre, M.; Sauter, T.; Hung, J.Y. Future energy systems: Integrating renewable energy sources into the smart power grid through industrial electronics. IEEE Ind. Electron. Mag. 2010, 4, 18–37. [Google Scholar] [CrossRef]
- Analytica, O. COP27 points to mixed progress on climate issues. Emerald Expert Briefings 2022. [Google Scholar] [CrossRef]
- Isaeva, A.; Salahodjaev, R.; Khachaturov, A.; Tosheva, S. The impact of tourism and financial development on energy consumption and carbon dioxide emission: Evidence from post-communist countries. J. Knowl. Econ. 2022, 13, 773–786. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mimi, S.; Ben Maissa, Y.; Tamtaoui, A. Optimization Approaches for Demand-Side Management in the Smart Grid: A Systematic Mapping Study. Smart Cities 2023, 6, 1630-1662. https://doi.org/10.3390/smartcities6040077
Mimi S, Ben Maissa Y, Tamtaoui A. Optimization Approaches for Demand-Side Management in the Smart Grid: A Systematic Mapping Study. Smart Cities. 2023; 6(4):1630-1662. https://doi.org/10.3390/smartcities6040077
Chicago/Turabian StyleMimi, Safaa, Yann Ben Maissa, and Ahmed Tamtaoui. 2023. "Optimization Approaches for Demand-Side Management in the Smart Grid: A Systematic Mapping Study" Smart Cities 6, no. 4: 1630-1662. https://doi.org/10.3390/smartcities6040077
APA StyleMimi, S., Ben Maissa, Y., & Tamtaoui, A. (2023). Optimization Approaches for Demand-Side Management in the Smart Grid: A Systematic Mapping Study. Smart Cities, 6(4), 1630-1662. https://doi.org/10.3390/smartcities6040077






