Novel Method for Speeding Up Time Series Processing in Smart City Applications
Abstract
:1. Introduction
2. Related Work
3. Adaptive Simulated Annealing Representation (ASAR) Based Distance Measure
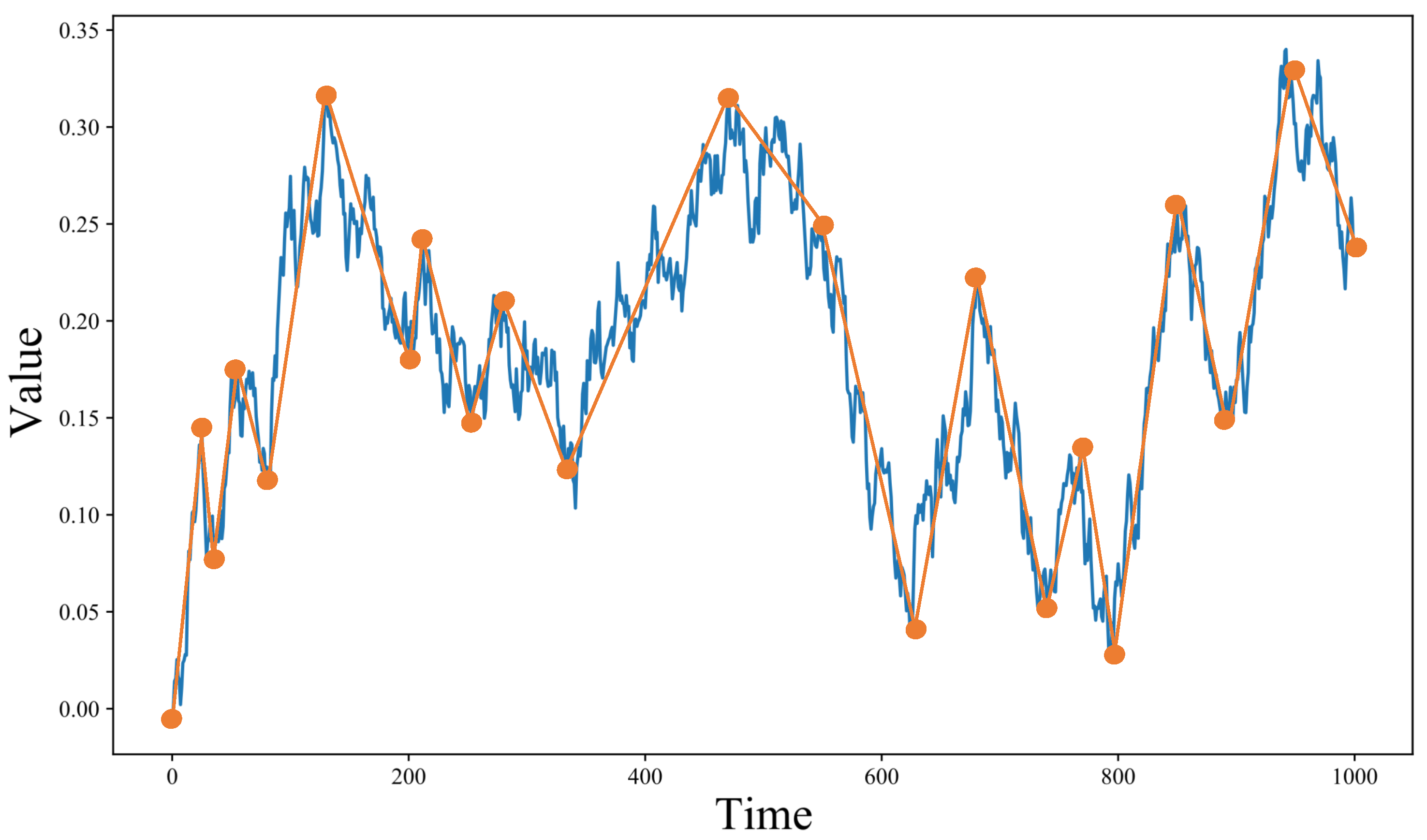
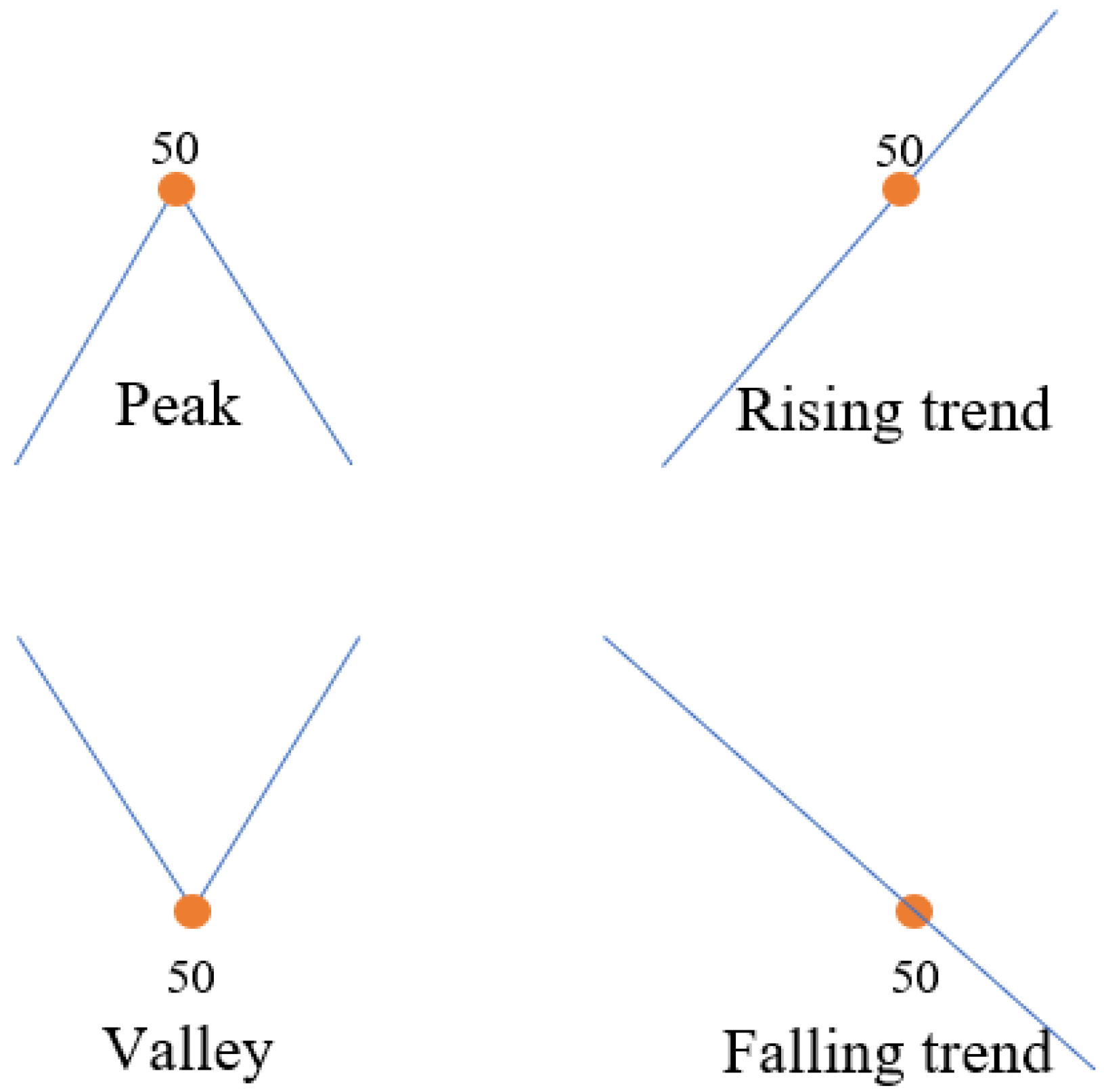
3.1. Adaptive Simulated Annealing Representation (ASAR)
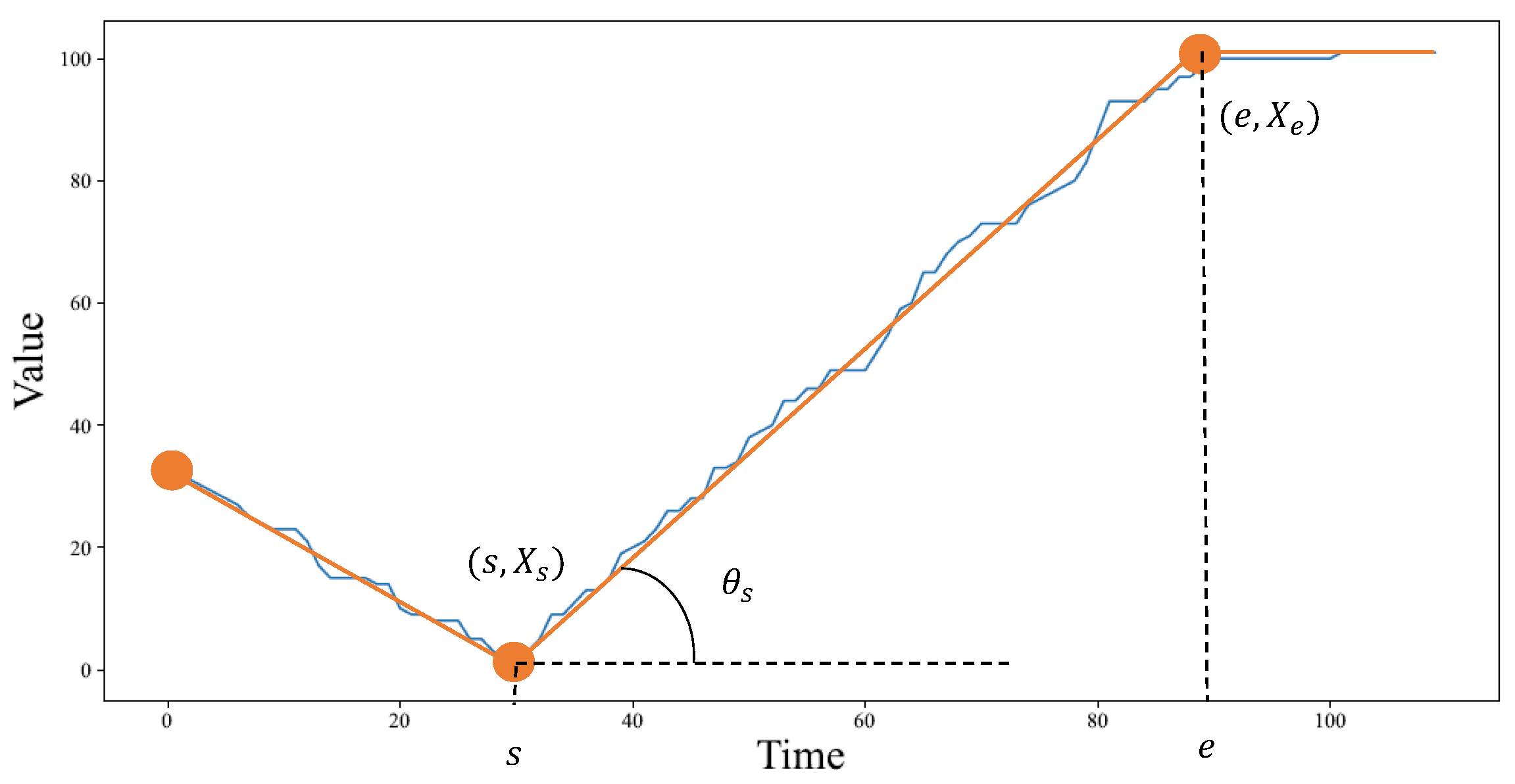
3.2. Enriching ASAR with the Slope Information
3.3. Adaptive Simulated Annealing Representation Based Distance Measure (ASAR-Distance)
4. Experimental Results and Discussion
4.1. Assessment Algorithms
4.1.1. One Nearest Neighbor Classification (1-NN)
4.1.2. Hierarchical Clustering
4.2. Assessment Criteria
4.3. Dataset Description
4.4. Effectiveness Evaluation
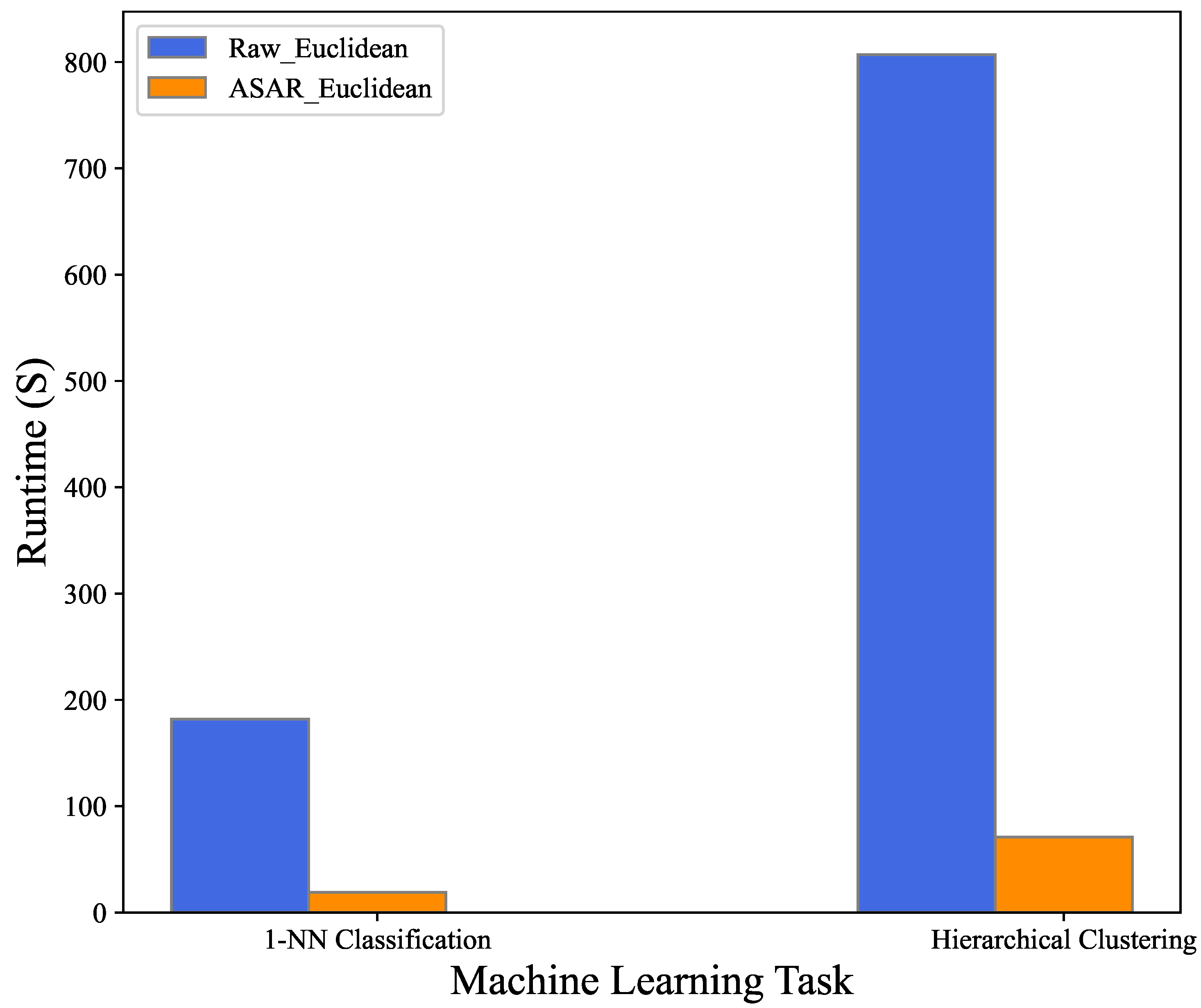
4.5. Results Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saqib, M.; Jasra, B.; Moon, A.H. A lightweight three factor authentication framework for IoT based critical applications. J. King Saud Univ. Comput. Inf. Sci. 2021; in press. [Google Scholar] [CrossRef]
- Syed, A.S.; Sierra-Sosa, D.; Kumar, A.; Elmaghraby, A. IoT in smart cities: A survey of technologies, practices and challenges. Smart Cities 2021, 4, 429–475. [Google Scholar] [CrossRef]
- Wu, J.; Guo, S.; Li, J.; Zeng, D. Big data meet green challenges: Greening big data. IEEE Syst. J. 2016, 10, 873–887. [Google Scholar] [CrossRef]
- Wu, J.; Guo, S.; Huang, H.; Liu, W.; Xiang, Y. Information and communications technologies for sustainable development goals: State-of-the-art, needs and perspectives. IEEE Commun. Surv. Tutor. 2018, 20, 2389–2406. [Google Scholar] [CrossRef] [Green Version]
- Doan, Q.T.; Kayes, A.; Rahayu, W.; Nguyen, K. Integration of iot streaming data with efficient indexing and storage optimization. IEEE Access 2020, 8, 47456–47467. [Google Scholar] [CrossRef]
- Koubaa, A.; Aldawood, A.; Saeed, B.; Hadid, A.; Ahmed, M.; Saad, A.; Alkhouja, H.; Ammar, A.; Alkanhal, M. Smart Palm: An IoT framework for red palm weevil early detection. Agronomy 2020, 10, 987. [Google Scholar] [CrossRef]
- Kim, H.; Choi, H.; Kang, H.; An, J.; Yeom, S.; Hong, T. A systematic review of the smart energy conservation system: From smart homes to sustainable smart cities. Renew. Sustain. Energy Rev. 2021, 140, 110755. [Google Scholar] [CrossRef]
- Khan, M.M.; Mehnaz, S.; Shaha, A.; Nayem, M.; Bourouis, S. IoT-Based Smart Health Monitoring System for COVID-19 Patients. Comput. Math. Methods Med. 2021, 2021, 8591036. [Google Scholar] [CrossRef]
- Bawaneh, M.; Simon, V. Anomaly detection in smart city traffic based on time series analysis. In Proceedings of the 2019 International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 19–21 September 2019; pp. 1–6. [Google Scholar]
- Pardini, K.; Rodrigues, J.J.; Kozlov, S.A.; Kumar, N.; Furtado, V. IoT-based solid waste management solutions: A survey. J. Sens. Actuator Netw. 2019, 8, 5. [Google Scholar] [CrossRef] [Green Version]
- Ali, G.; Ali, T.; Irfan, M.; Draz, U.; Sohail, M.; Glowacz, A.; Sulowicz, M.; Mielnik, R.; Faheem, Z.B.; Martis, C. IoT based smart parking system using deep long short memory network. Electronics 2020, 9, 1696. [Google Scholar] [CrossRef]
- Kaginalkar, A.; Kumar, S.; Gargava, P.; Niyogi, D. Review of urban computing in air quality management as smart city service: An integrated IoT, AI, and cloud technology perspective. Urban Clim. 2021, 39, 100972. [Google Scholar] [CrossRef]
- Ali, M.; Alqahtani, A.; Jones, M.W.; Xie, X. Clustering and classification for time series data in visual analytics: A survey. IEEE Access 2019, 7, 181314–181338. [Google Scholar] [CrossRef]
- Ciaburro, G.; Iannace, G. Machine Learning-Based Algorithms to Knowledge Extraction from Time Series Data: A Review. Data 2021, 6, 55. [Google Scholar] [CrossRef]
- Blázquez-García, A.; Conde, A.; Mori, U.; Lozano, J.A. A review on outlier/anomaly detection in time series data. ACM Comput. Surv. (CSUR) 2021, 54, 1–33. [Google Scholar] [CrossRef]
- Belhadi, A.; Djenouri, Y.; Nørvåg, K.; Ramampiaro, H.; Masseglia, F.; Lin, J.C.W. Space–time series clustering: Algorithms, taxonomy, and case study on urban smart cities. Eng. Appl. Artif. Intell. 2020, 95, 103857. [Google Scholar] [CrossRef]
- Abanda, A.; Mori, U.; Lozano, J.A. A review on distance based time series classification. Data Min. Knowl. Discov. 2019, 33, 378–412. [Google Scholar] [CrossRef] [Green Version]
- Torkamani, S.; Lohweg, V. Survey on time series motif discovery. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2017, 7, e1199. [Google Scholar] [CrossRef]
- Bawaneh, M.; Simon, V. A Novel Time Series Representation Approach for Dimensionality Reduction. Infocommun. J. 2022, 14, 44–55. [Google Scholar] [CrossRef]
- Faloutsos, C.; Ranganathan, M.; Manolopoulos, Y. Fast subsequence matching in time-series databases. Acm. Sigmod. Rec. 1994, 23, 419–429. [Google Scholar] [CrossRef] [Green Version]
- Berndt, D.J.; Clifford, J. Using dynamic time warping to find patterns in time series. In KDD Workshop; AAAI Press: Seattle, WA, USA, 1994; Volume 10, pp. 359–370. [Google Scholar]
- Yi, B.K.; Faloutsos, C. Fast time sequence indexing for arbitrary Lp norms. In Proceedings of the 26th International Conference on Very Large Data Bases Cairo (VLDB’00), Cairo, Egypt, 10–14 September 2000; pp. 385–394. [Google Scholar]
- Ahmadi, A.; Karray, F.; Kamel, M.S. Flocking based approach for data clustering. Nat. Comput. 2010, 9, 767–791. [Google Scholar] [CrossRef]
- Vlachos, M.; Kollios, G.; Gunopulos, D. Discovering similar multidimensional trajectories. In Proceedings of the 18th International Conference on Data Engineering, San Jose, CA, USA, 26 February–1 March 2002; pp. 673–684. [Google Scholar]
- Chen, L.; Özsu, M.T.; Oria, V. Robust and fast similarity search for moving object trajectories. In Proceedings of the 2005 ACM SIGMOD International Conference on Management of Data, Baltimore, MA, USA, 14–16 June 2005; pp. 491–502. [Google Scholar]
- Chen, L.; Ng, R. On the marriage of lp-norms and edit distance. In Proceedings of the Thirtieth International Conference on Very Large Data Bases-Volume 30, Toronto, ON, Canada, 31 August–3 September 2004; pp. 792–803. [Google Scholar]
- Chen, Y.; Nascimento, M.A.; Ooi, B.C.; Tung, A.K. Spade: On shape-based pattern detection in streaming time series. In Proceedings of the 2007 IEEE 23rd International Conference on Data Engineering, Istanbul, Turkey, 15–20 April 2007; pp. 786–795. [Google Scholar]
- Lin, J.; Keogh, E.; Lonardi, S.; Chiu, B. A symbolic representation of time series, with implications for streaming algorithms. In Proceedings of the 8th ACM SIGMOD Workshop on Research Issues in Data Mining and Knowledge Discovery, San Diego, CA, USA, 13 June 2003; pp. 2–11. [Google Scholar]
- Lin, J.; Keogh, E.; Wei, L.; Lonardi, S. Experiencing SAX: A novel symbolic representation of time series. Data Min. Knowl. Discov. 2007, 15, 107–144. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Pi, D. A new time series representation model and corresponding similarity measure for fast and accurate similarity detection. IEEE Access 2017, 5, 24503–24519. [Google Scholar] [CrossRef]
- Gullo, F.; Ponti, G.; Tagarelli, A.; Greco, S. A time series representation model for accurate and fast similarity detection. Pattern Recognit. 2009, 42, 2998–3014. [Google Scholar] [CrossRef]
- Kamalzadeh, H.; Ahmadi, A.; Mansour, S. Clustering time-series by a novel slope-based similarity measure considering particle swarm optimization. Appl. Soft Comput. 2020, 96, 106701. [Google Scholar] [CrossRef]
- Kamalzadeh, H.; Ahmadi, A.; Mansour, S. A shape-based adaptive segmentation of time-series using particle swarm optimization. Inf. Syst. 2017, 67, 1–18. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Lee, Y.H.; Wei, C.P.; Cheng, T.H.; Yang, C.T. Nearest-neighbor-based approach to time-series classification. Decis. Support Syst. 2012, 53, 207–217. [Google Scholar] [CrossRef]
- Murtagh, F.; Contreras, P. Algorithms for hierarchical clustering: An overview. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2012, 2, 86–97. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Dau, H.A.; Keogh, E.; Kamgar, K.; Yeh, C.C.M.; Zhu, Y.; Gharghabi, S.; Ratanamahatana, C.A.; Hu, B.; Begum, N.; Bagnall, A.; et al. The UCR Time Series Classification Archive. 2018. Available online: https://www.cs.ucr.edu/~eamonn/time_series_data_2018/ (accessed on 6 April 2022).
| Name | Type | Dataset Size | Time Series Length | Number of Classes |
|---|---|---|---|---|
| HandOutlines | Image | 1000 | 2709 | 2 |
| StarLightCurves | Sensor | 1000 | 1024 | 3 |
| Lightning2 | Sensor | 60 | 637 | 2 |
| OSULeaf | Image | 200 | 427 | 6 |
| WormsTwoClass | Motion | 180 | 900 | 2 |
| Yoga | Image | 1000 | 426 | 2 |
| Trace | Sensor | 100 | 275 | 4 |
| Car | Sensor | 60 | 577 | 4 |
| CricketX | Motion | 390 | 300 | 12 |
| InlineSkate | Motion | 550 | 1882 | 7 |
| UWaveGestureLibraryAll | Motion | 1500 | 945 | 8 |
| Dataset | Raw Time Series | ASAR Form | |||
|---|---|---|---|---|---|
| Euclidean | DTW | Euclidean | DTW | ASAR-Distance | |
| HandOutlines | 1.00 | 0.99 | 1.01 | 1.00 | 1.02 |
| StarLightCurves | 1.00 | 1.02 | 1.02 | 1.01 | 0.97 |
| Lightning2 | 1.00 | 0.88 | 0.80 | 0.91 | 1.04 |
| OSULeaf | 1.00 | 0.97 | 0.76 | 0.83 | 0.93 |
| WormsTwoClass | 1.00 | 0.91 | 1.02 | 1.06 | 1.06 |
| yoga | 1.00 | 1.01 | 0.84 | 0.85 | 0.87 |
| Trace | 1.00 | 0.97 | 1.19 | 1.30 | 1.30 |
| Car | 1.00 | 1.08 | 1.08 | 0.93 | 0.93 |
| CricketX | 1.00 | 1.08 | 0.84 | 0.84 | 0.84 |
| InlineSkate | 1.00 | 0.96 | 1.06 | 1.06 | 1.12 |
| UWaveGestureLibraryAll | 1.00 | 1.01 | 0.94 | 0.96 | 1.00 |
| Average | 1.00 | 0.99 | 0.96 | 0.98 | 1.01 |
| Dataset | Raw Time Series | ASAR Form | |||
|---|---|---|---|---|---|
| Euclidean | DTW | Euclidean | DTW | ASAR-Distance | |
| HandOutlines | 1.00 | 1.00 | 1.00 | 1.10 | 1.50 |
| StarLightCurves | 1.00 | 1.04 | 1.77 | 1.77 | 1.70 |
| Lightning2 | 1.00 | 1.02 | 0.84 | 0.84 | 1.14 |
| OSULeaf | 1.00 | 0.97 | 1.12 | 1.12 | 1.15 |
| WormsTwoClass | 1.00 | 0.96 | 1.02 | 1.04 | 0.94 |
| yoga | 1.00 | 1.05 | 1.05 | 1.12 | 1.14 |
| Trace | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Car | 1.00 | 1.00 | 0.95 | 0.60 | 0.60 |
| CricketX | 1.00 | 1.00 | 1.21 | 1.25 | 1.92 |
| InlineSkate | 1.00 | 1.02 | 1.00 | 1.00 | 1.11 |
| UWaveGestureLibraryAll | 1.00 | 1.02 | 0.95 | 0.45 | 1.08 |
| Average | 1.00 | 1.01 | 1.08 | 1.03 | 1.21 |
| Machine Learning Task | Raw Time Series | ASAR Form | |||
|---|---|---|---|---|---|
| Euclidean | DTW | Euclidean | DTW | ASAR-Distance | |
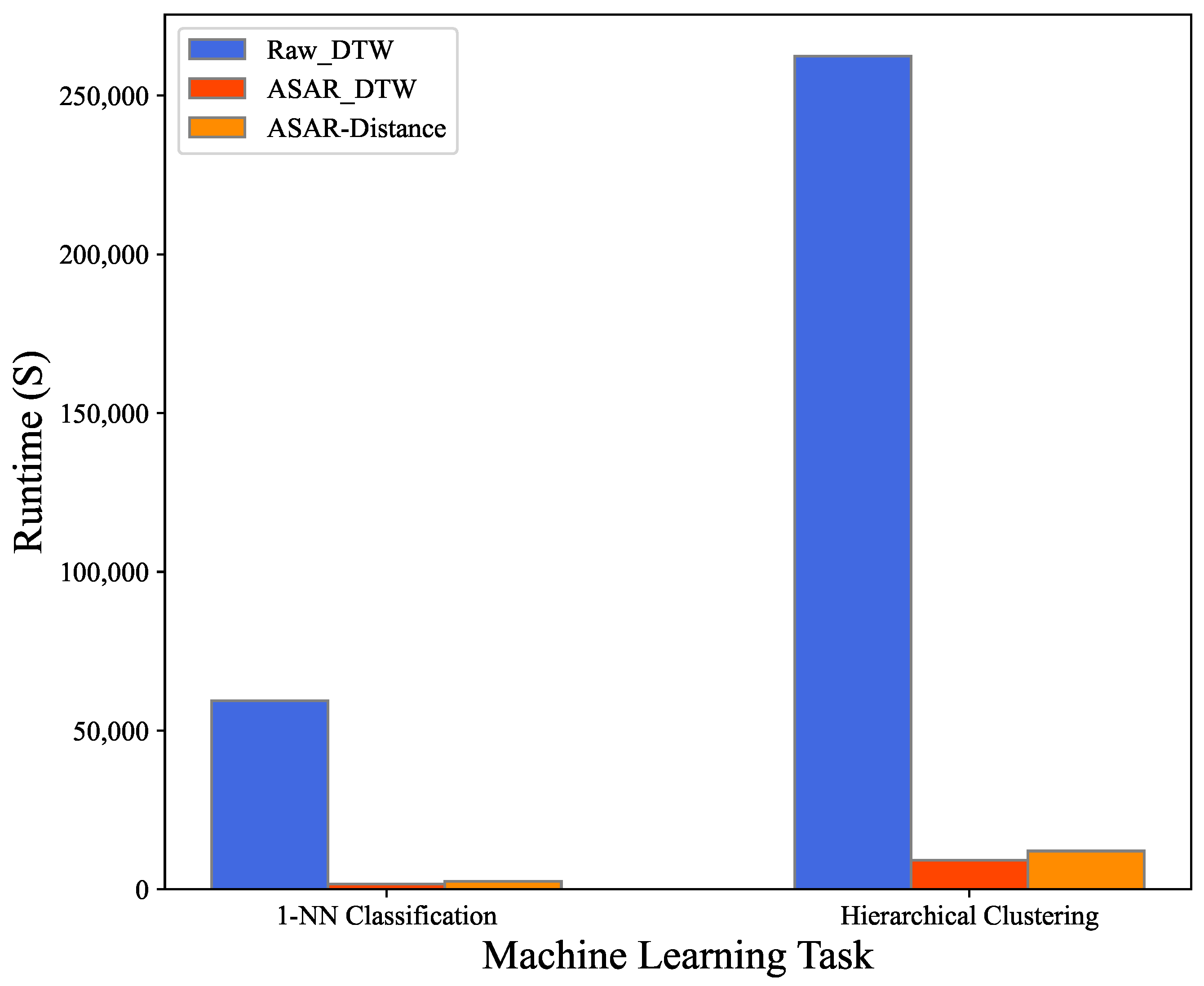
| 1-NN Classification | 182 | 59,439 | 19 | 1642 | 2556 |
| Hierarchical Clustering | 807 | 262,376 | 71 | 9217 | 12,081 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bawaneh, M.; Simon, V. Novel Method for Speeding Up Time Series Processing in Smart City Applications. Smart Cities 2022, 5, 964-978. https://doi.org/10.3390/smartcities5030048
Bawaneh M, Simon V. Novel Method for Speeding Up Time Series Processing in Smart City Applications. Smart Cities. 2022; 5(3):964-978. https://doi.org/10.3390/smartcities5030048
Chicago/Turabian StyleBawaneh, Mohammad, and Vilmos Simon. 2022. "Novel Method for Speeding Up Time Series Processing in Smart City Applications" Smart Cities 5, no. 3: 964-978. https://doi.org/10.3390/smartcities5030048
APA StyleBawaneh, M., & Simon, V. (2022). Novel Method for Speeding Up Time Series Processing in Smart City Applications. Smart Cities, 5(3), 964-978. https://doi.org/10.3390/smartcities5030048







