Discretization of Digital Controllers Comprising Second-Order Notch Filters

Abstract

Second-order notch filters (NFs) with constant coefficients are often used as part of feedback controllers in grid-connected power conversion systems to prevent unwanted harmonic content polluting the closed control loops. In practice, the value of the mains frequency resides within a certain known range rather than remaining constant. Hence, the correct selection of NF coefficients is crucial for ensuring that the desired performance is maintained within the whole expected mains frequency range. Bilinear transformation (BLT) with notch frequency prewarping is often adopted to convert an NF from a continuous to a digital form. While accurately preserving the notch frequency location, the method reduces the filter bandwidth. As a remedy, BLT with both notch frequency and damping ratio prewarping may be employed. Nevertheless, some inaccuracy remains under low sampling-to-notch frequency ratios. This technical note demonstrates that the issue may be solved by prewarping the boundary values of the expected harmonic frequency range rather than the notch frequency and/or damping factor before applying the BLT. Simulation results accurately support the presented issue and proposed solution.

1. Introduction

Notch filters are often employed in flexible mechatronic systems to suppress resonances [1,2,3,4,5,6,7,8,9,10] and mains-connected power electronic systems to cope with multiples of mains frequency harmonics [11,12,13,14,15,16]. Power grid interfacing energy conversion systems are required to comply with different power quality standards (e.g., IEC 61000, IEEE 519, etc.) when exchanging the current with the mains [17]. In particular, the mains current should follow a corresponding voltage shape (typically sinusoidal with some inevitable harmonic content). As a result, the power exchanged with the grid contains both DC and pulsating components. Consequently, real-time controllers directing the energy conversion system operation often comprise one (or several) second-order notch filter (NF) to minimize the influence of pulsating power components on closed-loop control performance [18,19,20,21,22]. The situation is further complicated by the fact that mains frequency does not remain constant, residing within a certain range around the nominal value [23]. Hence, the attenuation attained by the NF should be sufficient within the whole relevant frequency range. On the other hand, the sampling time should be reduced as much as possible to allow for low-cost digital controller implementation while accommodating all the necessary operations within a single sampling period. Nevertheless, NF discretization accuracy issues under low sampling-to-notch frequency ratios have been identified in the literature [24,25,26,27], and some remedies were proposed (e.g., prewarping of both the notch frequency and damping factor of the filter) [28,29]. Yet, this technical note demonstrates that some inaccuracy remains when bilinear transform (BLT)-based discretization [30] under ultra-low sampling-to-notch frequency ratios is carried out. To solve this issue, an alternative prewarping method is suggested, allowing the digital NF to accurately attain the desired attenuation within a prescribed bandwidth. Existing accuracy issues and the proposed methodology are validated by simulations.

2. Notch Filter Under Consideration

In this work, single second-order NF-based linear controllers for grid-connected converters of the Laplace domain form [31]

$$C(s)=C_1(s)F(s)$$

(1)

are considered for brevity (yet without loss of generality since a multi-notch structure would be typically realized by, e.g., cascaded connection of single-notch second-order sections), where C₁(s) denotes the stabilizing term (e.g., of P, PD, PI or PID type), and F(s) represents a second-order NF tuned to a certain (e.g., second [32]) mains frequency harmonic, typically present in the DC link voltage of unity power factor operating single-phase grid-interfacing power converters [33]. Discretization methods of the C₁(s) term have been widely studied in the literature (see, e.g., [34,35,36,37]) and are thus not included in this work. Thus, only the discretization of a generalized second-order NF given by

$$F(s)={\displaystyle \frac{s^2+{\omega }_f^2}{s^2+2{\xi }_f{\omega }_{f}s+{\omega }_f^2}}$$

(2)

with ω_f and ξ_f denoting corresponding notch frequency and damping factor, respectively, is discussed thereafter. While C₁(s) controls both the DC gain and crossover frequency of the control loop, the NF influences the certain harmonic frequency residing either within or outside the control bandwidth without affecting the two above-mentioned performance merits, since F(0) = F(∞) = 1. Meanwhile, the value of the mains frequency in practical power grids resides within a well-defined range rather than remaining constant [23]. Consequently, the NF should be designed to attain the required attenuation within the whole frequency range of interest (defined thereafter as [ω₁,ω₂]). In general, the requirement may be formulated as

$$\begin{array}{cc}\left|F(\omega )\right|\le G(\omega ),& {\omega }_1<\omega <{\omega }_2\end{array}$$

(3)

with G(ω) denoting the required attenuation envelope (typically linear in logarithmic scale [38,39]). In case the notch frequency in (2) is placed so that

$${\omega }_1<{\omega }_f<{\omega }_2$$

(4)

the constraint (3) reduces to

$$\begin{array}{cc}\left|F({\omega }_1)\right|\le G({\omega }_1)\triangleq G_1,& \left|F({\omega }_2)\right|\le G({\omega }_2)\triangleq G_2\end{array}$$

(5)

due to NF properties, as shown in Figure 1. Moreover, the required attenuation envelope (cf. (3)) is usually a monotonically increasing function of frequency [33], so that G₁ < G₂ is expected in practice (yet a generalized case is assumed in the subsequent discussion for the sake of completeness).

Noticing that the magnitude frequency response of the NF in (2) is given by

$$\left|F(\omega )\right|=\left|{\displaystyle \frac{1}{\sqrt{1+4{\xi }_f^2\frac{{\left(\omega {\omega }_f\right)}^2}{{\left({\omega }_f^2-{\omega }^2\right)}^2}}}}\right|$$

(6)

combining (5) with (6) yields two boundary conditions given by

$$\begin{array}{cc}\left|{\displaystyle \frac{1}{\sqrt{1+4{\xi }_f^2\frac{{\left({\omega }_1{\omega }_f\right)}^2}{{\left({\omega }_f^2-{\omega }_1^2\right)}^2}}}}\right|=G_1,& \left|{\displaystyle \frac{1}{\sqrt{1+4{\xi }_f^2\frac{{\left({\omega }_2{\omega }_f\right)}^2}{{\left({\omega }_f^2-{\omega }_2^2\right)}^2}}}}\right|=G_2\end{array}$$

(7)

Solving (7), the required notch frequency and damping factor of the NF in (2) are obtained as functions of the requirements in (5) as

$${\omega }_f={\omega }_2\sqrt{{\displaystyle \frac{1+\frac{{\omega }_1}{{\omega }_2}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}{1+\frac{{\omega }_2}{{\omega }_1}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}}}={\omega }_1\sqrt{{\displaystyle \frac{1+\frac{{\omega }_2}{{\omega }_1}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}{1+\frac{{\omega }_1}{{\omega }_2}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}}}$$

(8)

and

$${\xi }_f={\displaystyle \frac{1}{2}}\sqrt{G_1^{-2}-1}\left(\sqrt{{\displaystyle \frac{1+\frac{{\omega }_2}{{\omega }_1}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}{1+\frac{{\omega }_1}{{\omega }_2}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}}}-\sqrt{{\displaystyle \frac{1+\frac{{\omega }_1}{{\omega }_2}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}{1+\frac{{\omega }_2}{{\omega }_1}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}}}\right)$$

(9)

respectively. It is interesting to note that in the case

$$G_1=G_2=G_0$$

(10)

The notch frequency is the geometric mean of the expected harmonic frequency range boundary values

$${\omega }_f=\sqrt{{\omega }_1{\omega }_2}\triangleq {\omega }_{f0}$$

(11)

with the corresponding damping factor given by

$${\xi }_f={\displaystyle \frac{1}{2}}\sqrt{G_0^{-2}-1}{\displaystyle \frac{{\omega }_2-{\omega }_1}{{\omega }_{f0}}}\triangleq {\xi }_{f0}.$$

(12)

Consequently, the following notch frequency location shift is expected if G₁ ≠ G₂,

$$\begin{array}{cc}{G}_1<G_2\Rightarrow {\omega }_f<{\omega }_{f0},& G_1>G_2\Rightarrow {\omega }_f>{\omega }_{f0}\end{array}$$

(13)

Substituting (8) and (9) into (2), the transfer function in (2) may be reformulated as a function of constraints in (5), namely

$$F(s)={\displaystyle \frac{s^2+\frac{1+\frac{{\omega }_2}{{\omega }_1}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}{1+\frac{{\omega }_1}{{\omega }_2}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}{\omega }_1^2}{s^2+\sqrt{G_1^{-2}-1}\left(\frac{1+\frac{{\omega }_2}{{\omega }_1}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}{1+\frac{{\omega }_1}{{\omega }_2}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}-1\right){\omega }_{1}s+\frac{1+\frac{{\omega }_2}{{\omega }_1}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}{1+\frac{{\omega }_1}{{\omega }_2}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}{\omega }_1^2}}$$

(14)

3. Discretization Issues

As an example, consider the case presented in [39], where the NF in (2) is employed in a grid-interfacing AC/DC power converter as part of a DC link voltage controller to attenuate the magnitude of a second mains frequency harmonic inevitably entering the control loop. This is required to keep the total harmonic distortion of the grid-side current below a certain value (namely, 5%). A nominal grid frequency of 50 Hz with $\pm$2% uncertainty is considered so that (cf. (3)) (an interested reader is referred to [39] for further details).

$$2\pi \cdot 98={\omega }_1<\omega \hspace{0.17em}[rad/s]<{\omega }_2=2\pi \cdot 102$$

(15)

The required filter gain values at boundary frequencies (cf. (5)) were obtained in [35] as

$$\begin{array}{cc}\left|F({\omega }_1)\right|=0.0867=-21.24[dB],& \left|F({\omega }_2)\right|=0.0902=-20.89[dB].\end{array}$$

(16)

Substituting (15) and (16) into (8) and (9) yields

$$\begin{array}{cc}{\omega }_f=2\pi \cdot 99.94[rad/s],& {\xi }_f=0.2252.\end{array}$$

(17)

The resulting continuous transfer function of the NF in (2) is then given by

$$F(s)={\displaystyle \frac{s^2+3.943\cdot {10}^5}{s^2+282.9s+3.943\cdot {10}^5}}.$$

(18)

In the subsequent discussion, the sampling interval is denoted as T_s[s]. The corresponding angular frequency is then defined by

$${\omega }_s={\displaystyle \frac{2\pi }{T_s}}[rad/s]$$

(19)

3.1. Discretization by Notch Frequency Prewarping

Prewarping the notch frequency, there is

$${\omega }_{fp}=\left({\pi }^{-1}{\displaystyle \frac{{\omega }_s}{{\omega }_f}}\tan \left(\pi {\displaystyle \frac{{\omega }_f}{{\omega }_s}}\right)\right){\omega }_f.$$

(20)

Defining the sampling-to-notch frequency ratio as

$$r={\omega }_s/{\omega }_f,$$

(21)

The expression for the prewarped notch frequency in (20) may be rewritten as

$${\omega }_{fp}=\left({\displaystyle \frac{r}{\pi }}\tan \left({\displaystyle \frac{\pi }{r}}\right)\right){\omega }_f.$$

(22)

Substituting ω_f in (2) with ω_fp in (22) and applying the BLT defined by [30,40]

$$s={\displaystyle \frac{2}{T_s}}{\displaystyle \frac{z-1}{z+1}}={\displaystyle \frac{{\omega }_s}{\pi }}{\displaystyle \frac{z-1}{z+1}},$$

(23)

the corresponding digital filter is obtained as

$$F(z)={\displaystyle \frac{{\left(\frac{{\omega }_s}{\pi }\frac{z-1}{z+1}\right)}^2+{\left(\frac{{\omega }_s}{\pi }\tan \left(\pi \frac{{\omega }_f}{{\omega }_s}\right)\right)}^2}{{\left(\frac{{\omega }_s}{\pi }\frac{z-1}{z+1}\right)}^2+2{\xi }_f{\left(\frac{{\omega }_s}{\pi }\right)}^2\tan \left(\pi \frac{{\omega }_f}{{\omega }_s}\right)\frac{z-1}{z+1}+{\left(\frac{{\omega }_s}{\pi }\tan \left(\pi \frac{{\omega }_f}{{\omega }_s}\right)\right)}^2}}.$$

(24)

The magnitude frequency responses of the continuous NF in (18) and the digital NF in (24) for different values of r are depicted in Figure 2, with values of gains at boundary frequencies of interest summarized in

Table 1. Analog vs. digital (BLT with prewarped notch frequency) filter performances for different sampling-to-notch frequency ratios.

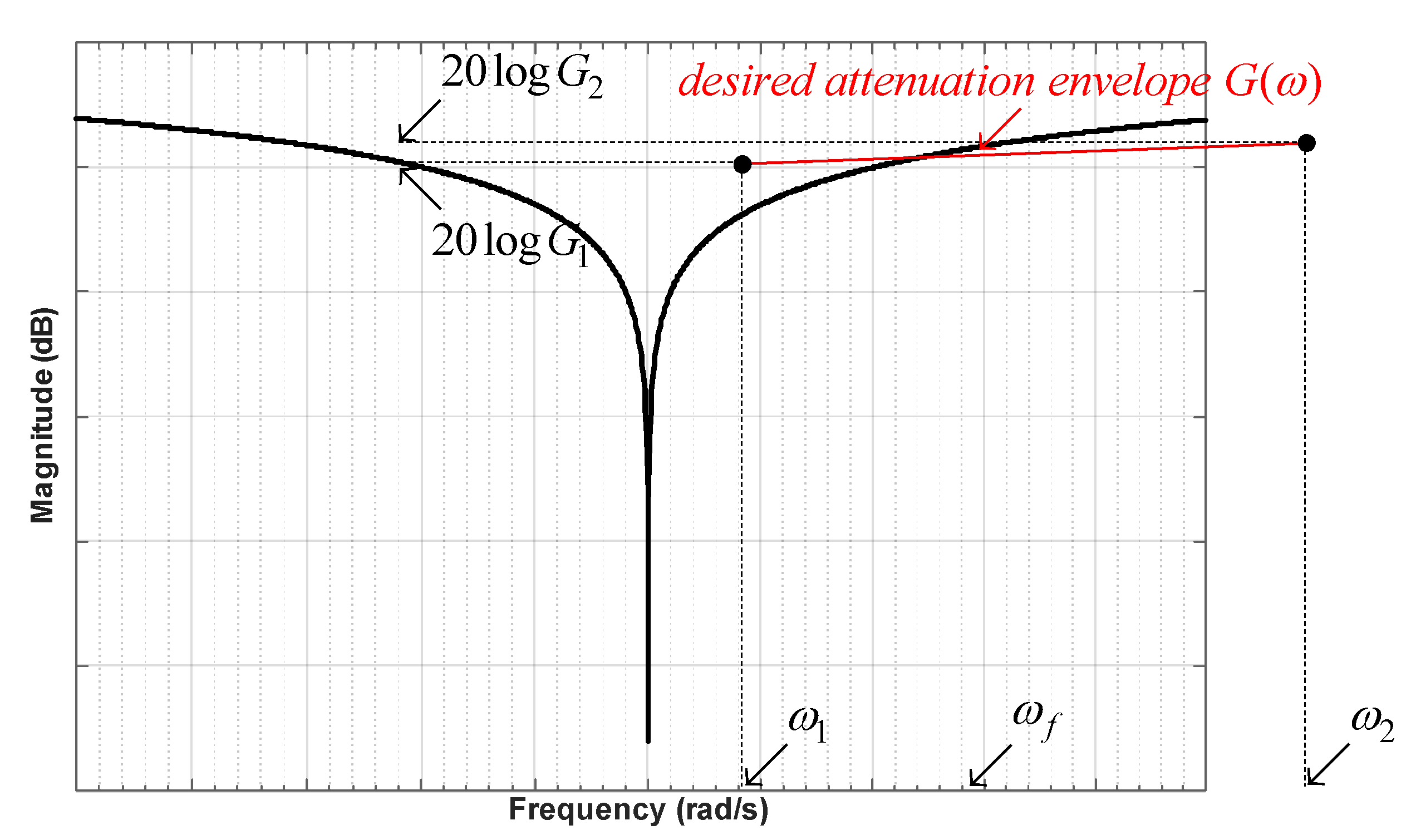
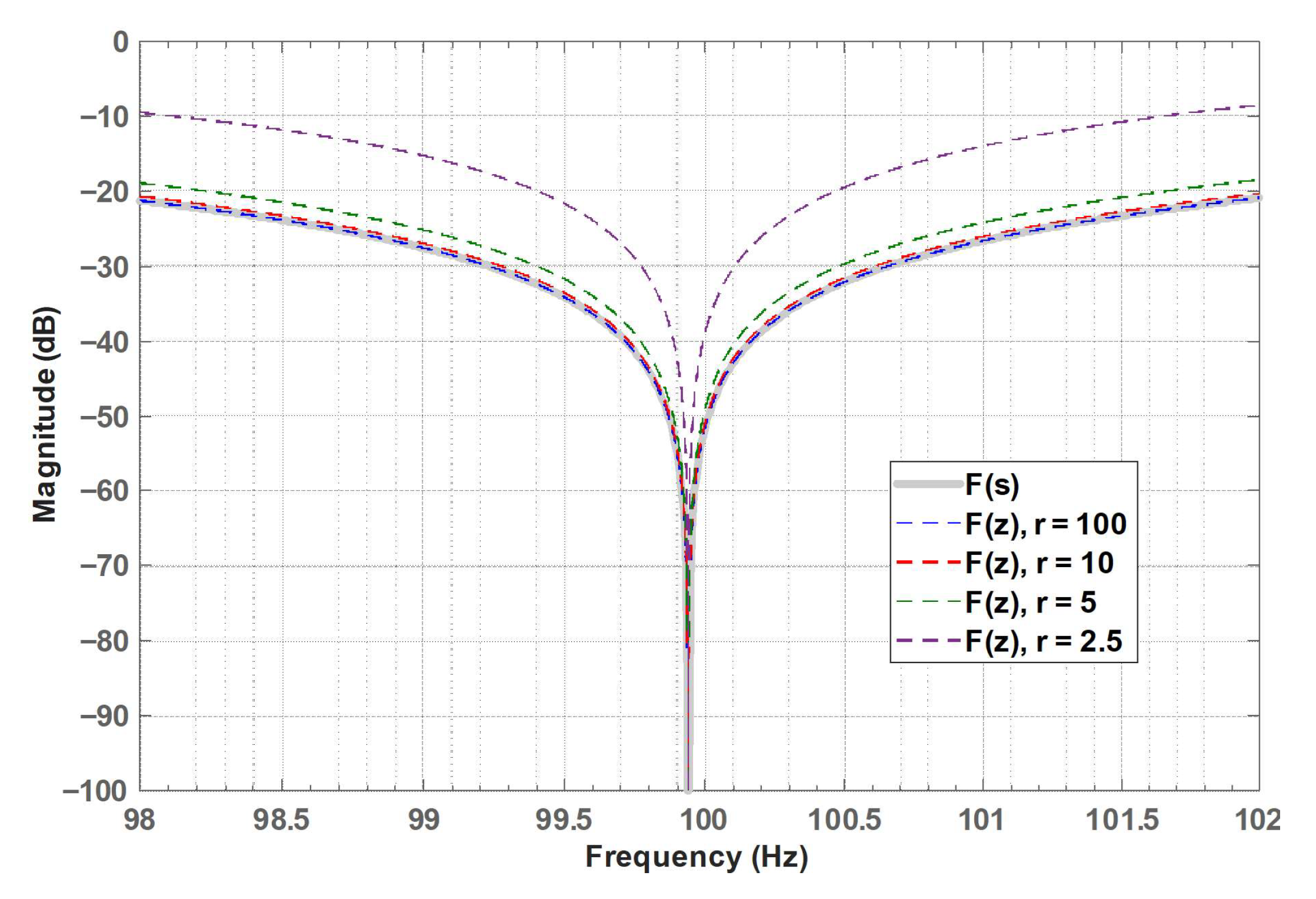
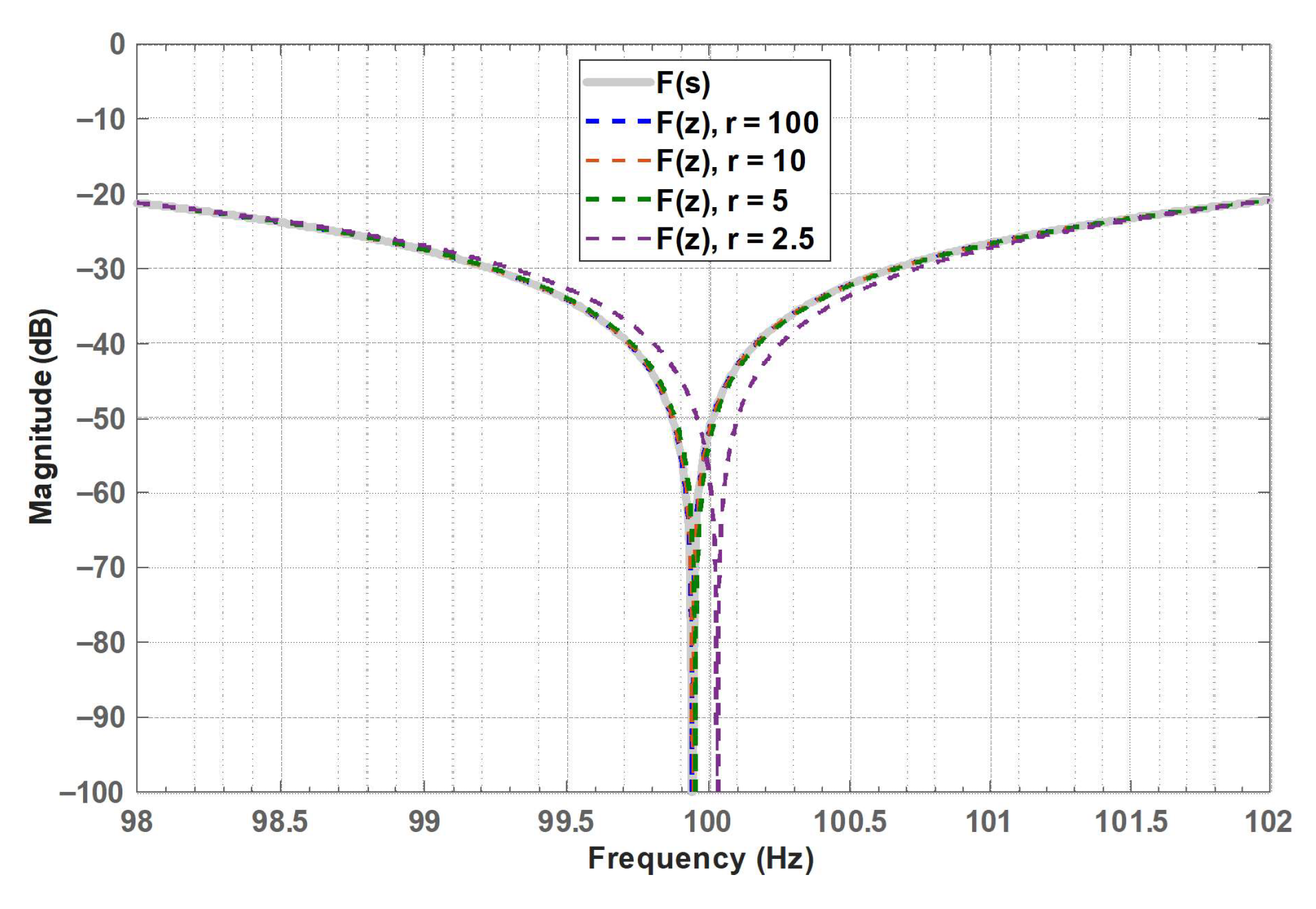
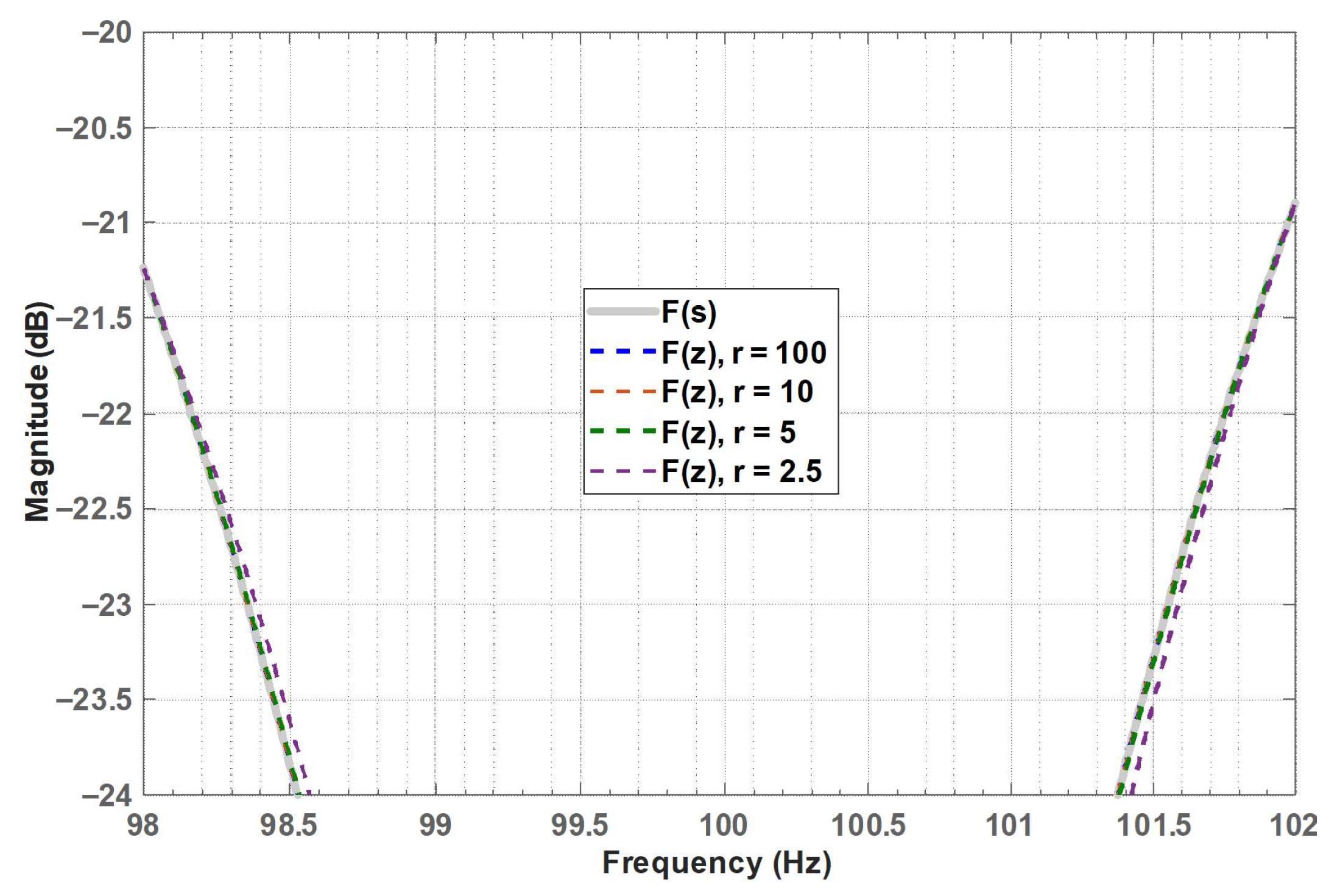
	Analog	r = 100	r = 10	r = 5	r = 2.5
G1 [dB]	−21.2	−21.2	−20.7	−18.9	−9.5
G2 [dB]	−20.9	−20.9	−20.3	−18.4	−8.5

. It may be concluded that while the digital filter matches well with its continuous counterpart for r > 10, a reduction in the sampling-to-notch frequency ratio below 10 yields significant bandwidth narrowing even though the notch frequency is accurately preserved.

3.2. Discretization by Notch Frequency and Damping Factor Prewarping

To improve the discretization accuracy under low sampling-to-notch frequency ratios, it was suggested in [28,29] to prewarp the filter damping factor as

$${\xi }_{fp}={\displaystyle \frac{{\omega }_f}{\sin \left({\omega }_f{T}_s\right)}}{\xi }_f$$

(25)

in addition to the notch frequency prewarping in (20). Applying the BLT in (23) to (2) with ω_f and ξ_f substituted with ω_fp in (22) and ξ_fp in (25), respectively, the corresponding digital filter is obtained as

$$F(z)={\displaystyle \frac{{\left(\frac{{\omega }_s}{\pi }\frac{z-1}{z+1}\right)}^2+{\left(\frac{{\omega }_s}{\pi }\tan \left(\pi \frac{{\omega }_f}{{\omega }_s}\right)\right)}^2}{{\left(\frac{{\omega }_s}{\pi }\frac{z-1}{z+1}\right)}^2+2\frac{{\omega }_f}{\sin \left(2\pi \frac{{\omega }_f}{{\omega }_s}\right)}{\xi }_f{\left(\frac{{\omega }_s}{\pi }\right)}^2\tan \left(\pi \frac{{\omega }_f}{{\omega }_s}\right)\frac{z-1}{z+1}+{\left(\frac{{\omega }_s}{\pi }\tan \left(\pi \frac{{\omega }_f}{{\omega }_s}\right)\right)}^2}}.$$

(26)

The magnitude frequency responses of the continuous NF in (18) and the digital NF in (26) for different values of r are depicted in Figure 3, with values of gains at boundary frequencies of interest summarized in

Table 2. Analog vs. digital (BLT with prewarped notch frequency and damping factor) filter performances for different sampling-to-notch frequency ratios.

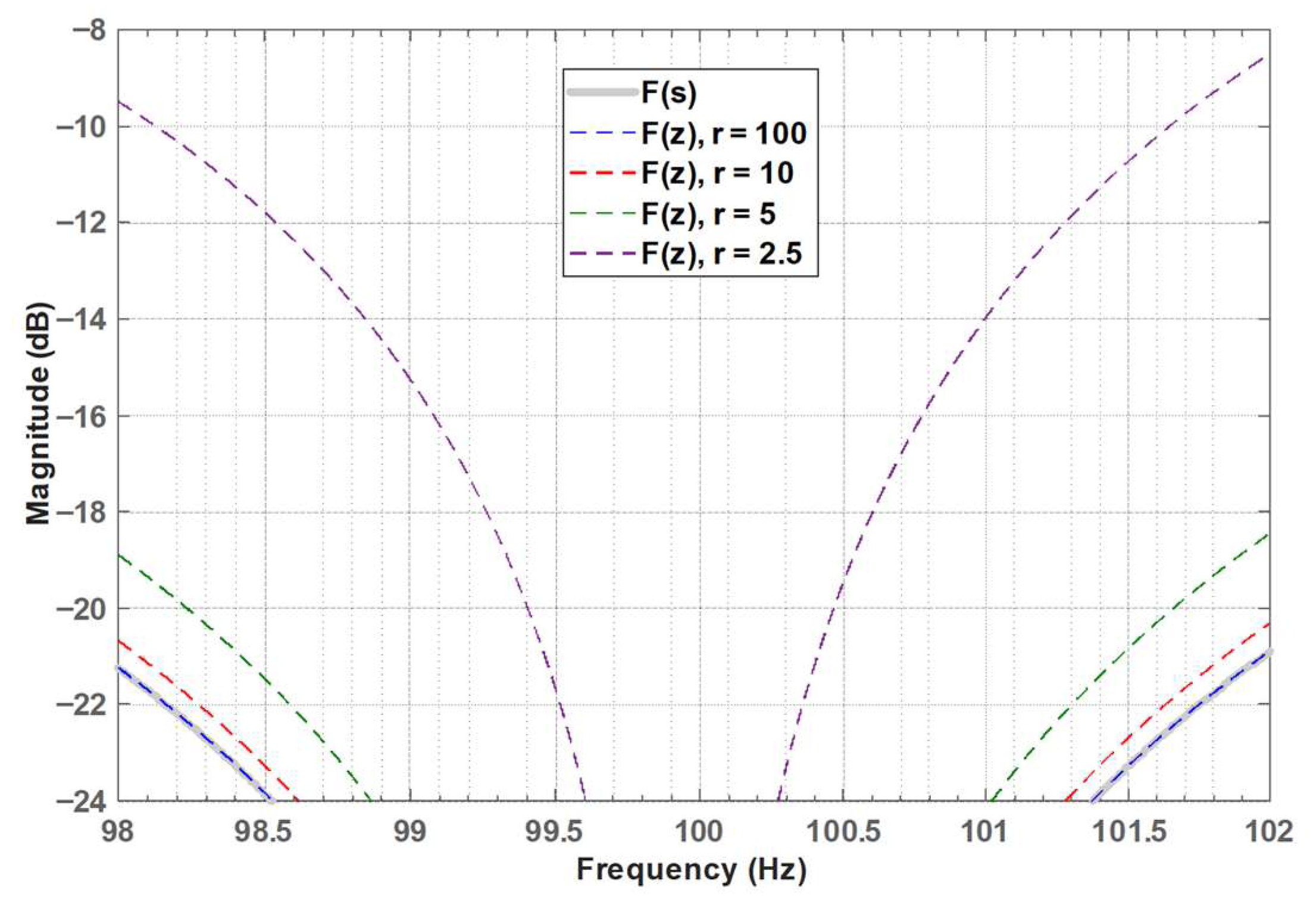
	Analog	r = 100	r = 10	r = 5	r = 2.5
G1 [dB]	−21.2	−21.2	−21.25	−21.3	−21.6
G2 [dB]	−20.9	−20.9	−20.88	−20.84	−20.45

. It may be concluded that while the digital filter matches well with its continuous counterpart for r > 5, a reduction in the sampling-to-notch frequency ratio to 2.5 yields a slight notch frequency shift, accompanied with a gain decrease at sub-resonant frequencies and a gain increase at super-resonant frequencies. As the result, the filter overperforms at ω₁ and underperforms at ω₂.

3.3. Discretization by Boundary Frequency Prewarping

To solve the above-demonstrated issue of the discretization accuracy under ultra-low sampling-to-notch frequency ratios, it is proposed to prewarp the boundary values of the relevant bandwidth of interest rather than the notch frequency and damping factor, i.e.,

$$\begin{array}{cc}{\omega }_{1p}=\left({\pi }^{-1}{\displaystyle \frac{{\omega }_s}{{\omega }_1}}\tan \left(\pi {\displaystyle \frac{{\omega }_1}{{\omega }_s}}\right)\right){\omega }_1,& {\omega }_{2p}=\left({\pi }^{-1}{\displaystyle \frac{{\omega }_s}{{\omega }_2}}\tan \left(\pi {\displaystyle \frac{{\omega }_2}{{\omega }_s}}\right)\right){\omega }_2.\end{array}$$

(27)

Applying the BLT in (23) to (14) with ω₁ and ω₂ substituted with ω_1p and ω_2p in (27), respectively, the corresponding digital filter is obtained as

$$F(z)={\displaystyle \frac{{\left(\frac{{\omega }_s}{\pi }\frac{z-1}{z+1}\right)}^2+\frac{1+\frac{\frac{{\omega }_s}{\pi }\tan \left(\pi \frac{{\omega }_2}{{\omega }_s}\right)}{\frac{{\omega }_s}{\pi }\tan \left(\pi \frac{{\omega }_1}{{\omega }_s}\right)}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}{1+\frac{\frac{{\omega }_s}{\pi }\tan \left(\pi \frac{{\omega }_1}{{\omega }_s}\right)}{\frac{{\omega }_s}{\pi }\tan \left(\pi \frac{{\omega }_2}{{\omega }_s}\right)}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}{\left(\frac{{\omega }_s}{\pi }\tan \left(\pi \frac{{\omega }_1}{{\omega }_s}\right)\right)}^2}{{\left(\frac{{\omega }_s}{\pi }\frac{z-1}{z+1}\right)}^2+A\frac{z-1}{z+1}+\frac{1+\frac{\frac{{\omega }_s}{\pi }\tan \left(\pi \frac{{\omega }_2}{{\omega }_s}\right)}{\frac{{\omega }_s}{\pi }\tan \left(\pi \frac{{\omega }_1}{{\omega }_s}\right)}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}{1+\frac{\frac{{\omega }_s}{\pi }\tan \left(\pi \frac{{\omega }_1}{{\omega }_s}\right)}{\frac{{\omega }_s}{\pi }\tan \left(\pi \frac{{\omega }_2}{{\omega }_s}\right)}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}{\left(\frac{{\omega }_s}{\pi }\tan \left(\pi \frac{{\omega }_1}{{\omega }_s}\right)\right)}^2}},$$

(28)

with

$$A=\sqrt{G_1^{-2}-1}\left({\displaystyle \frac{1+\frac{\frac{{\omega }_s}{\pi }\tan \left(\pi \frac{{\omega }_2}{{\omega }_s}\right)}{\frac{{\omega }_s}{\pi }\tan \left(\pi \frac{{\omega }_1}{{\omega }_s}\right)}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}{1+\frac{\frac{{\omega }_s}{\pi }\tan \left(\pi \frac{{\omega }_1}{{\omega }_s}\right)}{\frac{{\omega }_s}{\pi }\tan \left(\pi \frac{{\omega }_2}{{\omega }_s}\right)}\sqrt{\frac{G_1^{-2}-1}{G_2^{-2}-1}}}}-1\right){\left({\displaystyle \frac{{\omega }_s}{\pi }}\right)}^2\tan \left(\pi {\displaystyle \frac{{\omega }_1}{{\omega }_s}}\right).$$

(29)

Magnitude frequency responses of the continuous NF in (18) and the digital NF in (28) for different values of r are depicted in Figure 4, with values of gains at boundary frequencies of interest summarized in

Table 3. Analog vs. digital (BLT with prewarped boundary frequencies) filter performances for different sampling-to-notch frequency ratios.

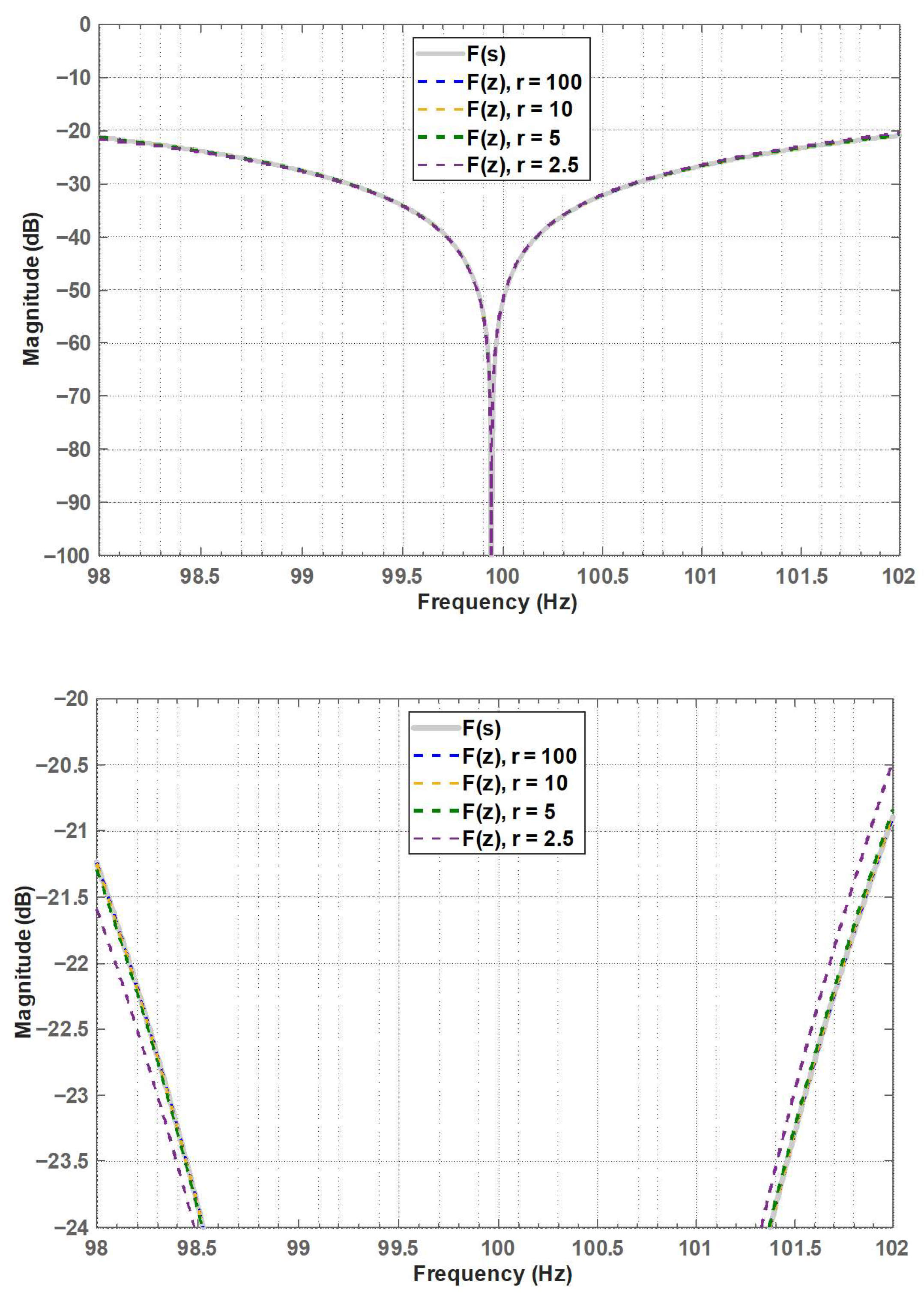
	Analog	r = 100	r = 10	r = 5	r = 2.5
G1 [dB]	−21.2	−21.2	−21.2	−21.2	−21.2
G2 [dB]	−20.9	−20.9	−20.9	−20.9	−20.9

. It is evident that despite the noticeable notch frequency shift at r = 2.5, the constraints in (16) are accurately met for all values of r, as desired.

4. Simulations

To validate both the revealed issue and the proposed solution, the worst case of r ≈ 2.5 (i.e., angular sampling frequency of ω_s = 2π∙250 rad/s) was examined by simulations using PSIM 2025 software.

The discretization of (18) by BLT with notch frequency prewarping (cf. (22)) yields a digital filter given by (cf. (24))

$$F_{d1}(z)={\displaystyle \frac{0.8829z^2+1.427z+0.8829}{z^2+1.427z+0.7657}}.$$

(30)

The discretization of (18) by BLT with notch frequency and damping factor prewarping (cf. (20), (25)) yields a digital filter given by (cf. (26))

$$F_{d2}(z)={\displaystyle \frac{0.6387z^2+1.032z+0.6387}{z^2+1.032z+0.2773}}.$$

(31)

The discretization of (18) by BLT with boundary frequency prewarping (cf. (27)) yields a digital filter of the following form (cf. (28)),

$$F_{d3}(z)={\displaystyle \frac{0.6381z^2+1.033z+0.6381}{z^2+1.033z+0.2761}}$$

(32)

Within the simulation framework (carried out at 1 μs step), unity magnitude sinusoids at different frequencies residing withing the range defined in (15) (at 1 Hz increments) were concurrently applied to the continuous filter, F(s) (cf. (18)), and the three digital filters, F_d1(z) F_d2(z) and F_d3(z) (cf. (30)–(32), respectively. Corresponding steady-state responses are depicted in Figure 5 (black waveforms are the continuous filter outputs), with the resulting filter gains summarized in

Table 4. Summary of steady-state filter gains at different frequencies within the range (14) for r ≈ 2.5.

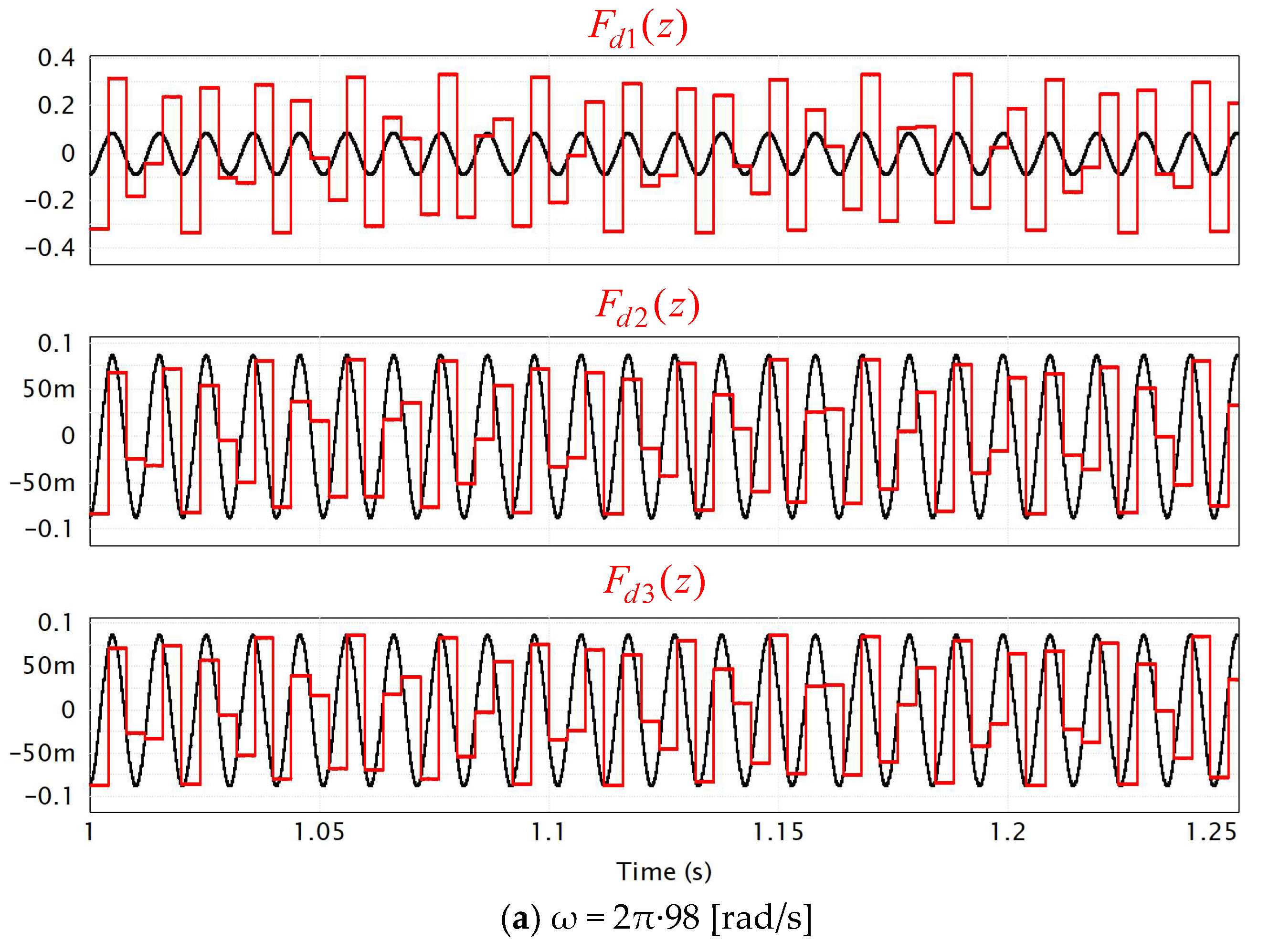
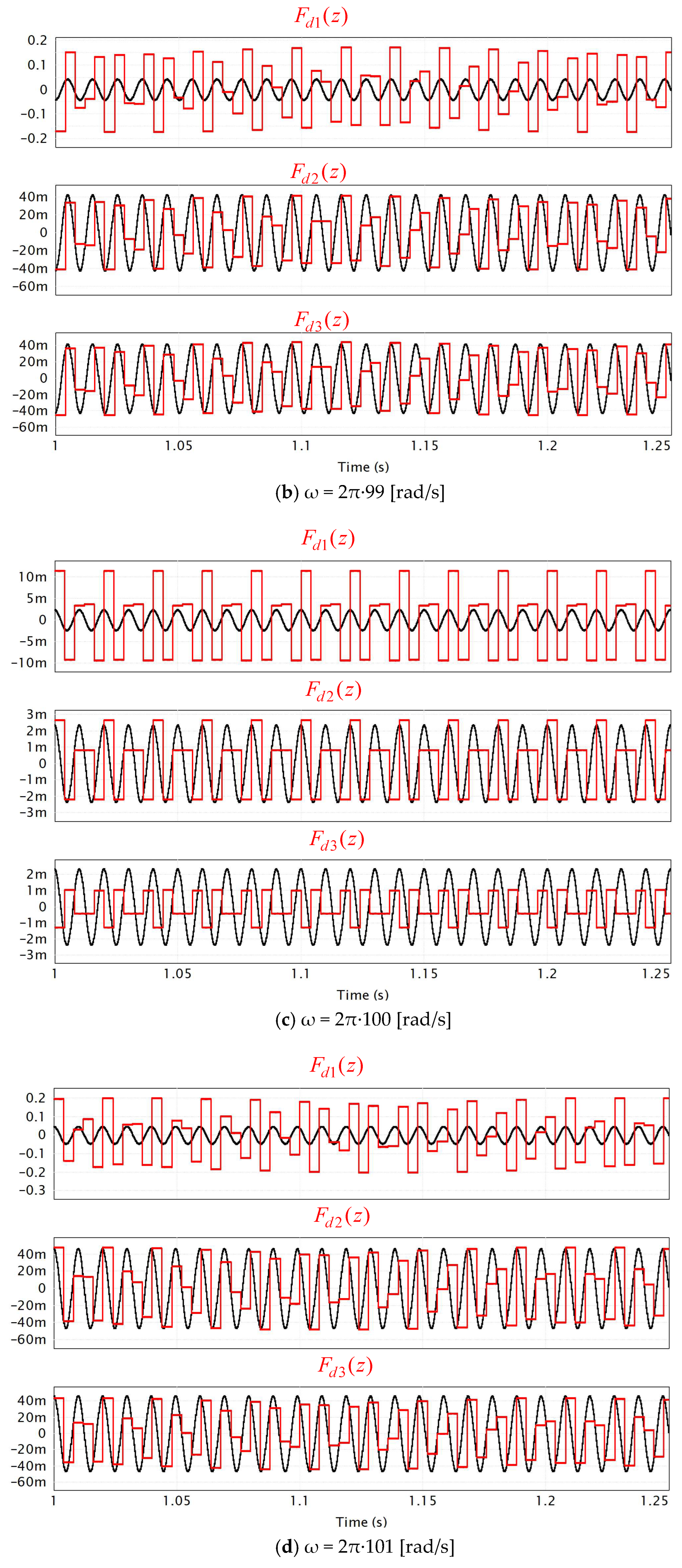
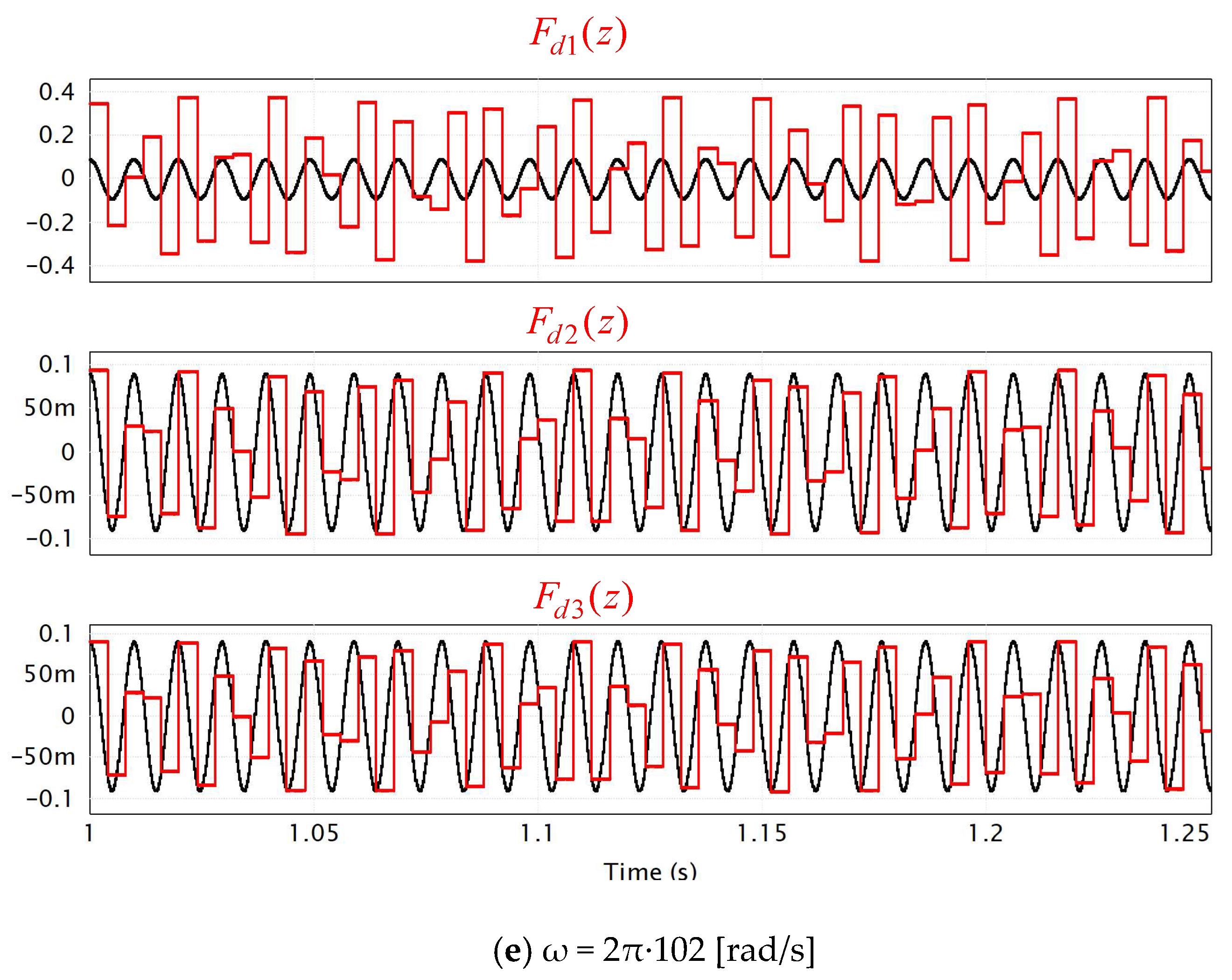
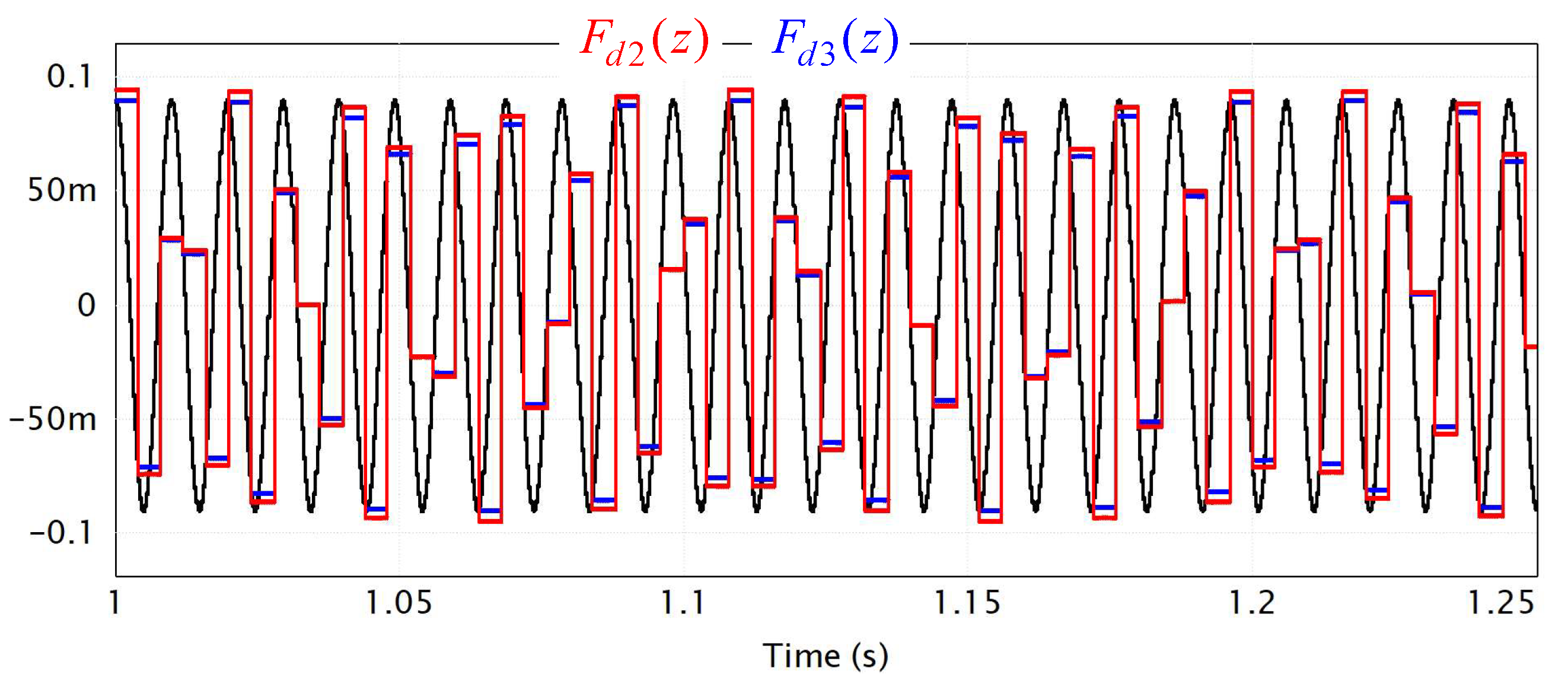
ω [rad/s]	2π∙98	2π∙99	2π∙100	2π∙101	2π∙102
F(s)	0.087	0.042	0.0026	0.047	0.09
Fd1(z)	0.336	0.172	0.012	0.2	0.376
Fd2(z)	0.083	0.041	0.0027	0.048	0.095
Fd3(z)	0.087	0.045	0.0012	0.044	0.09

. It is evident that steady-state time-domain responses accurately match corresponding analytical frequency-domain predictions (cf. Figure 2, Figure 3 and Figure 4 and Table 1, Table 2 and Table 3).

While the digital NF F_d1(z) obtained by the BLT with notch frequency prewarping is unable to meet either of the constraints in (15), its counterpart F_d2(z) created by the BLT with notch frequency and damping factor prewarping slightly overperforms at sub-resonant frequencies while underperforming at super-resonant frequencies, as expected. On the other hand, the digital NF F_d2(z) obtained by the BLT with the proposed boundary frequency prewarping accurately complies with both constraints in (15), even though its notch frequency does not match that of the continuous template. In order to further verify the difference between the performances of F_d2(z) and F_d3(z) at ω₂, corresponding responses were superimposed along with the response of F(s) in Figure 6. It is evident that while the magnitude of the F_d2(z) response slightly exceeds that of F(s), the response of F_d3(z) corresponds to that of F(s), as desired. Consequently, the discretization of the second-order NF by the BLT with notch frequency and/or damping ratio prewarping should be avoided under ultra-low sampling-to-notch frequency ratios, and boundary frequency prewarping should be adopted instead.

5. Conclusions

In this technical note, we demonstrated that adopting the bilinear transformation with notch frequency and/or dampling factor prewarping to convert an NF from a continuous to digital form results in some inaccuracy (~0.5 dB at super-resonant range) under low sampling-to-notch frequency ratios. Such an outcome may not be tolerable when the NF is employed within a real-time digital controller to attenuate certain harmonics residing within a defined frequency range. It was then suggested to resolve the issue by prewarping the boundary values of the frequency range of interest (instead of notch frequency and dampling factor) prior to applying the BLT. The simulation results accurately validated the proposed solution. Future work on this subject includes the experimental validation of the proposed methodology.