Explainable AI-Based Clinical Signal Analysis for Myocardial Infarction Classification and Risk Factor Interpretation

Abstract

Myocardial infarction (MI) remains one of the most critical causes of death worldwide, demanding predictive models that balance accuracy with clinical interpretability. This study introduces an explainable artificial intelligence (XAI) framework that integrates least absolute shrinkage and selection operator (LASSO) regression for feature selection, logistic regression for prediction, and Shapley additive explanations (SHAP) for interpretability. Using a dataset of 918 patients and 12 signal-derived clinical variables, the model achieved an accuracy of 87.7%, a recall of 0.87, and an F1 score of 0.89, confirming its robust performance. The key risk factors identified were age, fasting blood sugar, ST depression, flat ST slope, and exercise-induced angina, while the maximum heart rate and upward ST slope served as protective factors. Comparative analyses showed that the SHAP and p-value methods largely aligned, consistently highlighting ST_Slope_Flat and ExerciseAngina_Y, though discrepancies emerged for ST_Slope_Up, which showed limited statistical significance but high SHAP contribution. By combining predictive strength with transparent interpretation, this study addresses the black-box limitations of conventional models and offers actionable insights for clinicians. The findings highlight the potential of signal-driven XAI approaches to improve early detection and patient-centered prevention of MI. Future work should validate these models on larger and more diverse datasets to enhance generalizability and clinical adoption.

1. Introduction

Myocardial infarction (MI) is one of the leading causes of death globally, making early diagnosis and prevention critical. According to national cardiovascular disease statistics, the incidence rate of MI is 67.4 cases per 100,000 population, with 16.0% of patients dying within one year of occurrence [1,2]. Acute MI, in particular, is a life-threatening condition wherein coronary artery occlusion leads to myocardial necrosis, beginning within 30 min. As time progresses, the extent of necrosis increases, making it the main disease contributing to sudden adult death. Because ventricular fibrillation frequently occurs within the first hour following MI, early diagnosis and treatment are pivotal in improving patient survival rates [3,4,5,6]. Developing a risk prediction model for MI can enable early diagnosis and proactive preventive measures, thereby enhancing the responsiveness to critical situations [7].

Key risk factors for MI include age, gender, cholesterol levels, and hypertension [3,8,9]. By analyzing the relationships between these factors and MI occurrence, this study aims to identify significant contributing factors. Furthermore, by employing explainable artificial intelligence (XAI), the study explains the influence of key variables that are used in the prediction model, aiding both healthcare professionals and patients in understanding the predictions and improving the model’s reliability and performance.

Existing MI prediction models, despite the relatively extensive research that has been conducted in this area, have limited interpretability, which restricts their practical use in clinical settings [9,10,11,12,13,14,15]. This study seeks to enhance the interpretability of prediction models by utilizing XAI techniques to provide detailed explanations of how key variables impact MI predictions. XAI not only clarifies the rationale behind the model’s decision-making process but also supports medical professionals in making more informed decisions, thereby improving the model’s transparency and trustworthiness [4,16,17,18].

When datasets contain numerous risk factor variables, logistic regression models often face overfitting issues, leading to reduced predictive performance on new data [12]. To address this, this study employs the least absolute shrinkage and selection operator (LASSO) model, which effectively resolves overfitting by shrinking the coefficients of insignificant risk factors to exactly zero [12,19]. This approach allows the study to identify the most critical risk factors influencing the occurrence of MI, improving predictive accuracy for new datasets.

The contributions of this study can be summarized as follows:

• The application of the LASSO model to identify key risk factors for MI and angina while addressing overfitting issues, thereby enhancing the predictive performance on new data.
• The development of an XAI-based MI prediction model to overcome the limitations of low interpretability in existing models, providing detailed explanations of the influence of key variables and improving the model’s reliability, transparency, and practical utility.

2. Research Background

2.1. Related Works

Numerous studies on MI have been conducted across diverse fields [4,16,17,18,19,20]; in particular, undergraduate students have frequently analyzed MI as part of their course projects. Consequently, this paper aims to exclude undergraduate reports that are available online and focus on presenting research works that are published in SCI-level journals. These studies encompass a wide range of topics within the literature review and machine learning domains, as outlined below.

Jung et al. developed tailored risk prediction models for MI and ischemic stroke (IS) using health examination data from six million individuals in South Korea. To address the limitations of existing integrated cardiovascular risk prediction models, the researchers employed Cox proportional hazards models to construct 5-year risk prediction models. The analysis revealed that smoking, obesity, and dyslipidemia had a stronger influence on the risk of MI, whereas age and hypertension were identified as more critical factors for IS [14].

Park and Kim’s study utilized data from 166 patients, addressing the issue of imbalanced data distribution through the application of the Synthetic Minority Over-sampling Technique (SMOTE). Four machine learning algorithms—logistic regression, random forest, XGBoost, and multi-layer perceptron (MLP)—were implemented and comparatively analyzed. Among these, the MLP model demonstrated the highest performance with an accuracy of 97.05% and an F1 score of 0.80. However, all models exhibited low recall scores, highlighting their limitations in accurately predicting actual cases of acute myocardial infarction (AMI) [11].

Izabela Rojek et al. focused on developing an artificial intelligence (AI)-based tool to predict the risk of MI at an early stage for application in preventive medicine. The research team constructed a binary classification model utilizing patient characteristics such as sex, age, and chest pain type and compared the performance of various machine learning algorithms, including logistic regression, K-nearest neighbors (KNNs), random forest, and support vector classification (SVC). Among these, the logistic regression model demonstrated the highest performance with an accuracy of 88.5%, identifying key predictive factors such as chest pain type, exercise-induced angina, and resting blood pressure [20].

Yoo constructed and compared deep learning-based predictive models for acute MI using health examination data from the national health insurance service. Leveraging deep learning’s capability to handle large-scale data, recurrent neural networks such as long short-term memory (LSTM), gated recurrent unit (GRU), and the reverse time attention model (RETAIN) were employed. The LSTM model demonstrated the best performance, with an area under the curve (AUC) of 0.75 and an accuracy of 0.75. Notably, the RETAIN provided insights into the contribution of individual variables, addressing the “black-box” issue and showcasing the potential for using interpretable deep learning in healthcare [9].

Iim proposed a B-LASSO model to predict the occurrence of MI and angina and identify major risk factors using raw data from the sixth Korean national health and nutrition examination survey (2013–2015). The model exhibited superior predictive performance, achieving an AUC of 0.819 in validation data and thus outperforming traditional models such as LASSO and random forest (RF). The key risk factors identified included age, hypertension, and dyslipidemia [12].

2.2. Least Absolute Shrinkage and Selection Operator (LASSO) Model

The LASSO model is a regression analysis technique that simultaneously performs variable selection and regularization [12]. By applying L1 regularization, it penalizes the absolute values of regression coefficients, effectively reducing some coefficients to zero and thereby automatically selecting the most relevant variables [19]. LASSO is particularly useful in high-dimensional datasets or when the number of predictors exceeds the number of observations, as it maintains predictive performance while enhancing model interpretability through simplification [20].

In MI prediction models, LASSO was employed to identify the most critical factors among various physiological, environmental, and behavioral variables (e.g., age, sex, blood pressure, and cholesterol level). This approach enabled the removal of irrelevant variables, simplifying the model while preserving its predictive accuracy and preventing overfitting. Furthermore, the selected variables facilitated medical interpretability, allowing for an in-depth analysis of the primary factors contributing to MI. Utilizing LASSO in this context achieved a good predictive performance while creating a concise and efficient model.

2.3. Logistic Regression Model

Logistic regression is a supervised learning model that is designed for binary classification tasks, where the dependent variable takes on two possible outcomes (e.g., “yes/no,” “0/1”) [15,20,21]. While similar in structure to linear regression, the output of logistic regression is expressed as probabilities rather than continuous values. One of the primary advantages of logistic regression is its interpretability; the model’s coefficients provide insights into the importance of individual variables [20]. Additionally, it is computationally efficient, making it suitable for large datasets. Logistic regression is particularly well suited for binary classification problems and offers probabilistic outputs, which allow for the assessment of uncertainty in predictions [21].

In the context of MI prediction, logistic regression is an effective choice due to its ability to accurately classify binary outcomes, such as the presence or absence of MI. Its intuitive interpretability enables a clear understanding of the factors influencing the occurrence of MI, facilitating the development of prevention strategies. Furthermore, its computational efficiency and robust performance make it well suited for building predictive models based on complex medical data.

2.4. Shapley Additive Explanations (SHAP)

The SHAP method is designed to explain the predictions of machine learning models by quantifying and visualizing the contribution of each feature to the prediction [4,5,18]. Based on the Shapley values from game theory, SHAP ensures a fair distribution of contributions among all features, providing clear insights into the reasons behind specific model predictions [18]. SHAP calculates the contribution of each feature by considering all possible combinations of features and computing the average marginal effect of each feature on the model’s output. The total prediction can then be expressed as the sum of a baseline value and the SHAP values of all features: “Prediction = Baseline + Sum of SHAP values.” This additive property enables SHAP to present the contribution of features in a highly interpretable and visually intuitive manner [5].

The main advantages of SHAP include its ability to address the “black-box” nature of complex machine learning models by enhancing their transparency and providing clear assessments of features’ importance. Furthermore, SHAP explains the influence of each feature at both the global model level and the individual prediction level, making it a versatile tool that can be applied to various machine learning models [22,23].

In the context of MI prediction, SHAP was employed to improve the model’s interpretability and transparency, which are critical in the medical domain. By explicitly showing how each feature (e.g., age, smoking status, blood pressure) influences the prediction, SHAP enhances the trustworthiness of the model for medical professionals. It also allows for the identification of key risk factors for MI, enabling the development of targeted prevention strategies. Additionally, SHAP provides personalized explanations for individual patients, facilitating tailored diagnostic and treatment decisions. By integrating SHAP, the interpretability of the MI prediction model was significantly enhanced, increasing its reliability and utility in clinical settings.

3. Materials and Methods

3.1. Database

We utilized datasets from an open-source database on Kaggle (https://www.kaggle.com/code/tanmay111999/heart-failure-prediction-cv-score-90-5-models, accessed on 19 November 2024). This database comprises information on 12 parameters, collected from 918 patients across four European research centers. The features included for MI prediction were age, sex, chest pain type, resting blood pressure, serum cholesterol, fasting blood sugar, resting electrocardiographic results, maximum heart rate achieved, presence of exercise-induced angina, ST depression induced by exercise relative to rest, and slope of the ST peak exercise segment. These features were utilized to predict the target variable, indicating the presence or absence of heart disease, as detailed in

Table 1. Parameters of the dataset utilized in this study [24].

Variable	Details	Range (Min–Max)
Age	age of the patient [years]	28–77
Sex	sex of the patient [M: male; F: female]
ChestPainType	chest pain type [TA: Typical Angina; ATA: Atypical Angina; NAP: non-anginal pain; ASY: asymptomatic]
RestingBP	resting blood pressure [mm Hg]	0–200
Cholesterol	serum cholesterol [mm/dL]	0–603
FastingBS	fasting blood sugar [1: if FastingBS > 120 mg/dL; 0: otherwise]
RestingECG	resting electrocardiogram results [Normal: normal; ST: with ST-T wave abnormality (T wave inversions and/or ST elevation or depression of >0.05 mV); LVH: showing probable or definite left ventricular hypertrophy based on Estes’ criteria]
MaxHR	maximum heart rate achieved [numeric value between 60 and 202]	60–202
ExerciseAngina	exercise-induced angina [Y: yes; N: no]
Oldpeak	oldpeak = ST [numeric value measured in depression]	−2.6–6.2
ST_Slope	the slope of the peak exercise ST segment [Up: upsloping; Flat: flat; Down: downsloping]
HeartDisease	target class [1: heart disease; 0: normal]

[24]. We used 80% of the data for learning and the remaining 20% for testing.

In this study, missing values in the dataset were handled by either imputing them with 0 or replacing them with the mean. This approach was adopted to maintain the consistency of the dataset while minimizing unnecessary distortion during the training of predictive models. Additionally, categorical parameters were encoded into numerical formats to ensure compatibility with the model. For instance, parameters such as gender were encoded by assigning 0 to male and 1 to female.

3.2. Exploratory Data Analysis (EDA)

The scatter plot presented in Figure 1 visualizes the relationship between age, cholesterol levels, and the presence of heart disease, such as the category of “HeartDisease”. The x-axis represents age, while the y-axis represents cholesterol levels. Orange points indicate patients with heart disease (1), and blue points represent patients without heart disease (0). Cholesterol levels are primarily distributed between 100 and 400, with no significant variation across different age groups, showing a generally even distribution. Regarding the relationship between heart disease and age, patients with heart disease are predominantly concentrated in the age range of 40 to 70, with a notable cluster observed between the ages of 50 and 60. However, there is no clear correlation between cholesterol levels and the presence of heart disease, as most data points for both groups fall within the 200 to 300 range. Therefore, this graph suggests that while age and cholesterol levels may have some influence on the occurrence of heart disease, cholesterol levels alone are insufficient to accurately predict the presence of heart disease.

Figure 2 visualizes the relationship between resting blood pressure (RestBP), cholesterol levels (Cholesterol), and the presence of heart disease (HeartDisease). The x-axis represents the resting blood pressure, while the y-axis represents cholesterol levels. Orange points indicate patients with heart disease (1), and blue points represent patients without heart disease (0). Most data points are distributed within the range of 100–150 mmHg for resting blood pressure and 100–400 for cholesterol levels. When analyzing the relationship between heart disease and resting blood pressure, both patients with and without heart disease are primarily concentrated within the range of 120–140 mmHg, showing no significant distinction between the two groups. Similarly, in terms of cholesterol levels, both groups are predominantly distributed within the range of 200–300, with no noticeable difference between the groups. In conclusion, this graph suggests that, while the resting blood pressure and cholesterol levels may have some influence on the occurrence of heart disease, these two variables alone are insufficient to accurately predict the presence of heart disease.

Figure 3 plots the cholesterol levels on both the x-axis and y-axis, with heart disease status (HeartDisease) being indicated by different colors. Both axes represent cholesterol levels, where orange points indicate patients with heart disease (1), and blue points represent patients without heart disease (0). Patients with and without heart disease are primarily distributed within the cholesterol range of 100–400, and no clear distinction between the two groups is observed.

Figure 4 shows the relationship between age and resting blood pressure (RestBP), with the x-axis representing age and the y-axis representing the resting blood pressure. Overall, the resting blood pressure shows a slight upward trend with increasing age, but the correlation is very weak. Most data points are concentrated within the range of 125–150 mmHg, regardless of age. Additionally, a few data points with abnormally high blood pressure values exceeding 175 mmHg are observed, which are likely indicative of hypertensive patients. The data are predominantly concentrated between the ages of 40 and 70, with the resting blood pressure generally remaining stable within the range of 125–150 mmHg without significant variation.

4. Results

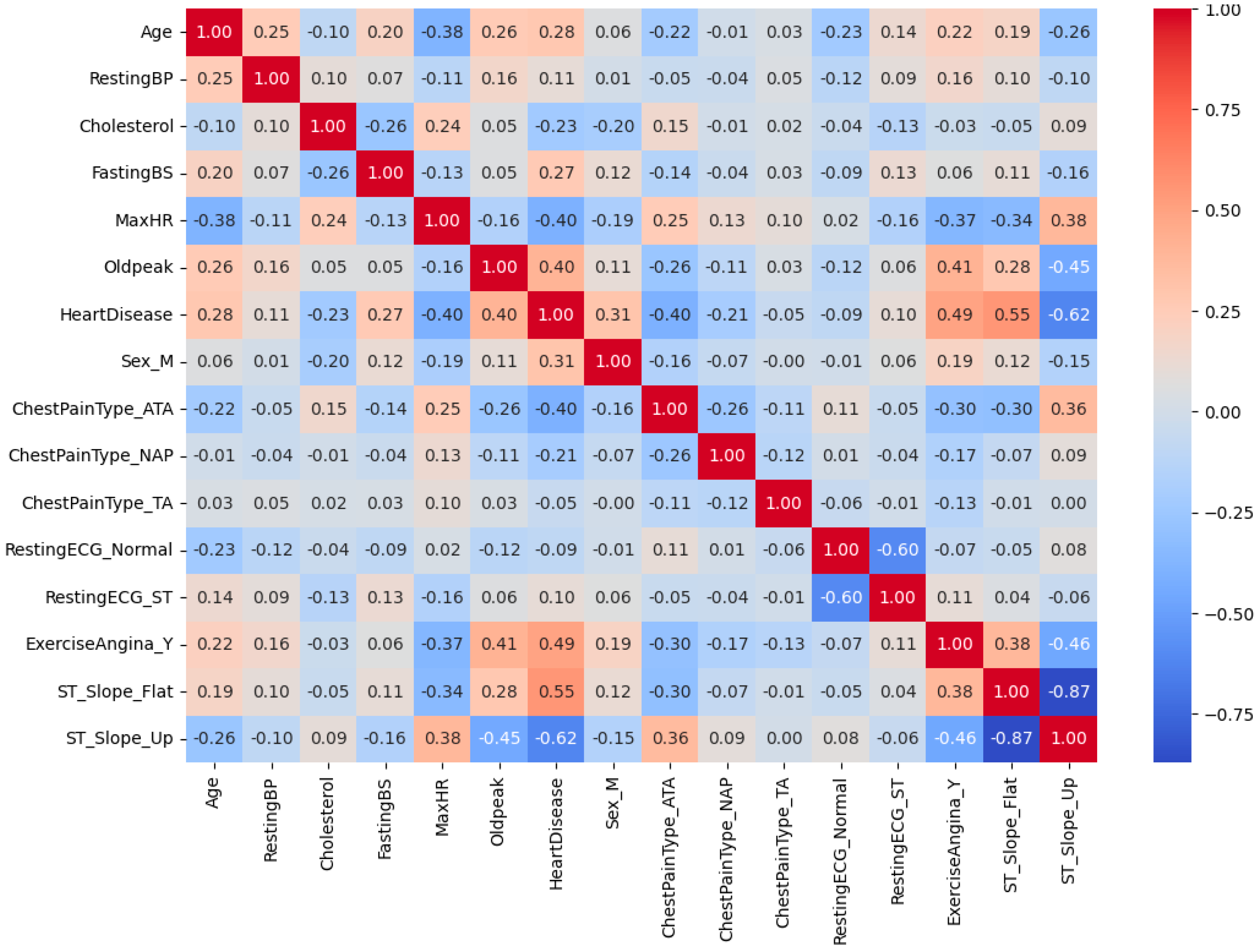
Figure 5 provides the correlation matrix [25] between various parameters, with the correlation coefficients being depicted using both colors and numerical values. Red indicates a positive correlation, blue represents a negative correlation, and white suggests little to no correlation. All variables, including binary and categorical ones, were numerically encoded (0/1) to construct this exploratory correlation matrix using Pearson’s correlation coefficients. The resulting visualization provides a descriptive overview of overall variable associations; however, correlations involving categorical variables should be interpreted with caution, as they primarily reflect proportional tendencies rather than true statistical correlations. Focusing on the relationship with “HeartDisease”, notable correlations are observed. “Oldpeak” exhibits a strong positive correlation (+0.40), while “ExerciseAngina_Y” also shows a positive association (+0.49). Conversely, “MaxHR” demonstrates a negative correlation (−0.40), indicating that a lower maximum heart rate may be associated with a higher likelihood of heart disease. Furthermore, a strong negative correlation (−0.87) exists between “ST_Slope_Flat” and “ST_Slope_Up”, suggesting that these two variables are mutually exclusive in their characteristics. The relationship between “Age” and “MaxHR” demonstrates a negative correlation (−0.38), highlighting a trend where the maximum heart rate decreases with increasing age. “RestingBP” (resting blood pressure) exhibits low correlations with other variables, implying that it may act as an independent feature. Gender (Sex_M) shows a moderate positive correlation (+0.31) with “HeartDisease”, suggesting that gender may have a partial influence on the risk of heart disease. Chest pain types (ChestPainType_ATA, ChestPainType_NAP, and ChestPainType_TA) display weak inter-correlations, indicating limited distinctiveness among these features. Overall, this heatmap effectively identifies key variables influencing heart disease prediction, such as “Oldpeak”, “ExerciseAngina_Y”, and “MaxHR”. These insights can guide feature selection when developing predictive models and inform further analysis of the relationships among these variables.

This study identified key factors that may significantly influence the occurrence of myocardial infarction (MI). Prior to modeling, all categorical variables were transformed using one-hot encoding, which increased the total number of predictors from the 12 original variables listed in Table 1 to 20 encoded predictors. By applying LASSO regression, the model shrank the coefficients of less relevant predictors to zero, thereby reducing the risk of overfitting and improving its generalization performance on unseen data. As a result, 15 significant predictors were selected out of the 20 encoded variables, and the results are summarized in

Table 2. The 15 explanatory variables and their coefficients.

Explanatory Variable	Coeffi.	Explanatory Variable	Coeffi.
Age	0.0210	ChestPainType_NAP	−0.0928
RestingBP	0.0024	ChestPainType_TA	−0.0393
Cholesterol	−0.0539	RestingECG_Normal	−0.0046
FastingBS	0.0545	RestingECG_ST	−0.0024
MaxHR	−0.0158	ExerciseAngina_Y	0.0668
Oldpeak	0.0522	ST_Slope_Flat	0.0785
Sex_M	0.0636	ST_Slope_Up	−0.1071
ChestPainType_ATA	−0.0952

.

Table 2 presents the 15 explanatory variables that were used in the heart disease prediction model, along with their respective coefficients, indicating the influence of each variable on the likelihood of heart disease. Positive coefficients (+) represent factors that increase the risk of heart disease, while negative coefficients (-) denote factors that reduce this risk. The major risk-increasing factors include age (Age), fasting blood sugar (FastingBS), ST depression (Oldpeak), male sex (Sex_M), exercise-induced angina (ExerciseAngina_Y), and a flat ST slope (ST_Slope_Flat). Notably, exercise-induced angina and a flat ST slope, which are both indicative of impaired cardiac function, emerged as the strongest risk factors. Conversely, risk-reducing factors include maximum heart rate (MaxHR), an upward ST slope (ST_Slope_Up), and specific chest pain types (ChestPainType_ATA, NAP, TA). A higher maximum heart rate and an upward ST slope suggest a healthier cardiac state, contributing to a reduced risk of heart disease. Additionally, normal (RestingECG_Normal) or mildly abnormal (RestingECG_ST) resting electrocardiogram results are associated with a lower risk. Interestingly, cholesterol (Cholesterol) displayed an inverse relationship, with higher levels correlating with a reduced risk of heart disease, which was contrary to conventional expectations. This anomaly may require further investigation to understand its cause. This result may also be influenced by factors such as sample imbalance and data heterogeneity, and thus should be interpreted with caution. In conclusion, this analysis clearly identifies key risk factors for heart disease, with exercise-induced angina and ST depression being highlighted as the most significant. These findings provide valuable insights for developing strategies for the prevention and management of heart disease.

Table 3. p-values calculated for various variables.

Explanatory Variable	p-Value	Explanatory Variable	p-Value
Age	0.2938	ChestPainType_NAP	0.0000 **
RestingBP	0.8558	ChestPainType_TA	0.0314 *
Cholesterol	0.0022 *	RestingECG_Normal	0.6930
FastingBS	0.0014 *	RestingECG_ST	0.3074
MaxHR	0.8191	ExerciseAngina_Y	0.0004 **
Oldpeak	0.0006 **	ST_Slope_Flat	0.0034 *
Sex_M	0.0002 **	ST_Slope_Up	0.1005
ChestPainType_ATA	0.0001 **

* and ** indicate statistical significance at the 0.05 and 0.01 levels, respectively.

summarizes the explanatory variables and their corresponding p-values, indicating the level of statistical significance. For continuous variables such as Age, RestingBP, Cholesterol, MaxHR, and Oldpeak, independent sample t-tests were conducted to compare the mean values between the MI and non-MI groups. For categorical and binary variables including Sex_M, Fasting blood sugar (FastingBS), Chest pain types—ATA, NAP, and TA, RestingECG, Exercise-induced angina (ExerciseAngina_Y), and ST slope categories (Flat and Up), Chi-squared tests were applied to assess their associations with myocardial infarction (MI). Variables such as Cholesterol, FastingBS, Oldpeak, Sex_M, Chest pain types (ATA, NAP, TA), ExerciseAngina_Y, and ST_Slope_Flat demonstrated statistically significant or highly significant results. These findings suggest that the aforementioned variables exert a substantial influence on MI occurrence and should be considered important predictors in the model development process.

Table 4. Confusion matrix of logistic regression analysis.

	Predicted
		Predicted positive (yes)	Predicted negative (no)	Total
Reference	Actual positive (yes)	100	12	112
	Actual negative (no)	22	142	164
	Total	122	154	276

presents the confusion matrix [26] results evaluating the performance of the logistic regression analysis of the 15 variables selected through LASSO, showcasing the model’s predictions for the presence of MI. The true positives (TPs, 100) refer to cases here MI was present and where the model correctly predicted these as positive. This indicates the model’s effectiveness in accurately detecting MI cases. The true negatives (TNs, 142) represent cases where MI was absent and where the model correctly predicted these as negative. In contrast, the false positives (FPs, 12) are cases where MI was absent, but the model incorrectly predicted them as positive. Similarly, the false negatives (FNs, 22) refer to cases where MI was present, but the model incorrectly predicted them as negative. Overall, the model accurately detected 100 out of 112 actual positive cases and correctly classified 142 out of 164 actual negative cases. However, the occurrence of 22 false negatives and 12 false positives indicates that the model missed some positive cases and incorrectly classified some negatives as positive. In conclusion, the model demonstrates reliable performance in predicting MI. However, addressing the false negatives and positives could further enhance its predictive accuracy.

Table 5. Classification performance of logistic regression model.

Performance	Value
Accuracy (%)	87.7%
Precision	0.82
Recall	0.89
F1 score	0.86

demonstrates a good performance in predicting the presence of MI. The default classification threshold of 0.5 was applied to convert the predicted probabilities from the logistic regression model into binary outcomes. The accuracy is 87.7%, indicating that the majority of cases were correctly classified. The precision is 0.82, meaning that 82% of the cases that were predicted as positive were actually positive. The recall is 0.89, reflecting that 87% of actual positive cases were correctly identified by the model. Furthermore, the F1 score, which balances precision and recall, is 0.86, highlighting the model’s robust and reliable performance in both positive and negative case predictions [26,27].

Figure 6 illustrates the importance of variables influencing model predictions based on their SHAP values. The importance of each variable is measured using the mean absolute SHAP value, which indicates the magnitude of the variable’s contribution to the model’s predictions. “ST_Slope_Flat” (a flat ST segment slope) emerged as the most influential variable, strongly associated with impaired cardiac function and playing a critical role in predicting heart disease risk. “ChestPainType_NAP” (non-anginal pain) and “ExerciseAngina_Y” (exercise-induced angina) also showed high importance, indicating a strong relationship with the risk of heart disease. Variables with moderate importance included “ST_Slope_Up” (upward ST segment slope), “ChestPainType_ATA” (asymptomatic angina), and “Oldpeak” (ST depression). These variables are closely linked to cardiac function and contributed significantly to the model’s predictive capabilities. In contrast, variables such as “RestingBP” (resting blood pressure), “RestingECG_Normal” (normal resting electrocardiogram), and “MaxHR” (maximum heart rate) demonstrated relatively lower importance, indicating a limited influence on the model’s predictions. In conclusion, “ST_Slope_Flat”, “ChestPainType_NAP”, and “ExerciseAngina_Y” were identified as the most critical variables in predicting heart disease, providing valuable insights for the prevention and management of cardiac conditions. Conversely, variables with lower importance may only contribute in specific cases, underscoring their limited role in the model’s overall performance. These findings offer a clear understanding of which variables the model relies on most heavily for its predictions.

Figure 7 demonstrates the process by which the model generated a prediction for a specific data point. Each feature’s contribution to the prediction is displayed, with the corresponding feature and SHAP values clearly indicating the individual impact of each feature. The model’s initial prediction value, 0.015, represents the average prediction value across the entire dataset. The final prediction for this data point is −3.478, indicating a low likelihood of MI. In terms of feature contributions, “ChestPainType_ATA” had the most significant impact, decreasing the prediction value by −1.02. This suggests that the presence of asymptomatic chest pain is a strong factor in reducing the risk of MI. Similarly, “Sex_M” (male gender) and “ST_Slope_Flat” (a flat ST segment slope) reduced the prediction value by −0.78 and −0.6, respectively, further lowering the likelihood of a positive outcome. Other important features include “ST_Slope_Up” (upward ST segment slope) and “ExerciseAngina_Y” (absence of exercise-induced angina), which decreased the prediction value by −0.5 and −0.47, respectively. On the other hand, “ChestPainType_NAP” (non-anginal chest pain) increased the prediction value by +0.35, while “Age” (63 years) contributed +0.16, slightly raising the likelihood of MI. In conclusion, this chart highlights how the model considers the interaction between features, with key features influencing the prediction value in different directions. “ChestPainType_ATA”, “Sex_M”, and “ST_Slope_Flat” significantly reduced the prediction value, while “ChestPainType_NAP” and “Age” increased it. This effectively explains why the model determined a low probability of MI for this specific data point. This analysis provides valuable insights into the model’s decision-making process and enhances its interpretability.

By combining the analysis of the SHAP graph and waterfall chart of Figure 6 and Figure 7, these visualizations illustrate how different variables influence the model’s predictions, both at the dataset level and in individual instances. The SHAP graph highlights the overall importance of variables across the dataset, showing that features such as “ST_Slope_Flat”, “ChestPainType_NAP”, and “ExerciseAngina_Y” play a critical role in predicting heart disease. These variables are strongly associated with the likelihood of heart disease and are key determinants in the model’s decision-making process. The waterfall chart, on the other hand, provides a detailed explanation for a specific data point. In this instance, “ChestPainType_ATA” and “Sex_M” significantly reduced the prediction value, indicating that asymptomatic chest pain and male gender are key factors that lower the risk of heart disease for the specific individual. Conversely, “ChestPainType_NA”P and “Age” increased the prediction value, suggesting that non-anginal chest pain and the patient’s age contributed to a higher likelihood of heart disease in this particular case. Together, the two visualizations demonstrate that the model consistently identifies certain variables, such as “ST_Slope_Flat”, “ChestPainType_NAP”, and “ExerciseAngina_Y”, as important predictors across both the entire dataset and individual data points. However, the impact and direction of these variables may vary depending on the unique characteristics of the data point. For example, “ChestPainType_NAP”, while relatively less influential at the dataset level, had a significant positive impact on the prediction for the specific data point analyzed. In conclusion, the SHAP analysis provides a clear understanding of how the model learns and utilizes interactions between variables and data characteristics. It underscores the central role of features such as “ST_Slope_Flat”, “ChestPainType_NAP”, “ExerciseAngina_Y”, and “Sex_M” in predicting heart disease, highlighting their clinical significance. This comprehensive analysis enhances the interpretability and transparency of the model, offering valuable insights for heart disease prevention and management.

The comparison between the p-value analysis and SHAP analysis demonstrates that these two approaches offer complementary insights when evaluating a variable’s importance and statistical significance. While the p-value analysis focuses on assessing the statistical significance of variables, SHAP analysis provides a visual representation of the relative contribution of each variable to the model’s predictions. In the SHAP analysis, variables such as “ST_Slope_Flat”, “ChestPainType_NAP”, and “ExerciseAngina_Y” were identified as having the greatest influence on the model’s predictions, which aligns with their statistical significance in the p-value analysis (p-values: 0.0034, 0.0000, and 0.0004, respectively). Conversely, variables such as “RestingBP” and “MaxHR”, with p-values of 0.8558 and 0.8191, were not statistically significant and exhibited low importance in the SHAP analysis, demonstrating consistency between the two methods. Variables such as “ChestPainType_ATA”, “Oldpeak”, “Sex_M”, “FastingBS”, and “Cholesterol” were deemed significant in both the p-value and SHAP analyses. However, ST_Slope_Up, despite a p-value of 0.1005 (not statistically significant), exhibited a relatively high contribution in the SHAP analysis. This discrepancy highlights the difference between p-value analysis, which evaluates statistical significance, and SHAP analysis, which assesses the actual contribution of variables within the model. The SHAP waterfall plot further illustrates the influence of individual variables on specific predictions. For instance, “ChestPainType_ATA” had the largest negative impact on the prediction (−1.02), while “ST_Slope_Flat” and “Sex_M” also contributed negatively. In contrast, “ChestPainType_NAP” contributed positively, increasing the predicted value. These variables were also statistically significant in the p-value analysis, emphasizing their important roles both in individual observations and the overall model, demonstrating consistency between the two methods. In conclusion, p-value analysis is effective for determining the statistical significance of variables, while SHAP analysis excels in visualizing the relative contribution of each variable to the model. Most variables showed consistent results across the two methods, but certain variables, such as “ST_Slope_Up”, exhibited differences, underscoring the complementary nature of these approaches and their potential for joint use in comprehensive evaluations.

5. Discussion

This study focuses on developing a predictive model for MI that balances predictive performance and interpretability, presenting a data-driven tool that is practical for clinical applications. By employing LASSO regression [12,19,20] and logistic regression [15,20,22], the model achieved robust predictive capabilities while performing a SHAP [4,5,22,23] analysis to visualize the feature contributions, significantly enhancing the transparency and trustworthiness of the results. This approach addresses the “black-box” limitations of many existing studies, representing a substantial advancement in the field [28].

The logistic regression model demonstrated strong performance, achieving an AUC of 87.7% and an F1 score of 0.89. The LASSO regression was instrumental in addressing overfitting and managing high-dimensional data [20], thereby simplifying the model and improving its interpretability and generalizability. The SHAP analysis provided visual insights into feature contributions, enabling medical professionals to better understand and trust the model’s outputs [18]. The key risk factors identified included age, fasting blood sugar (FastingBS), ST depression (Oldpeak), flat ST slope (ST_Slope_Flat), and exercise-induced angina (ExerciseAngina_Y). Protective factors such as maximum heart rate (MaxHR) and an upward ST slope (ST_Slope_Up) were also identified as reducing the risk of MI.

The comparison between the SHAP and p-value analyses provided complementary insights into assessing the importance and statistical significance of variables. The SHAP analysis identified “ST_Slope_Flat,” “ChestPainType_NAP,” and “ExerciseAngina_Y” as the most influential variables in model predictions, which aligned with their respective p-values (p = 0.0034, 0.0000, 0.0004). Conversely, “RestingBP” and “MaxHR” were consistently deemed less important across both the SHAP and p-value analyses (p = 0.8558, 0.8191), reinforcing the reliability of the two approaches. However, “ST_Slope_Up” presented a discrepancy, as it demonstrated a relatively high contribution in the SHAP analysis, despite being statistically insignificant (p = 0.1005). This difference highlights the distinct strengths of the two methods: while p-value analysis evaluates statistical associations, SHAP analysis captures the actual contribution of variables within the predictive model, underscoring the value of using these approaches in tandem for a comprehensive evaluation.

This study demonstrated notable differentiation compared with existing research, as summarized in

Table 6. An overview of recent studies on MI prediction.

Reference	Dataset	Proposed Model	Performance
Jung et al. [14]	Dataset from the National Health Insurance Service (NHIS) in South Korea.	Cox proportional hazards models	AUC 70.9%
Park and Kim [11]	166 actual patient surgery records in South Korea.	Multi-layer perceptron (MLP)	Accuracy 97.05%
Izabela Rojek et al. [20]	Dataset from the UCI Heart Disease Database, hosted on Kaggle (303 patient records).	Logistic regression	AUC 92% Accuracy 88.52%
Yoo [9]	Dataset from the National Health Insurance Service (NHIS) in South Korea.	Long short-term memory (LSTM)	AUC 71% Accuracy 75%
Iim [12]	Korea national health and nutrition examination survey (KNHANES) (6th Edition, 2013–2015).	Bagging + LASSO (B-LASSO)	AUC 81.9%

. Jung et al. [14] utilized data from the National Health Insurance Service (NHIS) and applied a Cox proportional hazards regression model, achieving an AUC of 70.9%, which was lower than the predictive performance of this study. Similarly, Yoo [9], who also employed NHIS data using a Long Short-Term Memory (LSTM) model, reported an AUC of 71% and an accuracy of 75%, indicating lower performance and limited interpretability compared with the present model. In contrast, Iim [12] used data from the Korea National Health and Nutrition Examination Survey (KNHANES) and adopted a B-LASSO model, yielding an AUC of 81.9% and demonstrating strong feature selection capability; however, the study lacked transparency in explaining feature contributions. Park and Kim [11] analyzed 166 actual patient surgery records from South Korea and addressed the issue of data imbalance using the SMOTE. Four machine learning models—logistic regression, random forest, XGBoost, and multi-layer perceptron (MLP)—were compared, among which the MLP achieved the highest accuracy of 97.05%. Nevertheless, all models exhibited low recall, indicating limitations in detecting true acute myocardial infarction (AMI) cases. Conversely, Izabela Rojek et al. [13] achieved superior predictive performance with an AUC of 92% and an accuracy of 88.52% using the UCI Heart Disease dataset. However, the small sample size (n = 303) limited the generalizability of their findings, unlike the broader applicability demonstrated in this study.

This study effectively identified critical risk and protective factors for MI and demonstrated the utility of SHAP analysis in providing detailed, case-specific explanations of model predictions. This explainability capability offers healthcare professionals actionable insights and builds a foundation for real-world clinical integration. However, reliance on the Kaggle dataset presents limitations in terms of sample size and population diversity, restricting the generalizability of the findings. Future research should focus on validating the model with larger and more diverse real-world clinical datasets and exploring additional variables that capture the multifactorial nature of MI. Furthermore, incorporating calibrated probability-based risk estimates to stratify patients into clinically meaningful categories (e.g., low-, intermediate-, and high-risk groups) would enhance the clinical interpretability of the model beyond binary classification and strengthen its potential utility in decision support.

In conclusion, this study represents a meaningful contribution to the literature by enhancing both the performance and interpretability of MI prediction models, distinguishing itself from prior research. With further external validation, probability calibration, and the integration of multi-source clinical data, such models hold strong potential to evolve into reliable and impactful tools for the early detection, personalized risk assessment, and prevention of cardiovascular diseases in clinical practice.

6. Conclusions

This study proposed a data-driven tool for predicting MI and identifying its risk factors, demonstrating its practical applicability in clinical settings. By employing LASSO regression for effective feature selection and building a logistic regression model, the study achieved a high prediction accuracy of 87.7% and an F1 score of 0.89, establishing the model’s reliability and robustness as a predictive tool for MI. Moreover, the integration of SHAP analysis significantly enhanced the interpretability of the model, providing a clear and trustworthy foundation for both healthcare professionals and patients to understand the predictive results.

This study identified age, fasting blood sugar (FastingBS), ST depression (Oldpeak), a flat ST slope (ST_Slope_Flat), and exercise-induced angina (ExerciseAngina_Y) as key risk factors, while the maximum heart rate (MaxHR) and an upward ST slope (ST_Slope_Up) were highlighted as protective factors. Both the SHAP and p-value analyses consistently identified “ST_Slope_Flat,” “ChestPainType_NAP,” and “ExerciseAngina_Y” as significant variables, whereas “RestingBP” and “MaxHR” were deemed less important based on both methods. However, a notable discrepancy was observed for “ST_Slope_Up,” which was statistically insignificant in the p-value analysis (p = 0.1005) but demonstrated a substantial contribution in the SHAP analysis. These findings underscore the complementary nature of SHAP analysis, which captures the actual contribution of variables to the model, and p-value analysis, which assesses statistical significance. Combining these methods provides a more comprehensive evaluation of a variable’s importance, offering deeper insights into the model’s behavior.

Notably, this study addressed the limitations of interpretability and transparency that are often associated with predictive models, demonstrating that such models can transcend basic data analysis to become practical decision-support tools in clinical applications. The results provide healthcare professionals with critical resources for designing personalized treatment and prevention strategies that are tailored to individual patients.

Future research should focus on validating the model with large-scale datasets encompassing diverse populations, as well as exploring additional variables and integrating real-time data to further enhance its performance and applicability. Furthermore, the LASSO-logistic regression model should be benchmarked against other regression-based methods to test the stability of the identified risk factors and provide stronger evidence of robustness. Strengthening the model’s patient-specific explanation capabilities and improving its utility in cardiovascular disease management will be essential for its evolution into a comprehensive and practical clinical tool.

In conclusion, this study proposed a predictive model that balances performance, interpretability, and practicality, laying a robust foundation for the management and prevention of cardiovascular diseases. These contributions highlight the potential of data-driven healthcare solutions to improve the quality and effectiveness of medical services.