A Fuzzy Model for Predicting the Group and Phase Velocities of Circumferential Waves Based on Subtractive Clustering
Abstract
1. Introduction
2. Fundamental Concepts of Fuzzy Logic System
2.1. Fuzzy Set Theory
2.2. Structure of Fuzzy Inference Systems
2.2.1. Mamdani Fuzzy Models
2.2.2. Takagi–Sugeno (TS)
2.2.3. Fuzzification
2.2.4. Inference Mechanism
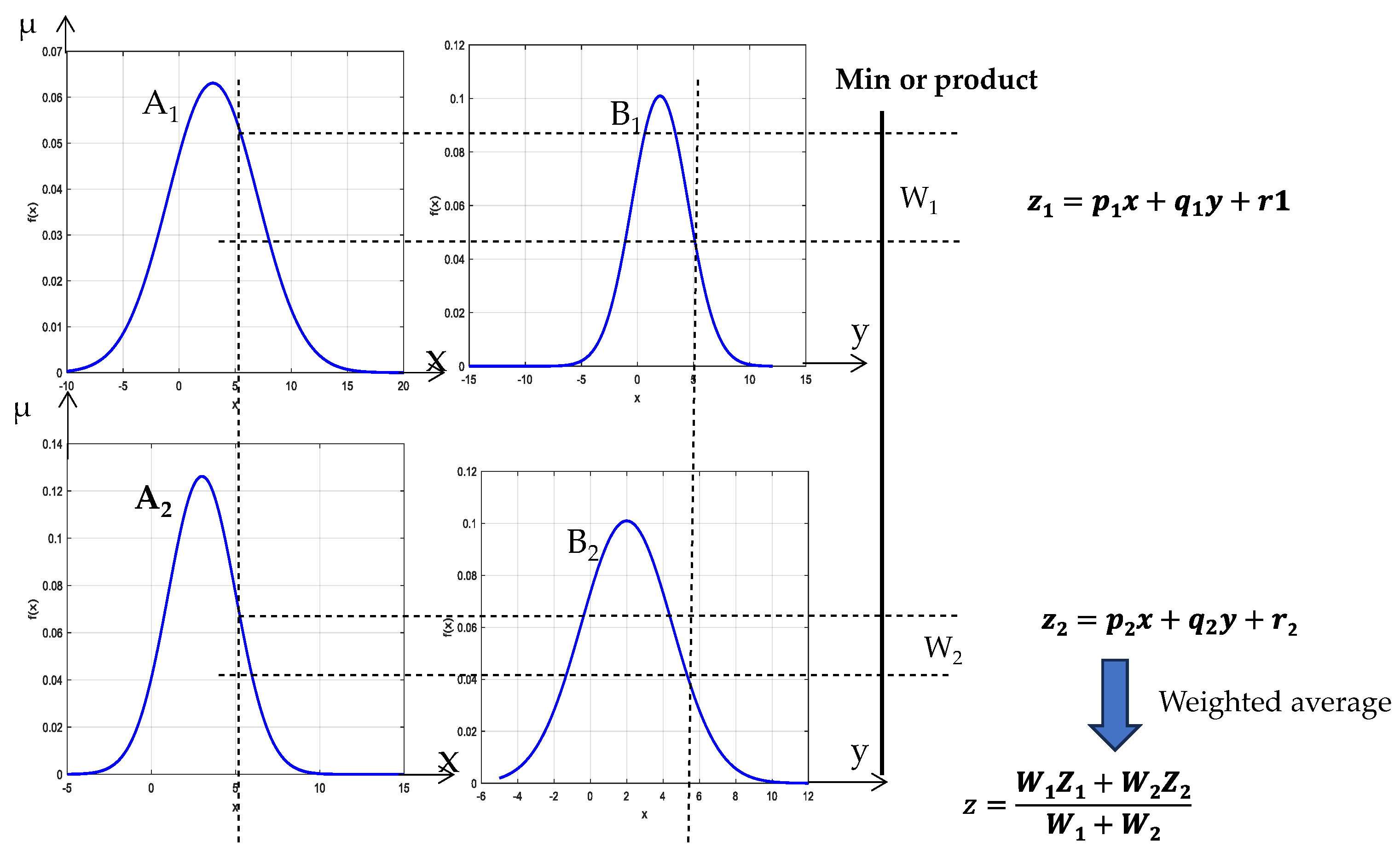
2.2.5. Defuzzification
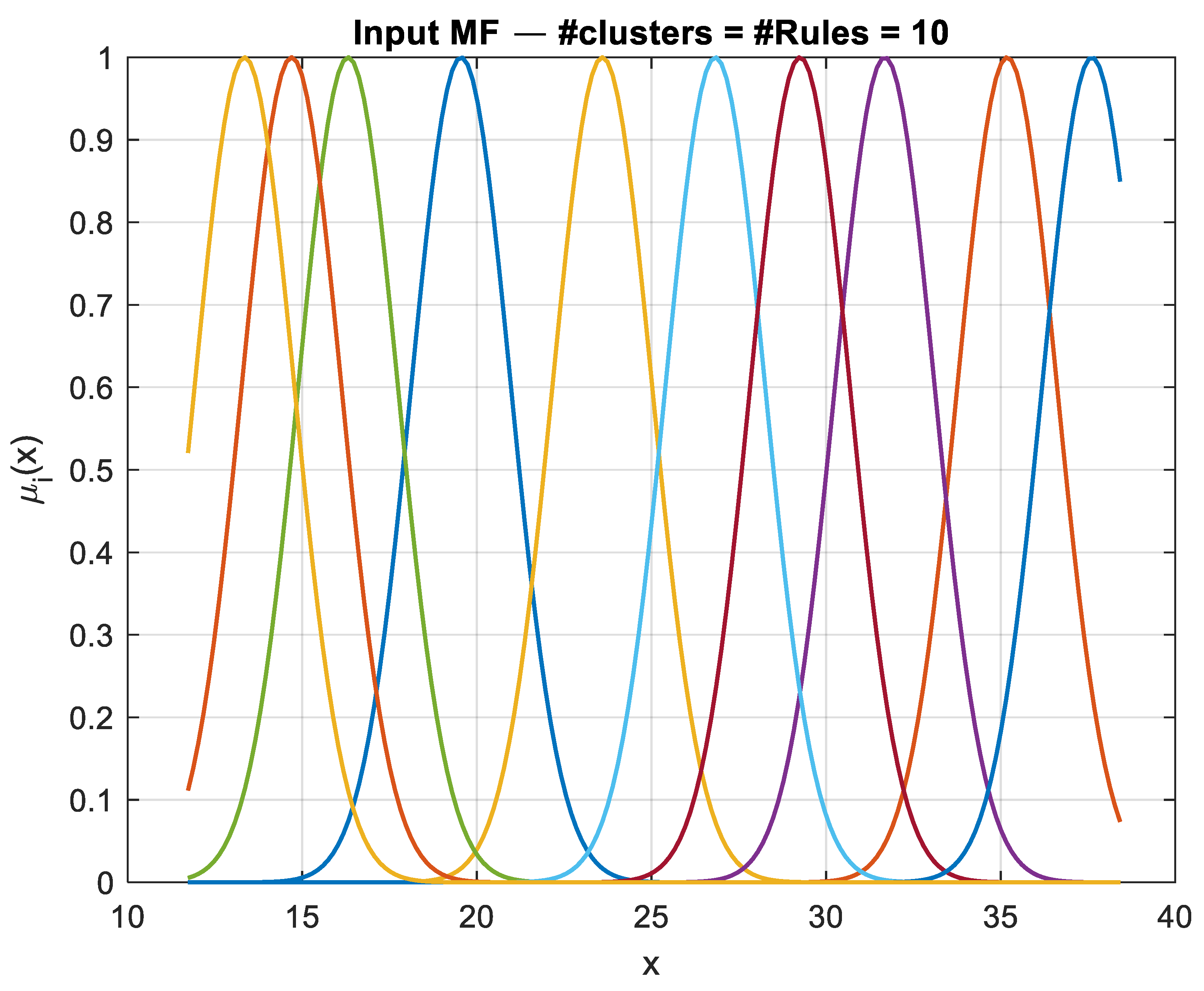
2.3. Subtractive Clustering
3. Theoretical Study
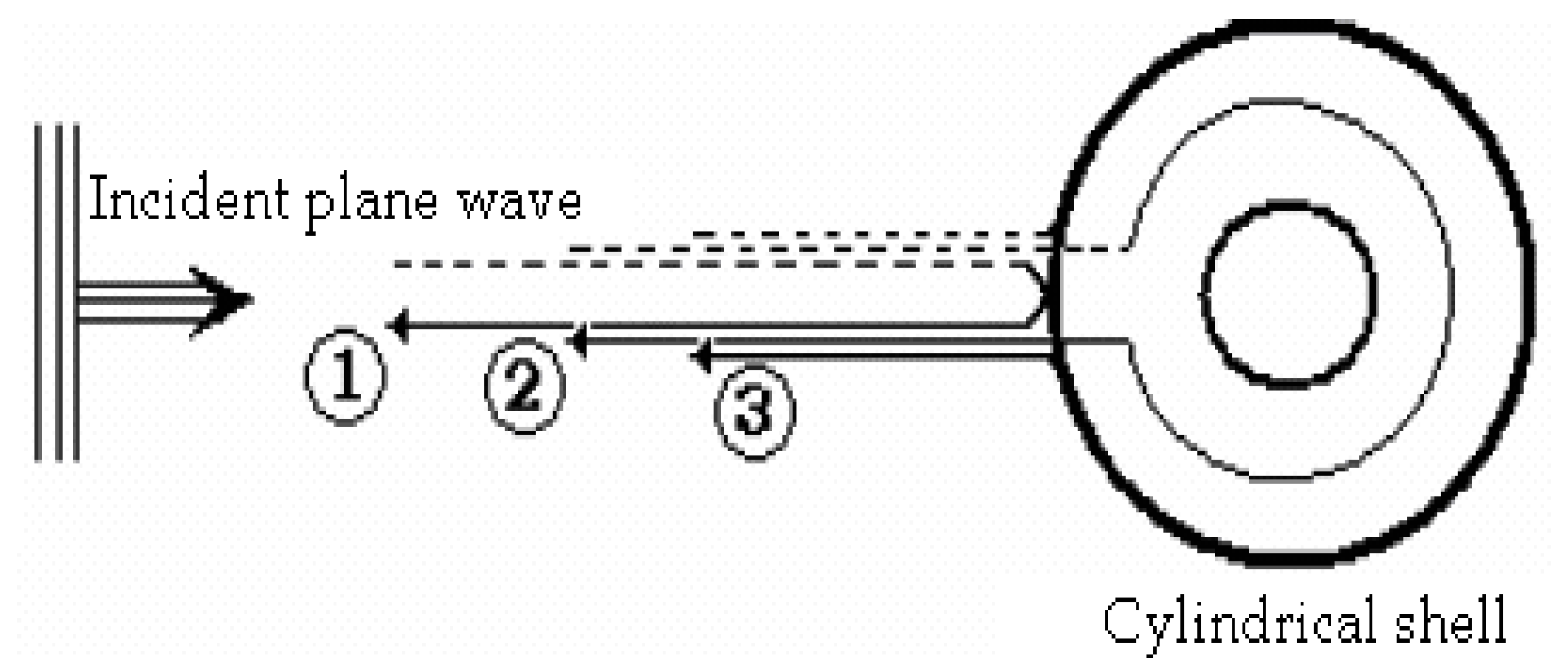
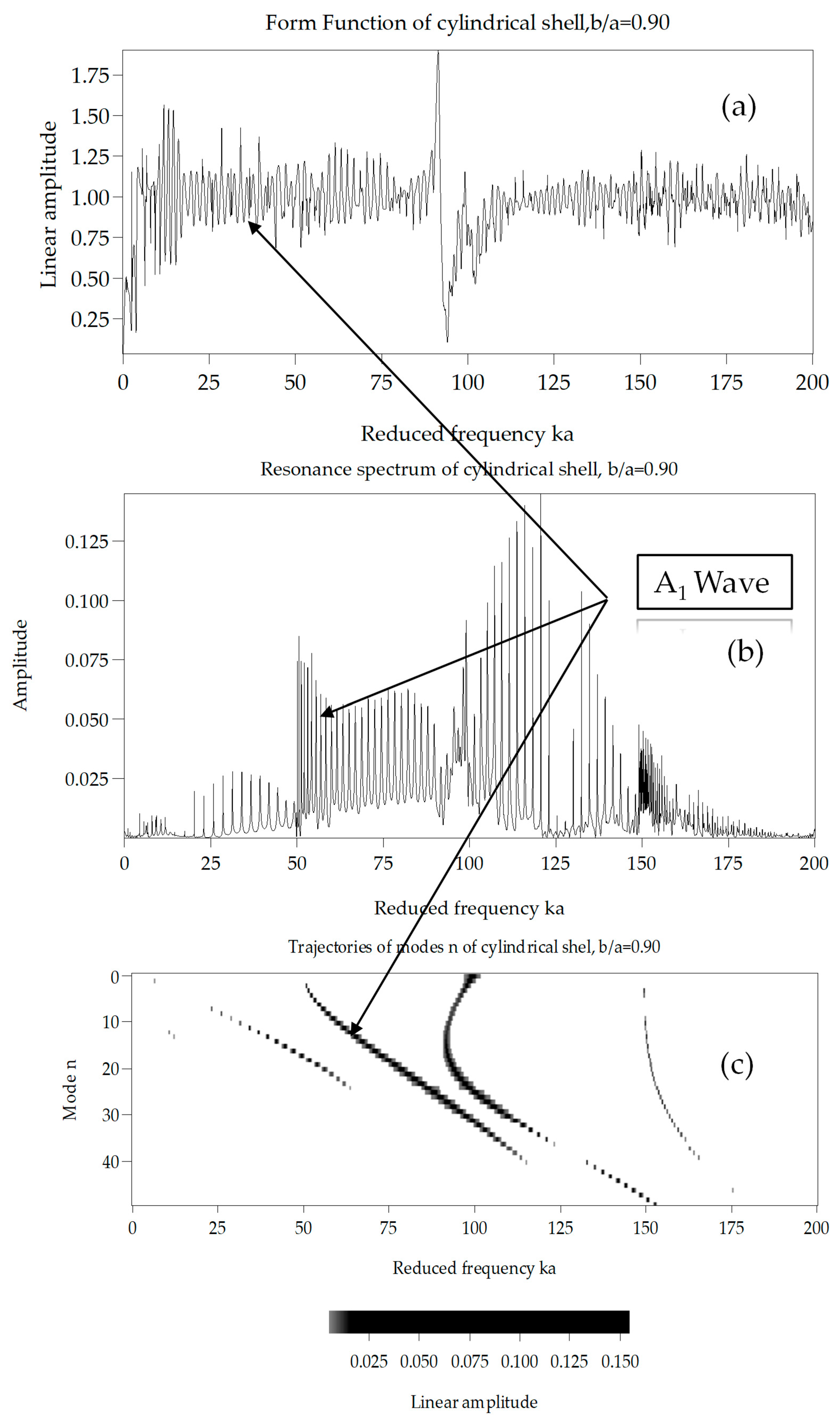
3.1. Acoustic Backscattering
3.2. Determination of Phase and Group Velocities
4. Methodology
- Choosing the most crucial elements to include in the modeling procedure.
- Creating a dataset, adapted to the chosen criteria, necessary for training and validation.
- Building the fuzzy model, which is a process that involves using a system identification technique based on subtractive clustering linked to a Sugeno fuzzy inference system.
- Modifying the clustering settings to obtain a model with the least amount of error.
- A hybrid optimization technique wherein functional signals progress and consequent parameters are determined using least squares estimation (LSE).
- The backpropagation optimization approach, which propagates error rates backward, updating the parameters based on the gradient descent technique.
5. Results and Discussion
6. Conclusions
7. Perspectives
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yin, T.; Ng, C.T.; Vidler, J.; Ho, V.D.; Kotousov, A. Amplitude-modulation vibro-acoustic technique for damage evaluation, Construction and Building Materials. Struct. Heal. Monit. 2022, 346, 128381. [Google Scholar]
- Hu, X.; Ng, C.T.; Kotousov, A. Numerical and experimental investigations on mode conversion of guided waves in partially immersed plates. Measurement 2022, 190, 110750. [Google Scholar] [CrossRef]
- Nahraoui, Y.; Aassif, E.H.; Maze, G. Modeling of the thickness of a Submerged Tube by the Artificial Neural Network. In Proceedings of the International Conference on Multimedia Computing and Systems, Mountain View, CA, USA, 27–31 October 2017; pp. 583–587. [Google Scholar]
- Flax, L.; Dragonette, L.; Uberall, H. Theory of elastic resonance excitation by sound scattering. J. Acoust. Soc. Amer. 1978, 63, 723–731. [Google Scholar] [CrossRef]
- Maze, G. Acoustic scattering from submerged cylinders. MIIR Im/Re: Experimental and theoretical study. J. Acoust. Soc. Amer. 1991, 89, 2559–2566. [Google Scholar] [CrossRef]
- Haumesser, L.; Décultot, D.; Léon, F.; Maze, G. Experimental identification of finite cylindrical shell vibration modes. J. Acoust. Soc. Am. 2002, 111, 2034–2039. [Google Scholar] [CrossRef] [PubMed]
- Maze, G. Diffusion D’une Onde Acoustique Plane Par des Cylindres et Tubes Immergés Dans L’eau: Isolement et Identification des Résonances, Thèse de Doctorat d’Etat és-Sciences; University of Rouen: Rouen, France, 1984. (In French) [Google Scholar]
- Maze, G.; Izbicki, J.L.; Ripoche, J. Resonances of plates and cylinders: Guided waves. J. Acoust. Soc. Amer. 1985, 77, 1352–1357. [Google Scholar] [CrossRef]
- Nahraoui, Y.; Aassif, E.; Elhanaoui, A.; Maze, G. A Neuro-Fuzzy Computing Technique for Modeling the Acoustic Form Function of Immersed Tubes. In Proceedings of the 3rd International Conference on Information Systems and Technologies, Tangier, Morocco, 22–24 March 2013. [Google Scholar]
- Dariouchy, A.; Aassif, E.H.; Decultot, D.; Maze, G. Acoustic characterization and prediction of the cut-off dimensionless frequency of an elastic tube by neural networks. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2007, 54, 1055–1064. [Google Scholar] [CrossRef]
- Tan, L.; Fan, J.; Wang, B.; Zhao, K.; Li, B. Backscattering enhancements by partially exposed cylindrical shells due to reflected flexural waves at air–water interfaces. J. Ocean Eng. Sci. 2023, 10, 274–280. [Google Scholar] [CrossRef]
- Thinh, T.I.; Nguyen, M.C. Dynamic stiffness method for free vibration of composite cylindrical shells containing fluid. Appl. Math. Model. 2016, 40, 9286–9301. [Google Scholar] [CrossRef]
- Latif, R.; Aassif, E.; Maze, G.; Moudden, A.; Faiz, B. Determination of the group and phase velocities from time-frequency representation of Wigner-Ville. J. Non-Destr. Test. Eval. Int. 1999, 32, 415–422. [Google Scholar] [CrossRef]
- Maze, G.; Léon, F.; Ripoche, J.; Überall, H. Repulsion phenomena in the phase-velocity dispersion curves of circumferential waves on elastic cylindrical shells. J. Acoust. Soc. Am. 1999, 105, 1695–1701. [Google Scholar] [CrossRef]
- Werro, N. Fuzzy Classification of Online Customers; Springer: Heidelberg, Germany, 2015; Volume 148, pp. 1–200. [Google Scholar]
- Wee, C.T. Advances in Fuzzy Rule-Based System for Pattern Classification. Ph.D. Thesis, National University of Singapore, Singapore, 2010. [Google Scholar]
- Babuška, R.; Babuška, R. Fuzzy Modeling for Control, 1st ed.; Springer: Dordrecht, The Netherlands, 1998; pp. 13–260. [Google Scholar]
- Zadeh, L. Outline of a new approach to the analysis of complex systems and decision processes. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 28–44. [Google Scholar]
- Mamdani, E. Application of fuzzy logic to approximate reasoning using linguistic systems. Fuzzy Sets Syst. 1977, 26, 1182–1191. [Google Scholar]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its application to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar]
- Dubois, D.; Prade, H. Fuzzy Sets and Systems—Theory and Applications; Academic Press: New York, NY, USA, 1980; pp. 1–400. [Google Scholar]
- Bouchon-Meunier, B. La logique floue et ses Applications; Addison-Wesley: Paris, France, 1995; pp. 1–320. [Google Scholar]
- Yager, R.R.; Filev, D.P. Essentials of Fuzzy Modeling and Control; John Wiley & Sons: New York, NY, USA, 1994; pp. 1–320. [Google Scholar]
- Zadeh, L. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Driankov, D.; Hellendoorn, H.; Reinfrank, M. An Introduction to Fuzzy Control; Springer: Berlin, Germany, 1993; pp. 1–304. [Google Scholar]
- Galichet, S. Contrôle Flou de L’interpolation Numérique au Codage de L’expertise. In Habilitation à Diriger des Recherches; Université de Savoie: Annecy, France, 2001. [Google Scholar]
- Singh, S.; Rattan, K.S. Implementation of a fuzzy logic controller on an FPGA using VHDL. In NAFIPS 2003 22nd International Conference of the North American; Fuzzy Information Processing Society: West Lafayette, IN, USA, 2003; pp. 110–115. [Google Scholar]
- Vuong, P.T.; Madni, A.M.; Vuong, B. VHDL Implementation for a Fuzzy Logic Controller. In Automation Congress; WAC ’06 World: Budapest, Hungary, 2006; pp. 1–8. [Google Scholar]
- Abu-Khudhair, A.; Muresan, R.; Yang, S.X. FPGA Based Real-Time Adaptive Fuzzy Logic Controller. In Proceedings of the 2010 IEEE International Conference on Automation and Logistics (ICAL), Beijing, China, 16–20 August 2010; pp. 539–544. [Google Scholar]
- Borne, P.; Rozinoer, I.; Dieulot, I.-Y.; Dubois, L. Introduction à la Commande Floue; Technip: Paris, France, 1998; pp. 1–320. [Google Scholar]
- Passino, K.M.; Yurkovich, S.; Reinfrank, M. Fuzzy Control; Addison-Wesley: Boston, MA, USA, 1998; Volume 42, pp. 15–21. [Google Scholar]
- Oliveira, D.N.; de Lima Henn, G.A.; da Mota Almeida, O. Design and implementation of a Mamdani Fuzzy Inference System on an FPGA using VHDL. In Proceedings of the Fuzzy Information Processing Society (NAFIPS), 2010 Annual Meeting of the North American, Toronto, ON, Canada, 12–14 July 2010; pp. 1–6. [Google Scholar]
- Chiu, S. Fuzzy model identification based on cluster estimation. J. Intell. Fuzzy Syst. 1994, 2, 267–278. [Google Scholar] [CrossRef]
- Demirli, K.; Muthukumaran, P. Higher order fuzzy system identification using subtractive clustering. J. Intell. Fuzzy Syst. 2000, 9, 129–158. [Google Scholar] [CrossRef]
- Jang, J.-S.R.; Sun, C.-T.; Mizutani, E. Neuro-Fuzzy and Soft Computing: A Computational Approach to Learning and Machine Intelligence; Prentice-Hall: Englewood Cliffs, NJ, USA, 1997; pp. 1–614. [Google Scholar]
- Mamdani, E.; Assilian, S. An Experiment in Linguistic Synthesis Using a Fuzzy Logic Controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Hayajneh, M.T.; Hassan, A.M.; Al-Wedyan, F. Monitoring Defects of Ceramic Tiles Using Fuzzy Subtractive Clustering-Based System Identification Method. Soft Comput. 2010, 14, 615–626. [Google Scholar] [CrossRef]
- Maze, G.; Ripoche, J.; Derem, A.; Rousselot, J.L. Diffusion d’une onde ultrasonore par des tubes remplis d’air immergés dans l’eau. Acustica 1984, 55, 69–85. [Google Scholar]
- Jang, J. ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar]
- Elouaham, S.; Nassiri, B.; Dliou, A.; Zougagh, H.; El Kamoun, N.; El Khadiri, K.; Said, S. Combination Time-Frequency and Empirical Wavelet Transform Methods for Removal of Composite Noise in EMG Signals. Telkomnika Telecommun. Comput. Electron. Control 2023, 21, 1373–1381. [Google Scholar] [CrossRef]
- El Khadiri, K.; Elouaham, S.; Nassiri, B.; El Melhoaui, O.; Said, S.; El Kamoun, N.; Zougagh, H. A Comparison of the Denoising Performance Using Capon Time-Frequency and Empirical Wavelet Transform Applied on Biomedical Signal. Int. J. Eng. Appl. (IREA) 2023, 11, 358–365. [Google Scholar] [CrossRef]
- Elouaham, S.; Dliou, A.; Laaboubi, M.; Latif, R.; Elkamoun, N.; Zougagh, H. Filtering and analyzing normal and abnormal electromyogram signals, Indonesia. J. Electr. Eng. Comput. Sci. 2020, 20, 176–184. [Google Scholar]



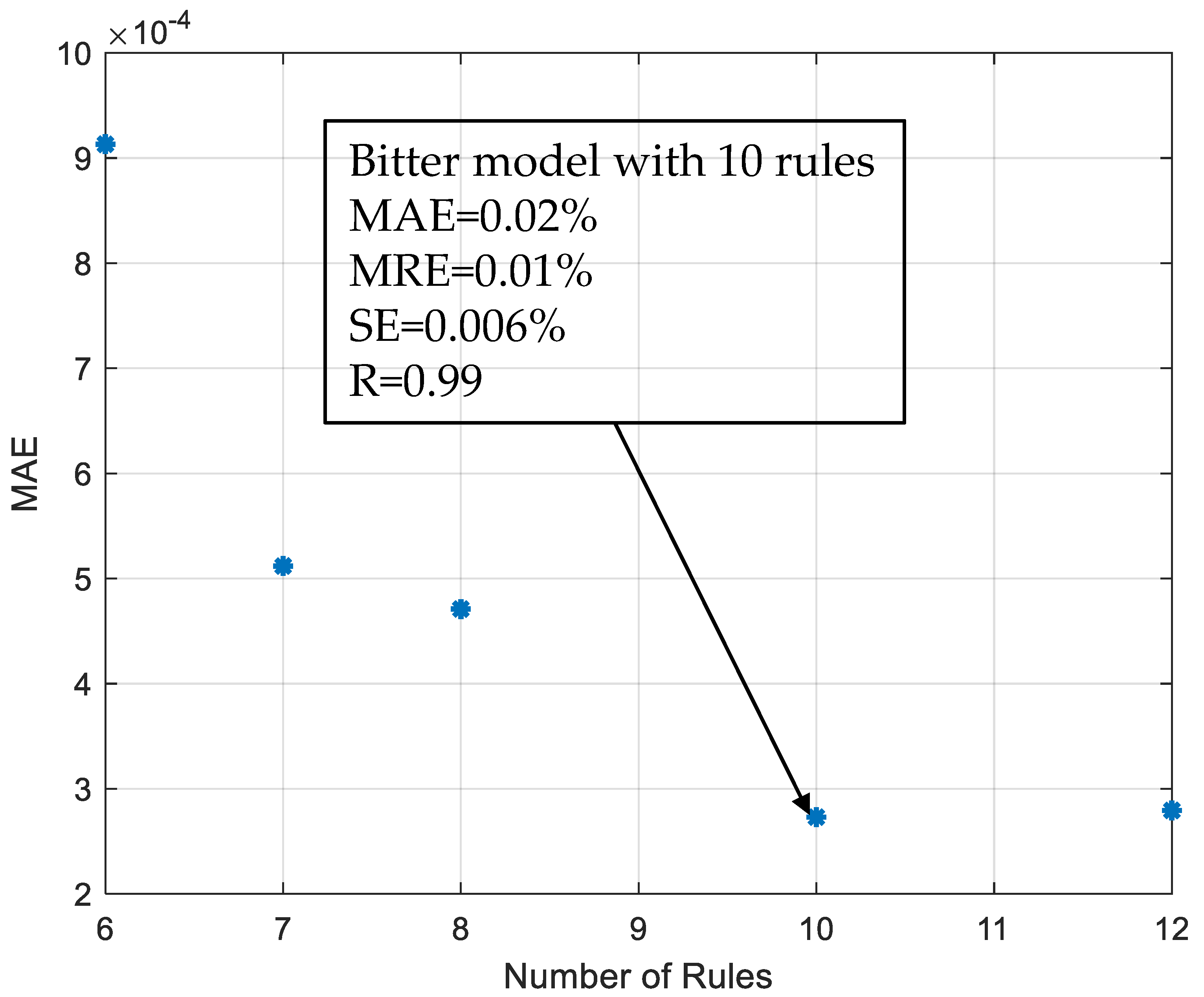


| Copper | Water (Fluid 1) | Air (Fluid 2) | |
|---|---|---|---|
| Density ρ (kg/m3) | 8930 | 1000 | 1.29 |
| CL: Longitudinal velocity (m/s) | 4760 | 1470 | 334 |
| CT: Transverse Velocity (m/s) | 2325 | ----------------- | ---------------- |
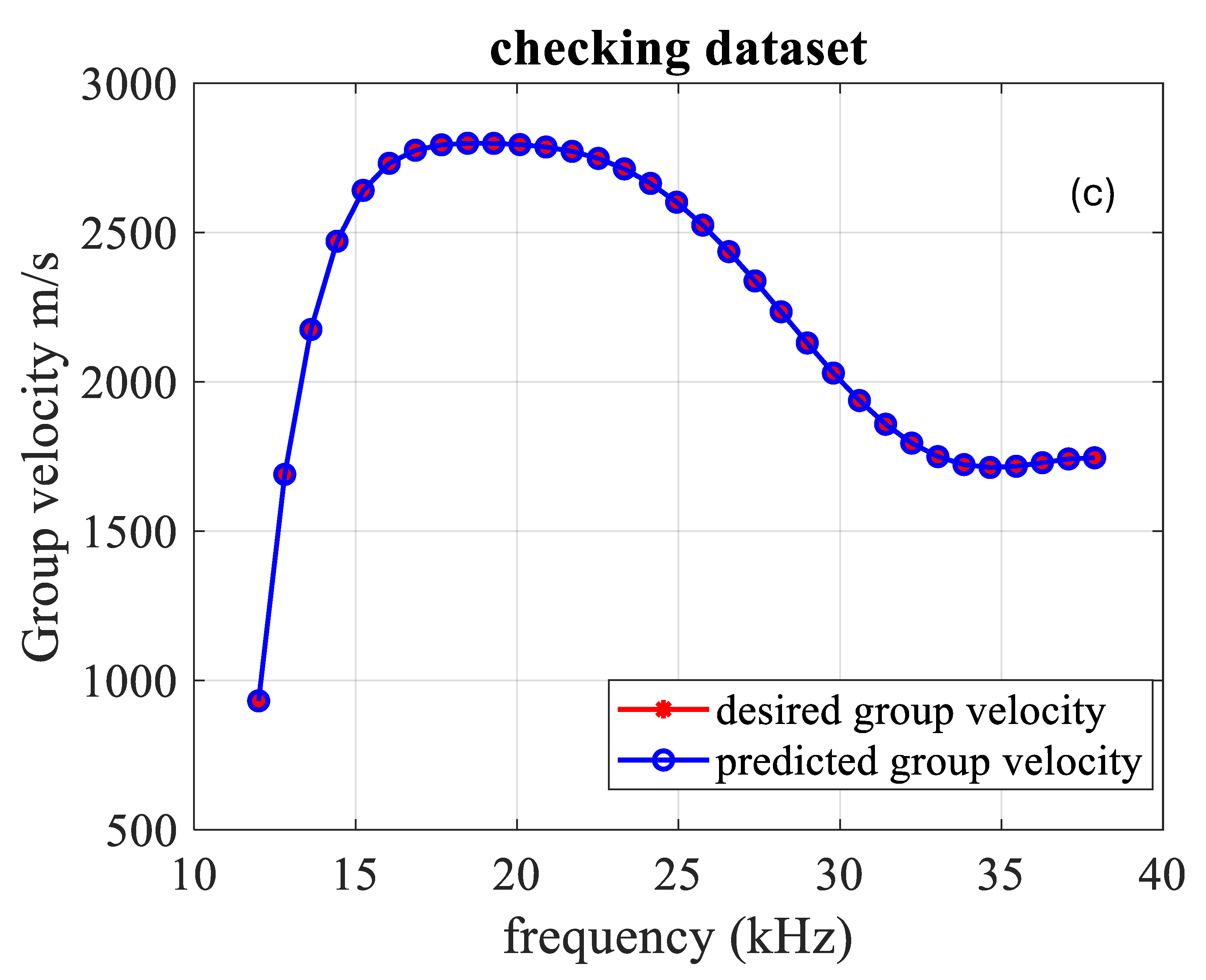
| N° | Frequency | Group Velocity Desired (×103) | Group Velocity Predicted (×103) |
|---|---|---|---|
| 1 | 11.7306 | 0.5996 | 0.5996 |
| 2 | 12.2698 | 1.2207 | 1.2207 |
| 3 | 12.5394 | 1.4722 | 1.4722 |
| 4 | 13.0786 | 1.8772 | 1.8771 |
| 5 | 13.3482 | 2.0378 | 2.0380 |
| 6 | 13.8874 | 2.2909 | 2.2905 |
| 7 | 14.1570 | 2.3887 | 2.3891 |
| 8 | 14.6961 | 2.5387 | 2.5382 |
| 9 | 14.9657 | 2.5948 | 2.5952 |
| 10 | 15.5049 | 2.6779 | 2.6780 |
| 11 | 15.7745 | 2.7078 | 2.7075 |
| 12 | 16.3137 | 2.7500 | 2.7506 |
| 13 | 16.5833 | 2.7643 | 2.7637 |
| 14 | 17.1225 | 2.7832 | 2.7828 |
| 15 | 17.3921 | 2.7891 | 2.7900 |
| 16 | 17.9313 | 2.7960 | 2.7955 |
| 17 | 18.7401 | 2.7990 | 2.7991 |
| 18 | 19.5489 | 2.7972 | 2.7981 |
| 19 | 20.3576 | 2.7919 | 2.7897 |
| 20 | 21.1664 | 2.7819 | 2.7846 |
| 21 | 21.4360 | 2.7771 | 2.7791 |
| 22 | 21.9752 | 2.7647 | 2.7629 |
| 23 | 22.2448 | 2.7568 | 2.7536 |
| 24 | 23.0536 | 2.7258 | 2.7255 |
| 25 | 23.5928 | 2.6980 | 2.7020 |
| 26 | 24.4016 | 2.6447 | 2.6426 |
| 27 | 24.6712 | 2.6237 | 2.6214 |
| 28 | 25.2103 | 2.5771 | 2.5774 |
| 29 | 25.4799 | 2.5515 | 2.5534 |
| 30 | 26.0191 | 2.4961 | 2.4973 |
| 31 | 26.2887 | 2.4664 | 2.4655 |
| 32 | 26.8279 | 2.4038 | 2.4024 |
| 33 | 27.0975 | 2.3711 | 2.3716 |
| 34 | 27.6367 | 2.3035 | 2.3051 |
| 35 | 27.9063 | 2.2689 | 2.2691 |
| 36 | 28.4455 | 2.1991 | 2.1972 |
| 37 | 28.7151 | 2.1642 | 2.1633 |
| 38 | 29.2543 | 2.0954 | 2.0974 |
| 39 | 29.5239 | 2.0618 | 2.0633 |
| 40 | 30.0631 | 1.9971 | 1.9950 |
| 41 | 30.3327 | 1.9664 | 1.9641 |
| 42 | 30.8718 | 1.9088 | 1.9106 |
| 43 | 31.1414 | 1.8824 | 1.8853 |
| 44 | 31.6806 | 1.8346 | 1.8332 |
| 45 | 31.9502 | 1.8134 | 1.8101 |
| 46 | 32.4894 | 1.7772 | 1.7760 |
| 47 | 32.7590 | 1.7621 | 1.7634 |
| 48 | 33.2982 | 1.7382 | 1.7420 |
| 49 | 33.5678 | 1.7293 | 1.7320 |
| 50 | 34.1070 | 1.7174 | 1.7132 |
| 51 | 34.9158 | 1.7128 | 1.7104 |
| 52 | 35.1854 | 1.7142 | 1.7158 |
| 53 | 35.7246 | 1.7202 | 1.7225 |
| 54 | 35.9941 | 1.7243 | 1.7251 |
| 55 | 36.5333 | 1.7334 | 1.7318 |
| 56 | 36.8029 | 1.7377 | 1.7361 |
| 57 | 37.3421 | 1.7442 | 1.7445 |
| 58 | 37.6117 | 1.7456 | 1.7466 |
| 59 | 38.1509 | 1.7428 | 1.7428 |
| 60 | 38.4205 | 1.7379 | 1.7375 |
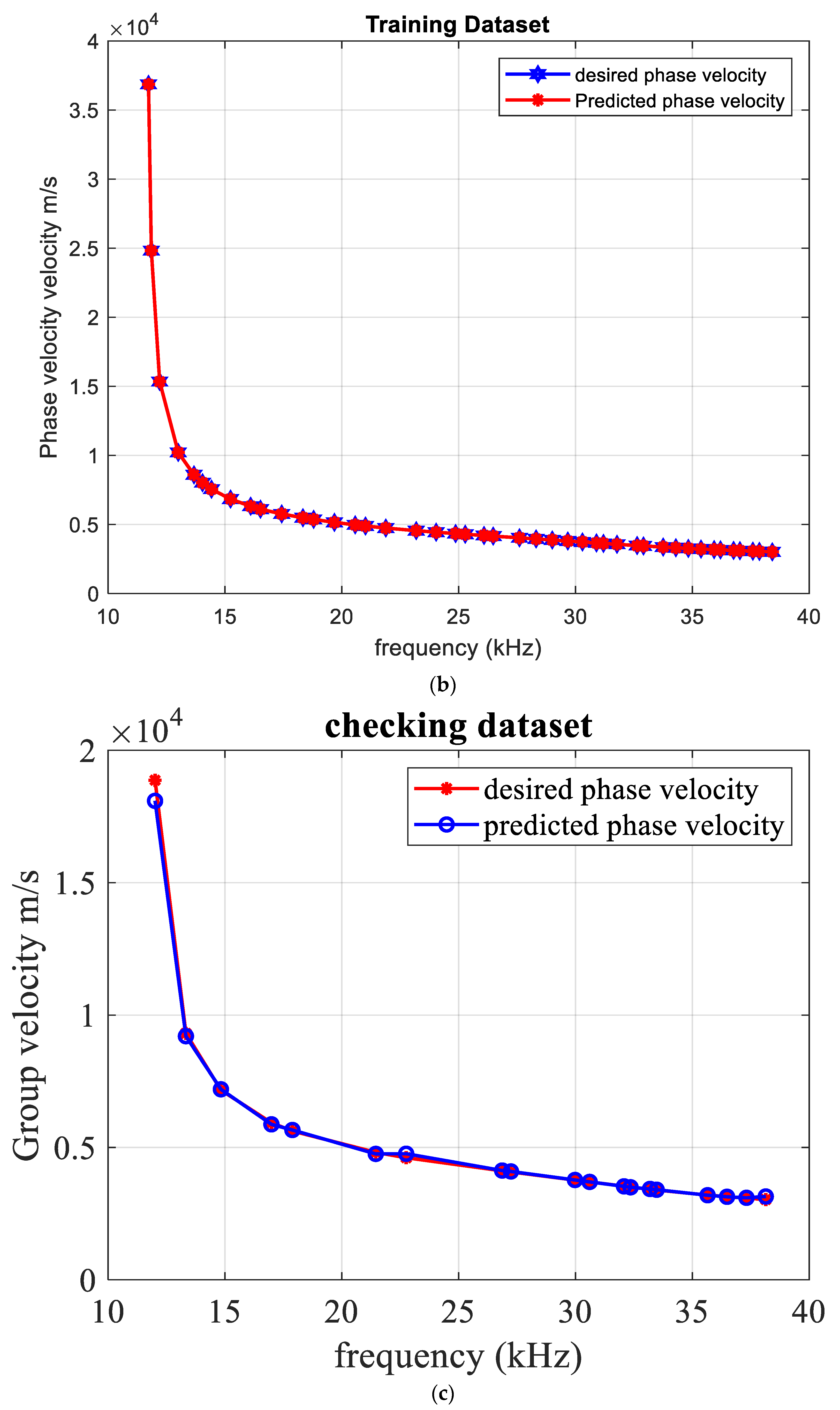
| Title 1 | Frequency | Group Velocity Desired (×103) | Group Velocity Predicted (×103) |
|---|---|---|---|
| 1 | 12.0002 | 0.9313 | 0.9071 |
| 2 | 14.4266 | 2.4706 | 2.4705 |
| 3 | 15.2353 | 2.6407 | 2.6415 |
| 4 | 16.0441 | 2.7314 | 2.7319 |
| 5 | 17.6617 | 2.7932 | 2.7942 |
| 6 | 18.4705 | 2.7987 | 2.7969 |
| 7 | 19.2793 | 2.7982 | 2.8003 |
| 8 | 20.0880 | 2.7941 | 2.7918 |
| 9 | 22.5144 | 2.7478 | 2.7441 |
| 10 | 23.3232 | 2.7127 | 2.7153 |
| 11 | 24.1320 | 2.6640 | 2.6638 |
| 12 | 26.5583 | 2.4356 | 2.4334 |
| 13 | 27.3671 | 2.3376 | 2.3395 |
| 14 | 28.1759 | 2.2341 | 2.2327 |
| 15 | 30.6023 | 1.9369 | 1.9363 |
| 16 | 31.4110 | 1.8576 | 1.8592 |
| 17 | 32.2198 | 1.7943 | 1.7911 |
| 18 | 34.6462 | 1.7128 | 1.7057 |
| 19 | 36.2637 | 1.7288 | 1.7281 |
| 20 | 37.8813 | 1.7453 | 1.7460 |
| Radius ra | Squash Factor ρ | Accept Ratio ) | Reject Ratio ) | Number of Rules | MAE |
|---|---|---|---|---|---|
| 0.5 | 0.4 | 0.2 | 0.1 | 7 | 0.0900 |
| 0.5 | 0.4 | 0.2 | 0.1 | 8 | 0.0130 |
| 0.5 | 0.3 | 0.2 | 0.1 | 11 | 0.0003 |
| 0.4 | 0.3 | 0.2 | 0.1 | 16 | 0.00028 |
| 0.3 | 0.3 | 0.2 | 0.1 | 19 | 0.00027 |
| 0.5 | 0.3 | 0.2 | 0.1 | 24 | 0.0002 |
| 0.5 | 0.3 | 0.2 | 0.1 | 25 | 0.00015 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nahraoui, Y.; Aassif, E.H.; Elouaham, S.; Nassiri, B. A Fuzzy Model for Predicting the Group and Phase Velocities of Circumferential Waves Based on Subtractive Clustering. Signals 2025, 6, 56. https://doi.org/10.3390/signals6040056
Nahraoui Y, Aassif EH, Elouaham S, Nassiri B. A Fuzzy Model for Predicting the Group and Phase Velocities of Circumferential Waves Based on Subtractive Clustering. Signals. 2025; 6(4):56. https://doi.org/10.3390/signals6040056
Chicago/Turabian StyleNahraoui, Youssef, El Houcein Aassif, Samir Elouaham, and Boujemaa Nassiri. 2025. "A Fuzzy Model for Predicting the Group and Phase Velocities of Circumferential Waves Based on Subtractive Clustering" Signals 6, no. 4: 56. https://doi.org/10.3390/signals6040056
APA StyleNahraoui, Y., Aassif, E. H., Elouaham, S., & Nassiri, B. (2025). A Fuzzy Model for Predicting the Group and Phase Velocities of Circumferential Waves Based on Subtractive Clustering. Signals, 6(4), 56. https://doi.org/10.3390/signals6040056








