Closed-Form Solution Lagrange Multipliers in Worst-Case Performance Optimization Beamforming
Abstract
1. Introduction
2. Mathematical Model of the Problem and Current Results
3. Derivation of the Closed Formula for Lagrange Multiplier λ
3.1. One Plane Wave Irradiation
3.2. Multiplane Wave Irradiation
4. Computer Simulations
4.1. Anti-Interference Performance and Estimation for Expected Signal
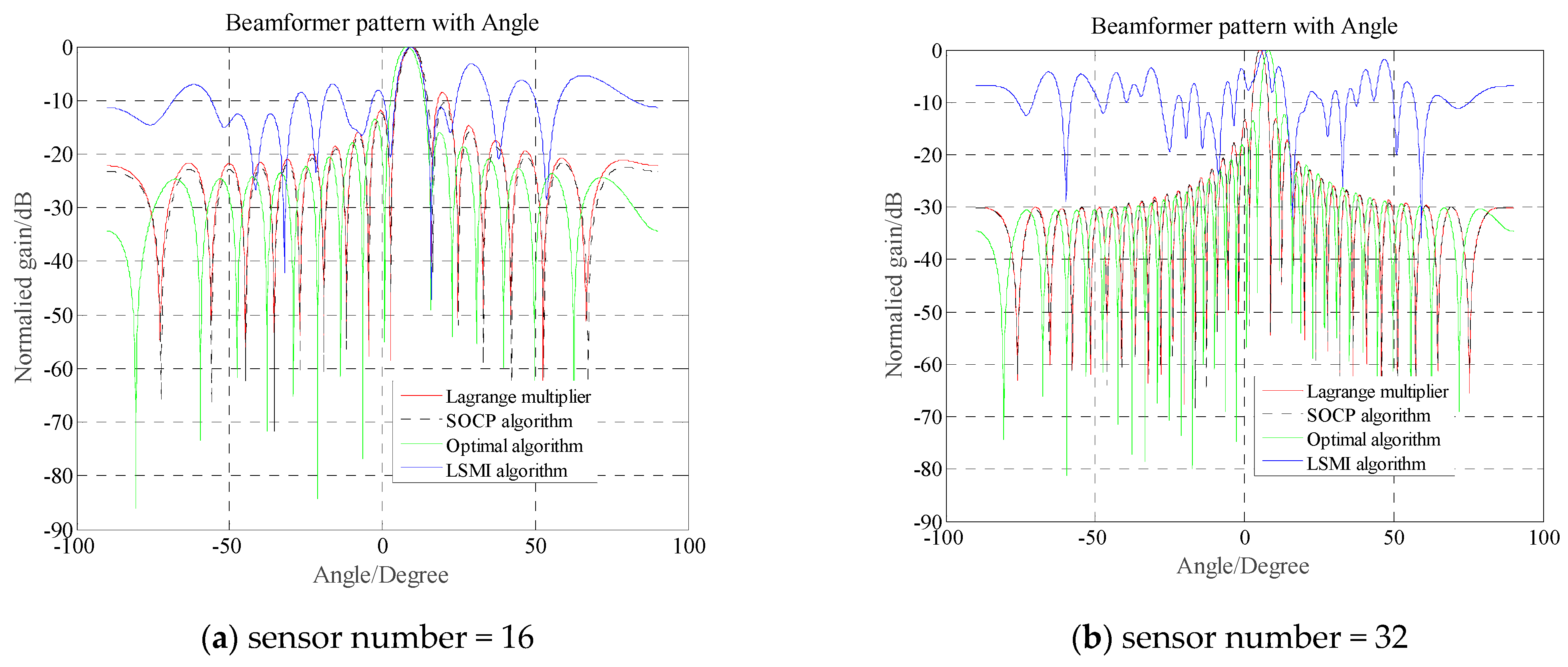
- Anti-interference performance. In this scenario, the expected signal direction was set to 8°, whereas the actual incoming wave signal direction randomly obeyed θ = 8° + (rand (.) − 0.5) 4°. Figure 1 shows that the output SINR varies with the input SNR. Figure 2 shows the directional gain with respect to the spatial angles. Four methods were used with arrays of 16 and 32 sensors for the simulations.

- DOA estimation of the expected signal. As shown in Figure 2a,b, the diagonal loading method has a significantly lower capability for identifying the direction of the incoming waves than the Lagrange multiplier and SOCP methods. The latter two methods exhibited nearly identical performances, with a relatively higher gain at 8° than at the other angles. By comparing Figure 2a,b, this phenomenon becomes more pronounced as the number of sensors increases. This indicates that the two methods using the WCPO have strong capabilities for resolving the direction of incoming waves.
- Comparison of the performance of Equations (16) and (21). To verify the effectiveness of (16), we perform a simulation using (21) with the same signals and array manifolds as those used in (16). The simulation results are shown in Figure 3a,b. By comparing Figure 1a and Figure 3a with Figure 1b and Figure 3b, respectively, they had the same performance characteristics. In particular, Equation (16) can approximately substitute Equation (21) for the design of robust adaptive beamforming.

4.2. Computation-Complexity Analysis
- (1)
- SOCP employs an interior-point approach with a computational complexity of approximately [17]. The convergence control parameter δ = 10−8. The parameter v denotes the number of independent variables in the constraints, which is equal to the number of array elements N in this study. Therefore, the computational complexity is .
- (2)
- The computational complexity of the proposed formula was determined using A, B, and C. The computational complexity of is , and that of is . Therefore, the computational loads for B, C, and A are , and , respectively. The complexity of this formula is known as .
- (3)
- The computational load of LSMI is .
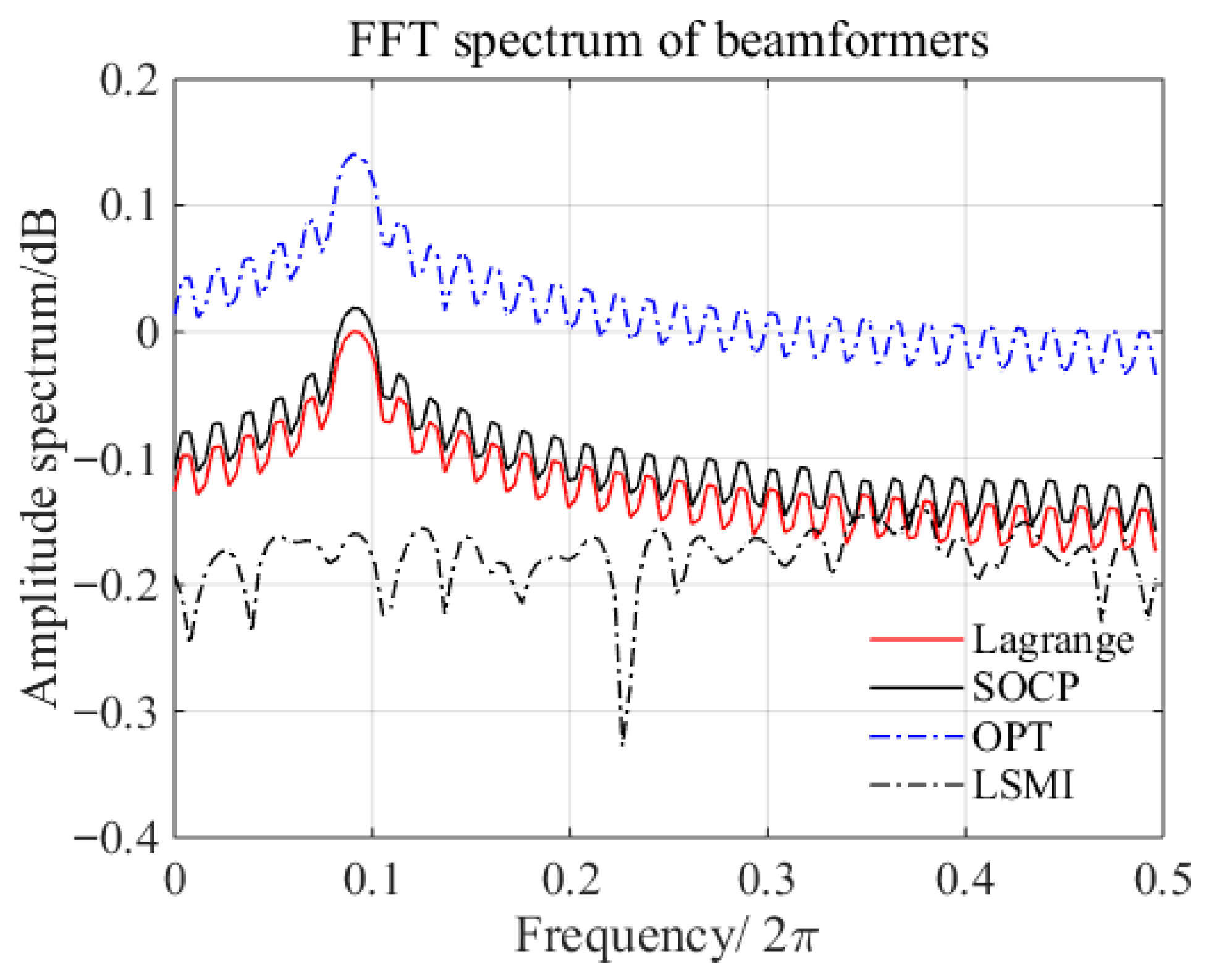
4.3. Feature Analysis and Comparison of Beamformers
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| WCPO | Worst-case performance optimization |
| SOCP | Second-order cone programming |
| DOA | Direction-of-arrival |
| SINR | Signal-to-interference-plus-noise ratio |
References
- Khabbazibasmenj, A.; Vorobyov, S.A.; Hassanien, A. Robust adaptive beamforming based on steering vector estimation with as little as possible prior information. IEEE Trans. Signal Process. 2012, 60, 2974–2987. [Google Scholar] [CrossRef]
- Zhang, P.; Yang, Z.; Jing, G.; Ma, T. Adaptive beamforming via desired signal robust removal for interference-plus-noise covariance matrix reconstruction. Circuits Syst. Signal Process. 2021, 40, 401–417. [Google Scholar] [CrossRef]
- Li, W.; Qu, X.; Yang, X.; Han, B.; Zhang, Z.; Fathy, A.E. Robust adaptive beamforming method based on steering vector phase correction and covariance matrix reconstruction. IEEE Commun. Lett. 2024, 28, 193–197. [Google Scholar] [CrossRef]
- Li, H.R.; Geng, J.; Xie, J.H. Robust adaptive beamforming based on covariance matrix reconstruction with RCB principle. Digit. Signal Process. 2022, 127, 103565. [Google Scholar] [CrossRef]
- Zhang, P.; Yang, Z.; Liao, G.; Jing, G.; Ma, T. An RCB-like steering vector estimation method based on interference matrix reduction. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 636–646. [Google Scholar] [CrossRef]
- Zhang, J.K.; Zheng, Z.; Wang, C. Robust adaptive beamforming based on covariance matrix reconstruction with Gaussian random dimensionality reduction. Circuits Syst. Signal Process. 2024, 43, 6035–6046. [Google Scholar] [CrossRef]
- Huang, Y.; Fu, H.; Vorobyov, S.A.; Luo, Z.-Q. Robust adaptive beamforming via worst-case SINR maximization with non-convex uncertainty sets. IEEE Trans. Signal Process. 2023, 71, 218–232. [Google Scholar] [CrossRef]
- Mohammadzadeh, S.; Nascimento, V.H.; Lamare, R.C.; Kukrer, O. Covariance Matrix Reconstruction Based on Power Spectral Estimation and Uncertainty Region for Robust Adaptive Beamforming. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3848–3858. [Google Scholar] [CrossRef]
- Huang, Y.; Zhou, M.; Vorobyov, S.A. New Designs on MVDR Robust Adaptive Beamforming Based on Optimal Steering Vector Estimation. IEEE Trans. Signal Process. 2019, 67, 3624–3638. [Google Scholar] [CrossRef]
- Irani, K.H.; Huang, Y.; Vorobyov, S.A. SINR Maximizing Distributionally Robust Adaptive Beamforming. IEEE Trans. Signal Process. 2025, 73, 2542–2557. [Google Scholar] [CrossRef]
- Vorobyov, S.A.; Gershman, A.B.; Luo, Z.Q. Robust Adaptive Beamforming Using Worst-Case Performance Optimization: A Solution to the Signal Mismatch Problem. IEEE Trans. Signal Process. 2003, 51, 313–324. [Google Scholar] [CrossRef]
- Lorenz, R.G.; Boyd, S.P. Robust Minimum Variance Beamforming. IEEE Trans. Signal Process. 2005, 53, 1684–1696. [Google Scholar] [CrossRef]
- Liao, B.; Chan, S.C.; Tsui, K.M. Recursive Steering Vector Estimation and Adaptive Beamforming under Uncertainties. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 489–500. [Google Scholar] [CrossRef]
- Zhang, P.; Yang, Z.W.; Jing, G. Further study on the RCB-like steering vector estimation method: Closed-form solution derivation via accurate Lagrange multiplier calculation. Signal Image Video Process. 2025, 19, 122. [Google Scholar] [CrossRef]
- Yin, J.; Wang, S.; Wang, H. A robust adaptive beamforming method based on variable constraint set. Acta Acust. 2021, 46, 871–883. (In Chinese) [Google Scholar]
- Trees, H.L. Optimum Array Processing; Wiley: Hoboken, NJ, USA, 2002; pp. 453–470. [Google Scholar]
- Tunçel, L. Polynomial Path-Following Algorithms for Linear and Convex Programming; Princeton University Press: Princeton, NJ, USA, 1999; pp. 89–95. [Google Scholar]
| Algorithm | Sensor Num. = 16 | Sensor Num. = 32 | Sensor Num. = 64 |
|---|---|---|---|
|
Operators/SOCP Operators/LSMI Operators/Proposed formula |
|
|
|
| Algorithms | SOCP/s | LSMI/s | Lagrange Multiplier/s |
|---|---|---|---|
| 16 sensors | 165.09375 | 0.01563 | 0.14063 |
| 32 sensors | 323.03125 | 0.51563 | 0.20313 |
| 48 sensors | 325.10938 | 0.25000 | 1.07813 |
| 64 sensors | 1233.79688 | 1.48438 | 1.59375 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pei, T.; Pei, B. Closed-Form Solution Lagrange Multipliers in Worst-Case Performance Optimization Beamforming. Signals 2025, 6, 55. https://doi.org/10.3390/signals6040055
Pei T, Pei B. Closed-Form Solution Lagrange Multipliers in Worst-Case Performance Optimization Beamforming. Signals. 2025; 6(4):55. https://doi.org/10.3390/signals6040055
Chicago/Turabian StylePei, Tengda, and Bingnan Pei. 2025. "Closed-Form Solution Lagrange Multipliers in Worst-Case Performance Optimization Beamforming" Signals 6, no. 4: 55. https://doi.org/10.3390/signals6040055
APA StylePei, T., & Pei, B. (2025). Closed-Form Solution Lagrange Multipliers in Worst-Case Performance Optimization Beamforming. Signals, 6(4), 55. https://doi.org/10.3390/signals6040055





