Abstract
Next-generation wireless communications aim to utilize mmWave/subTHz bands. In this regime, signal propagation is vulnerable to interferences and path losses. To overcome this issue, a novel technology has been introduced, which is called reconfigurable intelligent surface (RIS). RISs control digitally the reflecting signals using many passive reflector arrays and implement a smart and modifiable radio environment for wireless communications. Nonetheless, channel estimation is the main problem of RIS-assisted systems because of their direct dependence on the system architecture design, the transmission channel configuration and methods used to compute channel state information (CSI) on a base station (BS) and RIS. In this paper, a concise survey on the up-to-date RIS-assisted wireless communications is provided and includes the massive multiple input-multiple output (mMIMO), multiple input-single output (MISO) and cell-free systems with an emphasis on effective algorithms computing CSI. In addition, we will present the effectiveness of the algorithms computing CSI for different communication systems and their techniques, and we will represent the most important ones.
1. Introduction
The main goal of the sixth generation (6G) wireless technologies is to upgrade communication quality. Since the number of mobile devices is rapidly increasing, the issue concerning the efficient propagation of data at their distribution nodes unavoidably arises. For this reason, it is essential to study the improvement of bandwidth, system capacity and reliability, as well as quality of service (QoS). The percentage of energy consumption, carbon footprint and hardware costs are also considered [1]. In addition, the mmWave/subTHz band is already used in current research activity, which provides a large gain in the performance of 6G technology communication systems, although it is quite sensitive to physical obstacles and/or propagation attenuation effect. To avoid the above problems, the technology of RISs has emerged [2].
Specifically, an RIS consists of a surface designated by software that is typically connected to a prepared set-up system which mitigates blocking effects. It consists of many separately controllable, low-cost, and quasi-passive elements. The RIS succeeds in adapting to alterations in the propagation environment and modulating the radio waves, as each element can cause an adaptable phase shift to each detected signal, in order to enable a dynamic control over the wireless propagation channel [3]. Therefore, the RIS does not need complex signal processing units, as it is able to create a virtual path between the transmitter and receiver. Hence, throughput is improved, and a higher performance is achieved [2]. The contribution of the RIS is represented in [4] for reducing transmitted power at the BS using signal-to-interference-plus-noise ratio (SINR) constraints in multi-user MISO (MU-MISO) RIS-assisted systems for the joint improvement of the precoder and reflecting beamforming matrices (RBMs); in [5], the total rate reached the maximum under the transmit power limitation; in [6], the total rate was improved by considering the associated attenuation of Rayleigh waves and the usual hardware faults in both the transceiver and RIS; in [7], reaching the maximum of the minimum user equipment (UE) rate was investigated in the case of a large amount of antennas; in [8], the effect of hardware faults was assessed; in [9], the effect of incomplete CSI in the possibility of shutdown was demonstrated. Furthermore, there are discussions on how the technology of RIS contributes to the efficient transmission of energy consumption on the internet of vehicle (IoV) networks [10] and in passive meta surface-coated devices [11].
In addition, a new RIS structure, which reflects and absorbs the transmitted signal through an absorbing agent equipped with radio frequency chains, performs signal processing techniques, configures its phase shift matrix, and does not need incoming signal control [2]. It is called a hybrid RIS (HRIS) and research has been presented in [12,13,14,15]. In [16], concerning sparse antenna activation based on a channel extension strategy in a HRIS, a full one-hop channel optimization and beam searching scheme design for inclusion in channel subsampling are proposed.
Beamforming (i.e., precoding in transmission and combining in reception) is a key signal processing technique to ensure reliable communication between the transmitter and receiver. Although conventional MIMO systems widely consider single-stage all-digital beamforming, two critical challenges for mMIMO systems arise: high hardware costs due to a single dedicated radio frequency (RF) chain per antenna and large channel estimation overheads [17]. In several studies, such as [18,19,20,21], the hybrid beamforming (HBF) solution is proposed, which generates the RF stage through slow time-varying angular information and the digital baseband (BB)-stage through reduced-dimensional CSI. HBF has been studied, mainly in RIS-assisted mMIMO systems, to achieve the requirements for full CSI estimation [22,23]. In [22], the spectral performance is improved by the joint optimization of the RIS phase shift and hybrid precoder/compressor two-stage algorithm, while cost and energy consumption are reduced. In [24], the HBF scheme is used in a mmWave RIS-assisted broadband MIMO system with geometric mean beamforming decomposition in order to avoid complex bit/power allocation, while the authors in [23], designed a joint RIS phase shift matrix and HBF with a direct channel between the transmitter and receiver.
To make use of the advantages promised by the RIS, accurate CSI is essential, although it is difficult to achieve because a complex signal processing capability of the RIS [25] is missing. Furthermore, the RIS consists of passive components, which do not process signals and do not evaluate the UE-RIS and RIS-BS channel separately, but sequentially (i.e., the cascaded end-to-end channel). When there are many BS antennas and RIS reflectors, the number of sequential channel coefficients will be large; and so will be the number of pilots [26]. This causes a problem for channel estimation in any communication system. Other parameters that affect the channel estimation are the distance of the users from the RIS, the type of communication system used, but mainly the algorithm used for the channel estimation. We cannot assume which algorithm is the best for channel estimation in every RIS-assisted system architecture because each system has different requirements. Hence, there has been great contributions on channel estimation for RIS-assisted communication systems, such as those in [1,4,17,26,27].
The purpose of the current research is to provide an inclusive and up-to-date survey of papers in RIS-assisted wireless communications, such as MIMO and MISO system communications. Emphasis is given on the practical challenges of BS, RIS and user channels to estimate their value using optimized algorithms with different channel models and system configurations. This paper presents several methods to optimally solve critical issues of channel estimation, such as pilot overhead reduction. The complexity of these methods is presented and the communication systems in which they can be used are selected according to their positive outcome. In addition, the challenges of the proposed methods are mentioned in order to be handled in future research.
The rest of the paper is organized as follows: Section 2 presents system models for channel estimation in RIS-assisted systems with different system architectures. Section 3 presents optimal channel estimation algorithms using statistical CSI (S-CSI) or instantaneous CSI (I-CSI). Section 4 presents the results of the proposed optimal algorithms per communication system, and some concluding remarks are drawn in Section 5.
Notations: is a scalar, x is a vector, X represents a matrix, and denotes a set. , , and denote , , and the Frobenius norm, respectively. is the Kronecker product. , and are the -th element of vector a, the ()-th element of matrix and the ()-th element of tensor , accordingly. The notations , and each stand for the transpose, Hermitian transpose and trace operators. The is the expectation operator and denotes an diagonal matrix that consists of the elements of vector . is the symbol for a circularly symmetric complex Gaussian vector with zero mean and covariance matrix is the wavelength, is the discount factor, is the finite set of states, is the finite set of actions, is the vector of policy parameters and denotes the vector of policy parameters before the update; is the policy neural network with parameters denoted by and , and are the action and state of given time step t, respectively, with , is the reward function, is the phase shift introduced by the -th element of the RIS, is the velocity of the user, = 3 × 108 m/s is the speed of light and is the carrier frequency. Finally, stands for the identity matrix.
2. System Models for RIS-Assisted Systems
Table 1 summarizes the latest research on channel estimation in different RIS-assisted system settings. We noticed that most research has been carried out in narrowband for one or more users and channel estimation has been accomplished in cascaded channels. For the remaining categories, more research is needed.

Table 1.
RIS channel estimation for different system setups [28].
From Table 1 we observed that there are many different methods on how the channel can be estimated in RIS-assisted MISO and MIMO systems. For this reason, we searched and present below additional research on deep learning techniques, high user mobility scenarios, estimation in cascaded channels, use of neural networks and ZF detection techniques. We focused on these scenarios because most of the literature uses and develops them. In addition, we present other methods, such as tensor algorithms, which are used in more recent literature.
2.1. MISO Systems
The authors in [71,72] use S-CSI design passive beamformers for MISO systems and a purely S-CSI-based approach for the design of RIS-assisted multi-user downlink systems is proposed in [4]. Furthermore, in [73], the authors use a tensor algorithm and capitalize on the parallel factor (PARAFAC) decomposition to create an efficient iterative algorithm based on the alternating least squares (ALS) concept to answer the channel estimation issue in the downlink of a MISO network. For this reason, an approximate expression is established to employ the sum rate and formulate an active-passive joint beamforming design problem. Because of the non-convex constraint, the objective function is intractable and complicates the relationship between the BS transmit beamformer and RIS passive beamformer. In [27], the authors solve this optimization problem by using a proximal policy optimization (PPO) algorithm, which is a powerful reinforcement learning (RL) algorithm from the actor–critic family and outperforms other actor–critic algorithms. In the following subsection, we present the system and channel models for the considered RIS-assisted MISO communication systems, which are similar to those in [71,72,73,74].
2.1.1. System Model
The system and channel models for the considered RIS-assisted MISO communication systems are similar to those in [74]. Specifically, Figure 1 depicts an RIS-assisted MU-MISO system with M antennas at the BS, communicating with K users, and the RIS is equipped with antennas for signal transmission. Each -th reflective element of the RIS has a reflective coefficient and the reflectance matrix of the RIS panel is depicted as Ξ = diag(,…, ), where = with denoting the phase shift of the -th element of the RIS. All channel models follow the Rician distribution [74]. is the direct channel from BS to the -th UE, that from the BS to RIS and that from the RIS to the k-th UE. The corresponding effective channel from the transmitter to the -th UE would be [74].
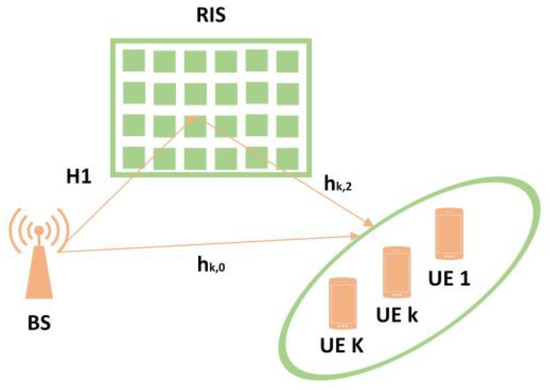
Figure 1.
Illustration of the RIS-assisted MU-MISO communication system.
The channel matrix between the RIS and -th UE is given as [74,75,76]
where is the distance dependent path-loss factor, is the Rician factor between the RIS and the -th UE. Furthermore, where is the azimuth and elevation angle of departure (AoD) from the RIS to the k-th UE, respectively, and is the array response vector at the RIS side. For is the assumed uniform planar arrays (UPAs) and is given by
where D is the distance between antenna elements and J = where and are the number of elements at the horizontal and vertical axes, accordingly [74].
The channels between the BS and RIS, and the direct one from the BS to the -th receiver are depicted as [75,76,77]
where is the distance dependent path-loss, is the Rician factor of the BS-RIS link. δu,0 and κu,0 stand for the distance dependent path-loss and the Rician factor between BS and the k-th UE link, correspondingly [74]. In addition, , where φ(RIS) and ψ(RIS) are the azimuth and elevation angle of the angle of arrival (AoA) to the RIS and φ(BS) and ψ(BS) express the azimuth and elevation AoD from the BS to the RIS direction. On the contrary, , where and are the azimuth and elevation AoD from the BS in the direction of the k-th UE [74].
Furthermore, there is no spatial correlation among the antennas and the distribution of the non-line-of-sight (NLoS) component of the channels , and are independently and identically distributed complex Gaussian random variables with zero-mean and unit-variance [74].
Finally, the obtained signal for the -th UE is equal to
where denotes the allocated power and xk is the signal for -th UE, is the beamforming vector for the -th UE, represents a circularly symmetric complex additive Gaussian noise with [74].
2.1.2. Problem Formulation
In the problem formulated by the authors in [74], it is assumed that the transmitter is not able to acquire CSI. Therefore, the trouble to reach the maximum total rate is based on the channel statistics, i.e., the information angle and Rician factors, through the recursive linkage [78]. Following the mathematical calculations, the authors in [74] arrive at the solution of the following optimized problem to be a function of the distance-dependent path loss, the Rician factors and other channel statistics, and the attenuation effect has been averaged on a small scale, using the proposed PPO algorithm.
(Theorem III.1. in [74]).
2.2. MIMO Systems
Studies in [1,2,3,17,25,26,69,70,79,80] focus on creating optimal channel estimation algorithms in RIS-assisted mMIMO and MIMO systems. In [3], the realistic characterization of the achievable downlink of the RIS-assisted mMIMO systems is presented, accounting for user mobility and I-CSI under correlated Rayleigh fading conditions, when regularized ZF (RZF) precoding is applied. In [25], a two-stage strategy is used for the estimation of cascaded uplink channels without using a standard user for the RIS-assisted MU mmWave system. In [26], an efficient three-stage channel estimation method with a low pilot overhead is presented in an RIS-assisted single-antenna MU mmWave communication system, and the BS, RIS and UE are equipped with UPA. In [17], an RIS angular-based hybrid beamforming (AB-HBF) system requires low CSI overhead for the mmWave mMIMO system with a mmWave channel model based on 3D geometry of three stages: (i) RF beamformers, (ii) BB precoder/combiner, and (iii) RIS phase shift design. In [1], the authors use a tensor algorithm for the joint estimation of involved channels and imperfections in an RIS-assisted MIMO system. In [69,70], the authors create phase shift design schemes in uplink with linear ZF detection in the receiver side of an RIS-assisted MIMO system. Furthermore, in [81,82], the authors develop simple iterative and closed-form channel estimation algorithms based on the PARAFAC modeling of the single-user MIMO scenario. Finally, in [79,80], the researchers focus on a cell-free RIS-assisted system architecture where channel estimation is achieved sequentially. Next, we present a cell-free and a cell RIS-assisted mMIMO mmWave system.
2.2.1. Cell-Free Communication System
- Scenario Caption and Signal Model
Figure 2 illustrates an RIS-assisted single user cell-free communication system. Based on [80], they assume a time division duplex (TDD) mMIMO system, where BSs with the assistance of RISs serve UE. The -th BS is equipped with antennas and each RIS has reflective elements, respectively, where = 1, 2, …, and = 1, 2, …, . In this model, the RISs function as antenna arrays far away from the BS to improve capacity and provide greater coverage at a low cost, to enhance cell-free communications. In addition, a central processing unit (CPU) facilitates the joint signal processing of multiple BSs. The RISs are managed by the wire to the BSs or CPU.
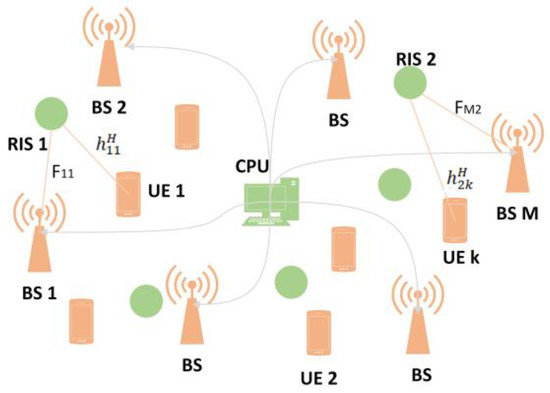
Figure 2.
An RIS-assisted cell-free communication system.
Quasi-static block-fading channels are considered; the channel matrices from the -th BS to the -th RIS are represented by and the channel matrices from the -th RIS to the -th UE are represented by . For the -th RIS, the reflection coefficient matrix is , where and is the reflection coefficient of the -th element of the -th RIS, = 1 and are the amplitude and phase, accordingly. The channel matrix from the -th BS to the -th UE affected by the -th RIS is . Additionally, the RIS has the same number of reflection elements, i.e., = = … = = . The downlink CSI can be achieved by the uplink channel estimation due to TDD systems. To estimate the uplink channel, the orthogonal pilot sequences and reflection coefficients for the channel measurement should be designed. It also consists of subframes Q for RISs, and each subframe contains symbol durations T, where [80].
The reflection vector of the -th RIS in the -th sub-frame is equal to , the pilot sequence of the -th UE is and , , where is the transmit power of each UE. The channel that directly links the BS and the UE considers all RISs to be disabled and the direct channel estimation is not considered. In the -th sub-frame, the received signal at the -th BS is written as
where represents the incoming Gaussian noise following [80].
In [80], since the orthogonal pilot sequences are employed and considering the low mobility scenarios for the -th UE, we obtain
where . By collecting the signals of the Q sub-frames via raw stacking, the received signal is expressed as
- Channel Model of Cell-Free Communication System
In [80], the BSs and RISs are supplied with a uniform linear array (ULA), and the physical channels defining the geometric arrangement are
where and are the number of paths of and , accordingly, and are the complex gains of the -th and -th paths of the two channels, accordingly. Additionally, and are AoDs from the -th BS to the -th RIS and from the -th RIS to the -th UE, accordingly. is the AoA from the -th BS to the -th RIS. is the antenna inter-element distancing. and are ULA steering vectors of BSs and RISs, accordingly. Not losing the generality, we have
where L is the number of antenna elements.
2.2.2. Cell Communication System
Figure 3 shows an RIS-assisted downlink cell mMIMO communication system [3], where the BS has antennas in communication with the single-antenna non-cooperative UEs behind the obstacles. The RIS has reflecting elements, where = 1 and 2, …, RIS is in the LoS of the BS to assist the contact with the UEs. The same scenario was considered where the BS and RIS are installed at a high altitude and with fixed locations. The size of each RIS element is , where and stand for its vertical height and its horizontal width, accordingly. The suggested model also examines the potential presence of direct links between the BS and the UEs.
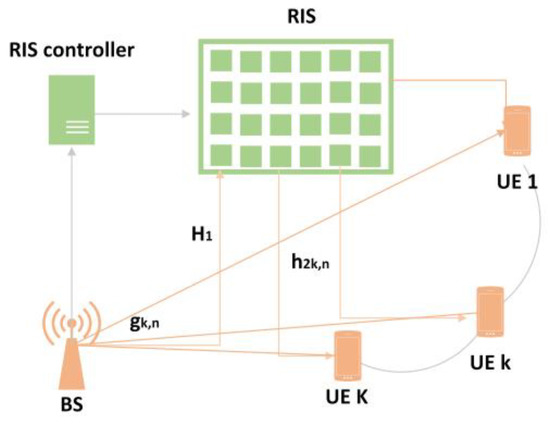
Figure 3.
RIS-assisted cell mMIMO communication system.
- Channel Model
A pseudo-static attenuation model with a larger bandwidth, rather than the channel bandwidth, is calculated. They generate a typical block attenuation model with each coherence interval/block included, for the channel usage, is the amplitude coherence (Hz) and is the time coherence (s). Inside the transmission of each relevance block and during the -th time slot, let and be the LoS channel between the BS and the RIS and the channel between the RIS and -thUE at the -th time instant. Consider that for = 1, …, expresses the -th column vector of . is the direct channel between the BS and -th UE at the -th moment. The greater part of existing studies e.g., [4,5], assumed the independent Rayleigh model, but, compared fading appeared and changed the performance [83]. and are depicted in terms of related Rayleigh fading distributions as
where and stand for the deterministic Hermitian-symmetric positive semi-definite correlation matrices at the RIS and the BS accordingly, with and given. Furthermore, expresses the path-losses of the RIS UE and is defined as the path-losses of the BS UE links. Particularly, is supposed to be small because of the blockages between the BS and the UEs. Furthermore, and indicate the matching fast-fading vectors at the -th moment. Notice that fast fading vectors shift within each coherence block, while the parallel matrices are believed to be continuous for many coherence blocks [3].
The high level LoS channel is illustrated as
where is the path-loss between the BS and RIS, while and are the inter-antenna partition at the BS and inter-element partition at the RIS, accordingly [49]. Moreover, and represent the elevation and azimuth line of sight (LoS) AoD at the BS regarding the RIS reflecting element , and represent the elevation and azimuth LoS AoA at the RIS. It is useful to point out that can be acquired similarly to the covariance matrices since the dependence of their statements on the distances and the angles is related [3].
The elements are defined by the diagonal RBMs ∈ , where ∈ [0, 2π] and ∈ [0, 1] are the phase and amplitude coefficient for the RIS element , accordingly. Maximum signal reflection is, i.e., = 1 ∀ [4]. The overall channel vector , conditioned on Θ is delivered as , where . Because depends on the path-losses, the correlation matrices can also be identified by the network and , which are all expected to be known as clarified earlier [3].
- Channel Aging
In practice, the UE mobility causes channel aging phenomenon [84,85,86,87]. In [3], authors assume that the RIS’s components move the same rating to a unique UE and this results in a Doppler shift that changes channel with time. Therefore, unlike the conventional block fading channel model, the flat fading channel coefficients differ from symbol to symbol. Still, they are fixed within a symbol. The symbol duration is expected to be less than or even to the coherence time of all UEs. Studies on the impact of channel aging assume the same in [84,85,86,87]. The channel use is represented by ∈ {1, …, } [3].
Arithmetically, the channel at the -th time instant is denoted as a function of its initial state . The advanced component is [87]
where is the separate innovation component at the -th time instant and is the sequential correlation coefficient of UE in the middle of the channel at time 0 and with are the zeroth-order Bessel function of the first kind, is the channel testing duration, is the maximum Doppler shift and [3].
3. Channel Estimation in the RIS-Assisted Communication Systems
In this section, we will present some optimized algorithms proposed for channel estimation in the MISO and MIMO model systems for RIS-assisted systems. First, the utility of S-CSI and I-CSI is explained.
3.1. S-CSI and I-CSI
In [9], it has been proven that large-scale antenna systems may be impaired from pilot contamination impact with many antennas. In frequency division duplex (FDD) systems, the BS accesses the CSI using a feedback channel. When users have high mobility, S-CSI is used, which varies more slowly than I-CSI [88]. The BS receives feedback for a longer time to reduce the amount of feedback [74]. The RIS-assisted communication systems are often hampered by the difficulty of obtaining accurate I-CSI [89]. Therefore, there are several studies on I-CSI in [90,91] and channel reciprocity in TDD systems and uplink training at the BS have been exploited, respectively. S-CSI has a much more balanced quantity and changes very gradually. First, channel statistics are collected and updated in sufficient time. Furthermore, signal exchange overhead and computation overhead can be decreased because the state of the RIS does not need to change often. Doing so, signal exchange overhead and computation overhead can be reduced, and S-CSI is used to verify RIS coefficients over an extended period. For all of these reasons, the CSIs of the BS-RIS and RIS-UEs links must be punctual to optimize the reflection coefficients of RIS-assisted systems. In addition, CSI can be difficult to determine, due to the large number of passive reflective elements in BS-RIS and RIS-UEs links. As a result, it is necessary to provide low training loads while maximizing the operation profits provided by the RIS. Overall, S-CSI provides an efficient direction in system design because it varies relatively slowly and can be obtained quite easily [74,75].
3.2. MISO Systems
In this section, we present the optimized algorithms, which use different techniques for the channel estimation in MISO systems.
3.2.1. Alternating Optimization with the Semidefinite Relaxation (SDR) Technique
In [4], the transmit beamforming at the BS is designed together with the phase shifts at the RIS based on all BS-RIS, UE-RIS and UE-BS channels, to fully realize the network beamforming gain. They apply the semidefinite relaxation (SDR) technique to avoid the non-convex SINR limitations, as well as the signal unit-modulus limitations imposed by the MU passive phase shifters. Furthermore, to reduce the computational complexity, an efficient algorithm is used based on the alternating optimization of the phase and transmission shifts of the beamforming vector in an iterative manner, where their optimal solutions are derived in closed form with the other being fixed. For more details see Algorithm 1 in [4].
3.2.2. PPO Algorithm
As we mentioned in Section 2, the authors of [74] use the PPO algorithm on the RIS-assisted MU-MISO system to solve optimization problem P1. PPO is presented in [27] and has been shown to outperform other benchmark algorithms, as it is easy to set up, useful and easy to execute, and is a model-free, policy-based, actor–critic strategy ranking method.
Think about an infinite-horizon discounted Markov decision process (MDP), specified by the tuple , where P: is the transition probability distribution and finally, [0, 1]. The purpose of PPO is to maintain the consistency of the trust region policy optimization (TRPO) algorithms because they guarantee monotonic improvements considering the Kullback–Leibler (KL) variance of policy updates using first-order optimization methods. The TRPO increases the objective purpose and limits the size of the policy update [74]. Specifically,
with the expectation showing the observed average over a fixed batch of samples, in an algorithm that varies between sampling and optimization. Furthermore, is an estimator of the gain function at timestep t and is given by
where and are the action-value of the value functions, accordingly, and are specified as follows
where . The valuation of the benefit task in the interval [0, T] is given by [27]
with and is a hyperparameter and represents the factor for the trade-off of bias and variance for the generalized advantage estimator (GAE) [74].
Then, let signify the probability ratio , then obviously = 1, hence, according to (17), the TRPO maximizes
where CPI is the conservative policy iteration. The major problem of optimization in (22) is the probability of a large policy update. If then becomes very large and policies change dramatically. To unravel this issue, PPO alters the objective function in (22), as follows
where is a hyperparameter. The simplification of the objective function (22) was carried out because using a small set of experiment sizes; the algorithm is not too acquisitive in favoring actions with positive benefit functions, nor too fast in preventing actions with negative benefit functions.
The PPO is an MDP with observation and action spaces. When resolving the joint active and passive beamforming problem on the BS, the RIS and UE of the MISO system are declared in the E environment, and the agent is the BS that controls the RIS. For more details, see Algorithm 1 in [74].
3.2.3. Pseudocode of Asynchronous One-Step Q-Learning
In [92], the authors propose an RL algorithm in an RIS-assisted MU-MISO system, where instead of repeating experience, they asynchronously execute multiple agents in parallel over multiple instances of the environment. This parallelism likewise decouples the agents’ data into a more stationary procedure, because at each time step, the parallel agents experience a variety of different states. This allows a wider range of fundamental RL algorithms within policy, such as critical action methods, and non-policy RL algorithms, such as Q-learning, to be robust and efficiently implemented using deep neural networks.
They believe the standard RL setting, where an agent relates with environment E over a few discrete time steps. At each time step t, the agent obtains a state and takes an action from some set of possible actions A, according to its policy π. In response, the agent obtains the next state and obtains a scalar reward . The method remains until the agent achieves a terminal state, after which the procedure restarts. The return Rt = is the total accumulated return from time step t with ω ∈ (0, 1]. The purpose of the agent is to improve the expected return from each state [92].
In value-based model-free RL methods, the action value function is characterized using a function approximator, such as a neural network. Let be an approximate action-value function with parameters . The updates to are obtained from a variety of RL algorithms. One example of such an algorithm is Q-learning, which directly estimates the optimal action value function: . In one-step Q-learning, the parameters of the action value function are studied by iteratively minimizing a sequence of loss functions, where the i-th loss function is described as
where is the state encountered after state s [92].
The above method is mentioned as one-step Q-learning because it renews the energy value to the one-step return . A disadvantage of utilizing one-step methods is that acquiring a reward r only immediately impacts the value of the pair of state actions s that led to the reward. The values of the other pairs of state actions are only indirectly affected through the updated value . This can make the learning process slow, as many updates are expected to generate a reward to the relevant previous states and actions [92]. For more details, see Algorithm 1 in [92].
3.3. MIMO Systems
In this section, we present the optimized algorithms, which use different techniques for the channel estimation in MIMO systems.
3.3.1. Three-Dimensional Multiple Measurement Vector (3D-MMV) and the Look Ahead Orthogonal Match Pursuit (3D-MLAOMP) Algorithm
In [80], the scenario focuses on a multi-BS and multi-UE in RIS-assisted cell-free systems and investigates the multi-BS cooperation and multi-UE joint estimation. For a cascaded channel estimation, a 3D-MMV framework has been used to jointly estimate the cascaded AoDs for all users in which the BS and RIS and multi-UE channels contribute to a common part (BS-RIS) (characteristic 1). They additionally use tensor contraction to present a 3D-MLAOMP algorithm. Moreover, when UE and RIS and multi-BS channels communicate on a common part (RIS-UE) (characteristic 2), it is not implemented in the cascaded channel estimation. For more details, see Algorithm 1 in [80].
3.3.2. Two-Stage Based Cascaded Channel Estimation for a Multi-User System
In [25], they propose a two-stage method for the uplink cascaded channel estimation without using a typical user in an RIS-assisted MU-MIMO cell system. Specifically, in the first stage, an ambiguous shared RIS-BS channel is constructed with all users jointly, to differentiate the multi-user gain and reduce propagation errors. In the second stage, each user estimates its channel together with the RIS and obtains full CSI of the cascaded channel and analyzes the required pilot overhead. For more details, see Algorithm 1 in [25].
3.3.3. Algorithm for an RIS-Assisted AB-HBF System
The authors in [17] create an RIS-assisted AB-HBF mMIMO cell system, as mentioned in Section 2. Their purpose is to maximize the achievable system rate by reducing the CSI overhead size and hardware complexity. First, the RF beamformers are designed based on slow-time varying angular parameters. Then, the BB precoder/combiner is designed with a SVD and water filling algorithm using an efficient channel with reduced size. Finally, to enhance the system capacity, the phase shifts of the RIS use a PSO method. For more details, see Algorithm 1 in [17].
3.3.4. Channel Estimation Algorithms for the Cases with Long-Term Imperfection (LTI) and Short-Term Imperfection (STI)
In [1], the authors propose different efficient tensor algorithms for channel estimation in RIS-assisted MIMO systems, with the RIS elements affected by real-world imperfections. Non-ideal channel estimation problems are solved with trilinear and quadrilinear PARAFAC. The proposed trilinear ALS (TALS)-based LTI algorithm solves with static imperfections. The TALS-STI and higher-order singular value decomposition (HOSVD)-STI algorithms are used for demanding scenarios with non-static behavior of RIS imperfections and with channel temporal coherence. Furthermore, the TALS-LTI and TALS-STI algorithms have iterative solutions, to relax the system requirements and work with more options for training parameters. The HOSVD-STI algorithm has a closed-form solution, has a lower computational complexity than ALS algorithms, and performs parallel processing. For more details, see Algorithms 1–3 in [1].
4. Results of the Proposed Algorithms
In this section, we present the results of the optimized algorithms for RIS-assisted MISO and MIMO systems.
4.1. MISO Systems
According to the results of [74], the PPO-based algorithm is used for joint active and passive beamforming for RIS-assisted MU MISO systems. They use S-CSI plots at the beamforming vectors of the BS and at the phase shifts at the RIS. According to their simulation results for the low and moderate SNR, the S-CSI models achieve equal performance to the I-CSI models and quickly converge to compare with others of the same category. In addition, the PPO-based method outperforms the asynchronous advantage actor–critic (A2C)-based method [92] and is robust against receiving many random actions, resulting from the use of the clip function. The studying time for the S-CSI PPO-based is considerably lower than that of the I-CSI PPO-based algorithm. Regarding the transmission power effect of the BS, the performance of the S-CSI PPO-based approach is compared with the alternating direction method of multipliers (ADMMs) suggested in [75]. Furthermore, the I-CSI-based method validates its operation against the algorithm proposed in [93]. Although the performance of all algorithms is the same at the low SNR, when the SNR rises, the I-CSI PPO-based algorithm outperforms the S-CSI PPO-based algorithms, the A2C and ADMM-based algorithms. Furthermore, the above algorithms perform significantly better than the RIS random phase shifts and the no-RIS case. For the effect of the Rician factor on the average sum, the I-CSI PPO-based algorithm is compared with the algorithm in [93]. According to the results of [74], by increasing the Rician factor, the performance of all algorithms with S-CSI and I-CSI enhances. Specifically, for the S-CSI approach, the LoS link becomes dominant as it increases, the BS-RIS-UE link turns out to be more deterministic.
In [92], the results show that in the proposed framework, it is possible to robustly train neural networks over RL with both value-based and policy-based techniques, non-policy, as well as policy methods and discrete and continuous domains. One of the main conclusions is that the use of peer actor-learners to inform a common model has a steadying effect on the learning process of the three value-based methods examined. Although this indicates that stable online Q-learning is possible without experience repetition, which was used for this objective in the deep Q-Networks (DQN) algorithm, it does not mean that experience repetition is not beneficial. Combining experience repetition into the framework of asynchronous RL could significantly increase the data efficiency of these methods by reprocessing old data. This leads to much quicker training times in areas, such as the open racing car simulator (TORCS), where cooperating with the environment is more costly than renewing the model for the architecture used.
In [72], the problem of planning the transmission joint beam and phase shifts in an RIS-assisted MISO communication system was addressed. Only S-CSI is available at the transmitter and efficient algorithms maximize the system performance. For the case of the Rician fading, an iterative algorithm is used, and the convergence of the algorithm is established. For the Rayleigh fading case, closed-form designs are used. Finally, the proposed S-CSI-based algorithm achieves a similar performance to the algorithm that requires I-CSI.
4.2. MIMO Systems
In [1], the authors use tensor algorithms for channel estimation in RIS-assisted MIMO systems, with trilinear and quadrilinear PARAFAC and it is referred to in Section 3. The results are that the proposed algorithms have a high-performance estimate for imperfections in the channel model and system settings. Furthermore, TALS-STI and HOSVD-STI algorithms have a similar performance. The TALS-STI algorithm is preferred for defect detection in the low SNR regime and when more flexible choices for the training parameters are required. Finally, HOSVD-STI is preferred when low processing latency is desired.
In [80], the authors analyze an RIS-assisted cell-free mMIMO system, investigate the multi-BS cooperation and multi-UE joint estimation. They use the 3D-MLAOMP algorithm, and it is referred to in Section 3. In future work, the derivation of the results for time-scale channel estimation through multi-BS cooperation will be explored. In addition, non-orthogonal pilot sequences based on RIS-assisted cell-free channel estimation in high-mobility scenarios will be investigated.
In [79], a closed-form analytical expression on the achievable sum of RIS-assisted cell-free systems is proposed, this evaluates the effect of key parameters of the system performance. To gain more information, a special case nLoS element was investigated with a power gain in the order of O(M). The proposed low-complexity algorithm uses a two-time-scale transmission protocol, so that the joint beamformers in the BS and RIS are optimized to increase the achievable weighted sum. In addition, the RIS beamformers were improved based on the penalty double decomposition (PDD) method exploiting S-CSI, while the BS beamformers were designed by the primal double degradation (PDS) method dependent on I-CSI. The influence of key system parameters, such as the number of RIS elements, CSI settings and the Rician factor was tested. Finally, the advantages of adopting the cell-free paradigm and developing the exploitation of RISs were demonstrated.
In [2], a joint channel estimation and data detection (JCEDD) scheme for a HRIS-assisted mmWave orthogonal time frequency space (OTFS) system was proposed. They suggested a transmission structure, where the OTFS blocks were escorted by several pilot sequences. In the duration of the pilot sequences, partial HRIS elements were alternatively initiated in passive mode, and the impinging signal was entirely absorbed. The time domain channel model was investigated. In addition, the received signal model at both the HRIS and the BS was presented. Because CSI between the UE and the HRIS is obtained by the pilot sequences. HRIS beamforming design strategy improves the received signal strength at the BS. For the OTFS transmission, a JCEDD scheme was proposed. In this scheme, they resorted to a probabilistic graphical model, and designed a message passing (MP) algorithm to concurrently recover the data symbols and assess the equivalent channel gain. Moreover, an expectation maximization (EM) algorithm was employed to acquire channel parameters, i.e., the channel sparsity, the channel covariance, and the Doppler frequency shift. By iteratively processing between the MP and EM algorithms, the delay-Doppler domain channel and the transmitted data symbols can be acquired at the same time. Simulation results were required to validate the proposed JCEDD scheme and its robustness to the user velocity.
In [3], the effect of channel aging on RIS-assisted mMIMO systems is studied and the effects of spatial correlation and I-CSI are considered. Correlation of channel aging and the Rayleigh attenuation in the data transmission phase and uplink training phase is introduced, the channel efficiency is estimated, and the DE attainable closed-form normalized zero-pressure RZF and sum SE is presented. Channel growth regarding the RIS phase shifts and power budget constraints is presented, applying the S-CSI-based alternating optimization (AO) algorithm to reduce computational complexity and feedback overhead. Therefore, the impact of channel aging and how it interacts with other fundamental parameters affecting the performance were illustrated. For example, the proper range of the numbers of RIS elements and frame duration reduces channel aging. In the future, the study of broadband systems is proposed.
Table 2 summarizes the contributions of some studies, that are mentioned above, on channel estimation in different RIS-assisted system settings.

Table 2.
Contributions of the proposed methods in RIS-assisted communication systems.
The research gaps arising from the mentioned literature for channel estimation in RIS-assisted MISO systems are related to improving the passive modulation of the received signals from the RIS to the BS and the other way around. Furthermore, it is worth researching and using more RL algorithms, expanding the use of neural networks, and improving their architecture. Furthermore, research gaps in RIS-assisted MIMO systems concerning channel estimation during multi-BS cooperation, in high user mobility scenarios, non-orthogonal pilot sequences and window refresh schemes have not been investigated. CSI estimation has not been investigated in broadband systems.
5. Conclusions
The current research delivered an inclusive and up-to-date survey of papers in RIS-assisted wireless communication, such as MIMO and MISO systems communications. Emphasis was placed on the practical challenges of BS, RIS and user channels to estimate them using optimized algorithms with different channel models and system configurations. Then, for various practical scenarios of available CSI, namely I-CSI and S-CSI, we introduced a detailed overview of the research results, depending on the system structure. Different model systems were presented for MISO and MIMO systems using techniques, such as tensor, RL, SDR and others to find the optimal channel estimation algorithm. For the MISO systems, the SDR technique algorithm, the Q-learning RL algorithm and the main PPO algorithm were presented. The PPO algorithm has presented a low and moderate SNR, the BS transmission power was similar to the ADMM algorithm. The preferred algorithms were I-CSI, S-CSI type and the BS-RIS-UE links, which were deterministic. The Q-learning RL algorithm increased the performance and reprocessed the received data. For MIMO systems that were divided into cell and cell-free, some of the algorithms presented were the 3D-MMV 3D-MLAOMP algorithm, two-stage based cascaded channel estimation algorithm, algorithm for an RIS-assisted AB-HBF system and algorithms that use LTI and STI methods. Of the mentioned algorithms, the 3D-MMV 3D-MLAOMP algorithm has been more interesting because it is a tensor-type algorithm, it has presented a low SNR and is preferred for low processing latency. Table 2 presented the characteristics of the above algorithms. Considering all the above, we found that channel estimation in RIS-assisted communication systems is improved by creating new or optimizing existing algorithms. Improvement was observed in estimation time, performance, how the BS-RIS and RIS-UE channels are calculated and create scenarios for users with high mobility. It was found that the performance of the system depends on the location of the RIS and how many elements it consists of. As a result, the optimized algorithms helped to reduce the pilot signal header and their complexity. For instance, for an RIS-assisted MU-MISO system in [74], an optimized PPO-based algorithm was proposed, which used S-CSI, and the algorithm had a fast convergence compared to same category algorithms. In addition, for an RIS-assisted mMIMO system in [3], they proposed an optimized algorithm for high user mobility with efficient complexity O(MN2 + N +M) and used S-CSI. According to the researchers, it is necessary to further study the methods in broadband systems, to study more the required number of RIS elements to have the maximum performance of the system and the window size to reduce the channel aging. The contribution of neural networks to channel estimation in RIS-assisted systems should be further investigated. In addition, there should be more scenarios for high user mobility versus channel aging. In our future work, we will simulate the mentioned algorithms for RIS-assisted MISO and MIMO systems, respectively, to confirm their optimization in terms of channel estimation. According to the settings of the systems used by these authors, but also by simulating them with other parameters. We hope this research provides information to researchers and professionals working on the new technologies of communication systems in order to further explore the problems that have emerged.
Author Contributions
Conceptualization, S.F.D. and N.I.M.; methodology, S.F.D.; validation, S.F.D., N.I.M., H.C.L. and P.A.K.; investigation, S.F.D.; resources, S.F.D.; data curation, S.F.D., N.I.M., H.C.L. and P.A.K.; writing—original draft preparation, S.F.D.; writing, editing, S.F.D., N.I.M., H.C.L. and P.A.K.; review H.C.L.; supervision, P.A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgment
This work is partially supported by University of West Attica.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| 1D | 1 dimension |
| 3D | 3 dimensions |
| 3D-MLAOMP | 3D-MMV look ahead orthogonal match pursuit |
| 3D-MMV | Three-dimensional multiple measurement vector |
| 6G | Sixth-generation |
| A2C | Asynchronous Advantage Actor–critic |
| AB-HBF | Angular-based Hybrid Beamforming |
| ADMM | Alternating Direction Method Of Multipliers |
| ALS | Alternating Least Squares |
| AO | Alternating Optimization |
| AoA | Angle of Arrival |
| AoD | Angle of Departure |
| BB | Baseband |
| BS | Base Station |
| CPI | Conservative Policy Iteration |
| CPU | Central Processing Unit |
| CS | Compression Sensing |
| CSI | Channel State Information |
| DE | Deterministic Equivalent |
| DFT | Discrete Fourier Transform |
| DQN | Deep Q-networks |
| EM | Expectation Maximization |
| FDD | Frequency Division Duplex |
| GAE | Generalized Advantage Estimator |
| HBF | Hybrid Beamforming |
| HOSVD | Higher-order Singular Value Decomposition |
| HRIS | Hybrid RIS |
| I-CSI | Instantaneous CSI |
| IoVs | Internet of Vehicles |
| JCEDD | Joint Channel Estimation and Data Detection |
| KL | Kullback–Leibler |
| LMMSE | Linear MMSE |
| LoS | Line of Sight |
| LS | Least Squares |
| LTI | Long-term Imperfection |
| MDP | Markov Decision Process |
| MIMO | Multiple Input-Multiple Output |
| MISO | Multiple Input-Single Output |
| mMIMO | massive Multiple Input-Multiple Output |
| MMSE | Minimum MSE |
| MMV | Multiple Measurement Vector |
| MP | Message Passing |
| MSE | Mean-Squared-Error |
| MU-MISO | multi-user MISO |
| NLoS | Non-line-of-sight |
| OMP | Orthogonal Matching Pursuit |
| OTFS | Orthogonal Time Frequency Space |
| PARAFAC | Parallel Factor |
| PDD | Penalty Double Decomposition |
| PDS | Primal Double Degradation |
| PPO | Proximal Policy Optimization |
| QoS | Quality of Service |
| RBM | Reflecting Beamforming Matrix |
| RF | Radio Frequency |
| RIS | Reconfigurable Intelligent Surface |
| RL | Reinforcement Learning |
| RZF | Regularized ZF |
| S-CSI | Statistical CSI |
| SE | Spectral Efficiency |
| SINR | Signal-to-Interference-Plus-Noise Ratio |
| STI | Short-term Imperfection |
| SVD | Singular Value Decomposition |
| TALS | Trilinear ALS |
| TDD | Time Division Duplex |
| TORCS | The Open Racing Car Simulator |
| TRPO | Trust Region Policy Optimization |
| UE | User Equipment |
| ULA | Uniform Linear Array |
| UPA | Uniform Planar Arrays |
| ZF | Zero Forcing |
| SDR | Semidefinite Relaxation |
| SCA | Successive Convex Approximation |
| DS-OMP | Double-Structured-OMP |
References
- Gomes, P.R.B.; Araujo, G.T.D.; Sokal, B.; Almeida, A.L.F.D.; Makki, B.; Fodor, G. Channel Estimation in RIS-Assisted MIMO Systems Operating under Imperfections. arXiv 2022, arXiv:2207.02700. [Google Scholar]
- Li, M.; Zhang, S.; Ge, Y.; Gao, F.; Fan, P. Joint Channel Estimation and Data Detection for Hybrid RIS aided Millimeter Wave OTFS Systems. IEEE Trans. Commun. 2022, 70, 6832–6848. [Google Scholar] [CrossRef]
- Papazafeiropoulos, A.; Krikidis, I.; Kourtessis, P. Impact of Channel Aging on Reconfigurable Intelligent Surface Aided Massive MIMO Systems with Statistical CSI. IEEE Trans. Veh. Technol. 2023, 72, 689–703. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Intelligent reflecting surface enhanced wireless network via joint active and passive beamforming. IEEE Trans. Wirel. Commun. 2019, 18, 5394–5409. [Google Scholar] [CrossRef]
- Pan, C.; Ren, H.; Wang, K.; Xu, W.; Elkashlan, M.; Nallanathan, A.; Hanzo, L. Multicell MIMO communications relying on intelligent reflecting surfaces. IEEE Trans. Wirel. Commun. 2020, 19, 5218–5233. [Google Scholar] [CrossRef]
- Papazafeiropoulos, A.; Pan, C.; Kourtessis, P.; Chatzinotas, S.; Senior, J.M. Intelligent reflecting surface-assisted MU-MISO systems with imperfect hardware: Channel estimation, beamforming design. IEEE Trans. Wirel. Commun. 2021, 21, 2077–2092. [Google Scholar] [CrossRef]
- Nadeem, Q.-U.; Kammoun, A.; Chaaban, A.; Debbah, M.; Alouini, M.-S. Asymptotic max-min SINR analysis of reconfigurable intelligent surface assisted MISO systems. IEEE Trans. Wirel. Commun. 2020, 19, 7748–7764. [Google Scholar] [CrossRef]
- Papazafeiropoulos, A.; Pan, C.; Elbir, A.M.; Nguyen, V.-D.; Kourtessis, P.; Chatzinotas, S. Asymptotic analysis of Max-Min weighted SINR for IRS-assisted MISO systems with hardware impairments. IEEE Wirel. Commun. Lett. 2021, 12, 192–196. [Google Scholar] [CrossRef]
- Yang, P.; Yang, L.; Wang, S.J. Performance analysis for RIS-Aided Wireless Systems with Imperfect CSI. IEEE Wirel. Commun. Lett. 2021, 11, 588–592. [Google Scholar] [CrossRef]
- Michailidis, E.T.; Miridakis, N.I.; Michalas, A.; Skondras, E.; Vergados, D.J. Energy Optimization in Dual-RIS UAV-Aided MEC-Enabled Internet of Vehicles. Sensors 2021, 21, 4392. [Google Scholar] [CrossRef] [PubMed]
- Tsiftsis, T.A.; Valagiannopoulos, C.; Liu, H.; Boulogeorgos, A.-A.A.; Miridakis, N.I. Metasurface-Coated Devices: A New Paradigm for Energy-Efficient and Secure 6G Communications. IEEE Veh. Technol. Mag. 2021, 17, 27–36. [Google Scholar] [CrossRef]
- Alexandropoulos, G.C.; Shlezinger, N.; Alamzadeh, I.; Imani, M.F.; Zhang, H.; Eldar, Y.C. Hybrid Reconfigurable Intelligent Metasurfaces: Enabling Simultaneous Tunable Reflections and Sensing for 6G Wireless Communications. arXiv 2021, arXiv:2104.04690. [Google Scholar]
- Albanese, A.; Devoti, F.; Sciancalepore, V.; Renzo, M.D.; Perez, X. MARISA: A Self-Configuring Metasurfaces Absorption and Reflection. arXiv 2021, arXiv:2104.04690. [Google Scholar]
- Hu, X.; Zhang, R.; Zhong, C. Semi-passive elements assisted channel estimation for intelligent reflecting surface-aided communications. IEEE Trans. Wirel. Commun. 2022, 21, 1132–1142. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.; Wu, Q.; Jin, Y.; Chen, Y.; Ai, B. RIS-Aided Next-Generation High-Speed Train Communications: Challenges, Solutions, and Future Directions. arXiv 2021, arXiv:2103.09484. [Google Scholar]
- Zhang, S.; Gao, F.; Ma, J.; Dobre, O.A. Deep learning optimized sparse antenna activation for reconfigurable intelligent surface assisted communication. IEEE Trans. Commun. 2021, 69, 6691–6705. [Google Scholar] [CrossRef]
- Yildirim, I.; Koc, A.; Basar, E.; Le-Ngoc, T. RIS-Aided Angular-Based Hybrid Beamforming Design in mmWave Massive MIMO Systems. 2022. Available online: https://arxiv.org/abs/2208.06622v1 (accessed on 1 January 2023).
- Ahmed, I.; Khammari, H.; Shahid, A.; Musa, A.; Kim, K.S.; De Poorter, E.; Moerman, I. A survey on hybrid beamforming techniques in 5G: Architecture and system model perspectives. IEEE Commun. Surv. Tutor. 2018, 20, 3060–3097. [Google Scholar] [CrossRef]
- Koc, A.; Masmoudi, A.; Le-Ngoc, T. 3D angular-based hybrid precoding and user grouping for uniform rectangular arrays in massive MU-MIMO systems. IEEE Access 2020, 8, 84689–84712. [Google Scholar] [CrossRef]
- Koc, A.; Le-Ngoc, T. Hybrid millimeter-wave massive MIMO systems with low CSI overhead and few-bit DACs/ADCs. In Proceedings of the IEEE Vehicular Technology Conference (VTC2020-Fall), Victoria, BC, Canada, 18 November–16 December 2020; pp. 1–5. [Google Scholar]
- Koc, A.; Le-Ngoc, T. Swarm Intelligence based Power Allocation in Hybrid Millimeter-Wave Massive MIMO Systems. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China; 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Wang, P.; Fang, J.; Dai, L.; Li, H. Joint transceiver and large intelligent surface design for massive MIMO mmWave systems. IEEE Trans. Wirel. Commun. 2021, 20, 1052–1064. [Google Scholar] [CrossRef]
- Hong, S.H.; Park, J.; Kim, S.-J.; Choi, J. Hybrid beamforming for intelligent reflecting surface aided millimeter wave MIMO systems. IEEE Trans. Wirel. Commun. 2022, 21, 7343–7357. [Google Scholar] [CrossRef]
- Ying, K.; Gao, Z.; Lyu, S.; Wu, Y.; Wang, H.; Alouini, M.-S. GMD-based hybrid beamforming for large reconfigurable intelligent surface assisted millimeter-wave massive MIMO. IEEE Access 2020, 8, 19530–19539. [Google Scholar] [CrossRef]
- Peng, Z.; Pan, C.; Zhou, G.; Ren, H. Error Propagation and Overhead Reduced Channel Estimation for RIS-Aided Multi-User mmWave Systems. 2022. Available online: https://arxiv.org/abs/2208.10732v1 (accessed on 1 January 2023).
- Peng, Z.; Zhou, G.; Pan, C.; Ren, H.; Swindlehurst, A.L.; Popovski, P.; Wu, G. Channel Estimation for RIS-Aided Multi-User mmWave Systems with Uniform Planar Arrays. 2022. Available online: https://arxiv.org/abs/2208.07069v1 (accessed on 1 January 2023).
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Zheng, B.; You, C.; Mei, W.; Zhang, R. A Survey on Channel Estimation and Practical Passive Beamforming Design for Intelligent Reflecting Surface Aided Wireless Communications. Available online: https://arxiv.org/abs/1911.00091 (accessed on 1 February 2022).
- Mishra, D.; Johansson, H. Channel estimation and low-complexity beamforming design for passive intelligent surface assisted MISO wireless energy transfer. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 4659–4663. [Google Scholar]
- Jensen, T.L.; Carvalho, E.D. An optimal channel estimation scheme for intelligent reflecting surfaces based on a minimum variance unbiased estimator. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 5000–5004. [Google Scholar]
- Wang, P.; Fang, J.; Duan, H.; Li, H. Compressed channel estimation for intelligent reflecting surface-assisted millimeter wave systems. IEEE Signal Process. Lett. 2020, 27, 905–909. [Google Scholar] [CrossRef]
- Gao, S.; Dong, P.; Pan, Z.; Li, G.Y. Deep multi-stage CSI acquisition for reconfigurable intelligent surface aided MIMO systems. IEEE Commun. Lett. 2021, 25, 2024–2028. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, S.; Zhong, C.; Ma, J.; Dobre, O.A. Ordinary differential equation-based CNN for channel extrapolation over RIS-assisted. IEEE Commun. Lett. 2021, 25, 1921–1925. [Google Scholar] [CrossRef]
- Kundu, N.K.; McKay, M.R. A Deep Learning-Based Channel Estimation Approach for MISO Communications with Large Intelligent Surfaces. In Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PRMIC), London, UK, 31 August–3 September 2020; pp. 1–6. [Google Scholar]
- Li, Z.; Chen, Z.; Ma, X.; Chen, W. Channel estimation for intelligent reflecting surface enabled terahertz MIMO systems: A deep learning perspective. In Proceedings of the IEEE/CIC International Conference on Communications in China (ICCC Workshop), Chongqing, China, 9–11 August 2020; pp. 75–79. [Google Scholar]
- Mao, Z.; Peng, M.; Liu, X. Channel estimation for reconfigurable intelligent surface assisted wireless communication systems in mobility scenarios. China Commun. 2021, 18, 29–38. [Google Scholar] [CrossRef]
- Cai, P.; Zong, J.; Luo, X.; Zhou, Y.; Chen, S.; Qian, H. Downlink channel tracking for intelligent reflecting surface-aided FDD MIMO systems. IEEE Trans. Veh. Technol. 2021, 70, 3341–3353. [Google Scholar] [CrossRef]
- Ardah, K.; Gherekhloo, S.; Almeida, A.L.; Haardt, M. TRICE: A channel estimation framework for RIS-aided millimeter-wave MIMO systems. IEEE Signal Process. Lett. 2021, 28, 513–517. [Google Scholar] [CrossRef]
- Jia, C.; Cheng, J.; Gao, H.; Xu, W. High-resolution channel estimation for intelligent reflecting surface-assisted mmWave communications. In Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PRMIC), London, UK, 31 August–3 September 2020; pp. 1–6. [Google Scholar]
- He, J.; Wymeersch, H.; Juntti, M. Channel estimation for RIS-aided mmWave MIMO systems via atomic norm minimization. IEEE Trans. Wirel. Commun. 2021, 20, 5786–5797. [Google Scholar] [CrossRef]
- He, J.; Leinonen, M.; Wymeersch, H.; Juntti, M. Channel estimation for RIS-aided mmWave MIMO systems. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar]
- Ma, X.; Chen, Z.; Chen, W.; Li, Z.; Chi, Y.; Han, C.; Li, S. Joint channel estimation and data rate maximization for intelligent reflecting surface assisted terahertz MIMO communication systems. IEEE Access 2020, 8, 99565–99581. [Google Scholar] [CrossRef]
- He, Z.-Q.; Yuan, X. Cascaded channel estimation for large intelligent metasurface assisted massive MIMO. IEEE Wirel. Commun. Lett. 2019, 9, 210–214. [Google Scholar] [CrossRef]
- Araujo, G.T.; Almeida, A.L.; Boyer, R. Channel estimation for intelligent reflecting surface assisted MIMO systems: A tensor modeling approach. IEEE J. Sel. Topics Signal Process. 2021, 15, 789–802. [Google Scholar] [CrossRef]
- Zegrar, S.E.; Afeef, L.; Arslan, H. Reconfigurable intelligent surfaces (RIS): Channel model and estimation. arXiv 2020, arXiv:2010.05623. [Google Scholar]
- Sun, S.; Yan, H. Channel estimation for reconfigurable intelligent surface-assisted wireless communications considering doppler effect. IEEE Wirel. Commun. Lett. 2021, 10, 790–794. [Google Scholar] [CrossRef]
- Zegrar, S.; Afeef, L.; Arslan, H. A general framework for RIS-aided mmWave communication networks: Channel estimation and mobile user tracking. arXiv 2020, arXiv:2009.01180. [Google Scholar]
- Nadeem, Q.-U.; Alwazani, H.; Kammoun, A.; Chaaban, A.; Debbah, M.; Alouini, M.-S. Intelligent reflecting surface-assisted multi-user MISO communication: Channel estimation and beamforming design. IEEE Open J. Commun. Soc. 2020, 1, 661–680. [Google Scholar] [CrossRef]
- Mishra, D.; Larsson, E.G. Passive intelligent surface assisted MIMO powered sustainable IoT. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 8961–8965. [Google Scholar]
- Buzzi, S.; D’Andrea, C.; Zappone, A.; Fresia, M.; Zhang, Y.-P.; Feng, S. RIS configuration, beamformer design, and power control in single-cell and multi-cell wireless networks. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 398–411. [Google Scholar] [CrossRef]
- Wei, X.; Shen, D.; Dai, L. Channel estimation for RIS assisted wireless communications—Part II: An improved solution based on double-structured sparsity. IEEE Commun. Lett. 2021, 25, 1403–1407. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, L.; Cui, S. Channel estimation for intelligent reflecting surface assisted multiuser communications: Framework, algorithms, and analysis. IEEE Trans. Wirel. Commun. 2020, 19, 6607–6620. [Google Scholar] [CrossRef]
- Chen, J.; Liang, Y.-C.; Cheng, H.V.; Yu, W. Channel estimation for reconfigurable intelligent surface aided multi-user MIMO systems. arXiv 2019, arXiv:1912.03619. [Google Scholar] [CrossRef]
- Hu, C.; Dai, L.; Han, S.; Wang, X. Two-timescale channel estimation for reconfigurable intelligent surface aided wireless communications. IEEE Trans. Commun. 2021, 69, 7736–7747. [Google Scholar] [CrossRef]
- Guan, X.; Wu, Q.; Zhang, R. Anchor-assisted channel estimation for intelligent reflecting surface aided multiuser communication. IEEE Trans. Wirel. Commun. 2021, 21, 3764–3778. [Google Scholar] [CrossRef]
- Kang, J.-M. Intelligent reflecting surface: Joint optimal training sequence and refection pattern. IEEE Commun. Lett. 2020, 24, 1784–1788. [Google Scholar] [CrossRef]
- Wei, L.; Huang, C.; Alexandropoulos, G.C.; Yuen, C.; Zhang, Z.; Debbah, M. Channel estimation for RIS-empowered multi-user MISO wireless communications. IEEE Trans. Commun. 2021, 69, 4144–4157. [Google Scholar] [CrossRef]
- Liu, H.; Yuan, X.; Zhang, Y.-J.A. Matrix-calibration-based cascaded channel estimation for reconfigurable intelligent surface assisted multiuser MIMO. IEEE J. Sel. Areas Commun. 2020, 38, 2621–2636. [Google Scholar] [CrossRef]
- He, Z.-Q.; Liu, H.; Yuan, X.; Zhang, Y.-J.A.; Liang, Y.-C. Semi-blind cascaded channel estimation for reconfigurable intelligent surface aided massive MIMO. arXiv 2021, arXiv:2101.07315. [Google Scholar]
- Elbir, A.M.; Papazafeiropoulos, A.; Kourtessis, P.; Chatzinotas, S. Deep channel learning for large intelligent surfaces aided mm-wave massive MIMO systems. IEEE Wirel. Commun. Lett. 2020, 9, 1447–1451. [Google Scholar] [CrossRef]
- Liu, C.; Liu, X.; Ng, D.; Yuan, J. Deep residual learning for channel estimation in intelligent reflecting surface-assisted multi-user communications. IEEE Trans. Wirel. Commun. 2021, 21, 898–912. [Google Scholar] [CrossRef]
- Jian, M.; Zhao, Y. A modified off-grid SBL channel estimation and transmission strategy for RIS-assisted wireless communication systems. In Proceedings of the International Wireless Communications and Mobile Computing Conference (IWCMC), Limassol, Cyprus, 15–19 June 2020; pp. 1848–1853. [Google Scholar]
- Liu, S.; Lei, M.; Zhao, M.-J. Deep learning based channel estimation for intelligent reflecting surface aided MISO-OFDM systems. In Proceedings of the IEEE Vehicular Technology Conference (VTC2020-Fall), Victoria, BC, Canada, 18 November–16 December 2020; pp. 1–5. [Google Scholar]
- Liu, S.; Gao, Z.; Zhang, J.; Di Renzo, M.; Alouini, M.-S. Deep denoising neural network assisted compressive channel estimation for mmWave intelligent reflecting surfaces. IEEE Trans. Veh. Technol. 2020, 69, 9223–9228. [Google Scholar] [CrossRef]
- Wan, Z.; Gao, Z.; Alouini, M.-S. Broadband channel estimation for intelligent reflecting surface aided mmWave massive MIMO systems. In Proceedings of the IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 July 2020. [Google Scholar]
- Lin, Y.; Jin, S.; Matthaiou, M.; You, X. Tensor-based algebraic channel estimation for hybrid IRS-assisted MIMO-OFDM. IEEE Trans. Wirel. Commun. 2021, 20, 3770–3784. [Google Scholar] [CrossRef]
- Elbir, A.; Coleri, S. Federated learning for channel estimation in conventional and IRS-assisted massive MIMO. arXiv 2020, arXiv:2008.10846. [Google Scholar]
- Wan, Z.; Gao, Z.; Gao, F.; Renzo, M.; Alouini, M.-S. Terahertz massive MIMO with holographic reconfigurable intelligent surfaces. IEEE Trans. Commun. 2021, 69, 4732–4750. [Google Scholar] [CrossRef]
- Miridakis, N.I.; Tsiftsis, T.A.; Yao, R. Zero Forcing Uplink Detection through Large-Scale RIS: System Performance and Phase Shift Design. Available online: https://arxiv.org/abs/2211.12794v1 (accessed on 23 November 2022).
- Miridakis, N.I.; Tsiftsis, T.A.; Yang, G.; Karkazis, P.A.; Leligou, H.C. Semi-Blind Multiuser Detection Under the Presence of Reconfigurable Intelligent Surfaces. Available online: https://arxiv.org/abs/2110.04736v1 (accessed on 10 October 2021).
- Han, Y.; Tang, W.; Jin, S.; Wen, C.-K.; Ma, X. Large intelligent surface-assisted wireless communication exploiting statistical csi. IEEE Trans. Veh. Technol. 2019, 68, 8238–8242. [Google Scholar] [CrossRef]
- Hu, X.; Wang, J.; Zhong, C. Statistical csi based design for intelligent reflecting surface assisted miso systems. Sci. China Inf. Sci. 2020, 63, 1–10. [Google Scholar] [CrossRef]
- Wei, L.; Huang, C.; Alexandropoulos, G.C.; Yuen, C. Parallel factor decomposition channel estimation in RIS-assisted multi-user MISO communication. In Proceedings of the IEEE Sensor Array AND Multichannel Signal Processing Workshop (SAM), Hangzhou, China, 8–11 June 2020. [Google Scholar]
- Eskandari, M.; Zhu, H.; Shojaeifard, A.; Wang, A.J. Statistical CSI-based Beamforming for RIS-Aided Multiuser MISO Systems using Deep Reinforcement Learning. 2022. Available online: https://arxiv.org/abs/2209.09856v1 (accessed on 1 January 2023).
- Gan, X.; Zhong, C.; Huang, C.; Zhang, Z. Ris-assisted multi-user miso communications exploiting statistical csi. IEEE Trans. Commun. 2021, 69, 6781–6792. [Google Scholar] [CrossRef]
- Wang, J.; Wang, H.; Han, Y.; Jin, S.; Li, X. Joint transmit beamforming and phase shift design for reconfigurable intelligent surface assisted mimo systems. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 354–368. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, R. Capacity characterization for intelligent reflecting surface aided mimo communication. IEEE J. Sel. Areas Commun. 2020, 38, 1823–1838. [Google Scholar] [CrossRef]
- Liu, P.; Luo, K.; Chen, D.; Jiang, T.; Matthaiou, M. Spectral efficiency analysis of multi-cell massive mimo systems with ricean fading. In Proceedings of the 2018 10th International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 18–20 October 2018; pp. 1–7. [Google Scholar]
- Gan, X.; Zhong, C.; Huang, C.; Yang, Z.; Zhang, Z. Multiple RISs Assisted Cell-Free Networks with Two-timescale CSI: Performance Analysis and System Design. 2022. Available online: https://arxiv.org/abs/2208.06072v1 (accessed on 1 January 2023).
- Yang, S.; Xie, C.; Wang, M.; Zhang, Z. Channel Estimation for Reconfigurable Intelligent Surface-Assisted Cell-Free Communications. 2022. Available online: https://arxiv.org/abs/2207.14182v1 (accessed on 1 January 2023).
- Araujo, G.; Almeida, A. PARAFAC-based channel estimation for intelligent reflective surface assisted MIMO system. In Proceedings of the IEEE Sensor Array AND Multichannel Signal Processing Workshop (SAM), Hangzhou, China, 8–11 June 2020. [Google Scholar]
- Araújo, G.; Pessoa, L.; Almeida, A. Channel estimation for MIMO system assisted by intelligent reflective surface. In Proceedings of the Stereotactic Body Radiation Therapy (SBrT), Santa Catarina, Brazil, 22–25 November 2020. [Google Scholar]
- Bjornson, E.; Sanguinetti, L. Rayleigh fading modeling and channel hardening for reconfigurable intelligent surfaces. IEEE Wirel. Commun. Lett. 2021, 10, 830–834. [Google Scholar] [CrossRef]
- Truong, K.T.; Heath, R.W. Effects of channel aging in massive MIMO systems. IEEE/KICS J. Commun. Net. 2013, 15, 338–351. [Google Scholar] [CrossRef]
- Papazafeiropoulos, A.K.; Ratnarajah, T. Deterministic equivalent performance analysis of time-varying massive MIMO systems. IEEE Trans. Wirel. Commun. 2015, 14, 5795–5809. [Google Scholar] [CrossRef]
- Papazafeiropoulos, A.K. Impact of general channel aging conditions on the downlink performance of massive MIMO. IEEE Trans. Veh. Technol. 2017, 66, 1428–1442. [Google Scholar] [CrossRef]
- Chopra, R.; Murthy, C.R.; Suraweera, H.A.; Larsson, E.G. Performance analysis of FDD massive MIMO systems under channel aging. IEEE Trans. Wirel. Commun. 2017, 17, 1094–1108. [Google Scholar] [CrossRef]
- Adhikary, A.; Nam, J.; Ahn, J.-Y.; Caire, G. Joint spatial division and multiplexing—The large-scale array regime. IEEE Trans. Inf. Theory 2013, 59, 6441–6463. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network. IEEE Commun. Mag. 2019, 58, 106–112. [Google Scholar] [CrossRef]
- You, C.; Zheng, B.; Zhang, R. Channel estimation and passive beamforming for intelligent reflecting surface: Discrete phase shift and progressive refinement. IEEE J. Sel. Areas Commun. 2020, 38, 2604–2620. [Google Scholar] [CrossRef]
- Rusek, F.; Persson, D.; Lau, B.K.; Larsson, E.G.; Marzetta, T.L.; Tufvesson, F. Scaling up mimo: Opportunities and challenges with very large arrays. IEEE Signal Process. Mag. 2012, 30, 40–60. [Google Scholar] [CrossRef]
- Mnih, V.; Badia, A.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning (PMLR), New York, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]
- Guo, H.; Liang, Y.-C.; Chen, J.; Larsson, E.G. Weighted sum-rate maximization for reconfigurable intelligent surface aided wireless networks. IEEE Trans. Wirel. Commun. 2020, 19, 3064–3076. [Google Scholar] [CrossRef]
- Zhao, M.; Wu, Q.; Zhao, M.; Zhang, R. Intelligent reflecting surface enhanced wireless networks: Two-timescale beamforming optimization. IEEE Trans. Wirel. Commun. 2021, 20, 2–17. [Google Scholar] [CrossRef]
- Zhi, K.; Pan, C.; Ren, H.; Wang, K. Power scaling law analysis and phase shift optimization of RIS-aided massive MIMO systems with statistical CSI. IEEE Trans. Commun. 2022, 70, 3558–3574. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).