Abstract
Grammatical inference of context-free grammars using positive and negative language examples is among the most challenging task in modern artificial and natural language technology. Recently, several implementations combining various techniques, usually including the Backus–Naur form, have been proposed. In this paper, we explore a new implementation of grammatical inference using evolution methods focused on the Greibach normal form and exploiting its properties, and also propose new solutions both in the evolutionary processes and in the corresponding fitness estimation.
1. Introduction
The theory of formal languages and grammars focuses on the description and the properties of sequences of symbols. Practical applications of this theory include the design of computer programming languages, compilers, computer processing of artificial and natural language texts, speech recognition and speech synthesis, computational biology problems dealing with biological sequences, processing, information extraction, annotation of web pages etc.
A Context-Free Grammar (CFG) is a 4-tuple G = (N,T,P,S), whereas N is a set of non-terminal symbols or variables, T is a set of terminal symbols, P is the set of production rules and S is the starting symbol. The rules in P have the form A a , a ∈ (N ∪ T)* and A ∈ (N ∪ S), whereas * is the Kleene star.
A string of terminal symbols can be generated by a CFG when starting from the symbol S and replacing continuously one variable of the string with the right part of a production rule included in P. The process is terminated when all variables in the string are eliminated. The finite or infinite set of all possible sentences generated by the CFG defines the corresponding language L(CFG) of the grammar. Typically, the description length of the CFG is significantly lower than the L(CFG), therefore CFGs are preferred in computer applications to encode and process artificial and natural languages due their compact description.
The inverse problem is known as the grammatical inference problem and is defined by a process to derive a CFG, given a finite sample of the language L(CFG) and a set of sentences not belonging to the L(CFG). Grammatical Evolution (GE) [1] is a hybrid computation technique which is used to solve the grammatical inference problem, combining genetic optimization methods [2] and CFG, mainly in the Backus–Naur Form (BNF).
Grammatical Evolution has been used in a variety of optimization problems with many variants and hybrid implementations with other well-known algorithms. Such variants with the use of heuristics and stochastic methods [3,4,5], with some rather interesting results, are common in this field. Moreover, GE has been used successfully with Neural Networks (NN) [6] or other Machine Learning (ML) methods such as SVMs [7]. Due to the strictness of the BNF representation of CFG, it is common for Grammatical Evolution (GE) algorithms to generate new chromosomes—through the operations of crossover and mutation—that are either not in the BNF form or even worse are not CFGs. In that case, these chromosomes should be dismissed and some other heuristic techniques must be used. It is clear that grammatical inference methods are a necessity in many applications where CFGs can be extracted from artificial or real string datasets. There have been many methods proposed for the inference problem both analytic [8,9], evolutionary [10,11] or using ant colony optimization tools [12]. In many cases, the complexity of the proposed method is polynomial and/or complex structures such as meta-grammars are introduced [13], which often increase the complexity of the proposed method.
Recently, the estimation of CFGs from positive and negative samples is derived as a Boolean satisfiability problem (SAT) [14]. The set of training strings is encoded and limits on the sizes of rule sets in Chomsky Normal Form (CNF) are used by a SAT solver to define the CFG. The experimental results suggest that the complexity of inferring CFG is related to its theoretical limitations. In [15,16], the tabular representation algorithm (TBL) and as an improved version is applied for CNF inference, using a dynamic programming method to store the exponential number of all possible grammatical structures in table similar to CYK of polynomial size. A genetic algorithm is used to solve the NP-hard partitioning problem of the non-terminals set.
A CFG definition method based on automatic distillation of structured patterns is presented in [17], relying on statistical pattern extraction and structured generalization. The proposed method is evaluated on artificial grammar data, on natural-language corpora such as ATIS and CHILDES, in languages as diverse as English and Chinese and in protein sequence data.
In this paper, a novel evolutionary method for grammatical inference [18] is described and evaluated adopting a simple and efficient grammar description method, the Greibach Normal Form (GNF) [19], which is used to describe the CFG in place of the BNF or any equivalent formalism. Additionally, several evolutionary techniques regarded as improvements by many researchers in the evolutionary programming field have been implemented. The proposed method has several advantages compared to previous reported methods, ensuring valid structure at each generated CFG after crossover and mutation, fast convergence to a reliable grammar under all restraints of a CFG in the GNF. Furthermore, a depth aware parser that enables more descriptive estimation of the fitness of each chromosome is presented. Quantitative results related to both advantages and disadvantages of the proposed method are presented in low complexity CFG inference problems and several qualitative issues is given in the last part of this paper.
In the following two sections, the proposed algorithm components and its detailed description are given.
2. Definition of the Key Components
2.1. Greibach Normal Form
The GNF is formally defined by the 4-tuple G = (N,T,P,S), where P is the production rules are in the form Aa a, with a∈ (N ∪ S)*, a ∈ T and A ∈ (N ∪ S) and the rule S , is the empty string, may exist.
A simple example of a GNF: . The language of the GNF is the infinite set
GNF was also used to show that each CFG can be accepted by a push-down automation as each CFG can be transformed to GNF [20].
2.2. Genetic Operations
In Genetic Programming, it is common for each chromosome, which is a candidate solution, to be represented by a string of arbitrary length where the genetic operations of selection, crossover and mutation will be applied when the new generation chromosomes are estimated. In Genetic Evolution [21], this string consists of either decimal or binary digits (chromosome) which is then mapped to the equivalent CFG (phenotype). All candidate grammars construct a current population and a fitness value proportional to the goodness of the problem description can be estimated at every chromosome. The operators of selective crossover and mutation are applied to the population for several generations until in the pool of chromosomes of the last generation, an acceptable maximum of the goodness value is reached or the maximum number of generations is achieved.
2.3. Over-Fitting and Generalization
In general artificial intelligence and machine learning implementations, one may come across over-fitting and generalization problems; over-fitting occurring when models or procedures that violate Occam’s razor principle or using too many adjustable variables which may result in under-performance on unseen data. Poor generalization also occurs when a model or a procedure validates not only what should be validated, the training data, but also the majority of any random inputs or data.
In grammatical inference, overfitting appears in GNFs with a small number of general production rule,s which validates almost any string of terminal symbols, while over-fitting in GNF occurs when there are too many production rules with respect to a given dataset. We tackle both problems in the proposed algorithm.
3. Proposed Algorithm of Grammatical Evolution for Greibach Context-Free Grammars
In this section, the proposed GE method for grammatical inference of GNF using positive and negative sequences of terminal symbols is given, as well as the actual implementation. The advantages of our method with respect to convergence accuracy and efficiency are also highlighted through the method’s analysis. Various evolutionary techniques are inspired by previous implementations, while the GNF has never been used before in GE for CFG inference from examples.
3.1. Data Requirements and Parameters Definition
The proposed GE inference algorithm for GFN estimation requires a number of data strings and the definition of several parameters which affect the algorithm’s convergence and efficiency.
- (1)
- Two training datasets. The positive set of terminal sequences is used to be effectively parsed by the GFN solution, i.e., and the negative set of terminal sequences is used to avoid generalization of the candidate solutions, i.e., ;
- (2)
- Evolutionary parameters:The mutation rate is the probability rate of applying the mutation operator.The elitism rate is the percentage of best chromosomes being migrated to a new population.The size of the population is the number of candidate solutions at every generation.The convergence criterion in the form of a fitness value that is considered sufficient for a good candidate solution.The Parental portion is the percentage of the best chromosomes that will be assigned with a probability to generate offsprings.
- (3)
- GNF parameters:The Size of the set N (non-terminal symbols), denoted by .The Terminal symbols set T which is inferred by the positive and negative examples and its size is denoted by .The maximum length of the production rule () and a maximum number of the production rules () in a GNF grammar to be used in the pool initialization step.The sub-parse parameter a (<1) that facilitates better estimation of a chromosome’s fitness
3.2. The Proposed Genetic Evolution Inference Method
Step 1 Initialization:
The three sets of the CNF: N,T,S are defined, whereas P will be estimated in the following steps. N is automatically estimated from the datasets, and T, S are calculated according to . In our implementation, all the sets are enumerated to accelerate the computer based processes. According to this approach, the starting symbol S , and the set T (with symbols) will be the one-to-one map of each unique character or terminal symbol to an integer value. We use the number of non-terminal symbols to generate the set N = { + }. On Table 1 the enumerated symbols map is shown.

Table 1.
Enumerated Symbols map
In the enumeration map, no integer number is skipped. In order to not interfere with the generality of our algorithm, we choose maximum chromosome length as * .
The maximum length of each production rule and the maximum number of production rules is used to generate random new chromosomes in the initial population up to the initial population size of the GNF in the first generation. If a random chromosome does not include the starting symbol S in the head of any production rule, this chromosome is discarded and the random generation process is re-activated for this chromosome. Each chromosome is stored in the population pool.
An example of the enumeration process with a phenotype to chromosome conversion follows.
Let the production rules set P = {S d A, A e B C, B e, C f}, N = {A,B,C}, T = {d,e,f} and S = {S}.
- (1)
- Every terminal and non-terminal is stored to the chromosome. In our example this chromosome is:
S d A A e B C B e C f - (2)
- The generated enumeration map becomes:
S d e f A B C 0 1 2 3 4 5 6 - (3)
- The phenotype is converted to an enumerated array as:
S d A A e B C B e C f 0 1 4 4 2 5 6 5 2 6 3
Step 2 Fitness calculation:
The inverse mapping of each chromosome to the corresponding grammar is estimated. The fitness value is calculated by parsing both positive and negative string databases with each chromosome GNF in the chromosome pool. After parsing the positive and negative examples, the well-known true positive (TP), false negative (FN), false positive (FP) and true negative (TN) rates are estimated. TPs and TNs contribute +1 to the fitness value of each chromosome GNF, while FPs contribute -1 and FNs contribute , where a is the sub-parse parameter defined in the previous paragraph. D is the ratio of the string length successfully parsed. From the above, it is obvious that maximum fitness equals the size of both datasets and minimum fitness equals minus the size of both datasets.
An example of the term D calculation follows. Let the production rules set P = {S d A, A e B C, B e, C f}, N = {A,B,C}, T = {d,e,f} and S = {S} as in the previous example. If the string deefd was in the positive dataset then the term D should be equal to 0.2 as deef can be parsed by the above grammar but in the string deefd only the four out of the five symbols can be reached. Hence, D should be 0.8. If the candidate string was deefde then D should be 0.666 and so forth.
Step 3 Convergence check:
The maximum fitness value of the current population GNFs is compared with the predefined convergence criterion. If the best chromosome fitness surpasses the convergence criterion or the maximum number of generations is reached, we accept the GNF with maximum value as a solution to the inference problem and the algorithm is terminated.
Step 4 Evolution:
In the crossover operator, two parents are used to derive a new candidate GNF, selected from the pool with respect to their crossover probability, which is estimated from the corresponding GNF fitness values following the typical procedure of GAs. A random offset from is generated for each chromosome. For the first parent, a sub-chromosome from is taken and for the second parent sub-chromosome from . Then, the two sub-chromosomes are concatenated in order to generate a new offspring. The offspring is discarded and the process is repeated only in two cases; if the resulting offspring is not in the GNF or if the starting symbol S is not found in the head of at least one production rule. An example follows. Let two chromosomes selected to produce an offspring , and the randomly generated offsets 3,4. Then, from the first parent the and from the second parent the is selected and the the resulting offspring’s chromosome is the concatenation of the selected sub-strings .
The process of crossover is repeated until the predefined size of the population pool is reached. Before an offspring enters the next generation, the mutation operator is applied with probability equal to mutation rate. In the proposed method, the resulting chromosome from the mutation rate is always checked in order to ensure valid GNF structure.
As the population evolves, the resulting grammars may have many small rules or a smaller number of lengthy rules. The only constraint applied across generations is the maximum length of each chromosome, but the maximum number of rules or maximum length of rules may be greater than originally defined. This relaxation of constraints helps diversify the new populations and better adapt to complex problems.
Step 5 Loop:
Go to step 2.
3.3. CFG and GNF Parsing Algorithms
In order to estimate the GE fitness of each chromosome GNF, a parsing algorithm must be implemented. Optimal parsing algorithms do exist for CFGs that solve the problem of whether a string can be generated by a CFG. Most of the parsers solve the problem of parsing in polynomial time O() up to O(), n being the length of the candidate string to be parsed. The computational complexity of the parsing algorithm depends on the implementation of the parser and the form of the CFG. Notable parsers are the CYK algorithm [22], Early algorithm [23] and GLR [24].
The CFG parsers can be divided in two main categories:
- (1)
- top-down parsers [25] which search the candidate string from left to right and usually implement a structure like a search tree;
- (2)
- bottom-up parsers [26] which search the candidate string from right to left and are usually implemented through dynamic programming techniques.
Top-down parsers fail when left-recursions occur [27] () and bottom-up parsers fail when right-recursions occur () in some production rules. For general CFGs, hybrid implementations of top-down and bottom-up parsers are used. Greibach Normal Form offers two interesting properties which accelerate the parsing process. GNF is a left-recursion free grammar which means that any top-down parser will halt at maximum depth n. Left-recursion-free means that one non-terminal symbol cannot exist both in the head of a production rule and also be the leftmost symbol in the body of a production rule. Additionally, every production rule consists of a terminal symbol which means that, at most, n production rules are used in a successful parsing path in the parsing tree. In our implementation we used a top-down parser which also provides an easy way to measure the sub-parsed string as a tree is generated.
Hybrid parsers for general CFGs are worst-case scenario O() but bottom-up parsers have lower order in respect to the candidate string compared to the general case. The parser used in our implementation is O() which furthermore accelerates the whole process.
The proposed parsing method was carried out in two steps used recurrently. First, the components of the method were analyzed and the pseudocode of the method will be presented after this.
The special notation used for the pseudocode is the sets of a 4-tuple GNF G represented as respectively and w is the candidate word to be parsed and consists only of symbols in set T. The notation means the sub-string from index n to index m ( and length of w). Additionally, the notations , and represent the body of the rule, without the terminal symbol in the GNF, the terminal symbol of a GNF production rule and the head of a production rule, respectively. Each component of the algorithm returns a 2-tuple Parsed,Depth whereas Parsed is a Boolean and Depth is an integer. The two steps are called ParseWord and Distribute.
{ Parsed,Depth } = ParseWord(StartSymbol,G,w)
Minimum Depth = length of w
for rule in
if == & == StartSymbol
case 1 : {rule length = 2 & word length = 1 }
return { true,0 }
case 2 : {rule length = 3 & word length > 1 }
Minimum Depth- = 1
check ParseWord{ , G , }
case 3 : {rule length > 3 & word length > 2 }
Minimum Depth -= 1
check Distribute{ , G , }
end for
return { False, Minimum Depth }
end ParseWord
In the above function, with the instruction check, it is meant that if the recurrent call of the function returns true, then the for loop is terminated and the 2-tuple of the called function is returned by the ParseWord{ … } function.
{ Parsed,Depth } = Distribute(array of Non-Terminals,G,w)
Minimum Depth = length of w
boolean
integer
for i in { 1,length of w -1 }
case 1 : size of array of Non-Terminals = 2
{ , } = ParseWord( NonTerminals, G, )
{ , } = ParseWord( NonTerminals, G, )
if < Minimum Depth : Minimum Depth =
if & return { True, Minimum Depth }
case 2 : size of array of Non-Terminals > 2
{ , } = ParseWord( NonTerminals, G, )
{ , } = Distribute( NonTerminals, G, )
if < Minimum Depth : Minimum Depth =
if & return { True, Minimum Depth }
end for
return { False, Minimum Depth }
end Distribute
In this implementation, the two components are called recursively. The stack of recurrent calls may be approximates of a DFS tree whereas the ParseWord function expands the nodes to lower leafs and the Distribute function generates the branches (breadth) of the parsing tree.
3.4. Advantages of the GNF Encoding
The GNF encoding offers a robust rule of thumb of whether the use of the crossover operator may lead to a grammar which is not in the GNF: the chromosome of any grammar in the GNF cannot have two consecutive terminal symbols. That means that we actually have a priori knowledge of whether the genetic operators lead to a valid GNF. For the mutation operator we only need to check whether the neighbouring symbols in the chromosome are leading to two consecutive terminal symbols in the new chromosome. So the validity of an offspring can be determined simply and robustly in fixed time. In cases in which an invalid mutation occurs, we can retry a different mutation to a specific chromosome.
GNF representation also eliminates the probability of new chromosomes not being a valid GNF with the crossover operator. An invalid offspring would be a chromosome with two consecutive terminal symbols, something that can not occur in a GNF. This probability for such cases is only 1/() whereas is the average length of a production rule counting all symbols in the head and the body of a production rule. This probability is easily derived, as for a grammar to be invalid the first subvector used in the crossover must end with a terminal symbol ( = 1/() in the GNF) and the second subvector must start with a terminal symbol ( = 1/() in the GNF). In these cases, our method chooses to reapply the crossover operation in different locations of the original chromosomes. With this method, the invalid offsprings probability is zero.
Finally, the use of GNF, facilitates a robust mapping of each grammar in a linear structure with no auxiliary data needed except from the mapping of the terminal and non terminal symbols.
The advantages of the GNF representation discussed offer a huge advantage in the proposed GNF inference method, because different CFG formulations tend to increase significantly the probability to introduce an invalid offspring through the crossover operator. This means, that, in our case, a new pool of candidate solutions always contains valid grammars adhering to the GNF structure and no parsing of chromosomes and discarding is needed before the evaluation step. Typical cases where invalid offsprings are created through genetic operations can be met in the bibliography in other forms of CFGs such as the Backus–Naur form. For example, if the average length of a production rule in a grammar is reported to be equal to 5, then the average probability, through the population, of two chromosomes’ crossover leading to an invalid offspring is 4%. Using the GNF constraints during crossover, these cases are discarded. Finally, the complexity of the proposed method is equal to whereas an efficient top-down parser such as the one presented can significantly drop the computational complexity.
3.5. Implementation Details
The complete GNF inference system using the GE method was implemented in ANSI C++, which can be executed in all systems running the GNU C++ compiler.
Multiple experiments were carried out to estimate the proposed algorithm behaviour in different datasets and parameter values.
4. Experiments
The proposed method was evaluated in several experiments estimating both quantitative and qualitative metrics. The code that was used to execute all experiments is publicly available on https://github.com/stranger-codebits/Greibach-Grammar-Inference, accessed on 1 March 2020. All experiments where conducted on a Linux machine with an Intel i7-3770K processor (7000 BogoMIPS) with 16 GigaBytes of RAM.
The eight languages used by Wieczorek et al. [12] were considered alongside language that showcases some key advantages of our method, and some special cases were selected as benchmark. All languages are context-free except for the third and ninth languages which are regular.
- 1
- 2
- balanced parentheses
- 3
- 4
- 5
- is a palindrome }
- 6
- 7
- : the language of Lukasiewicz
- 8
- or
- 9
- or
The first eight languages were used by Nakamura and Eyrad et al. [12,28,29], while the inherently ambiguous context-free language is the evaluation language showing that the method proposed by Nakamura and Matsumoto [30] is not convergent as mentioned by the authors.
The ninth language is a regular language in which each word has strings that contain either only odd or only even numbers. These examples are evenly distributed. This language was selected for a very specific reason. Due to having random negative examples, any inference algorithm may fall to a local minima where only strings with even, or only strings with odd numbers are parsed. This is the fastest path to reach a local minima. We used this grammar to compare the effect of the sub-parse variable to the convergence of the algorithm.
For the first seven languages, we listed all positive words with and for the eighth language we listed all positive words with . For , we generated 100 random positive examples (50 with odd numbers and 50 with even numbers) and 100 random negative examples.
4.1. Special Test Cases
We consider as a special test case. This is because the dataset contains two very distinct and strong local minima for the inference algorithm. The positive dataset can be described from two distinct context-free languages, one containing only even digits and one containing only odd numbers. This was developed and designed as an evolutionary technique can easily converge in the local minimum but it may be unable to also cover the rest of the dataset.
Finally, the last dataset considered was strings that represented the valid Collatz series. The corresponding Collatz series, for [31], were used as positive data and random number series were used as negative data. This dataset was created in order to evaluate the method on long and complex strings with no clear structure and dependencies as the previous nine languages.
4.2. Experiments Goals
For the first eight languages, all experiments where executed 10-fold with the defaults algorithm parameters. These are population = 500, generations = 500, mutation rate = 0.03, non-terminals set size = 10, elitism rate = 0.03, max chromosome length = 100, and D = 0.01. The goal of these experiments is to measure the generality of our method, analyze cases where results where unexpected and, finally, compare the method with other well-established techniques.
With experiments, we evaluate the ability of the proposed method to converge on a global minimum instead of the strong local minima described previously. That is the reason that we also used smaller population () and a smaller number of non-terminals () and .
Furthermore, with we evaluated the proposed method’s accuracy with respect to long structured strings and the ability to infer complex relationships inside a set of positive examples. For all experiments, the default parameters were used.
One final experiment we conducted was to test the algorithms’ capabilities with respect to the max chromosome length. The experiments were conducted using a positive dataset of 100 common English names and a negative dataset which consisted of the 114 most common English words (both datasets are downloaded from http://archive.ics.uci.edu/ml/index.php, accessed on 1 March 2020), population size 1000, mutation rate 3 %, elitism 3%, non-terminal symbols set size 30 and max chromosome length 30, 50 or 75, maximum number of generations 200 and number of candidates per generation 1000. The maximum fitness value for a chromosome is estimated to be 214 and the minimum is −214.
All experiments were conducted 10-fold with and without the sub-parse variable in order to have more quantitative results.
5. Results
In Table 2, the results from running 10-fold experiments on the first eight languages are presented. G, number of generations for convergence, , number of non-terminal symbols in the best solution, R, number of rules, , chromosome length, , accuracy, , true positive rate, , true negative rate and , experiments mean time are denoted.

Table 2.
Experimental results from .
As is presented for the majority of the languages, the accuracy of the proposed inference method is almost 1 (ACC). In the cases where the accuracy is less than optimal, we observed that, by changing the max chromosome length to 150 (as opposed to 100 that is the default parameter), the algorithm converged. This means that, given a large enough grammar, our method is capable of converging for any of the target languages. Furthermore, we executed the same set of experiments without the term D (sub-parse variable) and on average, the accuracy was less and the number of generations needed for convergence were more.
The number of non-terminal symbols in the best chromosome of the final generation is usually less than the default number. So, in many cases the method performs a reduction of the terminal symbols set during evolution. The mean number of non-terminals is similar in cases where we re-executed the experiments with 20 non-terminal symbols during method’s initialization.
These results, with a notably small chromosomes in the algorithm, lead to comparable results with Wieczorek [12] where, in this case, the success rate of the overall experiment was measured. Furthermore, if we used greater population sizes and chromosome sizes we can claim a success rate but we aim for realistic grammars with a small number of rules.
In the case of the special , we conducted experiments with the parameter values described in the previous subsection. In the majority of the experiments, the use of the sub-parse term led to faster convergence and with greater accuracy. In 10 experiments, the average accuracy was >10% greater when using the sub-parse variable while the algorithm converged in less generations.
In Figure 1, a comparison of the convergence of two typical experiments, one with the sub-parse variable and one without, is presented. It is clear that, when omitting the term D, the solution converges to one of the local minima described in the previous paragraphs. This is clearly not the case for the experiment using the sub-parse variable and we consider this behavior as an improvement of the typical ways to calculate the fitness in standard genetic algorithms for grammatical inference.
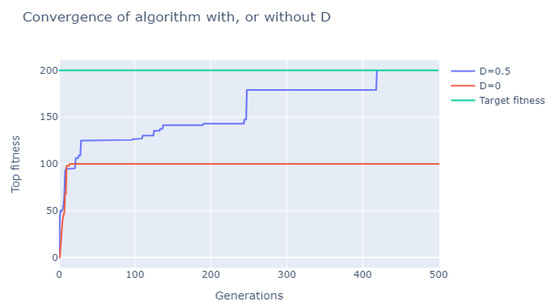
Figure 1.
Effect of sub-parse variable on .
For the special language , we executed 10-fold experiments with and without the sub-parse variable. The method was able to derive complex grammars that perfectly described the dataset. Again, the average accuracy was higher with the use of the sub-parse variable and the method converged faster.
Finally, in Figure 2, the maximum fitness value and the average fitness of the top 3% individuals at each generation is plotted for the chromosomes of lengths 30, 50 and 75 for the final experiment discussed in the previous section. Green and red lines show the corresponding best fitness and the average fitness of the best 3% candidates per generation using a chromosome length equal to 30, blue and orange lines show the corresponding fitness rates using a chromosome length equal to 50 and purple and brown lines show the corresponding fitness rates using a chromosome length equal to 75.
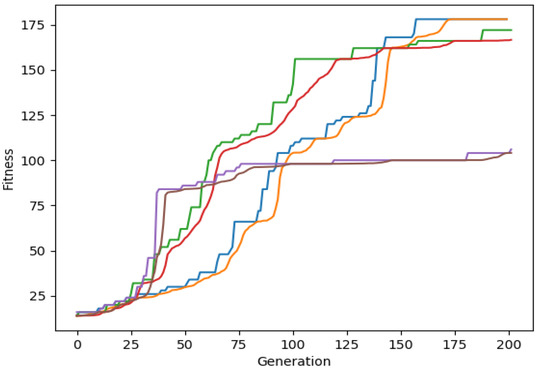
Figure 2.
Best population fitness rate with chromosomes of length 30, 50, 75.
It is clear that the convergence of the algorithm depends on the chromosome size, when target languages are complex and no clear pattern or structure is present.
6. Conclusions
In the vast majority of the conducted experiments it is clear that the proposed GNF inference algorithm follows the exponential learning curve after the first few iterations.
The main reason for some experiments with low accuracy is the use of too small chromosomes. In experiments with low accuracy, the same test was reevaluated with greater chromosome length and the algorithm converged to accuracy.
We also observed that the algorithm can perform a partial reduction of the non-terminal symbols set after convergence. In Table 2 especially, we can see how many symbols are on average the best solution developed by the method.
The use of the sub-parse variable heuristic significantly improved the convergence speed and in many cases replaced the random search in the first generations of the genetic algorithm with quantitative fitness estimation. This is evident from the comparisons from each experiment conducted.
Furthermore, the genetic algorithm converged even without the use of the sub-parse variable in many of the test cases presented. The premature calculation of Greibach chromosomes and the discard of any invalid offsprings during the crossover operator facilitates the algorithm to converge faster. Furthermore, due to the body of each GNF rule containing an arbitrary number of non-terminal symbols, complex rules can be easily created during crossover that can encode complex grammars.
7. Future Plans
Our future plans for this method include a more general overview of the algorithm for in-the-loop control of the algorithms’ variables (auto-tuning), making the chromosomes more robust using shuffled or permutated chromosomes reserving the phenotype, with more complex use of the sub-parse term, maybe converting it to exponential.
Author Contributions
The authors of this paper contributed on the following work items. Conceptualization, N.A. and E.D.; methodology, N.A. and E.D.; software, N.A.; formal analysis, N.A. and E.D.; writing—original draft preparation, N.A.; writing—review and editing, N.A. and E.D.; supervision, E.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data used for the analysis of this method are publicly available. The artificial languages are included in the open repository with the paper’s code and on any other case, the public datasets are linked.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ryan, C.; Collins, J.; O’Neill, M. Grammatical Evolution: Evolving Programs for an Arbitrary Language; Springer: Berlin/Heidelberg, Germany, 1998; pp. 83–96. [Google Scholar]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992; Volume 1. [Google Scholar]
- Bartoli, A.; Castelli, M.; Medvet, E. Weighted Hierarchical Grammatical Evolution. IEEE Trans. Cybern. 2018, 50, 476–488. [Google Scholar] [CrossRef] [PubMed]
- Kita, E.; Zuo, Y.; Sugiura, H.; Mizuno, T. Acceleration of Grammatical Evolution with Multiple Chromosome by Using Stochastic Schemata Exploiter. In Proceedings of the 2017 Fourth International Conference on Mathematics and Computers in Sciences and in Industry (MCSI), Corfu, Greece, 24–27 August 2017. [Google Scholar] [CrossRef]
- Sabar, N.R.; Ayob, M.; Kendall, G.; Qu, R. Grammatical Evolution Hyper-Heuristic for Combinatorial Optimization Problems. IEEE Trans. Evol. Comput. 2013, 17, 840–861. [Google Scholar] [CrossRef]
- Assuncao, F.; Lourenco, N.; Machado, P.; Ribeiro, B. Automatic generation of neural networks with structured Grammatical Evolution. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017. [Google Scholar] [CrossRef]
- Sousa, A.D.M.; Lorena, A.C.; Basgalupp, M.P. GEEK: Grammatical Evolution for Automatically Evolving Kernel Functions. In Proceedings of the 2017 IEEE Trustcom/BigDataSE/ICESS, Sydney, NSW, Australia, 1–4 August 2017. [Google Scholar] [CrossRef]
- Antonio-Javier, G.; López, D.; Calera-Rubio, J. Grammatical inference of directed acyclic graph languages with polynomial time complexity. J. Comput. Syst. Sci. 2018, 95, 19–34. [Google Scholar]
- Wojciech, W.; Nowakowski, A. Grammatical inference in the discovery of generating functions. In Man–Machine Interactions 4; Springer: Cham, Switzerland, 2016; pp. 627–637. [Google Scholar]
- Pandey, H.M.; Chaudhary, A.; Mehrotra, D.; Kendall, G. Maintaining regularity and generalization in data using the minimum description length principle and genetic algorithm: Case of grammatical inference. Swarm Evol. Comput. 2016, 31, 11–23. [Google Scholar] [CrossRef][Green Version]
- Pandey, H.M.; Chaudhary, A.; Mehrotra, D. Bit mask-oriented genetic algorithm for grammatical inference and premature convergence. Int. J. Bio-Inspired Comput. 2018, 12, 54–69. [Google Scholar] [CrossRef]
- Wieczorek, W. Inductive Synthesis of Cover-Grammars with the Help of Ant Colony Optimization. Found. Comput. Decis. Sci. 2016, 41, 297–315. [Google Scholar] [CrossRef][Green Version]
- Kogkalidis, K.; Melkonian, O. Towards a 2-Multiple Context-Free Grammar for the 3-Dimensional Dyck Language. In European Summer School in Logic, Language and Information; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Imada, K.; Nakamura, K. Learning context free grammars by using SAT solvers. In Proceedings of the 2009 International Conference on Machine Learning and Applications, Miami, FL, USA, 13–15 December 2009; pp. 267–272. [Google Scholar]
- Sakakibara, Y. Learning context-free grammars using tabular representations. Pattern Recognit. 2005, 9, 1372–1383. [Google Scholar] [CrossRef]
- Unold, O.; Jaworski, M. Learning context-free grammar using improved tabular representation. Appl. Soft Comput. 2010, 1, 44–52. [Google Scholar] [CrossRef]
- Solan, Z.; Horn, D.; Ruppin, E.; Edelman, S. Unsupervised learning of natural languages. Proc. Natl. Acad. Sci. USA 2005, 33, 11629–11634. [Google Scholar] [CrossRef] [PubMed]
- Yasubumi, S. Recent advances of grammatical inference. Theor. Comput. Sci. 1997, 185, 15–45. [Google Scholar]
- Greibach, S.A. A New Normal-Form Theorem for Context-Free Phrase Structure Grammars. J. ACM 1965, 12, 42–52. [Google Scholar] [CrossRef]
- Bals, M.; Jansen, C.; Noll, T. Incremental Construction of Greibach Normal Form. In Proceedings of the 2013 International Symposium on Theoretical Aspects of Software Engineering, Birmingham, Birmingham, UK, 1–3 July 2013; pp. 165–168. [Google Scholar] [CrossRef]
- O’Neill, M.; Ryan, C. Grammatical evolution. IEEE Trans. Evol. Comput. 2001, 5, 349–358. [Google Scholar] [CrossRef]
- Chappelier, J.-C.; Rajman, M. A generalized CYK algorithm for parsing stochastic CFG. In Proceedings of the 1st Workshop on Tabulation in Parsing and Deduction (TAPD’98), Paris, France, 2–3 April 1998. [Google Scholar]
- Schnelle, H.; Doust, R. A net-linguistic “Early” parser. In Connectionist Approaches to Natural Language Processing; Routledge: Oxfordshire, UK, 1992. [Google Scholar]
- McPeak, S.; Necula, G.C. Elkhound: A fast, practical GLR parser generator. In International Conference on Compiler Construction; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Brian, R. Probabilistic top-down parsing and language modeling. Comput. Linguist. 2001, 27, 249–276. [Google Scholar]
- Dowding, J.; Moore, R.; Andry, F.; Moran, D. Interleaving syntax and semantics in an efficient bottom-up parser. In Proceedings of the 32nd Annual Meeting on Association for Computational Linguistics, Las Cruces, NM, USA, 27–30 June 1994; Association for Computational Linguistics: Stroudsburg, PA, USA, 1994. [Google Scholar]
- Ludmila, F.; Baranov, S. Equivalent transformations and regularization in context-free grammars. Cybern. Inf. Technol. 2015, 14, 29–44. [Google Scholar]
- Eyraud, R.; de la Higuera, C.; Janodet, J. LARS: A learning algorithm for rewriting systems. Mach. Learn. 2007, 66, 7–31. [Google Scholar] [CrossRef]
- Nakamura, K.; Ishiwata, T. Synthesizing Context Free Grammars from Sample Strings Based on Inductive CYK Algorithm; LNAI 1891; Springer: Berlin/Heidelberg, Germany, 2000; pp. 186–195. [Google Scholar]
- Nakamura, K.; Matsumoto, M. Incremental learning of context free grammars based on bottom-up parsing and search. Pattern Recognit. 2005, 38, 1384–1392. [Google Scholar] [CrossRef]
- Ştefan, A.; Masalagiu, C. About the Collatz conjecture. Acta Inform. 1998, 35, 167–179. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).