Deep Ensembles Based on Stochastic Activations for Semantic Segmentation
Abstract
:1. Introduction
2. Methods
2.1. Deep Learning for Semantic Image Segmentation
- MobileNet-v2 [30] is a lightweight CNN designed for mobile devices based on depthwise separable convolutions.
- ResNet18 and ResNet50 [31] are two CNNs of the ResNet family, a set of architectures based on the use of residual blocks in which intermediate layers of a block learn a residual function concerning the block input.
- Xception [32] is a CNN architecture that relies solely on depthwise separable convolution layers.
- Inception-ResNet-v2 (IncR,) [33] combines the Inception architecture with residual connections. In the Inception-Resnet block, multiple-sized convolutional filters are combined with residual connections, replacing the filter concatenation stage of the Inception architecture.
- EfficentNet [34], is a family of CNNs designed to scale well with performance. EfficientNetB0 is a simple mobile-size baseline architecture, the other networks of the family are obtained applying an effective compound scaling method for increasing the model size to achieve maximum accuracy gains.
2.2. Stochastic Activation Selection
3. Results on Colorectal Cancer Segmentation
3.1. Datasets, Testing Protocol, and Metrics
- Accuracy/precision/recall/F1-score/F2-score can be defined for a bi-class problem (or for each class in the case of multiclass) starting from the confusion matrix (TP, TN, FP, and FN refer to the true positives, true negatives, false positives, and false negatives, respectively) as follows:is the number of pixels correctly classified over the total number of pixels in the image.is the fraction of the “polyp” that is correctly classified.is the fraction of the “polyp” predictions that were actually “polyp” pixels.are two measures that try to average precision and recall.
- Intersection over union (IoU): IoU is defined as the area of intersection between the predicted segmentation map A and the ground-truth map B, divided by the area of the union between the two maps:
- Dice: The Dice coefficient is defined as twice the overlap area of the predicted and ground-truth maps divided by the total number of pixels. For binary maps, with foreground as the positive class, the Dice coefficient is identical to the F1-score:
- All the above-reported metrics range in [0, 1] and must be maximized. The final performance is obtained averaging on the test set the performance obtained for each test image.
3.2. Experiments
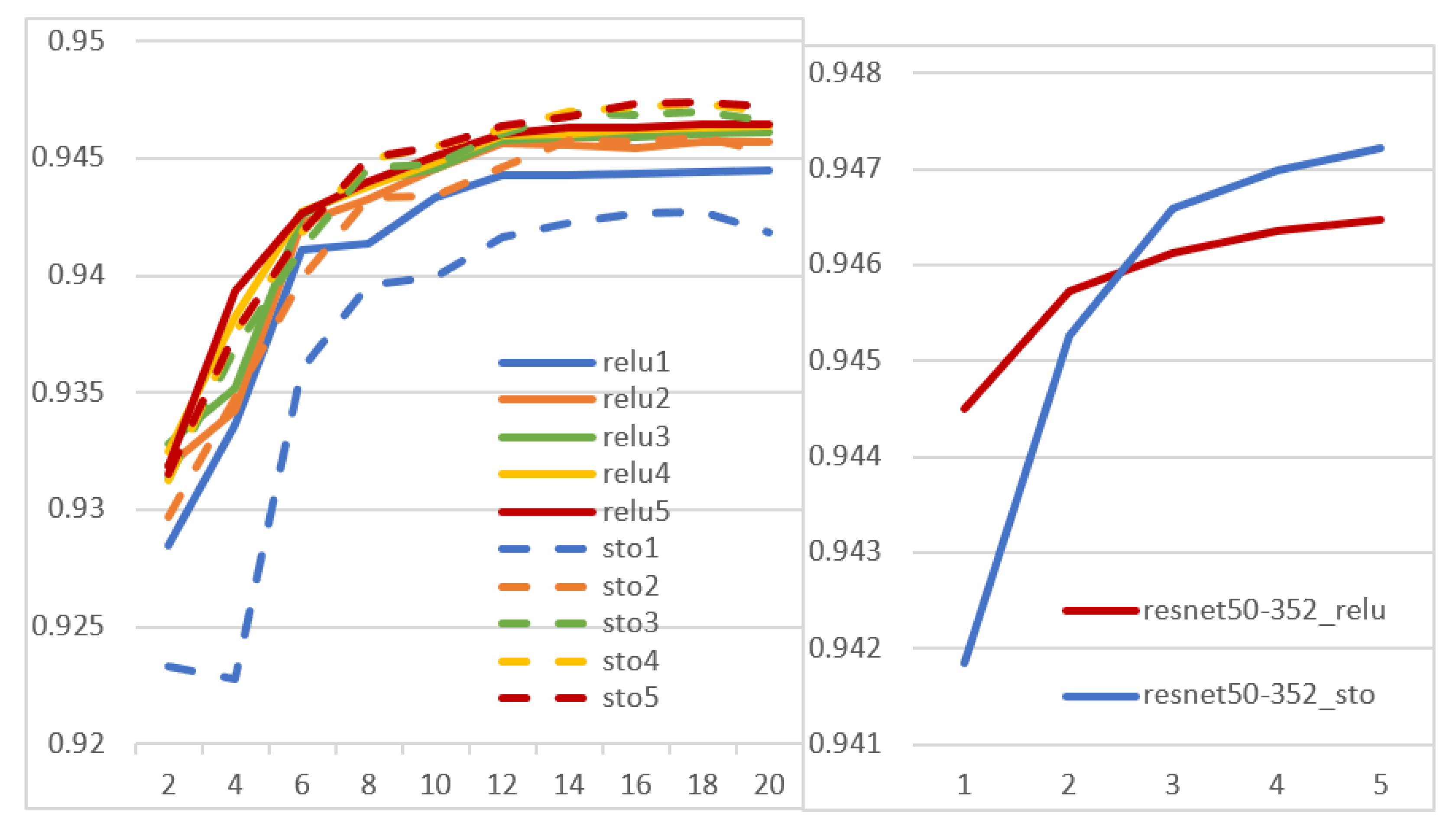
- _act: each network was obtained by deterministically substituting each activation layer with one of the activation functions of Section 2.2 (the same function for all the layers, but a different function for each network)
- _sto: ensembles of stochastic models, whose activation layers were replaced by a randomly selected activation function (which may be different for each layer)
- _sel: ensembles of “selected” stochastic models. The network selection was performed using cross-validation on the training set among 100 resnet50 stochastic models. The selection procedure was based on the idea of sequential forward floating selection (SFFS) [49], a selection method originally proposed for feature selection and used here for selecting the most performing/independent classifiers to be added to the ensemble. SFFS is an iterative method that, at each step, adds to the final ensemble the model that provides the highest incremental of performance to the existing subset of models. Then, a backtracking step is performed to exclude the worst model from the actual ensemble. Since SFFS requires a training phase, we performed threefold cross-validation on the training set. For a fair comparison with other ensembles, we selected a set of 14 networks, which were finally fine-tuned on the whole augmented training set at a larger resolution.
- _relu: an ensemble of original models that differ only for the random initialization before training. It means that all the starting models in the ensemble are the same, except for the initialization. This ensemble is the baseline for comparisons with the approaches above.
4. Result on Skin Detection
4.1. Datasets, Testing Protocol, and Metrics
4.2. Experiments
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Feng, D.; Haase-Schütz, C.; Rosenbaum, L.; Hertlein, H.; Glaeser, C.; Timm, F.; Wiesbeck, W.; Dietmayer, K. Deep multi-modal object detection and semantic segmentation for autonomous driving: Datasets, methods, and challenges. IEEE Trans. Intell. Transp. Syst. 2020, 22, 1341–1360. [Google Scholar] [CrossRef] [Green Version]
- Brandao, P.; Zisimopoulos, O.; Mazomenos, E.; Ciuti, G.; Bernal, J.; Visentini-Scarzanella, M.; Menciassi, A.; Dario, P.; Koulaouzidis, A.; Arezzo, A.; et al. Towards a computed-aided diagnosis system in colonoscopy: Automatic polyp segmentation using convolution neural networks. J. Med. Robot. Res. 2018, 3, 1840002. [Google Scholar] [CrossRef] [Green Version]
- Noh, H.; Hong, S.; Han, B. Learning deconvolution network for semantic segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1520–1528. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Bullock, J.; Cuesta-Lázaro, C.; Quera-Bofarull, A. XNet: A convolutional neural network (CNN) implementation for medical X-Ray image segmentation suitable for small datasets. In Proceedings of the Medical Imaging 2019: Biomedical Applications in Molecular, Structural, and Functional Imaging, San Diego, CA, USA, 15 March 2019; Volume 10953, p. 109531Z. [Google Scholar]
- Shelhamer, E.; Long, J.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017. [Google Scholar] [CrossRef]
- Roncucci, L.; Mariani, F. Prevention of colorectal cancer: How many tools do we have in our basket? Eur. J. Intern. Med. 2015, 26, 752–756. [Google Scholar] [CrossRef]
- Rein-Lien, H.; Abdel-Mottaleb, M.; Jain, A.K. Face detection in color images. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 696–706. [Google Scholar] [CrossRef] [Green Version]
- Argyros, A.A.; Lourakis, M.I.A. Real-time tracking of multiple skin-colored objects with a possibly moving camera. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2004; pp. 368–379. [Google Scholar] [CrossRef]
- Han, J.; Award, G.M.; Sutherland, A.; Wu, H. Automatic skin segmentation for gesture recognition combining region and support vector machine active learning. In Proceedings of the 7th International Conference on Automatic Face and Gesture Recognition, Southampton, UK, 10–12 April 2006; pp. 237–242. [Google Scholar]
- Wang, Y.; Tavanapong, W.; Wong, J.; Oh, J.; De Groen, P.C. Part-based multiderivative edge cross-sectional profiles for polyp detection in colonoscopy. IEEE J. Biomed. Health Inform. 2013, 18, 1379–1389. [Google Scholar] [CrossRef]
- Mori, Y.; Kudo, S.; Berzin, T.M.; Misawa, M.; Takeda, K. Computer-aided diagnosis for colonoscopy. Endoscopy 2017, 49, 813. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Xiao, X.; Brown, J.R.G.; Berzin, T.M.; Tu, M.; Xiong, F.; Hu, X.; Liu, P.; Song, Y.; Zhang, D.; et al. Development and validation of a deep-learning algorithm for the detection of polyps during colonoscopy. Nat. Biomed. Eng. 2018, 2, 741–748. [Google Scholar] [CrossRef]
- Thambawita, V.; Jha, D.; Riegler, M.; Halvorsen, P.; Hammer, H.L.; Johansen, H.D.; Johansen, D. The medico-task 2018: Disease detection in the gastrointestinal tract using global features and deep learning. arXiv 2018, arXiv:1810.13278. [Google Scholar]
- Guo, Y.B.; Matuszewski, B. Giana polyp segmentation with fully convolutional dilation neural networks. In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications, Prague, Czech Republic, 25–27 February 2019; pp. 632–641. [Google Scholar]
- Jha, D.; Smedsrud, P.H.; Riegler, M.A.; Halvorsen, P.; de Lange, T.; Johansen, D.; Johansen, H.D. Kvasir-SEG: A Segmented Polyp Dataset. In Proceedings of the 26th International Conference on Multimedia Modeling, Daejeon, Korea, 5–8 January 2020. [Google Scholar]
- Jha, D.; Ali, S.; Johansen, H.D.; Johansen, D.; Rittscher, J.; Riegler, M.A.; Halvorsen, P. Real-time polyp detection, localisation and segmentation in colonoscopy using deep learning. IEEE Access 2021, 9, 40496–40510. [Google Scholar] [CrossRef] [PubMed]
- Phung, S.L.; Bouzerdoum, A.; Chai, D. Skin segmentation using color pixel classification: Analysis and comparison. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 148–154. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roy, K.; Mohanty, A.; Sahay, R.R. Deep Learning Based Hand Detection in Cluttered Environment Using Skin Segmentation. In Proceedings of the IEEE International Conference on Computer Vision Workshops (ICCVW), Venice, Italy, 22–29 October 2017; pp. 640–649. [Google Scholar]
- Arsalan, M.; Kim, D.S.; Owais, M.; Park, K.R. OR-Skip-Net: Outer residual skip network for skin segmentation in non-ideal situations. Expert Syst. Appl. 2020, 141, 112922. [Google Scholar] [CrossRef]
- Shahriar, S.; Siddiquee, A.; Islam, T.; Ghosh, A.; Chakraborty, R.; Khan, A.I.; Shahnaz, C.; Fattah, S.A. Real-time american sign language recognition using skin segmentation and image category classification with convolutional neural network and deep learning. In Proceedings of the TENCON 2018-2018 IEEE Region 10 Conference, Jeju, Korea, 28–31 October 2018; pp. 1168–1171. [Google Scholar]
- Lumini, A.; Nanni, L. Fair comparison of skin detection approaches on publicly available datasets. Expert Syst. Appl. 2020, 160, 113677. [Google Scholar] [CrossRef]
- Huang, C.-H.; Wu, H.-Y.; Lin, Y.-L. HarDNet-MSEG: A Simple Encoder-Decoder Polyp Segmentation Neural Network that Achieves over 0.9 Mean Dice and 86 FPS. arXiv 2021, arXiv:2101.07172. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. Int. Conf. Learn. Represent. 2015, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the 15th European Conference in Computer Vision, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Minaee, S.; Boykov, Y.; Porikli, F.; Plaza, A.; Kehtarnavaz, N.; Terzopoulos, D. Image segmentation using deep learning: A Survey. IEEE Trans. Pattern Anal. Mach. Intelli. 2021. [Google Scholar] [CrossRef]
- Khan, A.; Sohail, A.; Zahoora, U.; Qureshi, A.S. A Survey of the Recent Architectures of Deep Convolutional Neural Networks. Artif. Intell. Rev. 2020, 53, 5455–5516. [Google Scholar] [CrossRef] [Green Version]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning. Proc. IEEE Int. Conf. Comput. Vis. 2017, 115, 4278–4284. [Google Scholar] [CrossRef] [Green Version]
- Tan, M.; Le, Q.V. EfficientNet: Rethinking model scaling for convolutional neural networks. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Sudre, C.H.; Li, W.; Vercauteren, T.; Ourselin, S.; Jorge Cardoso, M. Generalised dice overlap as a deep learning loss function for highly unbalanced segmentations. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef] [Green Version]
- Jadon, S. A survey of loss functions for semantic segmentation. In Proceedings of the 2020 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology, Viña del Mar, Chile, 27–29 October 2020. [Google Scholar]
- Nanni, L.; Lumini, A.; Ghidoni, S.; Maguolo, G. Stochastic selection of activation layers for convolutional neural networks. Sensors 2020, 20, 1626. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the 14th International Conference on Artificial Intelligence and Statistics (AISTATS) 2011, Fort Lauderdale, FL, USA, 26–29 August 2011. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier nonlinearities improve neural network acoustic models. In Proceedings of the in ICML Workshop on Deep Learning for Audio, Speech and Language Processing, Atlanta, GA, USA, 16 June 2013. [Google Scholar]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units (ELUs). In Proceedings of the 4th International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Jin, X.; Xu, C.; Feng, J.; Wei, Y.; Xiong, J.; Yan, S. Deep learning with S-shaped rectified linear activation units. In Proceedings of the 30th AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Agostinelli, F.; Hoffman, M.; Sadowski, P.; Baldi, P. Learning activation functions to improve deep neural networks. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Maguolo, G.; Nanni, L.; Ghidoni, S. Ensemble of Convolutional Neural Networks Trained with Different Activation Functions. Expert Syst. Appl. 2021, 166, 114048. [Google Scholar] [CrossRef]
- Cheng, Q.; Li, H.; Wu, Q.; Ma, L.; King, N.N. Parametric Deformable Exponential Linear Units for deep neural networks. Neural Netw. 2020, 125, 281–289. [Google Scholar] [CrossRef] [PubMed]
- Ramachandran, P.; Zoph, B.; Le, Q. V Searching for Activation Functions. arXiv 2017, arXiv:1710.05941. [Google Scholar]
- Zhou, Y.; Li, D.; Huo, S.; Kung, S.-Y. Soft-Root-Sign Activation Function. arXiv 2020, arXiv:2003.00547. [Google Scholar]
- Misra, D. Mish: A self regularized non-monotonic neural activation function. arXiv 2019, arXiv:1908.08681. [Google Scholar]
- Pudil, P.; Novovičová, J.; Kittler, J. Floating search methods in feature selection. Pattern Recognit. Lett. 1994, 15, 1119–1125. [Google Scholar] [CrossRef]
- Safarov, S.; Whangbo, T.K. A-denseunet: Adaptive densely connected unet for polyp segmentation in colonoscopy images with atrous convolution. Sensors 2021, 21, 1441. [Google Scholar] [CrossRef]
- Branch, M.V.L.; Carvalho, A.S. Polyp Segmentation in Colonoscopy Images using U-Net-MobileNetV2. arXiv 2021, arXiv:2103.15715. [Google Scholar]
- Tomar, N.K.; Jha, D.; Ali, S.; Johansen, H.D.; Johansen, D.; Riegler, M.A.; Halvorsen, P. DDANet: Dual Decoder Attention Network for Automatic Polyp Segmentation. In International Conference on Pattern Recognition; Springer: Cham, Switzerland, 2021; ISBN 9783030687922. [Google Scholar]
- Stöttinger, J.; Hanbury, A.; Liensberger, C.; Khan, R. Skin paths for contextual flagging adult videos. In Advances in Visual Computing; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Tan, W.R.; Chan, C.S.; Yogarajah, P.; Condell, J. A Fusion Approach for Efficient Human Skin Detection. Ind. Inf. IEEE Trans. 2012, 8, 138–147. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Xia, T.; Zhang, Y.; Lin, S. Human skin detection in images by MSER analysis. In Proceedings of the 2011 18th IEEE International Conference on Image Processing, Brussels, Belgium, 11–14 September 2011; pp. 1257–1260. [Google Scholar] [CrossRef]
- Ruiz-Del-Solar, J.; Verschae, R. Skin detection using neighborhood information. In Proceedings of the Proceedings—Sixth IEEE International Conference on Automatic Face and Gesture Recognition, Seoul, Korea, 17–19 May 2004; pp. 463–468. [Google Scholar]
- Jones, M.J.; Rehg, J.M. Statistical color models with application to skin detection. Int. J. Comput. Vis. 2002, 46, 81–96. [Google Scholar] [CrossRef]
- Casati, J.P.B.; Moraes, D.R.; Rodrigues, E.L.L. SFA: A human skin image database based on FERET and AR facial images. In Proceedings of the IX Workshop de Visao Computational, Rio de Janeiro, Brazil, 30 January–1 February 2013. [Google Scholar]
- Kawulok, M.; Kawulok, J.; Nalepa, J.; Smolka, B. Self-adaptive algorithm for segmenting skin regions. EURASIP J. Adv. Signal Process. 2014, 2014, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Schmugge, S.J.; Jayaram, S.; Shin, M.C.; Tsap, L.V. Objective evaluation of approaches of skin detection using ROC analysis. Comput. Vis. Image Underst. 2007, 108, 41–51. [Google Scholar] [CrossRef]
- Sanmiguel, J.C.; Suja, S. Skin detection by dual maximization of detectors agreement for video monitoring. Pattern Recognit. Lett. 2013, 34, 2102–2109. [Google Scholar] [CrossRef] [Green Version]
- Abdallah, A.S.; El-Nasr, M.A.; Abbott, A.L. A new color image database for benchmarking of automatic face detection and human skin segmentation techniques. World Academy of Science, Engineering and Technology, Open Science Index 12. Int. J. Comput. Inf. Eng. 2007, 1, 3782–3786. [Google Scholar]


| Network | Depth | Size (MB) | Parameters (Millions) | Input Size |
|---|---|---|---|---|
| mobilenetv2 | 53 | 13 | 3.5 | 224 × 224 |
| resnet18 | 18 | 44 | 11.7 | 224 × 224 |
| resnet50 | 50 | 96 | 25.6 | 224 × 224 |
| xception | 71 | 85 | 22.9 | 299 × 299 |
| IncR | 164 | 209 | 55.9 | 299 × 299 |
| efficientnetb0 | 82 | 20 | 5.3 | 224 × 224 |
| Backbone | IoU | Dice | F2 | Prec. | Rec. | Acc. |
|---|---|---|---|---|---|---|
| Mobilenetv2 | 0.734 | 0.823 | 0.827 | 0.863 | 0.841 | 0.947 |
| resnet18 | 0.759 | 0.844 | 0.845 | 0.882 | 0.856 | 0.952 |
| resnet50 | 0.751 | 0.837 | 0.836 | 0.883 | 0.845 | 0.952 |
| xception | 0.699 | 0.799 | 0.792 | 0.870 | 0.800 | 0.943 |
| IncR | 0.793 | 0.871 | 0.878 | 0.889 | 0.892 | 0.961 |
| efficientnetb0 | 0.705 | 0.800 | 0.801 | 0.860 | 0.814 | 0.944 |
| resnet18-299 | 0.782 | 0.863 | 0.870 | 0.881 | 0.883 | 0.959 |
| resnet50-299 | 0.798 | 0.872 | 0.876 | 0.898 | 0.886 | 0.962 |
| resnet18-352 | 0.787 | 0.865 | 0.871 | 0.891 | 0.884 | 0.960 |
| resnet50-352 | 0.801 | 0.872 | 0.884 | 0.881 | 0.900 | 0.964 |
| Ensemble Name | IoU | Dice | F2 | Prec. | Rec. | Acc. |
|---|---|---|---|---|---|---|
| resnet18_act | 0.774 | 0.856 | 0.856 | 0.888 | 0.867 | 0.955 |
| resnet18_relu | 0.774 | 0.858 | 0.858 | 0.892 | 0.867 | 0.955 |
| resnet18_sto | 0.780 | 0.860 | 0.857 | 0.898 | 0.864 | 0.956 |
| resnet50_act | 0.779 | 0.858 | 0.859 | 0.894 | 0.869 | 0.957 |
| resnet50_relu | 0.772 | 0.855 | 0.858 | 0.889 | 0.870 | 0.955 |
| resnet50_sto | 0.779 | 0.859 | 0.864 | 0.891 | 0.877 | 0.957 |
| resnet50-352_sto | 0.820 | 0.885 | 0.888 | 0.915 | 0.896 | 0.966 |
| resnet50-352_sel | 0.825 | 0.888 | 0.892 | 0.915 | 0.902 | 0.967 |
| Method | IoU | Dice | F2 | Prec. | Rec. | Acc. |
|---|---|---|---|---|---|---|
| resnet50-352 | 0.801 | 0.872 | 0.884 | 0.881 | 0.900 | 0.964 |
| resnet50-352_sel | 0.825 | 0.888 | 0.892 | 0.915 | 0.902 | 0.967 |
| U-Net [17] | 0.471 | 0.597 | 0.598 | 0.672 | 0.617 | 0.894 |
| ResUNet [17] | 0.572 | 0.69 | 0.699 | 0.745 | 0.725 | 0.917 |
| ResUNet++ [17] | 0.613 | 0.714 | 0.72 | 0.784 | 0.742 | 0.917 |
| FCN8 [17] | 0.737 | 0.831 | 0.825 | 0.882 | 0.835 | 0.952 |
| HRNet [17] | 0.759 | 0.845 | 0.847 | 0.878 | 0.859 | 0.952 |
| DoubleUNet [17] | 0.733 | 0.813 | 0.82 | 0.861 | 0.84 | 0.949 |
| PSPNet [17] | 0.744 | 0.841 | 0.831 | 0.89 | 0.836 | 0.953 |
| DeepLabv3+ResNet50 [17] | 0.776 | 0.857 | 0.855 | 0.891 | 0.861 | 0.961 |
| DeepLabv3+ResNet101[17] | 0.786 | 0.864 | 0.857 | 0.906 | 0.859 | 0.961 |
| U-Net ResNet34 [17] | 0.81 | 0.876 | 0.862 | 0.944 | 0.86 | 0.968 |
| ColonSegNet [17] | 0.724 | 0.821 | 0.821 | 0.843 | 0.850 | 0.949 |
| DDANet [52] | 0.78 | 0.858 | --- | 0.864 | 0.888 | --- |
| HarDNet-MSEG [23] | 0.848 | 0.904 | 0.915 | 0.907 | 0.923 | 0.969 |
| Short Name | Name | #Samples | Ref. |
|---|---|---|---|
| FV | Feeval Skin video DB | 8991 | [53] |
| Prat | Pratheepan | 78 | [54] |
| MCG | MCG-skin | 1000 | [55] |
| UC | UChile DB-skin | 103 | [56] |
| CMQ | Compaq | 4675 | [57] |
| SFA | SFA | 1118 | [58] |
| HGR | Hand Gesture Recognition | 1558 | [59] |
| Sch | Schmugge dataset | 845 | [60] |
| VMD | 5 datasets for human activity recognition | 285 | [61] |
| ECU | ECU Face and Skin Detection | 4000 | [18] |
| VT | VT-AAST | 66 | [62] |
| Method | FV | Prat | MCG | UC | CMQ | SFA | HGR | Sch | VMD | ECU | VT | Avg | Rank |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| resnet50-224 | 0.694 | 0.874 | 0.862 | 0.866 | 0.797 | 0.939 | 0.954 | 0.760 | 0.608 | 0.927 | 0.682 | 0.815 | 7 |
| resnet50-352 | 0.745 | 0.910 | 0.880 | 0.881 | 0.831 | 0.948 | 0.962 | 0.784 | 0.727 | 0.945 | 0.742 | 0.850 | 4 |
| HarDNet-224 | 0.674 | 0.890 | 0.882 | 0.894 | 0.819 | 0.949 | 0.963 | 0.792 | 0.677 | 0.936 | 0.756 | 0.839 | 3 |
| HarDNet-352 | 0.667 | 0.913 | 0.887 | 0.902 | 0.835 | 0.952 | 0.968 | 0.795 | 0.729 | 0.946 | 0.744 | 0.849 | 2 |
| resnet50-352_sel | 0.742 | 0.917 | 0.884 | 0.910 | 0.840 | 0.952 | 0.968 | 0.785 | 0.742 | 0.949 | 0.755 | 0.859 | 1 |
| FusAct3 [39] | 0.790 | 0.874 | 0.884 | 0.896 | 0.825 | 0.951 | 0.961 | 0.776 | 0.669 | 0.933 | 0.737 | 0.845 | 6 |
| FusAct10 [39] | 0.796 | 0.864 | 0.884 | 0.899 | 0.821 | 0.951 | 0.959 | 0.776 | 0.671 | 0.929 | 0.748 | 0.845 | 5 |
| SegNet [22] | 0.717 | 0.730 | 0.813 | 0.802 | 0.737 | 0.889 | 0.869 | 0.708 | 0.328 | - | - | - | |
| U-Net [22] | 0.576 | 0.787 | 0.779 | 0.713 | 0.686 | 0.848 | 0.836 | 0.671 | 0.332 | - | - | - | |
| DeepLab [22] | 0.771 | 0.875 | 0.879 | 0.899 | 0.817 | 0.939 | 0.954 | 0.774 | 0.628 | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lumini, A.; Nanni, L.; Maguolo, G. Deep Ensembles Based on Stochastic Activations for Semantic Segmentation. Signals 2021, 2, 820-833. https://doi.org/10.3390/signals2040047
Lumini A, Nanni L, Maguolo G. Deep Ensembles Based on Stochastic Activations for Semantic Segmentation. Signals. 2021; 2(4):820-833. https://doi.org/10.3390/signals2040047
Chicago/Turabian StyleLumini, Alessandra, Loris Nanni, and Gianluca Maguolo. 2021. "Deep Ensembles Based on Stochastic Activations for Semantic Segmentation" Signals 2, no. 4: 820-833. https://doi.org/10.3390/signals2040047
APA StyleLumini, A., Nanni, L., & Maguolo, G. (2021). Deep Ensembles Based on Stochastic Activations for Semantic Segmentation. Signals, 2(4), 820-833. https://doi.org/10.3390/signals2040047







