Abstract
Like many other brain productions, language is a complex tool that helps individuals to communicate with each other. Many studies from computational linguistics aim to exhibit and understand the structures and content production. At present, a large list of contributions can describe and manage it with different levels of precision and applicability, but there is still a requirement for generative purposes. This paper is focused on stating the roots to understand language production from a combination of entropy and fractals. It is part of a larger work on seven rules that are intended to help build sentences automatically, in the context of dialogs with humans. As part of the scope of this paper, a set of dialogs are outlined and pre-processed. Three of the thermodynamic rules of language production are introduced and applied. Also, the communication implications and statistical evaluation are presented. From the results, a final analysis suggests that the exploration of fractals explanations of the entropy and entropy perspectives could provide a prospective insight for automatic sentence generation in natural language.
1. Introduction
There are biological foundations for considering that the human brain works following a certain set of rules. For instance, it is known that children between 6 and 8 years old have patterns of estimates that progress from consistently natural logarithmic (ln) to a mixture of logarithmic and linear to a primary linear pattern []. Karen Wynn [] explains that the brain instinctively distinguishes mainly 1, 2, and many. Many ancient numerations are proof of that: they describe numbers 1 to 3 with a pattern that is different from the one used for numbers following 4. Language structure has something similar: there is a singular treatment for one object and plural for many. It is also very suggestive that in many languages (like in English and French), many words represent the treatment of couples, and many reflect a close relationship between 3 and many. For instance: three vs. Thrice y Trois vs. Très.
Regarding the rules related to mathematics, the fractal paradigm has been considered for explaining many sciences like biology, geography, astronomy, medicine, among others. In architecture, for instance, it is very related to geometry management and new alternate connectivity relations at architectural and urban levels []. This track of thinking leads to two main stands: deconstructionist and patterns language. The first one, by the French philosopher Jack Derrida, was influenced by Ferdinand du Saussure, Nietzeche, Freud, and mainly Heidegger from which he takes the German word Destruktion as a basis []. With High Tech materials, simple geometric shapes; others with outlandish and exaggerated irregular shapes, among other peculiarities. The second is more like grammar in the sense of language. It was first introduced in 1977 by the architect Christopher Alexander and considers patterns as building blocks combined with certain processes (let it consider to be rules of combination). It is like a language focused on explaining the physical world and using technology as just a tool (in fact one more among others). From this perspective, the architecture language considers cities like fractals as they respond to human needs at different scales. Then main highways, secondary connections and distribution of connections are related to traffic problems. This way, complex problems (like human specific requirements) derive in complex systems that are suited to fractals explanations.
Following the line of language expressions and fractals, but in the field of Natural Language Processing (NLP), a study performed by Ai21 Labs [] confirms that NLP requires expensive architectures. For that reason, the authors consider that an increasing complexity makes Neural Networks a transient solution for Language management. There is a need to expand the size of the network in order to reflect the external knowledge in the embedding space. Indeed, authors see several factors that may help tame this explosion and prevent things from getting out of hand. New trends in the field suggest that other perspectives need to be considered. It is important to note that most of the spoken interchange in Natural Language is complemented with the collective personality and a number of other visual and sound symbols whose analysis makes the study very complex. Linguists like Skinner, Chomsky, and Berwick [,,] performed a large study of it. However, this paper focuses just on the transcription of dialogs and introduces a subset of rules that feature the tactical formulation in linguistic thinking. Although a few historical precedents are introduced as part of the background, a full historical review is out of the scope of this work. The main focus here is a couple of rules and their application to a use case based on a dialog performed within the context of a game called 20Q. Statistics and analyses of the results suggest that a complete set of rules could serve as a simple way to understand deep meanings in dialog contexts and to insert semantics in automatic sentence generation. The following sections are the background (Section 2), materials and methods (Section 3), tests and results (Section 4), discussion (Section 5), and conclusion (Section 6).
2. Background
As Sala Torrent explains [] language distinguishes humans from the rest of the species. As a tool to communicate with people, it evolves since childhood and is very relevant for proper cognitive, emotional, and social maturity. Natural Language (NL) seems to follow the laws of chaos and presents logarithmic and fractal behaviors. Many researchers have found a dialectic, biological, practical, and technical background that supports these ideas. Some of them are part of this section.
2.1. Fractals and Language
Fractals can be described as mathematical models that describe and study objects and many phenomena in nature. They usually work well with processes that cannot be explained by classical theories and can be obtained mainly through simulations.
What becomes evident in fractal behaviors, is a pattern that provides information of the system behind it []. This chapter follows the prospective prescription recommended by many authors, in order to derive predictive patterns to understand and control the regularity in linguistic reasoning through sentences expressed in dialog contexts. It enables also to predict pattern disruptions [], that is, the main facts that produce communication failures. Fractals were introduced by the Polish mathematician Benoit Mandelbrot []. Its main feature is the invariance despite scale changes and a special new geometry that differs from Euclidean. While the traditional models better artificial objects (those man-made), the fractal is more like processes in nature.
This paper takes the following question: As a brain production, does language also have the complexity and baseline of geometry fractal? The results in section IV confirm that.
Fractal geometry exhibits a relationship with dimension as follows:
where
- D stands by fractal dimension
- N is the number of identical parts in the fractal
- L represents the total length of the fractal
Fractals show many further features that could be considered to better understand the processes modeled by them. For instance, when the scale decreasing is 1/ɸ, the branches do not touch each other and the spatial distribution of them is the maximum, covering all the available space.
2.2. Zipf–Mandelbrot, Chance, and Prediction
The first work that introduces a function to prescribe the use of words in texts was from George Kingsley Zipf. He suggested a power-law distribution for a given text corpus when the distribution of words is ranked by their frequency. The distribution is known as Zipf’s law [].
With:
- f the frequency of the nth word sorted from the most frequent one
- a is a positive real number, usually over 1.1
Benoit Mandelbrot improves its precision with the known Zipf–Mandelbrot distribution that derives from the work of Claude Shannon []. This law is a discrete probability distribution []. It is a power-law distribution on ranked data with a mass function given by:
With:
- k = rank of data
- q and s parameters
When N → ∞: f → Z(s,q) the Hurwitz Zeta function(A Zeta function is a function formed by the aggregation of an infinite number of functions powered to y powers, that converge. They can be expressed by a Dirichlet series, useful to many applications among them the geometric analysis of oscillating bodies.) [], one of many zeta functions that exist. It works with s as a Complex number and q Real:
This succession converges when q > 0 and Re(s) > 1. When N = q = 0: f (k; N,q,s) = fz (h, q, s) is the Zipf’s law. Probably, this equation is the best example of how language is more related to mathematics and probability than mere chance.
2.3. Thermodynamics as a Law of Complex Processes
This subsection analyzes how thermodynamics could be used to explain the linguistic process under study in this paper. It is strongly based on the work performed by Rebolledo in [] and Callen in [].
Probabilities are useful to model chance and its laws. Similarly, complexity may use mathematical concepts to describe complexity. This way emerges the entropy concept in physics. It was firsts introduced by Clausius in the XIX century and helps to assess the disorder degree of gas molecules, being the best way to explain thermodynamic equilibrium. It also has been used to study chance from other fields like Mathematics, Information Theory (IT), and Ergodic []. Chomsky, Eco, and many others extended IT applications to Linguistics and semiotics. According to Eco, for instance, encoding produces a decrease of a message entropy since it reduces the possibility of a chaotic interpretation. In other words, the possibility of addressing the meaning is an expression of the message complexity, and the related entropy its measure. From that framework this paper analyses the entropy of sentences considered as messages in the context of a dialog (in this case, a game named 20Q) with restricted conditions to close its context.
In messages interchange, many transformations take place, which is a complex process of the individual’s interpretation of reality (let it name its consciousness), a phenomenon that deserves to be evaluated from the entropy perspective. As the internal state of a person cannot be computed, it must be analyzed through the set of sentences interchanged. To do that, this paper evaluates the structure and sequence of sentences using entropy and how it evolves.
This way the knowledge flows have some throughput along with a dialog. The contribution of entropy here comes from the Knowledge theory and is given by a set of concepts like reversibility/irreversibility, equilibrium/instability, and a set of relationships named demarcations and breakouts in the cognitive process development [].
Despite Thermodynamics is a branch of physics that deals with systems energy and its transformations [] it applies also to Language. There is no heat, work, or matter in this new context, but concepts like the closed system, isolated system, status, and others are valid.
In thermodynamics, a process is irreversible if derives in chaos, that is when its entropy grows indefinitely. The corresponding system then reaches a steady state.
Extending that, a butterfly is a more complex system than the larva from which it derives. In this case, the process is a discontinuity, a breakout from larva given by the butterfly’s new status. There has been an increment of the entropy. However to conceive this change, it must be considered larva-butterfly as the new system extending the original larva system []. This change happens when there is a maximum quantity of local entropy. From the perspective of this paper, the global system is the concept or information to be transferred between two persons in a dialog, a set of sentences between them, and the knowledge status at both ends. The testing in section IV considers a word (concept) that is known just by one of the actors in the dialog, so the knowledge status of the second individual is null.
The description of a state relates to a local entropy and the global entropy is associated with the specific type of phenomenon that must explain []. Thus, the case under analysis in this paper (dialog in a 20Q game), every state has its complexity or local entropy value (denoted here as ETq) that relates dialectically with another measure: global entropy, which describes the complexity of the set of possible states.
All the above intrinsically supposes an evolution idea, a dynamic. Local entropy analyzes the complexity evolution for a determined phenomenon and corresponds to the category of dialectic transit from disorder/order to a new more developed stage. At the same, time new dialectic relationships emerge between the object under study and a set of phenomena.
The global entropy then expresses the increment in complexity due to them and depends on human observers []. In this paper, evolution is evaluated by the change of fractal dimension D according to ETq.
When entropy increases discontinuously, every discontinuity is a breakout in the evolution process. As will be seen in section IV, it is a sudden peak close to a valley in the D curve.
Among two breakouts, local entropy changes from a minimum to maximum, expressing a new stage that may be a transition to the next breakout. It represents a reconstitution of the new upgraded evolution level. In the current paper, successive breakouts were avoided by limiting the testing to dialogs with a certain number of sentences and to a unique concept to be communicated.
The shift from order to disorder and from disorder to a new upgraded order, in terms of complexity evolution, determine entropy as a category involving two opposites: local and global entropy. Both are defined by their mutual relationship.
According to the authors of [], another liaison level emerges when entropy is taken to analyze the knowledge development. The information progresses in a non-continuous manner where breakouts correspond to “epistemological rupture” [], an irreversible stage. In the context of the testing performed in this paper, this new status is obtained when a player discovers the target word, one that is initially hidden at the beginning of the dialog.
Laws of chaos were explored in a more general sense by others to understand language production systems as a normative universe [] with a set of variables with specific dynamics []; as an interdisciplinary extension of traditional complexity theory [] where there is thermodynamics defining the energy of cultural sources []. Other researchers studied language as a natural product with a high level of complexity [] with inborn behavior [,,], usually considered to be logarithmic [,], that sometimes is conversed by culture [] but explained by fractals as a proper language [,] to explain and reduce its complexity. Among them, a combination of fractals and entropy is also possible: considering entropy, the language to express information based on probabilities, this proposal takes fractals as the encoding for the essence of how information flows in a dialog. This is the main goal of the set of rules proposed here.
As in classical thermodynamics, language is also a system with its characteristics. Every science may assign a meaning to entropy and relate it with specific concepts in its field. The building blocks for equations explain different manifestations of the information as entropy (usually denoted by H and here with ET). Sometimes they are partially isolated, and it becomes an obstacle to completely understand the inner dynamics of the system. For that reason, in the testing performed in this paper, the dialog is restricted to a game named 20Q, and to one human interacting with an intelligent system (a trained Neural Network or NN).
The laws that explain how this type of behaviors work are simple and universal. In the case of gases, they explain how a system is considered in equilibrium with others (Law 1), how energy is preserved (Law 2), the global evolution of entropy (Law 2), and a specific limitation in the Temperature of a system (Law 3). A set of laws could also describe language dynamics. The subject under study is not a mere logical-formal definition as in the case of language pragmatics []. For language productions, laws become cumbersome and need to be determined practically. From this perspective, this paper presents three of seven laws (here described as rules) that are under the umbrella of this proposal.
3. Materials and Methods
The tests are a set of sentences produced in dialogs developed in a game named 20Q [], between a human player and an Intelligent System consisting of Artificial Neural Networks. A total of 20 plays were performed.
20Q target main goal is to guess a word initially thought by another player. The play consists of asking yes/no questions until the word is guessed. The restrictions are very few: any word in Spanish, or noun sentence can be the objective. The cases evaluated here are in Spanish, which has 93,000 words, according to RAE (Spain Royal Academy) in its Spanish Dictionary Edition of 2014 []. One of the players is an AI system trained online.
The implementation used for this research belongs to the Technological observatory of the Education and Sports Ministry of Spain State [].
The game has an implementation that is not identical to standard 20Q. Some considerations are:
- The original limit of 20 questions was changed to 30.
- This first question is changed to a selection between animal, vegetable, and another thing.
- When the ANN cannot guess the target, then it displays a candidate word.
- When ANN hits the word, it displays the answers that are different from the ones expected.
- The user can select extra answers besides yes and no, but they are not used in texts.
- Questions made by the AI can have small grammatical errors. They are neglected because the number and position of nouns and verbs are correct.
Volunteers were between 14 to 60 years old, and no one had played this game before nor had any previous contact with the online version.
The dataset had 20 different targets, 432 questions, a total of 3530 words, and 1042 sentences.
Target words were: WEB, Stomias, Cake, Sewing machine, Pen, Flag, Computer, Dog, Friend, Salt, Rose, Lamp, Sparrow, Onix, Church, Physician, Chair, Egg, Tree, and Keys. Table 1 is a summary of the dataset characteristics.

Table 1.
Dataset characteristics.
Sentences were collected and pre-processed to get a well-formed corpus in CSV format.
Regarding the hardware, all the processing is performed in two notebooks:
- A Processor Intel® Core™ i7-7600U CPU @ 2.80GHz × 4, with 7,4 GiB RAM and 256,1 GB Hard disk, an operating system Linux Ubuntu 20.04.2 LTS of 64 bits.
- A Processor Intel® Dual Core™ i7-7600U CPU @ 2.80GHz × 2, with 8 GiB RAM and 256 GB Hard disk, an operating system Linux Ubuntu 20.04.2 LTS of 64 bits.
Regarding the software, modules are in Python, and Octave (c). The IDE used is Pycharm 2021.2.1 version 11.0.11. Data analysis was carried out using WEKA (c), Open Office Calc (c), and PSPP (c). All the platforms and tools are open, multi-platform, and free.
The tagging was performed by hand with an expert reviewer, to guarantee a precision of 100%. It followed certain guidelines:
- Tag &V if there is an action (verb or verbal phrase o).
- Tag &N if there is any type of nominal reference (noun or short noun phrase).
- Tag &A if there is any type of qualification, description, properties, or characteristic.
4. Tests and Results
This section analyzes the dynamics of textual communication between two ends of a dialog that take place during a 20Q game (20Q, 2021), which is recommended for people over seven years old. The rules are:
- Player 1 thinks a word and keeps it in secret.
- Player 2 performs up to 20 Yes/No questions to guess the word.
- Player 1 answers the questions.
- At any time, player 2 can try a word.
- Player 2 wins if he can guess the secret word.
- Player 1 wins if player 1 asked 20 questions and never gets the correct word.
As explained in sections II and III, the dialogs are simple sentences in a game named 20Q. One of the players is an Artificial Intelligence (AI) system based on a Neural Networks (ANN), and the other is a human interacting through the WEB. The AI system tries to guess a word previously thought by the human. To do that, it performs yes/no questions. Interchanges are simple and up to 30 questions. Figure 1 presents the proportion between fails and hit games.
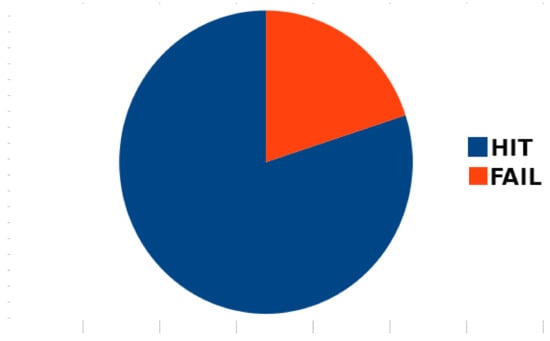
Figure 1.
Game results.
The results show that the machine is able to guess many of the target words or get close to them. It is important to note here that any of the 63,000 Spanish words could be selected, and that many times noun phrases. Despite that, the ANN was able to win most of the time. The only condition was that the chosen target must be previously known by the AI in a previous interchange. This section aims to test one after the other, each of the rules in Table 2.

Table 2.
Rules to be tested.
4.1. Rule R1
This section describes the steps performed to test the first rule on the corpus, which evaluates how the entropy changes in the dialogs, and how this evolution relates with the main goal of the 20Q game: to guess a target word. Every interchange is in Spanish.
Consider a communication C between the gamer (player 1) and the AI counterpart (player 2, the NN with the knowledge from previous plays):
C = {+t1 +t2 +t3 … +tn}
It is a sequence of n questions to infer a certain target word w that represents an ontological concept E. Rule 1 can be explained as the property of a communication C that succeeds after interchanging a certain amount of entropy if a concept E is correctly addressed by the receiver. The knowledge is transferred by sentences ti, with a quota of entropy.
The accumulative number of nouns and verbs in the successive questions for all the games are similar. The curves for verbs are softer and with a higher slope than nouns (Figure 2 is an example). In every case, the slope dispersion for verbs is smaller than for nouns.
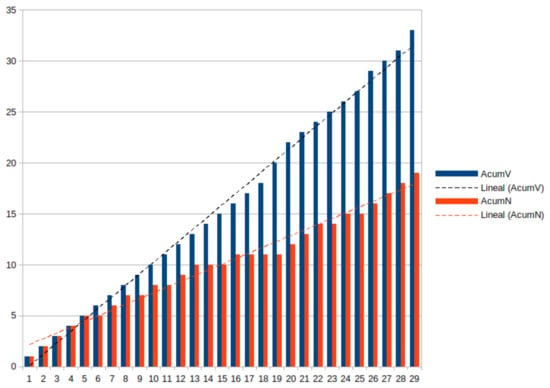
Figure 2.
Cumulative distribution for verbs (AcumV) and nouns (AcumN) for game #7.
This shows that verbs are used in a different way. It can be confirmed using clustering Data Mining with Expectation Maximization (EM), where natural similarities arise as five clusters. The maximum value of Log-likelihood (5.6) is obtained considering the number of nouns and verbs in the model training. Some clusters are typically at the beginning (#1, #2, and #4) and some others (#2 and #3) are at the end of the games. There are more verbs in clusters 2 and 3, but clusters 1 and 2 have more nouns. Cluster 0 has more nouns than cluster 1. Cluster 2 has more variation in the number of verbs than Cluster 3. Cluster 4 has a tiny part of the questions with no common patterns but are likely to be outliers. Table 3 shows a summary of the results obtained.

Table 3.
EM for questions.
CantV and CantN values are rounded to one decimal and represent the number of verbs and nouns in the clusters, and % q is the percentage of questions that belong to a cluster. The distribution confirms that there is a specific approach chosen to build sentences and it depends on the time in the game. It is important to note that every game with sentences from cluster #3 wins, which is another way to reinforce the above statement: sentences with certain characteristics and certain dispositions of them determine the chance to win.
4.2. Rule R2
The information is carried in sentences with the analysis centered on nouns (S) and verbs (V), change the amount of HS (entropy of the sentence S), and needs to be efficient to get a target word (the goal of the 20Q game). Rule 2 explains that sentences work not in a linear transmission of H:
There is a complement between V and N, though not perfect, they balance each other, and H has a certain rhythm and cycle.
In this context, rhythm is considered as its original sense: A regular movement or pattern of movements, and a regular pattern of change []. A cycle is a group of events that happen in a particular order, one following the other, and are often repeated [].
For the first (rhythm) H is considered as the pattern information, and the second (cycle) is a scaling of the original pattern, from a fractal perspective (see []). The scaling is measured with fractal dimension (D).
Entropy is calculated as usual []:
With:
X as the property to be measured. In the present context, it could be cantV (or #V, the number of verbs in a sentence), cantN (or #N, the number of nouns), or cantA (the number of attributes that describe the concept).
Pi represents the probability of that property (taken as the number of words of the type under study over the total).
k is the number of sentences in the game (usually a positive integer less than 30).
The standard entropy H is named in this paper with convenient labels like ET for total entropy, ET(V) for entropy due to verbs, ET(N) entropy due to nouns, and ET(A) entropy due to attributes. In certain tests, ET is evaluated sentence by sentence with a subscript notation as in ETq.
Analyzing the entropy by Verbs and nouns there is a behavior in all tests: ET(V), the variation of ET due to Verbs, is higher than ET(N) and ET(A), variations for Nouns and descriptors respectively. Also, the curve ET(N) is typically the lower one. Figure 3 shows the case of game 9.
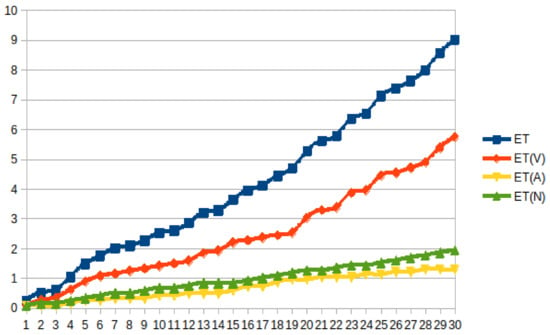
Figure 3.
Entropy for game 9.
ET shows a relationship with the result of the game. Table 4 shows that ET is in a specific interval out of scope of the cases when the ANN loses (Succeed = N) and similar intervals when it wins (Succeed = Y) or gets the concept but not the word (Succeed = C).

Table 4.
ET values for games that ANN wins (Y), get close (C), or loses (N).
The entropy conveyed through questions is centered here by using just nouns, verbs, and descriptors (adjectives, adverbs, etc.). Take Equation (5) and replace pi by p(s):
where:
- s: number of verbs (V), nouns (N), or descriptive word (A).
- T: total number of words.
Regarding the fractal dimension D is defined as []:
With:
- N: number of partitions.
- change rate.
When D is defined with:
x = 2
N = ΔET = ETq–ETq − 1
r = ET(A)q
Where ETq is the ET in question q, ETq−1 is ET in question (q − 1), and ET(A) is ET due to Attributes. The plots of D along every game show a unique pulse like in Figure 4.
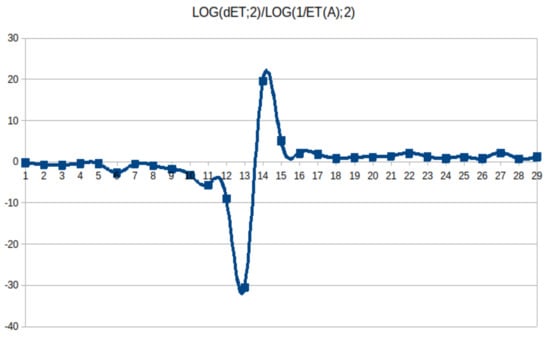
Figure 4.
D for test #2.
After analyzing the sentences, it is clear that the minimum represents a status where the concept represented by the target word is obtained by discarding other concepts. The peak, a fast increase of the entropy, fits after the class of object determination, decreasing as the specificity increases. This is like a strategy for the game: the best way to get success is to find the class and then the specific word.
Something similar can be obtained with:
x = 2
N = ΔET(V) = ET(V)q–ET(V)q−1
r = ET(N)q
Where ET(V)q and ET(N)q are ET values due to V and N respectively, at question q. But in this case, the peak comes after a valley as in Figure 5.
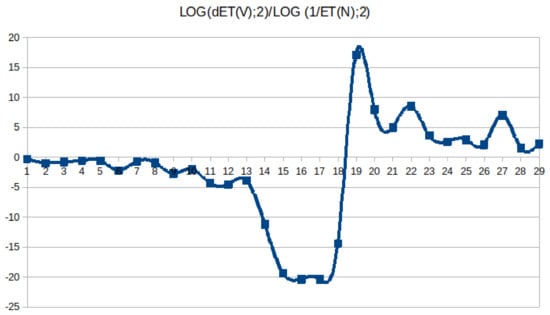
Figure 5.
D for test #2.
In this case, curves show four main behaviors: drop to negative values, a higher peak in negative, a higher peak in positive values, and Similar peaks in both directions. Evaluating them against the results, they model different strategies to gain entropy using N or V as the main approach for classifying or eliminating concepts.
Using the parameters:
x = 2
N = ET(V)q
r = ET(N)q
The curves are symmetric to the ones obtained previously, so there are again four types of curves. From this analysis, N and V can be seen as competing for entropy transference. When ET is based on V, N holds with the rest of the information required for finding out the specific concept.
4.3. Rule R3
As mentioned previously, concept E is not a displacement of H but forces the communication to perform that action in time ta. As the entropy of sender y is a negentropy for the receiver, it can be thought of as polarization and depolarization from the local (not global or system) perspective at time ta. Then the polarization is also an activity that happens during and due to the communication process. As can be seen in the text of this section, t can be predetermined and depends on ɸ.
For written text communications, the alterations are again the constituents (words) sorted to transfer sequentially the information to the receiver. During that process (p) the polarization is expressed by the pattern of the content and evaluated with probability and entropy relationships. The status at the receiver relates with ~p and its negentropy at time ta. The global system remains neutral in E.
From the E perspective, t is infinite and remains neutral for t in (−∞; ta), that is (for example) until finishing the text reading. Then the infinite set of possible partial expressions using E (let it be O) collapses to one meaning when it gets to the receiver.
Thus, E is one but is polarized due to the communication at ta, and emerges a triplet (O, E, C), which can also be considered as (O, E, <~p, p>). During p, t evolves (it increases to +∞) from the sender perspective (generation of the communication C), and t goes to −∞ from the reader (receiver) perspective, because the reading is going back to the generation process and when the cycle is perfect READING (E, tR) + WRITING (E, tE) = 0.
The rest of this section tests these characteristics, and the rule can be summarized as:
Any communication C is an activity with a triplet (O, E, C) composed of a cause, effect and evolution in t.
The evolution is p acting upon O, the evolution suffers a breakout related to ɸ as will be seen in Equation (13). After that moment the expansion of entropy starts a collapsing process as will be shown in Figure 6.
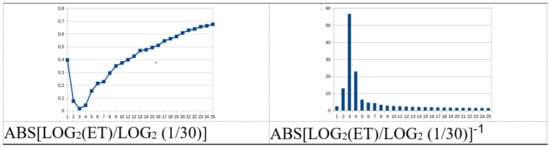
Figure 6.
Dimension with ET for test #20.
It is important to note the following properties that emerge from this rule:
- Language and its communication process imply a tuple (space, t), and involves a type of movement.
- There is always causation and an effect.
The evolution in t is produced by p and measured as in previous sections with the changes of D according to t. This way D(t + 1) depends on D(t).
Consider ER (Relation Entropy) a change in Equation (5) with:
with:
- Vq the number of verbs in sentence q.
- VNA total number of verbs, nouns, and qualifiers in the game.
EI (Intrinsic Entropy) another change in Equation (5) with:
with:
- Vq the number of verbs in sentence q.
- VN total number of verbs, and nouns in the game.
The relation EI/ER shows an evolution toward a target value (or rate). Figure 7 has 9 of the curves.
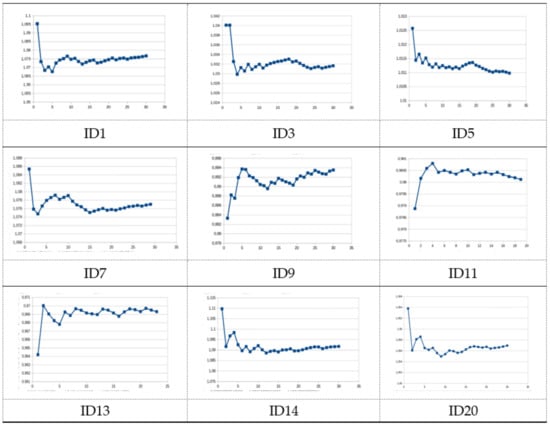
Figure 7.
EI/ER evolution for some Tests (1, 3, 5, 7, 9, 11, 13, 14, 20).
The process starts typically in some values but converges in every case. To test ta, where the entropy shows a peak and inverts polarization (see curves in Figure 4 and Figure 5), it is convenient to introduce constant ɸ:
It has been found to be related to many processes in nature like the Law of Ludwig [], in mathematics with Fibonacci Series [], and is considered a fractal scaling [].
Let evaluate total entropy ET through fractal dimension D using:
N = ET
x = 2
r = Number of questions in the game
The resulting curves exhibit a change in polarity, from positive to negative values. To remark this behavior, the absolute values are considered. The curves are as in Figure 6 in all cases.
For them, considering:
It verifies that:
The accumulated differences are E[1−k], from the starting point to the peak. This provides a tool to predetermine the sentence with the peak (which corresponds to ta). As explained in previous sections, this occurs when the amount of transferred information is the highest, and the target word classification is finished. After that starts, the process of looking for the specific word w to win the game.
Table 5 presents some examples of Equation (12) for games where the ANN wins the game.

Table 5.
Relation of minimum and ɸ when ANN wins.
It is interesting to note that in games where ANN loses, the proportion is not perfect and there are differences in the order of 10−2. Some cases are in Table 6.

Table 6.
Relation of minimum and ɸ when ANN loses.
5. Discussion
This paper evaluates three rules that relate entropy, fractals, and language in three of seven rules that might be like thermodynamics for language. The game 20Q was selected due to the restrictions and features of its implementation, which makes it simpler for the analysis to be performed.
The previous sections start considering a communication C between the gamer (player 1) and the AI counterpart (player 2, the NN with the knowledge from previous plays):
C = {+t1 +t2 +t3 … +tn}
Test of Rule 1: A communication C succeeds if it is composed of sentences able to transfer entropy in a proper way.
To do that, it shows the accumulative number of nouns and verbs and the relations between them. The behaviors are very different in all cases. EM determines five types of sentences, and specific distributions to win the game. When that distribution is not present the game is lost. The distribution exhibits the way to compose ti in C to let the ANN acquire enough entropy and find out the target word. This implies that the complete entropy required to get the goal is within the system. Since the player that collects the entropy is an ANN there is no extra information during the process and the entropy transferred does not come from elsewhere.
Let equilibrium in this context be the state where the system does not get or give any entropy to its environment (context), then the system holds its equilibrium by construction.
From the previous analysis, it can be said that:
- Global entropy does not change: Equilibrium.
- All the entropy remains within the system.
- No entropy is transferred out of the system but held as local entropy.
As a consequence of that, it can be said that there is a Main Behavior in C.
Test of Rule 2: There is a complement between V and N, though not perfect they balance each other, and H has a certain rhythm and cycle.
The information conveyed in ti is evaluated through total entropy, and its variations due to verbs, and nouns in every sentence. Curves show that C takes place during a limited lapse (the time from first to the last question in the game), therefore there are no changes in H out of this period.
There is a specific amount of entropy due to V and N, and a direct relationship between how they behave (see Figure 3, Figure 4 and Figure 5) and the result of the game (see Table 4).
There are peaks and valleys in the curves of every game where the entropy minimum (corresponding to the perfect classification) and starts with a maximum (starting the search for the specific word).
Also, the evolution of entropy values can be expressed by fractal dimension D, where a cycle could be devised at every scale change with entropy demarcation.
From the previous analysis, it can be said that:
- Time t є[−∞, +∞] holds the entire activity (sequence of sentences) in a lapse [t1; t2].
- No changes out of [t1; t2].
- H presents breakouts.
- H is cyclical.
Then there is a Dimension and Rhythm.
Test of Rule 3: Any communication C is an activity with a triplet (O, E, C) composed of a cause, effect, and evolution in t.
A general concept O collapses to a specific word w represented by a specific concept E, which is communicated through a set of sorted questions q composing the communication C. The process p evolves conversely from the perspective of a receiver and entropy H starts for him as negentropy with a process ~p. The local effect is like a transference between both ends, that in the case of a text could be devised as a displacement or movement in space and time.
Considering ER and EI, the change is explicit and exhibits evident progression towards a definite value for all cases.
The process has a specific time ta, that can be determined precisely with Equation (12) only when the ANN wins.
From the previous analysis, it can be said that:
- Language relates to a tuple (space, t) ≥ it involves movement.
- There is a causality: cause and effect.
- D evolves with t ≥ D(t + 1) depends on D(t).
Then there is a triplet that describes the activity as (O, E, C = <p;~p>).
6. Conclusions
Natural language is a complex production of the human brain, used to convey information in a very precise way. Many scientists provided elements used to interpret textual communications. But the generation of expressions artificially is still under work at the first stages. Many contributions use patterns and probabilities, but language is more than that. For that reason, this paper explores some rules that are part of a larger set to determine general principles that could allow artificial entities to automatically produce sentences in any natural language: a kind of thermodynamics for this field.
The proposed rules are three: Rule of the Main Behavior, Dimension and Rhythm, and Triplet activity. To understand the effects and relevance of each one, they are applied to a transcription of dialogs of the game 20Q. The main reasons to select these texts are analyzed here but most of them can be summarized as a simplification of the condition of the tests.
The dataset is a corpus based on 20 games performed among a human (a volunteer) and an AI. An EM shows a specific behavior, with a specific distribution of sentences during each game. Results also indicate that game evolution can be explained using global entropy (H, also ET in this context), and its variation due to nouns and verbs. Through dimensional analysis, it is possible to find out how ET must behave in order to win a game (which means to acquire enough amount of ET in order to find out a target word w).
Many properties were derived that are useful to understand the process of communication and to consider as parameters of a generative system. Among others: rhythmic and cyclical evolution of H, equilibrium, compensation between N and V, and the existence of a breakout point ta.
Some analyses rely on a definition of the fractal dimension (D) holding a macro rhythm along the time domain of the game. D helps to interpret the strategy during the game and confirms the analysis of section IV. It also represents the rate change during a cycle taken by the entropy during the process of fractal instantiation, that is, the messaging.
This proposal is still under work and has many pending. Other rules are being tested and evaluated as a complement of the ones introduced here. There are also some extra hypotheses and statements that aim to explain the most relevant part of language dynamics. All these rules aim to determine a model for the natural language sentences generation, a tool useful to provide better human interfaces and deeper analyses of certain anomalies in disorders like Autistic Spectrum Disorders.
After the complete set of rules is applied to the current dataset, it remains to test with other types of dialogs and texts and to evaluate how those rules work in the new contexts.
Funding
This research received no external funding.
Institutional Review Board Statement
IRB CI2S Labs committee expresses that research ethics during reviewing were performed and methods proposed for research are ethical.
Informed Consent Statement
Provided during submission.
Data Availability Statement
Data are available mailing to mdldl@ci2s.com.ar.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Siegler, R.S.; Booth, J.L. Development of numerical estimation in Young Children. Child Dev. 2004, 75, 428–444. [Google Scholar] [CrossRef] [PubMed]
- Wynn, K. Addition and Subtraction by human infants. Nature 1992, 358, 749–750. [Google Scholar] [CrossRef] [PubMed]
- Sulbarán Sandoval, J.A. Fractal as Architectural Paradigm: Deconstruction vs Vivid Patterns Language (El Fractal Como Paradigma arquitectónico: Deconstrucción vs Lenguaje de Patrones Viviente); Procesos Urbanos: Maracaibo, Venezuela, 2016; pp. 79–88. Available online: https://revistas.cecar.edu.co/index.php/procesos-urbanos/article/view/268 (accessed on 1 June 2021).
- Reyes, E. Breve introducción a Jacques Derrida y la Deconstrucción. Available online: http://hipercomunicacion.com/pubs/derrida-decons.html (accessed on 4 March 2016).
- Sharir, O.; Peleg, B.; Shoham, Y. The Cost of Training NLP Models: A concise overview. arXiv 2020, arXiv:2004.08900. Available online: https://arxiv.org/pdf/2004.08900.pdf (accessed on 4 March 2020).
- Skinner, B. Verbal Behavior; Appleton-Century-Crofts: New York, NY, USA, 1957. [Google Scholar]
- Chomsky, N. Reflections on Language; Random House: Manhattan, NY, USA, 1975. [Google Scholar]
- Berwick, R.; Weinberg, A. The Grammatical Basis of Linguistic Performance; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Sala Torrent, M. Trastornos del desarrollo del lenguaje oral y escrito. In Congreso de Actualización en Pediatría; 2020; pp. 251–263. Available online: https://www.aepap.org/sites/default/files/documento/archivos-adjuntos/congreso2020/251-264_Trastornos%20del%20desarrollo%20del%20lenguaje.pdf (accessed on 1 June 2021).
- Widyarto, S.; Syafrullah, M.; Sharif, M.W.; Budaya, G.A. Fractals Study and Its Application. In Proceedings of the 6th International Conference on Electrical Engineering, Computer Science and Informatics (EECSI), Bandung, Indonesia, 18–20 September 2019; pp. 200–204. [Google Scholar] [CrossRef]
- Spinadel, V.M. Fractals (Fractales). In Proceedings of the Segundo Congreso Internacional de Matemáticas en la Ingeniería y la Arquitectura, Madrid, Spain, 3, 4 and 7 April 2008; pp. 113–123. [Google Scholar]
- Zipf, G.K. Selected Studies of the Principle of Relative Frequency in Language; Harvard University Press: Cambridge, MA, USA, 1932. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 3, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Mandelbrot, B. Information Theory and Psycholinguistics; Wolman, B.B., Nagel, E., Eds.; Scientific Psychology: New York, NY, USA, 1965. [Google Scholar]
- Apostol, T.M. Introduction to Analytic Number Theory; Springer Verlag: Berlin/Heidelberg, Germany, 1976; ISBN 0-387-90163-9. [Google Scholar]
- Rebolledo, R. Complexity and Chance (Complejidad y azar). Humanit. J. Valpso. 2018. [Google Scholar] [CrossRef]
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1985. [Google Scholar]
- Billingsley, P. Ergodic Theory and Information; John Wiley & Sons: Hoboken, NJ, USA, 1965. [Google Scholar]
- Bunge, M. Probability and Law (Probabilidad y Ley). Magazine Diánoia. 1969, Volume 15, pp. 141–160. Available online: https://www.cairn.info/materiaux-philosophiques-et-scientifiques-vol-2--9782919694525-page-983.htm (accessed on 1 June 2021). [CrossRef] [Green Version]
- Von Bertalanffy, L. General System Theory; Foundations, Development, Applications (Teoría General de los Sistemas; Fundamentos, Aplicaciones); Fondo de Cultura Económica: Mexico City, Mexico, 1984. [Google Scholar]
- Rodríguez Duch, M.F. Chaos, Entropy and Public Health: Legal Analysis from a Multidimensional Perspective (Caos, Entropía y Salud pública: Análisis desde una Perspectiva Jurídica Multidimensional); Argentina Association of Administrative Law Magazine: Buenos Aires, Argentina, 2016. [Google Scholar]
- Esteva Fabregat, C. Follow-Up for a Complexity Theory (Acompañamientos a una Teoría de la Complejidad); Desacatos: Ciudad de Mexico, Mexico, 2008; Volume 12, Available online: https://dialnet.unirioja.es/servlet/articulo?codigo=5852219 (accessed on 1 June 2021).
- Eco, U. Tratado de Semiótica General; Lumen: Biblioteca Umberto Eco. Alessandria: Piamonte, Italy, 2000. [Google Scholar]
- Costa dos Santos, R.; Ascher, D. Popper Epistemology and Management as an Applied Social Science: A Theoretical Essay; Espacios: Curitiba, Brazil, 2017; Volume 38, p. 20. ISSN 07981015. Available online: http://www.revistaespacios.com/a17v38n16/a17v38n16p20.pdf (accessed on 1 June 2021).
- López De Luise, D.; Azor, R. Sound Model for Dialog Profiling. Int. J. Adv. Intell. Paradig. 2015, 9, 623–640. [Google Scholar] [CrossRef]
- 20Q. Available online: http://www.20q.net/ (accessed on 12 July 2021).
- Real Academia Española. Available online: https://www.rae.es/ (accessed on 7 July 2021).
- Ministery of Education of Spain. Ministerio de Educación de España. 2021. Available online: https://www.educacionyfp.gob.es/ (accessed on 7 July 2021).
- Cambridge Dictionary. Available online: https://dictionary.cambridge.org. (accessed on 7 July 2021).
- Rodriguez Santos, A.E. I.E.S. San Cristóbal de Los Ángeles. Madrid, Spain. 2011. Available online: https://m.facebook.com/profile.php?id=117806488264899 (accessed on 1 June 2021).
- Spinadel, V.W. Fractal geometry and Euclidean thermodynamics (Geometría fractal y geometría euclidiana). Mag. Educ. Pedagogy. Univ. Antioq. 2003, 15, 85–91. [Google Scholar]
- Cook, T.A. Capiulo V: “Botany: The Meaning of Spiral Leaf Arrangements”. In The Curves of Life; Constable and Company Ltd.: London, UK, 1914; p. 81. [Google Scholar]
- Cook, T.A. The Curves of Lifes; Dover Publications: New York, NY, USA, 1979. [Google Scholar]
- Fractal Foundation. Available online: http://fractalfoundation.org/ (accessed on 5 June 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).