Recovering Texture with a Denoising-Process-Aware LMMSE Filter

Abstract

Image denoising methods generally remove not only noise but also fine-scale textures and thus degrade the subjective image quality. In this paper, we propose a method of recovering the texture component that is lost under a state-of-the-art denoising method called weighted nuclear norm minimization (WNNM). We recover the image texture with a linear minimum mean squared error estimator (LMMSE filter), which requires statistical information about the texture and noise. This requirement is the key problem preventing the application of the LMMSE filter for texture recovery because such information is not easily obtained. We propose a new method of estimating the necessary statistical information using Stein’s lemma and several assumptions and show that our estimated information is more accurate than the simple estimation in terms of the Fréchet distance. Experimental results show that our proposed method can improve the objective quality of denoised images. Moreover, we show that our proposed method can also improve the subjective quality when an additional parameter is chosen for the texture to be added.

1. Introduction

Image denoising methods that can estimate a noiseless, clean natural image (original image) from a noisy observation are actively being studied [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. Many previous works have assumed that the noise in such a noisy observation is an additive white Gaussian noise (AWGN). One popular approach for image denoising is to use nonlocal self-similarity (NLSS), in which it is assumed that a local segment of an image (a patch) is similar to other local patches [10,11,12,13,14,15,16,17,18,19,20,21].

Weighted nuclear norm minimization for image denoising (WNNM) [16] is an optimization-based method based on an NLSS-based objective function. WNNM assumes that a matrix whose columns consist of similar patches extracted from a clean image is low rank and achieves state-of-the-art denoising performance among non-learning-based methods.

Image denoising methods such as WNNM can estimate the original image well in terms of the mean squared error (MSE) or the peak-signal-to-noise ratio (PSNR). However, as shown in Figure 1, texture is often lost in the estimated image. Because the texture carries important information about the aesthetic properties of the materials depicted in certain parts of an image (such as the feel of sand, fur, or tree bark), the texture losses severely degrade the subjective image quality.

On the other hand, it is difficult to obtain a good description of texture (we refer to such a description as a texture model) and to estimate its parameters because of its stochastic nature, and the performance of texture-aware image denoising methods [8,19,20,21] depends on these models and parameters. Thus, we can classify texture-aware image denoising methods based on the texture models they utilize.

The gradient histogram preservation (GHP) method [19] is a prominent texture model for texture-aware image denoising. GHP describes texture features in the form of a histogram of the spatial gradients of the pixel values (gradient histogram). GHP is based on an image denoising method called nonlocally centralized sparse representation [15], and it can recover texture by imposing the condition that the gradient histogram of the output image must be close to that of the original image. The parameters of GHP can be estimated from the observed image by solving an inverse problem.

However, GHP does not utilize the relationships between distant pixels. Nevertheless, these relationships can carry important texture information because textures are often repeated over long distances.

Zhao et al. addressed this problem by proposing a texture-preserving denoising method [20] that groups similar texture patches through adaptive clustering and then applies principal component analysis (PCA) and a suboptimal Wiener filter to each group. The Wiener filter is a special case of a linear minimum mean squared error estimator (LMMSE filter), and it requires an estimation of the covariance matrices of the original signals. In this texture model, the relationships between distant pixels can be expressed by the covariance matrices. The covariance matrices that are used in the suboptimal Wiener filter are calculated from sample observation patches, which are chosen using a nonfixed search window.

As another method of managing the distant relationships characterizing texture, a denoising method using the total generalized variation (TGV) and low-rank matrix approximation via nuclear norm minimization has been proposed [21]. In this method, the TGV is used to avoid the oversmoothing that is typically caused by low-rank matrix approximation methods [10,16]. The TGV and nuclear norm minimization are applied to capture the relationships between nearby pixels and distant pixels, respectively. Liu et al. claim that the latter are related to textures with regular patterns. The parameter of their texture model is the weight parameter of the TGV term. An iterative algorithm is required to estimate this parameter.

There is a trade-off between the complexity (or capacity) of a texture model and the simplicity of parameter estimation. For example, GHP [19] is a simple texture model with parameters that are easily estimated. However, this model cannot express textures in detail. By contrast, the covariance in the PCA domain [20] and the combination of the TGV and the nuclear norm [21] are complex texture models that can represent detailed textures well; however, their parameter estimation is relatively difficult.

To resolve this problem, we employ a slightly different definition of texture in this paper. We define texture as the difference between the original image and the corresponding denoised image (as obtained from an existing denoiser). We use the covariances within the texture component and between the texture and noise (covariance matrices) as our texture model, thereby capturing information about the relationships between distant pixels. Throughout this paper, we represent the covariance information in matrix form. Thus, we refer to this information as covariance matrices. It would appear to be difficult to estimate these matrices from a noisy observation. However, because we define the texture as the difference between the original and denoised images, we can utilize the information obtained in the denoising process to estimate the texture covariance matrices more easily.

We propose to use Stein’s lemma [22] and several empirical assumptions to estimate the covariance matrices. Then, we apply an LMMSE filter based on the covariance matrices to estimate the lost texture information. In general, the Wiener filter assumes that the target and the noise have zero covariance. However, in our case, there is nonzero covariance between the texture, which is the difference between the original and denoised images, and the noise because the denoised image depends on the noise. Thus, we propose to use the LMMSE filter for the case in which there is covariance between the signal and noise.

Moreover, our approach yields a separate texture image, which allows us to emphasize the texture with any desired magnitude. Such texture magnification can improve the subjective quality of an image. Figure 2 presents our motivation.

Our contributions are summarized as follows:

• We propose a new definition of texture for texture-aware denoising and a method of recovering texture information by applying an LMMSE filter.
• We introduce several nontrivial assumptions to estimate the covariance matrices regarding the texture and noise that are used in the LMMSE filter based on Stein’s lemma.
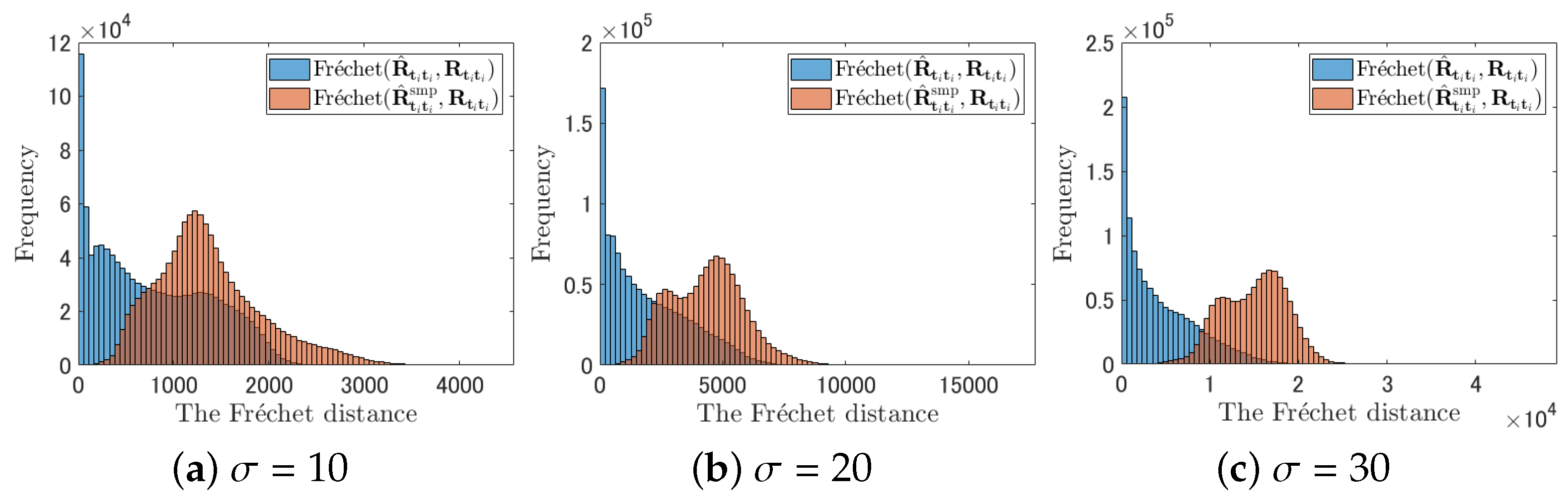
• We show an effectiveness of our method in terms of the PSNR and subjective quality (with texture magnification) through experiments. We also show similarities between our estimated covariance matrices and the corresponding true covariance matrices in terms of the Fréchet distance [23].

Recently, several image denoising methods based on neural networks have been proposed [9,18]. These methods achieve excellent denoising performance. However, understanding the process underlying such black-box methods is difficult. To the best of our knowledge, WNNM is still the state-of-the-art among denoising algorithms that are not based on machine learning approaches (i.e., white-box methods), and our proposed method represents the first successful attempt to significantly improve the performance of WNNM. Additionally, our method can explicitly extract the texture component from the noisy image, enabling us to maximize the perceptual quality of the denoised images by arbitrarily magnifying the obtained texture. In the pursuit of the inherent model of natural images, it is worthwhile to improve the denoising performance of white-box algorithms, as accomplished with the proposed method.

This paper is organized as follows. Section 2 introduces WNNM as the background to this study. Section 3 introduces our newly proposed method of texture recovery and analyzes the texture and noise covariance matrices using Stein’s lemma. We propose a linear approximation of WNNM to enable the application of Stein’s lemma. Section 4 compares our method with other state-of-the-art denoising methods. Section 5 concludes the paper. Appendix A proves that our LMMSE filter can successfully estimate the texture component of the original image. Appendix B shows experimental results to confirm our several assumptions.

Please note that this work on texture recovery has been previously presented in conference proceedings [24]. In this paper, we show the proof of the LMMSE filter and experimental results to confirm some assumptions. We also analyze the estimation accuracy of our texture covariance matrix used for texture recovery and the effectiveness of emphasizing the texture statistically. In conference proceedings, we only provided limited experimental results (24 images of Kodak Photo CD PCD 0992). On the other hand, in this paper, we show new experimental results obtained on two image datasets (contains 110 images in total) to confirm our method’s effectiveness.

2. Preliminaries and Notation

In this paper, $\mathbb{R}$ denotes the set of real numbers, small bold letters denote vectors, and large bold letters denote matrices. We denote the estimates of $\mathbf{a}$ and $\mathbf{A}$ by $\widehat{\mathbf{a}}$ and $\widehat{\mathbf{A}}$, respectively.

In this section, we describe WNNM [16] (a state-of-the-art denoising method based on NLSS) because our method estimates the texture information lost via the denoising process in WNNM.

In image denoising, a noisy observation is modeled as

$$\mathbf{y}=\mathbf{x}+\mathbf{n},$$

(1)

where $\mathbf{y}\in {\mathbb{R}}^m$ is the noisy observation with m pixels, $\mathbf{x}\in {\mathbb{R}}^m$ is the original image that is the target of estimation, and $\mathbf{n}\in {\mathbb{R}}^m$ is AWGN, of which the standard deviation is $\sigma$.

In WNNM, the observed image $\mathbf{y}$ is first divided into I overlapping focused patches ($\sqrt{L}\times \sqrt{L}$ pixels). The I depends on the image size and the noise level. Our experiment follows the default parameter of author’s implementation of WNNM. For example, in the case of $\sigma =20$, the patch size is $6\times 6$ pixels, and the focused patches are selected by 1 pixel skip (stride 2). Therefore, when the image size is $256\times 512$ pixels, the total number of focused patches I is 32,004 (note that similar patches are selected from $6\times 6$ pixels patches extracted from the neighborhood ($61\times 61$ pixels) of the focused patch. The overlapping focused patches are then vectorized. We denote the i-th focused patch of $\mathbf{y}$ by ${\mathbf{y}}_i\in {\mathbb{R}}^L$ ($i=1,\cdots ,I$). Then, a search is performed for the $M-1$ patches that are the most similar to each segmented patch ${\mathbf{y}}_i$, and for each ${\mathbf{y}}_i$, a patch matrix ${\tilde{\mathbf{Y}}}_i\in {\mathbb{R}}^{L\times M}$ is created that includes ${\mathbf{y}}_i$ as its leftmost column, while the remaining columns of ${\tilde{\mathbf{Y}}}_i$ are the patches that are similar to ${\mathbf{y}}_i$. For the i-th patches of the other components $\mathbf{x}$ and $\mathbf{n}$, we use similar notation, i.e., ${\mathbf{x}}_i$ and ${\mathbf{n}}_i$. We denote their corresponding patch matrices by ${\tilde{\mathbf{X}}}_i$ and ${\tilde{\mathbf{N}}}_i$. Note that the indices of the similar patches in ${\tilde{\mathbf{X}}}_i$ and ${\tilde{\mathbf{N}}}_i$ are the same as those in ${\tilde{\mathbf{Y}}}_i$.

For simplicity, we subtract the columnwise average of the matrix ${\tilde{\mathbf{Y}}}_i$ from each row of ${\tilde{\mathbf{Y}}}_i$ and denote the result by ${\mathbf{Y}}_i$. The same columnwise average subtraction method is used in the implementation provided by Gu et al.; however, this is not explicitly described in [16]. Because we assume that $\mathbf{n}$ is AWGN, each columnwise average of the noiseless matrix ${\tilde{\mathbf{X}}}_i$ is sufficiently similar to that of ${\tilde{\mathbf{Y}}}_i$. Thus, the objective of WNNM is to estimate ${\mathbf{X}}_i$ which is obtained by subtracting the columnwise average of ${\tilde{\mathbf{X}}}_i$ from ${\tilde{\mathbf{X}}}_i$.

The core of the denoising process of WNNM is the following equation based on the singular value decomposition (SVD) of the observed patch matrix ${\mathbf{Y}}_i$:

$${\widehat{\mathbf{X}}}_i=\mathbf{U}g\left({\mathsf{\Sigma }}_{{\mathbf{Y}}_i}\right){\mathbf{V}}^{\top },$$

(2)

where ${\widehat{\mathbf{X}}}_i$ is the denoised patch matrix, ${\mathbf{Y}}_i=\mathbf{U}{\mathsf{\Sigma }}_{{\mathbf{Y}}_i}{\mathbf{V}}^{\top }$ is the SVD and $g(·)$ is a threshold function. Each component $(k,k)$ of the diagonal matrix $g\left(\mathsf{\Sigma }\right)$ is expressed as

$$g{\left(\mathsf{\Sigma }\right)}_{k,k}=\left\{\begin{array}{cc}0\hfill & \mathrm{if}{c}_2<0\hfill \\ \frac{c_1+\sqrt{c_2}}{2}\hfill & \mathrm{if}{c}_2\ge 0\hfill \end{array}\right.,$$

(3)

where

$$c_1={\mathsf{\Sigma }}_{k,k}-ϵ,c_2={({\mathsf{\Sigma }}_{k,k}+ϵ)}^2-4{\sigma }^{2}C,$$

(4)

C is an arbitrary parameter, and $ϵ$ is a small number. This process corresponds to a closed-form solution of the iterative reweighting method applied to the singular value matrix of ${\mathbf{Y}}_i$ [16].

The singular value thresholding described above is applied to each focused patch and similar patches, and estimates of the original patches are obtained by adding the columnwise average to ${\tilde{\mathbf{Y}}}_i$. Then, the estimated original patches are combined to obtain a reconstructed image (overlapping patches are subjected to pixelwise averaging). In WNNM, this process is iterated to estimate the original image. In each iteration, the denoising target ${\mathbf{y}}^{\left(k\right)}$ is updated by calculating a weighted sum of the most recently estimated image ${\widehat{\mathbf{x}}}^{(k-1)}$ and the original noisy observation $\mathbf{y}$ (where k is the index of the iteration) with a weight parameter $\delta$, as follows: ${\mathbf{y}}^{\left(k\right)}={\widehat{\mathbf{x}}}^{(k-1)}+\delta (\mathbf{y}-{\widehat{\mathbf{x}}}^{(k-1)})$. This process is called iterative regularization, and the parameter $\delta$ is fixed to $0.1$ in [16]. The WNNM algorithm is given in Algorithm 1. For additional details on WNNM, please consult [16].

Algorithm 1 Image denoising via WNNM.

Input: Noisy observation $\mathbf{y}$

Initialize ${\widehat{\mathbf{x}}}^{\left(0\right)}=\mathbf{y}$ and ${\mathbf{y}}^{\left(0\right)}=\mathbf{y}$

for  $k=1:K$ do

Iterative regularization: ${\mathbf{y}}^{\left(k\right)}={\widehat{\mathbf{x}}}^{(k-1)}+\delta (\mathbf{y}-{\widehat{\mathbf{x}}}^{(k-1)})$

for $i=1:I$ do

Find the similar patch matrix ${\mathbf{Y}}_i^{\left(k\right)}$

Estimate the corresponding original patch matrix ${\mathbf{X}}_i$ by applying Equation (2); the result is ${\widehat{\mathbf{X}}}_i^{\left(k\right)}$

end for

Use the ${\widehat{\mathbf{X}}}_i^{\left(k\right)}$ to reconstruct the estimated image ${\widehat{\mathbf{x}}}^{\left(k\right)}$

end for

Output: Obtain the denoised image as $\widehat{\mathbf{x}}={\widehat{\mathbf{x}}}^{\left(K\right)}$

3. Recovering Texture via Statistical Analysis

In this section, we introduce our denoising method that recovers the texture lost by denoising a noisy observation. In this paper, we define a structure (or cartoon) component $\mathbf{s}=f\left(\mathbf{y}\right)\in {\mathbb{R}}^m$, where $f(·):{\mathbb{R}}^m\to {\mathbb{R}}^m$ is a map corresponding to the denoising process of WNNM. Then, in contrast to previous work [8,19,20,21], we define a texture component $\mathbf{t}$ as the difference between the original image $\mathbf{x}$ and the structure $\mathbf{s}$ (i.e., $\mathbf{t}=\mathbf{x}-\mathbf{s}$). Thus, we obtain our extended observation model, i.e.,

$$\mathbf{y}=\mathbf{s}+\mathbf{t}+\mathbf{n}.$$

(5)

Please note that the above equation is equivalent to Equation (1) since $\mathbf{x}=\mathbf{s}+\mathbf{t}$. Our goal is to estimate the texture component $\mathbf{t}$ that has been lost via WNNM.

First, we denoise the observation $\mathbf{y}$ with WNNM. Following WNNM, we estimate each texture patch matrix ${\mathbf{T}}_i$ from the corresponding structure patch matrix ${\mathbf{S}}_i$, which is obtained in the final iteration of the WNNM procedure, and the corresponding observation patch matrix ${\mathbf{Y}}_i$. Because we use an LMMSE filter to estimate ${\mathbf{T}}_i$, we need the statistical information on the relationship between the texture and noise; however, this information cannot be calculated directly because $\mathbf{t}$ and $\mathbf{n}$ are not observable. Instead, we estimate this information using Stein’s lemma and several assumptions, which are described below, and then reconstruct the estimated texture patch matrices to obtain the estimated texture component $\widehat{\mathbf{t}}$. Finally, we obtain an estimate of the original image, $\widehat{\mathbf{x}}$, by adding the estimated texture component $\widehat{\mathbf{t}}$ to the denoised image $\mathbf{s}$.

3.1. LMMSE Filter for Texture Recovery

We use an LMMSE filter to estimate each texture patch ${\mathbf{t}}_i$. The objective function of the LMMSE filter, ${\mathbf{W}}_i^{\ast }\in {\mathbb{R}}^{L\times L}$ is formulated as

$${\mathbf{W}}_i^{\ast }=\underset{\mathbf{W}}{\mathrm{argmin}}\mathbb{E}[\parallel \mathbf{W}({\mathbf{t}}_i+{\mathbf{n}}_i)-{\mathbf{t}}_i{\parallel }_2^2],$$

(6)

where $\mathbb{E}[·]$ denotes the expected value and ${\parallel ·\parallel }_2$ is the ℓ − 2 norm. Because this formula is quadratic, we can easily find the minimizer as follows:

$${\mathbf{W}}_i^{\ast }=({\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{t}}_i}+{\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{n}}_i}){\left({\mathbf{R}}_{({\mathbf{t}}_i+{\mathbf{n}}_i)({\mathbf{t}}_i+{\mathbf{n}}_i)}\right)}^{-1},$$

(7)

where we adopt the following covariance matrix notation: ${\mathbf{R}}_{\mathbf{a}\mathbf{b}}=\mathbb{E}\left[(\mathbf{a}-\mathbb{E}\left[\mathbf{a}\right]){(\mathbf{b}-\mathbb{E}\left[\mathbf{b}\right])}^{\top }\right]$ (where $\mathbf{a}$ and $\mathbf{b}$ are some random vectors). The proof is given in Appendix A.

Unfortunately, the covariance matrices ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{t}}_i}$ and ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{n}}_i}$ cannot be directly obtained because $\mathbf{t}$ and $\mathbf{n}$ are not observable. We solve this problem by using Stein’s lemma and introducing several assumptions.

3.2. Estimation of the Covariance Matrices

As mentioned above, we need to estimate ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{t}}_i}$ and ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{n}}_i}$. Since we define $\mathbf{t}$ as $\mathbf{x}-\mathbf{s}$, and the value of $\mathbf{s}$ is changed with respect to the value of $\mathbf{n}$, we can assume that $\mathbf{t}$ is the output of a function that takes $\mathbf{n}$ as an input. $\mathbf{n}$ also follows a normal distribution. Thus, we can estimate ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{n}}_i}$ using Stein’s lemma as follows:

$${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{n}}_i}={{\mathbf{R}}_{{\mathbf{n}}_i{\mathbf{t}}_i}}^{\top }={\sigma }^2\mathbb{E}\left[\frac{\partial {\mathbf{t}}_i}{\partial {\mathbf{n}}_i}\right].$$

(8)

The above equation shows that our desired covariance matrices can be obtained from the effects of the ${\mathbf{n}}_i$ on the ${\mathbf{t}}_i$. The texture patch ${\mathbf{t}}_i$ is equal to ${\mathbf{x}}_i-{\mathbf{s}}_i$ according to Equation (5); moreover, we assume that the effect of ${\mathbf{n}}_i$ on ${\mathbf{x}}_i$ is zero. Therefore, we can estimate the covariance matrix ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{n}}_i}$ as

$${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{n}}_i}={\sigma }^2\left[\frac{\partial {\mathbf{t}}_i}{\partial {\mathbf{n}}_i}\right]={\sigma }^2\left[\frac{\partial ({\mathbf{x}}_i-{\mathbf{s}}_i)}{\partial {\mathbf{n}}_i}\right]=-{\sigma }^2\left[\frac{\partial {\mathbf{s}}_i}{\partial {\mathbf{n}}_i}\right].$$

(9)

We need to analyze the variations in the WNNM output as the noise varies. As mentioned above, the WNNM process is complex. Thus, we need to approximate the WNNM process with a linear filter to simplify the analysis.

Surprisingly, the linear approximation of the WNNM process also provides us with an empirical method of estimating ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{t}}_i}$, which is more difficult to estimate than ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{n}}_i}$. In the next subsection, we describe how to approximate WNNM with a linear filter and how to estimate ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{t}}_i}$.

3.3. Linear Approximation of the WNNM Procedure

To simplify the analysis and determine the covariance matrix ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{n}}_i}$ by using Stein’s lemma, we assume that we can precisely approximate the whole process of WNNM as a linear filter:

$${\mathbf{S}}_i={\mathbf{F}}_i{\mathbf{Y}}_i.$$

(10)

The SVDs of ${\mathbf{Y}}_i$ and ${\mathbf{S}}_i$ are formulated as

$${\mathbf{Y}}_i={\mathbf{U}}_{{\mathbf{Y}}_i}{\mathsf{\Sigma }}_{{\mathbf{Y}}_i}{\mathbf{V}}_{{\mathbf{Y}}_i}^{\top }\mathrm{and}{\mathbf{S}}_i={\mathbf{U}}_{{\mathbf{S}}_i}{\mathsf{\Sigma }}_{{\mathbf{S}}_i}{\mathbf{V}}_{{\mathbf{S}}_i}^{\top }.$$

(11)

If we ignore the fact that the patch matrices are updated in WNNM via a similar patch search, reconstruction and iterative regularization in each iteration, then the SVDs of ${\mathbf{Y}}_i$ and ${\mathbf{S}}_i$ will have common right and left singular matrices. We assume that ${\mathbf{U}}_{{\mathbf{Y}}_i}$ and ${\mathbf{V}}_{{\mathbf{Y}}_i}$ are equal to ${\mathbf{U}}_{{\mathbf{S}}_i}$ and ${\mathbf{V}}_{{\mathbf{S}}_i}$, respectively. Thus, we can obtain the approximate WNNM filter ${\mathbf{F}}_i$ as follows:

$${\mathbf{F}}_i={\mathbf{U}}_{{\mathbf{S}}_i}{\mathsf{\Sigma }}_{{\mathbf{S}}_i}{\mathsf{\Sigma }}_{{\mathbf{Y}}_i}^{-1}{\mathbf{U}}_{{\mathbf{S}}_i}^{\top }.$$

(12)

The partial derivative of the columnwise average of ${\tilde{\mathbf{Y}}}_i$ with respect to $\mathbf{n}$ is considered to be very small because $\mathbf{n}$ is Gaussian and because the average of $\mathbf{n}$ is zero. Note that ${\mathbf{Y}}_i$ is obtained by subtracting the columnwise average of ${\tilde{\mathbf{Y}}}_i$ from ${\tilde{\mathbf{Y}}}_i$.

If this approximation of WNNM is sufficiently accurate, then $\frac{\partial {\mathbf{s}}_i}{\partial {\mathbf{n}}_i}\approx {\mathbf{F}}_i$. From Equation (9), we can estimate ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{n}}_i}$ as

$$\begin{array}{ccc}\hfill {\widehat{\mathbf{R}}}_{{\mathbf{t}}_i{\mathbf{n}}_i}& =& -{\sigma }^2{\mathbf{F}}_i.\hfill \end{array}$$

(13)

Additionally, we use the approximate WNNM filter ${\mathbf{F}}_i$ to estimate ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{t}}_i}$. We assume that ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{t}}_i}$ can be estimated as

$${\widehat{\mathbf{R}}}_{{\mathbf{t}}_i{\mathbf{t}}_i}=2{\sigma }^2{\mathbf{F}}_i.$$

(14)

This assumption is founded on preliminary experiments. The details of these preliminary experiments are presented in Appendix B.3.

3.4. Recovering the Texture of a Denoised Image

Based on the above discussion, we can calculate the LMMSE filter and estimate ${\mathbf{t}}_i$. However, ${\mathbf{R}}_{({\mathbf{t}}_i+{\mathbf{n}}_i)({\mathbf{t}}_i+{\mathbf{n}}_i)}$ is not invertible in practice because the number of patches M is smaller than L. Although an equivalent estimate of ${\mathbf{R}}_{({\mathbf{t}}_i+{\mathbf{n}}_i)({\mathbf{t}}_i+{\mathbf{n}}_i)}$ appears to be ${\widehat{\mathbf{R}}}_{{\mathbf{t}}_i{\mathbf{t}}_i}+{\widehat{\mathbf{R}}}_{{\mathbf{t}}_i{\mathbf{n}}_i}+{\widehat{\mathbf{R}}}_{{\mathbf{n}}_i{\mathbf{t}}_i}+{\sigma }^2\mathbf{I}$ (where $\mathbf{I}$ is the identity matrix), this choice does not provide good recovery performance. Instead, substituting ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{t}}_i}+{\sigma }^2\mathbf{I}$ into the sample covariance matrix ${\mathbf{R}}_{({\mathbf{t}}_i+{\mathbf{n}}_i)({\mathbf{t}}_i+{\mathbf{n}}_i)}$ was found to yield the best results in our preliminary experiments. Thus, we calculate the LMMSE filter as

$${\mathbf{W}}_i^{\ast }=({\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{t}}_i}+{\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{n}}_i}){({\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{t}}_i}+{\sigma }^2\mathbf{I})}^{-1}.$$

(15)

Substituting Equation (13) and (14) into (15), we can estimate ${\mathbf{T}}_i$ as

$${\widehat{\mathbf{T}}}_i=\left({\sigma }^2{\mathbf{F}}_i\right){(2{\sigma }^2{\mathbf{F}}_i+{\sigma }^2\mathbf{I})}^{-1}({\tilde{\mathbf{Y}}}_i-{\tilde{\mathbf{S}}}_i).$$

(16)

Then, we can obtain the desired estimated texture image $\widehat{\mathbf{t}}$ that is obtained by combining each ${\widehat{\mathbf{T}}}_i$ in the same manner used to reconstruct an image from the patches obtained in WNNM. Finally, we can obtain the final estimated image $\widehat{\mathbf{x}}$ with enhanced texture as

$$\widehat{\mathbf{x}}=\mathbf{s}+\widehat{\mathbf{t}}.$$

(17)

We use the LMMSE filter to obtain $\widehat{\mathbf{t}}$; however, minimizing the MSE often causes $\widehat{\mathbf{t}}$ to lose clarity. We can obtain a clearer texture-enhanced image as follows:

$$\widehat{\mathbf{x}}=\mathbf{s}+\alpha \widehat{\mathbf{t}},$$

(18)

where $\alpha$ is an arbitrary parameter used to control the magnitude of the texture that is added. Note that $\alpha =1$ means the proposed method applies the LMMSE filter and we can expect to obtain the denoised images with best PSNR if all of our assumptions hold. The entire proposed process is presented in Algorithm 2.

Algorithm 2 Texture recovery using the proposed method.

Input: Noisy observation $\mathbf{y}$

Initialize ${\mathbf{s}}^{\left(0\right)}=\mathbf{y}$ and ${\mathbf{y}}^{\left(0\right)}=\mathbf{y}$

for $k=1:K$ do

Iterative regularization: ${\mathbf{y}}^{\left(k\right)}={\mathbf{s}}^{(k-1)}+\delta (\mathbf{y}-{\mathbf{s}}^{(k-1)})$

for $i=1:I$ do

Find the similar patch matrix ${\mathbf{Y}}_i^{\left(k\right)}$

Estimate the corresponding original patch matrix ${\mathbf{X}}_i$ via Equation (2); the result is denoted by ${\mathbf{S}}_i^{\left(k\right)}$

if k=K then

Estimate ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{t}}_i}$ and ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{n}}_i}$ using Stein’s lemma via Equation (13) and (14)

Calculate ${\mathbf{W}}_i^{\ast }$ via Equation (9)

Estimate ${\mathbf{T}}_i$ via Equation (16) to obtain ${\widehat{\mathbf{T}}}_i$

end if

end for

Use the ${\mathbf{S}}_i^{\left(k\right)}$ to reconstruct the estimated image ${\mathbf{s}}^{\left(k\right)}$

end for

Use the ${\widehat{\mathbf{T}}}_i$ to reconstruct the estimated texture component $\widehat{\mathbf{t}}$

Output: Obtain the final estimated image as $\widehat{\mathbf{x}}={\mathbf{s}}^{\left(\mathrm{K}\right)}+\alpha \widehat{\mathbf{t}}$

4. Experimental Results

In this section, we discuss our experimental results. First, we present performance of our denoising method and compare it to other non-learning-based state-of-the-art denoising methods, namely, block matching and 3D filtering (BM3D) [11], GHP [19], and WNNM [16]. For comparison with learning-based denoising methods, we compare the denoising performance of the proposed method with that of a denoising convolutional neural network (DnCNN) [9]. We also confirm the effects of the parameter $\alpha$. Moreover, we present a histogram of the Fréchet distance to confirm the assumption of Equation (14).

We used two image datasets for validation. One dataset consists of ten grayscale natural images from [21], as shown in Figure 3 (dataset I). The other dataset contains 100 grayscale natural images from the Berkeley segmentation dataset [25] (BSD100). In all experiments, we used MATLAB R2018b for the implementation, and all noisy observations were simulated by adding noise generated by a pseudorandom number generator to the original images.

4.1. Image Denoising

The PSNR and structural self-similarity (SSIM) [26] results for the denoised images from dataset I with different noise levels $\sigma$ are given in

Table 1. The PSNR [dB] and SSIM results obtained after denoising on dataset I (with a noise standard deviation of $\sigma =10$).

	BM3D	GHP	WNNM	Proposed
Image01	34.31/0.932	34.31/0.925	34.70/0.935	34.74/0.937
Image02	32.99/0.887	32.97/0.884	33.12/0.889	33.23/0.896
Image03	31.64/0.907	31.79/0.909	31.86/0.910	31.95/0.916
Image04	30.58/0.898	30.66/0.904	30.76/0.900	30.80/0.905
Image05	32.59/0.946	32.52/0.932	32.88/0.948	32.89/0.949
Image06	33.61/0.917	33.61/0.905	33.90/0.921	33.99/0.925
Image07	34.19/0.898	34.11/0.894	34.41/0.902	34.48/0.906
Image08	31.48/0.908	31.51/0.907	31.73/0.912	31.80/0.917
Image09	35.12/0.946	34.96/0.934	35.30/0.946	35.35/0.948
Image10	31.71/0.912	31.76/0.907	31.84/0.913	31.92/0.917
Average	32.82/0.915	32.82/0.910	33.05/0.918	33.11/0.922

,

Table 2. The PSNR [dB] and SSIM results obtained after denoising on dataset I (with a noise standard deviation of $\sigma =20$).

	BM3D	GHP	WNNM	Proposed
Image01	30.47/0.868	30.58/0.869	30.81/0.872	30.91/0.875
Image02	29.55/0.765	29.67/0.778	29.64/0.765	29.77/0.777
Image03	27.82/0.796	28.10/0.816	28.06/0.802	28.21/0.815
Image04	26.61/0.793	26.74/0.803	26.80/0.798	26.91/0.809
Image05	28.30/0.881	28.48/0.884	28.58/0.883	28.70/0.888
Image06	29.96/0.828	30.21/0.841	30.25/0.833	30.38/0.841
Image07	30.97/0.812	31.00/0.816	31.03/0.811	31.11/0.817
Image08	27.22/0.806	27.41/0.818	27.54/0.815	27.69/0.827
Image09	31.35/0.895	31.39/0.896	31.52/0.895	31.60/0.896
Image10	27.82/0.803	27.98/0.813	27.96/0.807	28.11/0.819
Average	29.01/0.825	29.16/0.833	29.22/0.828	29.34/0.837

and

Table 3. The PSNR [dB] and SSIM results obtained after denoising on dataset I (with a noise standard deviation of $\sigma =30$).

	BM3D	GHP	WNNM	Proposed
Image01	28.51/0.817	28.57/0.818	28.75/0.822	28.83/0.824
Image02	28.03/0.688	28.03/0.700	28.07/0.684	28.13/0.694
Image03	26.08/0.719	26.21/0.738	26.29/0.727	26.39/0.740
Image04	24.57/0.703	24.68/0.718	24.81/0.714	24.92/0.729
Image05	26.04/0.813	26.28/0.819	26.38/0.823	26.51/0.831
Image06	28.22/0.762	28.43/0.778	28.50/0.770	28.59/0.776
Image07	29.37/0.756	29.24/0.757	29.43/0.755	29.45/0.759
Image08	25.13/0.724	25.34/0.744	25.46/0.738	25.60/0.751
Image09	29.48/0.854	29.47/0.855	29.65/0.856	29.70/0.855
Image10	26.00/0.718	26.09/0.733	26.14/0.725	26.25/0.738
Average	27.14/0.755	27.24/0.766	27.35/0.761	27.44/0.770

. Note that higher PSNR and SSIM values mean that the reference image is more similar to the original image. We highlight the highest PSNR and SSIM in each row in bold. We set the texture scaling parameter to $\alpha =1$ because we wish to measure how much improvement is achieved in terms of the PSNR. We recover the texture using the LMMSE filter; thus, the MSE is likely to be low, meaning that the PSNR should be high. These tables show that our denoising method outperforms the other state-of-the-art methods in terms of both the PSNR and SSIM. The largest difference in the PSNR between WNNM and our method is 0.15 dB. Additionally, the averages of the denoising results on BSD100 at each noise level are shown in

Table 4. The PSNR [dB] and SSIM results obtained after denoising on BSD100. The p-values were calculated by one-tailed paired t-tests on the difference of each PSNR and SSIM between the proposed method and WNNM.

	BM3D	GHP	WNNM	Proposed	p-Value
$\sigma =10$	33.13/0.913	33.10/0.911	33.36/0.916	33.42/0.920	$5.3\times {10}^{-16}$/$3.8\times {10}^{-20}$
$\sigma =20$	29.42/0.824	29.49/0.832	29.64/0.829	29.74/0.837	$4.6\times {10}^{-26}$/$3.3\times {10}^{-19}$
$\sigma =30$	27.56/0.759	27.58/0.769	27.78/0.766	27.84/0.773	$1.7\times {10}^{-16}$/$6.8\times {10}^{-13}$
Average	30.03/0.832	30.06/0.837	30.26/0.837	30.33/0.843	–

. This table shows that the performance improvement achieved with our method is independent of the dataset. For each image in BSD100, we performed one-tailed paired t-tests on the difference of each PSNR and SSIM between the proposed method and WNNM. In this test, the null hypothesis is that the PSNR/SSIM values obtained by proposed method are not greater than the corresponding values obtained by WNNM. The p-values are also shown in Table 4. From the results, since the p-values are small enough, we confirmed statistically significant differences between our proposed method and WNNM.

Moreover, we show the averages of computational time of WNNM and the proposed method in

Table 5. The averages of computational time (in seconds) of WNNM and the proposed method.

	WNNM	Proposed (WNNM + Texture Recovery)
$\sigma =10$	149	169
$\sigma =20$	148	167
$\sigma =30$	311	334

. The computational times were measured on 10 distinct observed images (the noise value of each observation is different) for each test image from BSD100. The additional computational time of our texture recovery is 7–13% of the computational time of WNNM. The PSNR/SSIM gain obtained by our texture recovery method is considered to be sufficient for the users to accept this additional cost.

We also compare the denoising performance of the proposed method with that of the DnCNN [9] on dataset I. The noise level $\sigma$ was set to 15 and the texture scaling parameter $\alpha$ was set to 1. We used the PyTorch implementation of DnCNN and the pretrained model parameters for noise level $\sigma =15$, which is published by the authors of [9]. The experimental results are shown in

Table 6. Comparison of non-learning-based methods (WNNM and the proposed method) and a learning-based method (DnCNN). The PSNR [dB] and SSIM results obtained after denoising on dataset I (with a noise standard deviation of $\sigma =15$). Note that the proposed method does not require any training and is fully explainable. The bold value means the highest PSNR or SSIM in non-learning-based methods.

	WNNM	Proposed	DnCNN
Image01	32.38/0.902	32.45/0.905	32.70/0.911
Image02	31.00/0.824	31.13/0.834	31.38/0.845
Image03	29.53/0.853	29.67/0.864	29.89/0.872
Image04	28.37/0.847	28.45/0.856	28.59/0.860
Image05	30.30/0.916	30.37/0.919	30.53/0.922
Image06	31.69/0.876	31.81/0.882	31.82/0.886
Image07	32.37/0.852	32.45/0.858	32.68/0.867
Image08	29.20/0.862	29.32/0.871	29.58/0.877
Image09	33.00/0.919	33.08/0.921	33.35/0.927
Image10	29.47/0.858	29.60/0.867	29.79/0.874
Average	30.73/0.871	30.83/0.878	31.03/0.884

. The improvement of DnCNN over WNNM is 0.30 dB in the average of PSNR while that of the proposed method is 0.10 dB. Note that the proposed method requires no training process and is fully explainable while the denoising mechanism of DnCNN is black box.

Next, to observe the effect of the parameter $\alpha$, we searched for the value of this parameter that would maximize the SSIM of the output image, denoted by ${\alpha }_{\mathrm{SSIM}}$. We obtained ${\alpha }_{\mathrm{SSIM}}$ via a line search in the range from 0 to 8 in increments of $0.01$. For several examples, the original image, the noisy observation, the output image obtained via GHP, the output image obtained via WNNM, and an output image obtained with our method are shown in Figure 4. From this figure, we can observe that the subjective quality and SSIM can be drastically improved by properly choosing the parameter $\alpha$. For example, as shown in Figure 4p–t for the image named 196073, the SSIM value obtained with our method is 0.073 higher than that achieved via WNNM. Moreover, we show $\mathbf{t}$ and $\alpha \widehat{\mathbf{t}}$ of each image of Figure 4 in Figure 5. Please note that the pixel value of each image is multiplied by a factor of 3. This figure shows that $\widehat{\mathbf{t}}$ is similar to $\mathbf{t}$ in each textured region such as surface of a stone, a coral, the skin of a snake, and the surface of the sea.

A histogram of the ${\alpha }_{\mathrm{SSIM}}$ values obtained on BSD100 is shown in Figure 6. We note that this histogram shows the frequency under three noise levels ($\sigma$ = 10, 20, 30). This figure indicates that there is no single optimal value of ${\alpha }_{\mathrm{SSIM}}$ that is common to all images. Nevertheless, the figure also shows that choosing $\alpha =2$ will almost always increase the expected value of the SSIM. Moreover, as with ${\alpha }_{\mathrm{SSIM}}$, we searched for the value of $\alpha$ that would maximize the PSNR of the output image, and denoted it by ${\alpha }_{\mathrm{PSNR}}$. We obtained ${\alpha }_{\mathrm{PSNR}}$ for each image via a line search in the range from 0 to 8 in increments of $0.01$. Figure 7 shows a histogram of the values of ${\alpha }_{\mathrm{PSNR}}$. We confirmed that $\alpha =1$ produces the denoised images with the best PSNR in most cases.

4.2. Accuracy of Texture Covariance Matrix Estimation

In this section, we compare the accuracy of two texture covariance matrices. One is our estimated texture covariance matrix, and the other is a simply sampled estimate that is calculated as

$${\hat{\mathbf{R}}}_{{\mathbf{t}}_i{\mathbf{t}}_i}^{\mathrm{smp}}=h(({\mathbf{T}}_i+{\mathbf{N}}_i){({\mathbf{T}}_i+{\mathbf{N}}_i)}^{\top }-{\sigma }^2\mathbf{I}),$$

(19)

where $h(·)$ is a function that replaces any negative eigenvalues of the input matrix with zero; this is equivalent to metric projection to a positive-semidefinite matrix.

We calculate the Fréchet distance to evaluate the accuracy of the texture covariance matrix. Dowson and Landau introduced the calculation of the Fréchet distance between multivariate normal (MVN) distributions [23]. The Fréchet distance is also used to measure the similarity between generated and real images [27]. We assume that the texture component $\mathbf{t}$ follows an MVN distribution. Consider a random MVN-distributed variable $\mathbf{a}\in {\mathbb{R}}^d$ whose mean vector is ${\mathbf{\mu }}_{\mathbf{a}}=\mathbb{E}\left[\mathbf{a}\right]\in {\mathbb{R}}^d$ and whose covariance matrix is ${\mathbf{R}}_{\mathbf{a}\mathbf{a}}$ ($\mathbf{a}\sim {\mathcal{N}}_d({\mathbf{\mu }}_{\mathbf{a}},{\mathbf{R}}_{\mathbf{a}\mathbf{a}})$); its probability density is denoted by

$$p\left(\mathbf{a}\right)=\frac{1}{(\sqrt{{\left(2\pi \right)}^{d}det({\mathbf{R}}_{\mathbf{a}\mathbf{a}}})}\exp (-\frac{1}{2}{(\mathbf{a}-{\mathbf{\mu }}_{\mathbf{a}})}^{\top }{\mathbf{R}}_{\mathbf{a}\mathbf{a}}^{-1}(\mathbf{a}-{\mathbf{\mu }}_{\mathbf{a}})).$$

(20)

Additionally, the Fréchet distance between the MVN distributions ${\mathcal{N}}_d({\mathbf{\mu }}_a,{\mathbf{R}}_{\mathbf{a}\mathbf{a}})$ and ${\mathcal{N}}_d({\mathbf{\mu }}_b,{\mathbf{R}}_{\mathbf{b}\mathbf{b}})$ is calculated as

$$\parallel {\mathbf{\mu }}_{\mathbf{a}}-{\mathbf{\mu }}_{\mathbf{b}}{\parallel }_2^2+\mathrm{tr}({\mathbf{R}}_{\mathbf{a}\mathbf{a}}+{\mathbf{R}}_{\mathbf{b}\mathbf{b}}-2{\left({\mathbf{R}}_{\mathbf{a}\mathbf{a}}{\mathbf{R}}_{\mathbf{b}\mathbf{b}}\right)}^{\frac{1}{2}}).$$

(21)

We assume that the mean vector of the texture is $\mathbf{0}$. Thus, we can calculate the Fréchet distance between the estimated texture covariance matrix ${\widehat{\mathbf{R}}}_{{\mathbf{t}}_i{\mathbf{t}}_i}$ and the true texture covariance matrix ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{t}}_i}$ from the ground truth as follows:

$$\mathrm{Fr}\acute{\mathrm{e}}\mathrm{chet}({\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{t}}_i},{\widehat{\mathbf{R}}}_{{\mathbf{t}}_i{\mathbf{t}}_i})=\mathrm{tr}({\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{t}}_i}+{\widehat{\mathbf{R}}}_{{\mathbf{t}}_i{\mathbf{t}}_i}-2{({\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{t}}_i}{\widehat{\mathbf{R}}}_{{\mathbf{t}}_i{\mathbf{t}}_i})}^{\frac{1}{2}}).$$

(22)

We can similarly calculate the Fréchet distance between the simply sampled estimate ${\widehat{\mathbf{R}}}_{{\mathbf{t}}_i{\mathbf{t}}_i}^{\mathrm{smp}}$ and ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{t}}_i}$ by replacing ${\widehat{\mathbf{R}}}_{{\mathbf{t}}_i{\mathbf{t}}_i}$ with ${\widehat{\mathbf{R}}}_{{\mathbf{t}}_i{\mathbf{t}}_i}^{\mathrm{smp}}$ in Equation (22).

Figure 8 shows histograms of these Fréchet distances. Note that we calculated the Fréchet distance for each patch matrix from dataset I. However, we ignored the very few outliers caused by numerical errors. This figure shows that ${\widehat{\mathbf{R}}}_{{\mathbf{t}}_i{\mathbf{t}}_i}$ is more similar to ${\mathbf{R}}_{{\mathbf{t}}_i{\mathbf{t}}_i}$ than ${\widehat{\mathbf{R}}}_{{\mathbf{t}}_i{\mathbf{t}}_i}^{\mathrm{smp}}$ is at each noise level.

5. Conclusions

In this paper, we have proposed a method of recovering texture information that has been oversmoothed by the denoising process in WNNM. For texture recovery, we apply an LMMSE filter to a noisy image. Because our filter requires covariance matrices between the texture and noise, we have also proposed a method of estimating this information based on Stein’s lemma and several key assumptions.

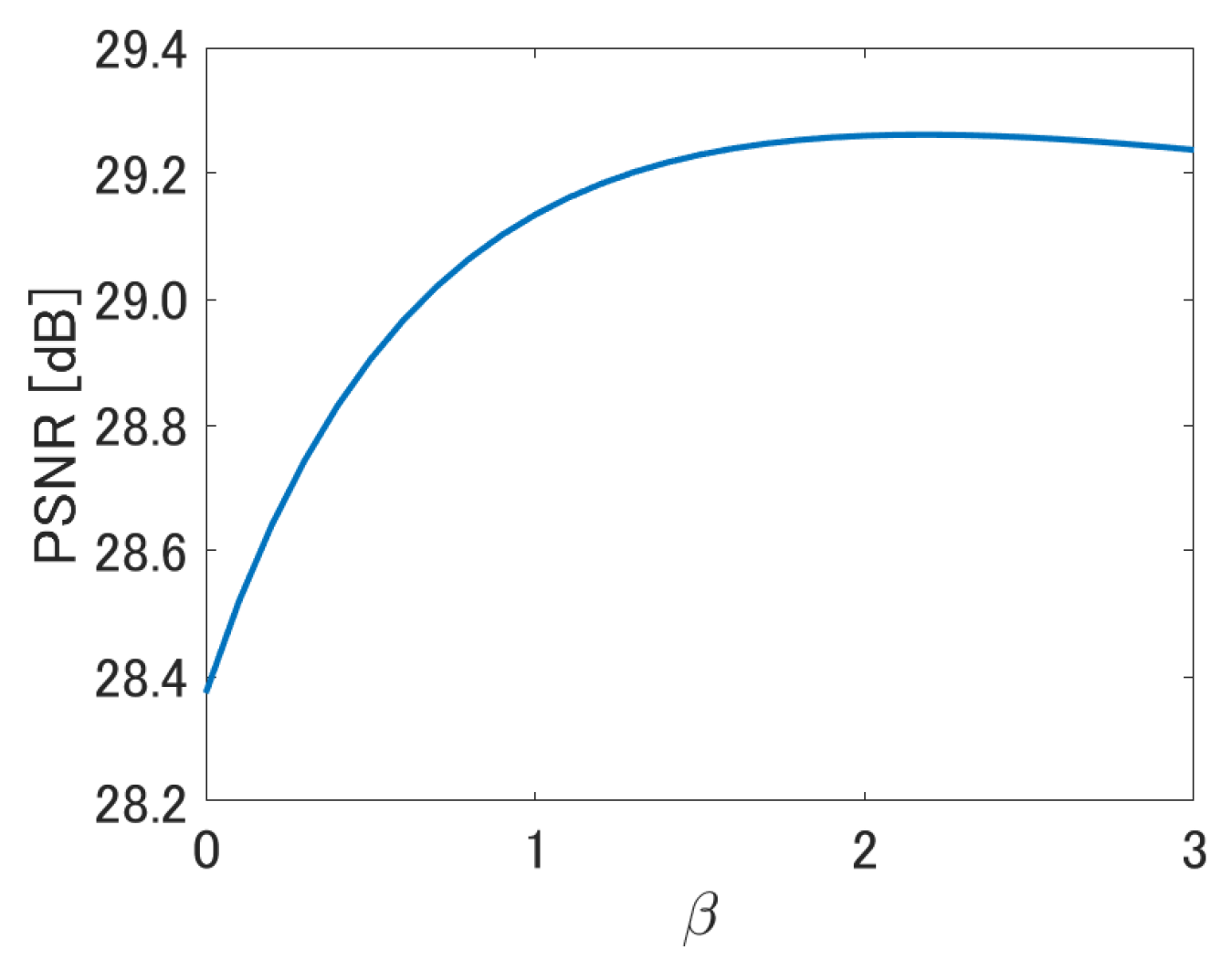
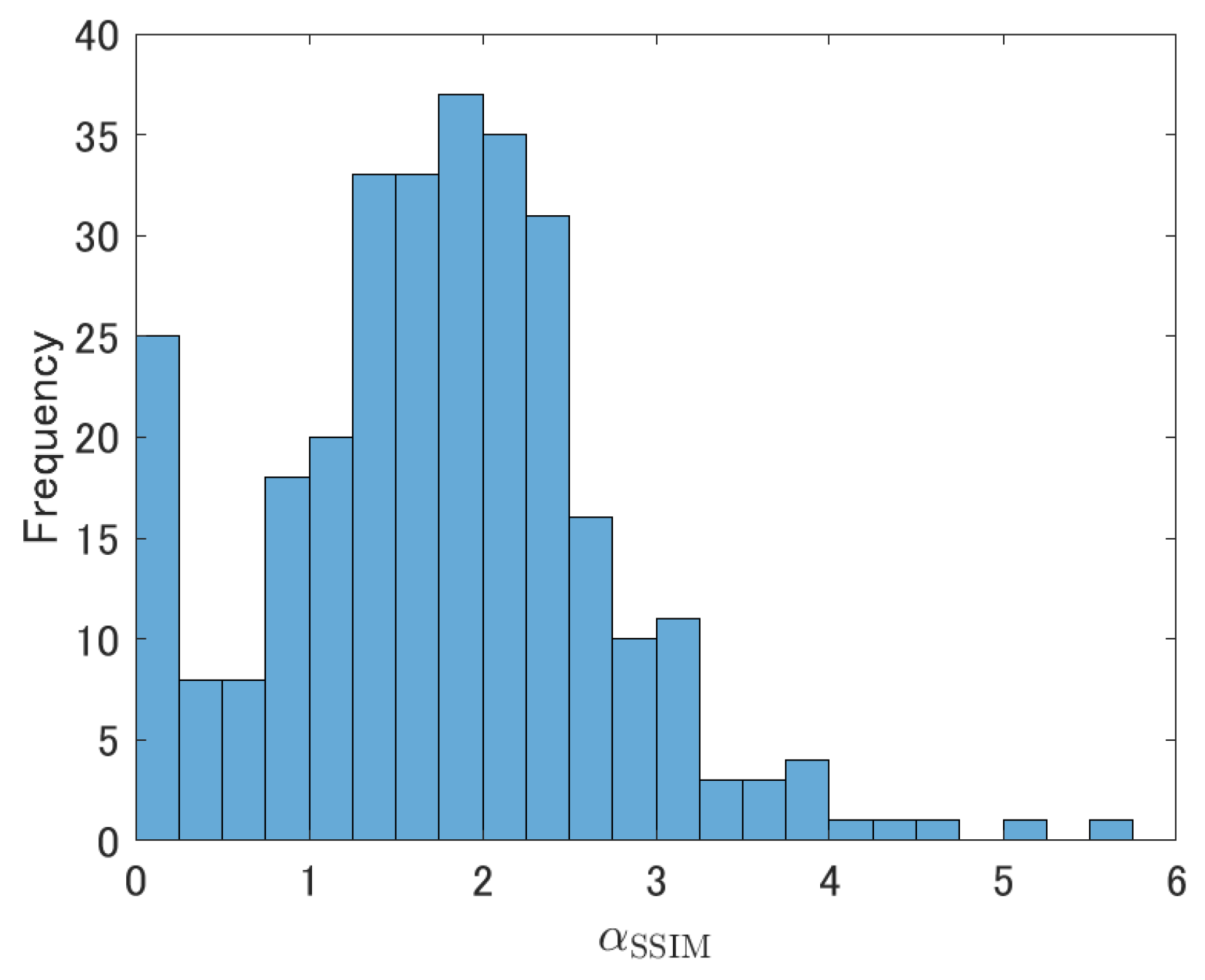
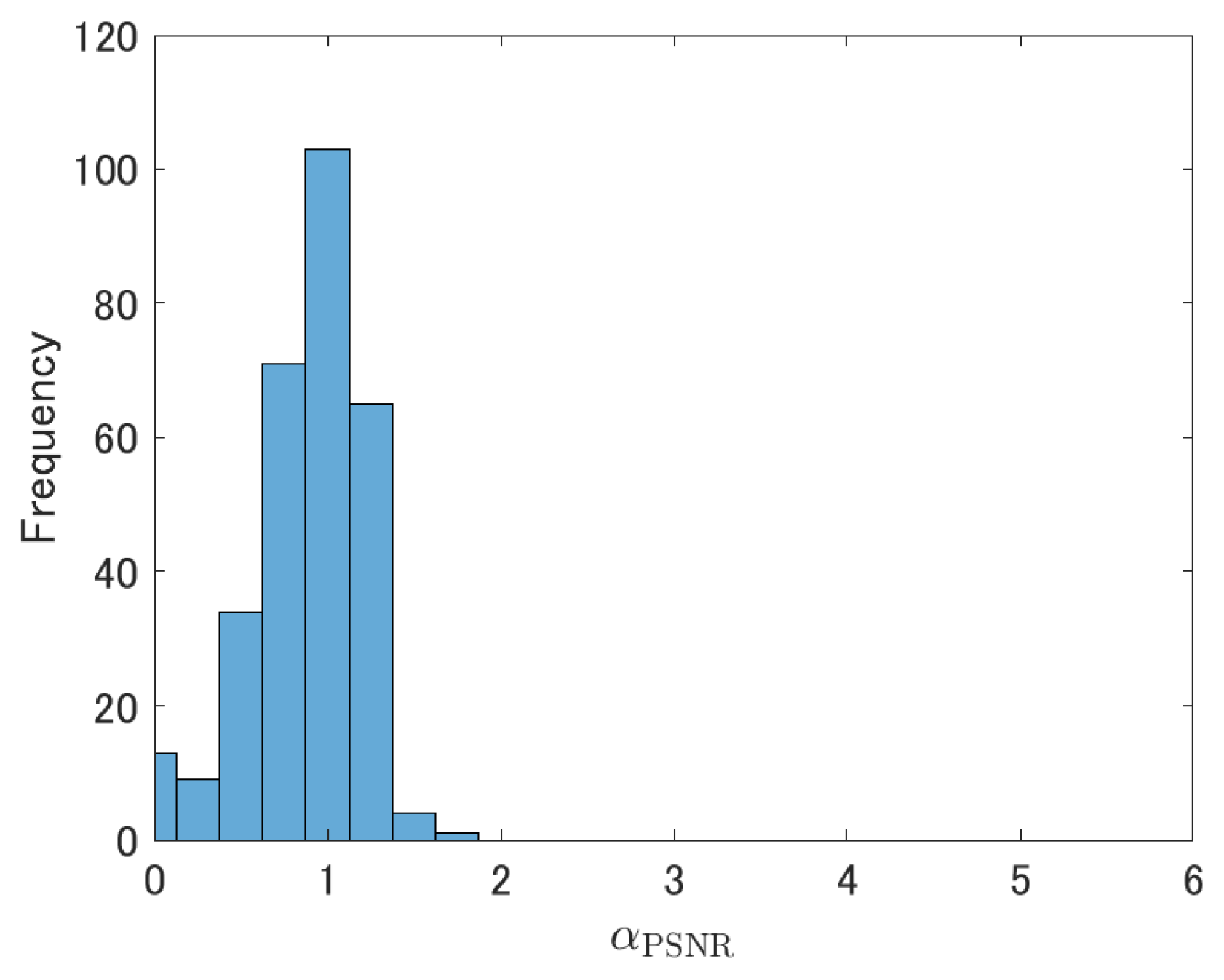
Experimental results obtained on various image datasets show that our method can improve PSNR and SSIM of WNNM and also outperforms other state-of-the-art methods with respect to both criteria. Moreover, we confirmed statistically significant differences between our method and WNNM. With our method, SSIM values can be further improved by choosing a suitable value for a scaling parameter that controls the magnitude of the added texture. Moreover, blurred edges and texture can be enhanced through a proper selection of this scaling parameter. Additionally, our estimated texture covariance matrices are more similar to the corresponding oracle covariance matrices in terms of the Fréchet distance than are simply sampled estimates obtained from the observed images. Finally, an additional computational time of our texture recovery is 7–13% of the computational time of WNNM. We consider the additional cost is acceptable considering the gain of PSNR and SSIM.

In the experiments, we chose almost all the parameters of the proposed method based on the default setting of WNNM. The only parameter that the user needs to choose is $\alpha$. When the user wants to maximize the PSNR, $\alpha$ = 1 gives the best result in most cases. If the user would like to enhance the texture, the user should choose the $\alpha$ larger than 1. In addition, our experimental results show that $\alpha =2$ almost always improves the SSIM.