Clipping Noise Compensation with Neural Networks in OFDM Systems
Abstract
:1. Introduction
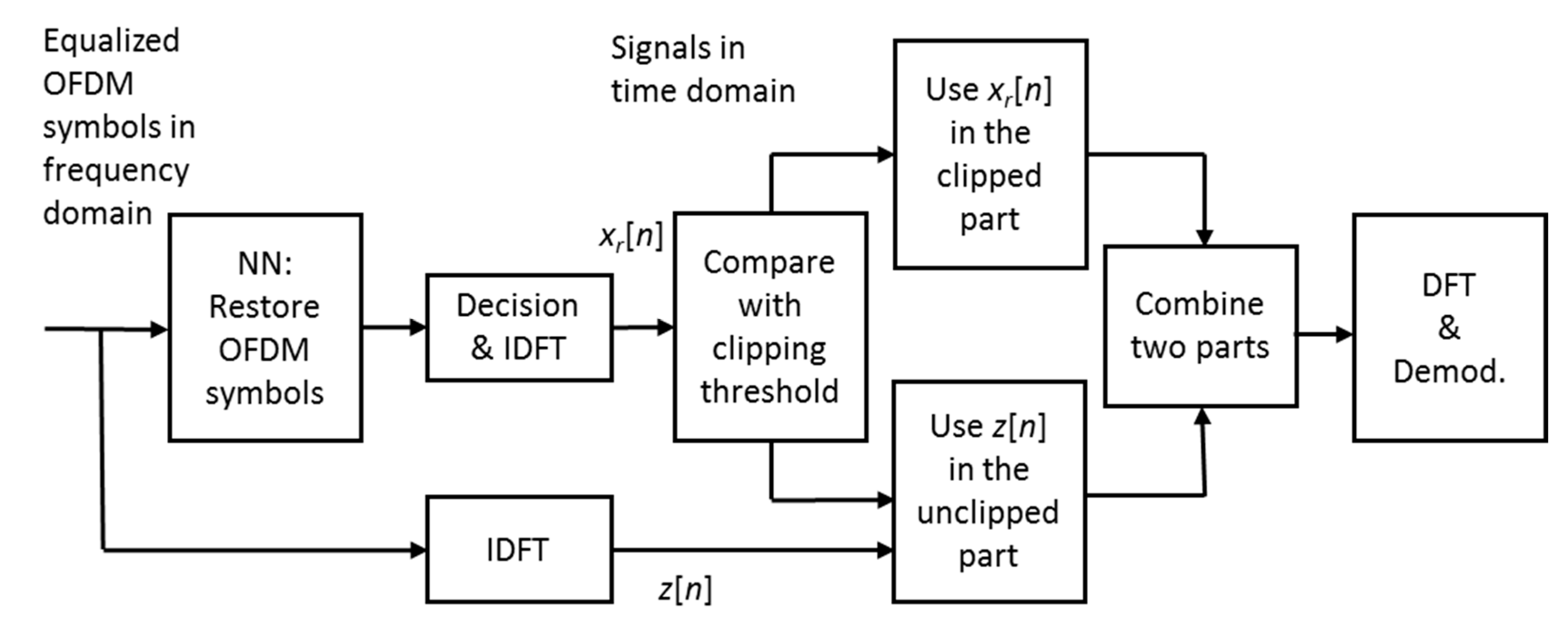
2. Clipping Noise Compensation
3. Results
3.1. Interpretation of NN Weight Matrices
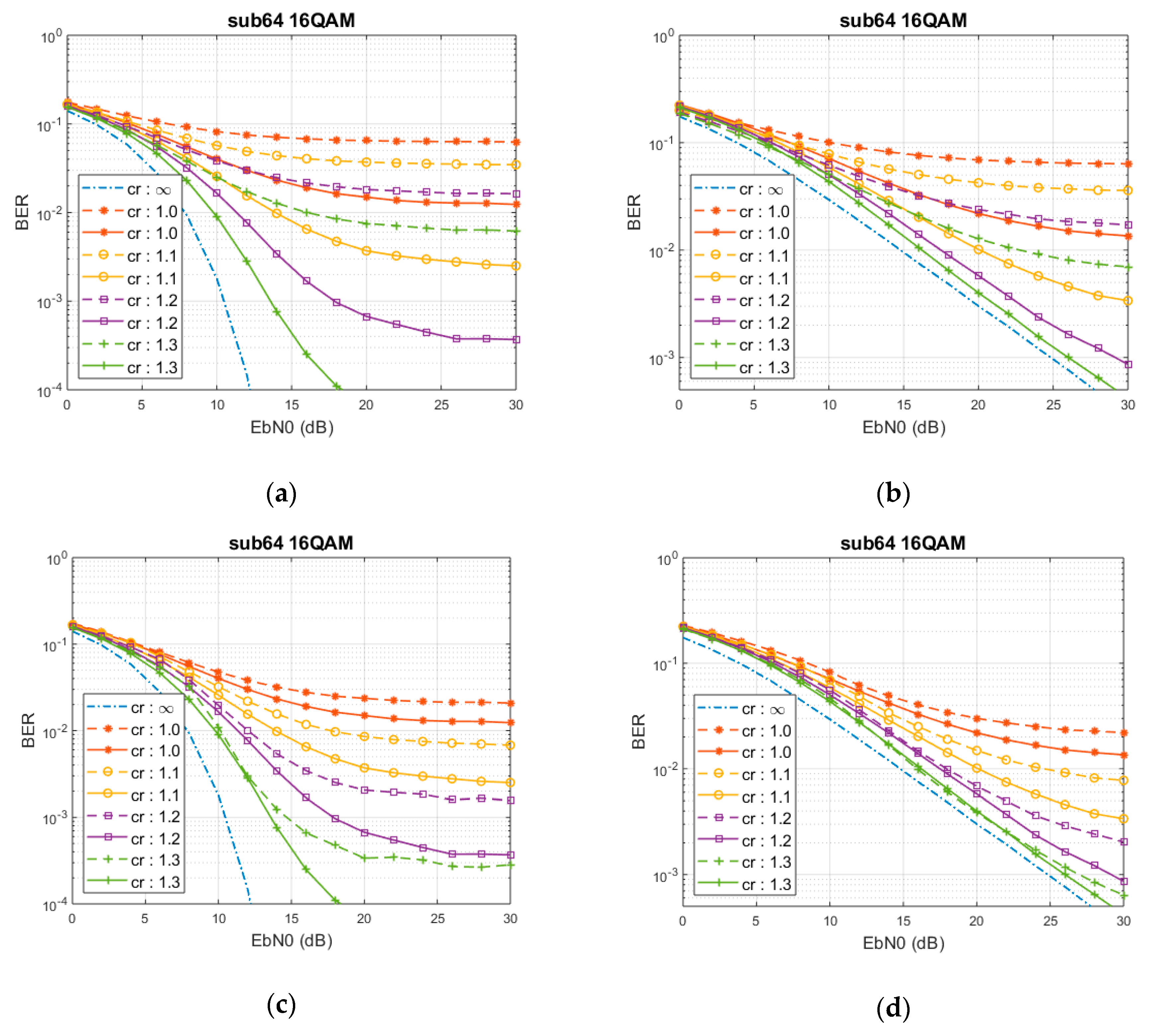
3.2. MSE and BER Performances
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge University Press: Cambridge, UK, 2005; pp. 95–99. [Google Scholar]
- Ochiai, H.; Imai, H. On the distribution of the peak-to-average power ratio in OFDM signals. IEEE Trans. Commun. 1995, 49, 282–289. [Google Scholar] [CrossRef]
- Cimini, L.J.; Sollenberger, N.R. Peak-to-average power ratio reduction of an OFDM signal using partial transmit sequences. IEEE Commun. Lett. 2000, 4, 86–88. [Google Scholar] [CrossRef]
- Bauml, R.W.; Fischer, R.F.H.; Huber, J.B. Reducing the peak-to-average power ratio of multicarrier modulation by selected mapping. Electron. Lett. 1996, 32, 2056–2057. [Google Scholar] [CrossRef] [Green Version]
- BKrongold, B.S.; Jones, D.L. An active-set approach for OFDM PAR reduction via tone reservation. IEEE Trans. Signal Proc. 2004, 52, 495–509. [Google Scholar] [CrossRef]
- Rahmatallah, Y.; Mohan, S. Peak-to-average power ratio reduction in OFDM systems: A survey and taxonomy. IEEE Commun. Surv. Tutor. 2013, 15, 1567–1592. [Google Scholar] [CrossRef]
- Ochiai, H.; Imai, H. Performance of the deliberate clipping with adaptive symbol selection for strictly band-limited OFDM systems. IEEE J. Sel. Areas Commun. 2000, 18, 2270–2277. [Google Scholar] [CrossRef]
- Ochiai, H.; Imai, H. Performance analysis of deliberately clipped OFDM signals. IEEE Trans. Commun. 2002, 50, 89–101. [Google Scholar] [CrossRef]
- O’Shea, T.; Hoydis, J. An introduction to deep learning for the physical layer. IEEE Trans. Cogn. Commun. Netw. 2017, 3, 563–575. [Google Scholar] [CrossRef] [Green Version]
- Ye, H.; Li, G.Y.; Juang, B. Power of deep learning for channel estimation and signal detection in OFDM systems. IEEE Wireless Commun. Lett. 2018, 7, 114–117. [Google Scholar] [CrossRef]
- Samuel, N.; Diskin, T.; Wiesel, A. Deep MIMO detection. In Proceedings of the IEEE 18th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Sapporo, Japan, 3–6 July 2017. [Google Scholar] [CrossRef]
- Farsad, N.; Goldsmith, A. Detection algorithms for communication systems using deep learning. arXiv 2017, arXiv:1705.08044. [Google Scholar]
- Nachmani, E.; Be’ery, Y.Y.; Burshtein, D. Learning to decode linear codes using deep learning. In Proceedings of the 54th Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 27–30 September 2016. [Google Scholar] [CrossRef] [Green Version]
- Saxena, V.; Jaldén, J.; Bengtsson, M.; Tullberg, H. Deep Learning for Frame Error Probability Prediction in BICM-OFDM Systems. In Proceedings of the IEEE ICASSP, Calgary, AB, Canada, 15–20 April 2018. [Google Scholar] [CrossRef] [Green Version]
- Darsena, D.; Gelli, G.; Melito, F.; Verde, F.; Vitello, A. Impulse noise mitigation for MIMO-OFDM wireless networks with linear equalization. In Proceedings of the IEEE M&N, Naples, Italy, 7–8 October 2013. [Google Scholar] [CrossRef]
- Anoh, K.; Tanriover, C.; Adebisi, B.; Hammoudeh, M. A new approach to iterative clipping and filtering PAPR reduction scheme for OFDM systems. IEEE Access 2017, 6, 17533–17544. [Google Scholar] [CrossRef]
- Kim, D.; Stuber, G.L. Clipping noise mitigation for OFDM by decision-aided reconstruction. IEEE Commun. Lett. 1999, 3, 4–6. [Google Scholar] [CrossRef]
- Kim, K.; Park, H.; No, J.; Chung, H.; Shin, D. Clipping noise cancelation for OFDM systems using reliable observations based on compressed sensing. IEEE Trans. Broadcast. 2015, 61, 116–118. [Google Scholar] [CrossRef]
- Samuel, N.; Diskin, T.; Wiesel, A. Learning to detect. IEEE Trans. Signal Proc. 2019, 67, 2554–2564. [Google Scholar] [CrossRef] [Green Version]
- Darsena, D.; Gelli, G.; Paura, L.; Verde, F. Widely linear equalization and blind channel identification for interference-contaminated multicarrier systems. IEEE Trans. Signal Proc. 2005, 53, 1163–1177. [Google Scholar] [CrossRef] [Green Version]
- Darsena, D.; Gelli, G.; Paura, L.; Verde, F. A constrained maximum-SINR NBI-resistant receiver for OFDM systems. IEEE Trans. Signal Proc. 2007, 55, 3032–3047. [Google Scholar] [CrossRef]
- Wang, H.W.; Lin, D.W.; Sang, T.H. OFDM signal detection in doubly selective channels with blockwise whitening of residual intercarrier interference and noise. IEEE J. Sel. Areas Comm. 2012, 30, 684–694. [Google Scholar] [CrossRef]
- Lin, H.D.; Sang, T.H.; Chen, J.T. Low-cost perturbation-based equalizers for OFDMA mobile systems. IEICE Trans. Comm. 2012, 95, 3509–3518. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.; Ba, J. ADAM: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the 13th International Conference on Artificial Intelligence and Statistics (AISTATS), Sardinia, Italy, 13–15 May 2010. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI), Savannah, GA, USA, 2–4 November 2016. [Google Scholar]
- Yang, F.; Gao, J.; Liu, S.; Song, J. Clipping noise elimination for OFDM systems by compressed sensing with partially aware support. IEEE Trans. Broadast. 2017, 63, 103–110. [Google Scholar] [CrossRef]
- Yang, L.; Song, K.; Siu, Y.M. Iterative clipping noise recovery of OFDM signals based on compressed sensing. IEEE Trans. Broadcast. 2017, 63, 706–713. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sang, T.-H.; Xu, Y.-C. Clipping Noise Compensation with Neural Networks in OFDM Systems. Signals 2020, 1, 100-109. https://doi.org/10.3390/signals1010005
Sang T-H, Xu Y-C. Clipping Noise Compensation with Neural Networks in OFDM Systems. Signals. 2020; 1(1):100-109. https://doi.org/10.3390/signals1010005
Chicago/Turabian StyleSang, Tzu-Hsien, and You-Cheng Xu. 2020. "Clipping Noise Compensation with Neural Networks in OFDM Systems" Signals 1, no. 1: 100-109. https://doi.org/10.3390/signals1010005
APA StyleSang, T.-H., & Xu, Y.-C. (2020). Clipping Noise Compensation with Neural Networks in OFDM Systems. Signals, 1(1), 100-109. https://doi.org/10.3390/signals1010005





