Modeling Volatility Characteristics of Epileptic EEGs using GARCH Models

Abstract

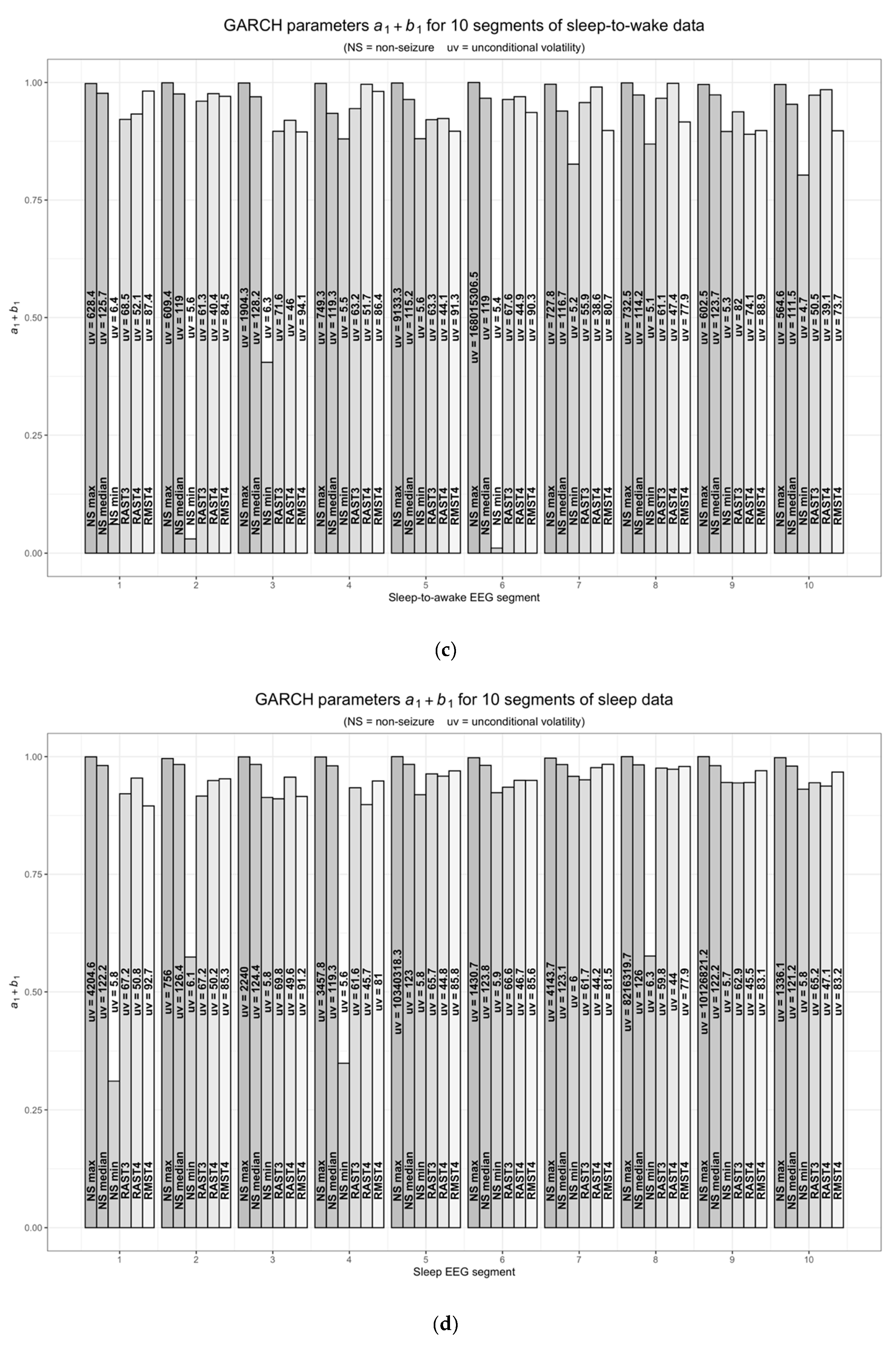
Objective: To determine if there was a difference in the volatility characteristics of seizure and non-seizure onset channels in the intracranial electroencephalogram (EEG) in a patient with temporal lobe epilepsy. Methods: The half-life of volatility for the different EEG channels was determined using Autoregressive Moving Average–Generalized Autoregressive Conditional Heteroscedasticity (ARMA–GARCH) models; confidence intervals were constructed using the delta method and an asymptotic method for comparing the half-lives. Results: Clinically determined seizure onsets occurred over strip electrodes named RAST (Right Anterior Subtemporal) and RMST (Right Mid Subtemporal), at locations 2, 3 and 4, on the strip electrodes. The half-lives of volatility for two of the three seizure channels, RAST3 and RAST4, were found to be significantly lower the rest of the channels for six one-minute EEG segments prior to seizure onset and nine one-minute EEG segments of an awake state. The half-lives of volatility for RAST3 and RAST4 were not significantly different to the non-seizure channels for ten one-minute segments of sleep and ten one-minute segments of sleep-to-awake states. The estimates for the half-lives were consistent for randomly selected one-minute EEG segments. Conclusions: The use of GARCH models may be a useful tool in determining hidden properties in epileptiform EEGs that may lead to better understanding of the seizure generating process.

1. Introduction

The visual examination of electroencephalograms (EEGs) is limited by potential subjectivity due to limited protocols and the inability to identify hidden patterns, characteristics or relationships in large amounts of data [1,2]. The introduction of quantitative methods in the analysis of EEGs attempt to overcome these limitations by introducing objective measures of EEG characteristics [1]. These methods give both the clinician and/or researcher access to the valuable information within the EEG concerning the dynamics of brain activity. Much of the quantitative research in epilepsy is based on the detection of changes (spikes, spike-waves, sharp waves, etc.,) in the properties of an EEG; the changes in the waveforms are associated with changes in behavioral and mental states. During an epileptic seizure, the EEG exhibits robust changes [3,4]. The amplitude of the EEG increases during an epileptic seizure due to episodic brief neuronal synchronous discharges; the seizure at onset may be seen in only a few EEG channels (local or partial seizure) or in all EEG channels (generalized seizure) [2]. The information obtained from EEGs using quantitative methods has been used in such areas as attempting to predict/anticipate the occurrence of seizures, attempting to detect the onset/occurrence of seizures, and in modeling seizure propagation/dynamics.

The EEG, like many physiological time series, is widely believed to be non-stationary due to its time-varying properties; the non-stationarity may arise from the fact that the observation time is shorter than the characteristic time scale of the EEG [3]. The non-stationarity of the EEG limits the use of classical time series analysis methods. However, early attempts at analyzing EEG signals in the time domain were based on a linear approach using autoregressive moving average (ARMA) modeling [5]. Even though the use of ARMA models in the analysis of EEG signals is limited because of the EEG’s time-varying properties, their usage contributed to the understanding of EEG signals [6]. Mormann et al. [7], citing studies by Rogowski et al., Salant et al., and Siegal et al., found changes in the autoregressive parameters seconds prior to the onset of a seizure as well as differences in characteristics between one-minute epochs prior to a seizure and control subjects. There are also studies on characterization of EEG time series using spectral and wavelet analysis [8,9,10,11,12,13,14].

Some EEG analyses have moved away from linear time series analysis methods and toward the use of non-linear time series analysis. Measures such as Lyapunov exponents, correlation dimension, correlation density, entropy, and dynamic similarity have been employed [15,16,17,18,19,20,21,22,23,24,25,26,27,28]. Additional techniques that have been used in quantitative EEG analysis either alone or combined with other methods include, but are not limited to, spatial-temporal modeling, wavelets, genetic algorithms, data mining, morphological filters, discriminant analysis, neural networks and support vector machines [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. Convolutional Neural Networks have also been used for feature classification and seizure detection [45,46,47,48]. Recent research has also focused on high-frequency oscillations (HFOs) in epileptic EEGs [45,48,49,50,51,52,53]

While the above listed methods have been used in EEG analysis, the use of GARCH models in characterizing volatility has not been explored. Conditional volatility models originated in finance with the ARCH (autoregressive conditional heteroscedastistic) model of Engle and the GARCH (generalized autoregressive conditional heteroscedastistic) model of Bollerslev [54,55]. These models and their extensions have been used to characterize the temporal behavior and clustering of volatility in financial markets. The use of these models to characterize the volatility of epileptiform EEG signals may be able to provide more insight into the seizure generating processes, may be used in identifying epileptogenic zones, and may have use in the prediction of seizures as well as aid in a diagnosis of epilepsy. In this study, volatility characteristics of epileptiform EEGs were examined for possible differences between seizure and non-seizure onset channels using GARCH models.

2. Methods

Data

The data used in this study were provided by the Department of Neurology at the University of Texas McGovern Medical School. Four epochs of intracranial EEG (awake, sleep, sleep to awake, and seizure) sampled at 200 Hz over various parts of the right hemisphere of a single individual’s brain were used in the analysis. The recordings were obtained from subdural grid and strip electrodes, placed directly over the brain surface through an operative procedure for the clinical investigation of temporal lobe epilepsy. The grids and strip electrodes were recorded from a total of sixty-six discrete channels over different brain regions. In the days following electrode placement, seizures were identified over contacts 2 and 3 on the strip electrode labeled RAST (Right Anterior Subtemporal) and over contact 4 on the strip electrode labeled RMST (Right Mid Subtemporal). The awake, sleep, and sleep to awake segments were approximately 10 min in length, with waking occurring in the sleep to wake signal at approximately 8 min; the segment with the seizure was approximately 15.5 min in length, with six minutes of pre-seizure data, 2.5 min of seizure data and seven minutes of post-seizure data. The onset of seizure was determined by conventional visual analysis by a clinical neurologist. All four segments were referenced to an external zero voltage reference. The data used in the analyses were de-identified.

3. Conditional Volatility Models

3.1. Autoregressive Moving Average Models

One of the traditional models used in modeling the dynamics of a time series $Y_t=\left\{y_1,y_2,\dots ,y_T\right\}$ is the Autoregressive Moving Average (ARMA) process. ARMA(p,q) processes are stationary. For stationary processes, the characteristics of the distribution for a sequence of $n$ observations are not dependent on the time origin [56]. A less restrictive requirement is that of a weakly stationary process, where, for a time series $Y_t=\left\{y_1,y_2,\dots ,y_T\right\}$, $E\left(Y_t\right)=\mu$ for all $t$, $Var\left(Y_t\right)={\sigma }_Y^2$ for all $t$, and $Corr\left(Y_t,Y_{t-s}\right)=\rho \left(s\right)$ for $t\ge s$, where $\rho (\cdot )$ is the autocorrelation function of a time series; thus, for a weakly stationary time series, the mean and variance are constant and the correlation between observations is only dependent on the time between the observations [56]. The property of weak stationarity is often employed in the analysis of time series [56]. Processes of the form under commonly used conditions

$$Y_t={\displaystyle \sum _{i=1}^p{\alpha }_i{Y}_{t-i}}+{\displaystyle \sum _{j=1}^q{\beta }_j{\epsilon }_{j-t}}+{\epsilon }_t,$$

(1)

where ${\epsilon }_t$ is a white noise sequence with variance ${\sigma }_{\epsilon }^2$ for all $t$ (for time series with non-zero mean, a mean term can be added to the model) [56,57].

If $p=0$ or $q=0$, then the processes are described as a moving average process of order q (MA(q)) or an autoregressive process of order $p$ (AR(p)) respectively. If a time series is non-stationary, Autoregressive Integrated Moving Average (ARIMA(p,d,q)) models may be used, where the dth difference of the time series is an ARMA(p,q) process [56]. The parameters of an ARMA model are useful in summarizing a time series, while the modeling may not reveal much information concerning the data generating process; however, ARMA processes are useful in forecasting [57].

3.2. Generalized Autoregressive Conditional Heteroscedasticity Models

One limitation of an ARMA model is the assumption of constant conditional variance ($Var\left(Y_t|F_{t-1}\right)={\sigma }_Y^2$ where $F_{t-1}$ is the set of information available at time $t-1$, mathematically, a σ-field generated from {Y_t-1, Y_t-2,…}), and, thus, is not satisfactory for use in modeling time series with time varying variance [56]. Variance that changes of over time may affect the inferential validity and efficiency of the parameters of an ARMA model [58]. Models that account conditionally for non-constant volatility (non-constant conditional variance) allow for better predictions of (local) variability and better prediction intervals [59]. Time series with non-constant volatility are common in finance, and the most common family of volatility models were developed to model financial time series; their use in biomedical research has been rarely utilized [60,61,62].

The Autoregressive Conditional Heteroscedasticity (ARCH) model was developed by Engle and generalized (GARCH) by Bollerslev [54,55]. The GARCH(p,q) model for a time series $Y_t=\left\{y_1,y_2,\dots ,y_T\right\}$ is

$$\begin{array}{l}{Y}_t=E_{t-1}\left[Y_t\right]+{\epsilon }_t\\ {\epsilon }_t=z_t{\sigma }_t\\ {\sigma }_t^2=a_0+{\displaystyle \sum _{i=1}^p{a}_i{\epsilon }_{t-i}^2+{\displaystyle \sum _{j=1}^q{b}_i}}{\sigma }_{t-j}^2\end{array}$$

(2)

where $E_{t-1}\left[Y_t\right]$ is the expectation conditional on information available at time $t-1$, $z_t$ are i.i.d. zero mean random variables with unit variance, $a_0>0$, $a_i,b_i\ge 0$ and

$${\displaystyle \sum _{i=1}^{\max \left(p,q\right)}\left(a_i+b_i\right)<1}$$

(3)

[63].

These constraints ensure positive and finite unconditional variance for ${\epsilon }_t$, with ${\displaystyle \sum _{i=1}^{\max \left(p,q\right)}\left(a_i+b_i\right)<1}$ a necessary and sufficient condition for weak stationarity. A less restrictive necessary and sufficient condition for strict stationarity is that $E\left(\log \left(a_1{\sigma }_t^2+b_1\right)\right)<0$, with certain conditions on the $z_t$. This allows the sum $a_1+b_1$ to equal or exceed one [55,64,65,66]. The ${\epsilon }_t$, often referred to as ‘shocks,’ are serially uncorrelated, but dependent. The $a_i$ and $b_i$ in the conditional variance equation are the ARCH and GARCH parameters respectively, with $E\left({\epsilon }_t\right)=0$ and the unconditional variance of ${\epsilon }_t$ is

$$E\left({\epsilon }_t^2\right)=\frac{a_0}{1-\left({\displaystyle \sum _{i=1}^p{a}_i+{\displaystyle \sum _{j=1}^q{b}_i}}\right)},$$

(4)

which will be positive due to the constraints. A GARCH model with $q=0$ is an ARCH(p) model and in order to identify the parameters, $A\left(\epsilon \right)={\displaystyle \sum _{i=1}^p{a}_i{\epsilon }^i}$ and $B\left(\epsilon \right)=1-{\displaystyle \sum _{i=1}^p{b}_i{\epsilon }^i}$ are co-primes [67].

If the conditional variance equation follows an ARCH(1) process, ${\sigma }_t^2=a_0+a_1{\epsilon }_{t-1}^2$, large values of ${\epsilon }_{t-1}$ result in a larger deviation from $E_{t-1}\left({\epsilon }_t\right)=0$, and the conditional variance of ${\epsilon }_t$ is larger as a result. This volatility will propagate since a large deviation of ${\epsilon }_t$ makes ${\sigma }_{t+1}^2$ and ${\epsilon }_{t+1}^2$ large (similarly for small values of ${\epsilon }_t$). Thus, the volatility will persist, but will eventually revert to the unconditional variance since $a_1<1$. For ARCH(p) processes, large past shocks ${\left\{{\epsilon }_{t-i}^2\right\}}_{i=1}^p$ lead to a large conditional variance for and a large value of ${\epsilon }_t$. Thus, the probability of a large shock following a large shock is greater than the probability of small shock. This leads to the volatility clustering often seen in financial time series [56,68].

The development of GARCH(p,q) models were motivated by the shortcomings in the ARCH(p) models and provide more flexibility than ARCH(p) models. Some weaknesses of an ARCH(p) model are that the order p may be high (leading to the need for estimating many parameters), that it is likely to overpredict the volatility, that it does not capture the excess kurtosis seen in financial time series, and that it assumes that positive and negative shocks produce the same effect on volatility [68]. ARCH(p) models also have high volatility in short bursts, or short volatility persistence, while GARCH($p,q$) models allow for more persistent volatility [56]. GARCH processes also tend to have heavy tails and GARCH models also tend to be more parsimonious, and the simplest form, GARCH($1,1$), has been successful in predicting conditional volatility [56,69]. GARCH models may be used to model the innovations of ARMA models (ARMA–GARCH) as well.

For a GARCH($1,1$) model, values of $b_1$ closer to 1 produce a high correlation between ${\sigma }_t^2$ and ${\sigma }_{t-1}^2$ which allows for longer persistence of volatility than an ARCH(1) model [68]. The speed with which the process reverts to the unconditional variance (persistence) is governed by the magnitude of $a_1+b_1$ [63]. The half-life (HL) of a volatility shock, a measure of the length of time it takes for a shock to decrease by one-half, is given by $HL=\ln \left(0.5\right)/\ln (a_1+b_1)$, and as $a_1+b_1$ approaches 1, the larger the half-life [63]. Models for which $a_1<b_1$ also imply longer volatility persistence [56]. These results can be extended to higher order GARCH($p,q$) models [63].

4. Confidence Intervals for Half-Life (HL)

To construct conventional two-sided confidence intervals, the standard errors for the half-life can be approximated using the delta method and using the large sample asymptotic properties of the estimated parameters. Using the delta method, the variance of a differentiable function of random variables, $f\left(X\right)$, where $X=\left(X_1,X_2,\dots ,X_n\right)$, can be approximated as

$$Var\left(f\left(X\right)\right)={{\displaystyle \sum _{i=1}^n{f}_i\prime \left(\theta \right)}}^{2}Var\left(X_i\right)+2{\displaystyle \sum _{i>j}{f}_i\prime \left(\theta \right)f_j\prime \left(\theta \right)Cov\left(X_i,X_j\right)},$$

(5)

where

$$\theta =\left(E\left(X_1\right),E\left(X_2\right),\dots ,E\left(X_n\right)\right),$$

and

$$f_i\prime \left(\theta \right)=\frac{\partial }{\partial X_i}f\left(x\right){|}_{x_1={\theta }_1,\dots ,x_n={\theta }_n}$$

Using the equation for half-life, $HL=\ln \left(0.5\right)/\ln \left(a_1+b_1\right)$, for a GARCH (1,1) model, taking partial derivatives and substituting into the variance equation above yields the following equation for the standard error:

$$\sigma \left(HL\right)=\frac{\ln \left(0.5\right)}{\left(a_1+b_1\right){\left[\ln \left(a_1+b_1\right)\right]}^2}{\left[Var\left(a_1\right)+Var\left(b_1\right)+2Cov\left(a_1,b_1\right)\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}.$$

(6)

Based on large sample asymptotics, the confidence interval for the half-life can be constructed as:

$$H{L}_{est}\pm 1.96\ast \sigma \left(H{L}_{est}\right).$$

(7)

Additionally, using the fact that the variance of the sum of random variables is the sum of the variances plus the sums of twice the respective covariances, confidence intervals can also be constructed for the sum of the coefficients. The 95% confidence intervals for large sample sizes can be constructed as:

$$Z\pm 1.96\ast \sigma (Z).$$

(8)

where Z is the sum of n random variables. The estimates for the upper and lower confidence limits can then be transformed using the half-life formula since it is a monotonic function in order to obtain a confidence interval for the half-life.

5. Analysis

All four datasets were divided into one-minute (12,000 values) segments for analysis. This resulted in 15 segments for the seizure data, 10 segments for the sleep and sleep to awake data, and 9 segments for the awake data. Of the 15 segments for the seizure data, there were six complete segments preceding seizure onset, one segment containing seizure onset, one segment of seizure, one segment containing the transition from ictal to post-seizure, and six post-seizure segments. The sleep-to-awake data had seven segments of sleep data, one segment containing the transition from sleep to awake and two segments of awake data. For each segment, ARMA–GARCH models were estimated for all 66 channels using MATLAB. The estimated parameters from the models were used to estimate unconditional volatility and half-lives. Confidence intervals for half-lives based on the GARCH coefficients were constructed. Additionally, models were estimated for one-minute segments with randomly selected starting points to see if the models were dependent on the particular segments.

6. Results

The onset of the seizure was identified at the three channels RAST3, RAST4 and RMST4. Based on these three channels, the ARMA(2,2)–GARCH(1,1) models were estimated for all channels. Using Equations (1) and (2), these models take the following form where $Y_{i,t}$ is the value of EEG signal i at time t:

$$Y_{i,t}=c_1{Y}_{i,t-1}+c_2{Y}_{i,t-2}+d_1{ϵ}_{i,t-1}+d_2{ϵ}_{i,t-2}+{ϵ}_{i,t},\left(\mathrm{ARMA}\right(2,2\left)\right)$$

where ${ϵ}_{i,t}=z_{i,t}{ϵ}_{i,t}$ and

$${\sigma }_{i,t}^2=a_0+a_1{ϵ}_{i,t-1}^2+b_1{\sigma }_{i,t-1}^2\left(\mathrm{GARCH}\right(1,1\left)\right)$$

Models were estimated for all segments of the seizure data. The models based on the seizure and post-seizure resulted in integrated models; thus, results only for the pre-seizure data are included. For the other three datasets, models were estimated for all segments.

The models used to estimate and examine volatility were ARMA(2,2)-GARCH(1,1) models. Since the EEG is believed to be non-stationary, one-minute (12,000 points) segments were selected and assumed to be (weakly) stationary. This particular model was selected for this analysis based on fitting an ARMA(2,2) model to the data, and checking the innovations (errors) for heteroscedasticity using an Ljung–Box Q test, and examining the autocorrelation and partial autocorrelation plots for GARCH characteristics, namely serial correlation in the squared innovations. These models were initially fit to the three seizure channels (RAST3, RAST4 and RMST4) and the standardized residuals were tested using the Ljung–Box Q test.

In addition to testing the standardized residuals, the fit of the GARCH(1,1) model to innovations of the ARMA(2,2) model, the estimated unconditional volatility from the GARCH coefficients and the variance of the innovations are listed in Figure 1a–d (all coefficients for models are included in supplementary Table S1a–d). For the three seizure channels, unconditional volatility estimates were within two percent of the innovation variance, with the exception of segment 3 of RAST3, which showed an approximate seven percent difference; this particular channel also had the highest estimated GARCH coefficient (0.7485) and coefficient sum (0.8763). The data for the other signals showed similar results with RAST3 awake segment 7, sleep to awake segment 3, sleep segments 1 and 3, RAST4 awake segment 5 and RMST4 sleep segments 1, 3, and 5 showing greater than five percent difference. For the other channels, three from the seizure data, fifteen from the awake data, twenty-two from the sleep to awake data and ninety from the sleep data had a greater than five percent difference between unconditional volatility and innovation variance.

6.1. GARCH Models

The estimated GARCH coefficients and unconditional volatilities for RAST3, RAST4 and RMST4 are listed in Table 1a–d, along with the minimum, median and maximum of the coefficients from the non-seizure channels. Table 1a shows the results for six one-minute segments preceding the onset of seizure. RAST3 and RAST4 show higher ARCH and lower GARCH parameters across all segments than the majority of the other signals; the sum of the ARCH and GARCH parameters are also lower than the majority of the other channels. Estimates for RMST4 do not appear to be different than the non-seizure channels. The unconditional volatility for all three channels do not show as marked a difference; however, each are less than the median of the unconditional volatility of all other signals for each segment. Similar results can be seen for the awake data (Table 1b). As with the seizure data, RAST3 and RAST4 show higher ARCH and lower GARCH coefficients than RMST4 and all of the other channels. The unconditional volatility for each of the three channels is also lower than the median for the other channels. The sleep to awake and sleep data (Table 1c,d) do not show as large of differences as the seizure and awake data. The estimated ARCH and GARCH coefficients of the sleep to awake and sleep data for RAST3 and RAST4 are higher (lower) than the median for the non-seizure channels. The unconditional volatility for the three channels are also lower than the median for the non-seizure channels and are similar to the those found in the seizure and awake data.

For the seizure data, the estimates across the six segments for the seizure channels for RAST3 show the most variation. RAST3 ranges from 0.4449 to 0.7485 for the GARCH coefficient, while the estimates for the ARCH coefficient only range from 0.1145 to 0.1516; the sum of the coefficients has a maximum of 0.8763 in the third segment, while the other sums are relatively similar. The unconditional volatility has a range of 79.1 to 96.5. The variation of the estimates for RAST4 and RMST4 do not show as large of differences as RAST3. The coefficients for RAST4 are similar across all segments; however, the unconditional volatility ranges from 62.4 to 80.9. RMST4 shows similar estimates across the first five segments, with noticeable differences in the sixth segment for the GARCH estimate. All three channels show jumps in unconditional volatility from the fifth to the sixth segment.

The estimates across the nine segments of the awake data do not show as much variation. Segments 5 and 7 for RAST3 and segment 5 for RAST4 have higher GARCH coefficients and higher coefficient sums than the estimates for the other segments. The unconditional variation is similar across all segments for all three channels. For the sleep to awake data, the estimates are similar across the segments with the exception of the unconditional volatility for segment 9 (first awake only segment) of RAST3 and RAST4. All three channels have their minimum unconditional volatility in the last segment. The sleep data estimates are similar across all segments.

6.2. Half-life and Confidence Intervals

To examine the volatility across all channels for the different segments of each dataset, the volatility half-life was calculated for each model along with 95% confidence intervals using the delta and asymptotic methods outlined above (Equations (6) and (7)). Only models with both significant ARCH and GARCH coefficients were used, and confidence intervals with negative confidence limits were used.

There were noticeable differences between the seizure and non-seizure channels in the pre-seizure and awake datasets (Table 1a,b and Table 2a,b). The half-life estimates for RAST3 and RAST4 were between one and two for all but three segments of the both datasets, indicating a volatility persisting half as long as most other channels, and at least four times shorter than at least half of all other channels. In examining the CIs for these two channels, they overlap with at most five of the CIs of the non-seizure channels using the delta method (Table 2a,b) and at most one using the asymptotic method (except for the segments where the half-life was greater than 2). For RMST4, the half-life for the segments varied, ranging from 6.33 to 268.82, with more than half below 6.50; the CIs for these overlapped more than half of the CIs for the non-seizure channels for all of the awake segments and approximately half for the pre-seizure data (for both methods). The CIs for RMST4 only overlapped the CIs of RAST3 and RAST4 in segment 6 of the pre-seizure data using the delta method.

For the sleep and sleep to awake data, the half-life estimates are higher than the pre-seizure and awake data for all channels (Table 2c,d). The half-life CIs for RAST3 and RAST4 overlap a greater number of non-seizure CIs in both datasets; however, in the sleep to awake data, both channels overlap approximately half of the non-seizure CIs. The half-life values appear to be highest in the sleep data relative to the other three datasets. For the non-seizure channels, the median half-life is higher for all segments in both datasets, with the exception of the last segment of the sleep to awake data (Table 2d). This particular segment is the second segment of awake data in the sleep to awake segment and has a median half-life of 14.58, which is similar to the values for the segments of the awake data. Similar behavior is seen for RMST4, which has similar half-life values to the awake data, but not in RAST3 and RAST4, which both have half-life values greater than the median.

7. Random Starting Points

To assess whether the estimated models were dependent on the particular segment, 100 models based on randomly selected starting points within each dataset were estimated for all 66 channels and sample statistics calculated (

Table 3. Summary of half-life estimates based on random starting points.

Signal	Channel	Mean (s.d.)	Min	Q1	Med	Q3	Max
Seizure	RAST3	2.11 (1.31)	1.18	1.45	1.70	1.89	5.56
	RAST4	1.86 (0.68)	1.44	1.59	1.75	1.91	5.64
	RMST4	22.49 (52.72)	6.28	6.39	6.45	8.11	276.91
	Others	38.33 (73.79)	0.16	6.44	17.15	42.05	2310.14
Awake	RAST3	2.27 (1.49)	1.15	1.46	1.71	1.91	5.70
	RAST4	2.61 (1.89)	1.29	1.43	1.56	2.17	6.62
	RMST4	20.99 (20.92	6.17	6.51	8.51	36.66	97.28
	Other	26.53 (83.71)	0.21	6.4	10.55	28.06	3465.39
Sleep	RAST3	12.92 (6.06)	5.20	9.19	11.62	15.61	50.25
	RAST4	15.76 (6.96)	5.95	10.06	14.43	19.04	33.30
	RMST4	18.39 (8.15)	5.84	11.72	17.8	23.03	36.52
	Other	56.57 (188.78)	0.16	28.29	37.32	49.16	6931.13
Sleep/Awake	RAST3	22.20 (49.86)	5.35	9.05	13.93	20.34	494.76
	RAST4	52.46 (114.55)	5.10	9.27	14.36	45.83	692.80
	RMST4	14.99 (16.58)	5.87	6.38	6.44	12.24	74.99
	Other	41.48 (152.17)	0.16	6.48	20.28	42.97	6931.13

). The average half-life for RAST3 (2.25 vs. 2.11) and RAST4 (1.75 vs. 1.86) were similar to the average of the half-life from the six pre-seizure segments. The third quartile score for each signal was also less than two; all half-life estimates for both channels were lower than 75% of the estimates for the non-seizure channels. RMST4 had higher estimates than the other two channels and at least 75% of the scores fell below the median for non-seizure channels. Similar results can be seen for the awake data. For the sleep to awake and sleep data, the estimates are lower on average, but without as large or noticeable differences as seen in the pre-seizure and awake data.

8. Discussion

In examining the volatility of EEG signals, two of the three channels where seizures originated (RAST3 and RAST4) had shorter volatility half-life relative to all other channels in the time leading up to the seizure (6 min) and during an awake state. During a sleep state and a sleep-to-awake state, the volatility half-life for the seizure channels were lower for most segments examined, but the respective confidence intervals (constructed from both methods) overlapped a larger proportion of non-seizure confidence intervals. The volatility also tended to persist longer in the sleep state than in the pre-seizure and awake states, but the half-life varied more than in the pre-seizure and awake data. The volatility half-life was similar to the non-seizure channels, especially in the awake data; however, for the sleep data, the half-lives were lower for half the segments.

For all of the models, the GARCH coefficient was larger than the ARCH coefficient, indicating larger volatility persistence. However, for some of models, the magnitudes of the coefficients could be an issue. While the coefficients were significant at the 5% level, some of the models had GARCH coefficients greater than 0.95 and ARCH coefficients smaller 0.01. The small ARCH coefficients make the effect of the past innovations negligible, which is an issue since GARCH models must have at least one non-zero ARCH parameter for the GARCH parameters to be identified. Additionally, the sum of the coefficients was greater than 0.99 (but less than 1.00), which is very close to being an integrated model. These extreme cases may indicate structural changes occurring in the signals during the one-minute interval, and a more dynamic model may be more appropriate.

The estimated confidence intervals for RAST3 and RAST4 constructed by both methods were similar for all datasets; however, the confidence limits were more in agreement when the half-life estimates were smaller (<10). The CIs for RMST4 were wider for similar half-life estimates, indicating higher variability in the RMST4 estimates. The non-seizure channels also had higher variability, leading to exclusion of some CIs because of negative confidence limits. It appears larger half-life estimates yield much wider CIs. This may be due to a higher covariance between the ARCH and GARCH parameters as their difference grows and/or their sum approaches unity.

The models estimated were based on one-minute segments of data, assuming that they were stationary, which may not be the case. However, in the cases of RAST3 and RAST4, it appears that the models were consistent across different segments for the pre-seizure and awake data, both in the segments used in the analyses and when randomly selecting starting points. This may indicate that these signals are ARMA–GARCH processes for these particular states. The differences in the estimates for the sleep and sleep to awake data may also be indicative of an underlying ARMA–GARCH structure, but they may have different lag structures. The non-seizure signals may also be ARMA–GARCH processes with different lag structures, especially the cases where the ARCH parameter was less than 0.01. All of the signals may also show different volatility properties with shorter segments, indicating possible regime changes.

The volatility half-life as a characteristic of epileptic EEG channels may be related to high frequency oscillations (HFOs), which may be possible characteristics in epileptic EEG channels ([48]. HFOs and their relationship to seizure onset zones have been studied using machine learning and deep learning methods [48,49,50,52,70]. These studies have found various accuracy, sensitivity and specificity in identifying under different conditions, but do pose another potential tool in studying EEGs.

9. Conclusions

To conclude, the use of ARMA–GARCH models to explore the volatility in the human EEG shows promise as a method of identifying otherwise unobservable properties in the signals. In particular, we suggest that identification of volatility properties may help in qualifying seizure dynamics.

This study modeled the innovations as GARCH(1,1) processes, which may be too simplistic—other types of GARCH models may be appropriate, possibly an Integrated GARCH (IGARCH) model, or one that takes leverage effects into account. Multivariate ARMA–GARCH models may also be considered since the signals may be correlated. Other models for estimating volatility may also be used, such as stochastic volatility models.