Fitting Methods for Empirical Models of Open-Pore Foams

Abstract

Sound-absorbing materials in the frequency range can be characterised upon the basis of their propagation constant and characteristic impedance. For a number of years, there have been empirical models, such as that of Delany and Bazley, which adjust these parameters to the flow resistivity and frequency, defining fitting coefficients. Based on the Delany–Bazley model, further adjustments of these coefficients have been proposed to improve the prediction of specific materials. The most commonly used adjustments are based on a quadratic error function for the normal incidence sound absorption coefficient or the surface impedance. Three adjustment methods are displayed in this paper to obtain new open-pore foam coefficients. The propagation constant and characteristic impedance measurements are adjusted, with different error functions and minimisation algorithms. New and improved models are obtained upon the basis of these three methods. The results obtained display satisfactory adjustments of all the material variables.

1. Introduction

Sound-absorbing materials in the frequency range can be characterised by the complex wave number k = G/j, where G is the sound propagation constant and characteristic impedance Zc. The most common parameter obtained from the two of them is the normal incidence absorption coefficient.

A wide range of models exist to predict the complex wave number kc (or the propagation constant G) and the characteristic impedance Zc. A classical model is presented in the paper by Delany and Bazley [1]. It adjusts the characteristic impedance and propagation coefficient values. They are represented by simple power-law functions that depend on the frequency and flow resistivity. These empirical equations have been constantly cited since the 1970s. For example, materials of similar flow resistivity are compared, and the Delany–Bazley model is used in Kino and Ueno [2]. They are used with sustainable sound absorbers in Oldham et al. [3]. A theoretical and experimental investigation of the coconut coir material is performed and measurements with the data obtained by the Delany–Bazley model are compared in Bhingare and Prakash [4]. The equations presented by Delany and Bazley also appear in annex B of the EN-12354-6:2003 standard for fibrous materials [5].

The Delany–Bazley model is simple and relies solely on the flow resistance. This parameter can be measured by the ISO 9053-1:2020 [6] and ISO 9053-2:2018 [7] standards and ASTM C522-03 [8], or with indirect methods such as those of Ingard and Dear [9] and Dragonetti et al. [10]. A comparison of these measurement procedures can be found in Del Rey et al. [11].

There are models that improve the prediction of the characteristic impedance and propagation coefficient. Attenborough [12] displays clear improvements by developing a model that predicts the acoustic characteristics of rigid fibrous absorbers upon the basis of five parameters. These parameters are porosity ϕ, flow resistivity σ, tortuosity α∞, steady flow shape factor s and dynamic shape factor n. This paper compares the new model with that of Delany and Bazley. Based on Attenborough’s paper, a series of models incorporating porosity and other parameters have appeared. These modifications are also made in Allard and Champoux [13] and compared with Delany and Bazley. Along these lines appears the Johnson–Champoux–Allard (JCA) model, based on the papers by Johnson et al. [14] and Champoux and Allard [15]. This model is extended by the paper by Lafarge et al. [16] and given the name of the JCAL model. There are six parameters involved in the calculation: the open porosity ϕ, the static air flow resistivity σ, the high frequency limit of the tortuosity α∞, the viscous characteristic length Λ, the thermal characteristic length Λ′ and the static thermal permeability k′₀. The drawback of these models is the need for six parameters. Several of them are not easy to obtain.

The Delany–Bazley model is also modified in other papers in different ways. The most common one is the use of the same equations, re-adjusting their coefficients. A modification of the Delany–Bazley model is proposed in Miki (1990) [17]. Other coefficients for open-pore foams are obtained in Dunn and Davern [18]. This paper also appears in annex B of the EN-12354-6:2020 standard [5]. Papers in which the coefficients are adjusted for specific materials can be found. All kinds of materials have been adjusted: synthetic fibres, vegetable fibres, animal fibres, nonwoven, different foams, etc. An adjustment for polyester fibre can be found in Garai and Pompoli [19]. Another paper based on the recycling of plastic bottles is that of Del Rey et al. [20]. More recently, another work can be found in Pelegrinis et al. [21], in which it is compared with Miki’s model, among others. In this case, the aim is to adjust the flow resistivity with an error function based on the normal incidence absorption coefficient.

Nonwoven materials appear in Hurrell et al. [22]. The Miki model, among others, is used and surface impedance adjustments are made with the MATLAB R2024b ‘fminsearchbnd minimisation subroutine [23]. The models of Delany and Bazley, Garay and Pompoli, Miki and Allard and Champoux are compared for non-woven fabric in Periyasamy [24].

The adjustment for coconut fibre can be found in Ramis et al. [25]. An adjustment of the natural jute is presented in Bansod and Mohanty [26], based on the model of Garai and Pompoli et al. A model for Kenaf fibre can be found in Ramis et al. [27]. Another model for esparto grass fibre can be found in Arenas et al. [28]. Sugarcane bagasse wastes fibres materials are presented in Haghighat et al. [29]. Sheep wool with blended recycled polyester can be found in Del Rey et al. [30]. Materials that are a mixture of sheep wool and soy protein appear in [31]. Different empirical models such as those listed above are reviewed and their degree of adjustment is studied in Oliva and Hongisto [32]. In Dunne et al. [33] an airflow resistivity database can be found and different empirical models are reviewed. The latter paper cites Dunne et al. [34], in which different comparisons of material adjustments are made. Dunn and Davern, among others, is used to characterise low pore density open-cell foams in Sachan and Ramamoorthy [35].

The obtaining of new coefficients is not the only modification of the Delany-Bazley model. A conversion to logarithms of the functions is performed and they are adjusted for poroelastic foam in Kessissoglou [36]. The Delany–Bazley and Miki models are improved in Komatsu [37], re-adjusting the models for glass rock and rock wool and performing a transformation with logarithmic functions. There are also papers with other adjustments to the JCA model. The machine learning approach is used to predict the Johnson–Champoux–Allard (JCA) parameters of a fibrous porous material in Yi et al. [38]. Adjustments can be found with the JCA model for both the normal incidence absorption coefficient and the transmission loss for palmyra palm fruit fibre composites in Chanlert et al. [39]. The JCA model and different kinds of adjustments also appear in Cai et al. [40]. Waste corn husk fibres as a sustainable material are investigated in Fattahi et al. [41]. The Attenborough and JCA models are used and compared with experimental measurements. The coefficients of the Dunn–Davern model are also optimised. The latter continue to be methods that entail directly or inversely obtaining the parameters of the JCA model.

We should also highlight the paper by Dunne [42], in which two adjustment methods are proposed. The first method is based on the airflow resistivity modified by Delany and Bazley, extending it to different kinds of materials. The second method performs a dimensional analysis by introducing a new parameter that depends on the fibre density, the thickness of the absorber, the bulk density, the frequency and the fibre diameter. The adjustments are made by means of the ANOVA analysis of variance of the functions, based on the sound absorption coefficient. Dunne could be considered to have made the last possible modification of the Delany–Bazley equations by acting on the frequency-dependent parameter. This second method is compatible with approaches such as that of the Bies–Hansen equation [43] and Garai and Pompoli [19], which relates a material’s airflow resistivity to its fibre diameter and bulk density. Equations for the flow resistivity based on these parameters are proposed in Pelegrinis et al. [21].

Recent papers such as the one by Santhanam and Subramanian [44] can also be found, in which sustainable polymer acoustic composites from waste cotton, coffee husk and sawdust for functional applications and their sound absorption properties are studied. In this case, the material is not modelled. Another example is Putra et al. [45], with pineapple-leaf fibres. Also is example Iannace et al. [46]. Airflow resistivity measurements could be proposed and adjusted to an empirical model in both works. This also occurs in Maderuelo-Sanz and Meneses-Rodríguez [47] where the flow resistivity has also been measured.

This paper is based on the original Delany–Bazley model and different open-pore foams are adjusted to obtain new coefficients in accordance with their flow resistivity. The innovation of the adjustment lies in the fact that, instead of using the normal incidence absorption coefficient or the surface impedance, error functions are constructed with measurements of the propagation constant G and the specific impedance Zc. The value of Г and Zc can be obtained with the two-thickness method, in accordance with ISO 10534-2:2023 [48] in Annex F. Improved predictions can thus be achieved. Moreover, three kinds of adjustments are used; the first adjustment is based on the Matlab “fminsearch” function [23], the second one is based on the construction of a genetic algorithm stemming from genetic algorithms (Matlab’s “ga” function [49]) and the third one is based on the least-squares method. The results of each adjustment and the associated error are shown.

2. Measurement

In order to adjust different porous materials to the empirical model, data on their airflow resistivity, their characteristic impedance, Zc, and their propagation constant Gamma are required.

The airflow resistivity is measured in a device built in the laboratory. This device is described in Del Rey et al. [11]. The apparatus consists of a cylindrical, polymethyl methacrylate (PMMA) tube 40 mm in diameter, 5 mm wall thickness and 169 cm in length. One end of the tube is equipped with a Beyma CP800TI high frequency compression driver with a 49 mm throat diameter, which permits emissions without considerable distortion at 100 Hz. The other end is closed, with a rigid, highly sound-reflective termination. The distance between the first microphone and the rigid termination was 84.5 cm. This value was chosen to be one-quarter wavelength at approximately 100 Hz. The two microphones used are 1/2 inch and mounted flush to the tube wall.

To determine the characteristic impedance Zc and the propagation constant G, annex F of the UNE-EN ISO 10534-2:2024 standard [48] is used. The surface impedance is measured with a sample of thickness d, Z₁, and the surface impedance with a sample of thickness 2d, Z₂. By applying Annex F of the standard, the propagation constant value G and the characteristic impedance Zc are obtained.

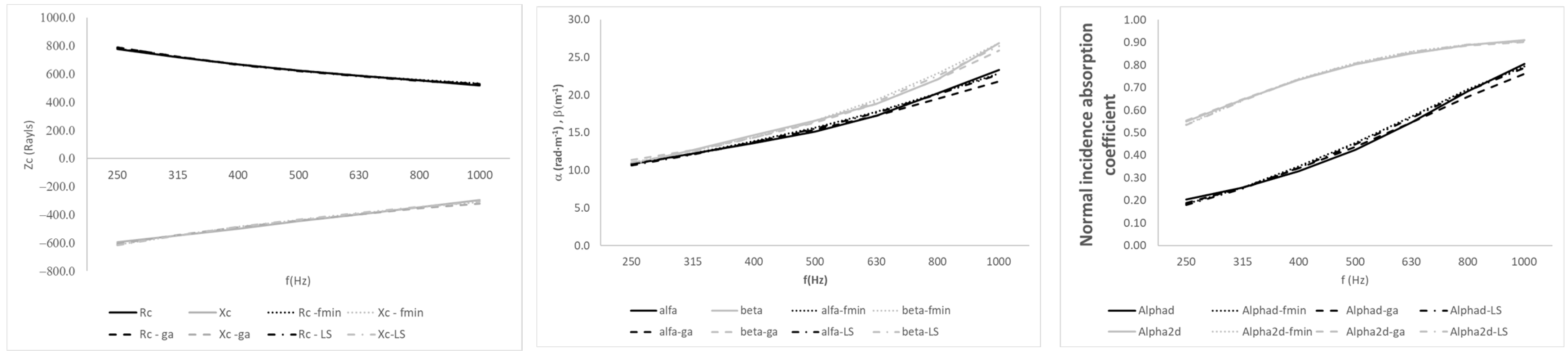
The different foams to be adjusted, with the airflow resistivity measurements obtained, are shown below in table format. Samples of open-pore foam, melamine foam (M1), polyurethane foam (M2, M3) and recycled foam (M4, M5, M6, M7) are chosen.

Table 1. Materials analysed.

Material		Density (kg/m3)	Thickness (mm)	Airflow Resistivity (kNs/m4)
M1: Melamine foam 4 cm		9.4	39.1	18.4
M2: Polyurethane foam 2.5 cm		26.4	25.0	3.8
M3: Polyurethane foam 4 cm		21.7	40.5	3.9
M4: Recycled foam 3 cm		59.7	31.6	10.8
M5: Recycled foam 2 cm		108.1	20.0	17.7
M6: Recycled foam 2 cm		106.0	20.0	21.0
M7: Recycled foam 3 cm		85.5	30.0	11.3
M8: Rockwool 2.7 cm		89.5	27.4	42.6

shows the materials studied, with the density, thickness and airflow resistivity values. Additionally, a sample of rockwool (M8) is included as a control material.

3. New Empirical Models

The construction of the models is based on the Delany–Bazley equations [1], which are as follows:

$$z_c=\rho c\left(1+c_1{\chi }^{-c_2}-j{c}_3{\chi }^{-c_4}\right)=R_c+j{X}_c$$

(1)

$$\mathsf{\Gamma }={\displaystyle \frac{\omega }{c}}\left(c_5{\chi }^{-c_6}+j{(1+c}_7{\chi }^{-c_8}\right))=\alpha +j\beta$$

(2)

where $z_c$ is the characteristic wave impedance, $\mathsf{\Gamma }$ is the propagation constant of the sound, σ is the airflow resistivity, $\rho$ is the air density, $c$ is the speed of the sound, $\omega$ is the angular frequency ($\omega =2\pi f$), $f$ is the frequency and $\chi ={\displaystyle \frac{\rho f}{\sigma }}$ is a dimensionless parameter.

From (1) and (2) we obtain:

$$\begin{gathered} R_c=\rho c\left(1+c_1{\chi }^{-c_2}\right) \\ {X}_c=\rho c\left(-c_3{\chi }^{-c_4}\right) \\ \alpha ={\displaystyle \frac{\omega }{c}}\left(c_5{\chi }^{-c_6}\right) \\ \beta ={\displaystyle \frac{\omega }{c}}{(1+c}_7{\chi }^{-c_8}) \end{gathered}$$

(3)

The real part and the imaginary part of the specific impedance, $R_c$ and $X_c$, are adjusted separately. The real part and the imaginary part of the sound propagation constant, α and β, respectively, are also adjusted separately. Three different kinds of adjustments are proposed. The first adjustment is based on Matlab’s “fminsearch” function. The values to be estimated are as follows:

$$\begin{gathered} {\widehat{z}}_c={\widehat{R}}_c+j{\widehat{X}}_c \\ \widehat{\mathsf{\Gamma }}=\widehat{\alpha }+j\widehat{\beta } \end{gathered}$$

(4)

After different error function tests, the following ones are chosen:

$$\begin{gathered} {\epsilon }_{R_c}=\sum _{i=1}^N{\left(\left|{\displaystyle \frac{R_{c,i}}{{\widehat{R}}_{c,i}}}\right|-1\right)}^2 \\ {\epsilon }_{X_c}=\sum _{i=1}^N{\left(\left|{\displaystyle \frac{X_{c,i}}{{\widehat{X}}_{c,i}}}\right|-1\right)}^2 \\ {\epsilon }_{\alpha }=\sum _{i=1}^N{\left(\left|{\displaystyle \frac{{\alpha }_i}{{\widehat{\alpha }}_i}}\right|-1\right)}^2 \\ {\epsilon }_{\beta }=\sum _{i=1}^N{\left(\left|{\displaystyle \frac{{\beta }_i}{{\widehat{\beta }}_i}}\right|-1\right)}^2 \end{gathered}$$

(5)

A sweep of the i-th frequency from 1 to N is performed. The “fminsearch” function requires an initial iteration to search for a local minimum. The Dunn–Davern coefficients are used [18] as the initial iteration, given that open-pore foams are measured. Although the error functions have a denominator, there are no discontinuity issues, as on no account do the measurements have a zero value. These error functions are not quadratic error functions. They have been chosen because they have returned fewer errors than the quadratic error function in previous results. The programmed algorithm uses a tolerance of 10⁻⁷ and a maximum of 1600 function evaluations as stopping criteria.

The second method is the use of genetic algorithms. The Matlab “ga” function is used for this purpose. The error functions are those proposed for the “fminsearch” case. The advantage of this method is that it does not require any initial values. Given that the algorithm generates random data populations, different coefficient results are obtained each time the algorithm is run, which is a drawback. To narrow down the results, all the coefficients to be adjusted, c1 to c8, are limited to between 0 and 1. In this case, the algorithm uses the same tolerance as the previous one. A maximum of 200 generations has been programmed. These two conditions define the stopping criteria.

The third method performs a least-squares adjustment. This is the most common one; it calculates a quadratic error function discarded in the first two methods. To make the adjustment, Equation (3) are previously converted into straight lines:

$$\begin{gathered} ln\left({\displaystyle \frac{R_c}{\rho c}}-1\right)=ln{(c}_1)-c_2\mathrm{l}\mathrm{n}(\chi ) \\ ln\left(-{\displaystyle \frac{X_c}{\rho c}}\right)=ln{(c}_3)-c_4\mathrm{l}\mathrm{n}(\chi ) \\ ln\left({\displaystyle \frac{\alpha c}{\omega }}\right)=ln{(c}_5)-c_6\mathrm{l}\mathrm{n}(\chi ) \\ ln\left({\displaystyle \frac{\beta c}{\omega }}-1\right)=ln{(c}_7)-c_8\mathrm{l}\mathrm{n}(\chi ) \end{gathered}$$

(6)

Equation (6) can be assimilated to a line in the form of y = ax + b, to which a least-squares adjustment can be applied. The Matlab “polyfit” function [50] also allows this adjustment to be made with ease. In this case, the function yields a fixed error or residual upon application, preventing further refinement of the results.

4. Results

This section shows the results obtained with the different adjustment methods.

Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 show the adjustments of the characteristic impedance Zc (=Rc + j Xc) and propagation constant Γ (=α + jβ) for materials M1 to M7. The adjustments of the normal incidence sound absorption coefficient obtained with the two sample thicknesses (d and 2d) are also shown. The measurements are shown as a solid line. The adjustments with “fminsearch” (fmin), the genetic algorithm (ga) and the least-squares adjustment (LS) are shown. A generally satisfactory adjustment of all the variables can be seen in the three methods.

Table 2. Fitting coefficients determined for M1: Melamine foam 4 cm.

Model	c1	c2	c3	c4	c5	c6	c7	c8	ε(Rc)	ε(Xc)	ε(α)	ε(β)
Fmin	0.0390	0.7756	0.2009	0.4937	0.3629	0.4562	0.0549	0.7926	3.2	4.6	0.9	1.0
Ga	0.0449	0.7382	0.2238	0.4657	0.3834	0.4374	0.0651	0.7427	3.7	4.4	1.0	1.1
LS	0.0316	0.8315	0.1962	0.5000	0.3649	0.4521	0.0472	0.8311	4.2	4.7	1.0	1.0

,

Table 3. Fitting coefficients determined for M2: Polyurethane foam 2.5 cm.

Model	c1	c2	c3	c4	c5	c6	c7	c8	ε(Rc)	ε(Xc)	ε(α)	ε(β)
Fmin	0.2897	0.2188	0.0907	0.3478	0.2200	0.2873	0.1973	0.4213	7.7	1.2	0.3	1.0
Ga	0.2897	0.2188	0.0903	0.3501	0.2200	0.2873	0.2005	0.4122	7.7	1.2	0.3	1.0
LS	0.3415	0.0414	0.0815	0.4221	0.2140	0.3082	0.2225	0.2843	8.7	1.2	0.3	1.2

,

Table 4. Fitting coefficients determined for M3: Polyurethane foam 4 cm.

Model	c1	c2	c3	c4	c5	c6	c7	c8	ε(Rc)	ε(Xc)	ε(α)	ε(β)
Fmin	0.1935	0.1697	0.0437	1.1506	0.1349	0.7634	0.2823	0.1028	4.2	2.6	0.4	0.8
Ga	0.1946	0.1648	0.0655	0.8958	0.1349	0.7635	0.2824	0.1025	4.2	2.3	0.4	0.8
LS	0.2121	0.0814	0.0466	1.1141	0.1355	0.7674	0.2542	0.1400	4.3	2.6	0.4	1.0

,

Table 5. Fitting coefficients determined for M4: Recycled foam 3 cm.

Model	c1	c2	c3	c4	c5	c6	c7	c8	ε(Rc)	ε(Xc)	ε(α)	ε(β)
Fmin	0.4248	0.2256	0.2393	0.3277	0.2836	0.4399	0.2857	0.3697	11.0	8.0	1.4	1.4
Ga	0.4247	0.2256	0.2393	0.3276	0.3063	0.4095	0.2727	0.3819	11.0	8.0	1.4	1.4
LS	0.3510	0.3029	0.1361	0.5355	0.2731	0.4518	0.2601	0.3972	11.8	6.9	1.4	1.5

,

Table 6. Fitting coefficients determined for M5: Recycled foam 2 cm.

Model	c1	c2	c3	c4	c5	c6	c7	c8	ε(Rc)	ε(Xc)	ε(α)	ε(β)
Fmin	0.2842	0.3200	0.1955	0.3596	0.3832	0.2874	0.2854	0.3438	11.5	4.2	1.1	1.6
Ga	0.2842	0.3201	0.2223	0.3075	0.3678	0.3009	0.2860	0.3431	11.5	4.5	1.1	1.6
LS	0.3773	0.2251	0.1694	0.4162	0.3370	0.3434	0.3151	0.2936	12.2	4.2	1.1	1.8

,

Table 7. Fitting coefficients determined for M6: Recycled foam 2 cm.

Model	c1	c2	c3	c4	c5	c6	c7	c8	ε(Rc)	ε(Xc)	ε(α)	ε(β)
Fmin	0.4248	0.2256	0.2393	0.3277	0.2836	0.4399	0.2857	0.3697	11.0	8.0	1.4	1.4
Ga	0.4247	0.2256	0.2393	0.3276	0.3063	0.4095	0.2727	0.3819	11.0	8.0	1.4	1.4
LS	0.3510	0.3029	0.1361	0.5355	0.2731	0.4518	0.2601	0.3972	11.8	6.9	1.4	1.5

and

Table 8. Fitting coefficients determined for M7: Recycled foam 3 cm.

Model	c1	c2	c3	c4	c5	c6	c7	c8	ε(Rc)	ε(Xc)	ε(α)	ε(β)
Fmin	0.3229	0.2636	0.0615	0.8181	0.1649	0.6322	0.3022	0.3459	8.3	4.2	0.8	1.2
Ga	0.3475	0.2275	0.0803	0.7022	0.1649	0.6323	0.3024	0.3458	8.3	3.9	0.8	1.2
LS	0.3460	0.2442	0.0659	0.7818	0.1705	0.6140	0.2691	0.3833	8.4	4.1	0.8	1.3

show the coefficients adjusted by the three methods for all the materials. The mean absolute error of each adjustment is also included. The coefficients obtained for each material are quite similar. The errors obtained are also very similar. This indicates that any of the models could be used. We should highlight the case of sample M3: Polyurethane foam 4 cm, in which there are coefficients greater than 1 for the Fmin and LS models. In this case, it is advisable to use the Ga adjustment, which keeps the coefficients between 0 and 1. The errors are expressed as absolute values and share the same units as the corresponding variable in each case.

5. Discussion

This section presents a discussion on the validity of the results. On one hand, the outcomes are compared with classical models. On the other hand, a control sample—rockwool—has been introduced to reapply the algorithms and perform comparative analyses.

A comparison has been carried out between the newly obtained models using the three proposed fitting approaches and the classical models of Delany and Bazley [1], Wu’s model for open-cell foams [51], and the Dunn and Davern model [18].

Table 9. Coefficients of the classical models.

Model	c1	c2	c3	c4	c5	c6	c7	c8
Delany and Bazley	0.0571	0.754	0.087	0.732	0.189	0.595	0.0978	0.700
Wu	0.212	0.454	0.105	0.607	0.163	0.592	0.188	0.544
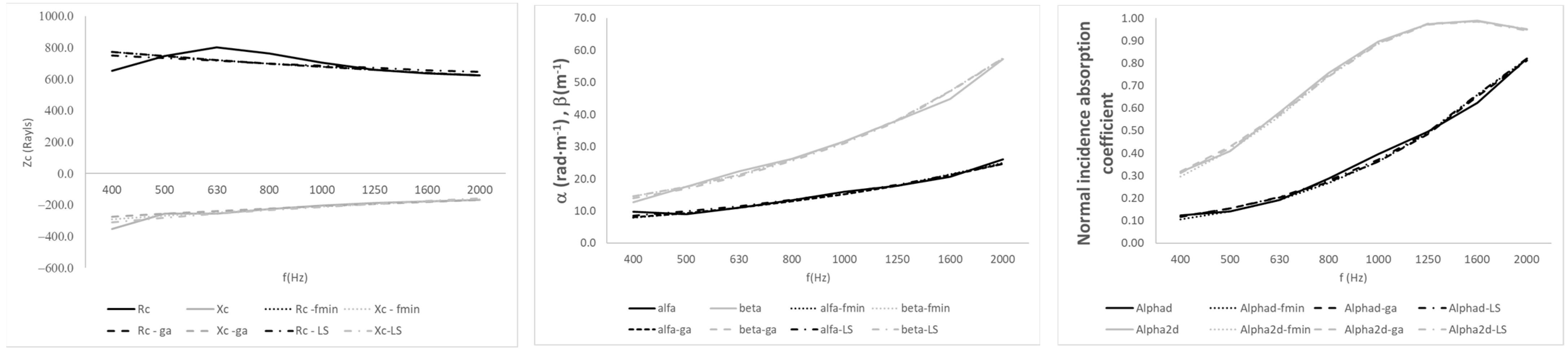
Dunn and Davern	0.114	0.369	0.0985	0.758	0.168	0.715	0.136	0.494

presents the coefficients of the three selected models.

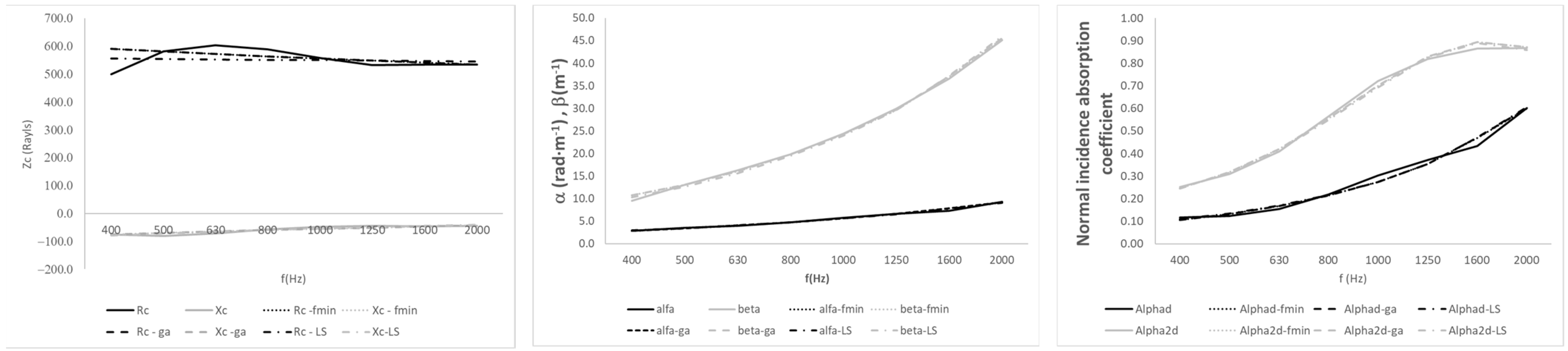
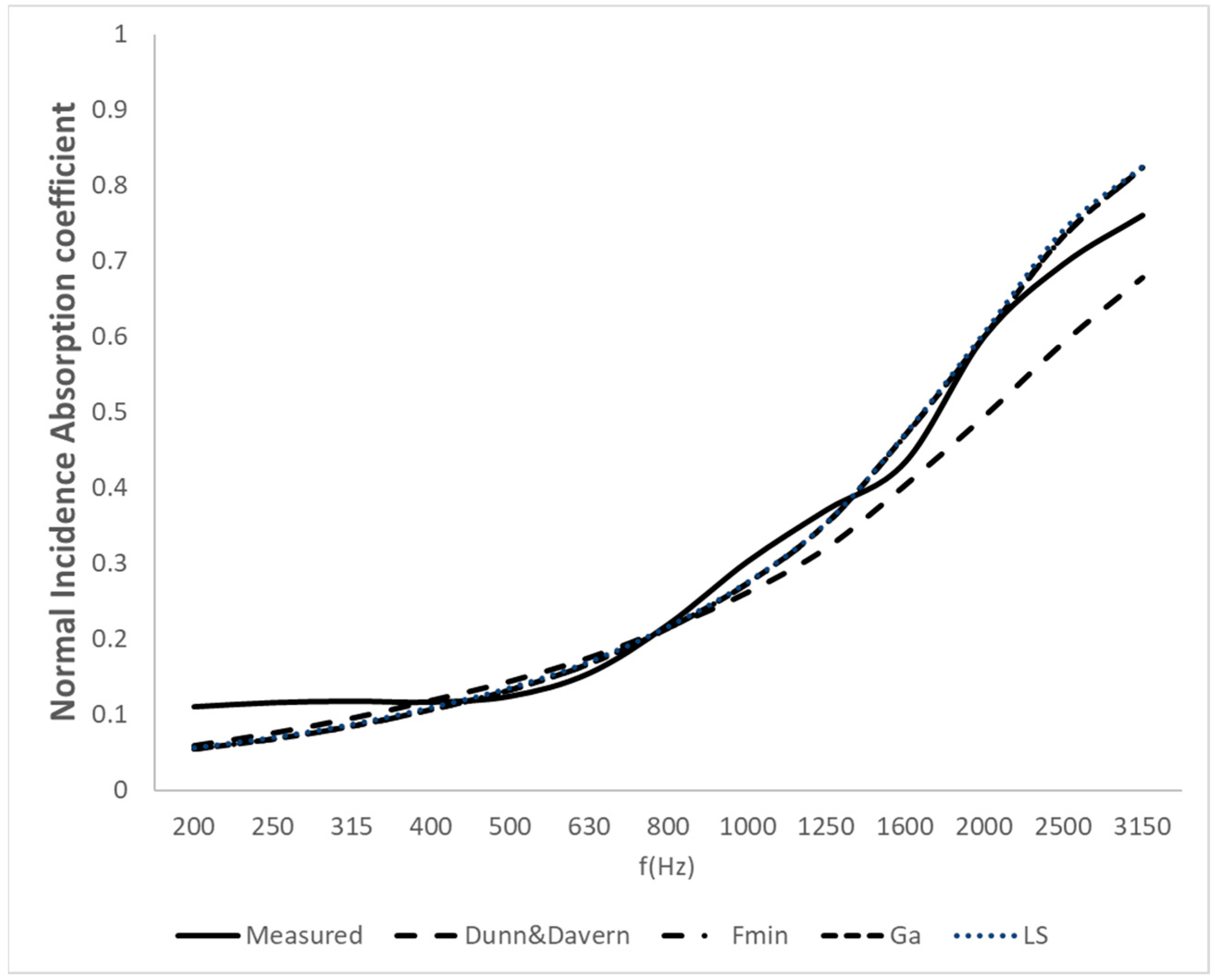
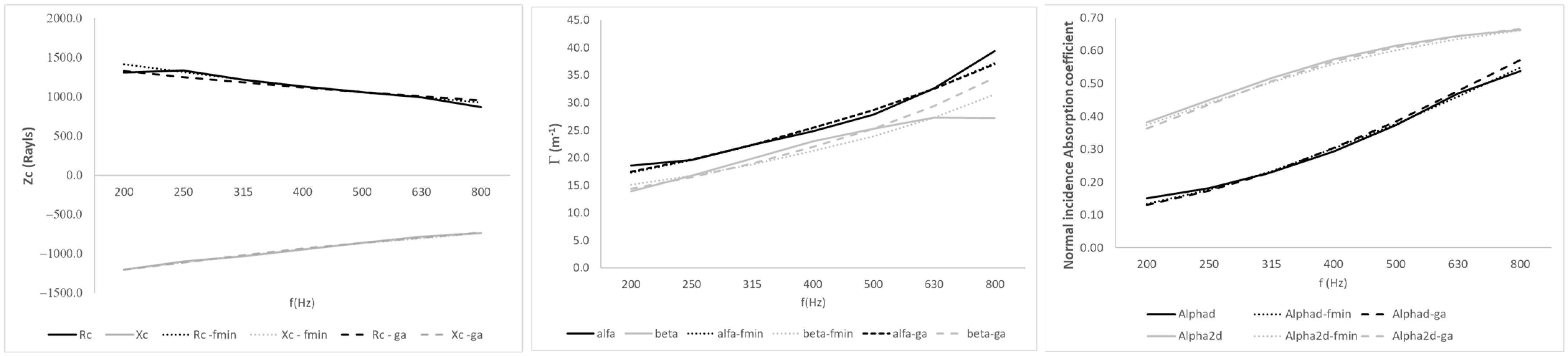
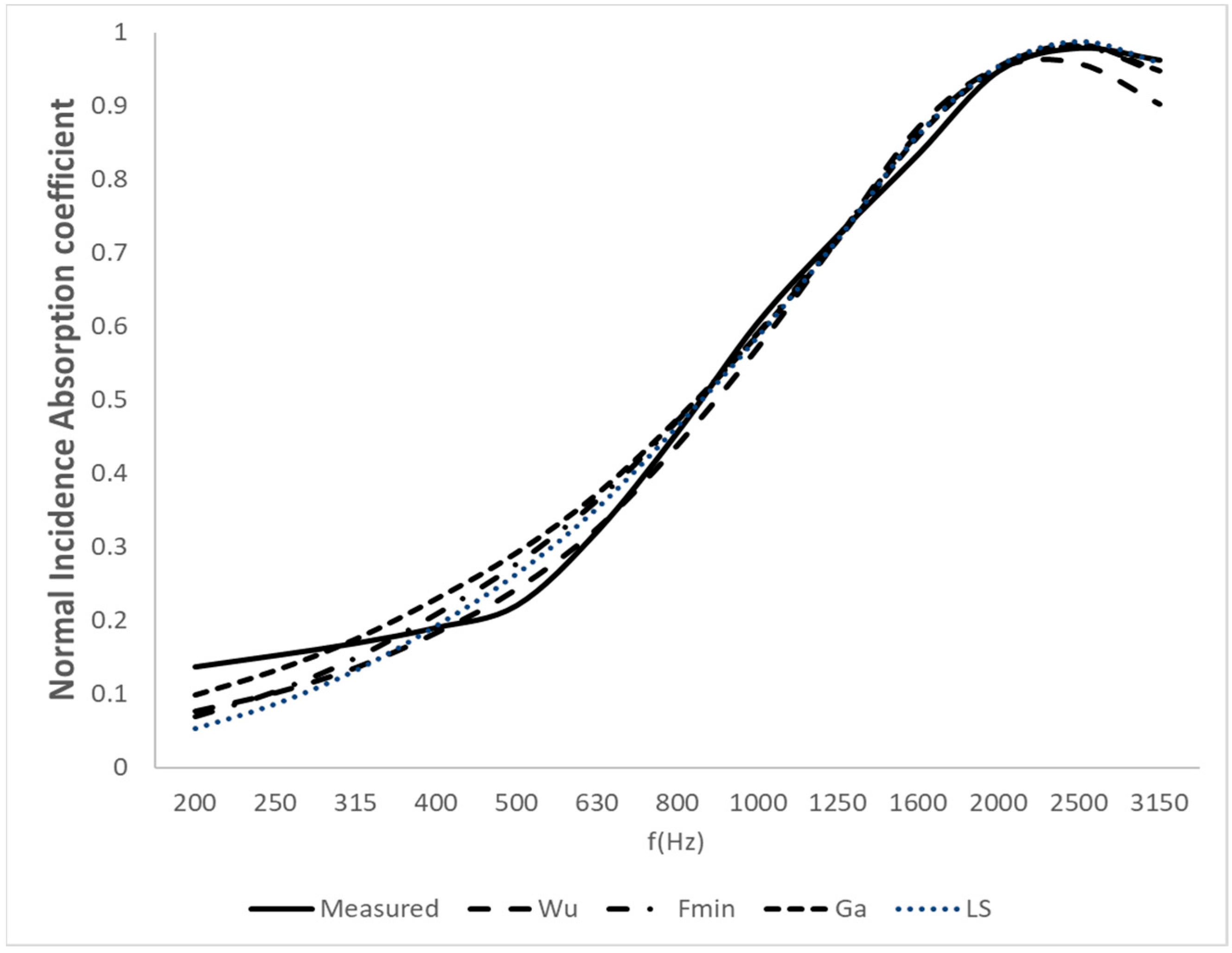
To discuss the results, sample M2 (polyurethane foam) is selected for comparison with the Dunn and Davern model, and sample M4 (recycled foam) is used for comparison with the Wu model. To discuss the results, sample M2 (polyurethane foam) is selected to compare the three newly fitted models with the Dunn and Davern model (Figure 8). The coefficients of the new models are presented in Table 3. Sample M4 (recycled foam) is selected to compare the three new models with the Wu model (Figure 9). The corresponding coefficients are shown in Table 5.

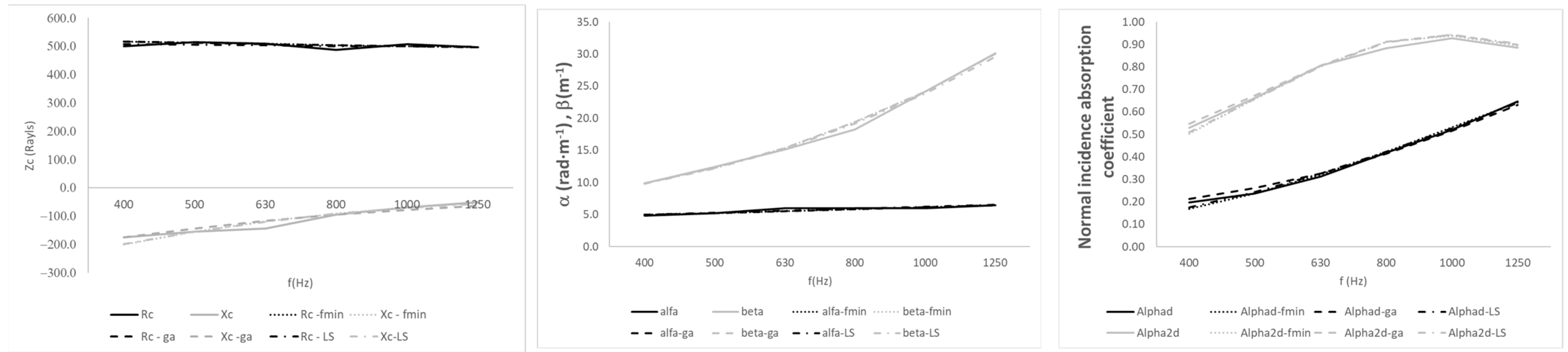
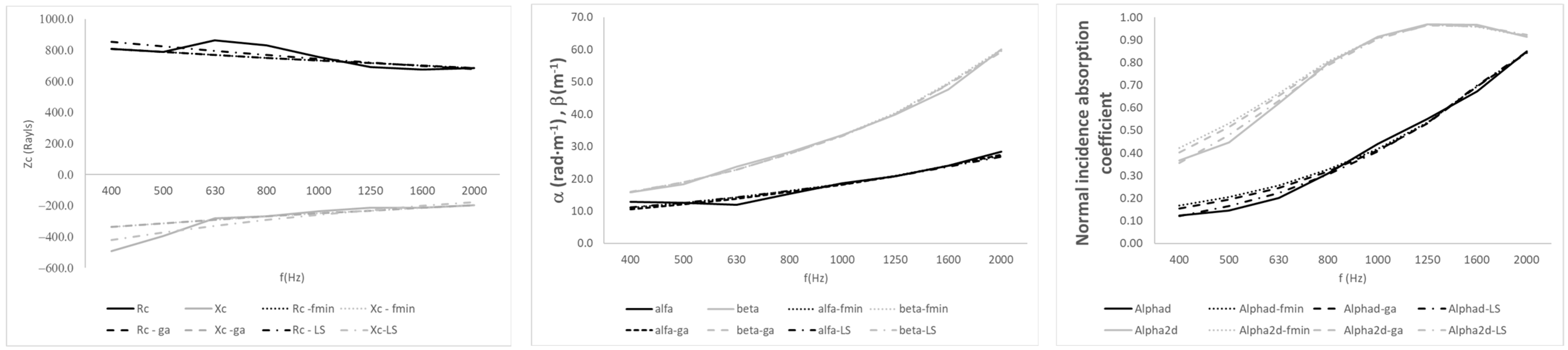
As previously mentioned, a control sample is included. This sample is M8 (rockwool). The same fitting procedures were applied to this fibrous material. Figure 10 shows details of these fittings. Results obtained using the LS algorithm are not included, as they exhibit high error levels.

Table 10. Fitting coefficients determined for M8: rockwool.

Model	c1	c2	c3	c4	c5	c6	c7	c8	ε(Rc)	ε(Xc)	ε(α)	ε(β)
Fmin	0.4248	0.2256	0.2393	0.3277	0.2836	0.4399	0.2857	0.3697	11.0	8.0	1.4	1.4
Ga	0.4247	0.2256	0.2393	0.3276	0.3063	0.4095	0.2727	0.3819	11.0	8.0	1.4	1.4

presents the fitted coefficients and the corresponding squared errors.

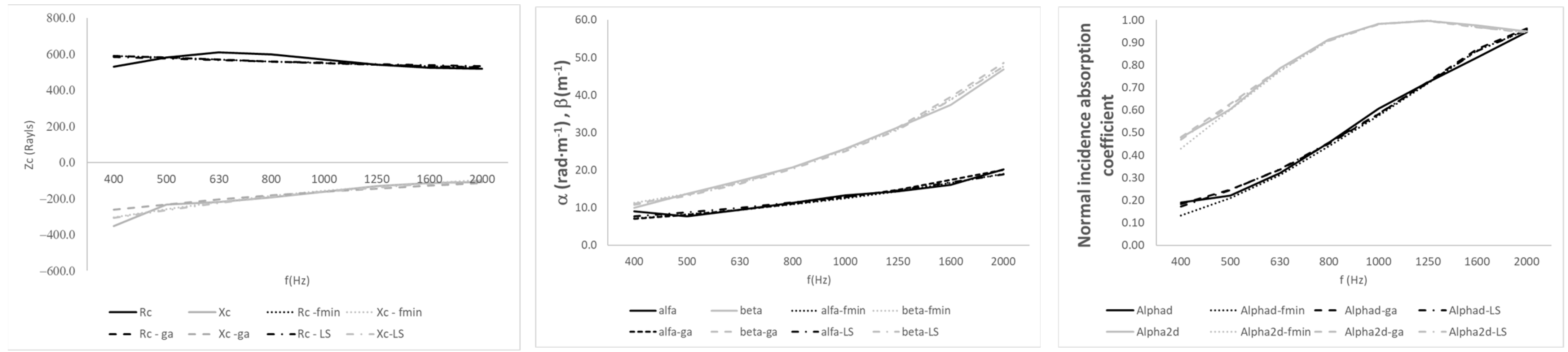
Additionally, sample M8 (rockwool) is compared with the Delany and Bazley model. The results are shown in Figure 11.

Table 11. Fitting errors of the sound absorption coefficient.

Material	Model	Fitting Error Model	Fmin	ga	LS
M2	Dunn and Davern	0.19	0.14	0.14	0.14
M4	Wu	0.14	0.13	0.14	0.13
M8	Delany and Bazley	0.22	0.30	0.19	0.33

presents the root mean square error of the sound absorption coefficient. The new models are compared with each of the reference models. For sample M2 (polyurethane foam), it can be seen that the Dunn and Davern model yields an error of 0.19, while the three new models show a lower error of 0.14. In this case, an improvement is clearly observed. For sample M4 (recycled foam), the Wu model has an error of 0.14, which is the same as the ‘ga’ model, and slightly higher than the other two models (0.13). In this case, the difference lies in the fact that the new models appear to better fit the high-frequency values, whereas the Wu model fits better at low frequencies.

For sample M8 (rockwool), the error for the Delany and Bazley model is 0.22. In this case, the ‘ga’ model shows a lower error of 0.19 and appears to provide a better fit at both low and high frequencies. The Delany and Bazley model, by contrast, deviates at low frequencies.

A sensitivity analysis has also been carried out to evaluate the effect of variations in the coefficients used to obtain the characteristic impedance and the propagation constant. This analysis is based on Equation (3). By applying differentiation, the sensitivity of each variable with respect to each coefficient is obtained. The equations that provide the relative error are as follows:

$$\begin{gathered} {\displaystyle \frac{\delta R_c}{R_c}}={\displaystyle \frac{1}{c_1{+\chi }^{c_2}}}\left(\delta c_1+{\displaystyle \frac{1}{c_2+1}}{\chi }^{-1}\delta c_2\right) \\ {\displaystyle \frac{\delta X_c}{X_c}}={\displaystyle \frac{1}{c_3}}\left(\delta c_3+{\displaystyle \frac{1}{c_4+1}}{\chi }^{-1}\delta c_4\right) \\ {\displaystyle \frac{\delta \alpha }{\alpha }}={\displaystyle \frac{1}{c_5}}\left(\delta c_5+{\displaystyle \frac{1}{c_6+1}}{\chi }^{-1}\delta c_6\right) \\ {\displaystyle \frac{\delta \beta }{\beta }}={\displaystyle \frac{1}{c_7{+\chi }^{c_8}}}\left(\delta c_7+{\displaystyle \frac{1}{c_8+1}}{\chi }^{-1}\delta c_8\right) \end{gathered}$$

(7)

The variation in each coefficient is represented by $\delta c_1$ to $\delta c_8$. The term ${\displaystyle \frac{\delta R_c}{R_c}}$ represents the relative error of the real part of the characteristic impedance, ${\displaystyle \frac{\delta X_c}{X_c}}$ corresponds to the relative error of the imaginary part of the characteristic impedance, ${\displaystyle \frac{\delta \alpha }{\alpha }}$ denotes the relative error of the real part of the propagation constant, and ${\displaystyle \frac{\delta \beta }{\beta }}$ that of the imaginary part of the propagation constant. It can be observed that, due to the dependence on $\chi ={\displaystyle \frac{\rho f}{\sigma }}$, the relative errors increase with higher flow resistivity. Additionally, the error is greater at low frequencies compared to high frequencies. Moreover, the smaller the coefficient, the larger the resulting error.

To quantify the effect of the variations, Equation (7) are applied to materials M2, M4, and M8 selected for this discussion. It is assumed that all models have four significant decimal digits. Thus, a possible variation in each coefficient of 0.0001 is considered.

Table 12. Relative errors (%) for M2.

	f = 200 Hz				f = 3150 Hz
Model	$\frac{\mathit{\delta }{\mathit{R}}_{\mathit{c}}}{{\mathit{R}}_{\mathit{c}}}$ (%)	$\frac{\mathit{\delta }{\mathit{X}}_{\mathit{c}}}{{\mathit{X}}_{\mathit{c}}}$ (%)	$\frac{\mathit{\delta }\mathit{\alpha }}{\mathit{\alpha }}$ (%)	$\frac{\mathit{\delta }\mathit{\beta }}{\mathit{\beta }}$ (%)	$\frac{\mathit{\delta }{\mathit{R}}_{\mathit{c}}}{{\mathit{R}}_{\mathit{c}}}$ (%)	$\frac{\mathit{\delta }{\mathit{X}}_{\mathit{c}}}{{\mathit{X}}_{\mathit{c}}}$ (%)	$\frac{\mathit{\delta }\mathit{\alpha }}{\mathit{\alpha }}$ (%)	$\frac{\mathit{\delta }\mathit{\beta }}{\mathit{\beta }}$ (%)
Fmin	0.17	1.43	0.61	0.24	0.01	0.19	0.08	0.01
Ga	0.17	1.43	0.61	0.24	0.01	0.19	0.08	0.01
LS	0.13	1.51	0.62	0.20	0.01	0.21	0.08	0.01
Dunn&Davern	0.27	1.03	0.62	0.30	0.02	0.16	0.10	0.01

presents the relative errors for sample M2 at 200 Hz (the case with the greatest deviation) and at 3150 Hz.

Table 13. Relative errors (%) for M4.

	f = 200 Hz				f = 3150 Hz
Model	$\frac{\mathit{\delta }{\mathit{R}}_{\mathit{c}}}{{\mathit{R}}_{\mathit{c}}}$ (%)	$\frac{\mathit{\delta }{\mathit{X}}_{\mathit{c}}}{{\mathit{X}}_{\mathit{c}}}$ (%)	$\frac{\mathit{\delta }\mathit{\alpha }}{\mathit{\alpha }}$ (%)	$\frac{\mathit{\delta }\mathit{\beta }}{\mathit{\beta }}$ (%)	$\frac{\mathit{\delta }{\mathit{R}}_{\mathit{c}}}{{\mathit{R}}_{\mathit{c}}}$ (%)	$\frac{\mathit{\delta }{\mathit{X}}_{\mathit{c}}}{{\mathit{X}}_{\mathit{c}}}$ (%)	$\frac{\mathit{\delta }\mathit{\alpha }}{\mathit{\alpha }}$ (%)	$\frac{\mathit{\delta }\mathit{\beta }}{\mathit{\beta }}$ (%)
Fmin	0.45	1.48	1.16	0.65	0.03	0.13	0.11	0.03
Ga	0.45	1.48	1.09	0.68	0.03	0.13	0.10	0.03
LS	0.54	2.26	1.19	0.70	0.03	0.21	0.11	0.03
Wu	0.84	2.81	1.82	0.98	0.04	0.27	0.17	0.04

shows the same analysis for sample M4, and

Table 14. Relative errors (%) for M8.

	f = 200 Hz				f = 3150 Hz
Model	$\frac{\mathit{\delta }{\mathit{R}}_{\mathit{c}}}{{\mathit{R}}_{\mathit{c}}}$ (%)	$\frac{\mathit{\delta }{\mathit{X}}_{\mathit{c}}}{{\mathit{X}}_{\mathit{c}}}$ (%)	$\frac{\mathit{\delta }\mathit{\alpha }}{\mathit{\alpha }}$ (%)	$\frac{\mathit{\delta }\mathit{\beta }}{\mathit{\beta }}$ (%)	$\frac{\mathit{\delta }{\mathit{R}}_{\mathit{c}}}{{\mathit{R}}_{\mathit{c}}}$ (%)	$\frac{\mathit{\delta }{\mathit{X}}_{\mathit{c}}}{{\mathit{X}}_{\mathit{c}}}$ (%)	$\frac{\mathit{\delta }\mathit{\alpha }}{\mathit{\alpha }}$ (%)	$\frac{\mathit{\delta }\mathit{\beta }}{\mathit{\beta }}$
Fmin	4.13	2.82	2.74	10.90	0.17	0.20	0.19	0.31
Ga	2.81	2.94	2.83	5.33	0.13	0.21	0.20	0.20
Delany and Bazley	1.76	12.09	6.04	8.63	0.10	0.88	0.43	0.28

for sample M8.

In general, the relative error for the imaginary part of the characteristic impedance is consistently the highest, due to its lower fitting coefficients. The second highest error corresponds to the real part of the propagation constant, also due to low coefficients. It can be observed that the errors increase from Table 12, Table 13 and Table 14, which is attributed to the increase in flow resistivity from M2 (Table 12) to M4 (Table 14). Additionally, the errors decrease with increasing frequency. Notably, the Delany and Bazley model shows significant error values at low frequencies in Table 14, which is consistent with the observations in Figure 11.

6. Conclusions

This paper reviews the empirical model of Delany and Bazley and new coefficients are adjusted for different kinds of open-pore foams: melamine, polyurethane foam and the recycled foams of different manufacturers. The airflow resistivity of samples of each material has been measured to do so. Their propagation constant and characteristic impedance have also been measured using the double thickness method.

Three adjustment methods have been proposed. Four error functions have been constructed for the first two methods, corresponding to the real and imaginary parts of the propagation constant and specific impedance. These error functions are not quadratic, and they have been previously chosen from different error function formats. They are adjusted with two Matlab functions, “fminsearch” for method 1 and “ga” for method 2. In method 1, the Dunn and Davern coefficients are introduced as the initial iteration. In method 2, for which no initial iteration is necessary, the coefficients are limited to between 0 and 1. The third method, LS, is based on linearising the equations and making a least-squares adjustment. This case does represent a least-squares adjustment.

Broadly speaking, the three methods converge into consistent solutions with a relatively low error. The value of the real part of the characteristic impedance is the most complex factor. Broadly speaking, “fmin” and “ga” return a slightly lower error than LS. Moreover, it can be seen that, in the case in which the adjustment returns values above 1 (or negative ones), the “ga” method is the only one that prevents one. This can be seen in the case of polyurethane foam 4 cm, in which this situation occurs.

The coefficients obtained from the characteristic impedance and propagation constant measurements adjust all the data properly, not only the normal incidence absorption coefficient.

A control material, M8 (rock wool), was also tested. In this case, it was found that the classical models provide a reasonably good fit. Only the genetic algorithm was able to outperform the classical models. This suggests that fitting the data to each specific material type is advisable in order to achieve better results.

In future lines, this discussion can be extended to adjusting models such as the JCAL in order to obtain a higher degree of accuracy in the model or inversely obtain parameters that are difficult to measure.