Broadband Acoustic Modal Identification by Combined Sensor Array Measurements
Abstract
1. Introduction
2. Measurement Theory
2.1. Combined Microphone Array Method
2.2. Advantage Analysis of the Combined Microphone Array Method
3. Numerical Simulation
3.1. Numerical Simulation Analysis of the Combined Microphone Array Method
3.2. Artificial Duct Broadband Noise Field
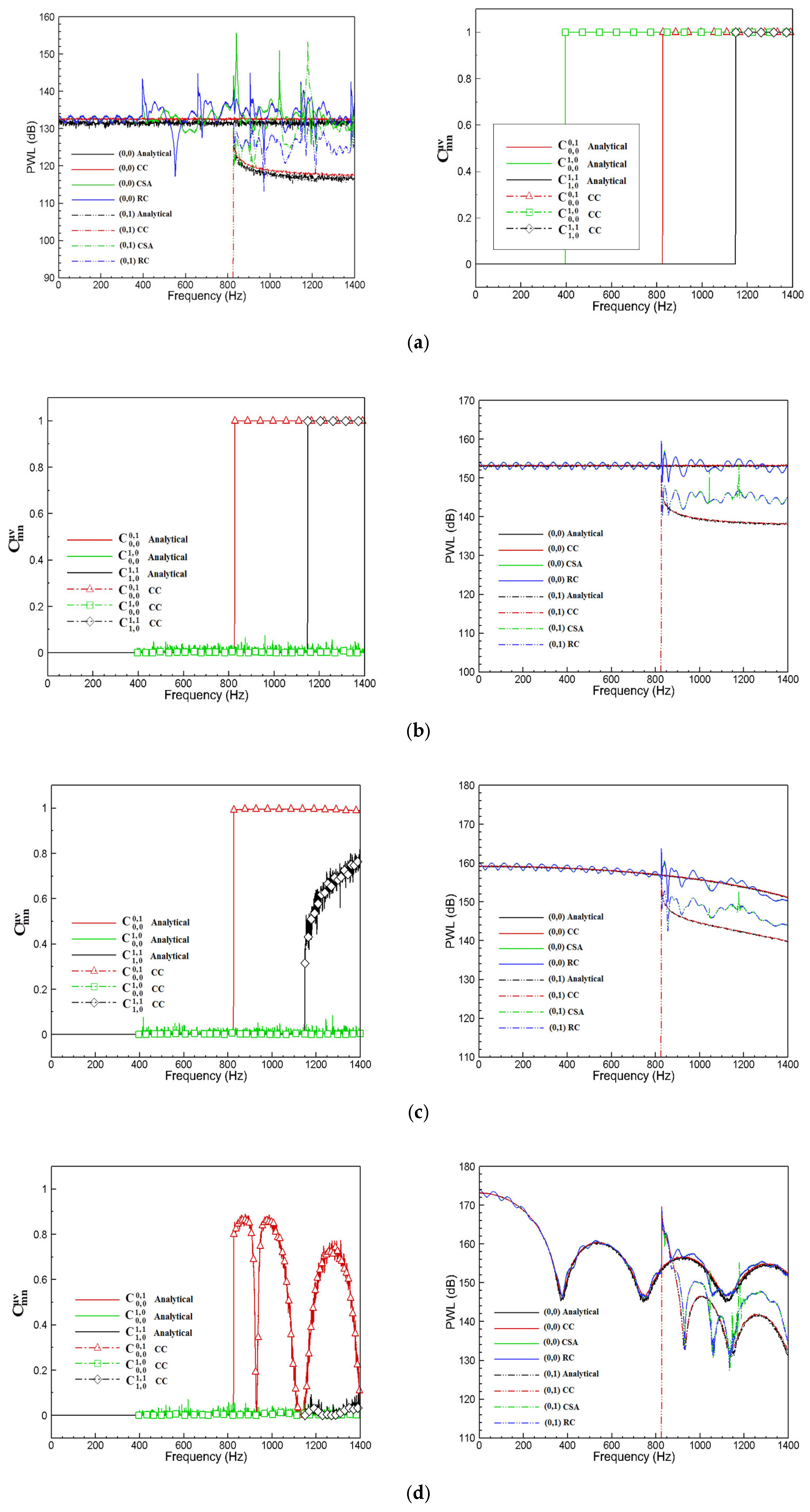
3.3. Numerical Verification and Error Analysis
4. Comparative Analysis of Measurement Results of Different Modal Identification Methods
4.1. Experimental Test Scheme Design
4.1.1. Fixed Microphone Array Scheme
4.1.2. Rotating Microphone Array Scheme
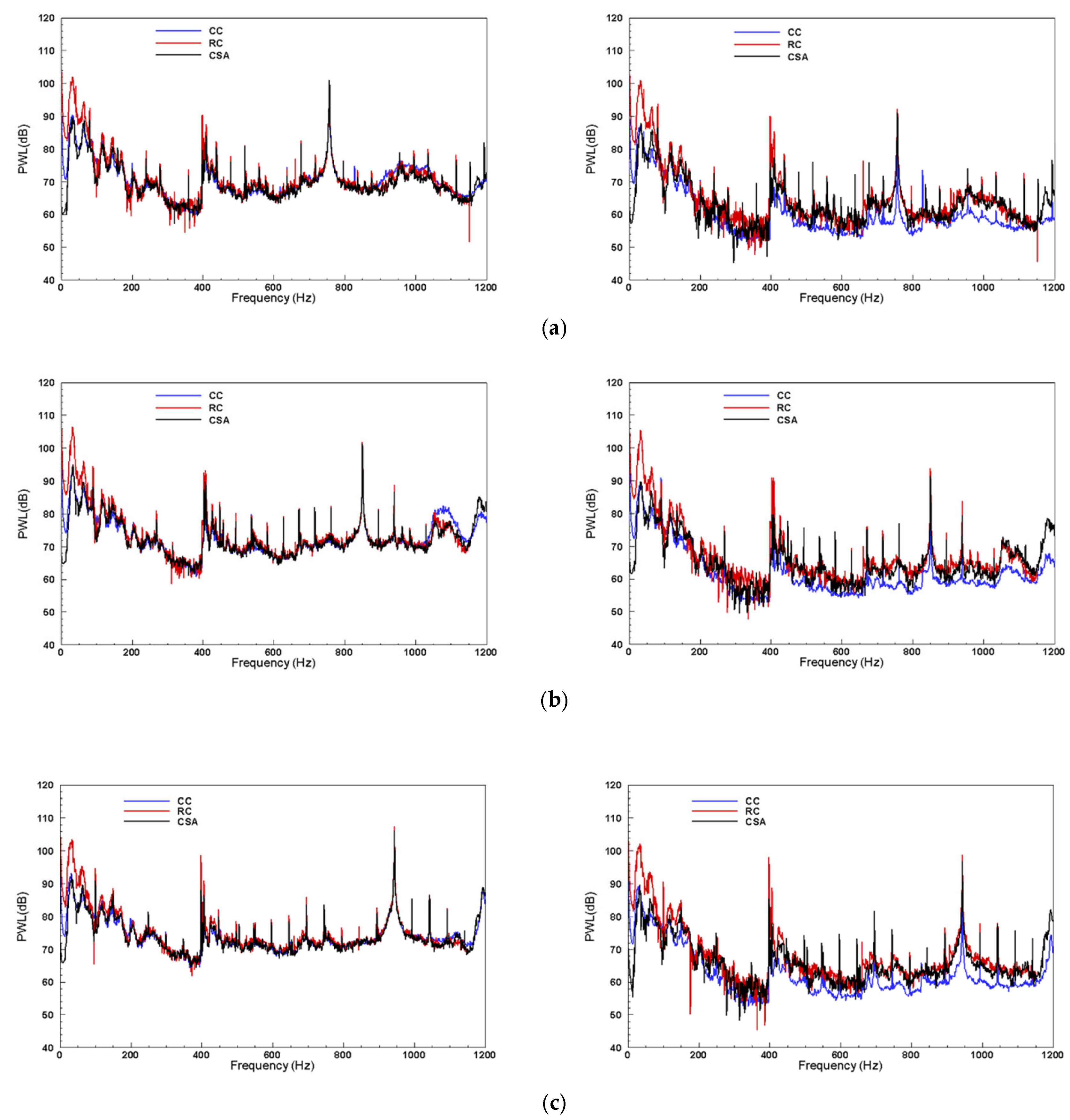
4.2. Comparative Analysis of Experimental Test Results of Fixed Microphone Array Scheme
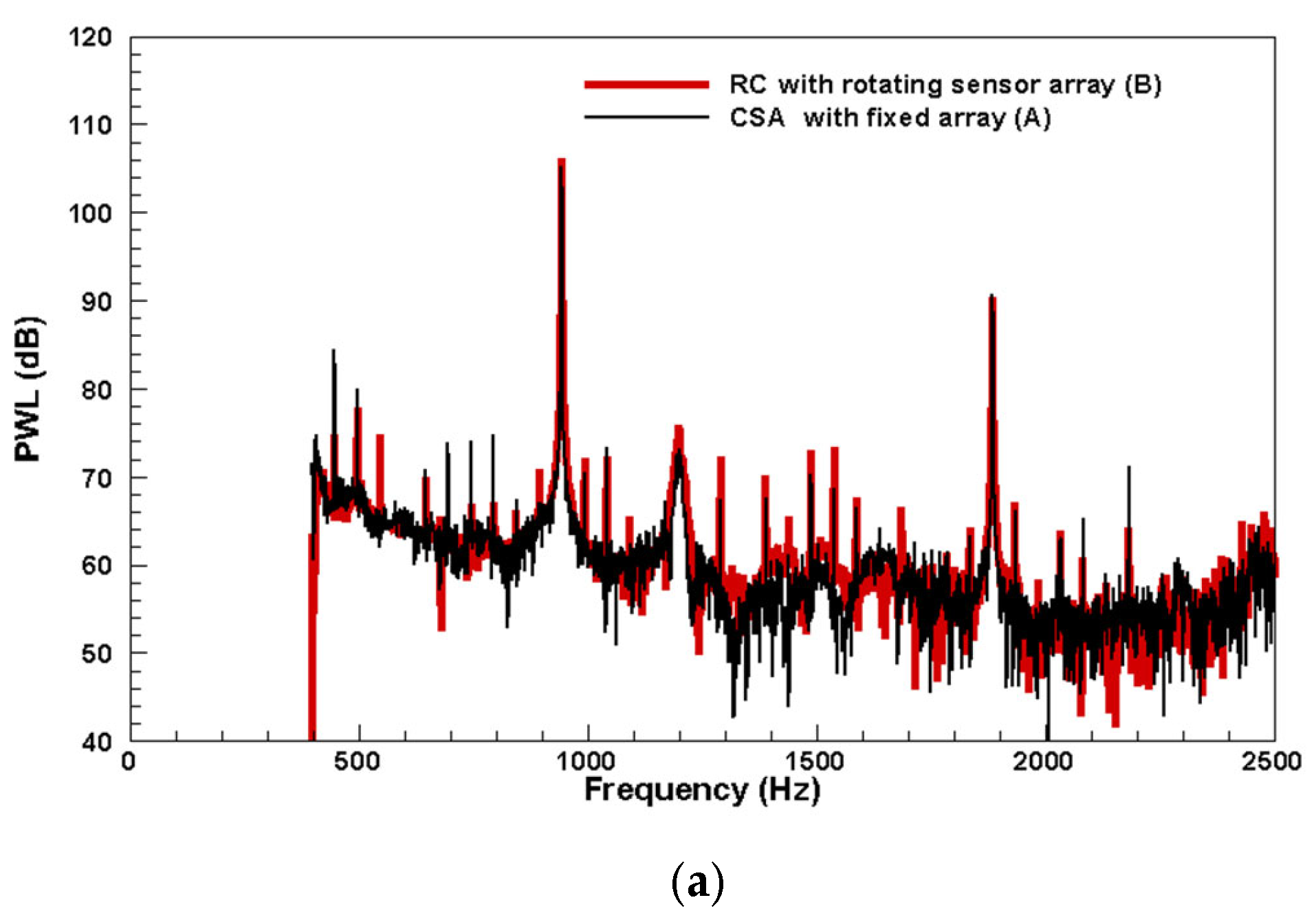
4.3. Comparative Analysis of Experimental Test Results of Rotating Microphone Array Scheme
5. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bolleter, U.; Crocker, M.J. Theory and measurement of modal spectra in hard-walled cylindrical ducts. J. Acoust. Soc. Am. 1972, 51, 1439–1447. [Google Scholar] [CrossRef]
- Moore, C.J. Measurement of radial and circumferential modes in annular and circular ducts. J. Sound Vib. 1979, 62, 235–256. [Google Scholar] [CrossRef]
- Morfey, C. Sound transmission and generation in ducts with flow. J. Sound Vib. 1971, 14, 37–55. [Google Scholar] [CrossRef]
- Gjoni, E. Numerical Study on Acoustic Phenomena in Cavities for Aero-engine Applications. Master’s Thesis, Politecnico di Torino, Torino, Italy, 2023. [Google Scholar]
- Sijtsma, P.; Brouwer, H. Deconvolution of azimuthal mode detection measurements. J. Sound Vib. 2018, 42, 1–14. [Google Scholar] [CrossRef]
- Xu, K.B.; Qiao, W.Y.; Huo, S.Y.; Wei, R.K.; Tong, F. Research of mode identification and error transfer property on fan tonal noise. J. Propuls. Technol. 2018, 39, 185–195. [Google Scholar]
- Enghardt, L.; Lowis, C.; Neuhaus, L. Broadband sound power determination in flow ducts. In Proceedings of the 10th AIAA/CEAS Aeroacoustic Conference, Manchester, UK, 10–12 May 2004. AIAA-2004–2940. [Google Scholar]
- Ganz, U.W.; Joppa, P.D.; Patten, T.J.; Scharpf, D.F. Boeing 18-Inch Fan Rig Broadband Noise Test; Technical Report CR-1998-208704; NASA: Washington, DC, USA, 1998. [Google Scholar]
- Xu, K.B.; Qiao, W.Y.; Huo, S.Y. Experimental of fan broadband noise determination based on rotating axial arrays. J. Acta Aeronaut. Astronaut. Sin. 2017, 38, 121–132. [Google Scholar]
- Kopiev, V.F.; Bersenev, Y.V.; Viskova, T.A.; Burdakov, R.V.; Palchikovskiy, V.V.; Belyaev, I.V.; Kustov, O.Y.; Ershov, V.V. Azimuthal modes measurement in an intake duct for a turbofan engine. Procedia Eng. 2017, 176, 273–277. [Google Scholar] [CrossRef]
- Bu, H.X.; Huang, X.; Zhang, X. A compressive-sensing-based method for radial mode analysis of aeroengine fan noise. J. Sound Vib. 2020, 464, 114930. [Google Scholar] [CrossRef]
- Yu, W.J.; Ma, Z.Y.; Lau, A.S.H.; Huang, X. Analysis and experiment of the compressive sensing approach for duct mode detection. AIAA J. 2018, 56, 648–657. [Google Scholar] [CrossRef]
- Jürgens, W.; Pardowitz, B.; Enghardt, L.; Tapken, U. Separation of broadband noise sources in aeroengine ducts with respect to modal decomposition. In Proceedings of the 17th AIAA/CEAS Aeroacoustic Conference, Portland, OR, USA, 5–8 June 2011. AIAA-2011-2879. [Google Scholar]
- Dyer, I. Measurement of noise sources in ducts. J. Acoust. Soc. Am. 1958, 30, 833–841. [Google Scholar] [CrossRef]
- Michalke, A.; Arnold, F.; Holste, F. On the coherence of the sound field in a circular duct with uniform mean flow. J. Sound Vib. 1996, 190, 261–271. [Google Scholar] [CrossRef]
- Enghardt, L.; Holewa, A.; Tapken, U. Comparison of different analysis techniques to decompose a broadband ducted sound field in its mode constituents. In Proceedings of the 13th AIAA/CEAS Aeroacoustics Conference, Rome, Italy, 21–23 May 2007. AIAA-2007-3520. [Google Scholar]
- Jürgens, W.; Tapken, U.; Pardowitz, B.; Kausche, P.; Bennett, G.J.; Enghardt, L. Technique to analyse characteristics of turbomachinery broadband noise sources. In Proceedings of the 16th AIAA/CEAS Aeroacoustics Conference, Stockholm, Sweden, 7–9 June 2010. AIAA-2010-3979. [Google Scholar]
- Tapken, U.; Gutsche, D.; Enghardt, L. Radial mode analysis of broadband noise in flow ducts using a combined axial and azimuthal sensors array. In Proceedings of the 20th AIAA/CEAS Aeroacoustics Conference, Atanta, GA, USA, 16–20 June 2014. AIAA-2014-3318. [Google Scholar]
- Venkateswaran, R.K. Characterization and Source Separation of Turbofan Broadband Noise Using Intra-Stage Measurements. Ph.D. Thesis, University of Southampton, Southampton, UK, 2025. [Google Scholar]
- Huang, G.; Jensen, J.R.; Chen, J.; Benesty, J.; Christensen, M.G.; Sugiyama, A.; Elko, G.; Gaensler, T. Advances in microphone array processing and multichannel speech enhancement. In Proceedings of the ICASSP 2025—2025 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Hyderabad, India, 6–11 April 2025; IEEE: Singapore, 2025; pp. 1–5. [Google Scholar]
- Jeong, W.; Lee, S.; Joseph, P. A wall-mounted source array for the excitation of incoherent broadband sound fields with prescribed modal distributions in ducts. J. Sound Vib. 2006, 290, 490–499. [Google Scholar] [CrossRef]
- Fauqueux, S.; Mons, V. Microphone array design for the modal analysis of in-duct broadband noise. J. Sound Vib. 2025, 618, 119356. [Google Scholar] [CrossRef]
- Du, S.; Dong, H.; Cong, L.; Li, S. Underwater target depth estimation: A shallow-water broadband acoustic source depth estimation method based on corrected warping transformation. PLoS ONE 2025, 20, e0318201. [Google Scholar]
- Lokhande, S.; Malarkodi, A.; Latha, G.; Srinivasan, S. Autonomous detection, localization and tracking of ships by underwater acoustic sensing using vector sensor array. Appl. Ocean Res. 2025, 154, 104389. [Google Scholar] [CrossRef]
- Yi, H.; Jiao, F.; Cao, H.; Zhang, J.; Zou, Y. Numerical simulations of molten pool dynamics in wire-arc directed energy deposition processes: A review. J. Manuf. Process. 2025, 134, 970–997. [Google Scholar] [CrossRef]
- Desiderio, L.; Falletta, S.; Ferrari, M.; Scuderi, L. On the coupling of the curved virtual element method with the one-equation boundary element method for 2D exterior Helmholtz problems. SIAM J. Numer. Anal. 2022, 60, 2099–2124. [Google Scholar] [CrossRef]
- Li, W.; Wen, H.; Guo, J. Acoustic Absorption and Radiation Features of Quasi-Periodic Acoustic Black Hole Rib Rings of Overlays. J. Vib. Eng. Technol. 2025, 13, 347. [Google Scholar] [CrossRef]
- Goldstein, M.E. Aeroacoustics; McGraw-Hill International Book Company: New York, NY, USA, 1976. [Google Scholar]
- Mao, Y.; Yoo, U.; Yao, Y.; Syed, S.N.; Bondi, L.; Francis, J.; Oh, J.; Ichnowski, J. Visuo-Acoustic Hand Pose and Contact Estimation. arXiv 2025, arXiv:2508.00852. [Google Scholar]
- Xu, K.; Liu, C.; Tong, F.; Qiao, W. Numerical and Experimental Investigations of Modal Coherence Characteristics for the Determination of Broadband Noise in Flow Ducts. Front. Energy Res. 2022, 10, 873749. [Google Scholar] [CrossRef]











| Sound Source Array No. | Total Number | ||
|---|---|---|---|
| Condition I | 1 | 1 | 1 |
| Condition II | 1 | 12 | 12 |
| Condition III | 2 | 12 | 24 |
| Condition IV | 10 | 12 | 120 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, K.; Liu, D.; Zong, Z.; Xiang, C.; Qiao, W.; Yu, L. Broadband Acoustic Modal Identification by Combined Sensor Array Measurements. Acoustics 2025, 7, 60. https://doi.org/10.3390/acoustics7040060
Xu K, Liu D, Zong Z, Xiang C, Qiao W, Yu L. Broadband Acoustic Modal Identification by Combined Sensor Array Measurements. Acoustics. 2025; 7(4):60. https://doi.org/10.3390/acoustics7040060
Chicago/Turabian StyleXu, Kunbo, Dongjun Liu, Zekai Zong, Chenzhe Xiang, Weiyang Qiao, and Liang Yu. 2025. "Broadband Acoustic Modal Identification by Combined Sensor Array Measurements" Acoustics 7, no. 4: 60. https://doi.org/10.3390/acoustics7040060
APA StyleXu, K., Liu, D., Zong, Z., Xiang, C., Qiao, W., & Yu, L. (2025). Broadband Acoustic Modal Identification by Combined Sensor Array Measurements. Acoustics, 7(4), 60. https://doi.org/10.3390/acoustics7040060








