Experimental and Theoretical Acoustic Performance of Esparto Grass Fibers

Abstract

Nowadays, natural fiber-based materials are widely used in the building sector, where the use of green and sustainable products is of growing interest. One of these fibrous materials is the esparto, a plant belonging to the Gramineae family, with a height up to 1 m. It grows in arid places with scarce rainfall, being common in some areas of the Iberian Peninsula. Due to its morphology, it can be used to replace conventional materials used in soundproofing and building applications. In this work, the acoustic properties of esparto fibers are studied using impedance tube measurements and via a phenomenological acoustic model where the input parameters are some non-acoustic properties such as porosity, density, tortuosity, and flow resistivity. The experimental results obtained showed the good acoustic performance of esparto fibers, with a high sound absorption coefficient along the usual frequency bandwidth. Furthermore, the theoretical results obtained using the phenomenological model exhibited a strong correlation with the sound absorption spectra obtained through experimental measurements.

1. Introduction

Nowadays, noise is considered to be one of the most important environmental pollutants affecting the health and well-being of citizens. Noise pollution, considered by the World Health Organization (WHO) as the second leading environmental cause of disease in Europe, can cause hearing loss, sleep disturbances, stress, fatigue, and cardiovascular problems [1]. According to the European Environment Agency (EEA), noise and related problems cause around 10,600 premature deaths and 39,800 new cases yearly of ischemic heart disease [2].

Usually, noise pollution is tackled through the use of building solutions that incorporate materials of synthetic origin from petroleum by-products. These show high efficiency in noise reduction, but are expensive to produce and difficult to recycle or reuse [3]. For this reason, in recent decades, building construction has begun to use building solutions that incorporate recycled materials or materials derived from natural sources [4,5,6,7,8,9,10,11], achieving more sustainable buildings. By using this type of raw material, it is possible to achieve adequate insulation and acoustic conditioning. This contributes to improved energy consumption, lower CO₂ emissions, and energy savings [4].

Regarding the use of materials derived from natural sources, numerous studies have been produced in which natural fibers were investigated because this kind of raw material usually shows good acoustic properties. Waste corn husk fibers were used to obtain sound fibrous absorbers with relatively low bulk densities (200–250 kg/m³), thicknesses between 20 and 40 mm, and sound absorption coefficients higher than 0.5 for frequencies above 1000 Hz [12]. The acoustic behavior of a blend composed of yucca and kenaf fibers, present in different proportions in terms of mass (70:30, 50:50, and 30:70), was experimentally and theoretically studied. The result was that the highest sound absorption average was achieved at low frequencies when the proportion of kenaf in the mass was greater than that of yucca [13]. Water hyacinth fibers bonded with 10% polyvinyl alcohol, with different bulk densities and a thickness of 40 mm, were acoustically tested, showing that samples with low densities (118 kg/m³) presented the highest sound absorption average, while samples with high densities (282 kg/m³) presented the greatest transmission loss average. This indicated the existence of an inverse relationship between the bulk density and the sound absorption coefficient, and that there was a direct relationship between the bulk density and the acoustic insulation [14]. The sound absorption properties of date palm fiber samples, with thicknesses between 25 mm and 55 mm, average fiber diameter of 265 μm, and two densities (125 and 175 kg/m³), were studied, experimentally and theoretically, by Taban et al. [15], showing that the sample with the higher thickness and density showed the best acoustical performance, mainly due to its relatively high flow resistivity and thickness. Moreover, we found good agreement between the proposed model (Johnson–Champoux–Allard (JCA) model) and the experimental measurements.

In this work, the acoustic performance of esparto fibers coming from Extremadura crops was experimentally and theoretically studied. Esparto grass (stipa tenacissima), scientifically belonging to the Gramineae family, is a perennial plant that grows extensively in the western Mediterranean basin and in areas of North Africa, which have low rainfall, covering large areas [16]. Its stem has a regular length of 1 m. From its leaves, it is possible to extract the esparto fibers, which are short cellulose-based fibers. The main uses of esparto fibers are ropes, sandals, mats, and decorative products for dwellings. Only some research has studied the acoustic and thermal behavior of esparto grass, as part of natural fiber composites, for its use in building solutions. Sair et al. [17] developed an esparto–fiber/polyurethane composite for use as a thermal and acoustic insulation material in buildings. This offered enhanced acoustic, thermal, and mechanical properties when a 10% alkaline solution was introduced in its manufacture. Bousshine et al. [18] studied samples of esparto fibers with low density (120 kg/m³), 8 cm in thickness, using frequencies below 1400 Hz. Composites made of petiole and esparto displayed good thermal properties, with a value of thermal conductivity equal to 0.065 W/mK. In the study conducted by Ouakarrouch et al. [19], insulation panels made of cardboard and esparto fibers were studied. They showed a good insulation performance when the mass ratio was 60:40 and the bulk density was equal to 278.6 kg/m³, with a thermal conductivity value of 0.072 W/mK. Only the work of Arenas et al. [20] studied the sound absorption coefficient of esparto fibers and its correlation with an empirical model, without previous chemical treatment or the use of a binder. These fibers originated from Pakistan, Tunisia, and Egypt.

The present work constitutes an experimental and theoretical investigation of the acoustic performance of an eco-efficient material with low energy cost, such as esparto grass. This eco-efficient material was the esparto grass fiber from Extremadura crops. The physical properties of esparto fibers, such as fiber diameter, bulk and real density, porosity, tortuosity, and flow resistivity, were determined. The evaluation of the sound absorption coefficient at a normal incidence was performed using an acoustic impedance tube. Finally, theoretical sound absorption was determined using an acoustic phenomenological model and compared with experimental measurements to evaluate the efficiency of this model. The results showed that esparto fibers had the potential to serve as a substitute for conventional materials frequently employed in noise control applications.

Although both Arenas et al. [20] and this work deduced flow resistivity using an acoustic method, obtained the normal incidence absorption coefficient spectra and compared them to the predictions of one model, and investigated the effect of the thickness in the sound absorption spectra, some differences can be found between them: (i) the origin of the esparto grass fibers, (ii) the fiber diameters (in the range of several mm and lower than 1 mm, respectively), and (iii) the frequency range. Moreover, the authors of this work are aware that no phenomenological model has been previously used to predict the acoustic behavior of this type of fiber.

2. Materials and Methods

The materials used in this work were esparto fibers (EFs) from Extremadura crops. The samples had different lengths and thicknesses (Figure 1). Previously, to manufacture the samples for testing, esparto fibers were immersed in distilled water and stirred in a magnetic stirrer for 1 h to remove possible impurities. Subsequently, esparto fibers were drained and placed in an oven at a temperature of 60 °C for a period of 72 h to remove the possible moisture. The fibers were finally introduced into cylindrical-shaped molds with two different internal diameters, 29 and 100 mm, and then compacted with the hard-back termination of the impedance tube, with the objective of reaching three different bulk densities (denoted throughout this paper with EF1, EF2 and EF3), and thicknesses between 0.1 m and 0.6 m (denoted throughout this paper with the suffix “_1” to “_6”). No bonding method was used.

2.1. Fiber Size

Fiber size was determined using confocal microscopy. The microscope used was a Sensofar Plu Neox laser scanning confocal microscope with the required configuration, an objective of 20X (0.80 NA), a spatial sampling of 2.6 μm, optical and vertical resolutions of 1.7 μm and 10 nm, respectively, and a z-step interval of 0.1 mm.

2.2. Porosity

Porosity (ϕ), a pivotal property in the assessment of acoustic performance, is defined as the proportion of air volume in relation to the global volume of fibrous material. It is widely accepted that an increase in porosity results in the enhanced dissipation of sound energy within the fibrous absorber, thereby leading to an increase in the effectiveness of sound absorption. The measurement of porosity was conducted using a helium pycnometer (Quantachrome SPY-3, Quantachrome Instruments, Boynton Beach, FL, USA), an instrument that employs Boyle’s law to determine the skeletal volume of esparto grass fibers through the displacement of the inert gas. This method was subsequently employed to calculate the porosity using the following expression:

$$\varphi =1-{\displaystyle \frac{{\rho }_m}{{\rho }_s}}$$

(1)

In this expression, the bulk density of the sample (in kg/m³) is denoted by ρ_m, and the skeletal density of the porous material (in kg/m³) is denoted by ρ_s. A precision balance (model AX 205, Mettler Toledo, Greifensee, Switzerland) was used to weigh the samples, and the volume and bulk density of the esparto grass samples were obtained from a measuring cylinder. To obtain the bulk density, this process was repeated five times for each sample, and subsequently the individual results were averaged.

2.3. Flow Resistivity

Sound is attenuated in porous media by the viscous friction between the air particle motion and the relatively motionless pore walls (viscous effects), and by thermal exchange between compressions and rarefactions in the pore-borne sound wave and the relatively constant-temperature pore walls (thermal effects). Moreover, in fibrous material there can be friction between fibers, which contributes to energy loss. But this is taken as negligible in models of acoustic properties that assume the porous frame to be rigid. The attenuation due to viscous effects depends on the resistance to air flow through the material commonly measured independently as flow resistivity (σ), i.e., the ratio of volumetric air flow to pressure drop per unit thickness across a known thickness of material. This physical property is indicative of the extent to which sound energy is dissipated within the sound absorber due to the effects of thermal and viscous conduction as air passes through it [21]. It has been established that low resistance values to air flowing through the fibrous absorber are associated with low values of bulk density, and so high sound absorption values may be expected. In the case of a complex porous structure, characterized by the high bulk density values of the fibrous absorber, it is to be expected that low sound absorption values will be observed. Therefore, it can be concluded that flow resistivity is clearly linked to bulk density, and thus both properties can be considered directly proportional [22]. The methodology established by Ingard and Dear [21] was employed in order to ascertain the flow resistivity of the samples in this study. Flow resistivity values were obtained by employing a closed cylindrical tube (with diameter D). This tube had a loudspeaker at one end, and a rigid termination that closed the opposite end (Figure 2). The loudspeaker emits a sound wave with a wavelength greater than 1.7D. It is imperative that the distance between the fibrous sample position and the rigid termination, L, is an odd number of quarter wavelengths, i.e., L + d = (2n − 1) λ/4, where n = 1, 2, 3, … The sound pressure level (SPL) inside the cylindrical tube was measured by two microphones, with one microphone (SPL₁) placed at the front of the fibrous sample of thickness d, and the other microphone (SPL₂) placed at the rigid termination of the tube. The flow resistivity of the fibrous sample can be evaluated using the following expression:

$$\sigma ={\displaystyle \frac{{\rho }_0{c}_0}{d}}·{10}^{{\displaystyle \raisebox{1ex}{$\left({SPL}_1-{SPL}_2\right)$}\!\left/ \!\raisebox{-1ex}{$20$}\right.}}$$

(2)

In this expression, the air density is denoted by ρ₀, the sound propagation velocity in air is denoted by c₀, and SPL₁ and SPL₂ are the sound pressure levels in the microphone positions 1 and 2, respectively. Each sample was measured five times and subsequently the results were averaged.

2.4. Tortuosity

Tortuosity (α_∞) is a structural parameter that indicates the straightforward nature of the path of the sound wave inside the porous absorber [23]. This parameter is found to be solely dependent on the pore geometry and the interconnectedness of the pores [24]. Consequently, higher fiber density in a sound porous absorber tends to result in a more complex path, implying a higher level of interaction between fibers and sound waves passing through it. This, in turn, results in the increased dissipation of sound energy as heat. Furthermore, it has been demonstrated that this parameter exerts a significant influence on the value of the absorption coefficient and the frequency at which sound absorption maxima are obtained. The evaluation of this parameter was conducted through the utilization of an empirical expression, derived in terms of porosity [25]:

$${\alpha }_{\infty }=1+{\displaystyle \frac{1-\varphi }{2\varphi }}$$

(3)

2.5. Sound Absorption Coefficient

The ISO standard 10534-2 [26] was used to determine the acoustic performance of esparto fibers. The sound absorption coefficient at normal incidence was obtained according to this standard using an impedance tube type 4206T and a portable PULSE System, both from Brüel & Kjaer, Narum, Denmark. The impedance tube system was composed of two different tubes. One tube had a diameter of 100 mm and was used for measurements over the frequency range 100 Hz–1600 Hz. The second tube had a diameter of 29 mm and was used for the frequency range of 500 Hz–6400 Hz. The frequency resolution was 4 Hz. The employment of dual tubes is predicated on the imperative to circumvent the occurrence of non-plane wave mode propagation within the tubes. For this reason, the ISO standard 10534-2 requires that the working frequency range be f₁ < f < f_u, where f₁ is the lower frequency of the tube, limited by the spacing between the two microphones and the uncertainty of the signal processing equipment, and f_u is the upper working frequency of the tube that must meet this condition, f_u · d < 0.58 · c₀, where d is the tube diameter, and c₀ the speed sound. In our case, this condition is fulfilled for both tubes: for the first tube, d (0.1 m) < 0.12 m, and for the second tube, d (0.029 m) < 0.033 m. The tube was closed, showing a loudspeaker at one end and a rigid termination at the opposite end. The sample was positioned in close proximity to the rigid termination, with its surface oriented perpendicularly to the direction of the sound waves incoming from the loudspeaker. The loudspeaker generated random pink noise inside the impedance tube and the signals, measured by two microphones separated by distance s, were analyzed by the PULSE system (Figure 3). The influence of atmospheric pressure on the variation in the sound velocity, relative humidity, and air temperature, were previously measured and introduced in the software PULSE system. The measurement process was repeated five times and the results were averaged.

2.6. Phenomenological Model

The sound absorption coefficient at the normal incidence of a sound fibrous absorber can be determined using physical–mathematical models [27,28]. In this way, it is possible to save time and avoid a lot of experimental tests. In these acoustic models, the characteristic acoustic impedance (composed by real and imaginary parts), as a function of the frequency, is determined in order to fit theoretical results and experimental measurements in a standing wave tube [29]. Two types of models are the most widely used: these are empirical models, which are mainly based on a large number of measurements, and phenomenological models, which introduce additional variables to optimize the behavior of the acoustic wave inside the fibrous material. The latter option has been shown to provide superior accuracy when compared with the former, primarily due to the inhomogeneity of the fibrous materials [10,11,28]. In the phenomenological models, the sound absorber is defined as a combination of air, a known fluid filling the pores, and solid material acting as a rigid frame (fiber) that reacts differently when the sound wave passes through it. Therefore, regarding the dissipation mechanisms, it is imperative to acknowledge those with viscous, thermal, and structural natures as a consequence of the vibration of the rigid frame [30,31].

Therefore, the characteristic acoustic impedance, Z_c(ω), and the propagation wavenumber, k(ω), for the fibrous sound absorber can be defined by the dynamic density of the fluid, ρ(ω), and the bulk modulus, K(ω), as follows:

$$Z_c\left(\omega \right)=\sqrt{\rho \left(\omega \right)·K\left(\omega \right)}$$

(4)

$$k\left(\omega \right)=\sqrt{\rho \left(\omega \right)/K\left(\omega \right)}$$

(5)

where the dynamic density of the fluid is expressed as follows:

$$\rho \left(\omega \right)={\alpha }_{\infty }{\rho }_0-{\displaystyle \frac{\sigma \varphi }{\omega }}F\left(\lambda \right)$$

(6)

$$\lambda =c\sqrt{{\displaystyle \frac{8{\alpha }_{\infty }{\rho }_0\omega }{\sigma \varphi }}}$$

(7)

In this expression, an adimensional shape factor λ, an adjustment parameter c (related to viscous effects in the pores), and a complex function related to the Bessel functions of zero and first order denoted by F(λ), are formulated. The parameter c is generally accepted to range between 0.3 and 3 [32]. To simplify the expression (6), Johnson et al. [33] established a sufficient degree of precision for F(λ) for cylindrical pores, and so the dynamic density of the fluid finally can be expressed as follows:

$$\rho \left(\omega \right)={\alpha }_{\infty }{\rho }_0\left(1+{\displaystyle \frac{\sigma \varphi }{j\omega {\rho }_0{T\alpha }_{\infty }}}·c\sqrt{1+{\displaystyle \frac{{\lambda }^2}{16}}}\right)$$

(8)

Taking into account the simplification established by Johnson et al. [33] for cylindrical pores, the bulk modulus can be expressed as follows:

$$K\left(\omega \right)={\displaystyle \frac{\gamma P_0}{\frac{\gamma -(\gamma -1)}{1+\frac{c^{\prime }\sigma \varphi }{j{N}_{pr}\omega {\alpha }_{\infty }{\rho }_0}·\sqrt{1+{jN}_{pr}{\left(\frac{\lambda }{4c{c}^{\prime }}\right)}^2}}}}$$

(9)

In this expression, the porosity is denoted by ϕ, c’ is formulated as another adjustment shape parameter (related to thermal effects in the pores, which is generally accepted to be expressed as 1/c [32]), the air density is denoted by ρ₀, j² = −1, ω is the angular frequency (ω = 2πf), γ is the ratio of the specific heat capacity (≈1.4), the atmospheric pressure is denoted by P₀ (≈101,320 N·m⁻²), and the Prandtl number is denoted by N_pr (≈0.71).

The sound absorption coefficient α of a fibrous absorber (having a thickness d) can be determined using the surface acoustic impedance Z(ω) as follows:

$$Z\left(\omega \right)=-j{Z}_c\left(\omega \right)cot\left(k\left(\omega \right)·d\right)$$

(10)

$$\alpha ={1-\left|{\displaystyle \frac{Z\left(\omega \right)-{\rho }_0{c}_0}{Z\left(\omega \right)+{\rho }_0{c}_0}}\right|}^2$$

(11)

An iterative numerical method was used to minimize the differences between the experimental and the predicted sound absorption spectra, allowing us to obtain c and c′.

In order to evaluate the degree to which the measurements aligned with the phenomenological model, the frequency-dependent relative error between the experimental and theoretical sound absorption coefficient was used, using the following expression:

$$\epsilon =\left|{\displaystyle \frac{{\alpha }_{meas}-{\alpha }_{model}}{{\alpha }_{meas}}}\right|·100$$

(12)

3. Results

Fiber diameters, bulk and skeletal density, porosity, tortuosity, and air flow resistivity were measured and analyzed (

Table 1. Physical properties—bulk density (ρ_m), porosity (ϕ), tortuosity (α_∞) and flow resistivity (σ)—of the esparto fiber samples studied in this work.

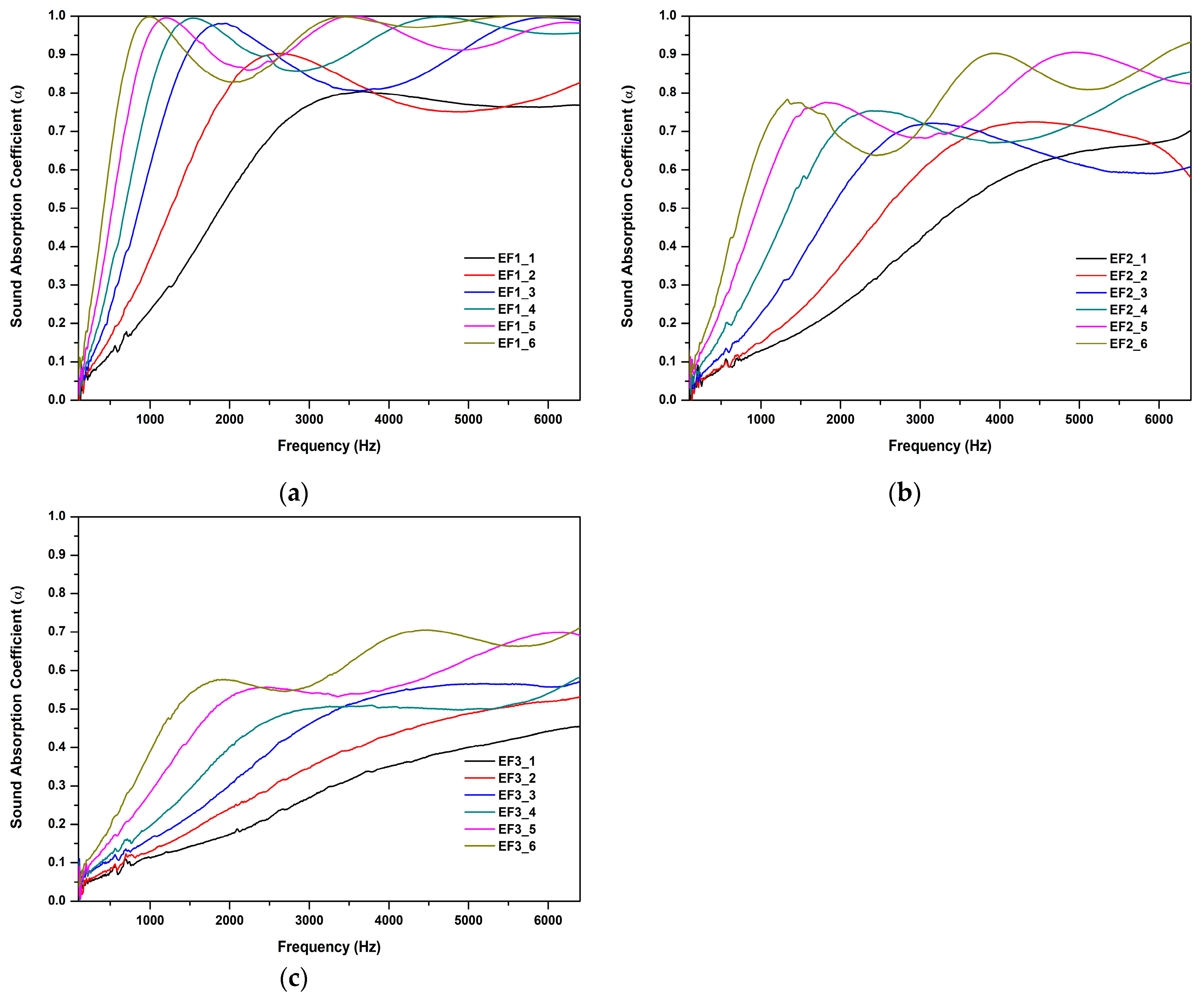
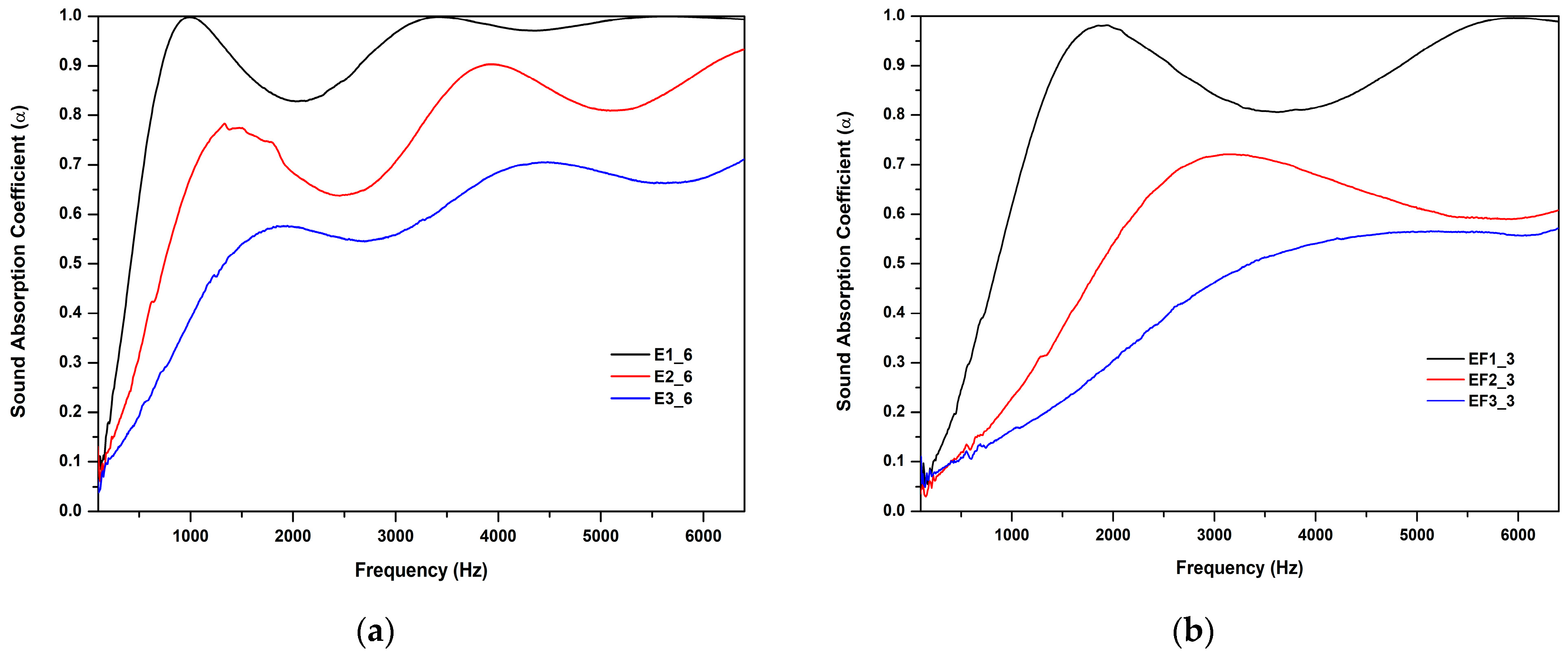
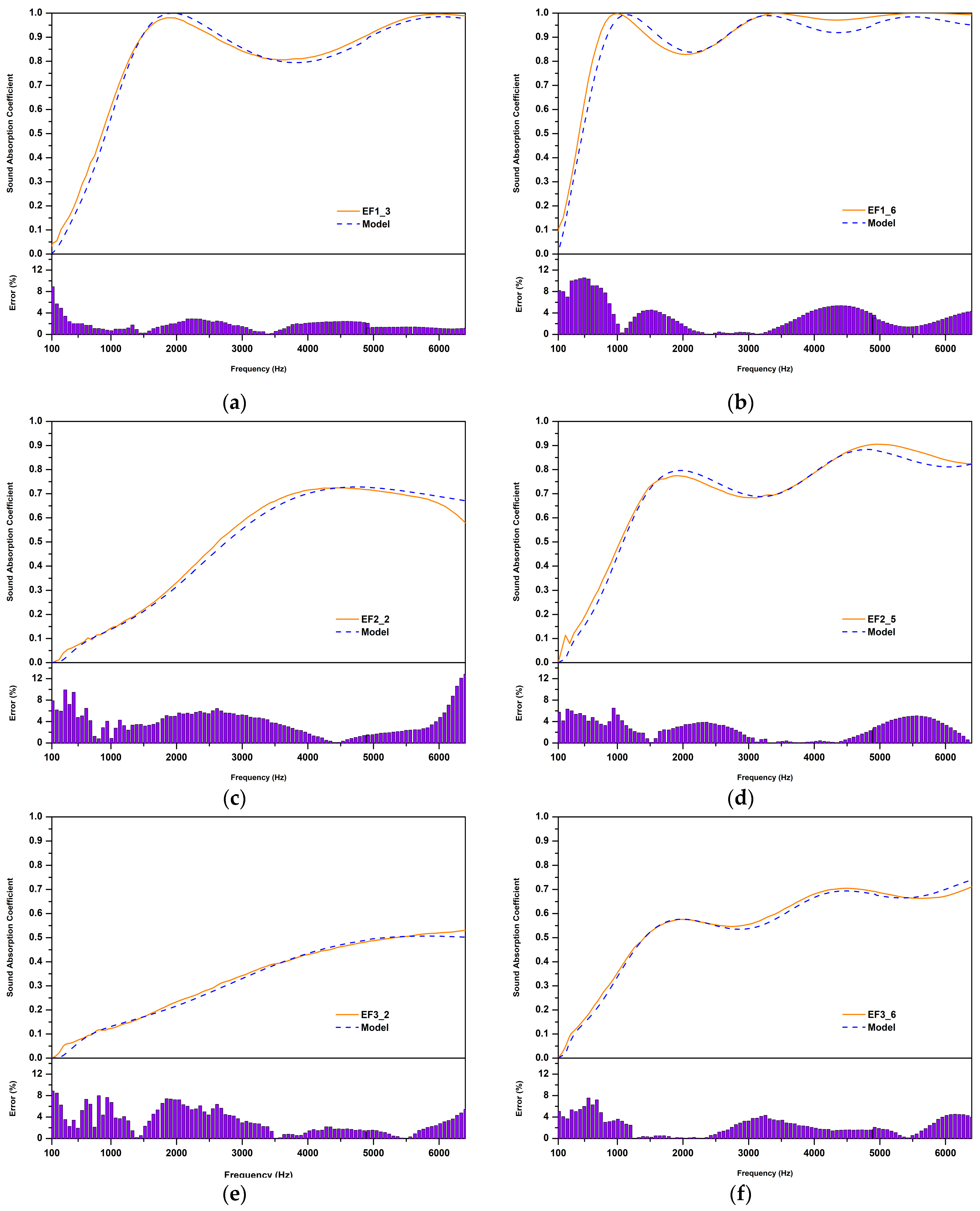
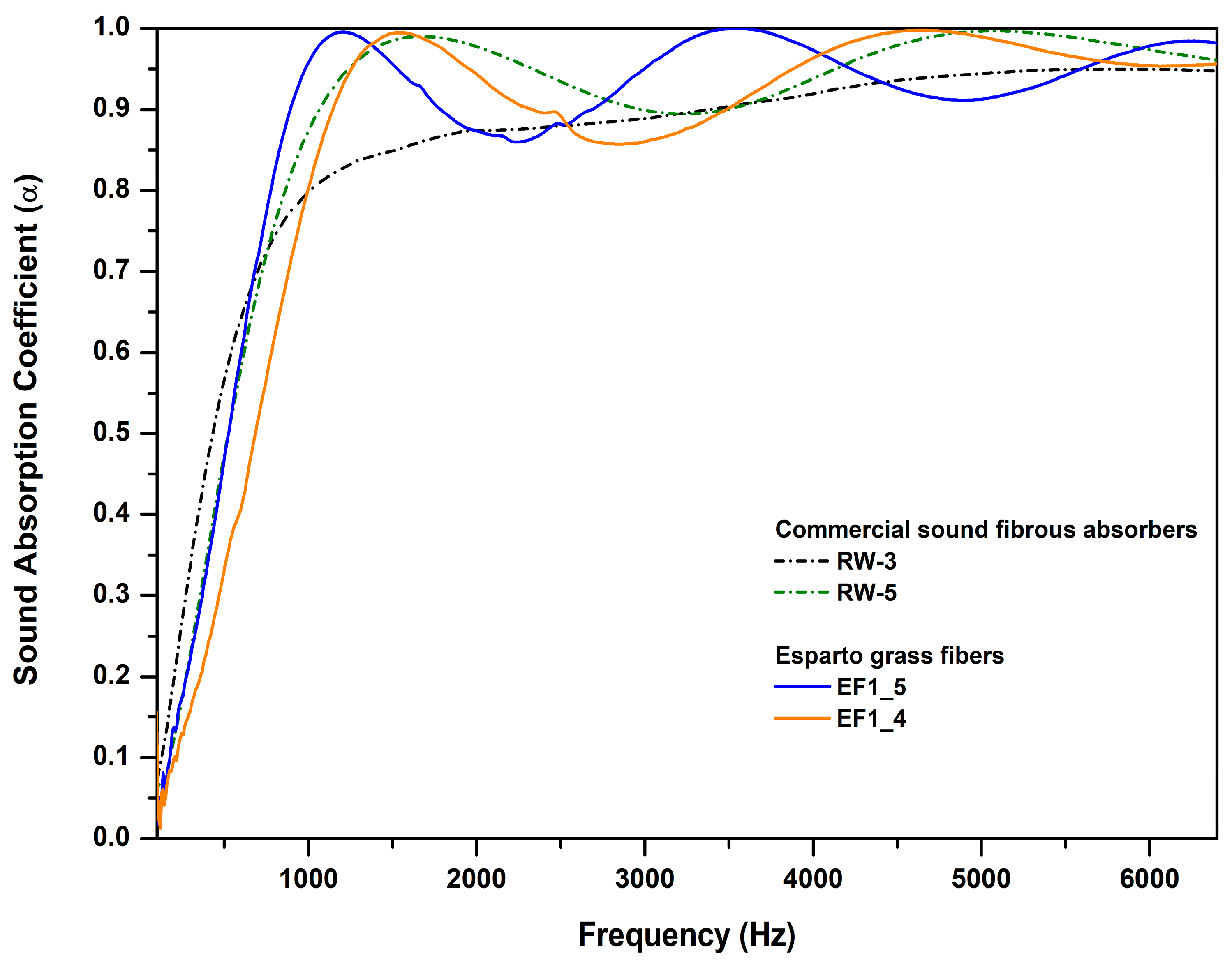
Sample ID	ρm (kg/m3)	ϕ (%)	α∞	σ (Pa s/m2)
EF1	199.8 ± 8.1	84.6 ± 1.2	1.091 ± 0.009	13,199 ± 227
EF2	104.0 ± 6.2	91.9 ± 1.4	1.044 ± 0.010	3692 ± 163
EF3	56.8 ± 3.5	95.6 ± 1.1	1.023 ± 0.005	917 ± 82

). Average fiber diameters were determined by confocal microscopy. Then, 20 samples of esparto fibers were measured and the diameters were averaged. The diameters of fibers (Figure 4) ranged between 161 μm and 239 μm, with an average fiber diameter of 210 ± 22 μm. The values obtained were in accordance with the values obtained for esparto fibers in previous works, where these kinds of fibers showed irregular shapes and diameters [34,35].

The bulk density (ρ_m) of the esparto fibers was determined based on the relationship between the mass and the volume of each sample (Table 1), while the skeletal density of the esparto fibers was determined using a helium pycnometer. The value obtained for the skeletal density was 129.9 ± 6.8 kg/m³. With this value, the open porosity of each sample was calculated. It is widely accepted that the open porosity of fibrous materials can exert a considerable influence on their acoustic behavior. The values of open porosity are shown in Table 1. These values ranged from 84.6% to 95.6%, showing that there was an inverse relationship between porosity and bulk density; the higher the bulk density, the lower the porosity. This was due to the higher number of pores in the fibrous material, as was observed by many other authors [11,12,13,15]. Flow resistivity values ranged from 917 to 13,199 Pa s/m². The results indicated that an increase in the bulk density of the samples resulted in a reduction in the porosity. Consequently, this led to an increase in the airflow resistivity of the samples, showing a direct relationship between porosity and flow resistivity [36].

Figure 5 shows the effect of the thickness on the sound absorption spectra. This figure shows the sound absorption spectra of the samples studied in this work, displaying the same value of bulk density and different thicknesses, when applying a rigid-back wall to the samples in the impedance tube. It was established that an increase in the thickness of the fibrous sound absorber resulted in the occurrence of the first absorption maximum, which showed lower amplitude, and the frequency bandwidth shifted towards lower frequencies, increasing the value of the sound absorption coefficient for this first interference maximum. Therefore, a higher quarter-wavelength resonance maximum was obtained when the thickness of the sample corresponded to a quarter wavelength of the sound wave inside the sample. This effect could be attributed to the absorption suffered by the higher-wavelength acoustic waves when increasing the thickness, which was attributable to the heightened dissipative energy process occurring within the fibrous absorber, based on the viscous and thermal effects when the sound wave passed through the fibrous absorber. The values of the sound absorption coefficient for the first maximum were close to 1. Specifically, values of 0.9981, 0.9953, and 0.9946 were achieved at 992, 1208 and 1536 Hz for samples of 6, 5 and 4 cm, respectively. This was also the case for the samples with higher density and flow resistivity (EF1). In the case of samples with lower values of density and flow resistivity, the values of the sound absorption coefficient for the first maximum were 0.573, 0.5563 and 0.5101, which were achieved at 1904, 2464 and 3784 Hz, for samples of 6, 5, and 4 cm, respectively. The lower values of the sound absorption coefficient were due to the lower dissipative energy process inside the fibrous absorber because of the lower amount of fibers in the samples. If we compare these results with those obtained by Arenas et al. [20], it is possible to affirm that sound absorption spectra present a similar trend in the case of comparable thicknesses and densities.

Figure 6 shows the effect of the density on the sound absorption spectra. This Figure shows the sound absorption spectra for samples with the same thickness and different bulk densities when applying a rigid-back wall to the samples in the impedance tube. The findings demonstrated that the value of the sound absorption coefficient exhibited a substantial increase with rising bulk density for samples of equivalent thickness. This phenomenon was observed across the low-, medium-, and high-frequency ranges. Considering that the tortuosity of these samples increased with the density, the path of the sound wave inside the fibrous sample was more complex, resulting in greater sound energy loss inside the sample. Moreover, as is well known, tortuosity affects the frequency where the first absorption maximum is achieved [10]. The higher the tortuosity, the higher the sound absorption coefficient. Thus, this first absorption maximum shifts to lower frequencies and displays decreased amplitude. In the case of Figure 6a, the first interference maximum was achieved at 992, 1328, and 1904 Hz with sound absorption coefficients equal to 0.9981, 0.7832, and 0.5763, respectively. In the case of Figure 6b, 3 cm in thickness, the first interference maximum was achieved at 1994, 3152, and 5200 Hz with sound absorption coefficients equal to 0.9813, 0.7213, and 0.5650, respectively.

Figure 7 shows the experimental sound absorption spectra and those predicted by the model described in Equations (4) to (10), using the experimental values of porosity, flow resistivity, tortuosity, and thickness as input parameters for each sample. In general, the values obtained from the phenomenological model were in good agreement with the experimental results. In general, the frequency-dependent relative errors for frequencies lower than 1000 Hz ranged from 0.8% to 10.6% as could be expected, with frequency-dependent relative errors below 5.3% obtained for frequencies above 1000 Hz. In some samples, such as EF1_6, EF3_2, and EF2_2, the frequency-dependent relative error was up to 8% for frequencies below 600 Hz. The frequency-dependent relative errors between the experimental and the theoretical sound absorption coefficient were above 12%, but only for the small broad bandwidth (6200–6400 Hz) seen for sample EF2_2. Nevertheless, these errors, comparable to the errors obtained in other studies [11,12,15,36,37] using a phenomenological model to predict the acoustic performance of natural fibrous materials, could be regarded as negligible in relation to the overall frequency range observed across all samples. If we compare the results from the prediction sound absorption spectra obtained in the work of Arenas et al. [20] and those obtained in the present work, it can be observed that the empirical model underestimated the sound absorption at low frequencies, with an average error for all data of less than 4%. For the phenomenological model, the sound absorption was better fitted at low frequencies, and the average error for all data ranged between 1.8% and 3.9%. The phenomenological model demonstrated a satisfactory degree of accuracy in predicting the frequency of the absorption maximums and their corresponding sound absorption coefficient values for all the samples. However, due to the inhomogeneity of the samples, their porosity, and flow resistivity measurements, relative errors could be introduced in the theoretical sound absorption spectra of the samples.

To compare the sound absorption spectra of esparto fibers with some commercial sound fibrous absorbers, currently used in construction, two different fibrous materials made of rock wool, RW-3 (d = 3 cm; ρ_m = 30 kg/m³; fiber diameter = 10 μm; σ = 8248 Pa s/m²) and RW-5 (d = 5 cm; ρ_m = 110 kg/m³; fiber diameter = 15 μm; σ = 12,547 Pa s/m²) [23], were tested and compared with samples EF1_4, EF1_5, and EF2_6 (Figure 8).

It is a well-established fact that the values of the sound absorption coefficient of fibrous absorbers are predominantly influenced by their bulk density, which is a critical factor for porous materials, playing a pivotal role. Despite the relatively high values of the bulk density of the esparto grass fibers, regarding the synthetic fibers, an increase in sound absorption coefficient at medium and high frequencies was observed due to surface friction rises leading to a greater energy loss. Conversely, lower frequencies (700 Hz) can be absorbed by less dense and more open structures, while denser structures prove effective at absorbing sounds above 1000 Hz. The sound absorption spectra for samples EF1_5 and RW-5 were slightly different, with both samples having the same thickness. It was established that the initial absorption maximum of the two samples was observed at distinct frequencies (1208 Hz and 1680 Hz). However, the attainment of comparable sound absorption coefficient values, 0.995 and 0.991, respectively, is noteworthy. Something similar happened with the samples EF1_4 and RW-3, although the thickness of the samples was different. The sound absorption spectra for both samples were different. Whilst the first absorption maximum of the sample EF1_4 occurred at 1536 Hz, achieving a sound absorption coefficient value of 0.994, no absorption maximum was found for the sample RW-3.

4. Conclusions

The objective of this study was to conduct an experimental and theoretical investigation into the acoustic performance of eco-efficient fibrous materials, such as esparto grass. To achieve this objective, samples with 3 different bulk densities, with 6 different thicknesses for each sample, were manufactured. Certain properties such as porosity, bulk and real density, and flow resistivity were measured, while tortuosity was evaluated by using a simple model. Subsequently, the sound absorption coefficients at normal incidence were measured. The effect of the thickness and the density were evaluated, showing in both cases that increasing the thickness and density caused an increase in the sound absorption coefficient toward lower frequencies and a reduction in bandwidth.

Moreover, a phenomenological model was tested to predict the sound absorption coefficients of esparto fibers. With this model, it was possible to determine the sound absorption spectra with enough accuracy for samples made of esparto fibers when the thickness, porosity, tortuosity, and flow resistivity were known, showing average relative errors below 6%. However, some samples and some frequencies presented discrepancies between experimental and theoretical results, which might be due to the inhomogeneity of the samples.

Finally, comparative analysis was conducted on the sound absorption performance of esparto grass fibers and several commercially available fibrous absorbers. The findings indicated that esparto grass fibers exhibited acoustic performances comparable to those of fibrous absorbers commonly employed in the building sector.