Sonic Boom Impact Assessment of European SST Concept for Milan to New York Supersonic Flight
Abstract
1. Introduction
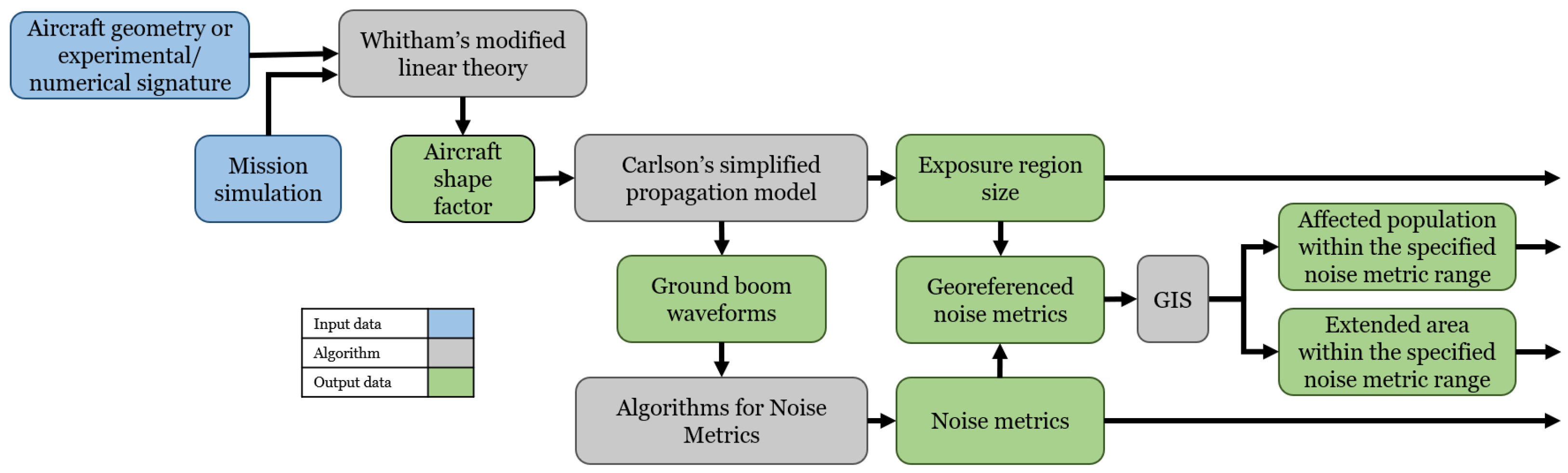
2. Surrogate Model for Sonic Boom Analysis
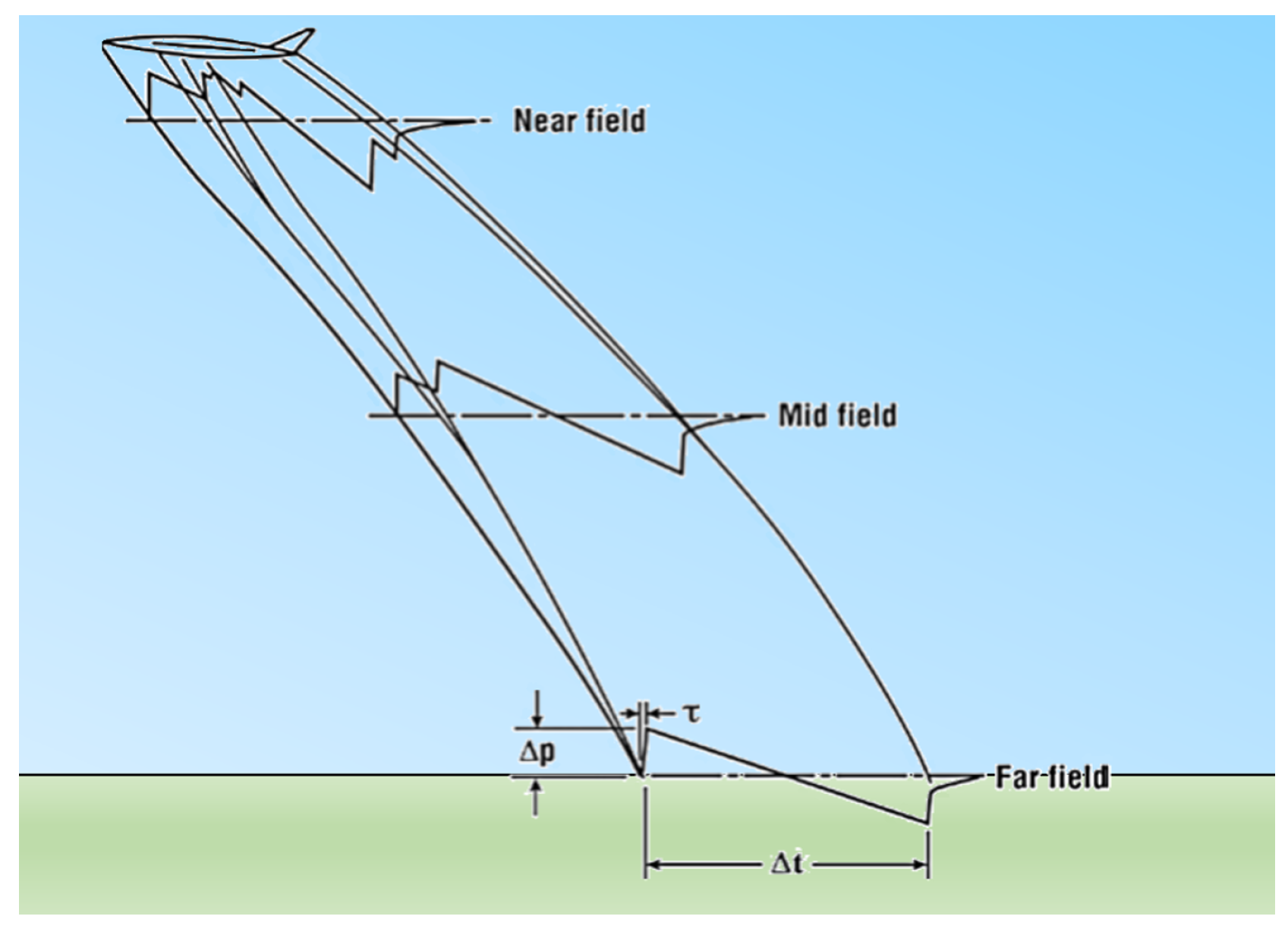
2.1. Near-Field Pressure Signatures
2.2. Whitham’s Modified Linear Theory
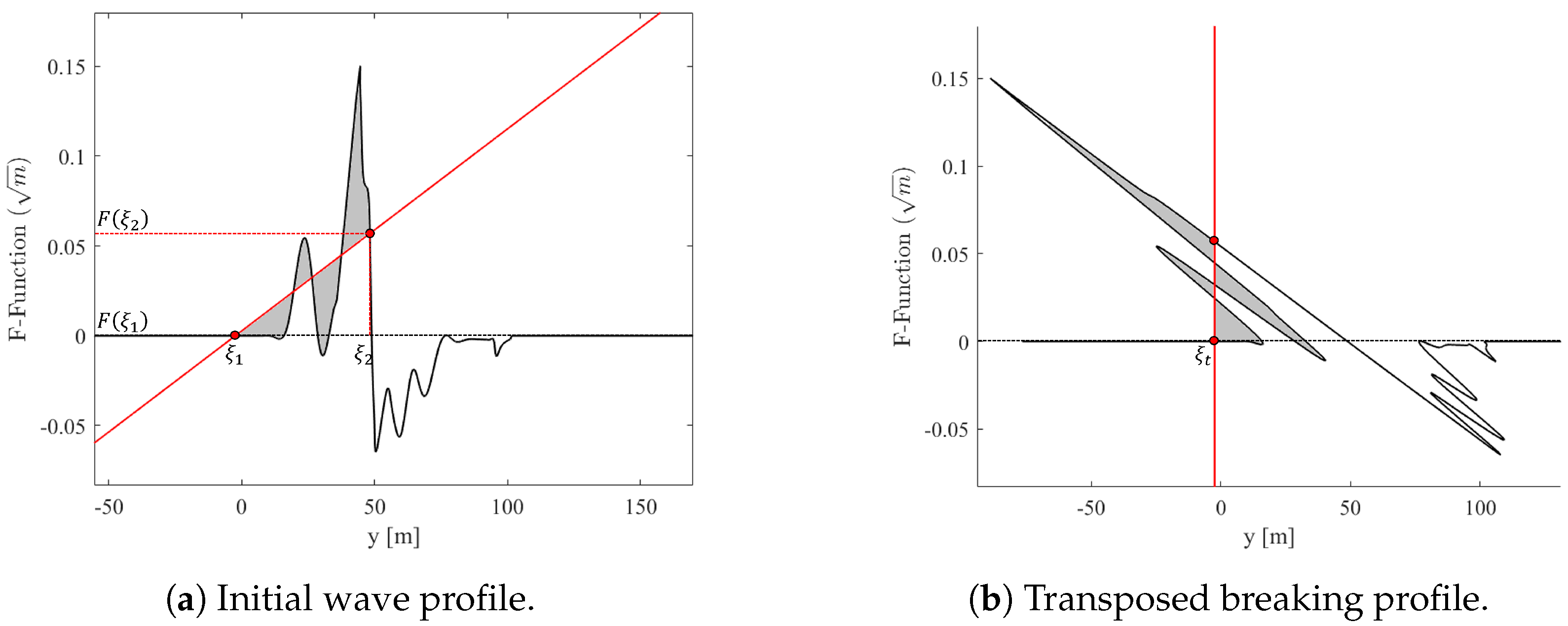
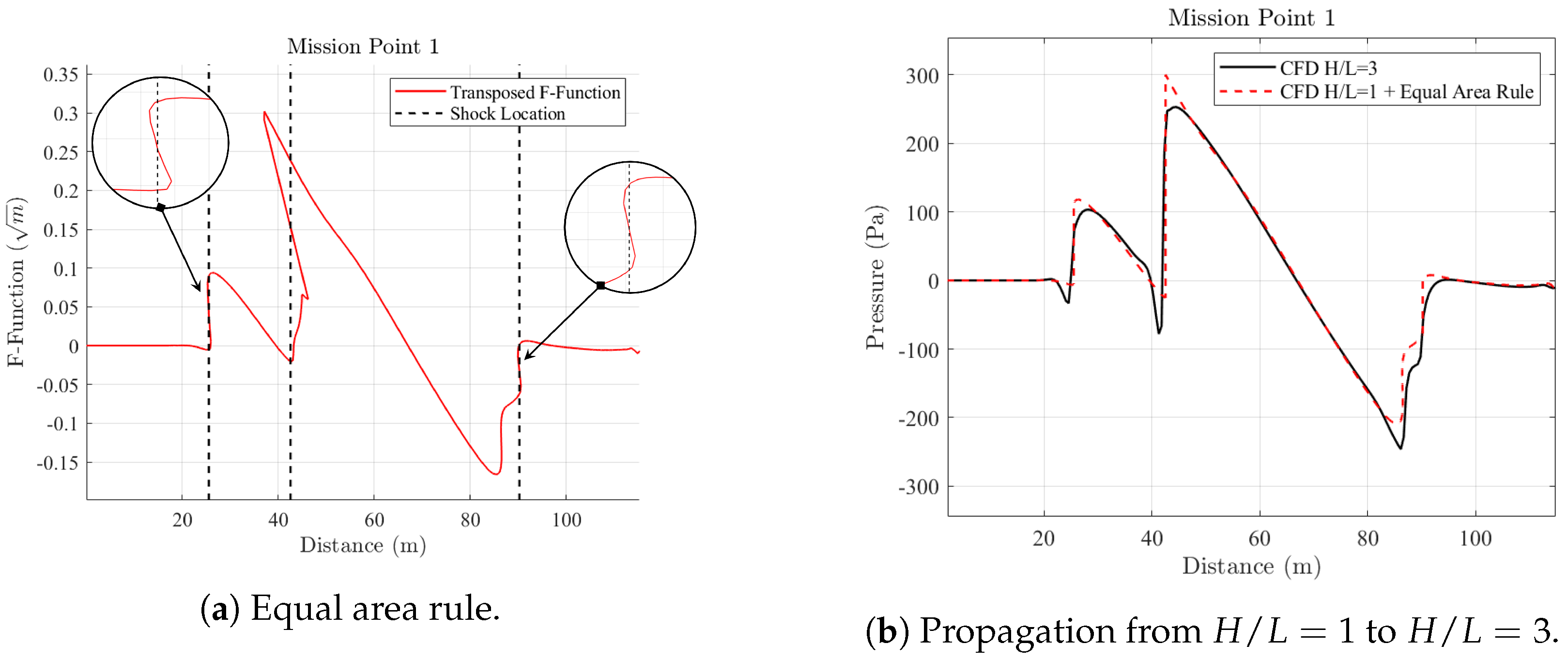
Whitham’s Equal Area Rule
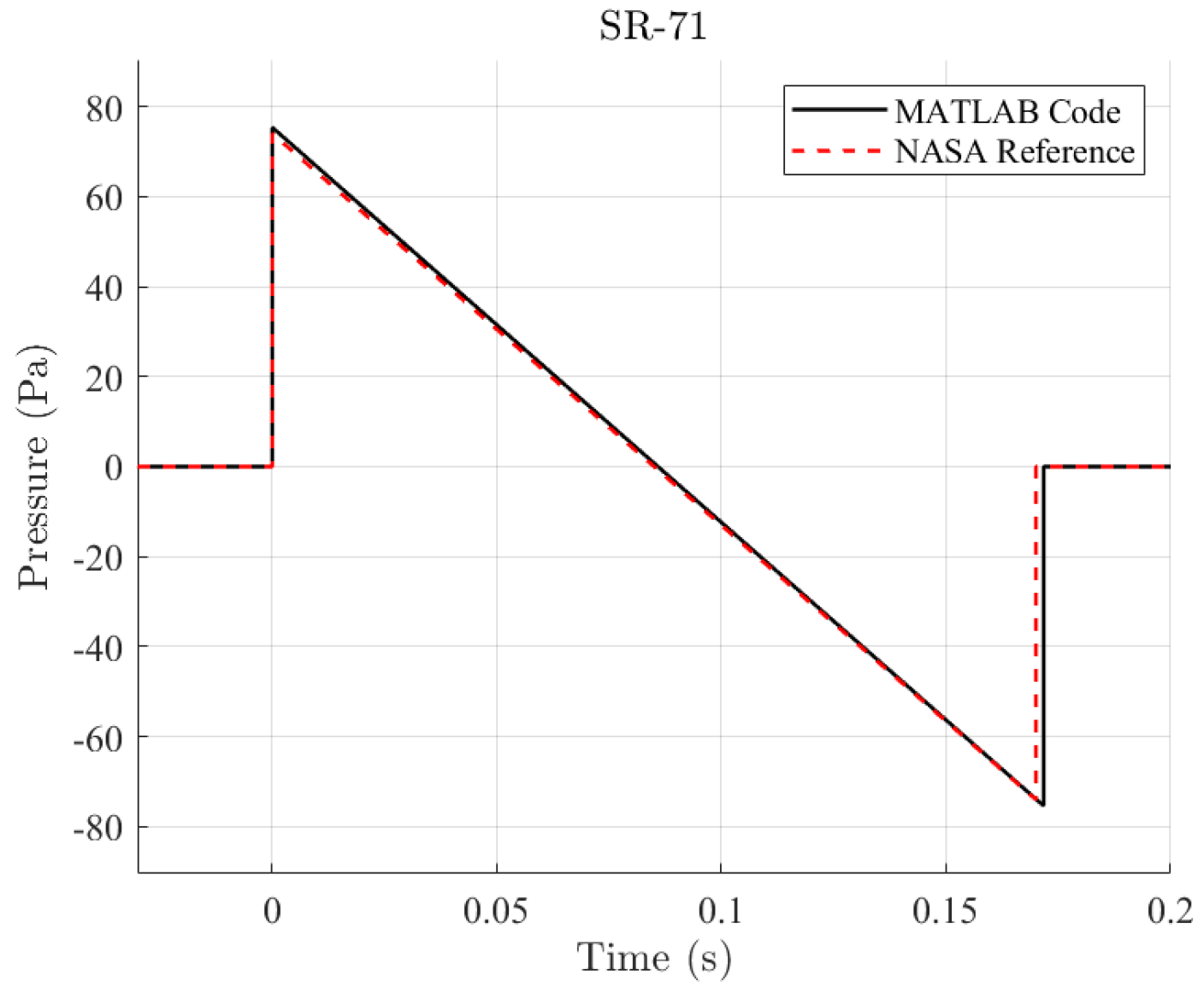
2.3. Propagation of Sonic Boom Signatures to Ground Level Through Homogeneous Atmosphere
2.4. Propagation of Sonic Boom Signatures to Ground Level Through Standard Atmosphere
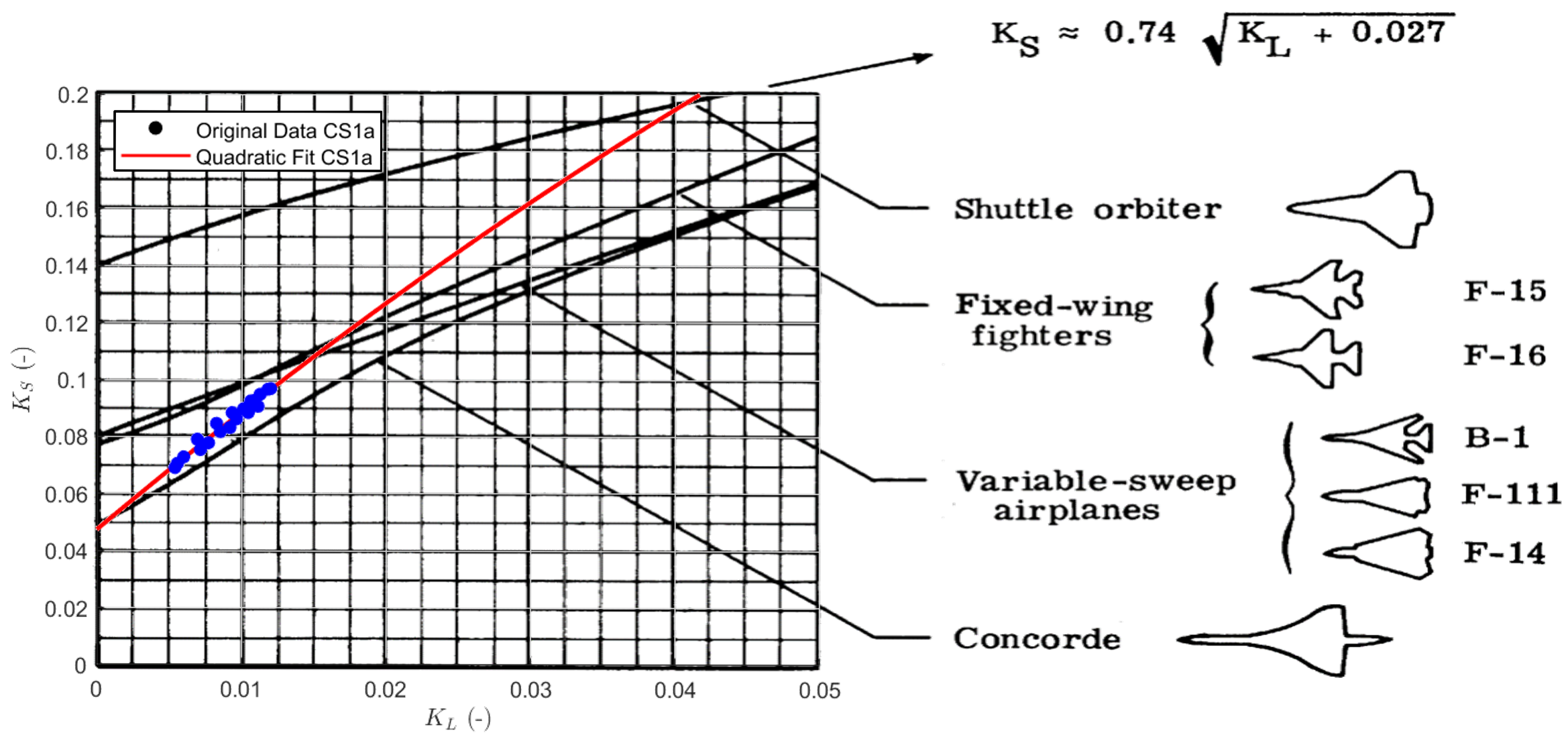
2.5. Aircraft Shape Factor and Mission Profile Regression Model
3. Results of the Presented Procedure on Sonic Boom Impact
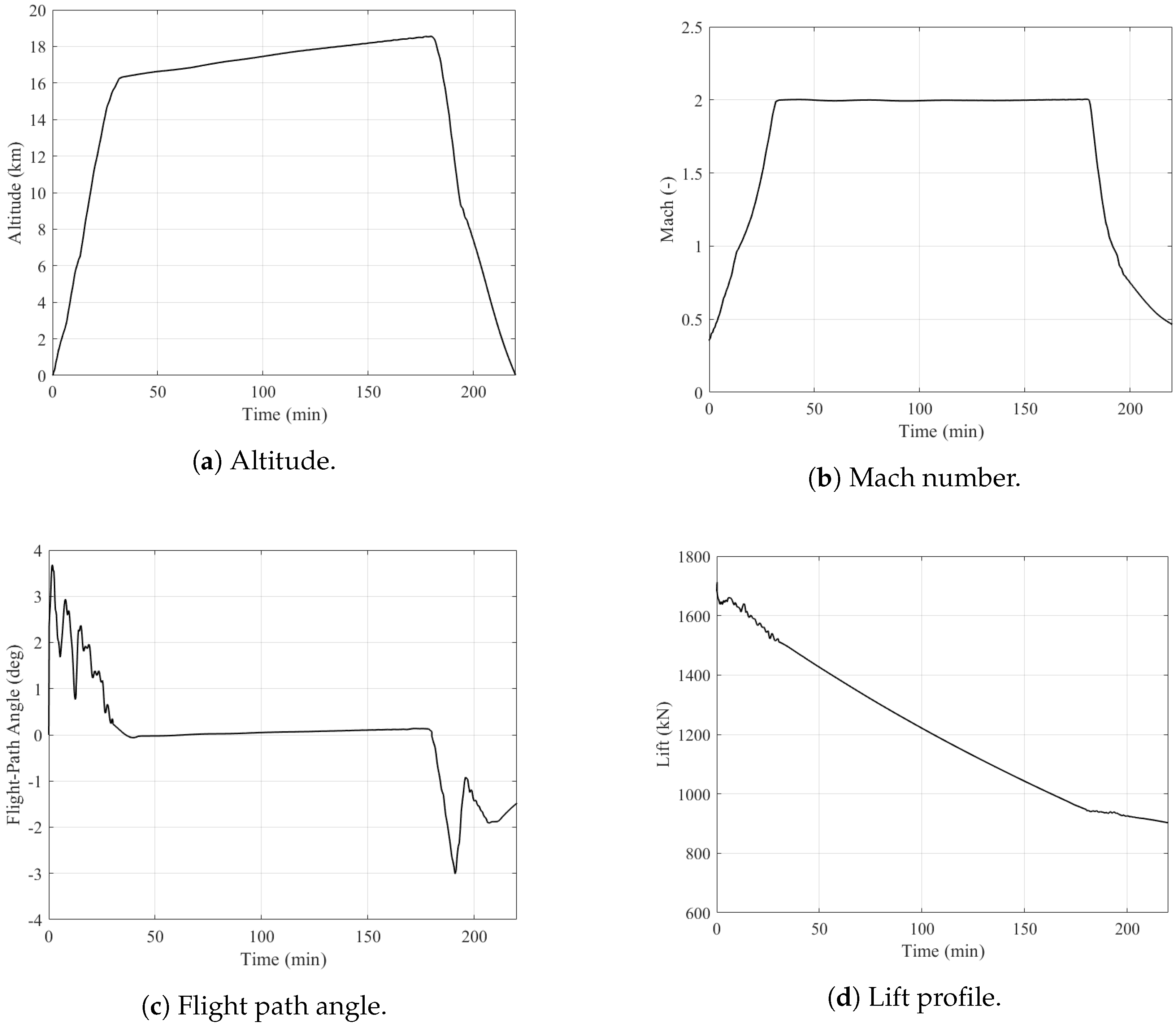
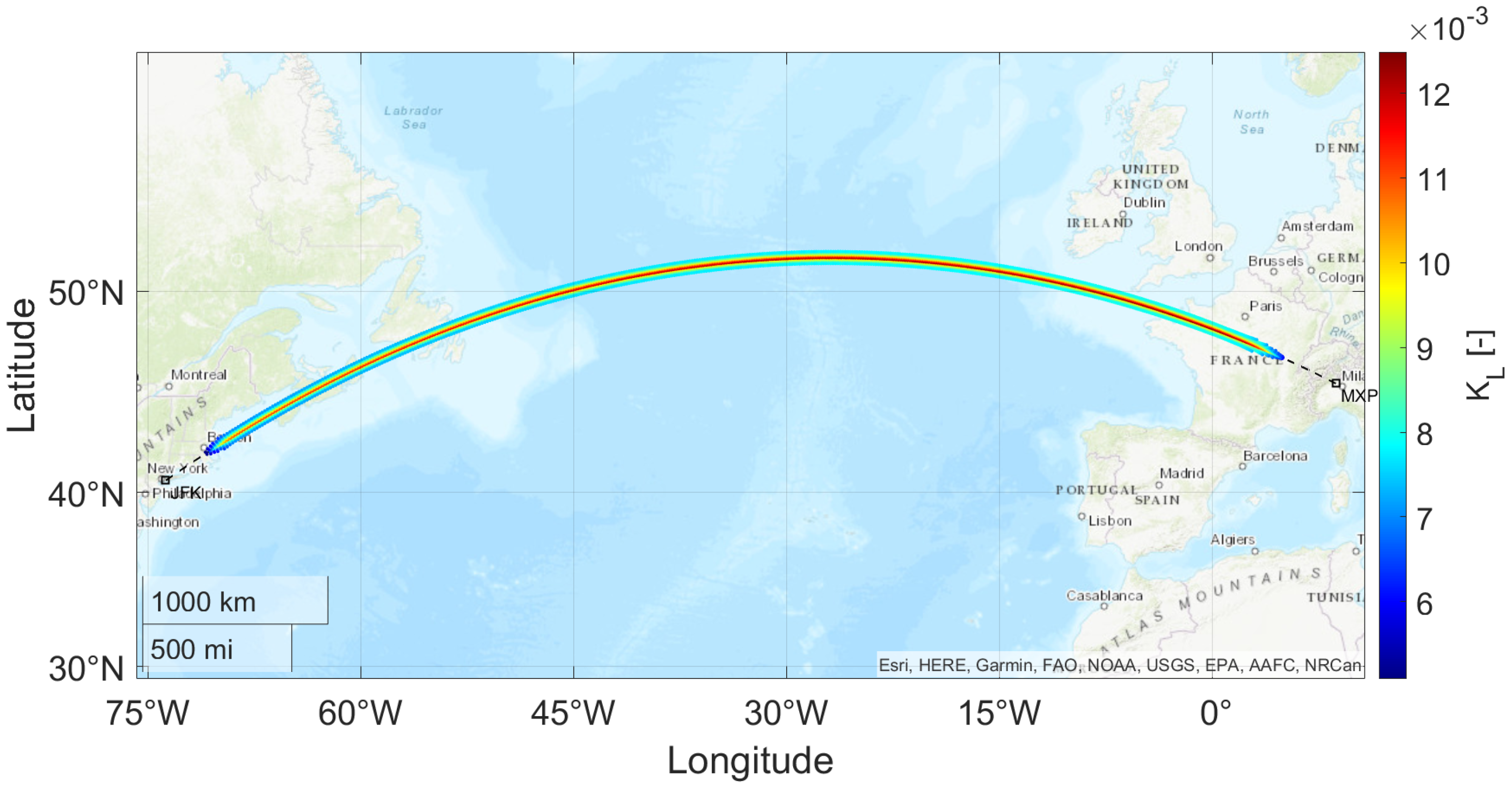
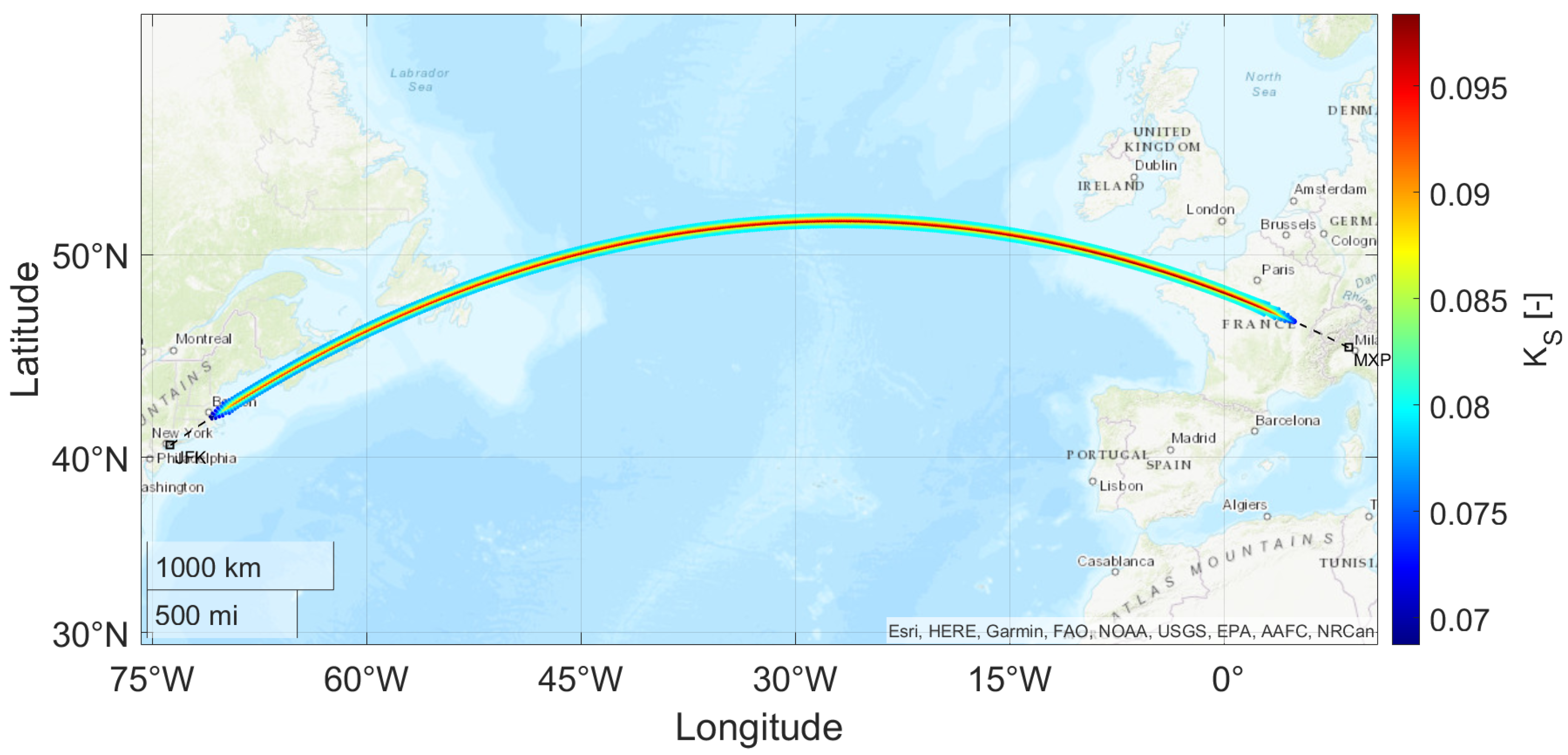
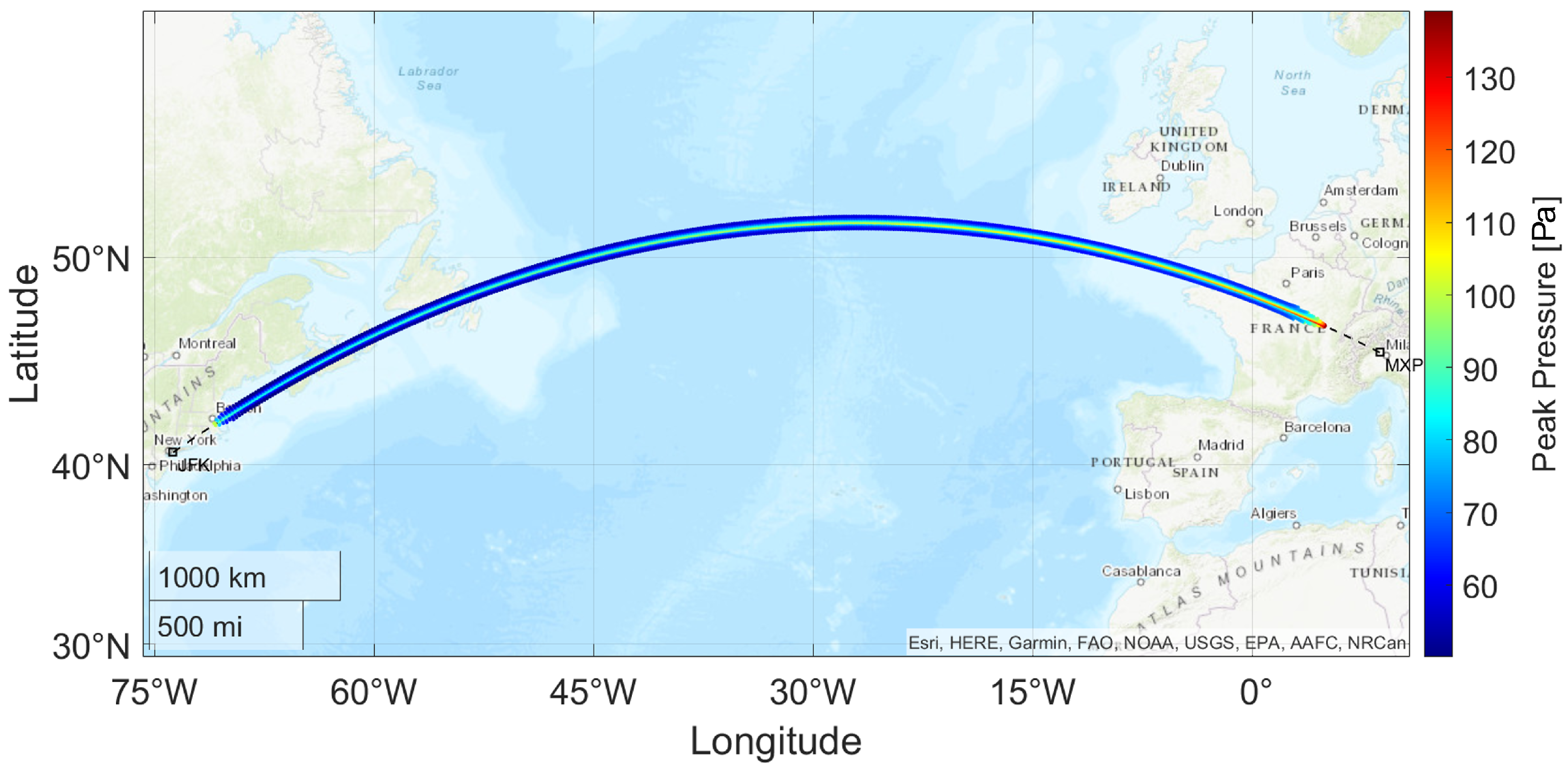
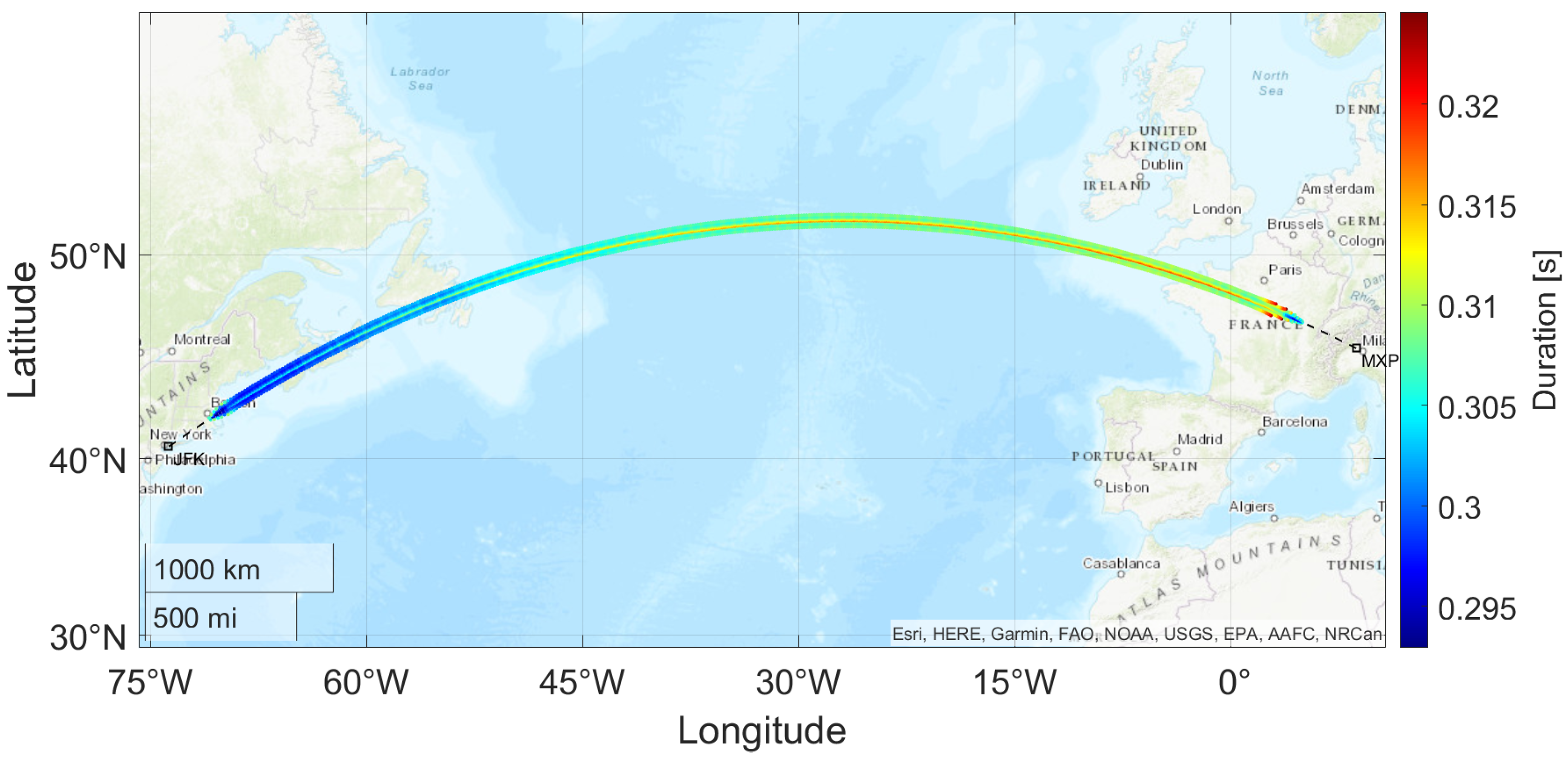
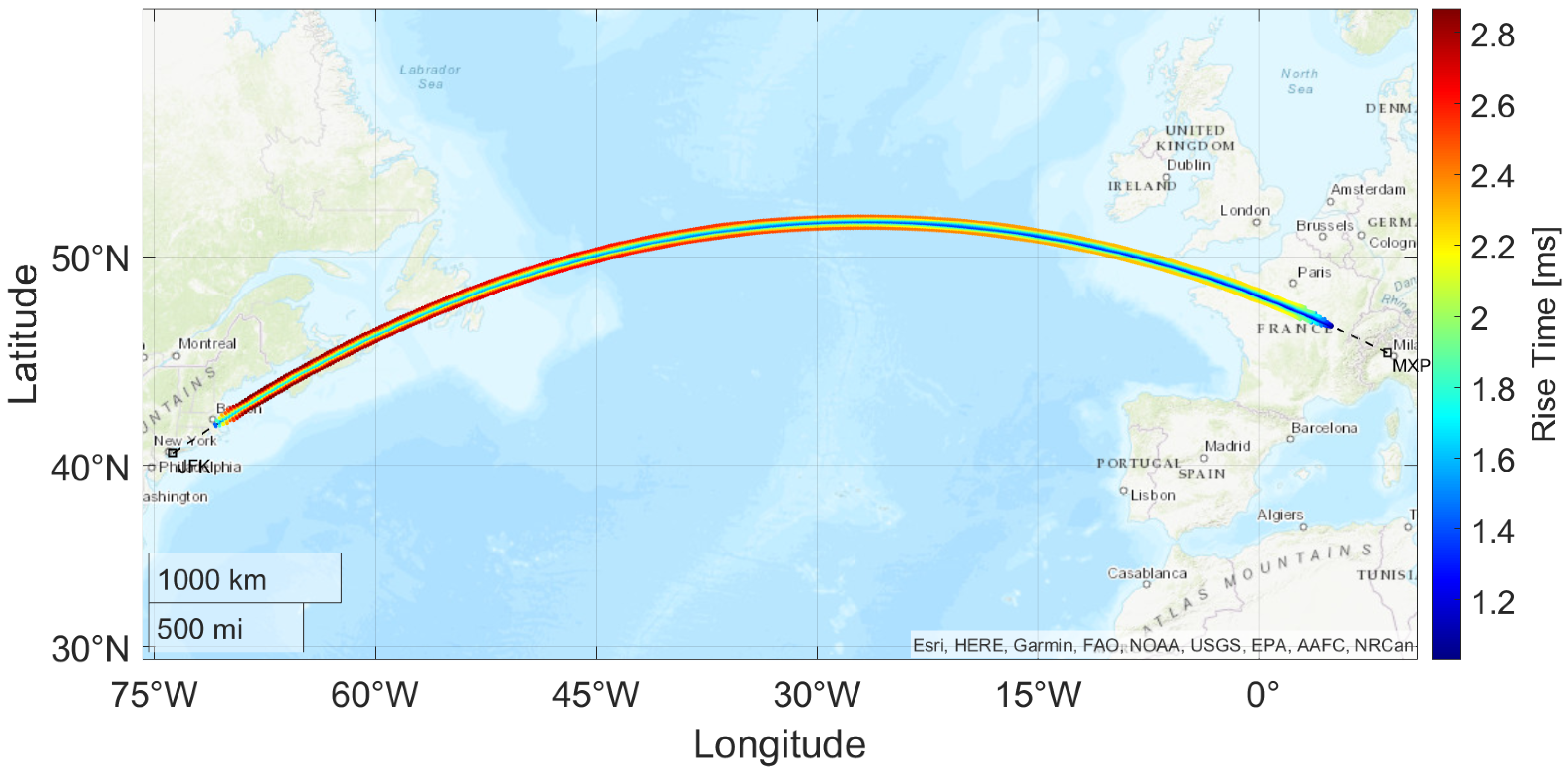
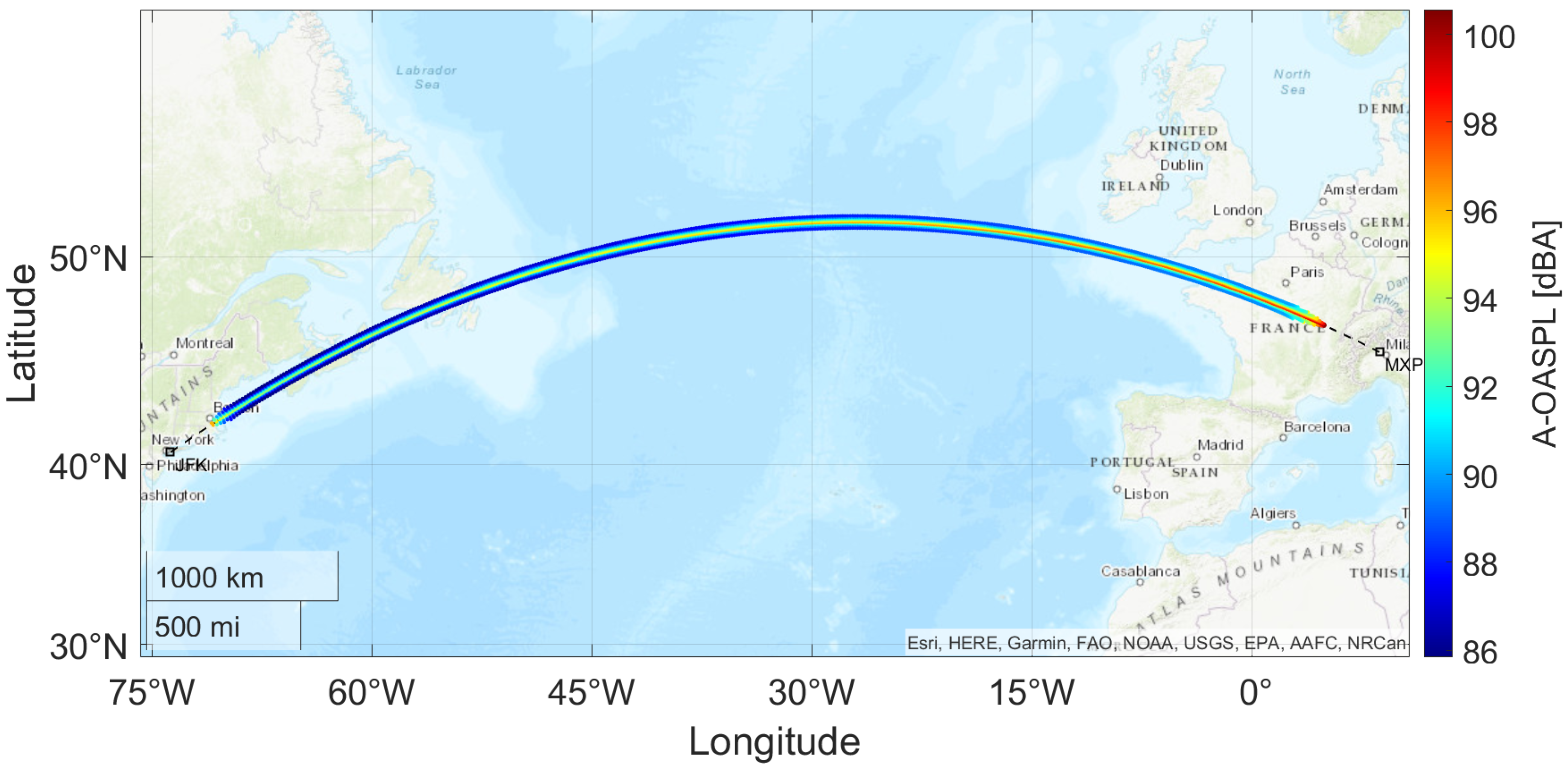
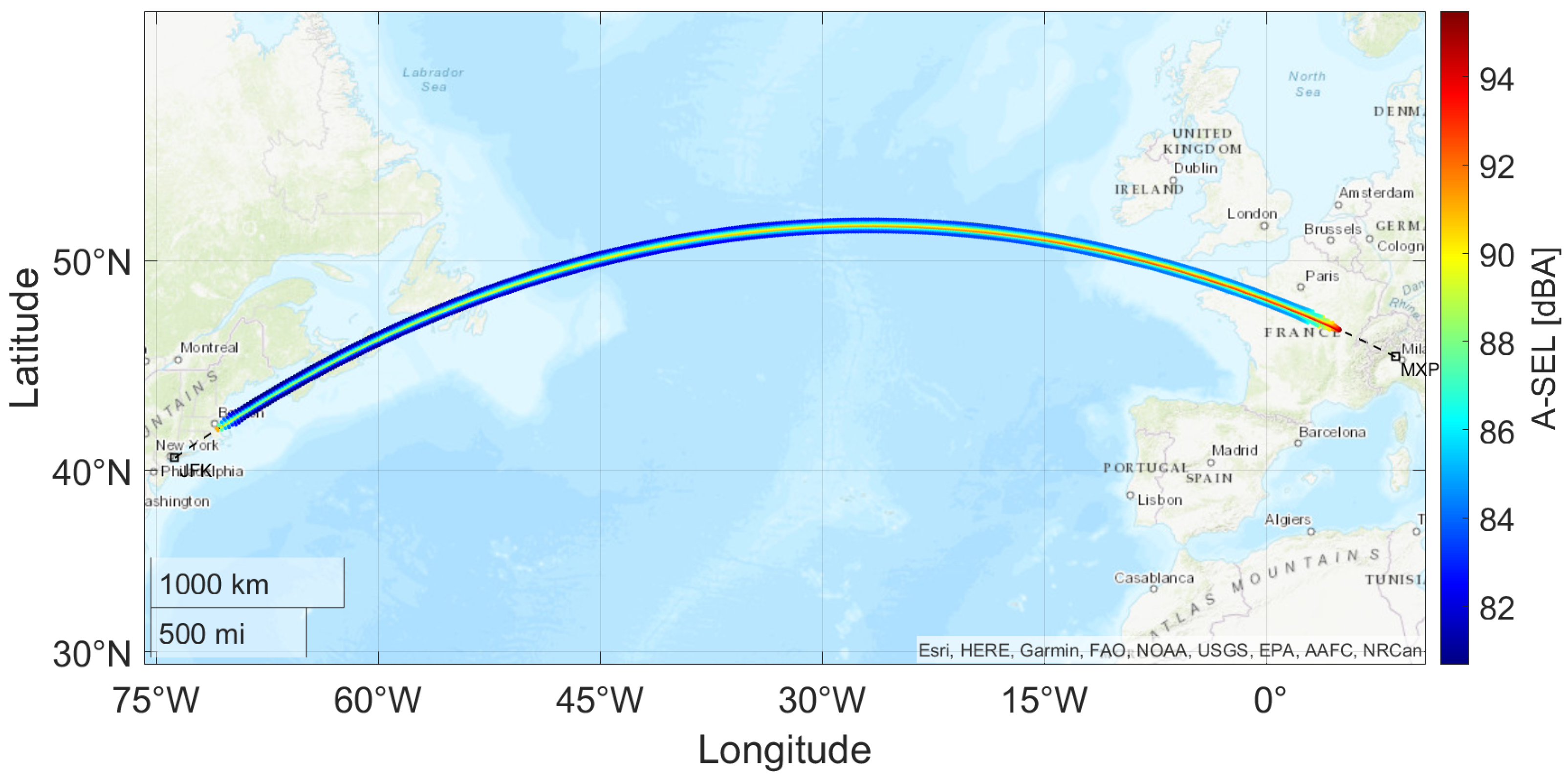
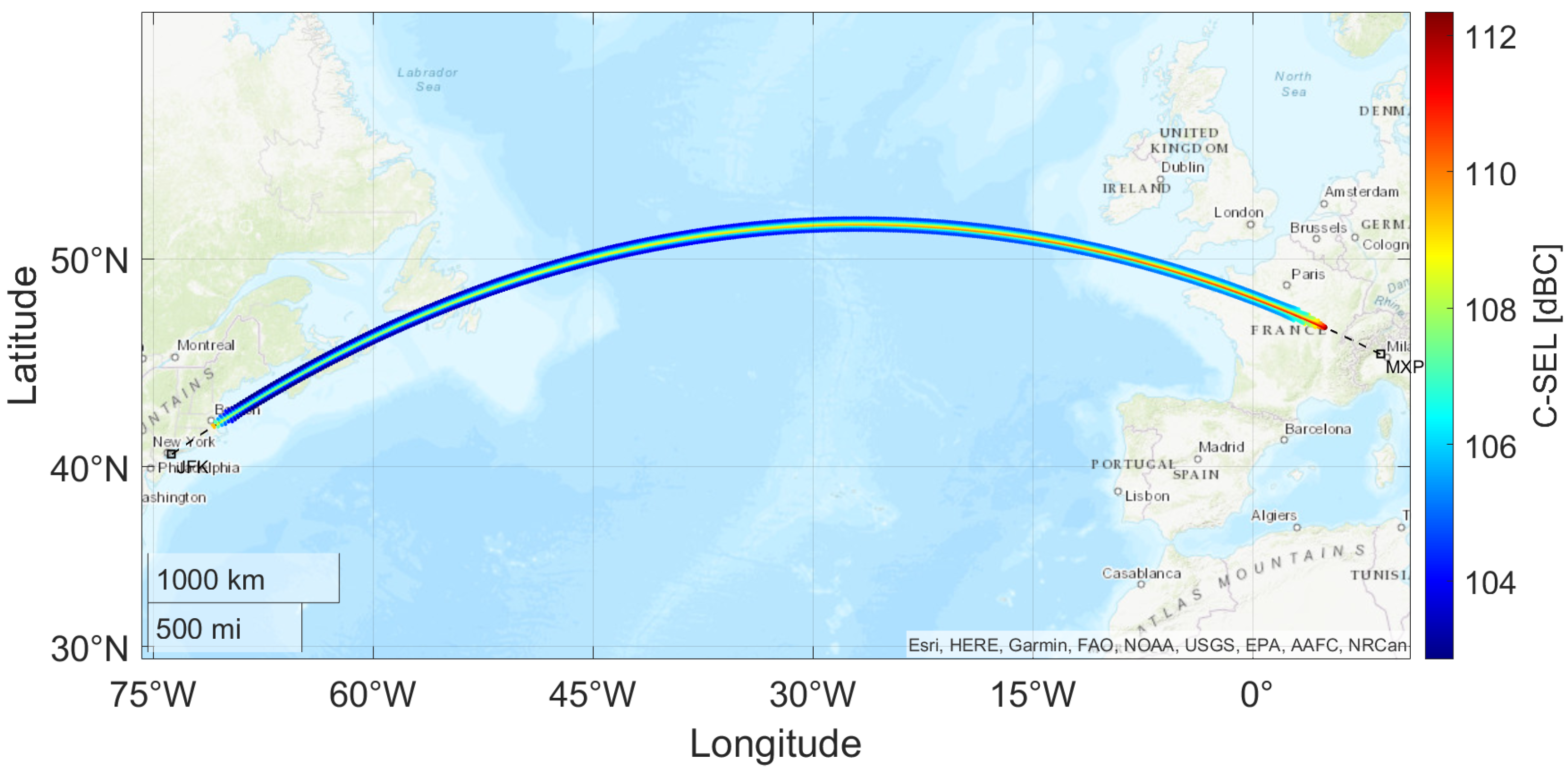
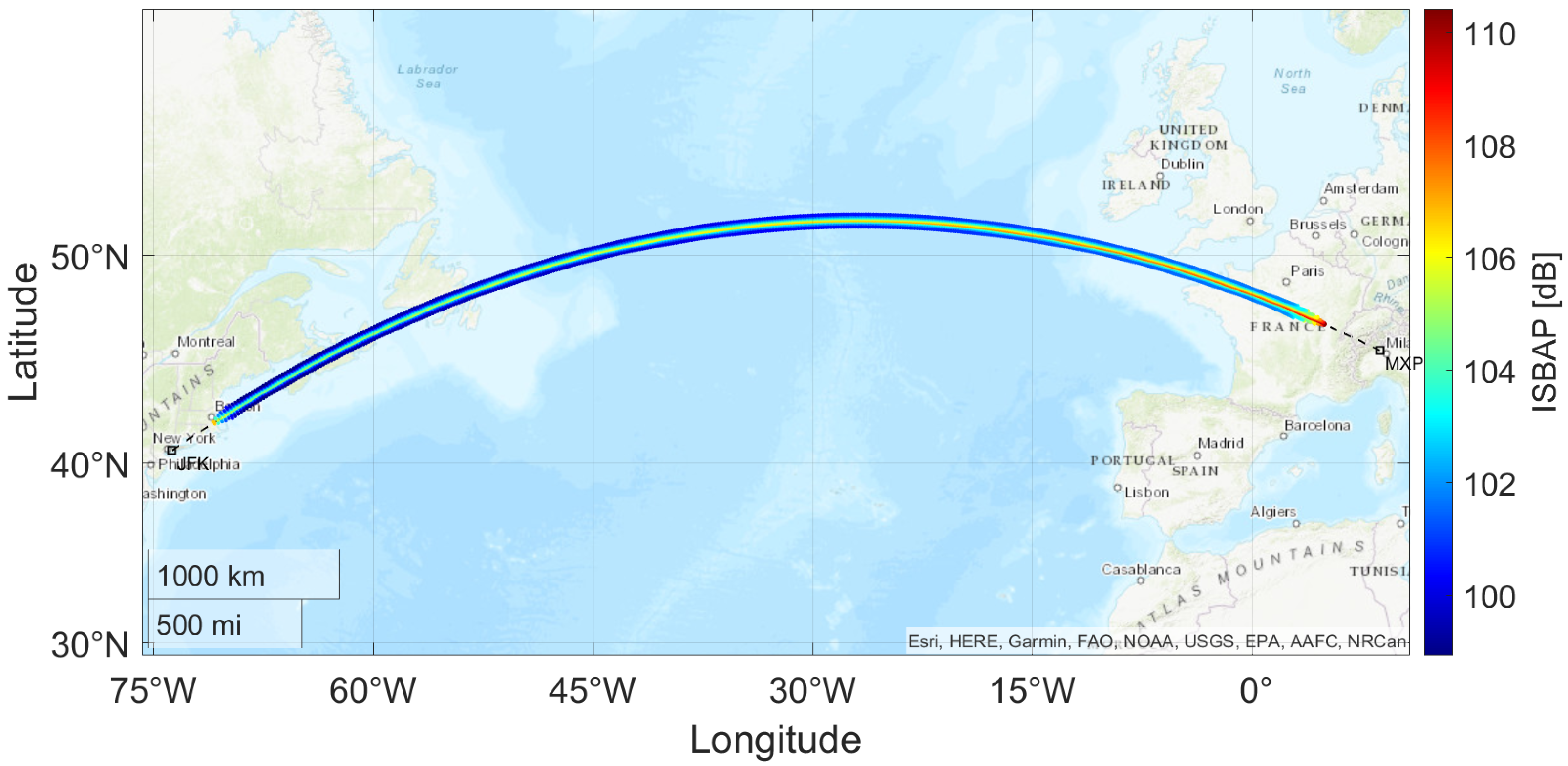
3.1. Transatlantic Route Impact Assessment: Milan to New York Case Study
- Engineering metrics, which quantify physical sound characteristics;
- Loudness metrics, which account for human perception of sound;
- Hybrid metrics, which integrate multiple metrics to provide a comprehensive sonic boom assessment.
- The increasing altitude causes the rays to cover a greater distance, reducing the sonic boom intensity;
- Fuel burn results in a lighter aircraft, thereby lowering the lift requirement and further decreasing the peak pressure along the ground track.
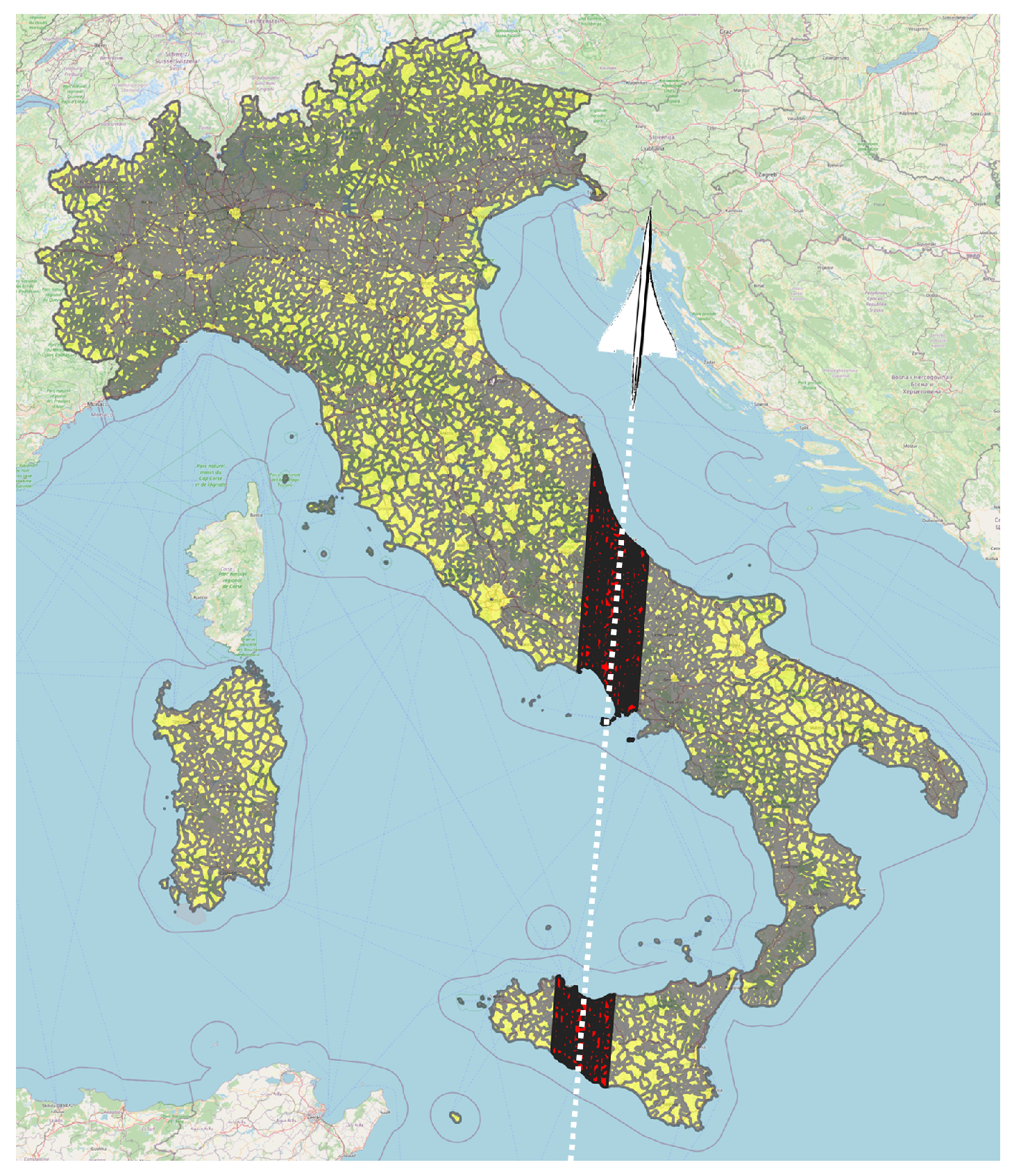
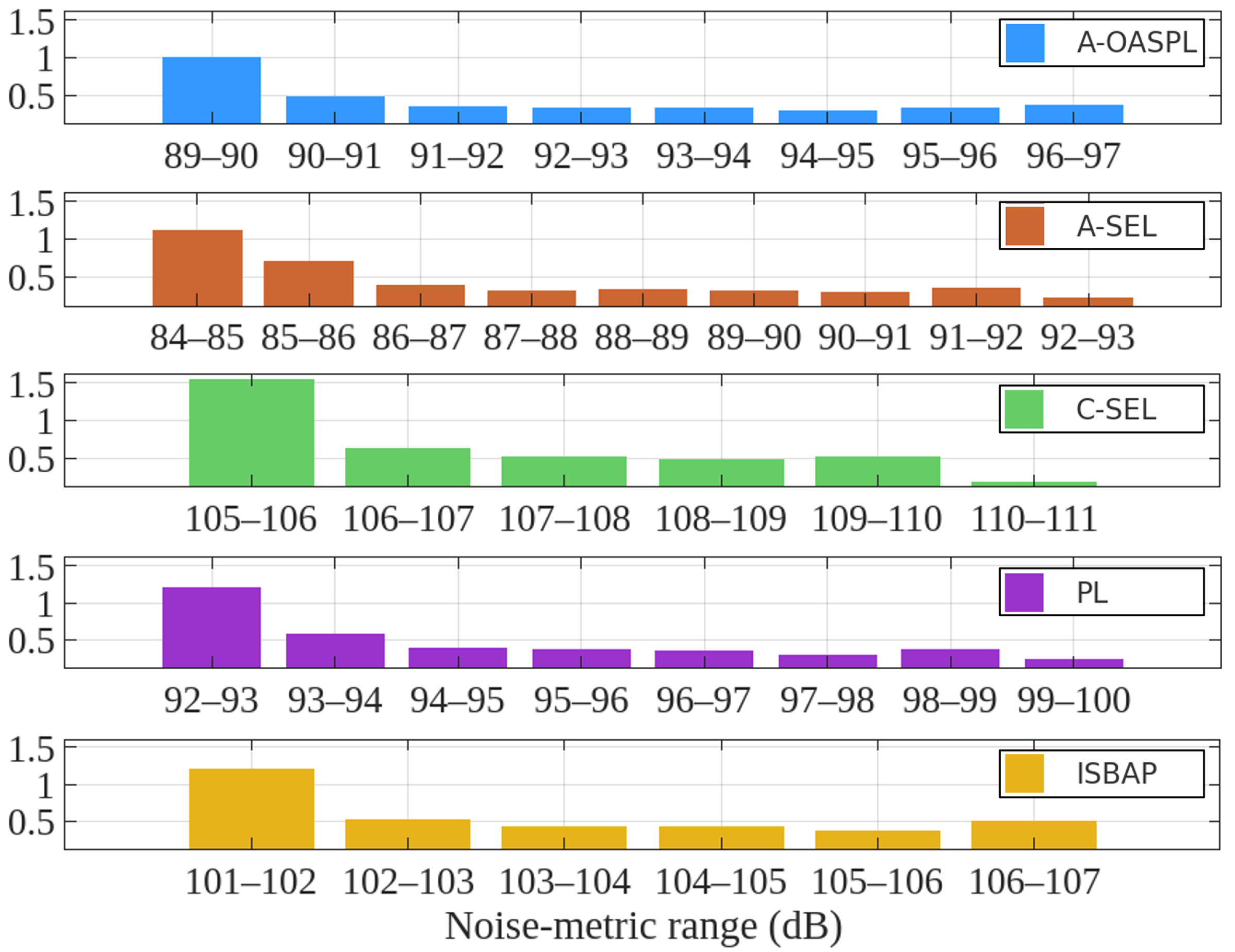
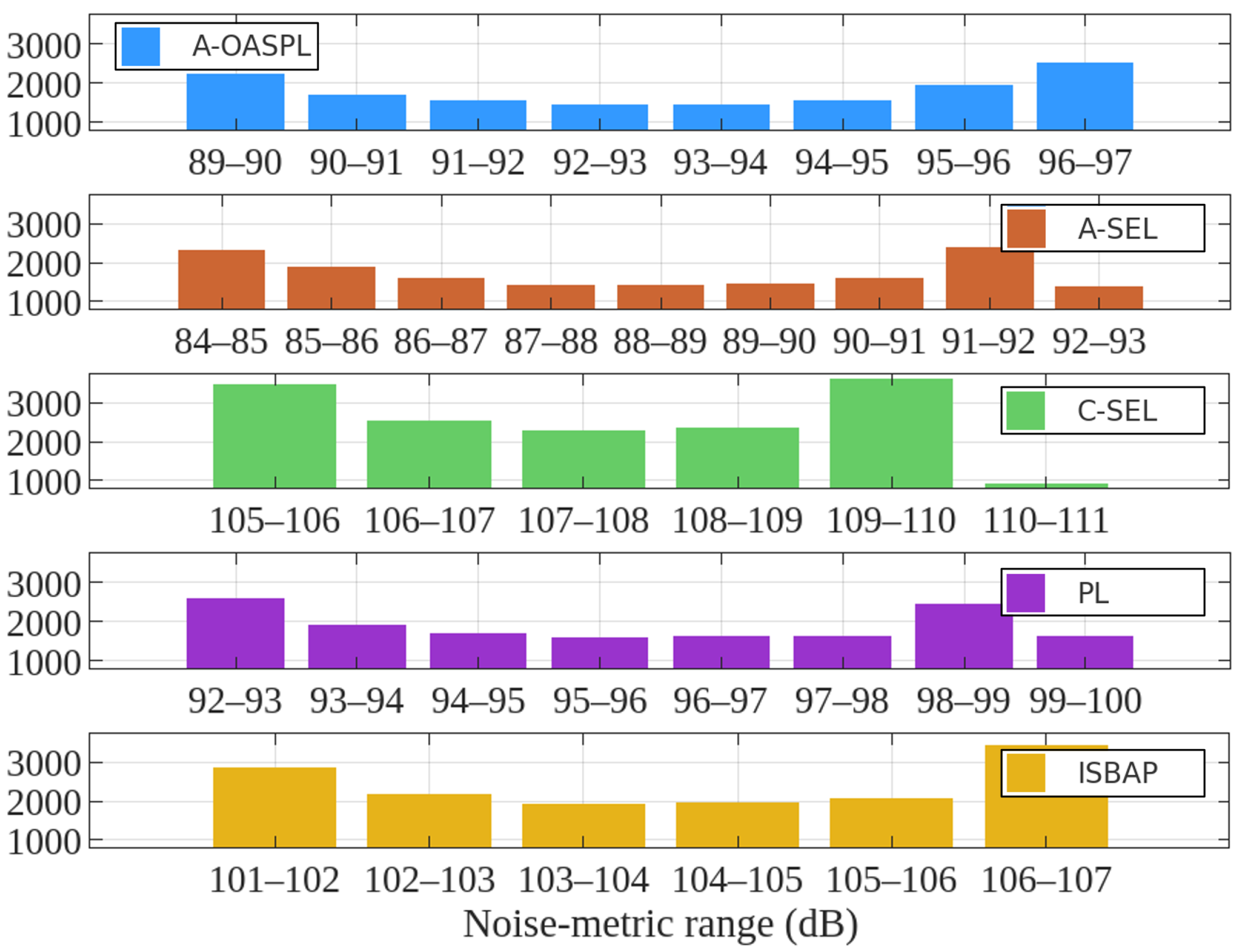
3.2. Supersonic Flight Impact over Italy
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| dB | Decibel |
| PLdB | Perceived level of noise in decibel |
| FAA | Federal Aviation Administration |
| ICAO | International Civil Aviation Organization |
| CAEP | ICAO’s Committee on Aviation Environmental Protection |
| AEDT | Aviation Environmental Tools Suite |
| CFD | Computational fluid dynamics |
| SPL | Sound pressure level |
| SEL | Sound exposure level |
| PSD | Power spectral density |
| ISBAP | Indoor Sonic Boom Annoyance Predictor |
| DNL | Day–Night Average Sound Level |
| FFT | Fast Fourier transform |
| OASPL | Overall Sound Pressure Level |
| MXP | Milan Malpensa Airport |
| JFK | New York John F. Kennedy International Airport |
References
- Bonavolontà, G.; Lawson, C.; Riaz, A. Review of sonic boom prediction and reduction methods for next generation of supersonic aircraft. Aerospace 2023, 10, 917. [Google Scholar] [CrossRef]
- Pawlowski, J.; Graham, D.; Boccadoro, C.; Coen, P.; Maglieri, D. Origins and overview of the shaped sonic boom demonstration program. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005; p. 5. Available online: https://ntrs.nasa.gov/citations/20050165091 (accessed on 27 December 2024).
- Cowart, R.; Grindle, T. An overview of the Gulfstream/NASA Quiet SpikeTM flight test program. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008; p. 123. [Google Scholar]
- Honda, M.; Yoshida, K. D-SEND project for low sonic boom design technology. In Proceedings of the 28th International Congress of the Aeronautical Sciences, Brisbane, Australia, 23–28 September 2012; pp. 1–8. [Google Scholar]
- CORDIS. Environmentally Friendly High Speed Aircraft. Available online: https://cordis.europa.eu/project/id/516132 (accessed on 27 December 2024).
- CORDIS. (LTO) noiSe and EmissioNs of supErsoniC Aircraft. Available online: https://cordis.europa.eu/project/id/101006742 (accessed on 27 December 2024).
- CORDIS. MDO and REgulations for Low-Boom and Environmentally Sustainable Supersonic Aviation. Available online: https://cordis.europa.eu/project/id/101006856 (accessed on 27 December 2024).
- NASA. Quesst Mission Overview. Available online: https://www.nasa.gov/mission/quesst/ (accessed on 27 December 2024).
- Lockheed Martin. X-59 Quiet Supersonic Technology (QueSST) Product Card. Available online: https://www.lockheedmartin.com/content/dam/lockheed-martin/aero/documents/Product%20Card%20X-59.pdf (accessed on 27 December 2024).
- Doebler, W.J.; Wilson, S.R.; Loubeau, A.; Sparrow, V.W. Simulation and regression modeling of NASA’s X-59 low-boom carpets across America. J. Aircr. 2023, 60, 509–520. [Google Scholar] [CrossRef]
- Morgenstern, J.; Buonanno, M.; Norstrud, N. N+2 Low Boom Wind Tunnel Model Design and Validation. In Proceedings of the 30th AIAA Applied Aerodynamics Conference, New Orleans, LO, USA, 25–28 June 2012; Volume 3217. [Google Scholar]
- Rathsam, J.; Coen, P.; Loubeau, A.; Ozoroski, L.; Shah, G. Scope and goals of NASA’s Quesst Community Test Campaign with the X-59 aircraft. In Proceedings of the 14th ICBEN Congress on Noise as a Public Health Problem, Belgrade, Serbia, 18–22 June 2023. [Google Scholar]
- Boom Supersonic. Boom Fact Sheet. Available online: https://boomsupersonic.com/wp-content/uploads/2024/03/Boom-Fact-Sheet.pdf (accessed on 28 December 2024).
- Federal Aviation Administration. Aviation Environmental Design Tool (AEDT). Available online: https://aedt.faa.gov/ (accessed on 16 December 2024).
- Yamashita, R.; Suzuki, K. Full-field sonic boom simulation in stratified atmosphere. AIAA J. 2016, 54, 3223–3231. [Google Scholar] [CrossRef]
- Rallabhandi, S.K. Advanced sonic boom prediction using the augmented Burgers equation. J. Aircr. 2011, 48, 1245–1253. [Google Scholar] [CrossRef]
- Loubeau, A.; Coulouvrat, F. Effects of meteorological variability on sonic boom propagation from hypersonic aircraft. AIAA J. 2009, 47, 2632–2641. [Google Scholar] [CrossRef]
- Leal, P.B.C.; Schrass, J.A.; Giblette, T.N.; Hunsaker, D.F.; Shen, H.; Logan, T.S.; Hartl, D.J. Effects of atmospheric profiles on sonic boom perceived level from supersonic vehicles. AIAA J. 2021, 59, 5020–5028. [Google Scholar] [CrossRef]
- Iura, R.; Ukai, T.; Yamashita, H.; Kern, B.; Misaka, T.; Obayashi, S. Impact of atmospheric variations on sonic boom loudness over 10 years of simulated flights. J. Acoust. Soc. Am. 2024, 156, 1529–1542. [Google Scholar] [CrossRef]
- Park, M.A.; Carter, M.B. Nearfield Summary and Analysis of the Third AIAA Sonic Boom Prediction Workshop C608 Low Boom Demonstrator. In Proceedings of the AIAA 2021-0345. AIAA Scitech 2021 Forum, Virtual Event, 11–15 & 19–21 January 2021. [Google Scholar] [CrossRef]
- Carlson, H.W. Simplified Sonic-Boom Prediction. NASA Technical Paper 1122. 1978. Available online: https://ntrs.nasa.gov/citations/19780012135 (accessed on 27 December 2024).
- Bass, H.; Raspet, R. Comparison of sonic boom rise time prediction techniques. J. Acoust. Soc. Am. 1992, 91, 1767–1768. [Google Scholar] [CrossRef]
- Robinson, L.D. An evaluation of rise time characterization and prediction methods. In NASA Conference Publication; NASA Langley Research Center: Hampton, VA, USA, 1994; p. 39. Available online: https://ntrs.nasa.gov/api/citations/19950008467/downloads/19950008467.pdf (accessed on 27 December 2024).
- Loubeau, A.; Page, J. Human perception of sonic booms from supersonic aircraft. Acoust. Today 2018, 14, 23–30. Available online: https://acousticstoday.org/human-perception-sonic-booms-supersonic-aircraft-alexandra-loubeau-juliet-page/ (accessed on 27 December 2024).
- Vaughn, A.B.; Doebler, W.J.; Christian, A.W. Cumulative noise metric design considerations for the NASA Quesst community test campaign with the X-59 aircraft. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Chiba, Japan, 20–23 August 2023; Volume 268, pp. 1485–1496. [Google Scholar]
- Vaughn, A.B. Literature Review of Cumulative Noise Metrics Relevant to X-59 Supersonic Overflights. NASA Technical Memorandum. June 2024. Available online: https://ntrs.nasa.gov/citations/20240005399 (accessed on 27 December 2024).
- European Parliament and Council. Directive 2002/49/EC of the European Parliament and of the Council of 25 June 2002 Relating to the Assessment and Management of Environmental Noise. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32002L0049 (accessed on 28 December 2024).
- Whitham, G.B. The flow pattern of a supersonic projectile. Commun. Pure Appl. Math. 1952, 5, 301–348. [Google Scholar] [CrossRef]
- Glorioso, A.; Petrosino, F.; Aprovitola, A.; Barbarino, M.; Pezzella, G. Sonic Boom generation using open source CFD approach. In Proceedings of the AIAA 2023-4168. AIAA AVIATION 2023 Forum, San Diego, CA, USA, 12–16 June 2023. [Google Scholar] [CrossRef]
- Graziani, S.; Petrosino, F.; Jäschke, J.; Glorioso, A.; Fusaro, R.; Viola, N. Evaluation of Sonic Boom Shock Wave Generation with CFD Methods. Aerospace 2024, 11, 484. [Google Scholar] [CrossRef]
- Economon, T.D.; Palacios, F.; Copel, S.R.; Lukaczyk, T.W.; Alonso, J.J. SU2: An Open-Source Suite for Multiphysics Simulation and Design. AIAA J. 2016, 54, 828–846. [Google Scholar] [CrossRef]
- Maglieri, D.J. Sonic Boom: Six Decades of Research; Langley Research Center: Hampton, VA, USA, 2014.
- Darden, C.M.; Powell, C.A.; Hayes, W.D.; George, A.R.; Pierce, A.D. Status of Sonic Boom Methodology and Understanding; Langley Research Center: Hampton, VA, USA, 1988.
- Whitham, G.B. Linear and Nonlinear Waves; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Walkden, F. The shock pattern of a wing-body combination, far from the flight path. Aeronaut. Q. 1958, 9, 164–194. [Google Scholar] [CrossRef]
- Hayes, W.D.; Haefeli, R.C.; Kulsrud, H.E. Sonic Boom Propagation in a Stratified Atmosphere, with Computer Program. NASA CR-1299. NASA: Contractor Report. April 1969. Available online: https://ntrs.nasa.gov/citations/19690013184 (accessed on 27 December 2024).
- Emmanuelli, A.; Dragna, D.; Ollivier, S.; Blanc-Benon, P. Characterization of topographic effects on sonic boom reflection by resolution of the Euler equations. J. Acoust. Soc. Am. 2021, 149, 2437–2450. [Google Scholar] [CrossRef] [PubMed]
- Emmanuelli, A.; Dragna, D.; Ollivier, S.; Blanc-Benon, P. Sonic boom propagation over real topography. J. Acoust. Soc. Am. 2023, 154, 16–27. [Google Scholar] [CrossRef]
- Dragna, D.; Emmanuelli, A.; Ollivier, S.; Blanc-Benon, P. Sonic boom reflection over urban areas. J. Acoust. Soc. Am. 2022, 152, 3323–3339. [Google Scholar] [CrossRef]
- Yamashita, R.; Nikiforakis, N. Three-dimensional full-field simulation of sonic boom emanating from complex geometries over buildings. Shock Waves 2023, 33, 149–167. [Google Scholar] [CrossRef]
- Riegel, K.; Sparrow, V.W. Sonic boom propagation in urban canyons using a combined ray tracing/radiosity method. J. Acoust. Soc. Am. 2024, 155, 1527–1533. [Google Scholar] [CrossRef]
- Miles, J.H. Method of Representation of Acoustic Spectra and Reflection Corrections Applied to Externally Blown Flap Noise; NASA: Washington, DC, USA, 1975.
- Brüel & Kjær. Application Notes—Leq, SEL WHAT? WHY? WHEN?; Brüel & Kjær Sound & Vibration Measurement A/S. Available online: https://www.bksv.com/doc/bo0051.pdf (accessed on 14 December 2024).
- Stevens, S. Perceived level of noise by Mark VII and decibels. J. Acoust. Soc. Am. 1972, 51, 575–601. [Google Scholar] [CrossRef]
- Jackson, G.; Leventhall, H. Calculation of the perceived level of noise (PLdB) using Stevens’ method (Mark VII). Appl. Acoust. 1973, 6, 23–34. [Google Scholar] [CrossRef]
- Rathsam, J.; Loubeau, A.; Klos, J. Simulator Study of Indoor Annoyance Caused by Shaped Sonic Boom Stimuli with and Without Rattle Augmentation; Langley Research Center: Hampton, VA, USA, 2013.
- Loubeau, A. Evaluation of the Effect of Aircraft Size on Indoor Annoyance Caused by Sonic Booms. J. Acoust. Soc. Am. 2014, 136, 2223–2224. [Google Scholar] [CrossRef]
- Hayes, M.H. Statistical Digital Signal Processing and Modeling; John Wiley & Sons: Hoboken, NJ, USA, 1996; ISBN 978-0-471-59431-4. [Google Scholar]
- ASTOS Solutions GmbH. ASTOS, version 2023; Computer Software; Astos Solutions GmbH: Stuttgart, Germany, 2023.







| MP1 | MP2 | MP3 | ||
|---|---|---|---|---|
| Phase | Descent | Climb | Cruise | |
| Mach number | M [-] | 1.5 | 1.5 | 2 |
| Free stream pressure | p [Pa] | 8120.51 | 12,044.6 | 6935.86 |
| Free stream temperature | T [K] | 216.6 | 216.6 | 216.6 |
| Aircraft length | L [m] | 61.7 | 61.7 | 61.7 |
| Altitude | H [m] | 17,500 | 15,000 | 18,500 |
| Speed of sound | a [m/s] | 295 | 295 | 295 |
| Aircraft weight | W [kN] | 940 | 1550 | 950 |
| Flight angle | [deg] | −1.2 | 1.2 | 0 |
| Phase | Cruise | |
|---|---|---|
| Mach number | M [-] | 2 |
| Free stream pressure | p [Pa] | 7506 |
| Altitude | H [m] | 18,000 |
| Speed of sound | a [m/s] | 295 |
| Aircraft weight | W [kN] | 1500 |
| Flight angle | [deg] | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fasulo, G.; Glorioso, A.; Petrosino, F.; Barbarino, M.; Federico, L. Sonic Boom Impact Assessment of European SST Concept for Milan to New York Supersonic Flight. Acoustics 2025, 7, 29. https://doi.org/10.3390/acoustics7020029
Fasulo G, Glorioso A, Petrosino F, Barbarino M, Federico L. Sonic Boom Impact Assessment of European SST Concept for Milan to New York Supersonic Flight. Acoustics. 2025; 7(2):29. https://doi.org/10.3390/acoustics7020029
Chicago/Turabian StyleFasulo, Giovanni, Antimo Glorioso, Francesco Petrosino, Mattia Barbarino, and Luigi Federico. 2025. "Sonic Boom Impact Assessment of European SST Concept for Milan to New York Supersonic Flight" Acoustics 7, no. 2: 29. https://doi.org/10.3390/acoustics7020029
APA StyleFasulo, G., Glorioso, A., Petrosino, F., Barbarino, M., & Federico, L. (2025). Sonic Boom Impact Assessment of European SST Concept for Milan to New York Supersonic Flight. Acoustics, 7(2), 29. https://doi.org/10.3390/acoustics7020029









