Enhancement of Subharmonic Intensity in a Cavity Filled with Bubbly Liquid Through Its Nonlinear Resonance Shift
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Nonlinear Resonance of Subharmonics in a Free Bubbly Liquid (Study vs. Acoustic Pressure Amplitude)
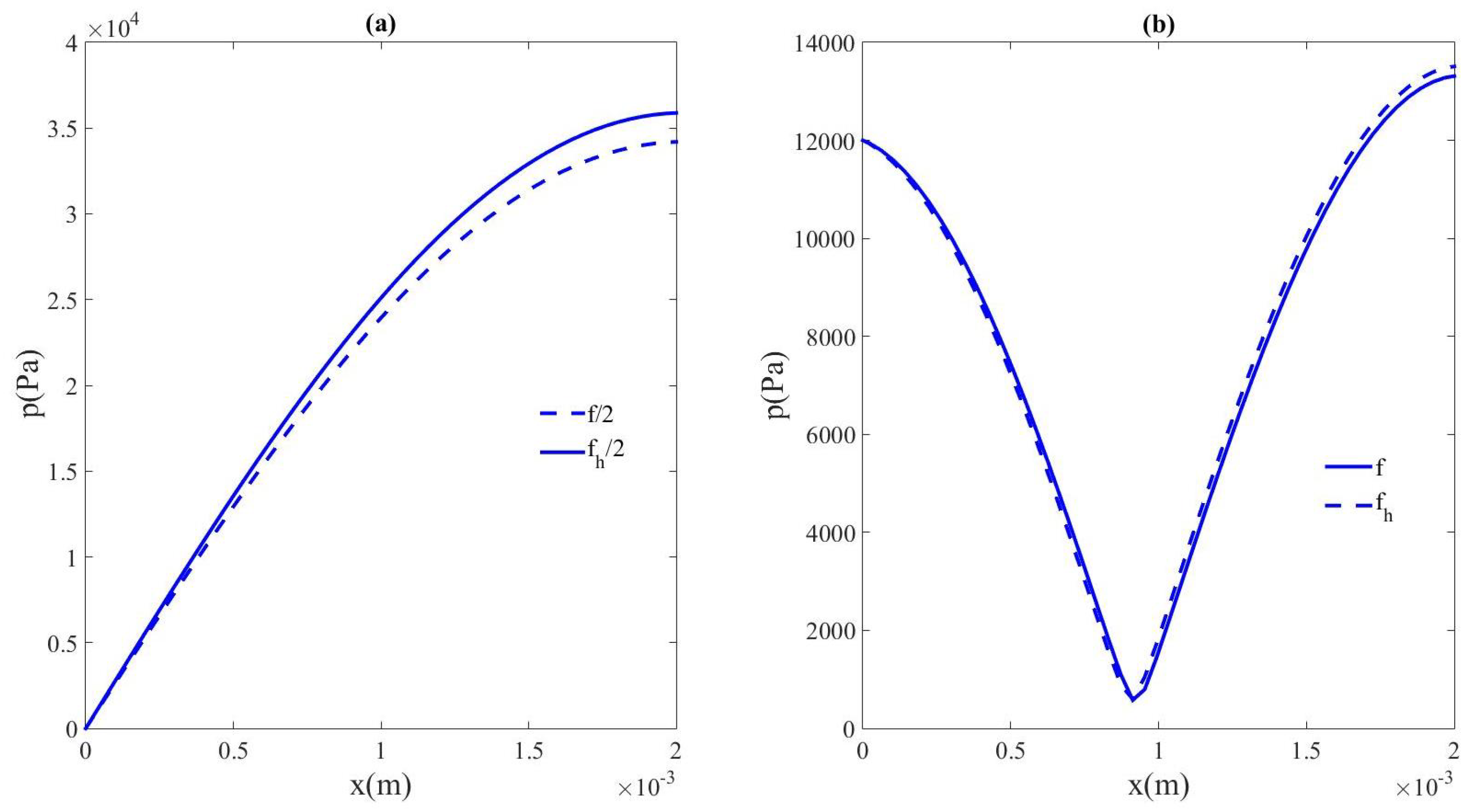
3.2. Nonlinear Resonance of Subharmonics in a Compressed Bubbly Liquid (Study vs. Acoustic Pressure Amplitude)
3.3. Nonlinear Resonance of Subharmonics in a Decompressed Bubbly Liquid (Study vs. Acoustic Pressure Amplitude)
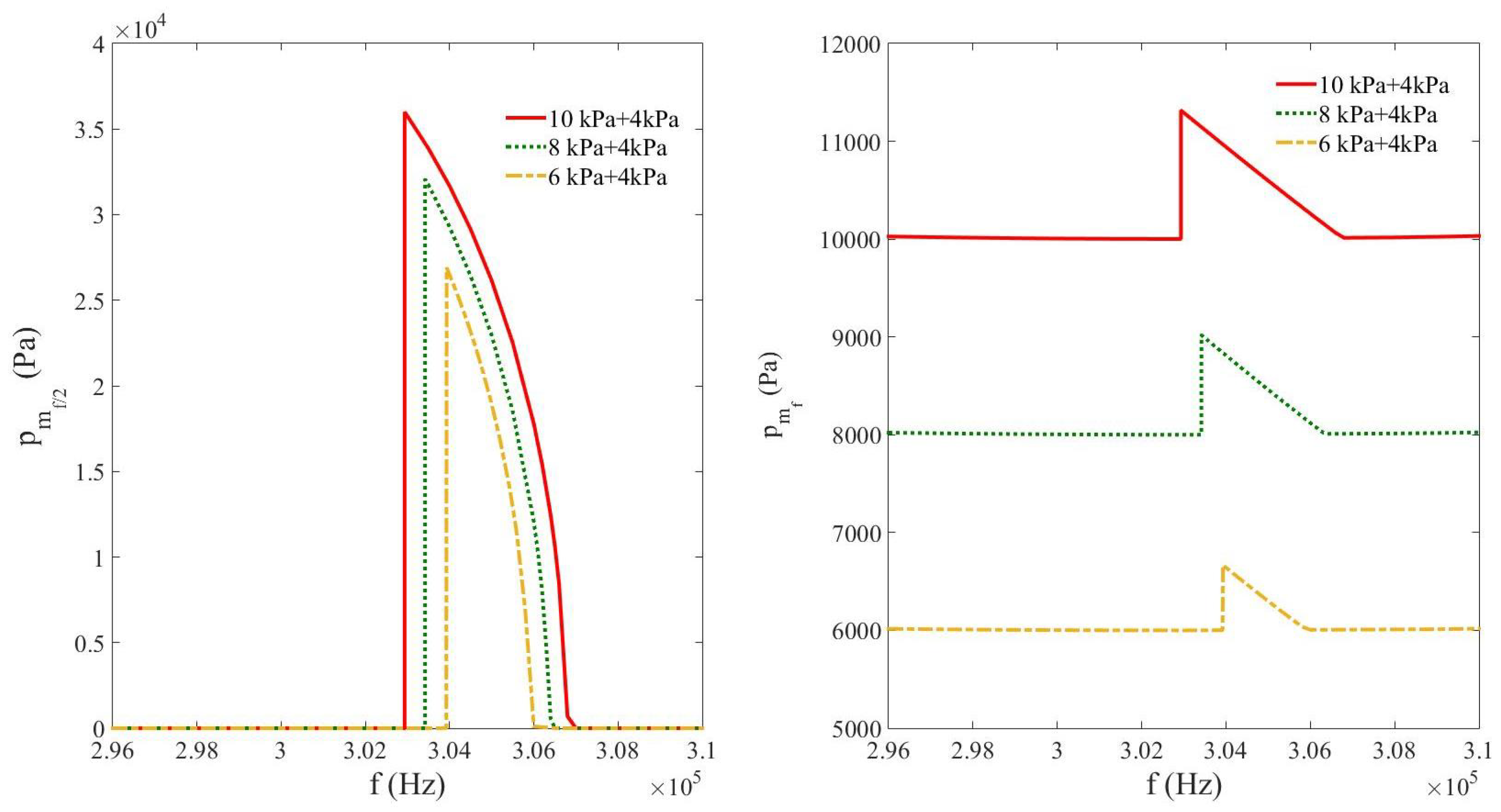
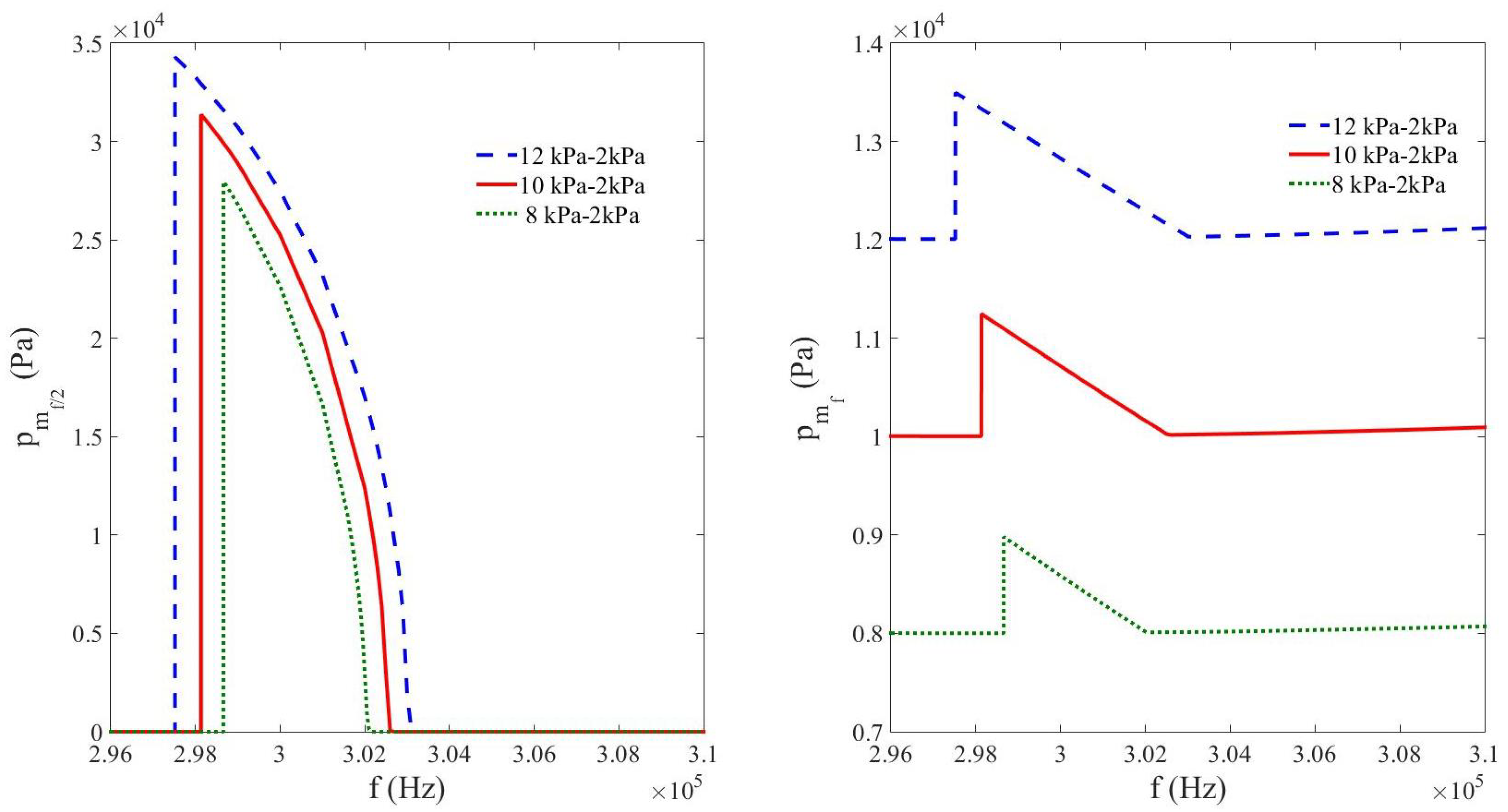
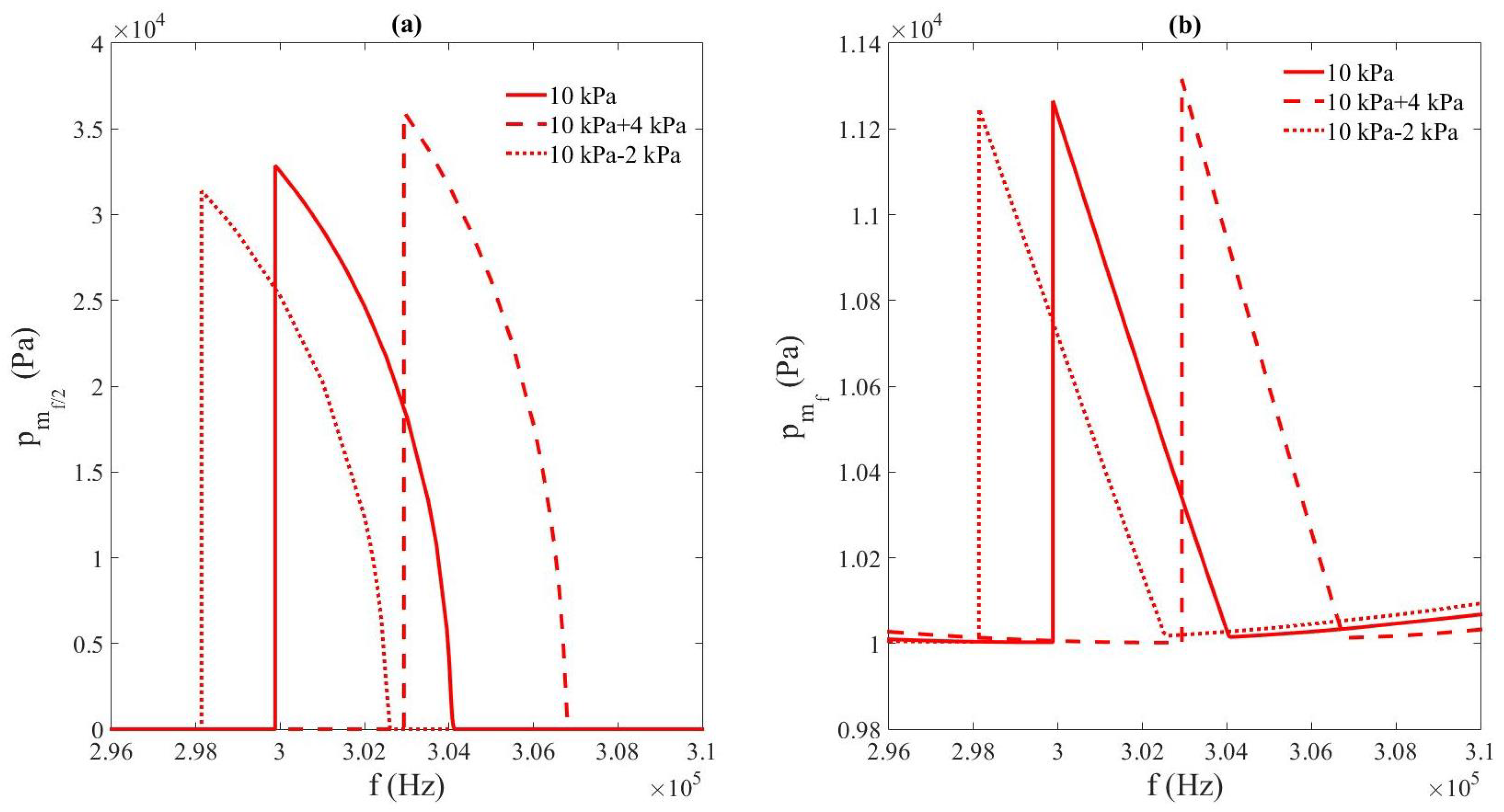
3.4. Comparison of the Nonlinear Resonance of Subharmonics Between Free, Compressed, and Decompressed Bubbly Liquids (Study vs. Net Bulk Pressure)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grieser, F.; Choi, P.; Enomoto, N.; Harada, H.; Okitsu, K.; Yasui, K. Sonochemistry and the Acoustic Bubble; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Hamilton, M.; Blackstock, D. Nonlinear Acoustics; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Naugolnykh, K.; Ostrovsky, L. Nonlinear Wave Processes in Acoustics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Berry, J.; Sidhu, P. Microbubble contrast-enhanced ultrasound in liver transplantation. Eur. Radiol. 2004, 14 (Suppl. S8), 96–103. [Google Scholar]
- Gong, Q.; Gao, X.; Liu, W.; Hong, T.; Chen, C. Drug-Loaded Microbubbles Combined with Ultrasound for Thrombolysis and Malignant Tumor Therapy. BioMed Res. Int. 2019, 35, 6792465. [Google Scholar] [CrossRef]
- Hernot, S.; Klibanov, A.L. Microbubbles in ultrasound-triggered drug and gene delivery. Adv. Drug Deliv. Rev. 2008, 10, 1153–1166. [Google Scholar] [CrossRef]
- Yusof, N.S.; Babgi, B.; Alghamdi, Y.; Aksu, M.; Madhavan, J.A.M. Physical and chemical effects of acoustic cavitation in selected ultrasonic cleaning applications. Ultrason. Sonochem. 2016, 29, 568–576. [Google Scholar]
- Mason, T.; Lorimer, J. Applied Sonochemistry: The Uses of Power Ultrasound in Chemistry and Processing; Wiley-VCH: Weinheim, Germany, 2002. [Google Scholar]
- Desser, T.; Jeffrey, R. Tissue harmonic imaging tecniques: Physical principles and clinical aplications. Semin. Ultrasound CT MRI 2001, 22, 1–10. [Google Scholar]
- Newhouse, V.L.; Shankar, P.M. Bubble size measurements using the nonlinear mixing of two frequencies. J. Acoust. Soc. Am. 1984, 75, 1473–1477. [Google Scholar]
- Buckey, J.C.; Knaus, D.A.; Alvarenga, D.L.; Kenton, M.A.; Magari, P.J. Dual-frequency ultrasound for detecting and sizing bubbles. Acta Astronaut. 2005, 56, 1041–1047. [Google Scholar]
- Zhang, W.; Liu, Y.; Ratilal, P.; Cho, B.; Makris, N.C. Active Nonlinear Acoustic Sensing of an Object with Sum or Difference Frequency Fields. Remote Sens. 2017, 9, 954. [Google Scholar] [CrossRef]
- Westervelt, P.J. Parametric Acoustic Array. J. Acoust. Soc. Am. 1963, 35, 1535–1537. [Google Scholar]
- Sinha, D.N.; Pantea, C. Broadband unidirectional ultrasound propagation using sonic crystal and nonlinear medium. Emerg. Mater. Res. 2013, 2, 117–126. [Google Scholar] [CrossRef]
- Forsberg, F.; Shi, W.; Goldberg, B. Subharmonic imaging of contrast agents. Ultrasonics 2000, 38, 93–98. [Google Scholar] [CrossRef]
- Shankar, P.; Krishna, P.; Newhouse, V. Advantages of Subharmonic Over Second Harmonic Backscatter for Contrast-To-Tissue Echo Enhancement. Ultrasound Med. Biol. 1998, 24, 395–399. [Google Scholar]
- Eller, A.; Flynn, H. Generation of subharmonics of order one-half by bubbles in a sound field. J. Acoust. Soc. Am. 1969, 46, 722–727. [Google Scholar]
- Lauterborn, W. Numerical investigation of nonlinear oscillations of gas bubbles in liquids. J. Acoust. Soc. Am. 1976, 59, 283–293. [Google Scholar]
- Fan, Y.; Li, H.; Fuster, D. Optimal subharmonic emission of stable bubble oscillations in a tube. Phys. Rev. E 2020, 102, 013105. [Google Scholar] [CrossRef] [PubMed]
- Sojahrood, A.; Earl, R.; Kolios, M.; Karshafian, R. Investigation of the 1/2 order subharmonic emissions of the period-2 oscillations of an ultrasonically excited bubble. Phys. Lett. A 2020, 384, 126446. [Google Scholar]
- Sojahrood, A.; Haghi, H.; Shirazi, N.; Karshafian, R.; Kolios, M. On the threshold of 1/2 order subharmonic emissions in the oscillations of ultrasonically excited bubbles. Ultrasonics 2021, 112, 106363. [Google Scholar]
- Shankar, P.; Krishna, P.; Newhouse, V. Subharmonic backscattering from ultrasound contrast agents. J. Acoust. Soc. Am. 1999, 106, 2104–2110. [Google Scholar]
- Prosperetti, A. A general derivation of the subharmonic threshold for non-linear bubble oscillations. J. Acoust. Soc. Am. 2013, 133, 3719–3726. [Google Scholar] [PubMed]
- Katiyar, A.; Sarkar, K. Excitation threshold for subharmonic generation from contrast microbubbles. J. Acoust. Soc. Am. 2011, 130, 3137–3147. [Google Scholar] [CrossRef] [PubMed]
- Katiyar, A.; Sarkar, K. Effects of encapsulation damping on the excitation threshold for subharmonic generation from contrast microbubbles. J. Acoust. Soc. Am. 2012, 132, 3576–3585. [Google Scholar] [PubMed]
- Tejedor Sastre, M.T.; Louisnard, O.; Vanhille, C. Generation of subharmonics in acoustic resonators containing bubbly liquids: A numerical study of the excitation threshold and hysteretic behavior. Ultrason. Sonochem. 2022, 88, 106068. [Google Scholar]
- Omta, R. Oscillations of a cloud of bubbles of small and not so small amplitude. J. Acoust. Soc. Am. 1987, 82, 1018–1033. [Google Scholar]
- Matsumoto, Y.; Yoshizawa, S. Behaviour of a bubble cluster in an ultrasound field. Int. J. Numer. Methods Fluids 2005, 47, 591–601. [Google Scholar]
- Doc, J.B.; Conoir, J.M.; Marchiano, R.; Fuster, D. Nonlinear acoustic propagation in bubbly liquids: Multiple scattering, softening and hardening phenomena. J. Acoust. Soc. Am. 2016, 139, 1703–1712. [Google Scholar] [CrossRef] [PubMed]
- Tejedor-Sastre, M.; Vanhille, C. Nonlinear Resonance of Cavities Filled with Bubbly Liquids: A Numerical Study with Application to the Enhancement of the Frequency Mixing Effect. Shock Vib. 2018, 2018, 1570508. [Google Scholar]
- Tejedor Sastre, M.T.; Vanhille, C. Definition of Bubbly Liquids Parameters for the Optimization of Their Nonlinear Effects on Ultrasound. Appl. Sci. 2023, 13, 3882. [Google Scholar] [CrossRef]
- Tejedor-Sastre, M.; Vanhille, C. A numerical model for the study of the difference frequency generated from nonlinear mixing of standing ultrasonic waves in bubbly liquids. Ultrason. Sonochem. 2017, 34, 881–888. [Google Scholar]
- Doinikov, A. Bjerknes forces and translational bubble dynamics. Bubble Part. Dyn. Acoust. Fields Mod. Trends Appl. 2005, 661, 95–143. [Google Scholar]

| Liquid (Water) | Gas (Air) | Bubbles |
|---|---|---|
| m/s | m/s | µm |
| kg/ | kg/ | MHz |
| /s | 1/ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tejedor-Sastre, M.T.; Vanhille, C. Enhancement of Subharmonic Intensity in a Cavity Filled with Bubbly Liquid Through Its Nonlinear Resonance Shift. Acoustics 2025, 7, 17. https://doi.org/10.3390/acoustics7020017
Tejedor-Sastre MT, Vanhille C. Enhancement of Subharmonic Intensity in a Cavity Filled with Bubbly Liquid Through Its Nonlinear Resonance Shift. Acoustics. 2025; 7(2):17. https://doi.org/10.3390/acoustics7020017
Chicago/Turabian StyleTejedor-Sastre, María Teresa, and Christian Vanhille. 2025. "Enhancement of Subharmonic Intensity in a Cavity Filled with Bubbly Liquid Through Its Nonlinear Resonance Shift" Acoustics 7, no. 2: 17. https://doi.org/10.3390/acoustics7020017
APA StyleTejedor-Sastre, M. T., & Vanhille, C. (2025). Enhancement of Subharmonic Intensity in a Cavity Filled with Bubbly Liquid Through Its Nonlinear Resonance Shift. Acoustics, 7(2), 17. https://doi.org/10.3390/acoustics7020017







