Porous Metal Backing for High-Temperature Ultrasonic Transducers
Abstract
1. Introduction
2. Materials and Methods
2.1. Metallic Porous Materials for High-Temperature Applications
2.2. Experimental Measurements
3. Results
4. Discussion
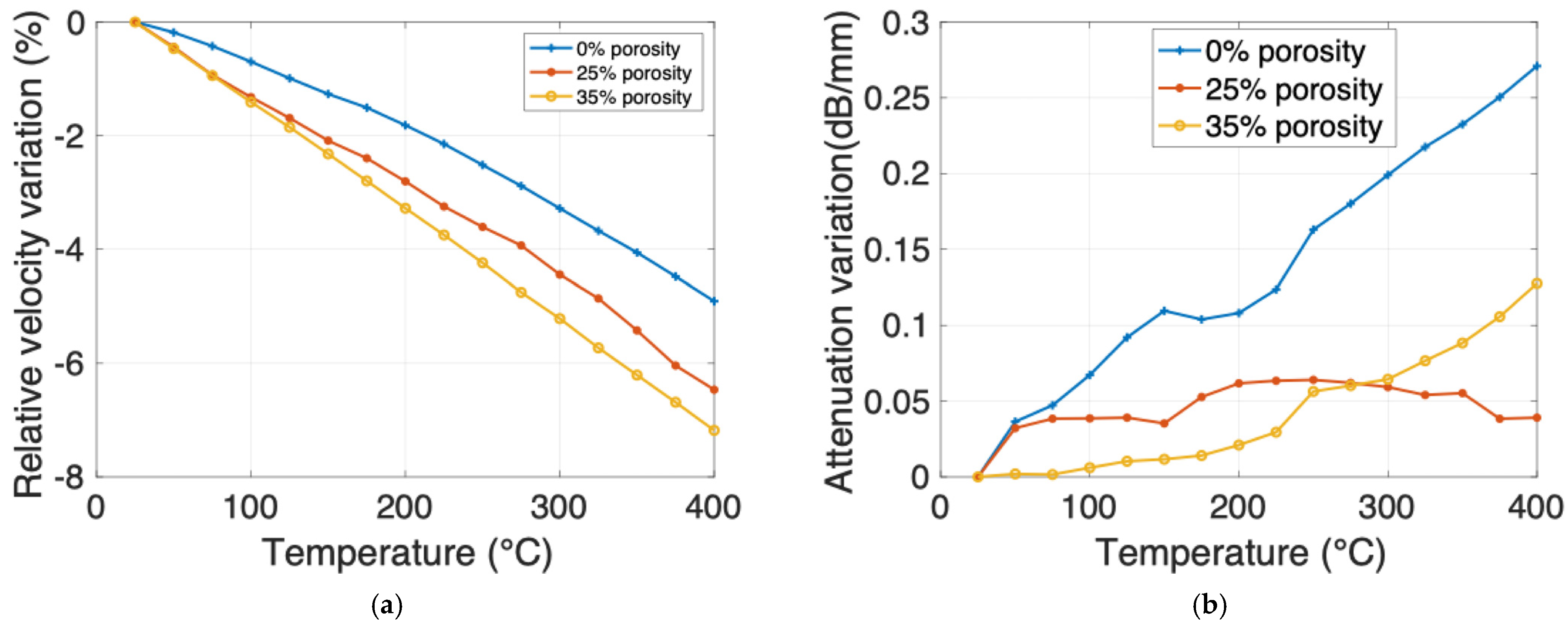
4.1. Measurementsas a Function of Temperature
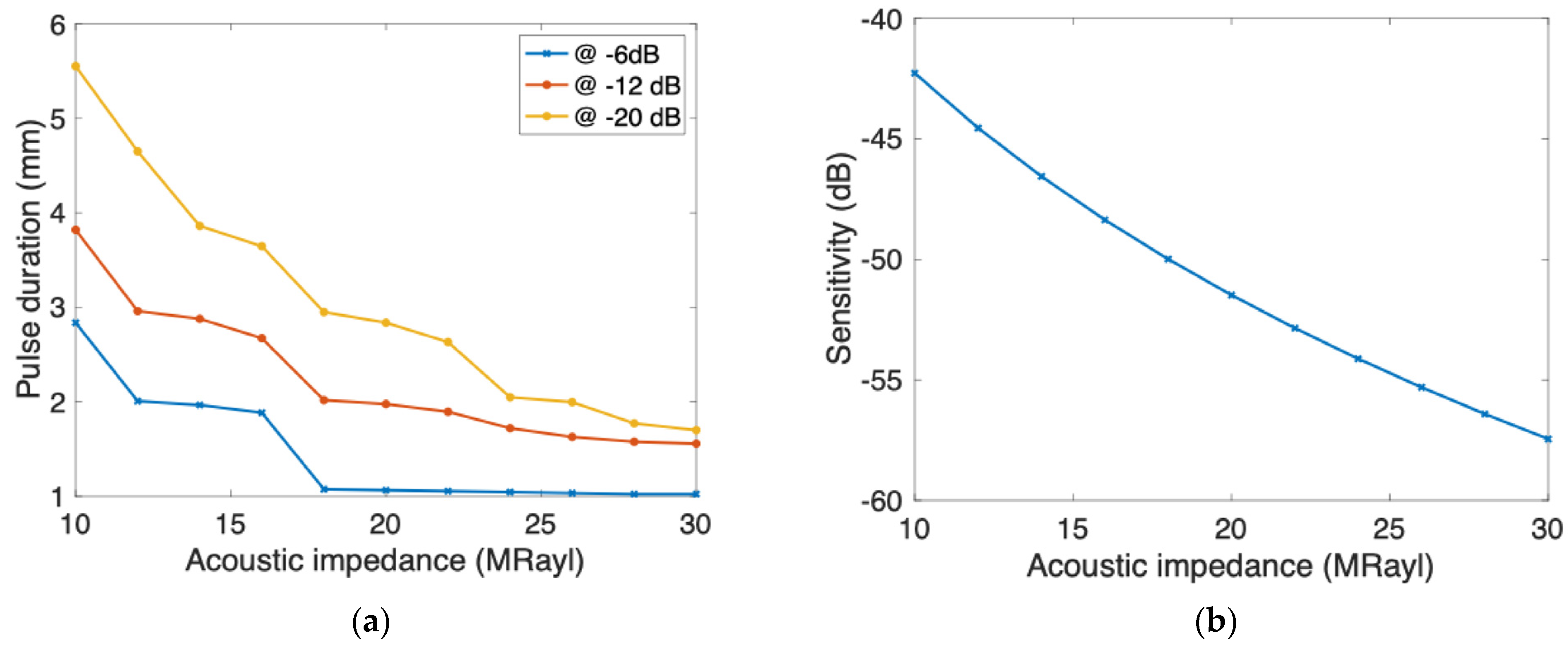
4.2. Influence of the Backing Acoustic Impedance
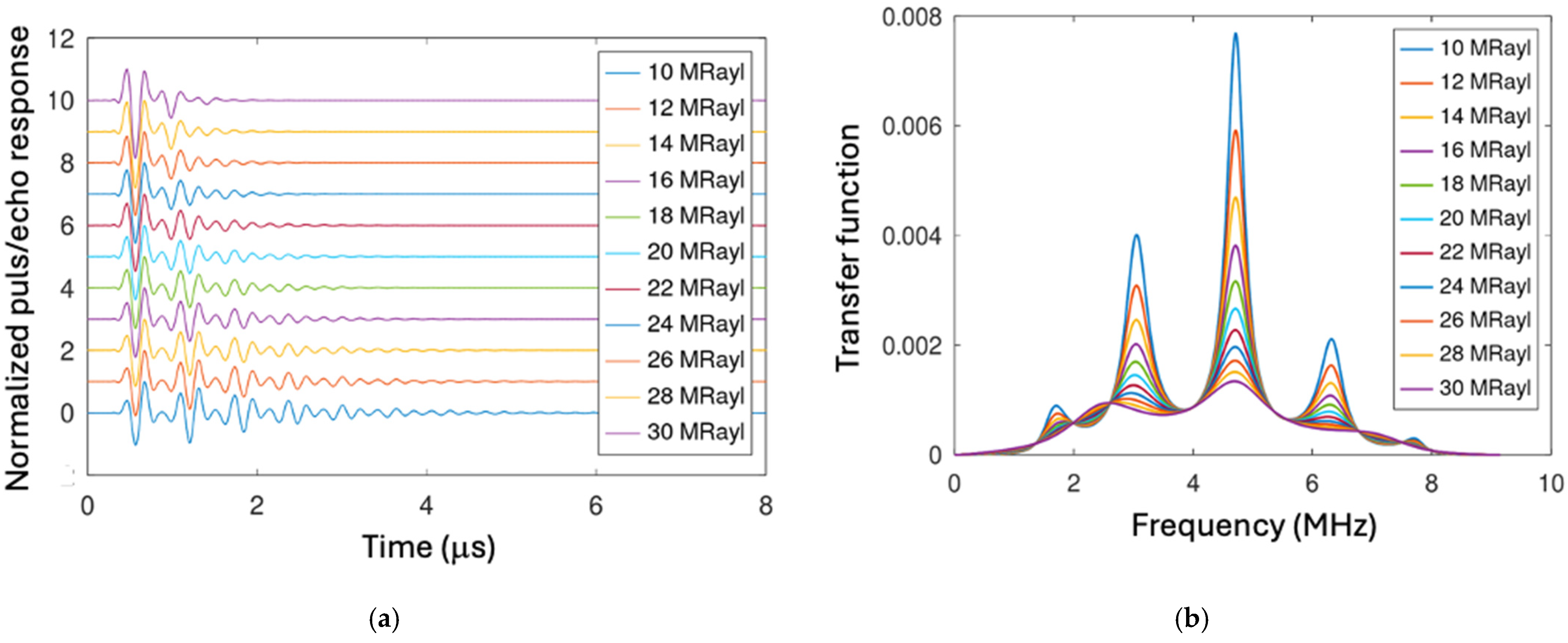
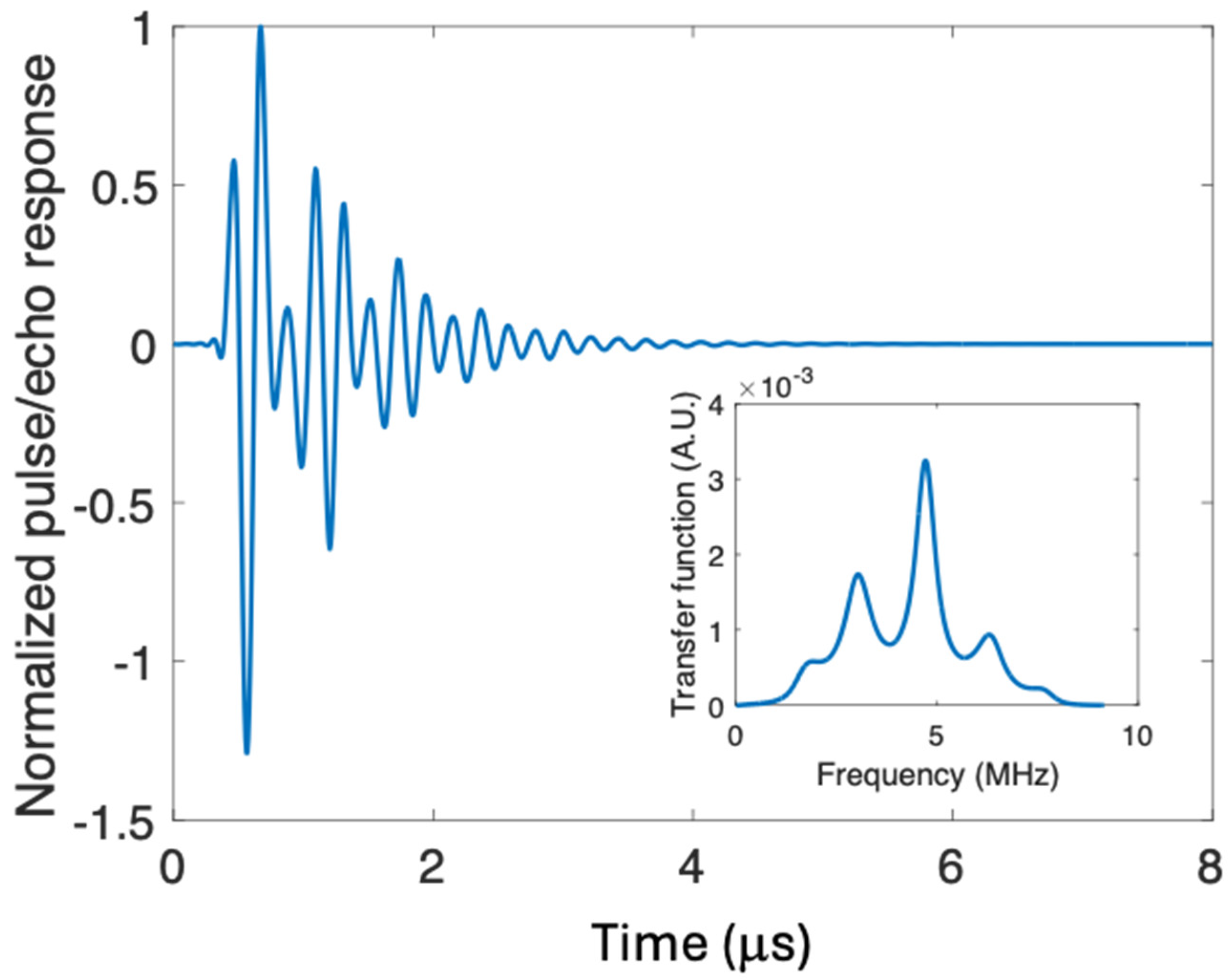
4.3. Transducer Simulation
5. Conclusions
6. Patents
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cochran, S. Piezoelectricity and Basic Configurations for Piezoelectric Ultrasonic Transducers. In Ultrasonic Transducers: Materials and Design for Sensors, Actuators and Medical Applications; Nakamura, K., Ed.; Woodhead Publishing Series in Electronic and Optical Materials; Woodhead Publishing: Sawston, UK, 2012; pp. 3–35. ISBN 978-0-85709-630-2/978-1-84569-989-5. [Google Scholar]
- Jensen, J.A. Medical Ultrasound Imaging. Prog. Biophys. Mol. Biol. 2007, 93, 153–165. [Google Scholar] [CrossRef] [PubMed]
- Drinkwater, B.W.; Wilcox, P.D. Ultrasonic Arrays for Non-Destructive Evaluation: A Review. NDT E Int. 2006, 39, 525–541. [Google Scholar] [CrossRef]
- Song, S.-J.; Shin, H.J.; Jang, Y.H. Development of an Ultra Sonic Phased Array System for Nondestructive Tests of Nuclear Power Plant Components. Nucl. Eng. Des. 2002, 214, 151–161. [Google Scholar] [CrossRef]
- Tang, L.; Cao, W. Temperature Dependence of Self-Consistent Full Matrix Material Constants of Lead Zirconate Titanate Ceramics. Appl. Phys. Lett. 2015, 106, 052902. [Google Scholar] [CrossRef]
- Baptista, F.G.; Budoya, D.E.; de Almeida, V.A.D.; Ulson, J.A.C. An Experimental Study on the Effect of Temperature on Piezoelectric Sensors for Impedance-Based Structural Health Monitoring. Sensors 2014, 14, 1208–1227. [Google Scholar] [CrossRef]
- Amini, M.H.; Sinclair, A.N.; Coyle, T.W. A New High-Temperature Ultrasonic Transducer for Continuous Inspection. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 448–455. [Google Scholar] [CrossRef]
- Kazys, R.; Vaskeliene, V. High Temperature Ultrasonic Transducers: A Review. Sensors 2021, 21, 3200. [Google Scholar] [CrossRef]
- Baba, A.; Searfass, C.T.; Tittmann, B.R. High Temperature Ultrasonic Transducer up to 1000 °C Using Lithium Niobate Single Crystal. Appl. Phys. Lett. 2010, 97, 232901. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, F. Piezoelectric Materials for High Temperature Sensors. J. Am. Ceram. Soc. 2011, 94, 3153–3170. [Google Scholar] [CrossRef]
- Yamada, T.; Iwasaki, H.; Niizeki, N. Piezoelectric and Elastic Properties of LiTaO3: Temperature Characteristics. Jpn. J. Appl. Phys. 1969, 8, 1127. [Google Scholar] [CrossRef]
- Sinclair, A.N.; Malkin, R. Sensors for Ultrasonic Nondestructive Testing (NDT) in Harsh Environments. Sensors 2020, 20, 456. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.J.; Zhang, S.; Bar-Cohen, Y.; Sherrit, S. High Temperature, High Power Piezoelectric Composite Transducers. Sensors 2014, 14, 14526–14552. [Google Scholar] [CrossRef] [PubMed]
- Kazys, R.; Voleisis, A.; Sliteris, R.; Mazeika, L.; Van Nieuwenhove, R.; Kupschus, P.; Abderrahim, H.A. High Temperature Ultrasonic Transducers for Imaging and Measurements in a Liquid Pb/Bi Eutectic Alloy. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 525–537. [Google Scholar] [CrossRef]
- Kobayashi, M.; Jen, C.-K. Transducers for Non-Destructive Evaluation at High Temperatures. In Ultrasonic Transducers: Materials and Design for Sensors, Actuators and Medical Applications; Nakamura, K., Ed.; Woodhead Publishing Series in Electronic and Optical Materials; Woodhead Publishing: Sawston, UK, 2012; pp. 408–443. ISBN 978-0-85709-630-2/978-1-84569-989-5. [Google Scholar]
- Parks, D.A.; Zhang, S.; Tittmann, B.R. High-Temperature (>500/Spl Deg C) Ultrasonic Transducers: An Experimental Comparison among Three Candidate Piezoelectric Materials. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 1010–1015. [Google Scholar] [CrossRef]
- Song, W.; Yuan, X.; Yu, S.; Yu, X. A Novel Design of Piezoelectric Ultrasonic Transducer with High Temperature Resistance. In Proceedings of the 2018 IEEE International Ultrasonics Symposium (IUS), Kobe, Japan, 22–25 October 2018; pp. 1–9. [Google Scholar]
- Bhadwal, N.; Torabi Milani, M.; Coyle, T.; Sinclair, A. Dry Coupling of Ultrasonic Transducer Components for High Temperature Applications. Sensors 2019, 19, 5383. [Google Scholar] [CrossRef]
- Bilgunde, P.N.; Bond, L.J. Resonance Analysis of a High Temperature Piezoelectric Disc for Sensitivity Characterization. Ultrasonics 2018, 87, 103–111. [Google Scholar] [CrossRef]
- Saillant, J.-F.; Marlier, R.; Navacchia, F.; Baqué, F. Ultrasonic Transducer for Non-Destructive Testing of Structures Immersed in Liquid Sodium at 200 °C. Sensors 2019, 19, 4156. [Google Scholar] [CrossRef]
- Zu, H.; Wu, H.; Wang, Q.-M. High-Temperature Piezoelectric Crystals for Acoustic Wave Sensor Applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 486–505. [Google Scholar] [CrossRef]
- Hamidon, M.N.; Skarda, V.; White, N.M.; Krispel, F.; Krempl, P.; Binhack, M.; Buff, W. High-Temperature 434 MHz Surface Acoustic Wave Devices Based on GaPO/Sub 4/. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 2465–2470. [Google Scholar] [CrossRef]
- Cheong, Y.-M.; Kim, K.-M.; Kim, D.-J. High-Temperature Ultrasonic Thickness Monitoring for Pipe Thinning in a Flow-Accelerated Corrosion Proof Test Facility. Nucl. Eng. Technol. 2017, 49, 1463–1471. [Google Scholar] [CrossRef]
- Pucci, L.; Raillon, R.; Taupin, L.; Baqué, F. Design of a Phased Array EMAT for Inspection Applications in Liquid Sodium. Sensors 2019, 19, 4460. [Google Scholar] [CrossRef] [PubMed]
- CEA. Sodium-Cooled Nuclear Reactors; François, P.J., Ed.; Edition du Moniteur: Saclay, France, 2016; ISBN 978-2-281-14055-2. [Google Scholar]
- Lhuillier, C.; Marchand, B.; Augem, J.-M.; Sibilo, J.; Saillant, J.-F. Generation IV Nuclear Reactors: Under Sodium Ultrasonic Transducers for Inspection and Surveillance. In Proceedings of the 2013 3rd International Conference on Advancements in Nuclear Instrumentation, Measurement Methods and Their Applications (ANIMMA), Marseille, France, 23–27 June 2013; pp. 1–6. [Google Scholar]
- Feuillard, G.; Hue, L.P.T.H.; Saadaoui, N.; Nguyen, V.T.; Lethiecq, M.; Saillant, J.F. Symmetric Reflector Ultrasonic Transducer Modeling and Characterization: Role of the Matching Layer on Electroacoustic Performance. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 3608–3615. [Google Scholar] [CrossRef] [PubMed]
- Warner, A.W.; Onoe, M.; Coquin, G.A. Determination of Elastic and Piezoelectric Constants for Crystals in Class (3m). J. Acoust. Soc. Am. 1967, 42, 1223–1231. [Google Scholar] [CrossRef]
- Nguyen, D.C.; Navacchia, F.; Tran-Huu-Hue, L.P.; Feuillard, G. Ultrasonic Characterization, Simulation of Porous Metal in the Interest of High Frequency Applications. In Proceedings of the 4th Singapore International Non-Destructive Testing Conference and Exhibition, Singapore, 7–8 November 2022. [Google Scholar]
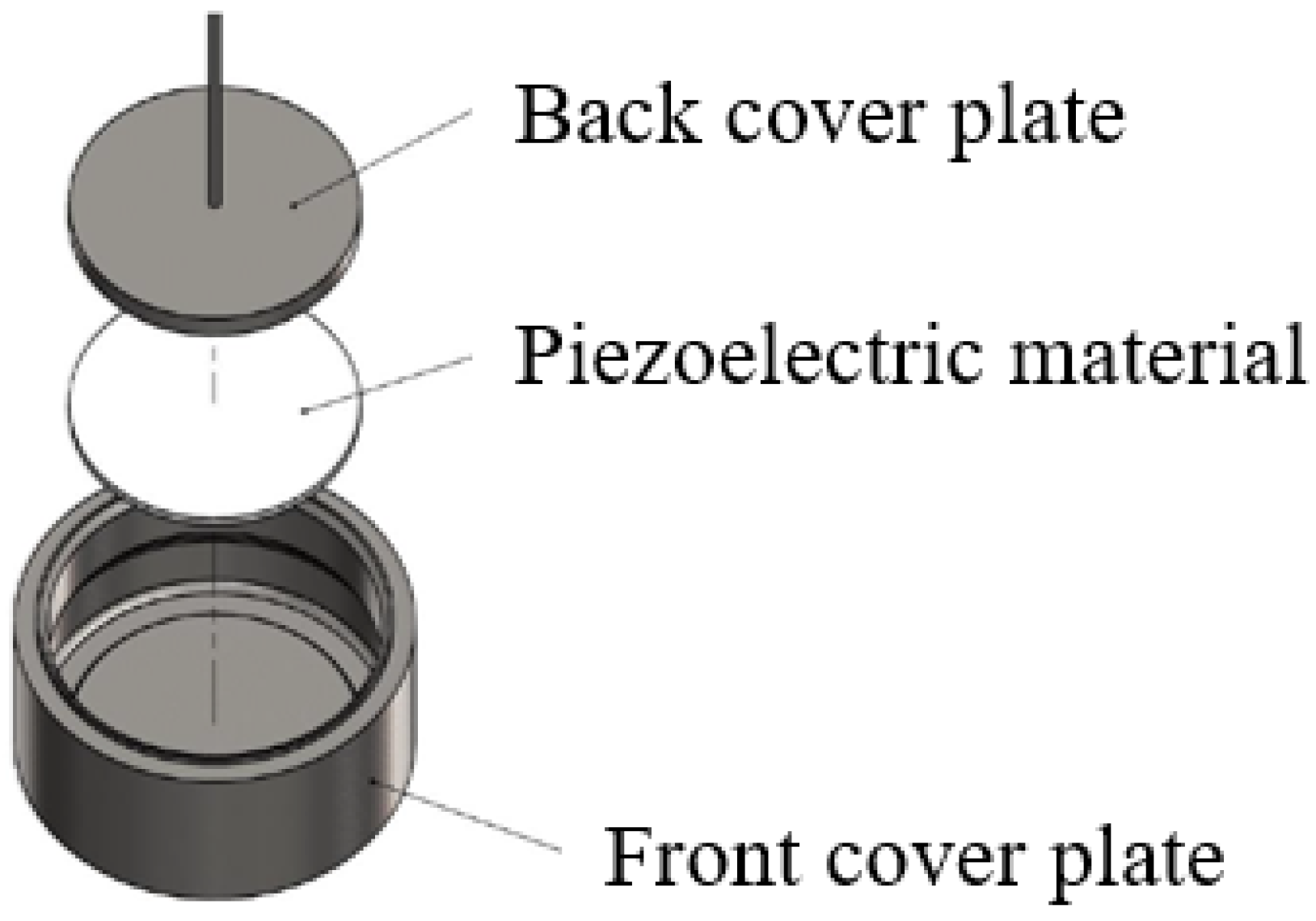
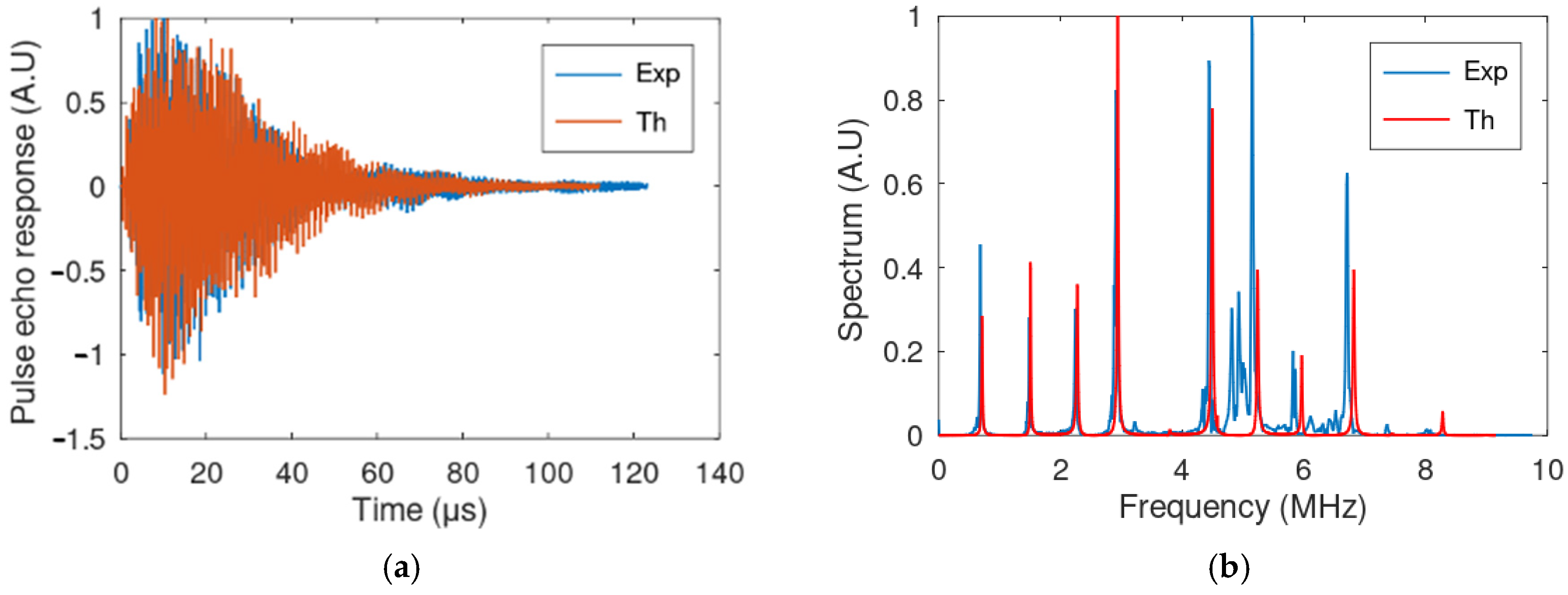

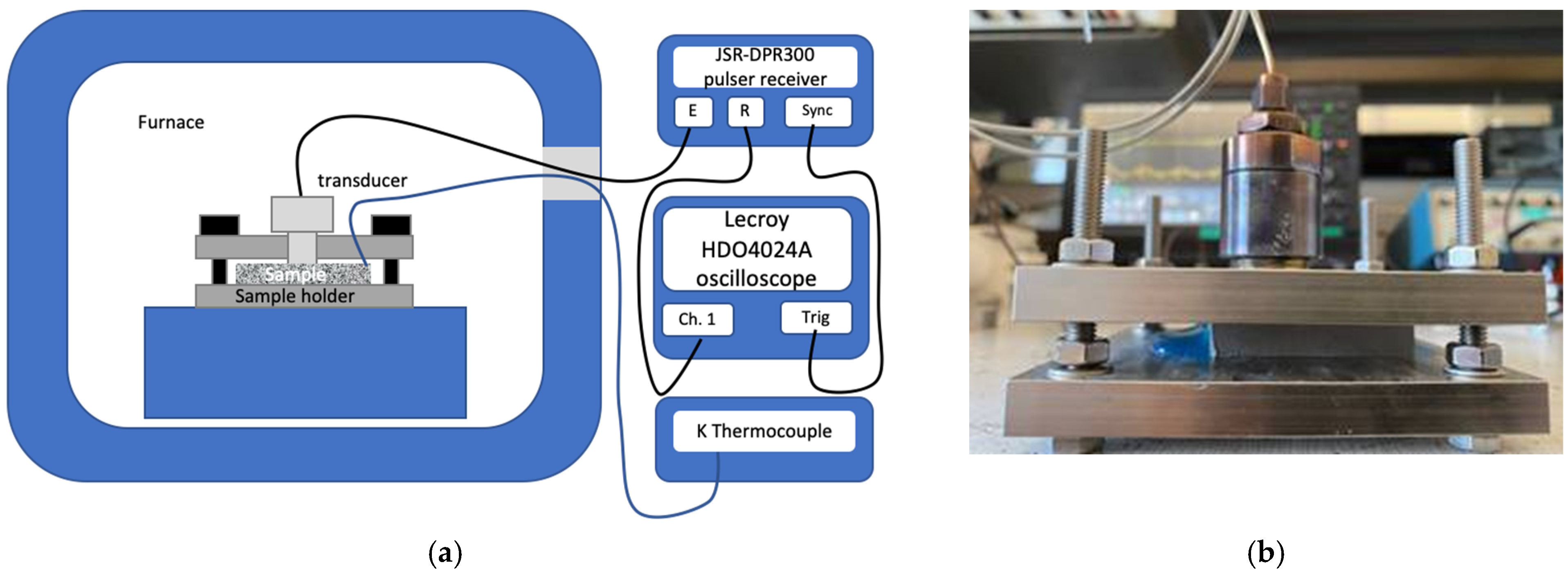
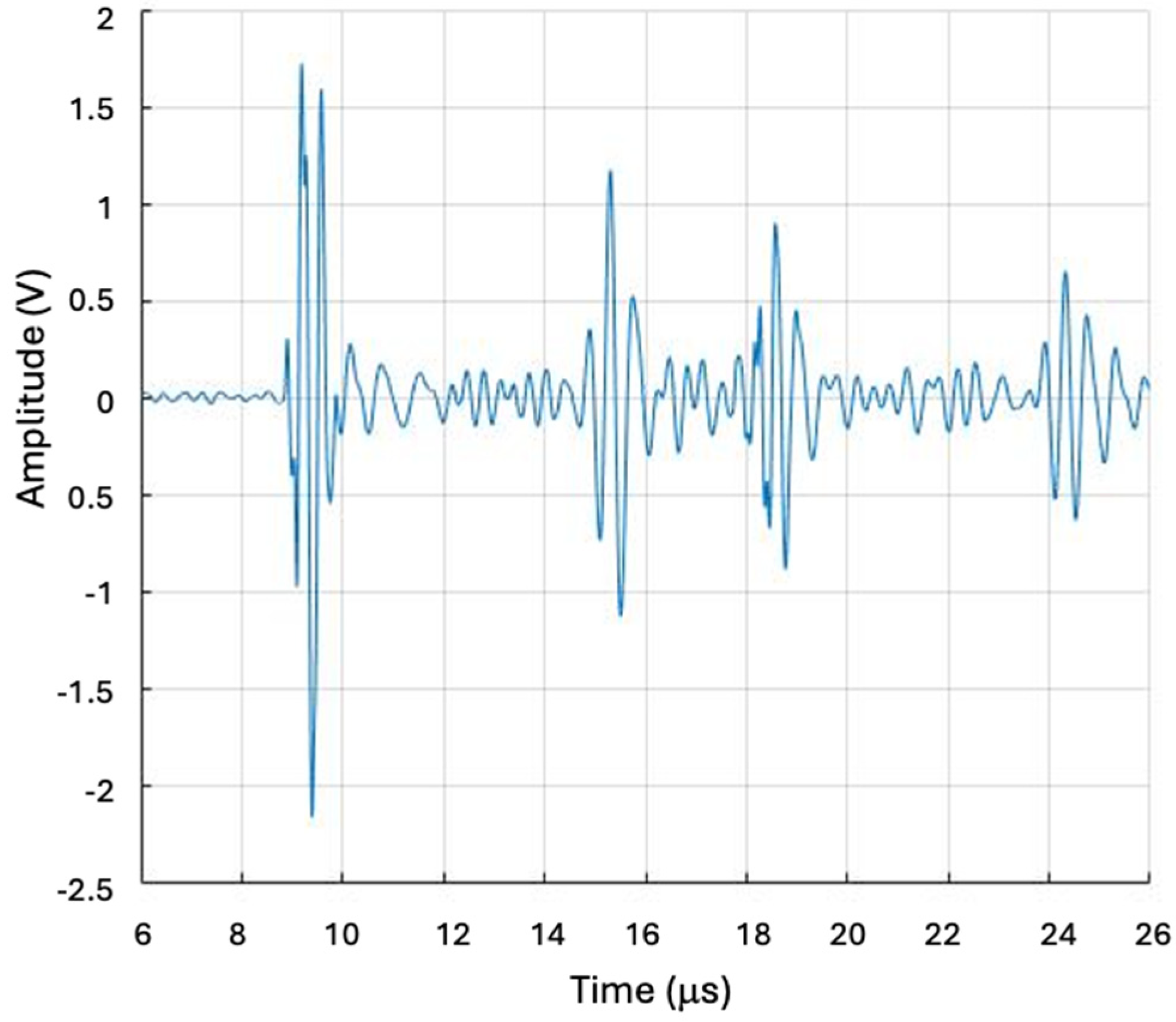

| Active Element | |
|---|---|
| Single crystal | LiNbO3 Z-cut * |
| Diameter (mm) | 40 |
| Thickness (mm) | 0.78 |
| Density (kg m−3) | 4700 |
| Wave velocity (m s−1) | 7220 |
| Acoustic impedance (MRayl) | 33.9 |
| Relative dielectric constant | 29 |
| Thickness coupling coefficient | 0.17 |
| Front layer/rear layer | |
| Thickness (mm) | 1.2/2 |
| Wave velocity (m.s−1) | 5740 |
| Loss tangent | 0.001 |
| Acoustic impedance (MRayl) | 46.2 |
| Propagation medium (water) | |
| Acoustic impedance (MRayl) | 1.5 |
| Material | Measured Thickness (mm) | Measured Density (kg m−3) | Measured Porosity (%) | Nominal Pore Size (µm) |
|---|---|---|---|---|
| SSU00 | 10.00 | 7918 | - | - |
| SSU02 | 9.98 | 6059 | 25.20 | 1.7 |
| SSU10 | 10.13 | 5268 | 34.2297 | 10.9 |
| Material | Average Porosity (%) | Average Wave Velocity (m s−1) | Standard Deviation (%) | Average Acoustic Impedance (MRayls) | Standard Deviation (%) | Average Attenuation (dB mm−1) | Standard Deviation (%) |
|---|---|---|---|---|---|---|---|
| SSU00 | 0 | 5780 | 1.10 | 45.11 | 1.07 | 0.12 | 7.13 |
| SSU02 | 25.20 | 4402 | 1.90 | 26.73 | 2.46 | 0.46 | 12.75 |
| SSU10 | 34.97 | 3751 | 1.57 | 19.75 | 2.80 | 0.46 | 26.05 |
| SSU00 | SSU02 | SSU10 | ||||
|---|---|---|---|---|---|---|
| Temperature (°C) | Wave Velocity (m s−1) | Attenuation Variation (dB mm−1) | Wave Velocity (m s−1) | Attenuation Variation (dB mm−1) | Wave Velocity (m.s−1) | Attenuation Variation (dB mm−1) |
| 25 | 5807.50 | 0.00 | 4417.50 | 0.00 | 3511.70 | 0.00 |
| 50 | 5796.90 | 0.04 | 4398.00 | 0.03 | 3495.30 | 0.00 |
| 75 | 5782.90 | 0.05 | 4376.30 | 0.04 | 3478.60 | 0.00 |
| 100 | 5767.00 | 0.07 | 4359.10 | 0.04 | 3462.20 | 0.01 |
| 125 | 5750.00 | 0.09 | 4342.90 | 0.04 | 3446.70 | 0.01 |
| 150 | 5734.00 | 0.11 | 4325.30 | 0.04 | 3430.20 | 0.01 |
| 175 | 5720.00 | 0.10 | 4311.60 | 0.05 | 3413.50 | 0.01 |
| 200 | 5702.00 | 0.11 | 4293.60 | 0.06 | 3396.60 | 0.02 |
| 225 | 5682.90 | 0.12 | 4274.10 | 0.06 | 3380.10 | 0.03 |
| 250 | 5661.40 | 0.16 | 4258.20 | 0.06 | 3362.90 | 0.06 |
| 275 | 5640.00 | 0.18 | 4243.80 | 0.06 | 3344.80 | 0.06 |
| 300 | 5617.00 | 0.20 | 4221.20 | 0.06 | 3328.60 | 0.06 |
| 325 | 5594.20 | 0.22 | 4202.80 | 0.05 | 3310.50 | 0.08 |
| 350 | 5572.00 | 0.23 | 4178.00 | 0.06 | 3293.70 | 0.09 |
| 375 | 5547.50 | 0.25 | 4150.70 | 0.04 | 3276.90 | 0.11 |
| 400 | 5522.40 | 0.27 | 4131.90 | 0.04 | 3259.50 | 0.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feuillard, G.; Nguyen, D.C.; Lethiecq, M.; Jean, M.; Navacchia, F. Porous Metal Backing for High-Temperature Ultrasonic Transducers. Acoustics 2024, 6, 1074-1087. https://doi.org/10.3390/acoustics6040058
Feuillard G, Nguyen DC, Lethiecq M, Jean M, Navacchia F. Porous Metal Backing for High-Temperature Ultrasonic Transducers. Acoustics. 2024; 6(4):1074-1087. https://doi.org/10.3390/acoustics6040058
Chicago/Turabian StyleFeuillard, Guy, Dang Chi Nguyen, Marc Lethiecq, Mathieu Jean, and Frédéric Navacchia. 2024. "Porous Metal Backing for High-Temperature Ultrasonic Transducers" Acoustics 6, no. 4: 1074-1087. https://doi.org/10.3390/acoustics6040058
APA StyleFeuillard, G., Nguyen, D. C., Lethiecq, M., Jean, M., & Navacchia, F. (2024). Porous Metal Backing for High-Temperature Ultrasonic Transducers. Acoustics, 6(4), 1074-1087. https://doi.org/10.3390/acoustics6040058







