Feasibility Analysis for Active Noise Cancellation Using the Electrical Power Steering Motor
Abstract
1. Introduction
2. Materials and Methods
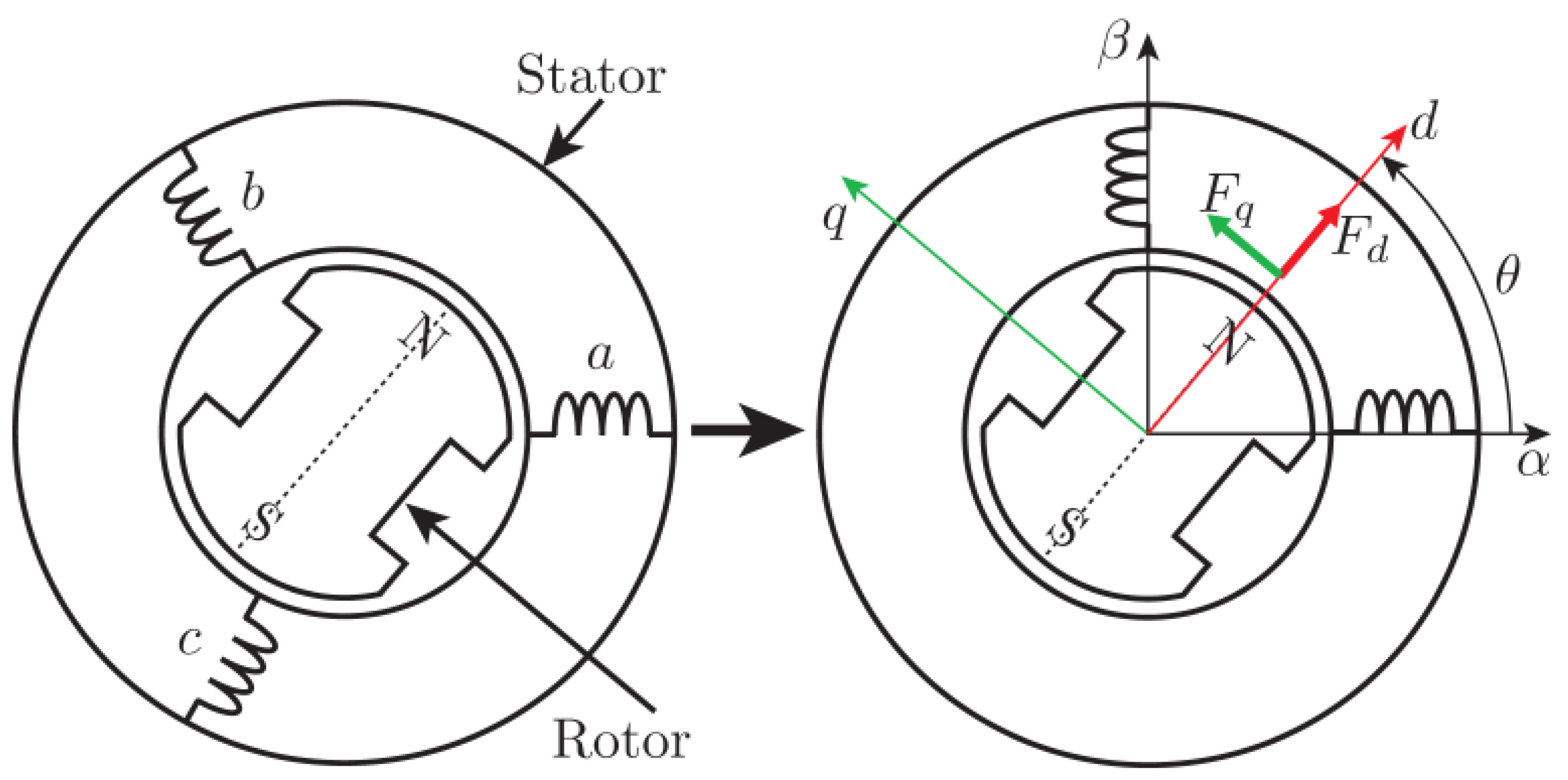
2.1. Control Structure
2.2. Experimental Setup
- Acoustic Sensors:
- –
- Accelerometers: To measure the structure-borne noise level, a PCB Piezotronics triaxial accelerometer is used. It has a linear frequency range from 2 Hz to 6 kHz. Its sensitivity is 1.02 mV/(m/s2).
- –
- Microphones: The airborne level is measured using a 1/2” condenser microphone mafufactured by Microtech Gefell GmbH (07926 Gefell, Germany). It has a linear frequency range from 20 Hz to 10 kHz. Its sensitivity is 50 mV/Pa.
- Measurement Systems:
- –
- PAK MK II: A frontend MK II with highly sensitive measurement inputs from Müller-BBM is used for acoustic data acquisition. Its measurement inputs support the IEPE standard with a 24-bit resolution in the measuring range ±1 V.
- –
- SQuadriga II: For acoustical data acquisition during test drives, a SQuadriga II mobile recording and playback system from HEAD acoustics is used. The inputs with a 24-bit resolution are used in the measuring range ±2.83 V.
2.3. Active Noise Cancellation
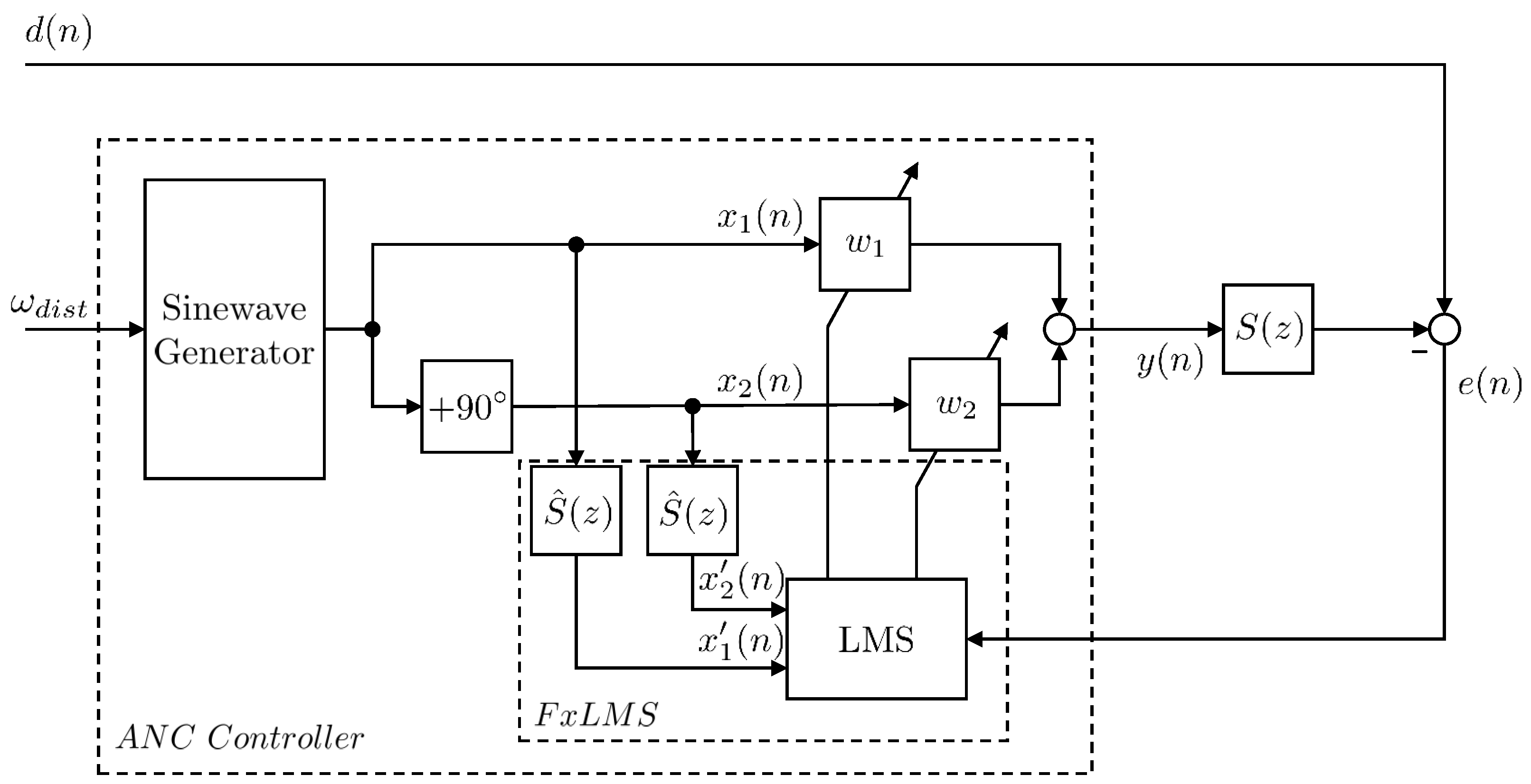
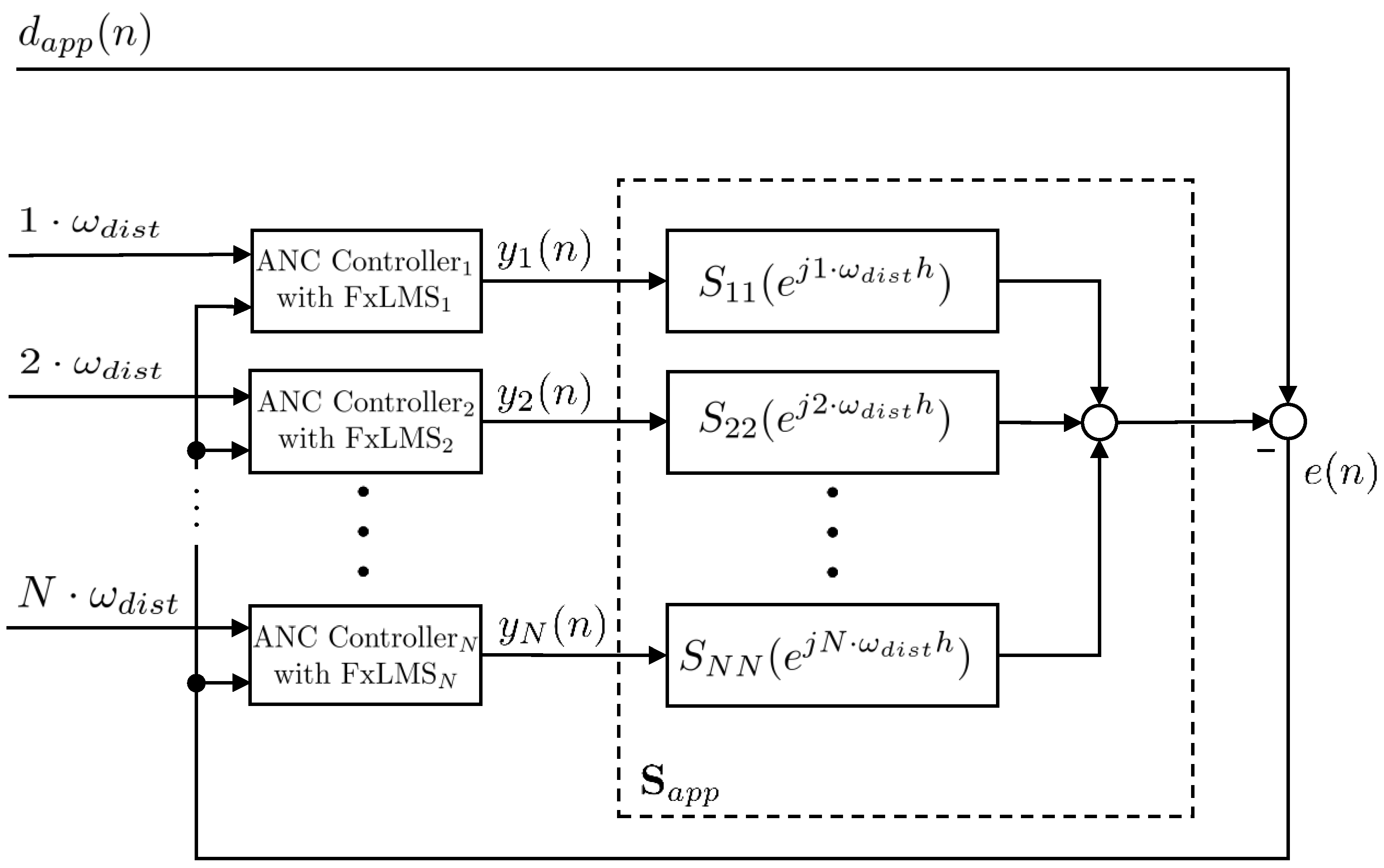
2.3.1. ANC Algorithm
2.3.2. Reduction of the Higher Harmonics
Higher Harmonics Reduction Method 1: Filter Weight Limitation
Trial Hypotheses
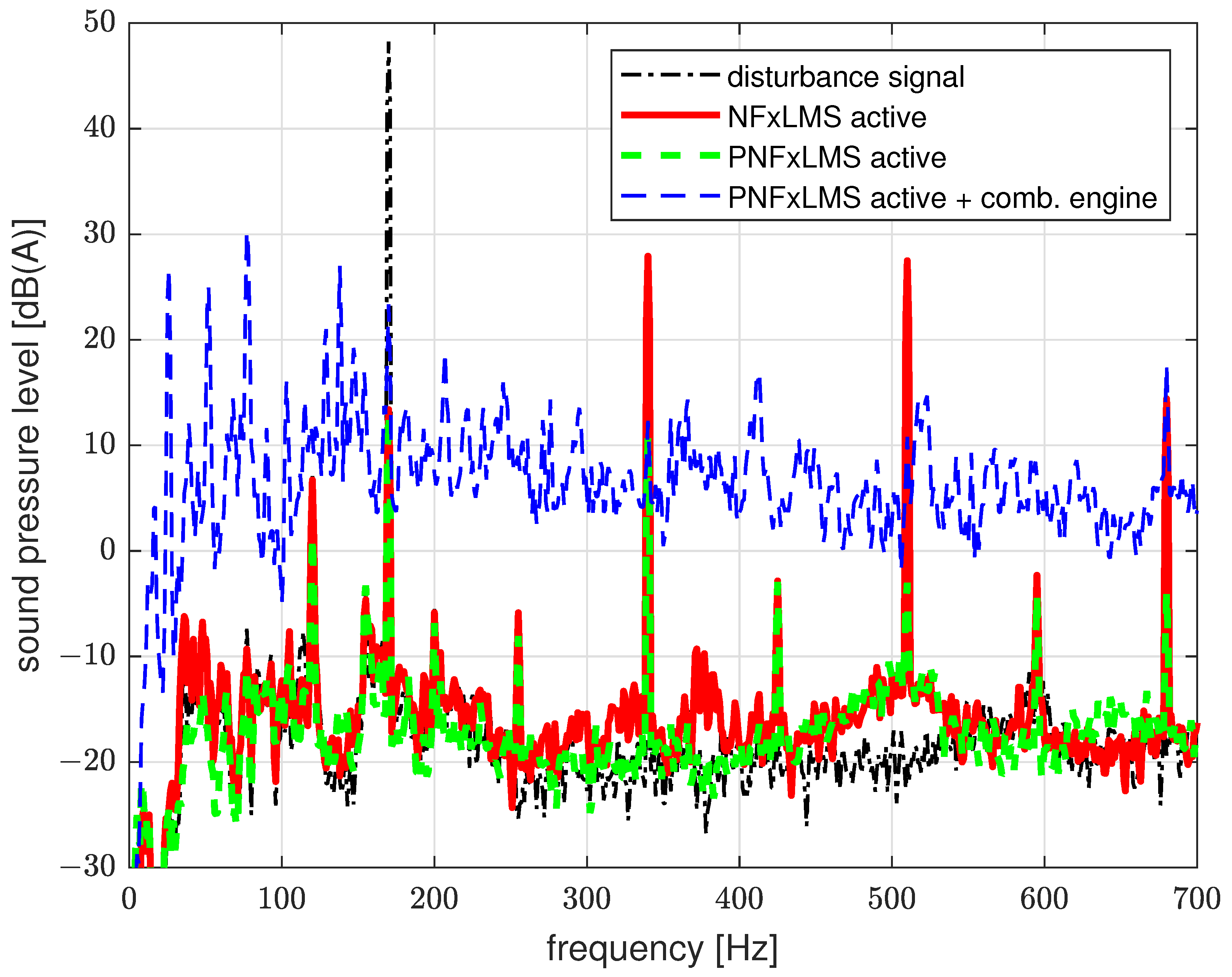
Higher Harmonics Reduction Method 2: Parallel NFxLMS Controller
- Dependency of the compensation level on the noise level: this can be more sensitive during traffic light phases, for example, than during highway driving and high interference levels. The noise level and the associated filter limitation could be implemented in a control unit in the form of a lookup table.
- Compensation of the higher harmonics due to a parallel form of the FxLMS algorithm: several adaptive filters will be connected in parallel to reduce the dominating harmonics.
3. Results
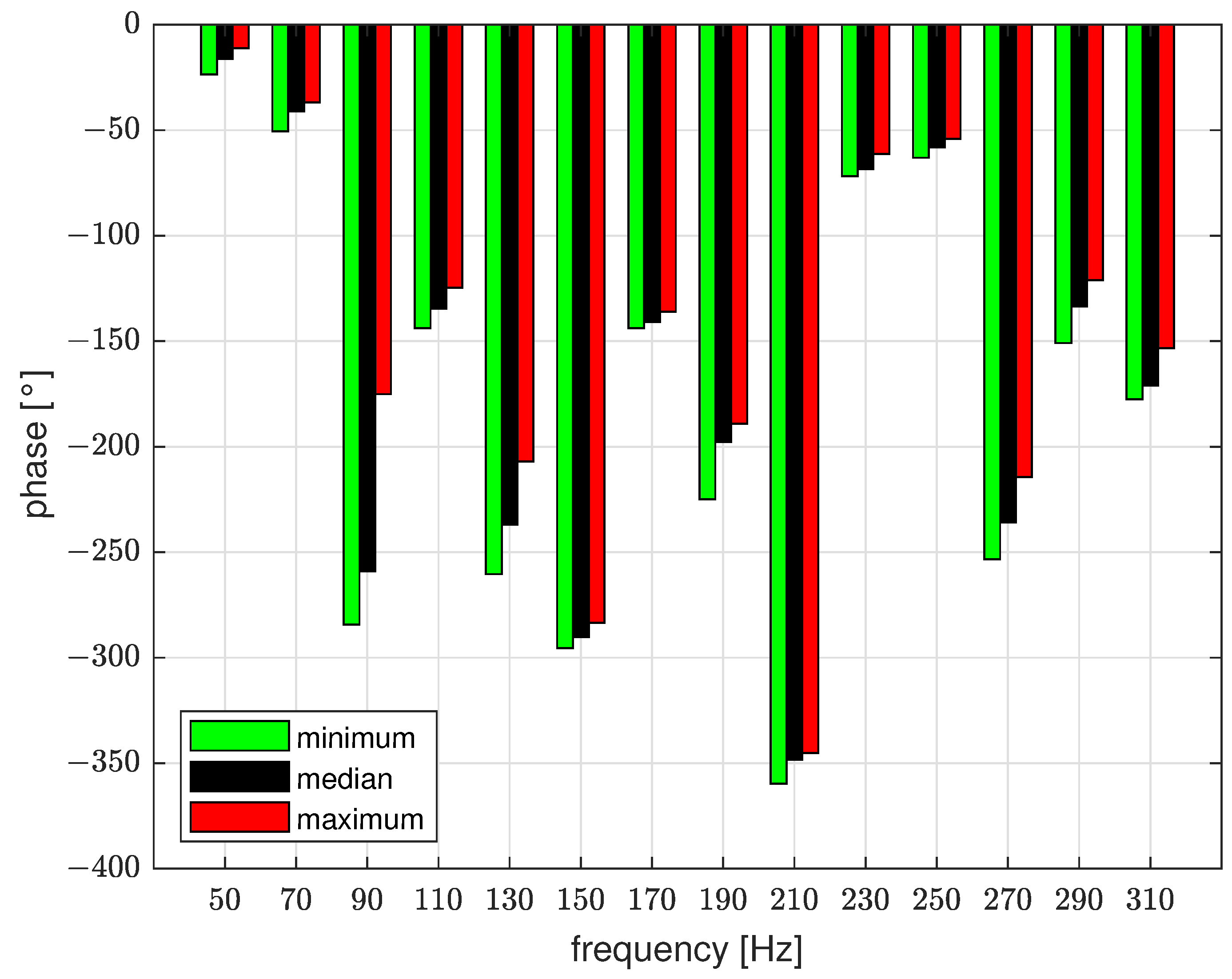
3.1. Constant Synthetic Disturbance Source
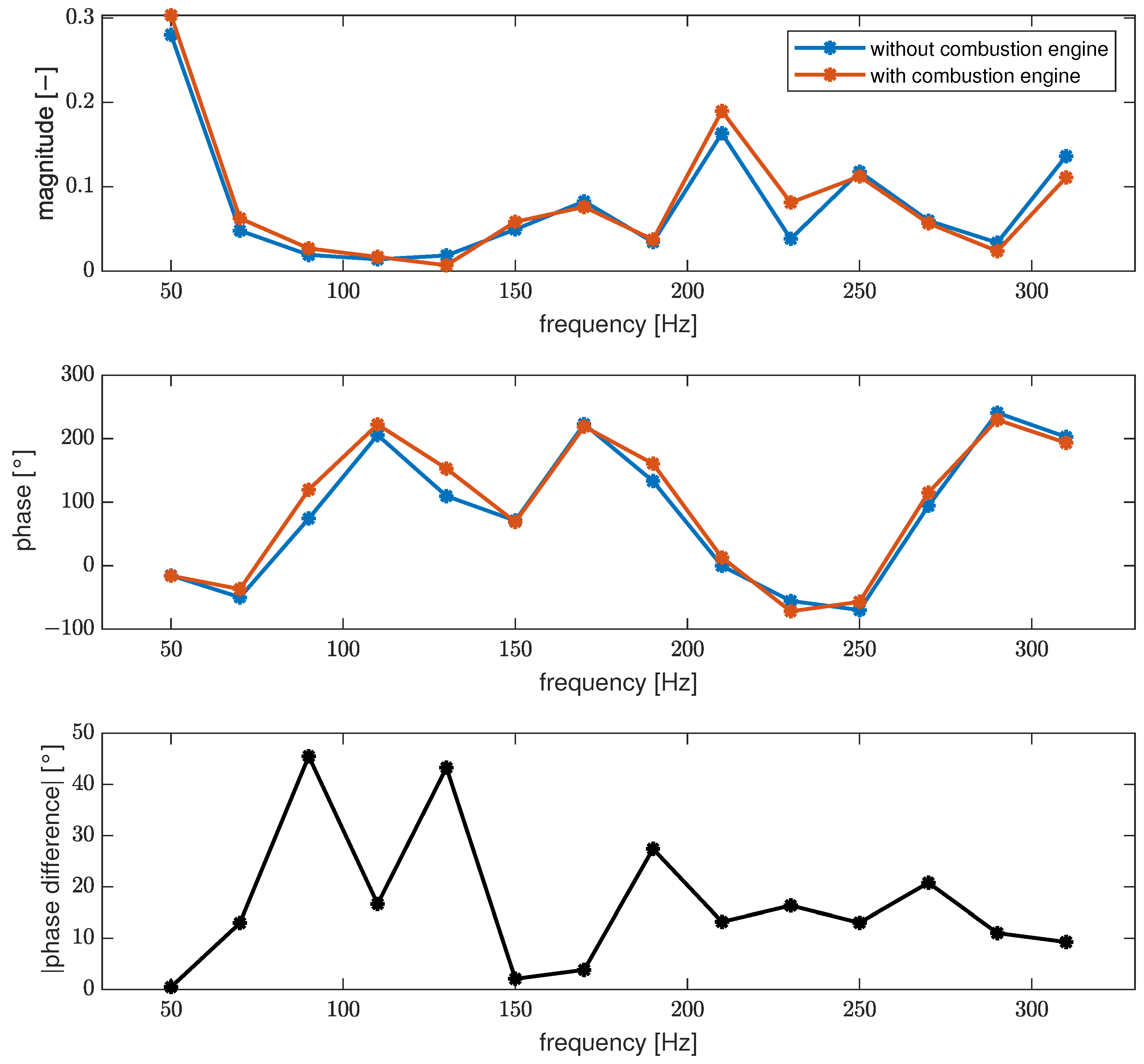
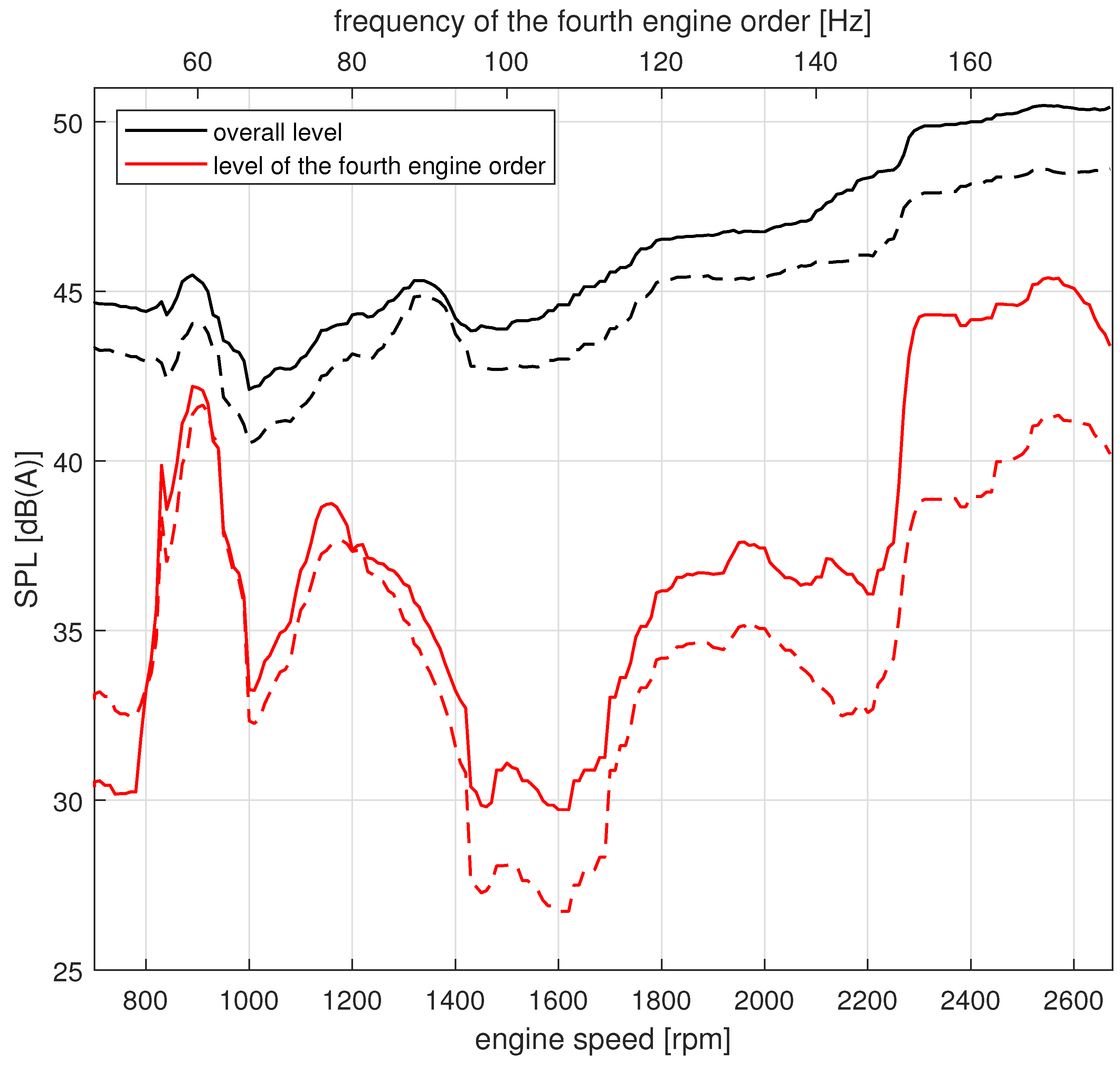
3.2. Reduction in Combustion Engine Order
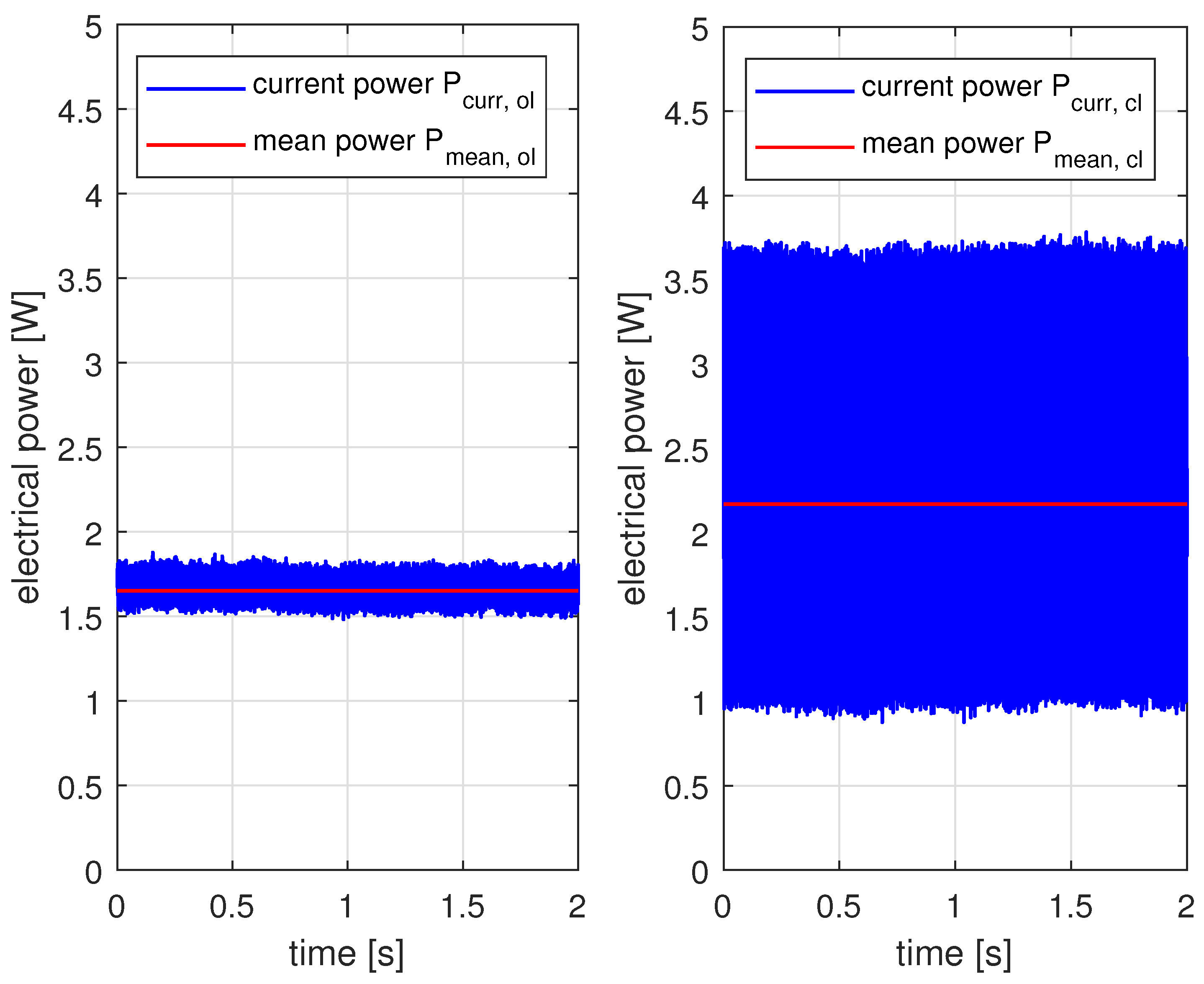
3.3. Energetic Considerations
- The procedure described in the previous section is used to determine the amplitude of the ANC algorithm needed to cancel the order of the combustion engine. After the ANC algorithm has converged, the values of the constant filter weights are stored. The output amplitude can be calculated using Equation (6).
- To eliminate the thermal impact due to the combustion engine, the ANC algorithm is replaced by a harmonic signal with the calculated amplitude and a constant frequency. Therefore, it is possible to stimulate the motor with a realistic signal without using an error signal.
- Since the ambient temperature is also not constant and to obtain an identical dynamic behavior of the temperature without the ANC function, a second EPS motor of the same type is placed near the stimulated one, while the surface temperature is also measured.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANC | Active Noise Cancellation |
| NVH | Noise, Vibration, Harshness |
| EPS | Electrical Power Steering |
| PMSM | Permanent Magnet Synchronous Machine |
| FIR | Finite Impulse Response |
| LMS | Least Mean Squares |
| FxLMS | Filtered-x Least Mean Squares |
| NFxLMS | Narrowband Filtered-x Least Mean Squares |
| PNFxLMS | Parallel Narrowband Filtered-x Least Mean Squares |
| FOC | Field Oriented Control |
| ECU | Electrical Control Unit |
| PWM | Pulse Width Modulation |
| SVM | Space Vector Modulation |
| IEPE | Integrated Electronics Piezo Electric |
References
- Wolf, A.; Portal, E. Requirements to Noise Reduction Concepts and Parts in Future Engine Compartments. In SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2000. [Google Scholar] [CrossRef]
- Hausberg, F.; Scheiblegger, C.; Pfeffer, P.; Plöchl, M.; Hecker, S.; Rupp, M. Experimental and analytical study of secondary path variations in active engine mounts. J. Sound Vib. 2014, 340, 22–38. [Google Scholar] [CrossRef]
- Bohn, C.; Cortabarria, A.; Härtel, V.; Kowalczyk, K. Active control of engine-induced vibrations in automotive vehicles using disturbance observer gain scheduling. Control Eng. Pract. 2004, 12, 1029–1039. [Google Scholar] [CrossRef]
- Schubert, D.; Henneberger, R.; Hecker, S.; Sentpali, S.; Marburg, S. Active Noise Cancellation in Passenger Cars using the Electrical Power Steering Motor. In Proceedings of the 2017 IEEE Conference on Control Technology and Applications (CCTA), Maui, HI, USA, 27–30 August 2017; pp. 255–260. [Google Scholar] [CrossRef]
- Widrow, B.; McCool, J.; Ball, M. The Complex LMS Algorithm. In Proceedings of the IEEE; IEEE: Piscataway, NJ, USA, 1975. [Google Scholar] [CrossRef]
- Morgan, D. An Analysis of Multiple Correlation Cancellation Loops with a Filter in the Auxiliary Path. IEEE Trans. Acoust. Speech Signal Process. 1980, 28, 454–467. [Google Scholar] [CrossRef]
- Widrow, B.; Walach, E. Adaptive Inverse Control: A Signal Processing Approach, Reissue Edition; IEEE Press Series on Power Engineering; IEEE Press Wiley-Interscience and IEEE Xplore: Piscataway, NJ, USA, 2008. [Google Scholar]
- Burgess, J.C. Active adaptive sound control in a duct: A computer simulation. J. Acoust. Soc. Am. 1981, 70, 715–726. [Google Scholar] [CrossRef]
- Kuo, S.M.; Morgan, D.R. Active Noise Control Systems: Algorithms and DSP Implementations; A Wiley-Interscience Publication; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Elliott, S.J. Signal Processing for Active Control; Academic Press: San Diego, CA, USA, 2005. [Google Scholar]
- Hillis, A.J. Multi-input multi-output control of an automotive active engine mounting system. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2011, 225, 1492–1504. [Google Scholar] [CrossRef]
- Bao, C.; Sas, P.; van Brussel, H. Comparison of two-on-line identification algorithms for active noise control. In Proceedings of the 2nd Conference on Recent Advances in Active Control of Sound and Vibration, Blacksburg, VA, USA, 1 January 1993; pp. 38–54. [Google Scholar]
- van der Broeck, H.W.; Skudelny, H.C.; Stanke, G.V. Analysis and Realization of a Pulsewidth Modulator Based on Voltage Space Vectors. IEEE Trans. Ind. Appl. 1988, 24, 142–150. [Google Scholar] [CrossRef]
- Widrow, B.; Hoff, M.E. Adaptive Switching Circuits. In Proceedings of the 1960 IRE WESCON Convention Record, Part 4, Los Angeles, CA, USA, 23–26 August 1960; pp. 96–104. [Google Scholar]
- Morgan, D.R.; Sanford, C. A Control Theory Approach to the Stability and Transient Analysis of the Filtered-X LMS Adaptive Notch Filter. IEEE Trans. Signal Process. 1992, 40, 2341–2346. [Google Scholar] [CrossRef]
- Snyder, S.D.; Hansen, C.H. The Influence of Transducer Transfer Functions and Acoustic Time Delays on the Implementation of the LMS Algorithm in Active Noise Control Systems. J. Sound Vib. 1990, 141, 409–424. [Google Scholar] [CrossRef]
- Elliott, S.; Stothers, I.; Nelson, P. A Multiple Error LMS Algorithm and Its Application to the Active Control of Sound and Vibration. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 1423–1434. [Google Scholar] [CrossRef]
- Rupp, M.; Sayed, A.H. Robust FxLMS Algorithms with Improved Convergence Performance. IEEE Trans. Speech Audio Process. 1998, 6, 78–85. [Google Scholar] [CrossRef]
- Hansen, C.H. Active Control of Noise and Vibration, 2nd ed.; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2012. [Google Scholar]
- Qiu, X.; Hansen, C.H. A study of time-domain FXLMS algorithms with control output constraint. J. Acoust. Soc. Am. 2001, 109, 2815–2823. [Google Scholar] [CrossRef] [PubMed]
- Lan, H.; Zhang, M.; Ser, W. A Weight-Constrained FxLMS Algorithm for Feedforward Active Noise Control Systems. IEEE Signal Process. Lett. 2002, 9, 1–4. [Google Scholar] [CrossRef]
- Belicchi, C.; Opinto, A.; Martalo, M.; Tira, A.; Pinardi, D.; Farina, A.; Ferrari, G. ANC: A Low-Cost Implementation Perspective. In SAE Technical Paper Series 2022; SAE International: Warrendale, PA, USA, 2022. [Google Scholar] [CrossRef]
- Sutton, T.J.; Elliott, S.J. Active Attenuation of Periodic Vibration in Nonlinear Systems Using an Adaptive Harmonic Controller. J. Vib. Acoust. 1995, 117, 355. [Google Scholar] [CrossRef]
- Blondel, L.A.; Elliott, S.J. Electropneumatic Transducers as Secondary Actuators for Active Noise Control. Part III: Experimental Control in Ducts with the Subsonic Source. J. Sound Vib. 1999, 219, 451–481. [Google Scholar] [CrossRef]
- Kuo, S.M.; Ji, M. Passband Disturbance Reduction in Periodic Active Noise Control Systems. IEEE Trans. Speech Audio Process. 1996, 4, 96–103. [Google Scholar] [CrossRef]
- Hausberg, F.; Plöchl, M.; Rupp, M.; Pfeffer, P.; Hecker, S. Combination of map-based and adaptive feedforward control algorithms for active engine mounts. J. Vib. Control 2016, 23. [Google Scholar] [CrossRef]



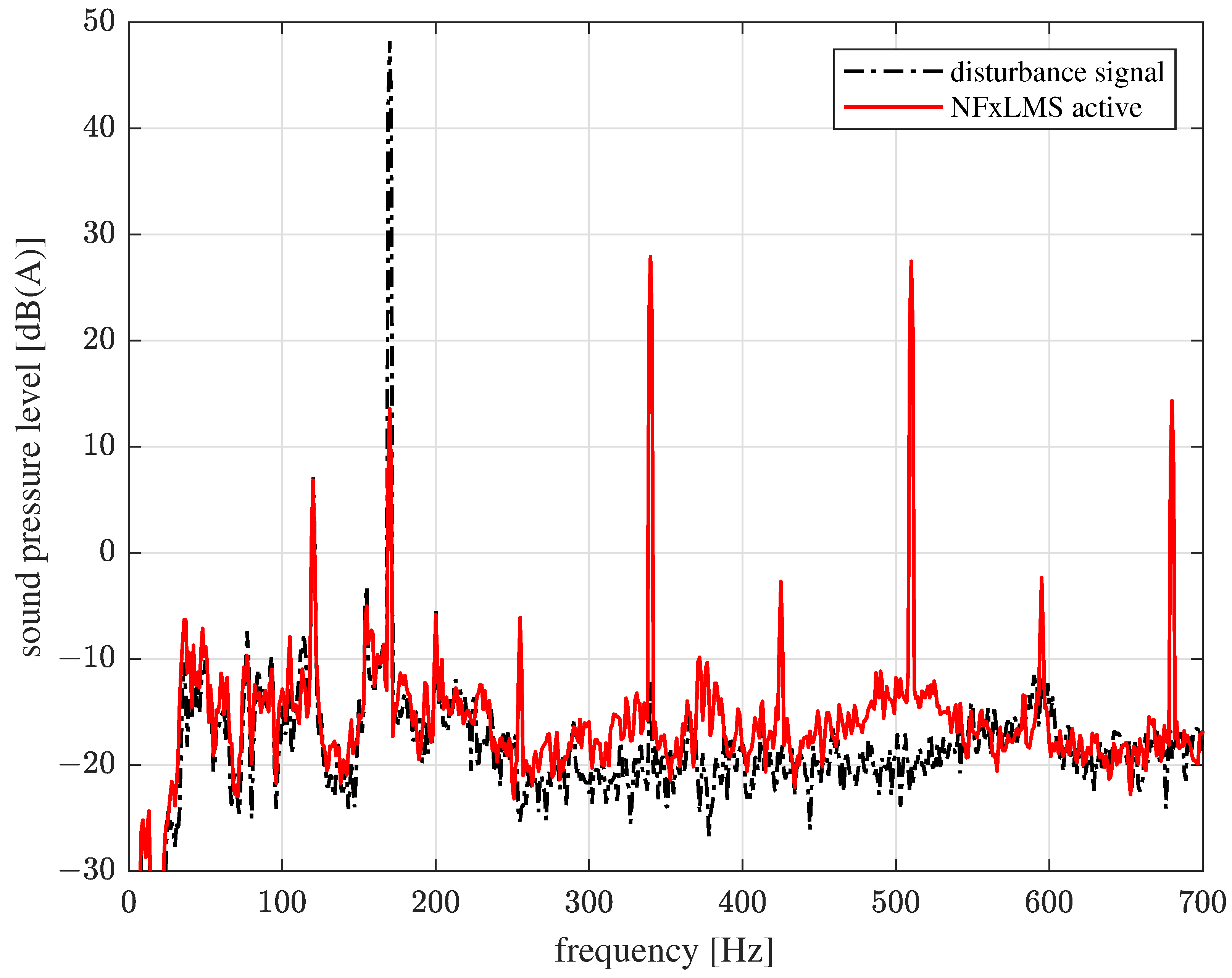

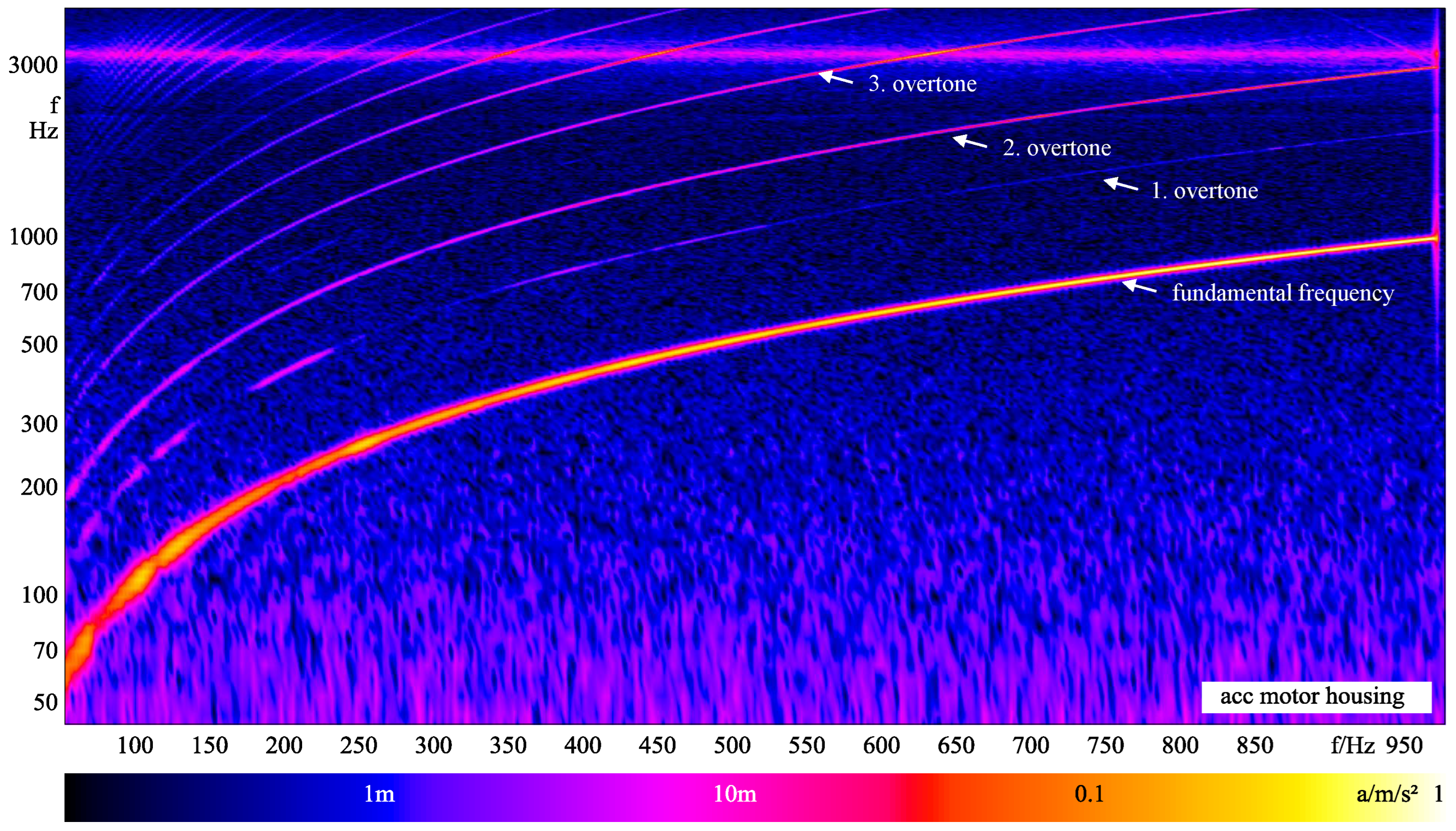

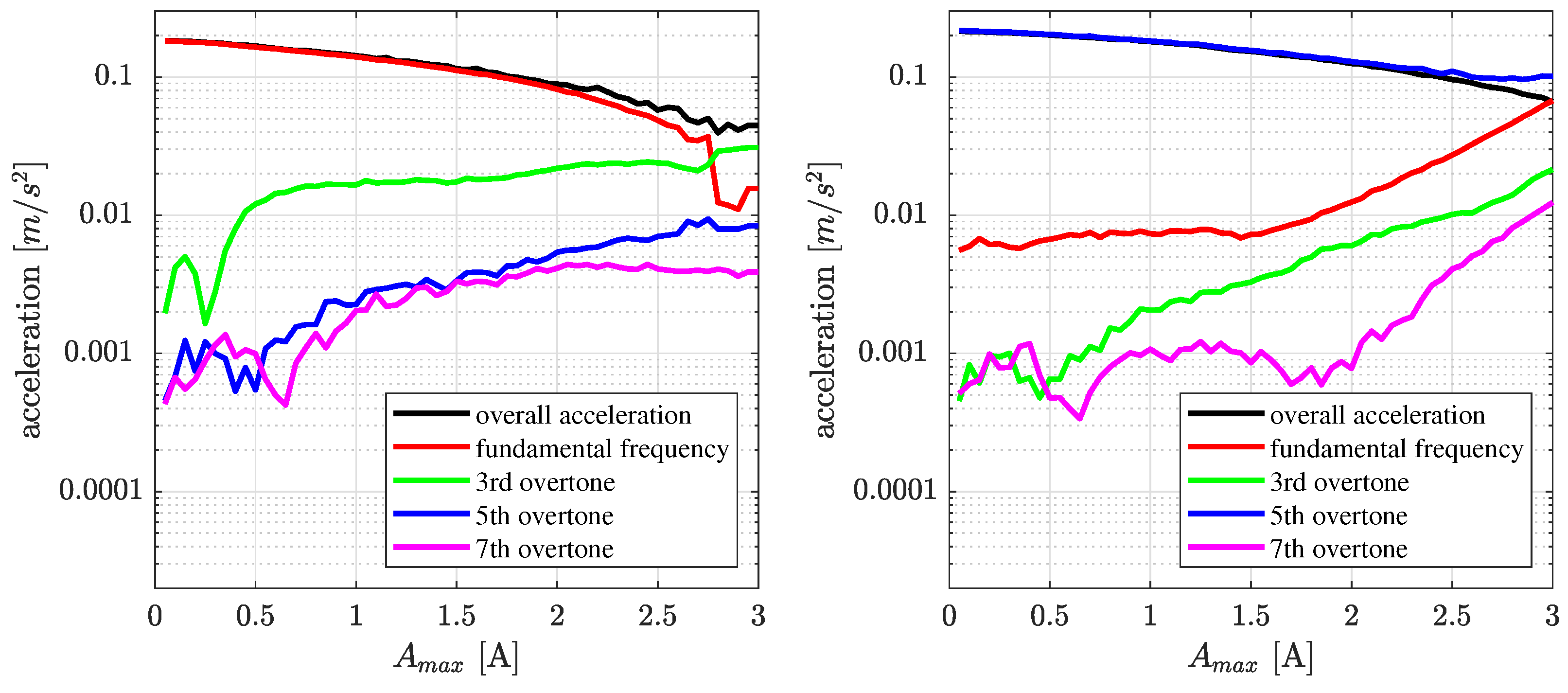
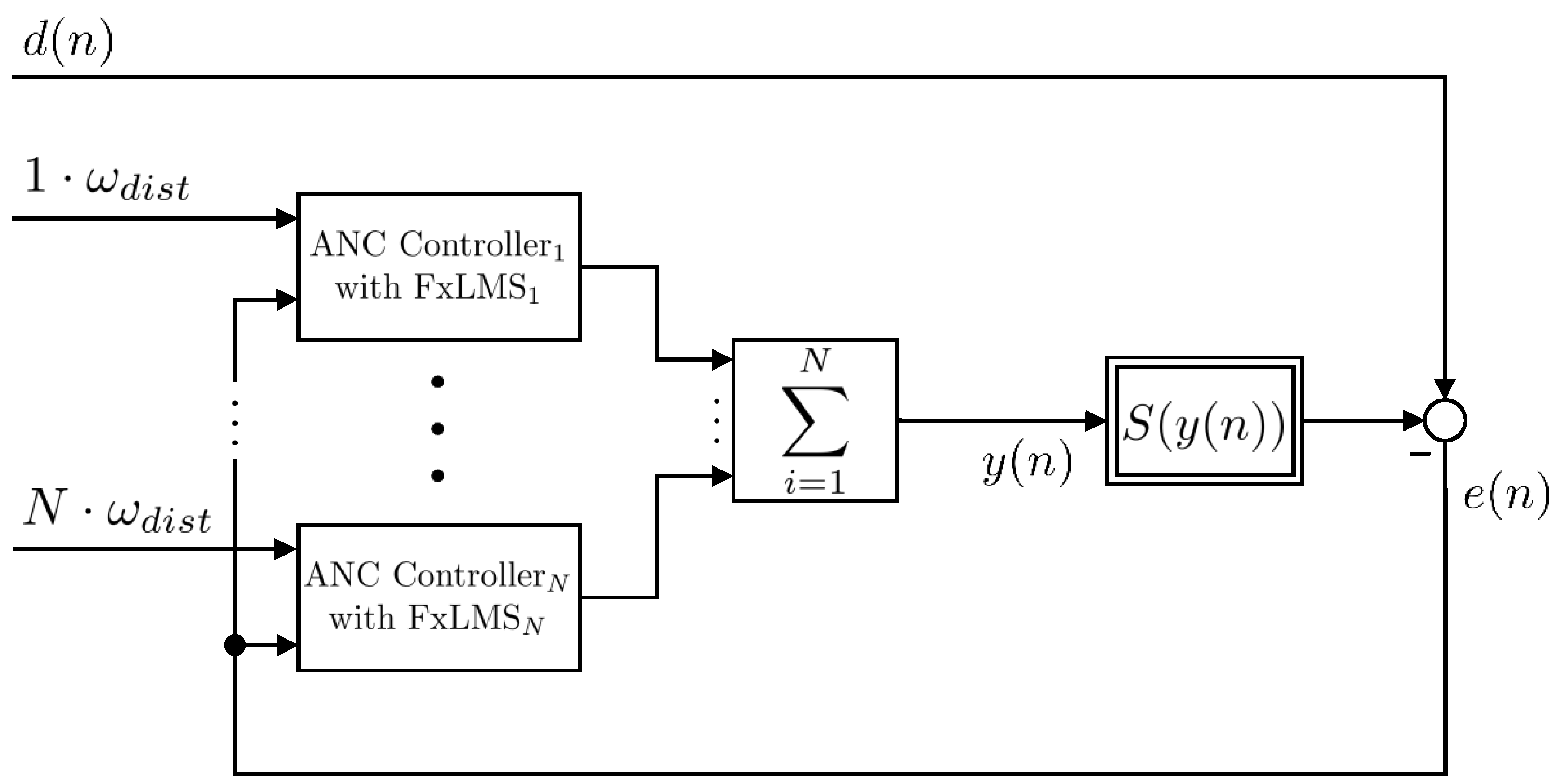
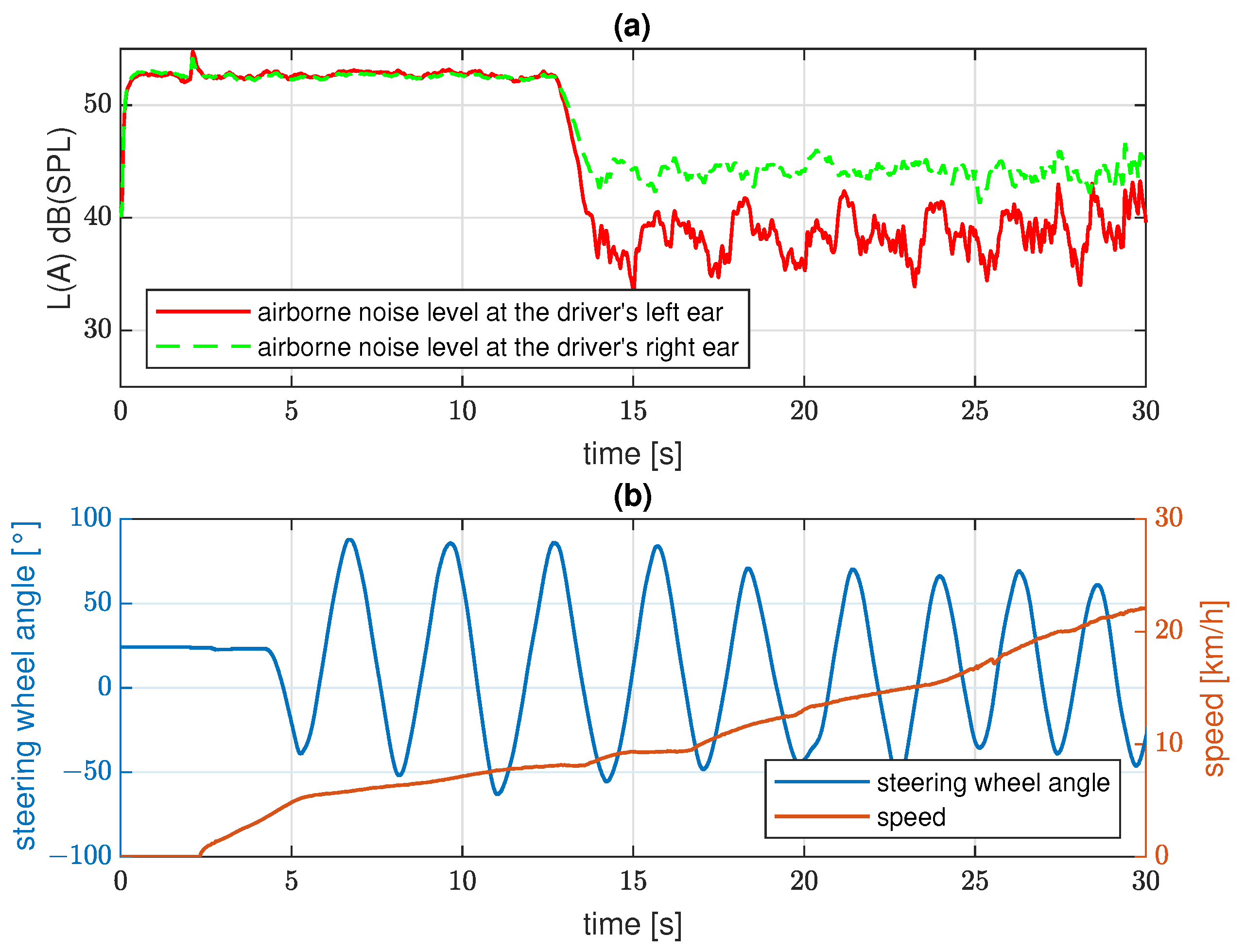

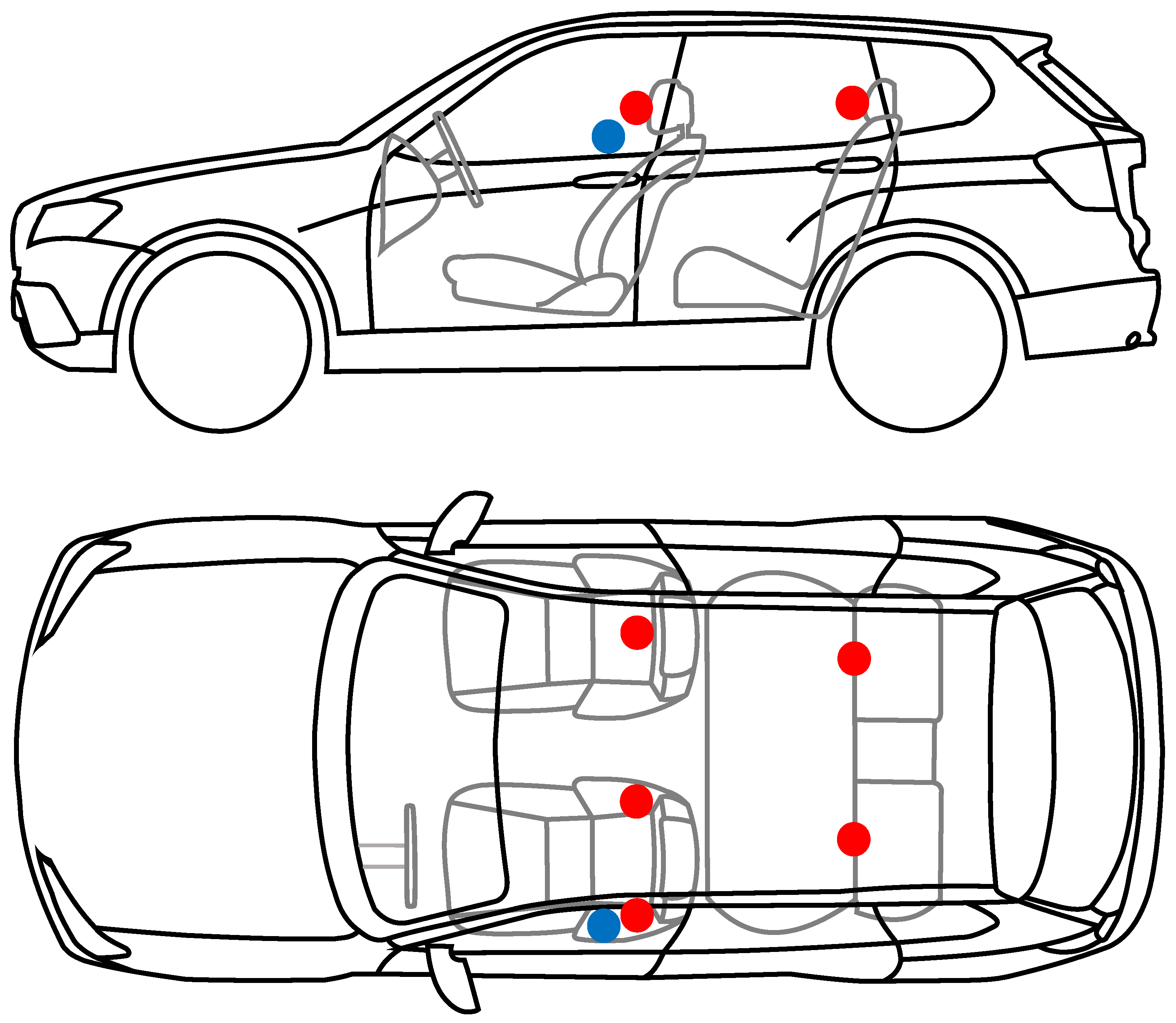
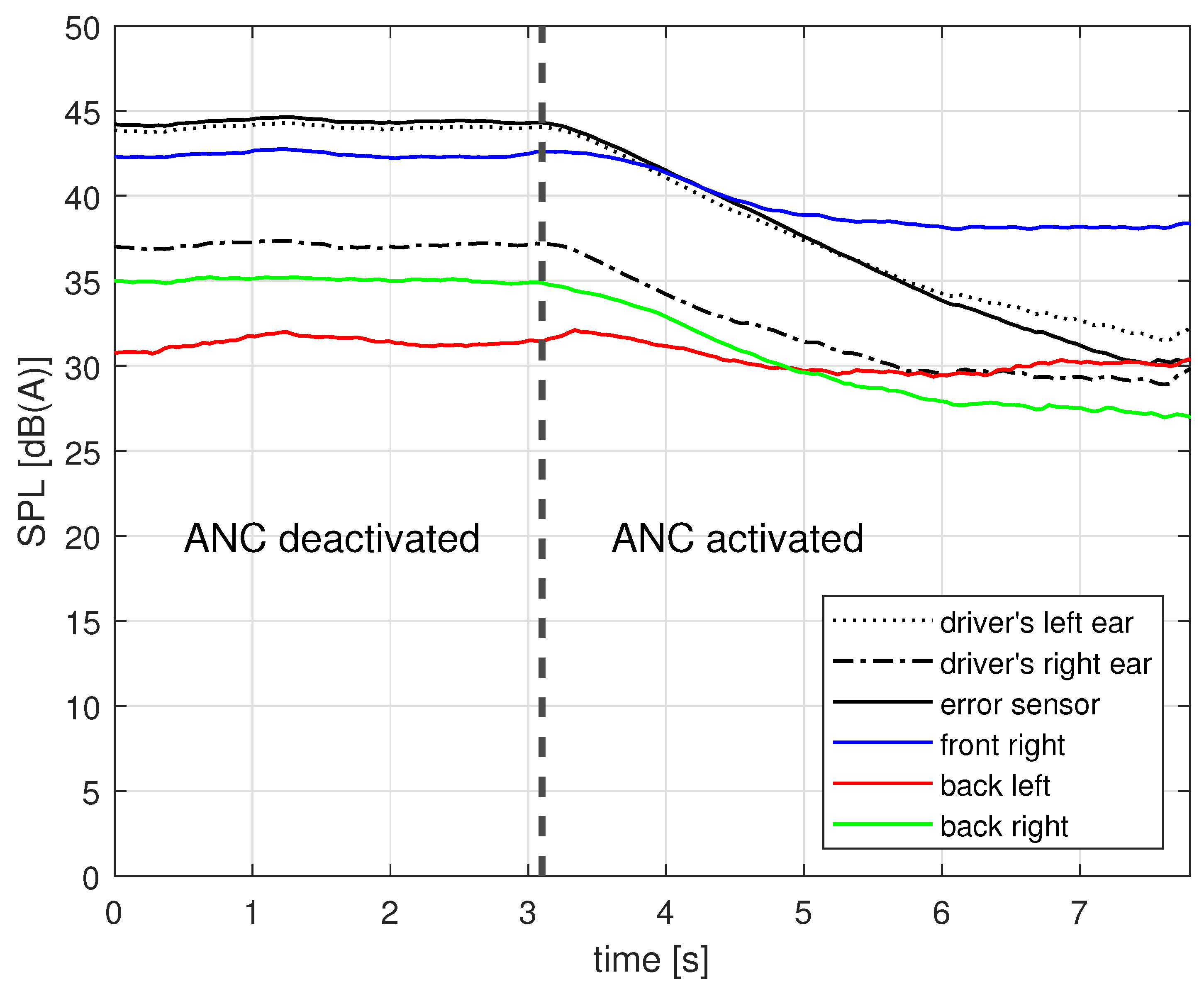

| Position | ANC Deactivated | ANC Activated | Reduction |
|---|---|---|---|
| error sensor | 44.4 dB(A) | 29.6 dB(A) | 14.8 dB(A) |
| driver’s seat | |||
| left | 44.1 dB(A) | 31.8 dB(A) | 12.3 dB(A) |
| right | 37.3 dB(A) | 29.9 dB(A) | 7.4 dB(A) |
| front right | 42.5 dB(A) | 38.4 dB(A) | 4.1 dB(A) |
| back left | 31.4 dB(A) | 31.1 dB(A) | 0.3 dB(A) |
| back right | 35.0 dB(A) | 26.1 dB(A) | 8.9 dB(A) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schubert, D.; Hecker, S.; Sentpali, S.; Buss, M. Feasibility Analysis for Active Noise Cancellation Using the Electrical Power Steering Motor. Acoustics 2024, 6, 730-753. https://doi.org/10.3390/acoustics6030040
Schubert D, Hecker S, Sentpali S, Buss M. Feasibility Analysis for Active Noise Cancellation Using the Electrical Power Steering Motor. Acoustics. 2024; 6(3):730-753. https://doi.org/10.3390/acoustics6030040
Chicago/Turabian StyleSchubert, Dominik, Simon Hecker, Stefan Sentpali, and Martin Buss. 2024. "Feasibility Analysis for Active Noise Cancellation Using the Electrical Power Steering Motor" Acoustics 6, no. 3: 730-753. https://doi.org/10.3390/acoustics6030040
APA StyleSchubert, D., Hecker, S., Sentpali, S., & Buss, M. (2024). Feasibility Analysis for Active Noise Cancellation Using the Electrical Power Steering Motor. Acoustics, 6(3), 730-753. https://doi.org/10.3390/acoustics6030040







