Abstract
For some sound sources, the function of the square of sound pressure amplitudes on the sphere in the far field is an integrable function or can be integrated with geometrical simplifications, so an exact or approximated analytical expression for the sound power can be calculated. However, often the sound pressure on the sphere in the far field can only be defined in discrete points, for which a numerical integration is required for the calculation of the sound power. In this paper, two new algorithms, Anchored Radially Projected Integration on Spherical Triangles (ARPIST) and Spherical Quadrature Radial Basis Function (SQRBF), for surface numerical integration are used to calculate the sound power from the sound pressures on the sphere surface in the far field, and their solutions are compared with the analytical and the finite element method solution. If function values are available at any location on a sphere, ARPIST has a greater accuracy and stability than SQRBF while being faster and easier to implement. If function values are available only at user-prescribed locations, SQRBF can directly calculate weights while ARPIST needs data interpolation to obtain function values at predefined node locations, which reduces the accuracy and increases the calculation time.
1. Introduction
Two basic approaches for calculating the sound power of sound sources are used in the literature. In the first approach, the sound power is calculated directly from the vibrations of the sound source and the sound pressure on the surface of the source. In the second approach, the sound power is calculated from the sound pressure on a sphere in the far field. References [1,2,3,4,5,6] provide a detailed overview of both approaches. This article deals with the second approach, i.e., the calculation of the sound power from the sound pressures in the far field.
The calculation of sound power from sound pressures in the far field is based on a sufficiently large distance to the sound source at which the sound pressure is approximately in phase with the approximately radially directed fluid particle velocity [2]. The sound field described is similar to the plane sound field; hence, this is the reason its theory and expressions are used.
The sound pressures in the far field are calculated from the plane sound source vibrations using the surface integral (Rayleigh integral). The vibrational field can be defined with approximated analytical functions, e.g., with a series of expansions, so that the surface integral is an integrable function; i.e., an analytic solution can be obtained, at least an approximate one. There are a number of sound sources for which an analytical solution for sound pressures or for sound power is obtained (rigid piston, beam, plate) and they are often cited in the relevant literature [7,8]. In practice, such solutions can sometimes be associated with real sound sources, e.g., a rigid piston with a loudspeaker, but the added value of such solutions is the possibility for a comparison with other methods which are also used in this paper. For example, a mathematical derivation for sound pressure on a hemisphere in the far field with a vibrating circular rigid piston in its center uses an approximation [7] to define a function of distance between a point on the source and a point on the hemisphere, for which the Rayleigh surface integral has an analytical solution. So, the surface integral for sound power calculated from the function of the sound pressures has an approximate analytical solution with sufficient accuracy for reference, which points to the importance of using other approximate methods for the confirmation of the results, e.g., numerical surface integrals.
The numerical surface integral on a plane surface is often applied, and its accuracy has been confirmed [9]. However, numerical surface integration on the sphere is still under development [10,11,12,13], and there is a lack of articles dealing with the application of this method for the calculation of sound power. Recently, new algorithms, SQRBF and ARPIST, for the calculation of the surface numerical integral on the sphere have been proposed [10,14], and their accuracy for the calculation of sound power is analyzed in this article.
2. Sound Power from Sound Pressure in the Far Field
The radiated sound power can be obtained by integrating the far-field intensity over a spherical surface centered on the source [2] as follows:
where the unit vector is normal to the infinitesimal surface dS on the sphere, ω is the sound source vibration angular frequency, and ¯ represents a time average. Directivity of the sound field on the sphere in the far field for two indentical point sources vibrating in phase on the opposite sides and on distance e from the reference horizontal plane is shown in Figure 1, while the directivity of the sound field on the hemisphere in the far field created by a vibrating rigid circular flat piston in a baffle is shown in Figure 2 [8].
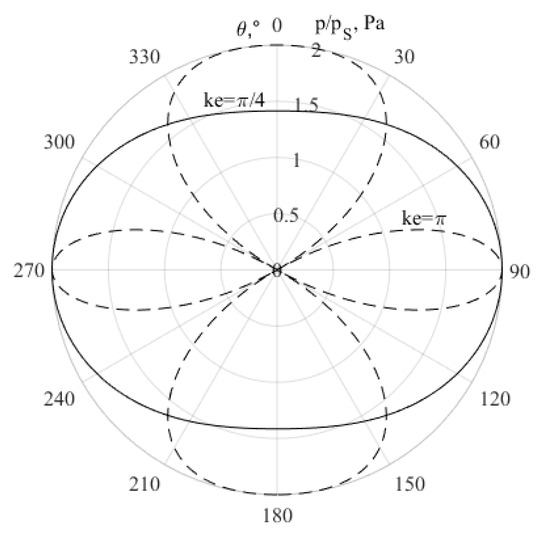
Figure 1.
Directivity of two indentical point sources vibrating in phase.
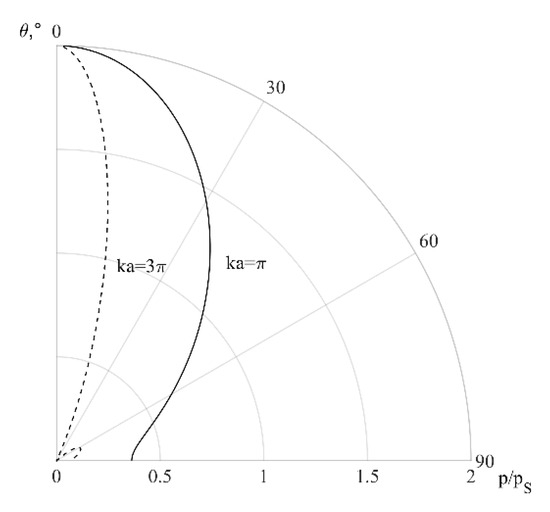
Figure 2.
Directivity of the baffled rigid circular piston.
In both cases, it is necessary to calculate the surface integral on the sphere surface in the far field in order to define the sound power. The sound pressure in the far field for curved (or irregularly shaped) sound sources [2] can be calculated using the Kirchhoff–Helmholtz integral equation. This method includes knowledge of sound pressures and their normal derivative on the surface of a sound source from which the sound power can be defined directly, so in practice, the far field is not used for the calculation of the sound power for this type of source. Therefore, the plane sound source is used as a reference example in this article, and the theory of sound radiation around curved sound sources is not described.
For plane sound sources in the baffle, the coordinate system in Figure 3 is used, so the sound power can be calculated with the following expression:
where θ, ϕ, and R are the coordinates of dS on the hemisphere.
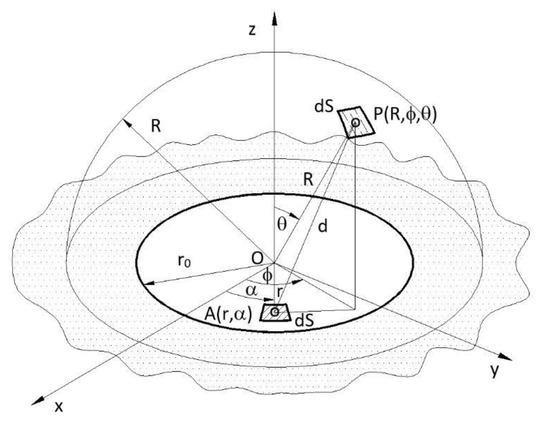
Figure 3.
The hemisphere and vibrating sound source with referent coordinates.
It can be assumed that the functions of sound pressures are smooth in the periods between zero values (Figure 1 and Figure 2), which is the basis for the selection of the surface numerical integral.
The time-averaged sound intensity at a point on a hemisphere of radius R and for a defined excitation frequency is a vector quantity given by the time-averaged product of the sound pressure p and the particle velocity vector :
where t is the time and T is a suitable interval of time.
In the far field, the component of the air particle velocity that is in-phase with the pressure is radially directed [2]. Consequently, the sound intensity vector is also radially directed () and, as in the plane sound wave, is given by the product of the sound pressure and particle velocity. Just as with the plane sound wave, the particle velocity in the far field for the harmonic vibration of the source is equal to the following:
where is the density of the sound media, c is the sound velocity, and represents the complex amplitude (phasor). It follows that the sound intensity is equal to the following:
where is the amplitude of the sound pressure p(R, ϕ, θ, t), * represents the conjugate complex number, and the intensity is directed radially from the sound source. Therefore, the only variable that should be defined for the calculation of sound power is the sound pressure on a hemisphere in the far field.
The sound infinitesimal pressure dp for a point P in the far field produced by the velocity of the oscillation of an infinitesimal element of a plane sound source, , with the surface dS can be calculated as follows [1,2]:
where d is the distance between the far-field point and the infinitesimal element of a plane sound source, and k is the sound wave number.
The sound pressure in the point P produced by the whole vibrating source, with the surface S, can then be calculated by a Rayleigh surface integral [1]:
where the oscillation of the source infinitesimal surface dS is given by the product of the complex amplitude of the surface velocity and the phase change ωt.
The next step consists of the introduction of the expression for the distance from the far-field point to the point on the sound source surface into Equation (7). The formula for the distance is as follows [8]:
where α is the angle in the sound source plane (Figure 3), and r is the distance between the infinitesimal surface dS of the sound source and coordinate system origin.
Equation (8) can be simplified for the point in far-field (R >> r) when the distance R can be approximated as equal to d in the denominator for all infinitesimal surfaces dS of Equation (7). However, in the exponent, the distance d can only be approximated as follows:
At a long range, where R >> r, the term r2 can be dropped, thus implying that (r2/R) is negligible. Once the simplified expressions are introduced into Equation (7), the simplified formula becomes the following:
The solution of the sound power for plane sound sources in the baffle includes the surface integral on the hemisphere as follows:
and the existence of its analytical solution depends on the sound pressure function. The chosen examples in this article include the functions of sound pressures which have an analytical solution for the surface integral so that a comparison with the numerical results can be made.
3. New Algorithms for Numerical Surface Integral on a Sphere
In this article, two algorithms for numerical integration on the surface of a sphere are analyzed (SQRBF and ARPIST). For each technique, the integration of any smooth distribution of acoustical pressures over the whole sphere is the sum of the scalar product of the function values at the quadrature points and the weights.
3.1. SQRBF
SQRBF or Spherical Quadrature Radial Basis Function (SQRBF) of Reeger and Fornberg [14,15,16] is used for the numerical surface integration on a sphere so it can be used for the calculation of sound power from known sound pressures on a sphere in the far field. SQRBF creates quadrature weights for N arbitrarily scattered nodes and the numerical integration is performed using the following expression:
where S2 is a spherical surface, f(x, y, z) represents the function of scalar values to be integrated on a sphere, N is the number of triangle vertices defining a net of spherical triangles over a sphere (Figure 4), and Wi is a weighting set derived from several coordinate transformations, .
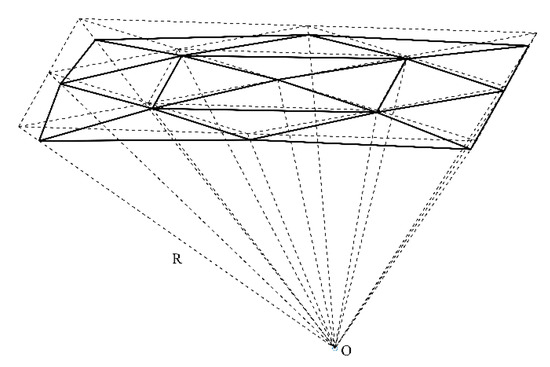
Figure 4.
An example of n = 12 nearest neighbors.
As shown in [14], the triangle vertices on a sphere are firstly optimally positioned with spherical Delaunay triangulation, which results in a new set of spherical triangles . The surface integral of a complete sphere is also defined as being equal to the sum of the surface integrals of all the spherical triangles on a spherical surface.
where K is the number of spherical triangles.
Then, the projection of triangle vertices to a tangent plane is performed by using a gnomic projection (Figure 4). For each of the spherical triangles τk with the midpoint , the projection is realized by a transformation of the vertices’ coordinates. The midpoint is taken to be the average of the vertices of the spherical triangle τk in the plane they form, projected radially to the sphere’s surface; however, any point contained in the spherical triangle would also be suitable. The sphere of radius R is rotated so that the midpoint of the triangle lies on the vertex of the sphere. The coordinates of the vertices projected on the tangent plane are then given by the following [14]:
All coordinates refer to the same Cartesian coordinate system whose origin is in the center of a sphere. The integral, Equation (12), for a triangle is now defined on the surface of its tangent plane, and an expression for a complete sphere is as follows:
The approximation of the last expression for each projected triangle τk is performed by interpolating the integrand over the projected vertices in the tangent plane, based on the radial basis function (RBF) finite differences (FD) method [14] and then integrating the interpolant. Then, an RBF-FD type weight set wk is created for a current reference triangle, and the new approximated expression is as follows:
where n represents the number of the nearest neighbors (the nodes projected to the same tangent plane as the current reference triangle; see Figure 2). If Ki (i = 1, 2,…, N) represents a set of all pairs (k,j), the surface integral takes the final form:
after the transformation of the coordinates . Equation (17) represents the solution for the surface numerical integral on a sphere. The MATLAB implementations of SQRBF for a complete sphere are available at https://www.mathworks.com/matlabcentral/fileexchange/51214-spherical_quadrature_rbf-quadrature_nodes (accessed on 15 October 2023.) and for a smooth surface with boundaries at https://www.mathworks.com/matlabcentral/fileexchange/63938-bounded-smooth-surface-quadrature-rbf (accessed on 15 October 2023). For more details, see articles [14,17,18].
3.2. ARPIST
ARPIST or Anchored Radially Projected Integration on Spherical Triangles is an algorithm for the computation of the numerical integration of a sufficiently smooth function over a spherical triangle. The algorithm is based on an easy-to-implement transformation to the spherical triangle from its corresponding linear triangle via radial projection (Figure 5).
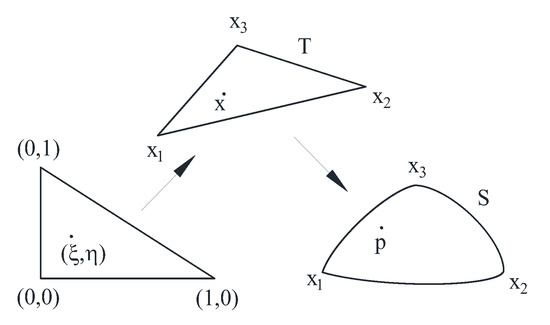
Figure 5.
Projection from a reference triangle to a spherical triangle via a linear triangle.
For a spherical triangle S, the vertices are defined as vertices , and . Without a loss of generality, assume the vertices are in counterclockwise order with respect to the outward normal to the sphere. Let r denote the radius of the sphere, i.e., . Let T denote its corresponding flat (linear) triangle , and let (ξ, η) denote the natural coordinates of T, so that T has the parameterization as follows:
for and . Let , which projects a point x ∈ T onto a point in S. We then obtain a radial projection as follows:
See Figure 5 for a schematic of the mapping.
Given a function f on the spherical triangle S, the integral is as follows:
where is the Jacobian determinant of the mapping from the reference triangle to the curved triangle.
Although the idea of radial projection is simple, care is taken to ensure the stable computation of the Jacobian determinant of the transformation. The algorithm overcomes potential instabilities in computing the Jacobian determinant of the transformation, even for poorly shaped triangles, by properly selecting one of the vertices as the “anchor” to avoid catastrophic cancellation errors. After a number of mathematical transformations, the next expression is defined as follows (for details, please see [1])
An efficient quadrature rule based on the Gaussian quadrature over the linear triangle T is then obtained where additional quadrature point locations are predefined from the position of a triangle and the degree of the quadrature. If defines the degree-p quadrature over T, where ξi are the quadrature points, wi are the corresponding weights, and the integrand is continuously differentiable to the pth order, then the following expression can be used:
where h denotes the longest edge of the triangle and A = area(T). This theorem follows from the two-dimensional Taylor series expansion [19] and the high-order chain rule [20]. The MATLAB and Python implementations of ARPIST are available at https://github.com/numgeom/arpist (accessed on 15 October 2023.). For more details, see article [10].
4. Examples
The following are examples of a comparison of the results for the sound pressures and the sound power of a vibrating circular flat rigid piston in an infinite baffle, calculated using the proposed methods. The results are verified using the finite element method (Ansys, version 2020R1).
4.1. Sound Pressures on a Sphere in the Far Field
The accuracy of the calculation of the sound power from the sound pressures in the far field is affected by the accuracy of the sound pressure calculation. Therefore, the simplest geometry (circular flat rigid piston) is chosen because the sound pressure in the far field can be expressed by an analytic function.
The properties of the sound medium (air) are the density ρ0 = 1.225 kg/m3 and the velocity of sound c = 340 m/s, while the properties of the circular flat rigid piston are the vibration displacement amplitude W0 = 0.005 m and the radius of the piston a = 0.075 m.
The far field is defined as the space behind the last local energy minimum where the amplitude of the sound pressure attenuates with inverse proportionality to the distance from the source. Also, the far field can be defined as the space where the pattern of the radiation (i.e., the positions of the local minima and maxima in the space) do not depend on the distance from the source. This definition is equal to Fraunhofer diffraction in optics, which is valid when the Fresnel number, , where a is the radius of the sphere which surrounds the sound source, is much smaller than 1. The reference distance of the far field that is common in engineering practice is as follows:
so for a maximum frequency of analysis f = 12,000 Hz and velocity of sound c, the reference distance is 1.58 m. This value is higher than the radius of the near field which is defined with the Rayleigh distance, [9,21]. The radius of the far-field hemisphere is taken as R = 2.5 m.
In this example, sound pressures in the far field are calculated with the analytical solution of the Rayleigh integral (Equation (29)), the surface numerical integration of the Rayleigh integral (Equation (27)), and the finite element method (Ansys).
For the definition of the analytical solution of the sound pressure around a vibrating circular flat rigid piston, it is useful to provide the expression (10) in polar coordinates because of its circular geometry:
where v0 is the amplitude of the velocity.
The complete surface of a rigid piston vibrates in-phase so the initial phase is set to zero and the complex amplitude just has the real part, which is equal to the following:
where W0 is the displacement amplitude of the piston vibration, and the velocity function for the harmonically vibrating circular rigid piston has the following form:
The final equation for the sound pressure of the circular rigid piston (Rayleigh integral) can be written as follows:
where a is the piston radius, and the pressure is equal for all values of ϕ due to the symmetry of the piston (Figure 3).
A part of Equation (27), , is used to define the instanteneous velocity v(t) of the infinitesimal elements in Equation (26) and is written outside of the integral because the velocity of all infinitesimal elements has the same amplitude and phase.
Now, the real part of Equation (27) is tabulated in terms of the Bessel function.
and after the analytical integration of the Rayleigh integral, a pressure field around the vibrating circular rigid piston in the far field (a ≪ R) can be defined as follows:
For a comparison of the results, a numerical integration of the Rayleigh integral for a flat piston, Equation (27), was performed via MATLAB’s vpaintegral function (high-precision numerical integration which uses variable-precision arithmetic and a semi-symbolic quadrature) [17].
Also, a finite element model was created using Ansys. The finite element model consisting of approximately 500,000 nodes was used for the final simulation. The types of finite elements used were FLUID29 and FLUID129, which are commonly used in the modelling of the interaction of body and fluids and whose main usage is the modelling of sound waves [22]. Two-dimensional elements (Figure 6) were used because the radiation of a rigid piston is an axisymmetric problem.
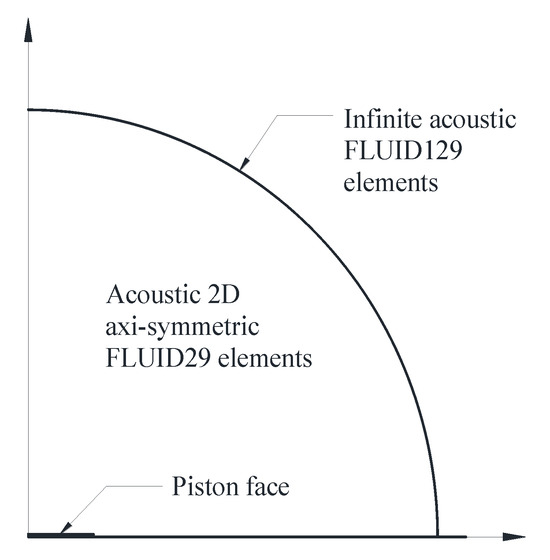
Figure 6.
Schematic representation of the finite element model of the circular piston in an infinite baffle.
The analytical and numerical results of the Rayleigh integral are equal when rounded to four decimal places, which proves the quality of numerical surface integration on a flat surface. The results were obtained using the MATLAB programming language and are shown in Table 1 as “Rayleigh integral”.

Table 1.
Comparison of sound pressures obtained with the Rayleigh integral and the finite element model.
The results obtained using the finite element model created with Ansys (Figure 7) were slightly different but very close, which verifies the results. The comparison is shown in Table 1.

Figure 7.
Sound pressure at the intersection of the hemisphere and the plane perpendicular to the piston plane (e.g., plane xz with r = R in Figure 3).
In Figure 8, the sound pressures on the sphere in the far field for different circular frequencies ω are shown in order to refer to the nature of pressure distribution (the existence of smooth curves). The sound pressures on the sphere in the far field shown in Figure 8a was calculated for ω = 500 rad/s, and the sound pressures in in Figure 8b for ω = 12,000 rad/s, while corresponding sound powers are listed in Table 1.
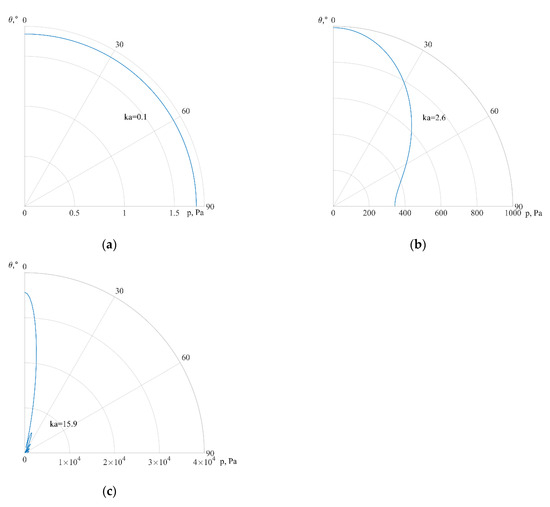
Figure 8.
Sound pressures in far field: (a) ω = 500 rad/s, (b) ω = 12,000 rad/s, and (c) ω = 72,000 rad/s.
4.2. Sound Power from Sound Pressure, Analytical vs. Numerical Solution
Now, when a function of the sound pressures on a hemisphere of radius R in the far field is defined, the sound intensity at a point can be defined with Equation (5) and the sound power of a vibrating circular rigid piston can be defined from Equation (2) as follows:
where Ap is the piston area [23]. This integral has only approximate solutions, analytical and numerical.
In this example, the sound power is calculated using an approximate analytical solution of the integral of the series expansion of the Bessel function, Equation (33), and the numerical integration of a function of one scalar θ, Equation (30). The results are verified using the finite element method (Ansys). The numerical integration for one coordinate or for two coordinates on a plane are performed with the MATLAB function vpaintegral. The obtained results for the sound pressure on the sphere in the far field (27) and for the sound power of a vibrating circular rigid flat piston in a baffle (30) are used for comparison in our examples.
The properties of the rigid piston and the sound medium (air) are the same as in Example 1.
The approximation in the form of series expansion of the Bessel function can be used [24]:
and after inclusion in Equation (30), the sound power expression for a circular rigid piston of radius a can be found as follows:
where the sum of q arises due to the squaring of the Bessel function.
If the first two values (0 and 1) of the indices q and s are considered, there are four different combinations of them: (q,s) = (0,0), (0,1), (l,0), and (1,1). Substituting these combinations into Equation (32) separately, integrating them, adding them up, and simplifying them, the total approximate sound power can be obtained as follows:
In Figure 9, it can be seen that the results obtained using the different approaches are almost exactly the same except for the analytical solution in Equation (33). Normally, it is expected that the analytical solution is the most accurate, but Equation (33) is a rough approximation.
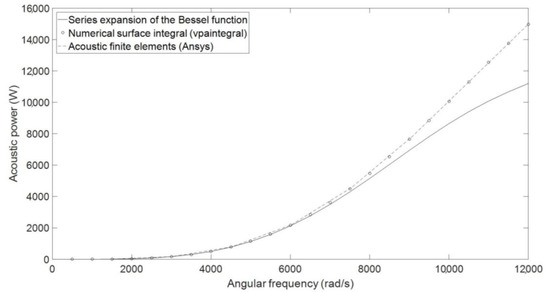
Figure 9.
Sound power results.
The values obtained with the numerical integration of a function of one scalar θ in Equation (30) were also compared with the values obtained using the acoustic finite elements for a wider range of angular frequency values. The results were, again, very close and almost identical for the most part of it (Figure 10) but discrepancies occurred at very high frequencies, which indicates the inaccuracy of the Ansys.
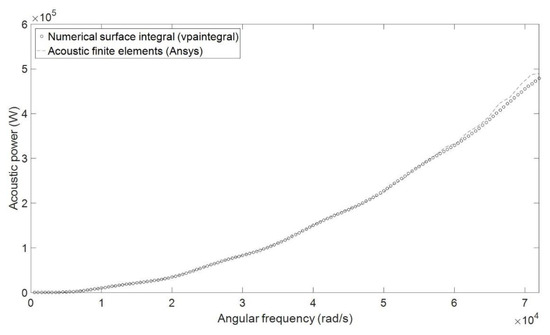
Figure 10.
Sound power results (higher frequencies).
4.3. Sound Power from Sound Pressure, New Algorithms for Numerical Integration on the Sphere
In the next example, the new algorithms ARPIST and SQRBF for surface numerical integration on a sphere are tested for calculating the sound power by the surface integration of sound pressures in the far field. For a vibrating circular flat rigid piston, the function of the sound pressures on a hemisphere in the far field is known so its values in referent points can be defined. In practice, an analytic function may not be available; for example, the data values may be sampled at some scattered data points. Mathematically, it simply means that the values at the quadrature points of the numerical integration must be reconstructed from the scattered data values, and the sound power can only be solved by the numerical surface integral. Consequently, such a procedure reduces the accuracy and increases the calculation time.
The results are compared with a numerical integration of a function of one scalar θ in Equation (30).
For the calculation of the sound power for a vibrating flat circular rigid piston in a baffle, the surface integral of the hemisphere is needed. In this article, SQRBF and ARPIST were used to calculate the sound power for a complete sphere, and the results are divided by two. This approach is based on the equivalent sound pressures of a point on the hemisphere and of imagined mirror point on a sphere (on the opposite side of the baffle). In such a case, expression (2) gives the same result as the following expression:
The algorithms ARPIST and SQRBF for the numerical quadrature on a sphere were performed with different parameters, ensuring its usefulness even on computers with a lower computing capacity.
The parameters for SQRBF that were changed in different runs of the model are the order of the polynomial (m), number of the nearest neighbors (n), and number of nodes (N). The “rules” for the choice of the values of these parameters are as follows: (a) the order of the polynomial should be equal to or lower than 13 because of MATLAB code limitations; and (b) the expressions N/n ≥ 10 and n ≥ (m + 1)(m + 2)/2 must be fulfilled to ensure accurate results.
Two sets of input parameters were used. The first set of results was obtained for the “lowest value” parameters that would ensure the results to be within the 0.2% of those obtained using the numerical integration of a scalar function of one scalar θ in Equation (30).
The parameters were calibrated with a trial-and-error procedure, and the following set of parameters was shown to provide both accurate results and a relatively low calculation time for the computers used: polynomial order m = 7, number of the nearest neighbors n = 80, and number of nodes N = 2500.
In order to check the accuracy of the model for its use on computers with a much lower capacity, significantly lower parameters were used for the second simulation: polynomial order m = 4, number of the nearest neighbors n = 20, and number of nodes N = 200.
The parameters for the ARPIST were the number of triangle elements and Gaussian quadrature rule. In this article, degree-4 with six quadrature points per triangle and the Gaussian quadrature rules for linear triangles from [25] were used. Also, the sphere was divided with equal triangles creating an icosahedron.
A comparison of the results obtained with the new algorithms ARPIST and SQRBF is shown in Table 2.

Table 2.
Comparison of numerical results.
From Table 2, it can be seen that very accurate results can be obtained with both algorithms but ARPIST gives a higher accuracy. However, additional tests are performed for the ARPIST and SQRBF algorithms for higher values of the input parameters to compare them. The results are presented in Table 3. The sound power for ω = 72,000 rad/s is listed in Table 3 while the sound pressures on a sphere in the far-field is shown in Figure 8c.

Table 3.
Comparison of higher set of input parameters.
From these simulations, it is obvious that the accuracy of the quadrature further increases with the increase in the parameters and that it approaches a 0% difference to the reference numerical solution (Equation (30)). Both algorithms have a high accuracy, and it can be concluded that for the same number of triangle vertices in SQRBF and quadrature points in ARPIST, ARPIST has a higher accuracy. Both algorithms are relatively fast (the calculation time was in the order of several seconds).
5. Conclusions
In this paper, the accuracy and efficiency of new algorithms for numerical integration on a spherical surface (ARPIST and SQRBF) and the possibility of its use for calculating the sound power of sound sources were analyzed. The calculations were performed for a vibrating rigid flat circular piston because analytical solutions for the sound pressure and the sound power exist, so they can be compared with the results of the numerical surface integration.
The detailed analyses described in this paper led to the following conclusions:
- -
- For some sources, it is possible to define integrable functions for the calculation of sound pressure or sound power with an accuracy corresponding to the mathematical simplifications used;
- -
- For other sources, it is not possible to define integrable functions so that numerical surface integration must be used;
- -
- The accuracy of the algorithms ARPIST and SQRBF for numerical integration on a sphere’s surface increases with the increase of its parameters, approaching almost a 0% difference to the reference numerical solution;
- -
- If function values are available at any location on a sphere, ARPIST has a higher accuracy and stability than SQRBF while being faster and easier to implement;
- -
- If function values are available only at user-prescribed locations, SQRBF can directly calculate weights while ARPIST requires high-accuracy scattered data interpolation to obtain function values at these Gaussian quadrature locations from the (coarser sampled) data at the original scattered nodes. Such a procedure reduces the accuracy and increases the calculation time.
All the calculated results were in good agreement.
Author Contributions
Conceptualization, S.P., A.S., R.Ž. and L.T.; methodology, S.P., A.S., R.Ž. and L.T.; software, S.P. and A.S.; validation, S.P. and A.S.; formal analysis, S.P. and A.S.; investigation, S.P. and A.S.; writing—original draft preparation, S.P., A.S., R.Ž. and L.T.; writing—review and editing, S.P., A.S., R.Ž. and L.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Univsersity of Rijeka under the project number uniri-tehnic-18-225, and partially by the European Union’s Horizon 2020 research and innovation program under grant agreement No 769355 (“Port IoT for Environmental Leverage—PIXEL”). Their support is gratefully acknowledged.
Data Availability Statement
The data presented in this study are available in the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rayleigh, J.W.S. The Theory of Sound; Dower Publications: New York, NY, USA, 1897. [Google Scholar]
- Fahy, F.; Gardonio, P. Sound and Structural Vibration; Radiation, Transmission and Response; Elsevier: Oxford, UK, 2007. [Google Scholar]
- Cunefare, K.A. Effect of Modal Interaction on Sound Radiation from Vibrating Structures. AIAA J. 1992, 30, 2819–2828. [Google Scholar] [CrossRef]
- Herrin, D.W.; Martinus, F.; Wu, T.W.; Seybert, A.F. An assessment of the high frequency boundary element and Rayleigh integral approximations. Appl. Acoust. 2006, 67, 819–833. [Google Scholar] [CrossRef]
- Arenas, J.P. Numerical Computation of the Sound Radiation from a Planar Baffled Vibrating Surface. J. Comput. Acoust. 2008, 16, 321–341. [Google Scholar] [CrossRef]
- Bai, M.R.; Tsao, M. Estimation of sound power of baffled planar sources using radiation matrices. J. Acoust. Soc. Am. 2002, 112, 876–883. [Google Scholar] [CrossRef] [PubMed]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics; John Wiley & Sons, Inc.: New York, NY, USA, 2000. [Google Scholar]
- Junger, M.C.; Feit, D. Sound, Structures, and Their Interaction; MIT Press: London, UK, 1972. [Google Scholar]
- Kirkup, S.M. Computational solution of the acoustic field surrounding a baffled panel by the Rayleigh integral method. Appt. Math. Modelling 1994, 18, 403–407. [Google Scholar] [CrossRef]
- Li, Y.; Jiao, X. ARPIST: Provably Accurate and Stable Numerical Integration over Spherical Triangles. J. Comput. Appl. Math. 2023, 420, 114822. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Oh, B.H. Efficient Numerical Integration on the Surface of a Sphere. ZAMM-Z. Angew. Math. U. Mech. 1986, 66, 37–49. [Google Scholar] [CrossRef]
- Rosca, D. Spherical quadrature formulas with equally spaced nodes on latitudinal circles. Electron. Trans. Numer. Anal. 2009, 35, 148–163. [Google Scholar]
- Shivaram, K.T. Generalised Gaussian Quadrature over a Sphere. Int. J. Sci. Eng. Res. 2013, 4, 1530–1534. [Google Scholar]
- Reeger, J.A.; Fornberg, B. Numerical Quadrature over the Surface of a Sphere. Stud. Appl. Math. 2016, 137, 174–188. [Google Scholar] [CrossRef]
- Fornberg, B.; Martel, J.M. On spherical harmonics based numerical quadrature over the surface of a sphere. Adv. Comput. Math. 2014, 40, 1169–1184. [Google Scholar]
- Reeger, J.A.; Fornberg, B.; Wats, M.L. Numerical quadrature over smooth, closed surfaces. Proc. R. Soc. A 2016, 472, 20160401. [Google Scholar] [CrossRef] [PubMed]
- The Mathworks, Inc. Symbolic Math ToolboxTM, Matlab, R2017a; The Mathworks, Inc.: Natick, MA, USA, 2017. [Google Scholar]
- Reeger, J.A.; Fornberg, B. Numerical quadrature over smooth surfaces with boundaries. J. Comput. Phys. 2018, 355, 176–190. [Google Scholar] [CrossRef]
- Humpherys, J.; Jarvis, T.J.; Evans, E.J. Foundations of Applied Mathematics, Volume I: Mathematical Analysis; SIAM -Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2017. [Google Scholar]
- Ma, T.-W. Higher chain formula proved by combinatorics. Electron. J. Comb. 2009, 16, N21. [Google Scholar] [CrossRef] [PubMed]
- Kuntz, H.L.; Hixon, E.L.; Ryan, W.W. The Rayleigh distance and geometric nearfield size of nonplane sound radiators. J. Acoust. Soc. Am. 1983, 74, S82. [Google Scholar] [CrossRef]
- Howard, C.Q.; Cazzolato, B.S. Acoustic Analyses Using Matlab and Ansys; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Abingdon, UK, 2015. [Google Scholar]
- Akkaya, N. Acoustic Radiation from Baffled Planar Sources. In A Series Approach; Master of Science, Graduate Faculty of Texas Tech University: Lubbock, TX, USA, 1999. [Google Scholar]
- McLachlan, N.W. Bessel Functions for Engineers; Clarendon Press: Oxford, UK, 1955. [Google Scholar]
- Cools, R. An encyclopedia of cubature formulas. J. Complex. 2003, 19, 445–453. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).