A Novel Algorithm for Directional Scattering in Acoustic Ray Tracers
Abstract
:1. Introduction
2. A Directional Scattering Algorithm
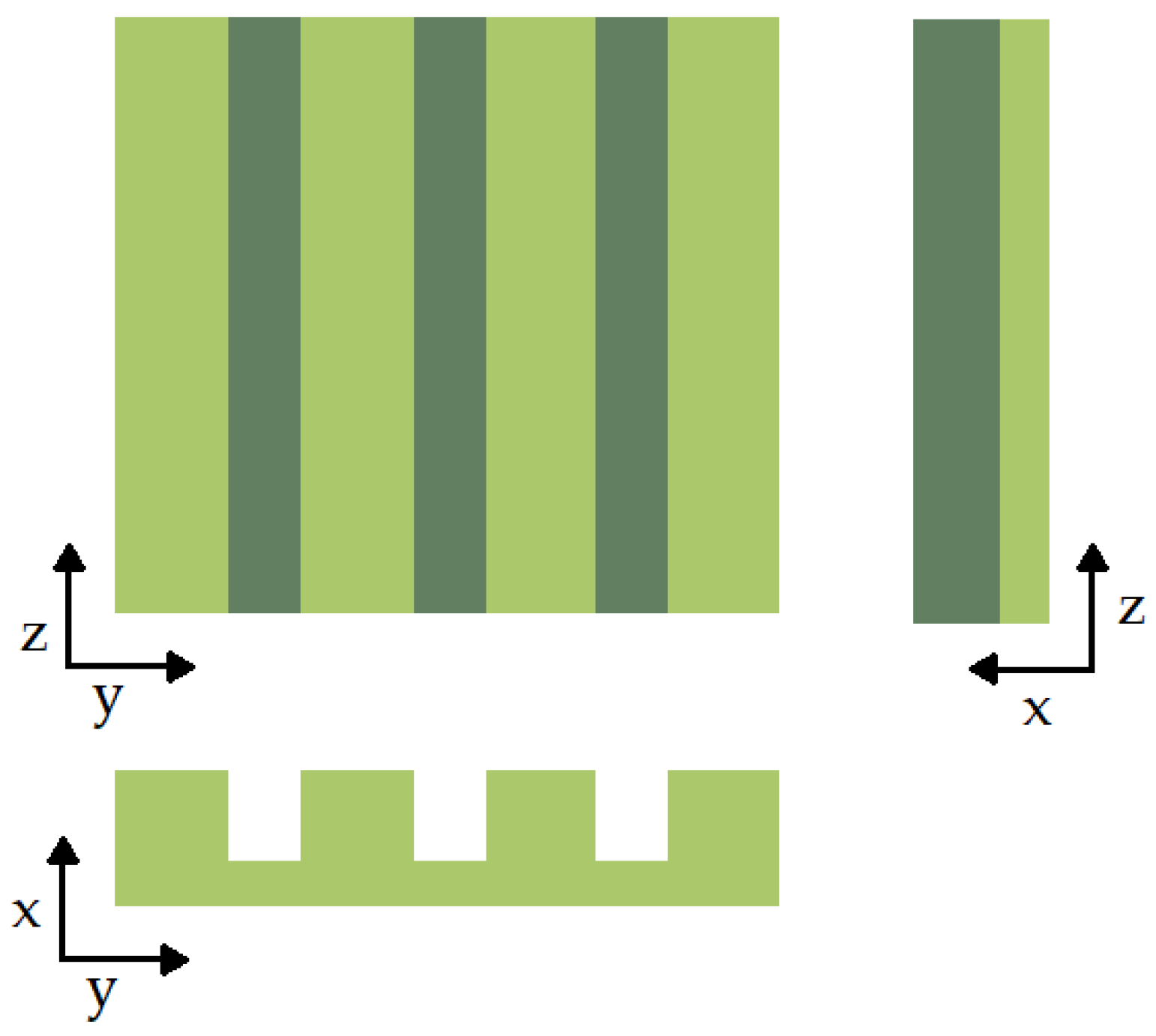
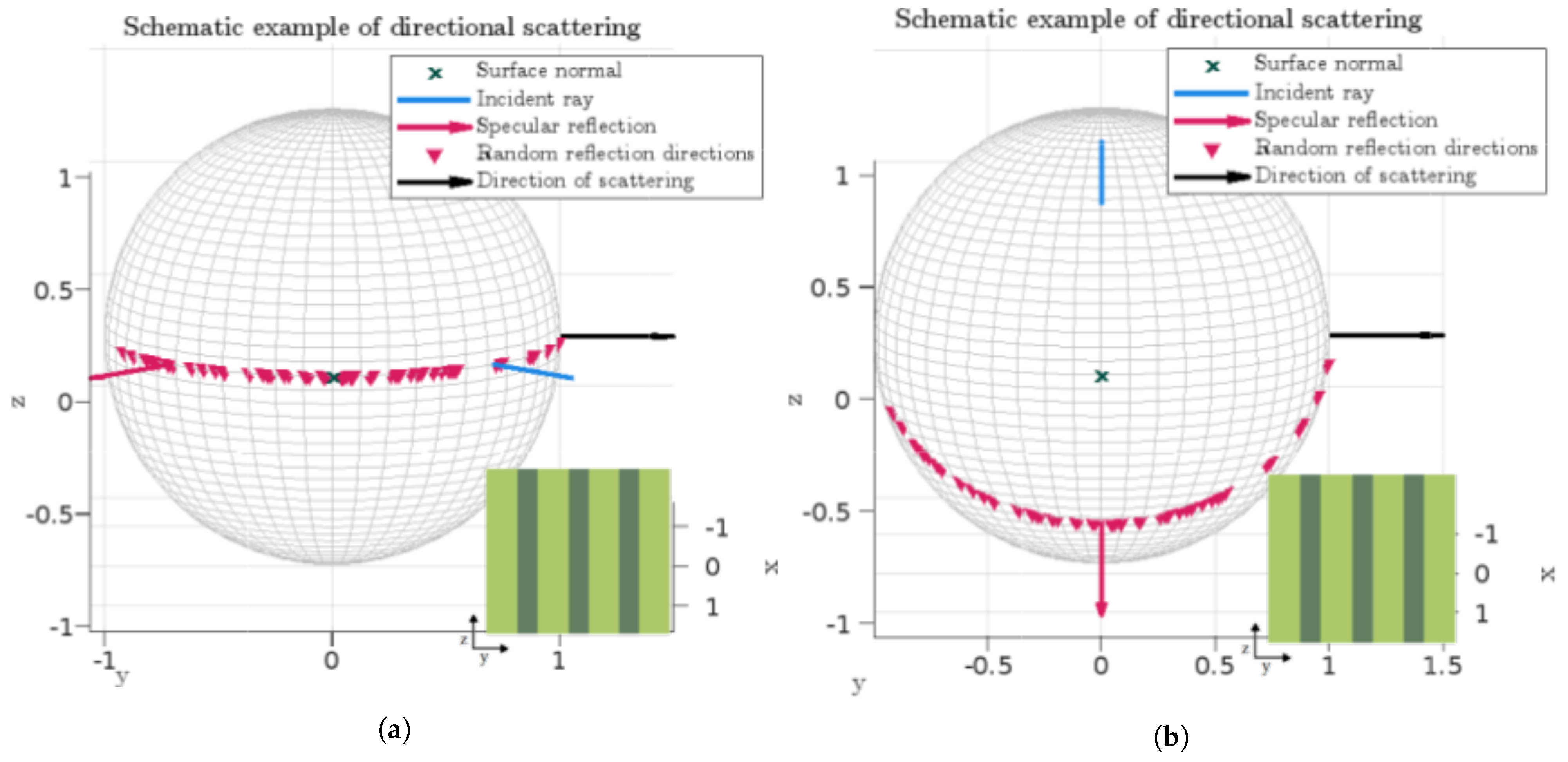
2.1. Model for an Ideal 1D Scatterer
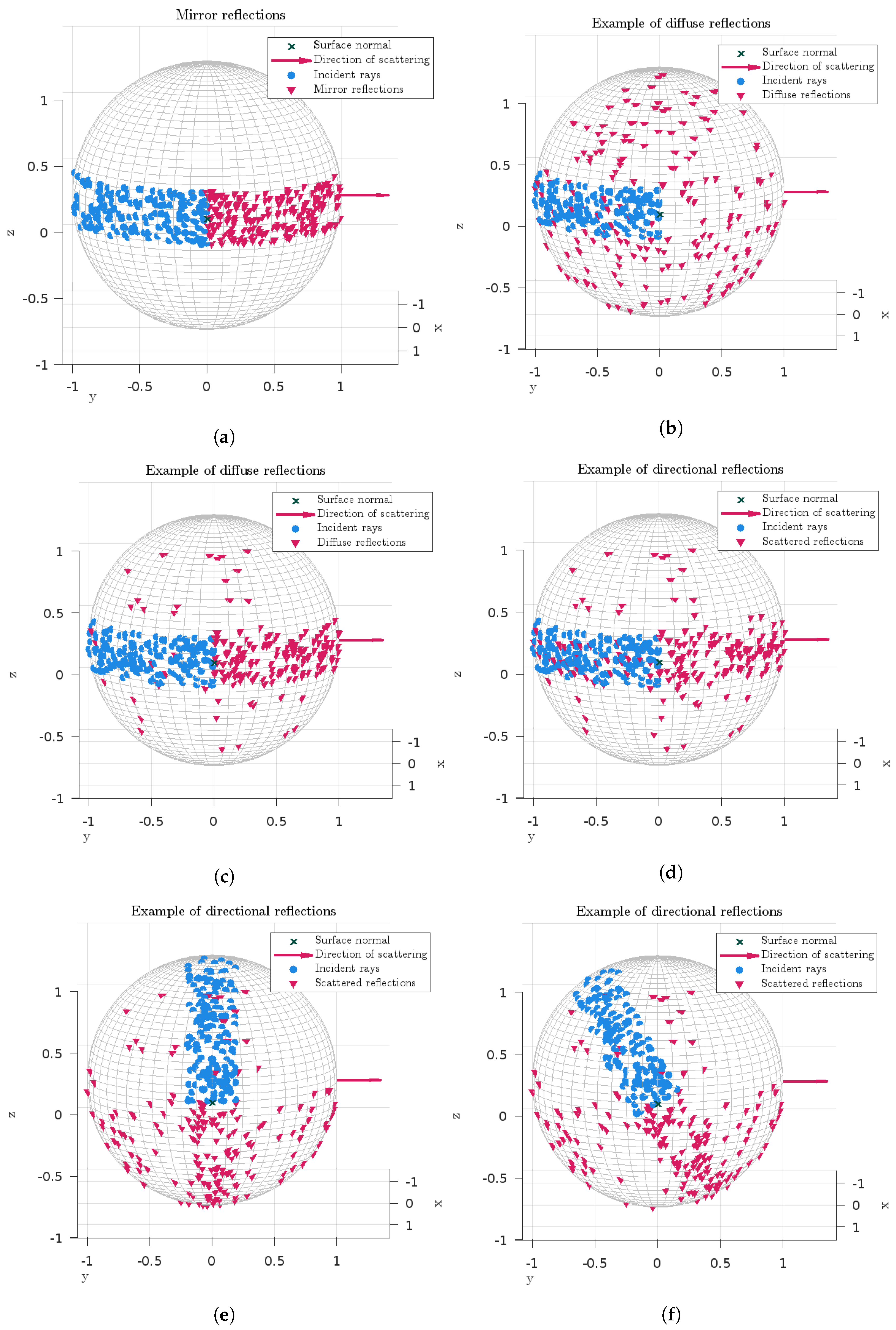
2.2. Implementation
| Listing 1. Pseudo code for the directional reflection algorithm. |
| // Generate a random value to determine if the ray is scattered float rnd=rand(0,1); if (rnd < s_d) { // Ray is diffusely reflected new_direction=generate_lambert(); } else if (rnd > s_s) { // Ray is not scattered new_direction=reflect(incident, surface_normal); } else { // Ray is partially scattered // Generate a random direction on a semi-circle new_direction=generate_cosine_circle(); // Determine the desired angle between the xy-plane // and the reflected ray float z_angle=rotation_angle(xy_plane, incident_local); // Calculate the new direction by rotation around the // y-axis new_direction=rotate(new_direction, z_angle, y_axis); } |
2.3. Directional Scattering Coefficients
3. Materials and Methods
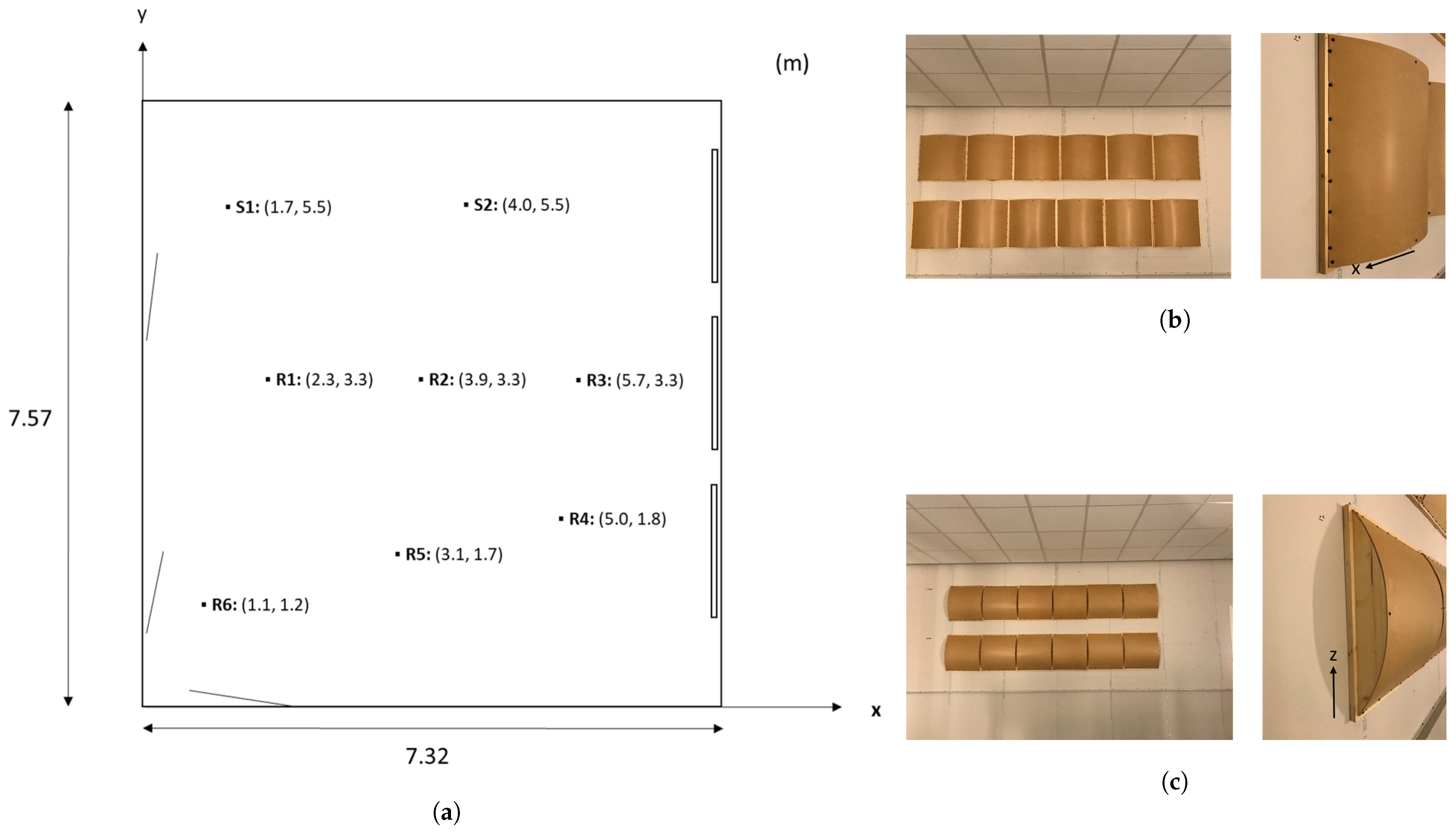
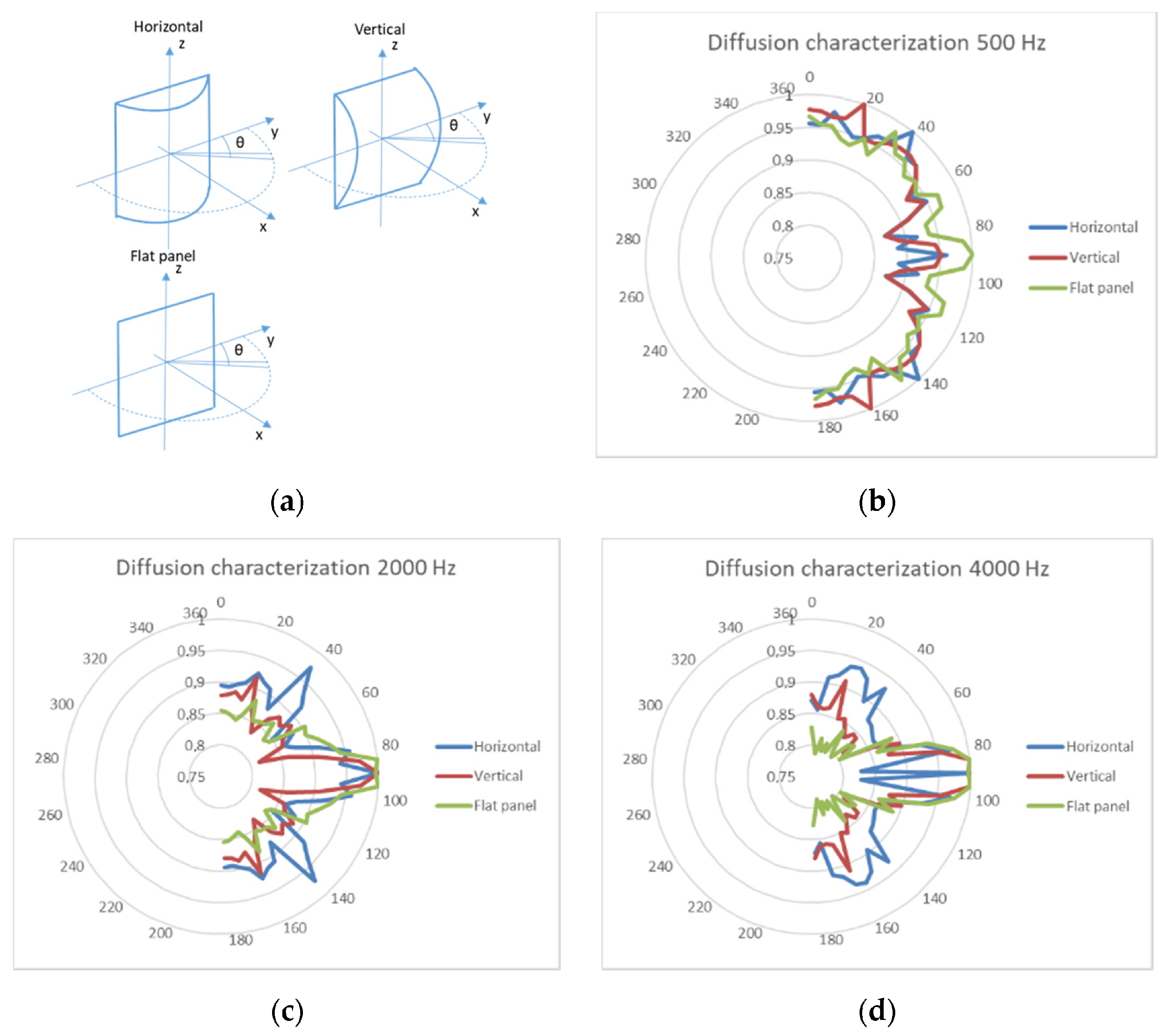
3.1. Measurements
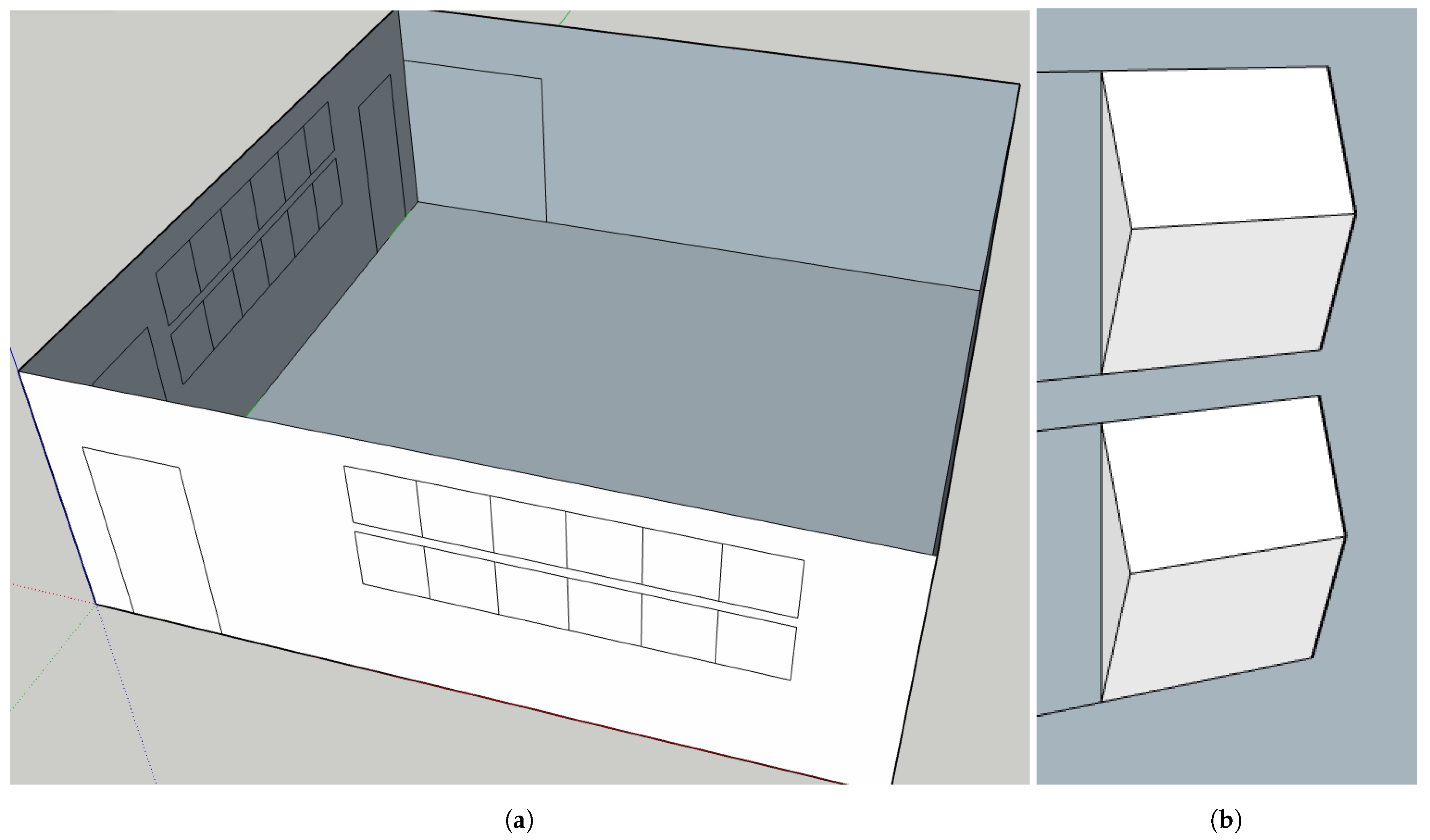
3.2. Modelling the Scatterers in the Ray Tracer
3.3. Surface Absorption and Scattering Parameter Selection
4. Results
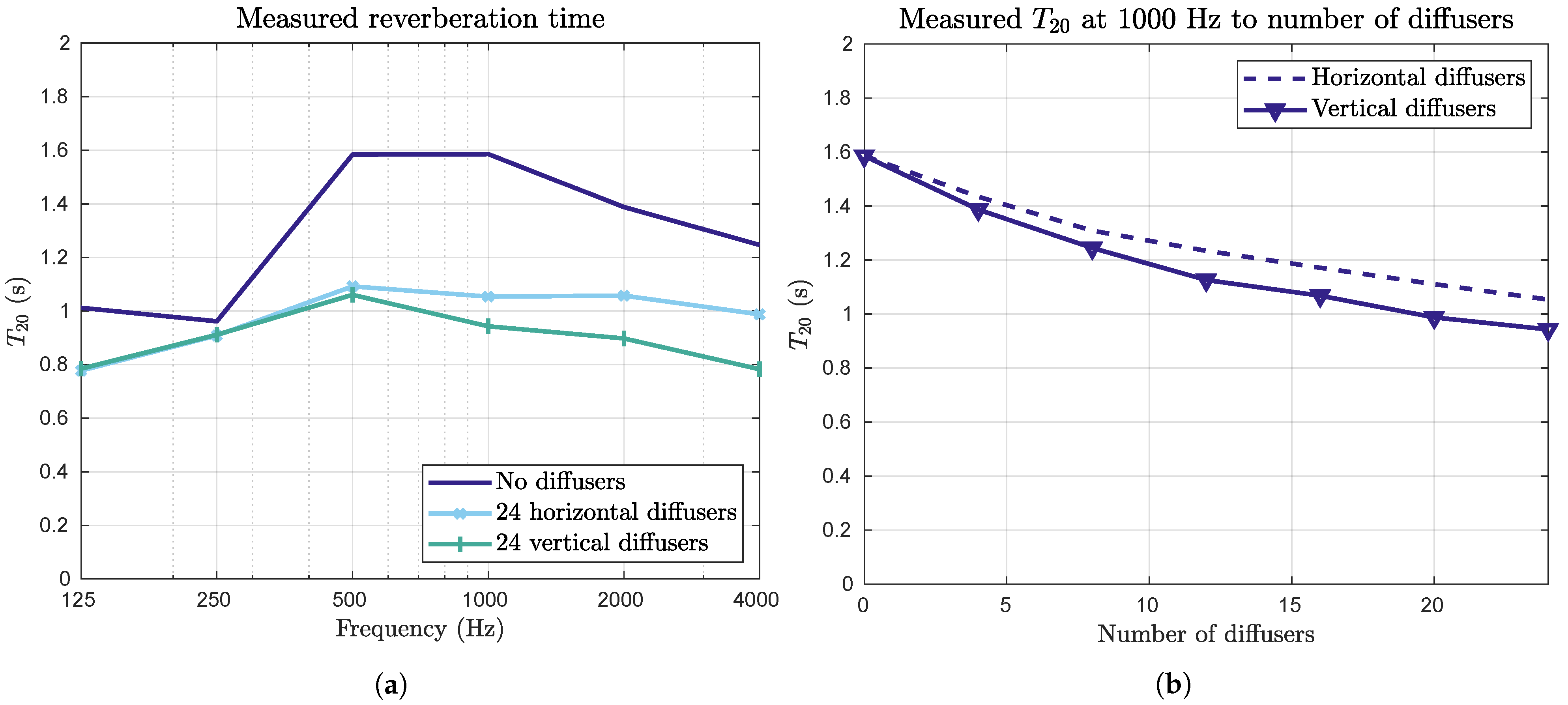
4.1. Measurements
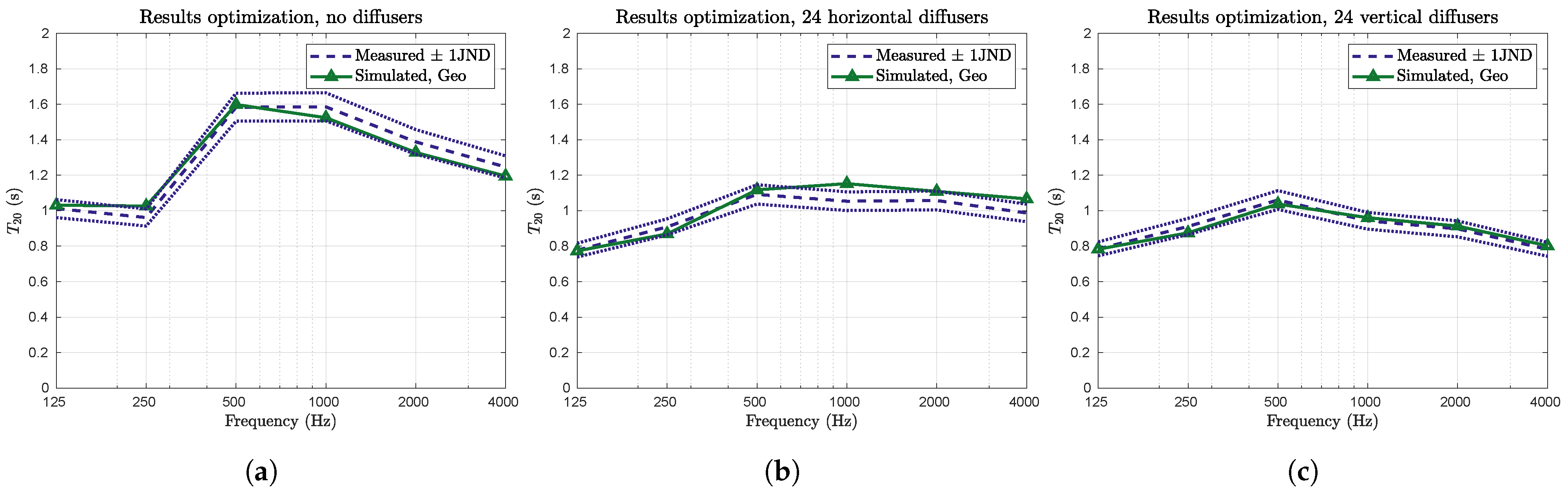
4.2. Optimization Results
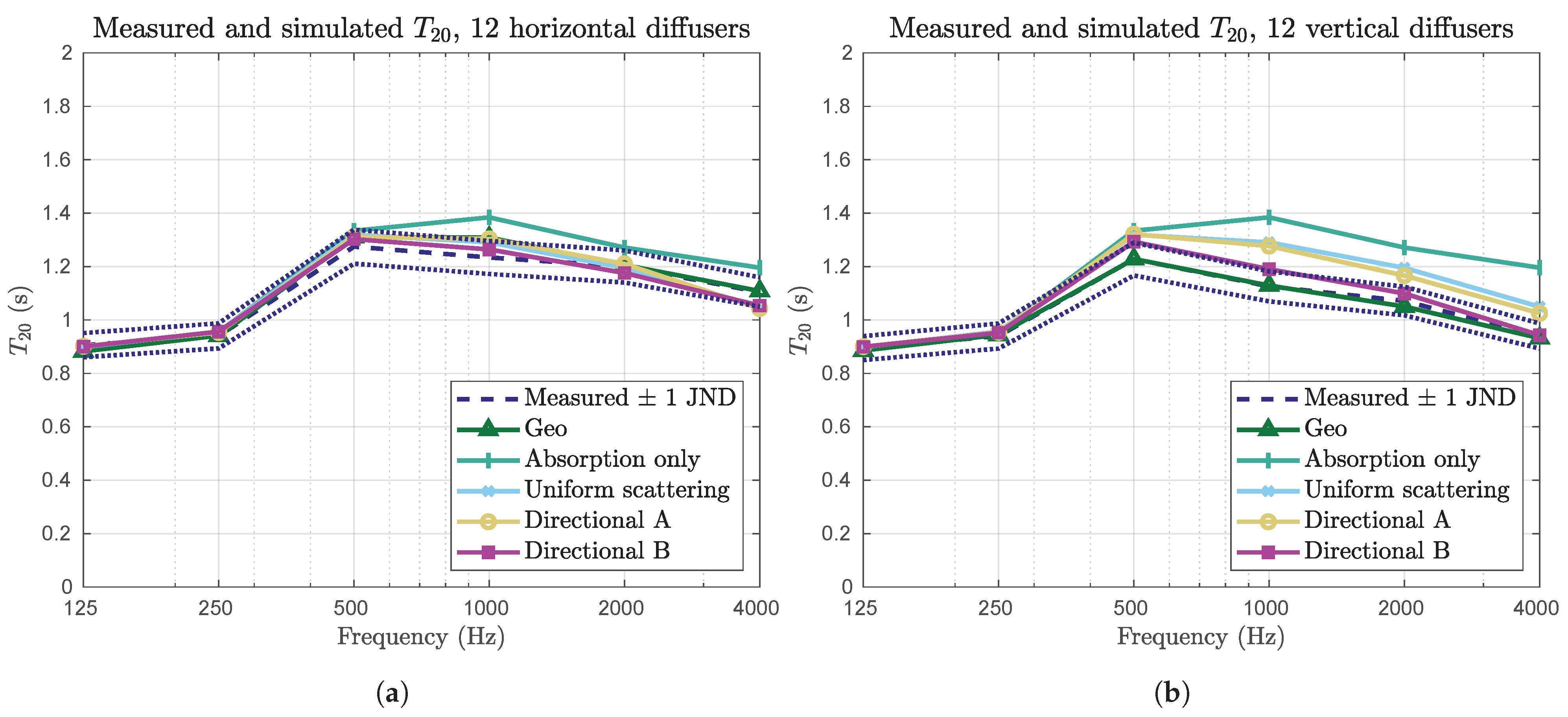
4.3. Simulation Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Savioja, L.; Svensson, P. Overview of geometrical room acoustic modeling techniques. J. Acoust. Soc. Am. 2015, 138, 708–730. [Google Scholar] [CrossRef] [PubMed]
- Vorländer, M. Auralization. Fundamentals of Acoustics, Modelling, Simulation, Algorithms and Acoustic Virtual Reality; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–335. [Google Scholar] [CrossRef]
- Cox, T.J.; D’Antonio, P. Acoustic Absorbers and Diffusers, 3rd ed.; Taylor & Francis Group: Boca Raton, FL, USA, 2017. [Google Scholar]
- Kuttruff, H. Room Acoustics, 5th ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Cox, T.J.; Dalenback, B.I.; D’Antonio, P.; Embrechts, J.J.; Jeon, J.Y.; Mommertz, E.; Vorländer, M. A tutorial on scattering and diffusion coefficients for room acoustic surfaces. Acta Acust. United Acust. 2006, 92, 1–15. [Google Scholar]
- Morse, P.M.; Ingard, K.U. Theoretical Acoustics; McGraw-Hill Book Company: New York, NY, USA, 1968. [Google Scholar]
- Autio, H.; Vardaxis, N.G.; Bard Hagberg, D. The Influence of Different Scattering Algorithms on Room Acoustic Simulations in Rectangular Rooms. Buildings 2021, 11, 414. [Google Scholar] [CrossRef]
- Dalenbäck, B.I. Modeling 1D-Diffusers—The Missing Link. 2011. Available online: http://www.catt.se/Lambert-1D-CATT.pdf (accessed on 18 October 2023).
- Svensson, U.P.; Fred, R.I.; Vanderkooy, J. An analytic secondary source model of edge diffraction impulse responses. J. Acoust. Soc. Am. 1999, 106, 2331–2344. [Google Scholar] [CrossRef]
- Lu, B.; Darmon, M.; Potel, C.; Zernov, V. Models Comparison for the scattering of an acoustic wave on immersed targets. J. Phys. Conf. Ser. 2012, 353, 012009. [Google Scholar] [CrossRef]
- Lü, B.; Darmon, M.; Fradkin, L.; Potel, C. Numerical comparison of acoustic wedge models, with application to ultrasonic telemetry. Ultrasonics 2016, 65, 5–9. [Google Scholar] [CrossRef] [PubMed]
- Chehade, S.; Kamta Djakou, A.; Darmon, M.; Lebeau, G. The spectral functions method for acoustic wave diffraction by a stress-free wedge: Theory and validation. J. Comput. Phys. 2019, 377, 200–218. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Y.; Lian, H.; Atroshchenko, E.; Ding, C.; Bordas, S. Seamless integration of computer-aided geometric modeling and acoustic simulation: Isogeometric boundary element methods based on Catmull-Clark subdivision surfaces. Adv. Eng. Softw. 2020, 149, 102879. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, F.; Li, P.W.; Qu, W. Singular boundary method for 2D and 3D acoustic design sensitivity analysisImage 1. Comput. Math. Appl. 2022, 119, 371–386. [Google Scholar] [CrossRef]
- Li, J.; Fu, Z.; Gu, Y.; Zhang, L. Rapid calculation of large-scale acoustic scattering from complex targets by a dual-level fast direct solver. Comput. Math. Appl. 2023, 130, 1–9. [Google Scholar] [CrossRef]
- Shaaban, A.M.; Anitescu, C.; Atroshchenko, E.; Rabczuk, T. 3D isogeometric boundary element analysis and structural shape optimization for Helmholtz acoustic scattering problems. Comput. Methods Appl. Mech. Eng. 2021, 384, 113950. [Google Scholar] [CrossRef]
- Wang, F.; Gu, Y.; Qu, W.; Zhang, C. Localized boundary knot method and its application to large-scale acoustic problems. Comput. Methods Appl. Mech. Eng. 2020, 361, 112729. [Google Scholar] [CrossRef]
- Odeon A/S. ODEON Room Acoustics Software—User’s Manual. 2020. Available online: https://odeon.dk/download/Version17/OdeonManual.pdf (accessed on 23 October 2023).
- Dalenbäck, B.I. CATT-Acoustic v9.1 Powered by TUCT v2. 2022. Available online: https://www.catt.se/ (accessed on 18 October 2023).
- Arvidsson, E.; Nilsson, E.; Hagberg, D.B.; Karlsson, O.J.I. The Effect on Room Acoustical Parameters Using a Combination of Absorbers and Diffusers—An Experimental Study in a Classroom. Acoustics 2020, 2, 505–523. [Google Scholar] [CrossRef]
- Arvidsson, E.; Nilsson, E.; Bard-Hagberg, D.; Karlsson, O.J.I. Subjective Experience of Speech Depending on the Acoustic Treatment in an Ordinary Room. Int. J. Environ. Res. Public Health 2021, 18, 12274. [Google Scholar] [CrossRef] [PubMed]
- Arvidsson, E.; Nilsson, E.; Bard Hagberg, D.; Karlsson, O.J.I. The Difference in Subjective Experience Related to Acoustic Treatments in an Ordinary Public Room: A Case Study. Acoustics 2021, 3, 442–461. [Google Scholar] [CrossRef]
- Kuttruff, H. Room Acoustics, 6th ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- ISO 17497-1:2004; Acoustics—Sound-Scattering Properties of Surfaces—Part 1: Measurement of the Random-Incidence Scattering Coefficient in a Reverberation Room. ISO: Geneva, Switzerland, 2004.
- Givens, W. Computation of plain unitary rotations transforming a general matrix to triangular form. J. Soc. Ind. Appl. Math. 1958, 6, 26–50. [Google Scholar] [CrossRef]
- Postma, B.N.J.; Katz, B.F.G. Creation and calibration method of acoustical models for historic virtual reality auralizations. Virtual Real. 2015, 19, 161–180. [Google Scholar] [CrossRef]
- Arvidsson, E.; Nilsson, E.; Bard Hagberg, D.; Karlsson, O.J.I. Quantification of the Absorption and Scattering Effects of Diffusers in a Room with Absorbent Ceiling. Buildings 2021, 11, 612. [Google Scholar] [CrossRef]
- ISO 3382-1:2009; Acoustics—Measurement of Room Acoustic Parameters—Part 1: Performance Spaces. ISO: Geneva, Switzerland, 2009.
- Schröder, D. Physically Based Real-Time Auralization of Interactive Virtual Environments. Ph.D. Thesis, Institute of Technical Acousitcs, Aachen, Germany, 2011. [Google Scholar]
- Zhu, X.; Kang, J.; Ma, H. The impact of surface scattering on reverberation time in differently shaped spaces. Appl. Sci. 2020, 10, 4880. [Google Scholar] [CrossRef]
- Nilsson, E.; Arvidsson, E. An Energy Model for the Calculation of Room Acoustic Parameters in Rectangular Rooms with Absorbent Ceilings. Appl. Sci. 2021, 11, 6607. [Google Scholar] [CrossRef]



| f (Hz) | Floor | Doors | Scatterers | Walls | Absorptive Ceiling |
|---|---|---|---|---|---|
| 125 | 0.01 | 0.2 | 0.72 | 0.13 | 0.21 |
| 250 | 0.01 | 0.2 | 0.48 | 0.15 | 0.17 |
| 500 | 0.01 | 0.04 | 0.49 | 0.07 | 0.28 |
| 1000 | 0.01 | 0.02 | 0.32 | 0.04 | 0.60 |
| 2000 | 0.01 | 0.02 | 0.18 | 0.07 | 0.50 |
| 4000 | 0.01 | 0.02 | 0.02 | 0.06 | 0.80 |
| f (Hz) | Floor | Doors | Scatterers | Walls | Absorptive Ceiling | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Geo | Uniform | Dir A, | Dir B, | Dir A, | Dir B, | |||||
| 125 | 0.05 | 0.1 | 0.1 | 0.12 | 0.12 | 0.1 | 0.12 | 0.1 | 0.13 | 0.13 |
| 250 | 0.05 | 0.1 | 0.1 | 0.15 | 0.15 | 0.1 | 0.15 | 0.1 | 0.15 | 0.15 |
| 500 | 0.05 | 0.1 | 0.15 | 0.23 | 0.23 | 0.35 | 0.23 | 0.5 | 0.05 | 0.05 |
| 1000 | 0.05 | 0.1 | 0.15 | 0.32 | 0.27 | 0.45 | 0.36 | 0.75 | 0.07 | 0.07 |
| 2000 | 0.05 | 0.15 | 0.25 | 0.37 | 0.31 | 0.45 | 0.42 | 0.8 | 0.05 | 0.05 |
| 4000 | 0.05 | 0.15 | 0.25 | 0.46 | 0.36 | 0.45 | 0.56 | 0.9 | 0.05 | 0.05 |
| Average Error, Measurements vs. Simulations | (s) | (s) | (dB) |
|---|---|---|---|
| Geometric | 0.074 | 0.178 | 2.025 |
| Absorption only | 0.153 | 0.175 | 2.076 |
| Uniform scattering | 0.100 | 0.178 | 2.069 |
| Directional scattering A | 0.097 | 0.175 | 2.058 |
| Directional scattering B | 0.078 | 0.178 | 2.049 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Autio, H.; Nilsson, E. A Novel Algorithm for Directional Scattering in Acoustic Ray Tracers. Acoustics 2023, 5, 928-947. https://doi.org/10.3390/acoustics5040054
Autio H, Nilsson E. A Novel Algorithm for Directional Scattering in Acoustic Ray Tracers. Acoustics. 2023; 5(4):928-947. https://doi.org/10.3390/acoustics5040054
Chicago/Turabian StyleAutio, Hanna, and Erling Nilsson. 2023. "A Novel Algorithm for Directional Scattering in Acoustic Ray Tracers" Acoustics 5, no. 4: 928-947. https://doi.org/10.3390/acoustics5040054
APA StyleAutio, H., & Nilsson, E. (2023). A Novel Algorithm for Directional Scattering in Acoustic Ray Tracers. Acoustics, 5(4), 928-947. https://doi.org/10.3390/acoustics5040054






