A Modification of the Monte Carlo Filtering Approach for Correcting Negative SEA Loss Factors
Abstract
:1. Introduction
- All elements off the main diagonal are negative.
- Elements on the main diagonal are positive and greater than the sum of the absolute values of the remaining elements for a given column.
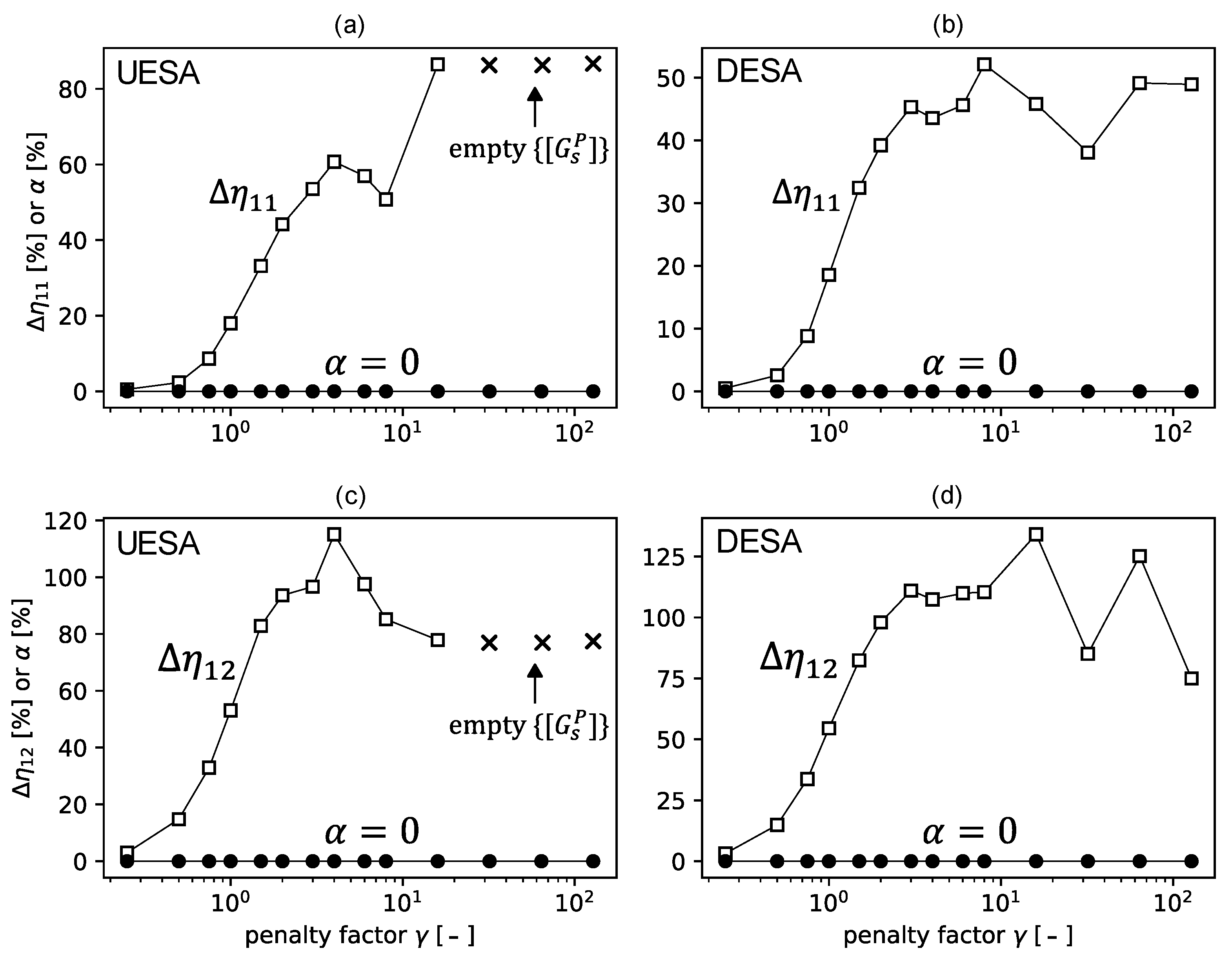
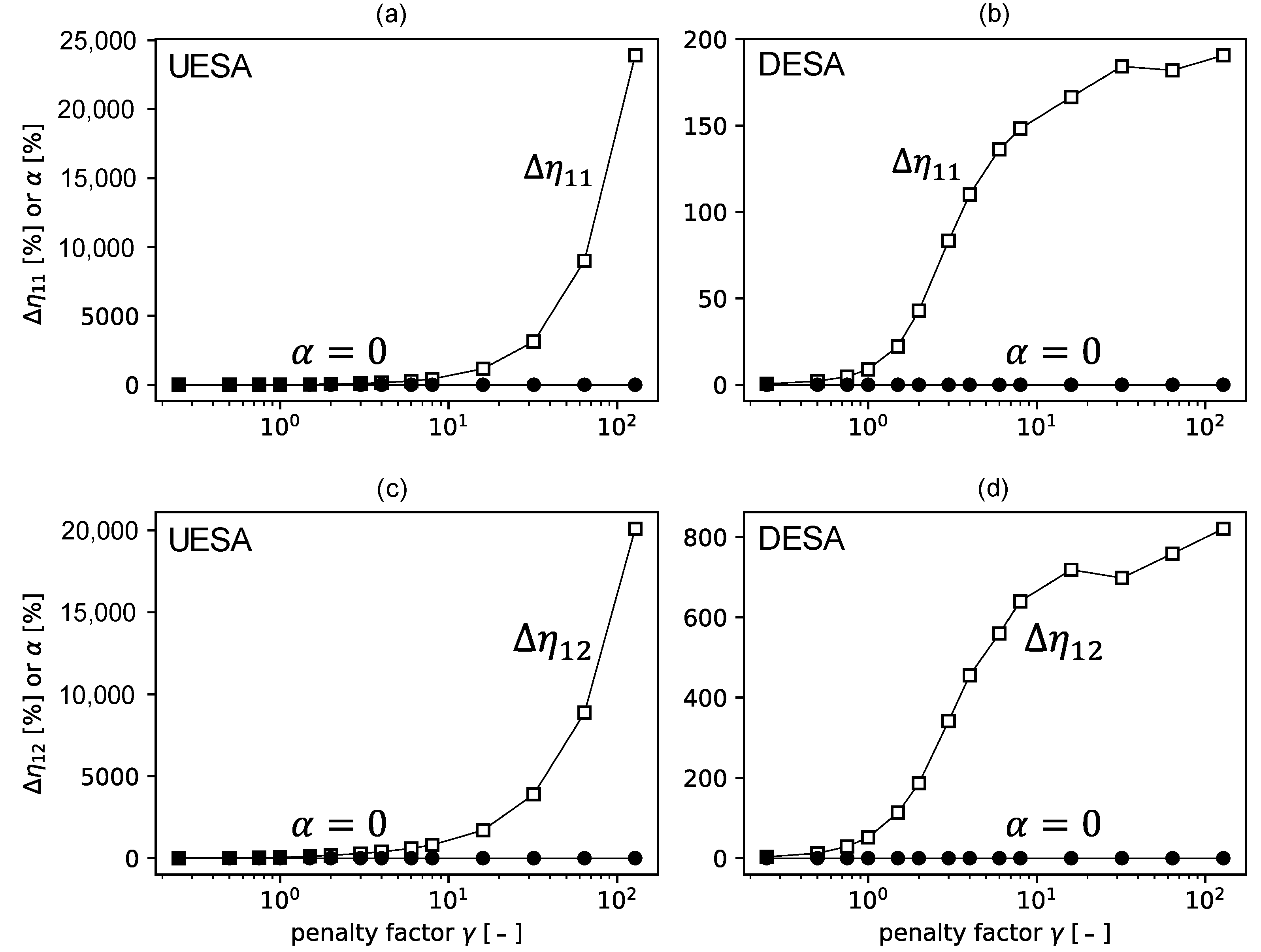
- The present paper proposes a modification of the MCF method. The modification is called DESA (Diagonal Expansion of the Search Area), which is the main contribution to the experimental SEA field. DESA consists of applying a correction during the MCF, which causes a non-uniform expansion of the search area (Section 2.1). This novel approach expands the range of vibroacoustic systems that can be properly identified by MCF. It can be applied in the frequency bands for which correct results could not be obtained using the MCF method in the basic version (using a homogeneous expansion of the search area for the population with a normal distribution), as will be demonstrated by the example presented in Section 3.
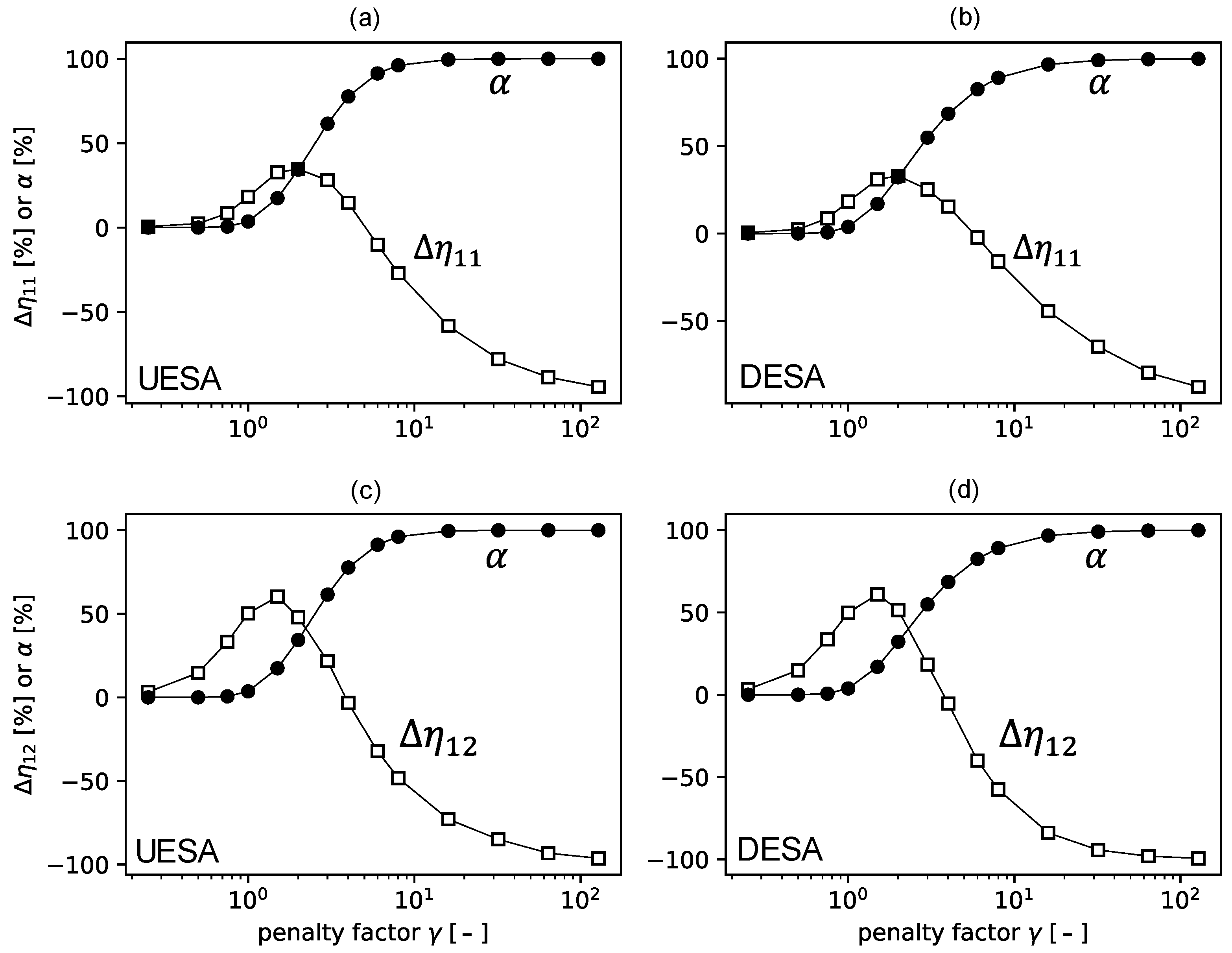
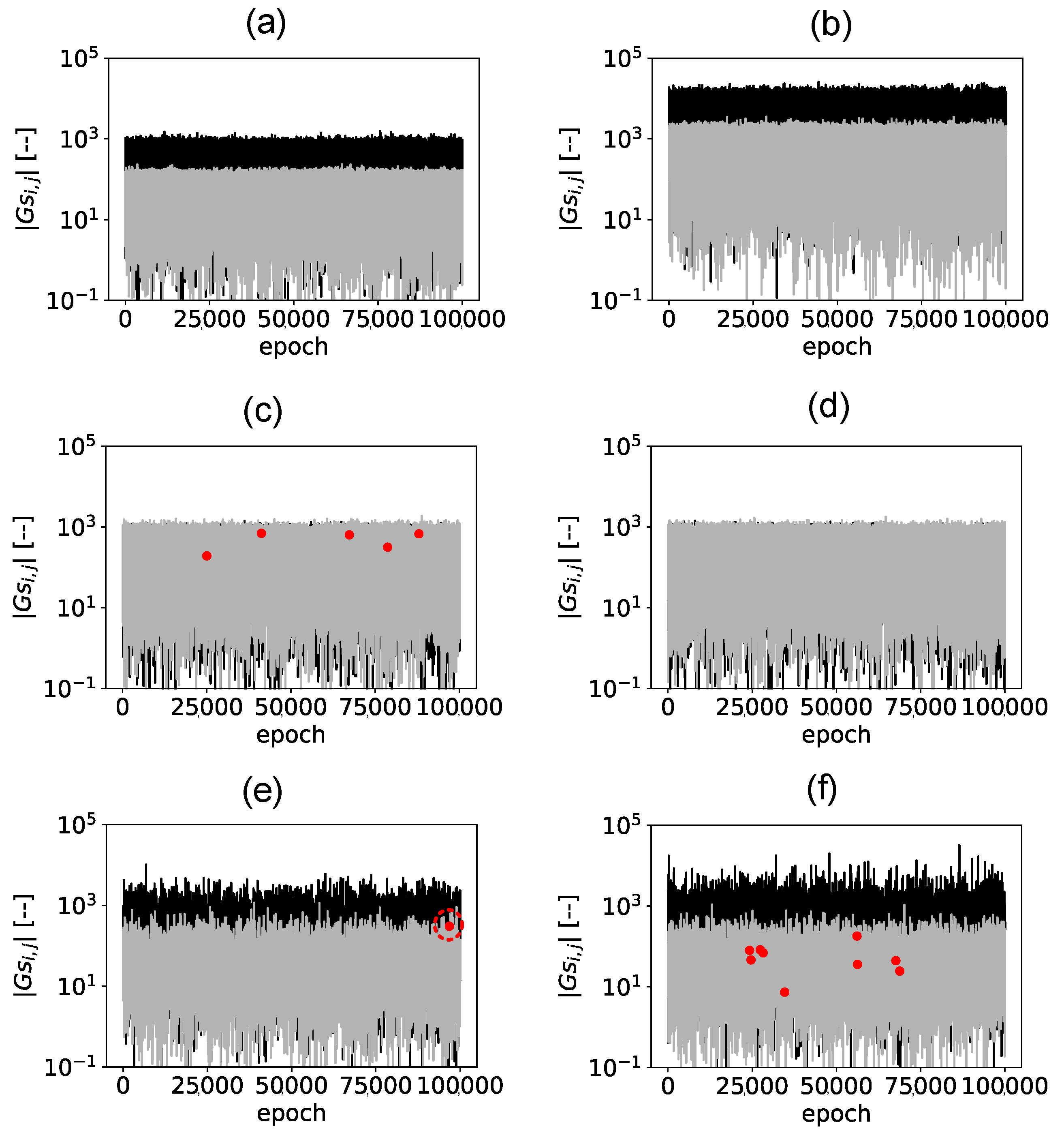
- The effect of the expansion of the search area (parameter ) on the errors introduced into the loss factors was investigated. The so-called shift error was observed and related to the asymmetry present in the generated population of the energy matrices. We pointed out that the asymmetry of the population increases with an increase in .
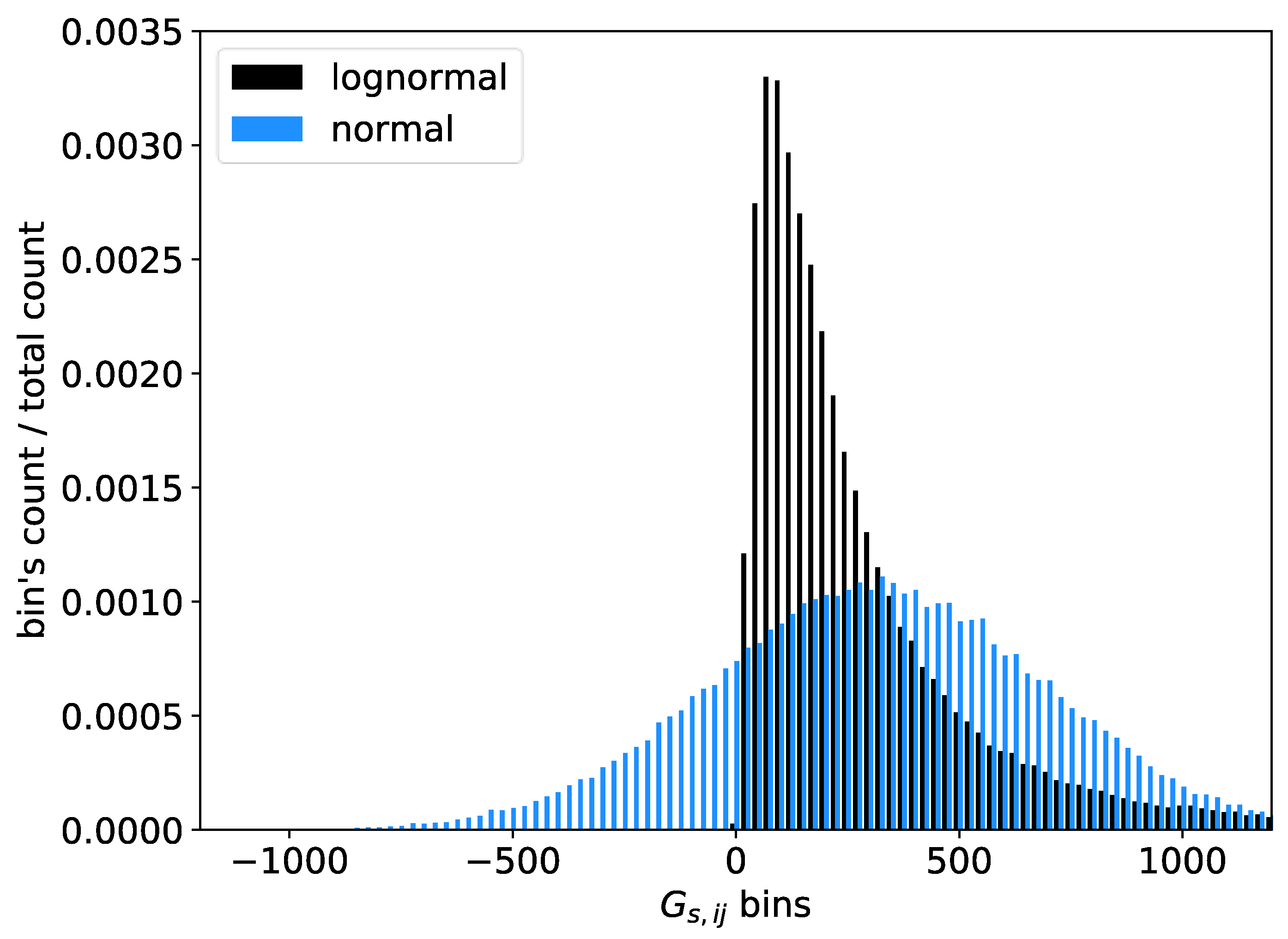
- We introduced a new parameter describing the degree of asymmetry of the energy matrix population, the asymmetry index , and proposed two methods (A and B) for eliminating the shift error. Method A involves detecting matrices that introduce asymmetry and rejecting them from the calculation, while method B involves using a log-normal distribution when generating the energy matrix population. A common feature of both methods is the need to perform minimization.
2. Materials and Methods
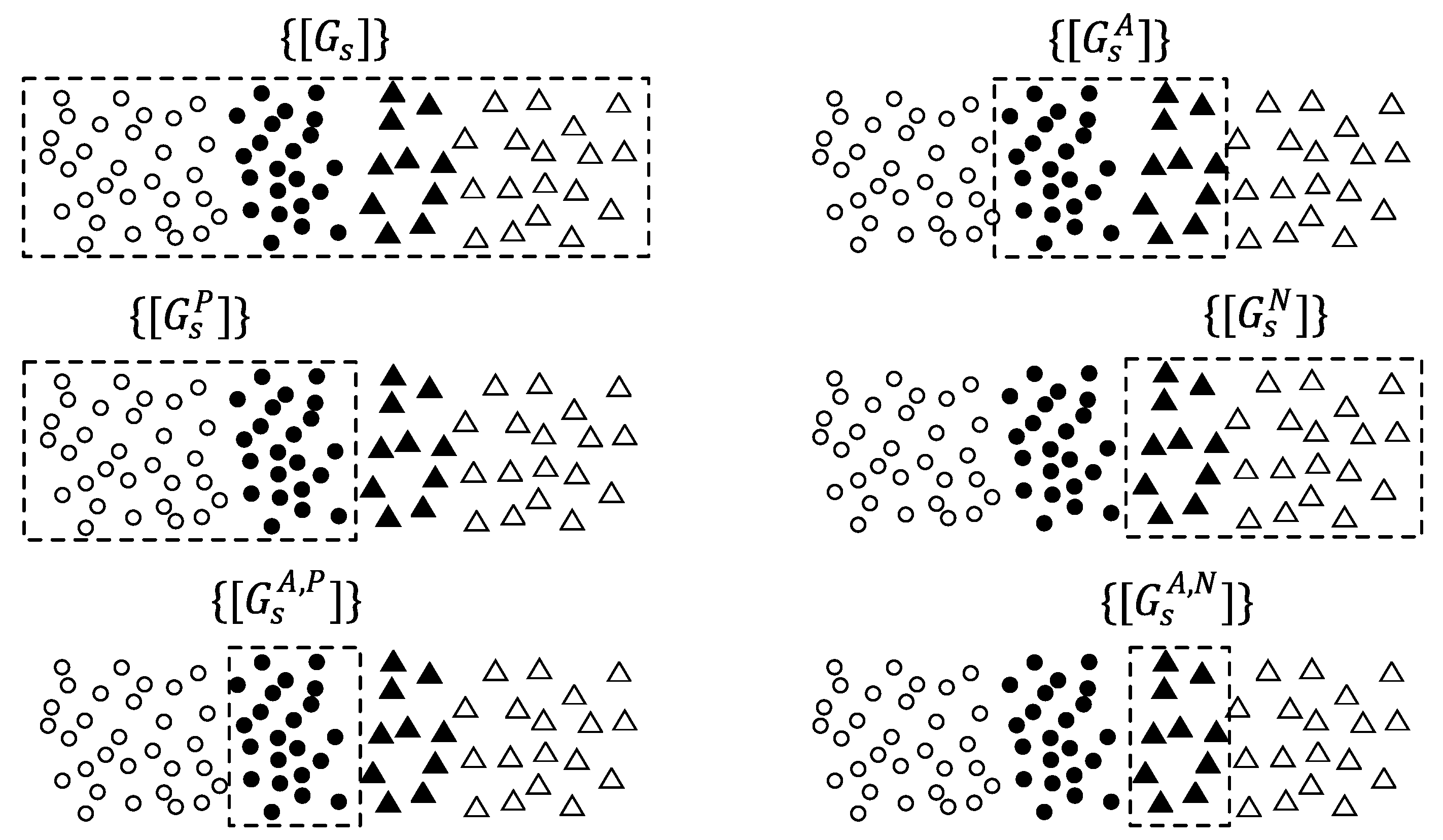
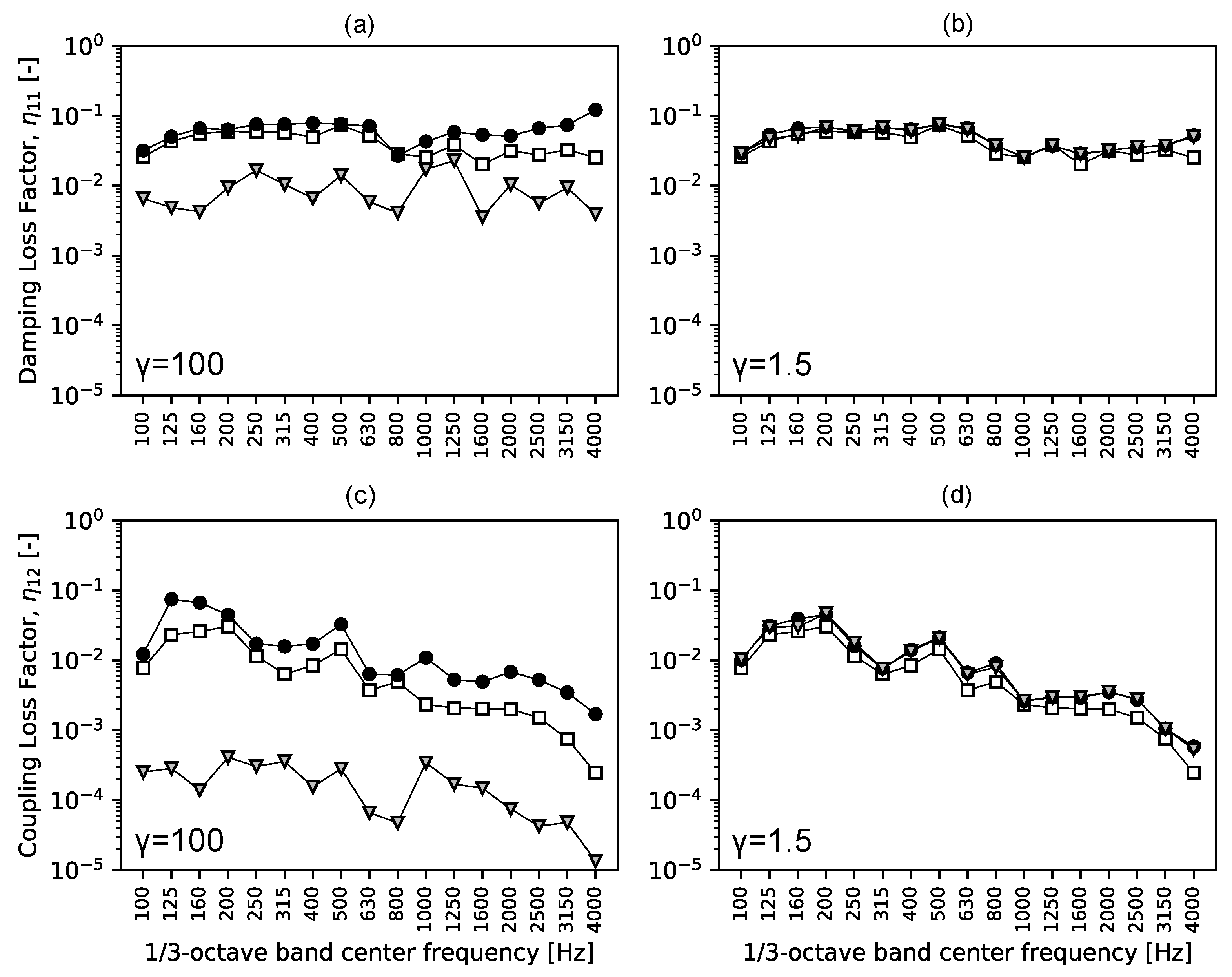
2.1. Expansion of the Search Area (UESA and DESA)
2.2. Errors Associated with ESA
2.2.1. Population Asymmetry and Shift Error
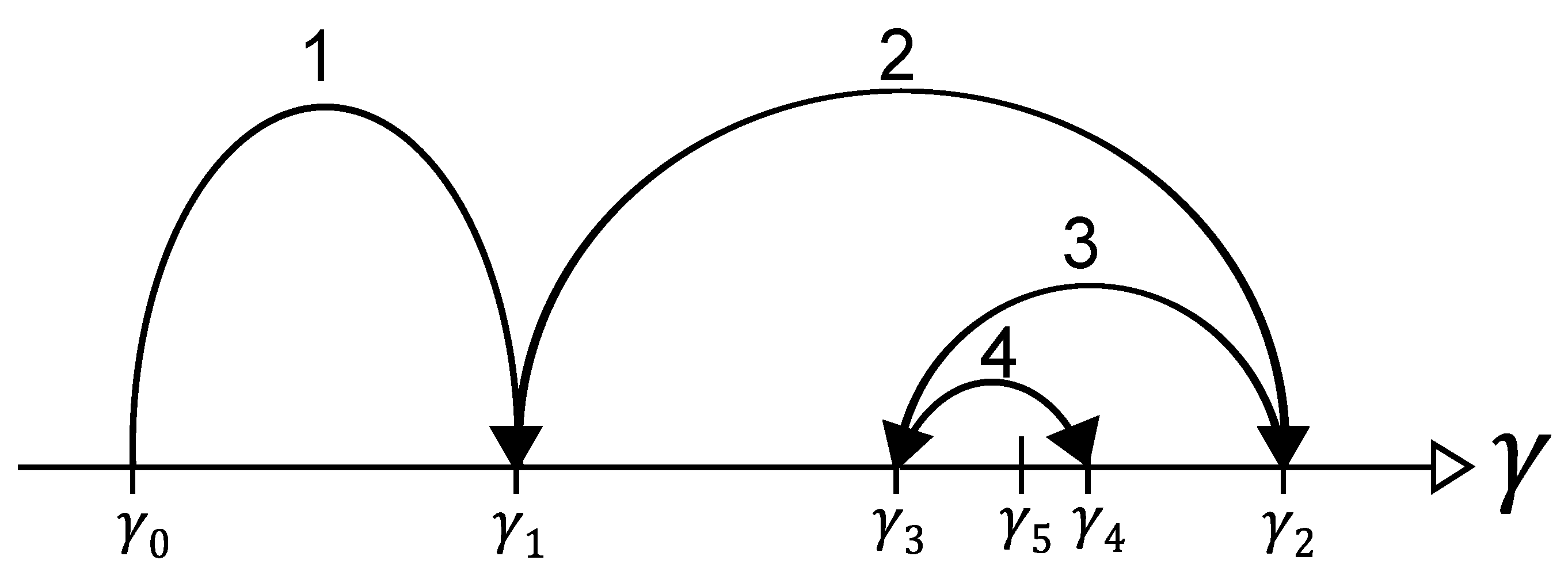
2.2.2. Scaling Factor Minimization
2.2.3. Enforcing Symmetry of the Population
- Method A, which involves discarding from the calculation matrices that fall into the tail of the normal distribution.
- Method B, which involves generating a population with a log-normal distribution.
- The use of one of the presented SFM methods in combination with -minimization allows us to:
- Correct negative loss factors and replace them with factors that are free of offset error.
- Obtain results close to the original results in bands that do not require correction, which can be good in terms of the quality control of the applied methods.
- When , or equivalently , the result obtained will be free of both shift error and negative LF. Then, the identification result obtained by Method A can be considered correct, and occurs for the resulting population.
- When , or equivalently (which also means that ), all correct matrices will be discarded and the correction of negative LF coefficients will not take place. Method A is then ineffective. However, it is possible to take the LF coefficients determined for an asymmetric population of matrices as the final result. In such a situation, the result obtained will be affected by a shift error. However, this error will be minimized by using during the calculation (the distance between the matrices and the original matrix will be relatively small).
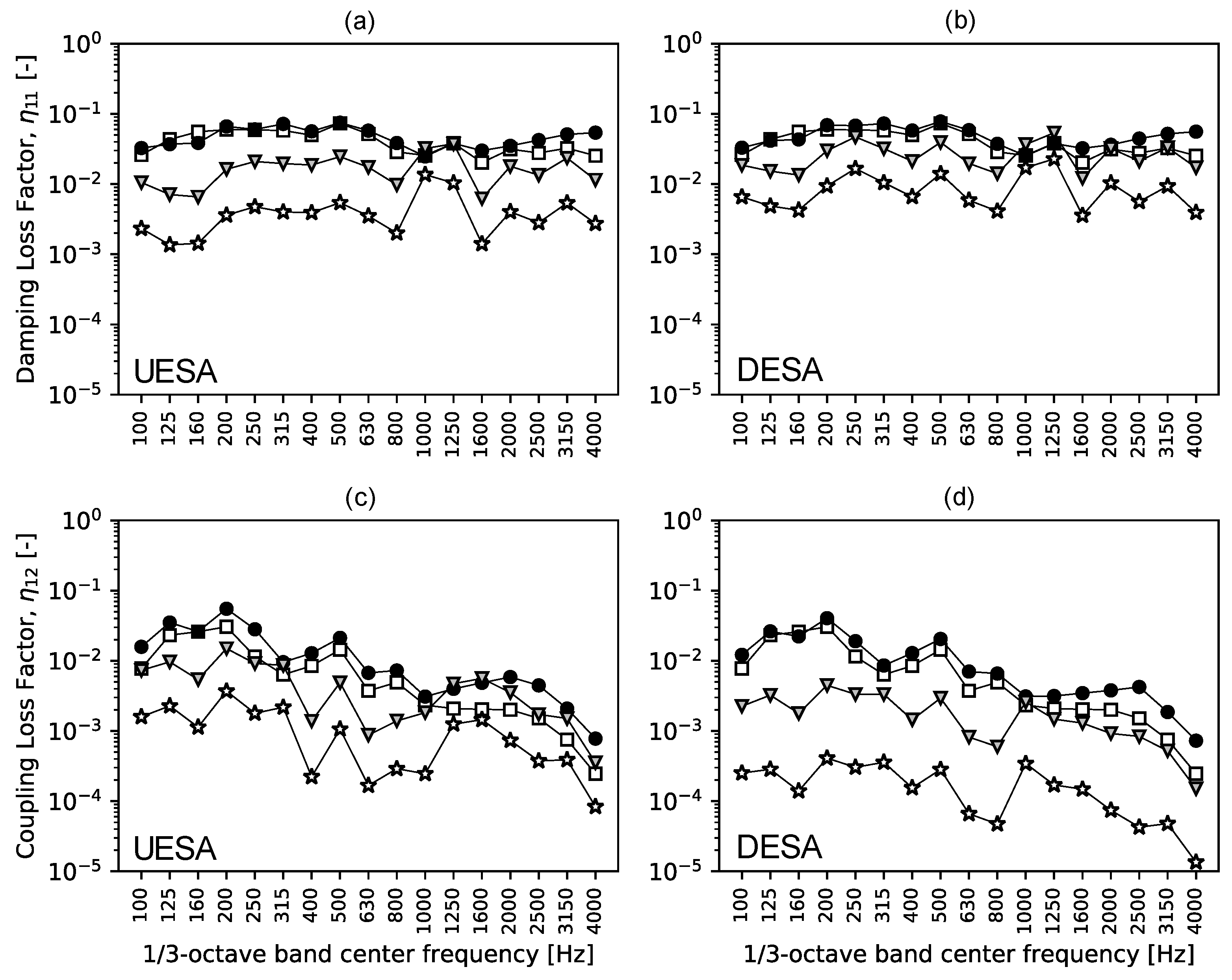
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lyon, R.H.; DeJong, R.G.; Heckl, M. Theory and Application of Statistical Energy Analysis. J. Acoust. Soc. Am. 1995, 98, 3021. [Google Scholar] [CrossRef]
- Hwang, H.J. Prediction and Validation of High Frequency Vibration Responses of NASA Mars Pathfinder Spacecraft due to Acoustic Launch Load Using Statistical Energy Analysis. Technical report, California Institute of Technology, Jet Propulsion Laboratory. 28 April 2002. Available online: https://trs.jpl.nasa.gov/bitstream/handle/2014/11593/02-0107.pdf?sequence=1 (accessed on 12 December 2022).
- Chen, X.; Wang, D.; Ma, Z. Simulation on a car interior aerodynamic noise control based on statistical energy analysis. Chin. J. Mech. Eng. 2012, 25, 1016–1021. [Google Scholar] [CrossRef]
- Craik, R. The prediction of sound transmission through buildings using statistical energy analysis. J. Sound Vib. 1982, 82, 505–516. [Google Scholar] [CrossRef]
- Bies, D.; Hamid, S. In situ determination of loss and coupling loss factors by the power injection method. J. Sound Vib. 1980, 70, 187–204. [Google Scholar] [CrossRef]
- Iwaniec, M. Damping loss factor estimation in plates. Mol. Quantum Acoust. 2003, 24, 61–68. [Google Scholar]
- Bloss, B.; Rao, M.D. A Comparison Between Power Injection and Impulse Response Decay Methods for Estimating Frequency Averaged Loss Factors for SEA. SAE Trans. 2003, 1878–1890. [Google Scholar] [CrossRef]
- Fahy, F.J.; Ruivo, H.M. Determination of statistical energy analysis loss factors by means of an input power modulation technique. J. Sound Vib. 1997, 203, 763–779. [Google Scholar] [CrossRef]
- Sun, J. Measuring Method of Dissipation and Coupling Loss Factors for Complex Structures. In Chinese Science Abstracts Series A; Elsevier Science: Amsterdam, The Netherlands, 1995; Volume 4, Number 14; p. 24. [Google Scholar]
- Gu, J.; Sheng, M. Improved energy ratio method to estimate coupling loss factors for series coupled structure. J. Mech. Eng. 2015, 45, 37–40. [Google Scholar] [CrossRef] [Green Version]
- Cuschieri, J.; Sun, J. Use of Statistical Energy Analysis for Rotating Machinery, Part I: Determination of Dissipation and Coupling Loss Factors Using Energy Ratios. J. Sound Vib. 1994, 170, 181–190. [Google Scholar] [CrossRef]
- Guasch, O. A direct transmissibility formulation for experimental statistical energy analysis with no input power measurements. J. Sound Vib. 2011, 330, 6223–6236. [Google Scholar] [CrossRef]
- Fahy, F. An alternative to the SEA coupling loss factor: Rationale and method for experimental determination. J. Sound Vib. 1998, 214, 261–267. [Google Scholar] [CrossRef]
- Ming, R. An experimental comparison of the sea power injection method and the power coefficient method. J. Sound Vib. 2005, 282, 1009–1023. [Google Scholar] [CrossRef]
- Ming, R. The measurement of coupling loss factors using the structural intensity technique. J. Acoust. Soc. Am. 1998, 103, 401–407. [Google Scholar] [CrossRef]
- Cacciolati, C.; Guyader, J.L. Measurement of SEA coupling loss factors using point mobilities. Philosophical Trans-actions of the Royal Society of London. Ser. A Phys. Eng. Sci. 1994, 346, 465–475. [Google Scholar]
- Hopkins, C. Statistical energy analysis of coupled plate systems with low modal density and low modal overlap. J. Sound Vib. 2002, 251, 193–214. [Google Scholar] [CrossRef]
- Lalor, N. Practical Consideration for the Measurement of Internal and Coupling Loss Factors on Complex Structures, ISVR Technical Report No. 182. June 1990.
- de las Heras, M.F.; Manguán, M.C.; Millán, E.R.; de las Heras, L.F.; Hidalgo, F.S. Determination of SEA loss factors by Monte Carlo Filtering. J. Sound Vib. 2020, 479, 115348. [Google Scholar] [CrossRef]
- Liesen, J.; Rozlozník, M.; Strakos, Z. Least squares residuals and minimal residual methods. SIAM J. Sci. Comput. 2002, 23, 1503–1525. [Google Scholar] [CrossRef] [Green Version]
- Hodges, C.; Nash, P.; Woodhouse, J. Measurement of coupling loss factors by matrix fitting: An investigation of numerical procedures. Appl. Acoust. 1987, 22, 47–69. [Google Scholar] [CrossRef]
- Lawson, C.L.; Hanson, R.J. Solving Least Squares Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1995. [Google Scholar]
- Cimerman, B.; Bharj, T.; Borello, G. Overview of the Experimental Approach to Statistical Energy Analysis. In SAE Conference Proceedings P; Soc Automative Engineers Inc.: Warrendale, PA, USA, 1997; Volume 2, pp. 783–788. [Google Scholar]
- Bouhaj, M.; von Estorff, O.; Peiffer, A. An approach for the assessment of the statistical aspects of the SEA coupling loss factors and the vibrational energy transmission in complex aircraft structures: Experimental investigation and methods benchmark. J. Sound Vib. 2017, 403, 152–172. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Jobe, J.M. Log-Normal Distributions: Theory and Applications; Dekker: New York, NY, USA, 1989. [Google Scholar]


| Geometry | |
|---|---|
| Thickness | 20 mm |
| Length | 80 mm |
| Width | 500 mm |
| Mechanical Parameters | |
| Material | Steel |
| Density | 7827 kg/m3 |
| Young’s modulus | 205 GPa |
| Poisson number | 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nieradka, P.; Dobrucki, A. A Modification of the Monte Carlo Filtering Approach for Correcting Negative SEA Loss Factors. Acoustics 2022, 4, 1028-1044. https://doi.org/10.3390/acoustics4040063
Nieradka P, Dobrucki A. A Modification of the Monte Carlo Filtering Approach for Correcting Negative SEA Loss Factors. Acoustics. 2022; 4(4):1028-1044. https://doi.org/10.3390/acoustics4040063
Chicago/Turabian StyleNieradka, Paweł, and Andrzej Dobrucki. 2022. "A Modification of the Monte Carlo Filtering Approach for Correcting Negative SEA Loss Factors" Acoustics 4, no. 4: 1028-1044. https://doi.org/10.3390/acoustics4040063
APA StyleNieradka, P., & Dobrucki, A. (2022). A Modification of the Monte Carlo Filtering Approach for Correcting Negative SEA Loss Factors. Acoustics, 4(4), 1028-1044. https://doi.org/10.3390/acoustics4040063






