Impact of Damping on Oscillation Patterns on the Plain Piano Soundboard
Abstract
:1. Introduction
2. Methods
2.1. Finite-Difference Model
2.2. Parameter Space
2.3. Driving Mechanisms
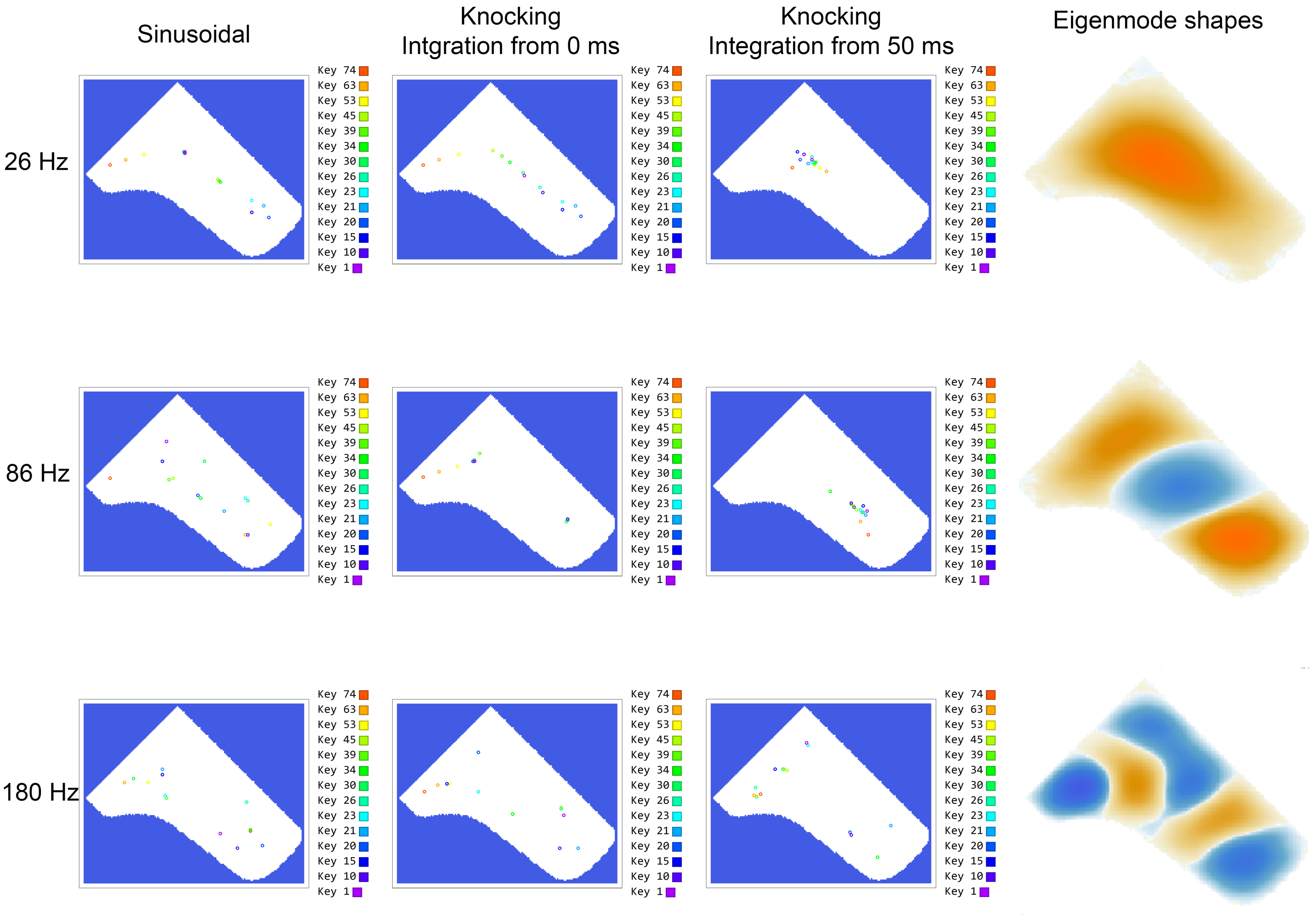
2.4. Spatial Analysis
2.5. Damping Estimations
2.5.1. Simulation
2.5.2. Measurements
3. Results
3.1. Damping of Piano Soundboards
3.2. Forced Oscillation Patterns vs. Eigenmodes
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pierce, A. Intrinsic damping, relaxation processes, and internal friction in vibrating systems. POMA 2010, 9, 1–16. [Google Scholar]
- Norris, A.N.; Photiadis, D.M. Thermoelastic Relaxation in Elastic Structures, with Applications to Thin Plates. arXiv 2004, arXiv:cond-mat/0405323v2. [Google Scholar]
- French, A.D.; Johnson, G.P. Advanced conformational energy surfaces for cellobiose. Cellulose 2004, 11, 449–462. [Google Scholar] [CrossRef]
- Tramer, A.; Jungen, C.; Lahmani, F. Energy Dissipation in Molecular Systems; Springer: Heidelberg, Germany, 2005. [Google Scholar]
- Zhou, X.Q.; Yu, D.Y.; Shao, X.Y.; Zhang, S.Q.; Wang, S. Research and applications of viscoelastic vibration damping materials: A review. Compos. Struct. 2016, 135, 460–480. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Yu, D.Y.; Shao, X.Y.; Wang, S.; Tian, Y.H. Asymptotic analysis on flexural dynamic characteristics for a sandwich plate with periodically perforated viscoelastic damping material core. Compos. Struct. 2015, 119, 487–504. [Google Scholar] [CrossRef]
- Zhou, X.Q.; Yu, D.Y.; Shao, X.; Wang, S.; Tian, Y.H. Band gap characteristics of periodically stiffened-thin-plate based on center-finite-difference-method. Thin-Walled Struct. 2014, 82, 115–123. [Google Scholar] [CrossRef]
- Brémaud, I. What do we know on “resonance wood” properties? Selective review and ongoing research. In Proceedings of the Acoustics 2012 Nantes Conference, Nantes, France, 23–27 April 2012. [Google Scholar]
- Brémaud, I.; Gril, J.; Thibaut, B. Anisotropy of wood vibrational properties: Dependence on grain angle and review of literature data. Wood Sci. Technol. 2011, 45, 735–754. [Google Scholar] [CrossRef]
- Brémaud, I.; Ruelle, J.; Thibaut, A.; Thibaut, B. Changes in viscoelastic vibrational properties between compression and normal wood: Roles of microbril angle and of lignin. Holzforschung 2013, 67, 75–85. [Google Scholar] [CrossRef] [Green Version]
- Obataya, E.; Umezawa, T.; Nakatsubo, F.; Norimoto, M. The effects of water soluble extractives on the acoustics properties of reed (Arundo donax L.). Holzforschung 1999, 53, 63–67. [Google Scholar] [CrossRef]
- Schleske, M. On the Acoustical Properties of Violin Varnish. CAS 1998, 3, 27–43. [Google Scholar]
- Romanillos, J.L. Antonio De Torres: Guitar Maker-His Life and Work; Yehudi Menuhin music guides; Bold Strummer Ltd.: Westport, CT, USA, 1997. [Google Scholar]
- Hansing, S. Das Pianoforte und seine akustischen Anlagen [The Pianoforte and Its Acoustical Properties]; Im Selbstverlage des Verfassers: Schwerin, Germany, 1910. [Google Scholar]
- Bilhuber, P.H. Diaphragm Unit and Method of Fabricating Same. U.S. Patent No. 2,529,862, 14 November 1950. [Google Scholar]
- Bilhuber, P.H.; Johnson, C.A. The Influence of the Soundboard on Piano Tone Quality. J. Acoust. Soc. Am. 1940, 11, 311–320. [Google Scholar] [CrossRef]
- Conlona, S.C.; Fahnline, J.B. Numerical analysis of the vibroacoustic properties of plates with embedded grids of acoustic black holes. J. Acoust. Soc. Am. 2015, 137, 447–457. [Google Scholar] [CrossRef] [PubMed]
- Adrien Mamou-Mani, J.F.; Besnainou, C. Numerical simulation of a piano soundboard under downbearing. J. Acoust. Soc. Am. 2008, 123, 2401–2406. [Google Scholar] [CrossRef] [PubMed]
- Mamou-Mani, A.; Moyne, S.L.; Ollivier, F.; Besnainou, C.; Frelat, J. Prestress effects on the eigenfrequencies of the soundboards: Experimental results on a simplified string instrument. J. Acoust. Soc. Am. 2012, 131, 872–877. [Google Scholar] [CrossRef] [PubMed]
- Petersen, S. Craftsmen- Turned- Scientists? The Circulation of Explicit and Working Knowledge in Musical- Instrument Making, 1880–1960. OSIRIS 2013, 28, 212–231. [Google Scholar] [CrossRef]
- Chaigne, A.; Lambourg, C. Time-domain simulation of damped impacted plates. I. Theory and experiments. J. Acoust. Soc. Am. 2001, 109, 1422–1432. [Google Scholar] [CrossRef]
- Lambourg, C.; Chaigne, A.; Matignon, D. Time-domain simulation of damped impacted plates. II. Numerical model and results. J. Acoust. Soc. Am. 2001, 109, 1433–1447. [Google Scholar] [CrossRef] [Green Version]
- Bader, R. Computational Mechanics of the Classical Guitar; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Bader, R. Finite-Difference model of mode shape changes of the Myanmar pat wain drum circle using tuning paste. Proc. Mtgt. Acoust. 2016, 29, 035004. [Google Scholar]
- Schroeder, M.R. New Method of Measuring Reverberation Time. J. Acoust. Soc. Am. 1965, 37, 409. [Google Scholar] [CrossRef]
- Farina, A. Simultaneous measurement of impulse response and distortion with a swept-sine technique. In Proceedings of the Audio Engineering Society Convention 108, Paris, France, 19–22 February 2000; pp. 1–24. [Google Scholar]
- Plath, N.; Pfeifle, F.; Koehn, C.; Bader, R. Radiation Characteristics of Grand Piano Soundboards in Different Stages of Production. In Proceedings of the 2017 International Symposium on Musical Acoustics, Montreal, QC, Canada, 18–22 June 2017. [Google Scholar]
- Plath, N.; Pfeifle, F.; Koehn, C.; Bader, R. Driving Point Mobilities of a Concert Grand Piano Soundboard in Different Stages of Production. In Proceedings of the 3rd Annual COST FP1302 WoodMusICK Conference, Barcelona, Spain, 7–9 September 2016; pp. 117–123. [Google Scholar]
- Lawergren, B. Acoustics and Evoluation of Arched Harps. Galpin Soc. J. 1981, 34, 110–129. [Google Scholar] [CrossRef]
- Williamson, M. The Burmese Harp: Its Classical Music, Tunings, & Modes; Northern Illinois Monograph Series of Southeast Asia; Northern Illinois University: DeKalb, IL, USA, 2000; Volume 1. [Google Scholar]
- Koe, Y.; Liu, B.; Tian, J. Radiation efficiency of damped plates. J. Acoust. Soc. Am. 2015, 137, 1032–1035. [Google Scholar] [CrossRef] [PubMed]
- Giordano, N. Simple model of a piano soundboard. J. Acoust. Soc. Am. 1997, 102, 1159–1168. [Google Scholar] [CrossRef]
- Moore, T.R.; Zietlow, S.A. Interferometric studies of a piano soundboard. JASA 2006, 119, 1783–1793. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mokdat, F. Fully Parameterized Finite Element Model of a Grand Piano Soundboard for Sensitivity Analysis of the Dynamic Behavior. Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, 2013. [Google Scholar]
- Beurmann, A.; Bader, R.; Schneider, A. An acoustical study of a Kirkman harpsichord from 1766. Galpin Soc. J. 2010, 63, 61–72. [Google Scholar]
- Bader, R. Nonlinearities and Synchronization in Musical Acoustics and Music Psychology; Current Research in Systematic Musicology; Springer: Berlin/Heidelberg, 2013; Volume 2, pp. 157–284. [Google Scholar]
- Fahy, F. Sound and Structural Vibration: Radiation, Transmission and Response, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Loredo, A.; Plessy, A.; Hafidi, A.E.; Hamzaoui, N. Numerical vibroacoustic analysis of plates with constrained-layer damping patches. J. Acoust. Soc. Am. 2011, 129, 1905–1918. [Google Scholar] [CrossRef]
- Plath, N. From Workshop to Concert Hall: Acoustic Observations on a Gran Piano under Construction. Ph.D. Thesis, University of Hamburg, Hamburg, Germany, 2019. [Google Scholar]
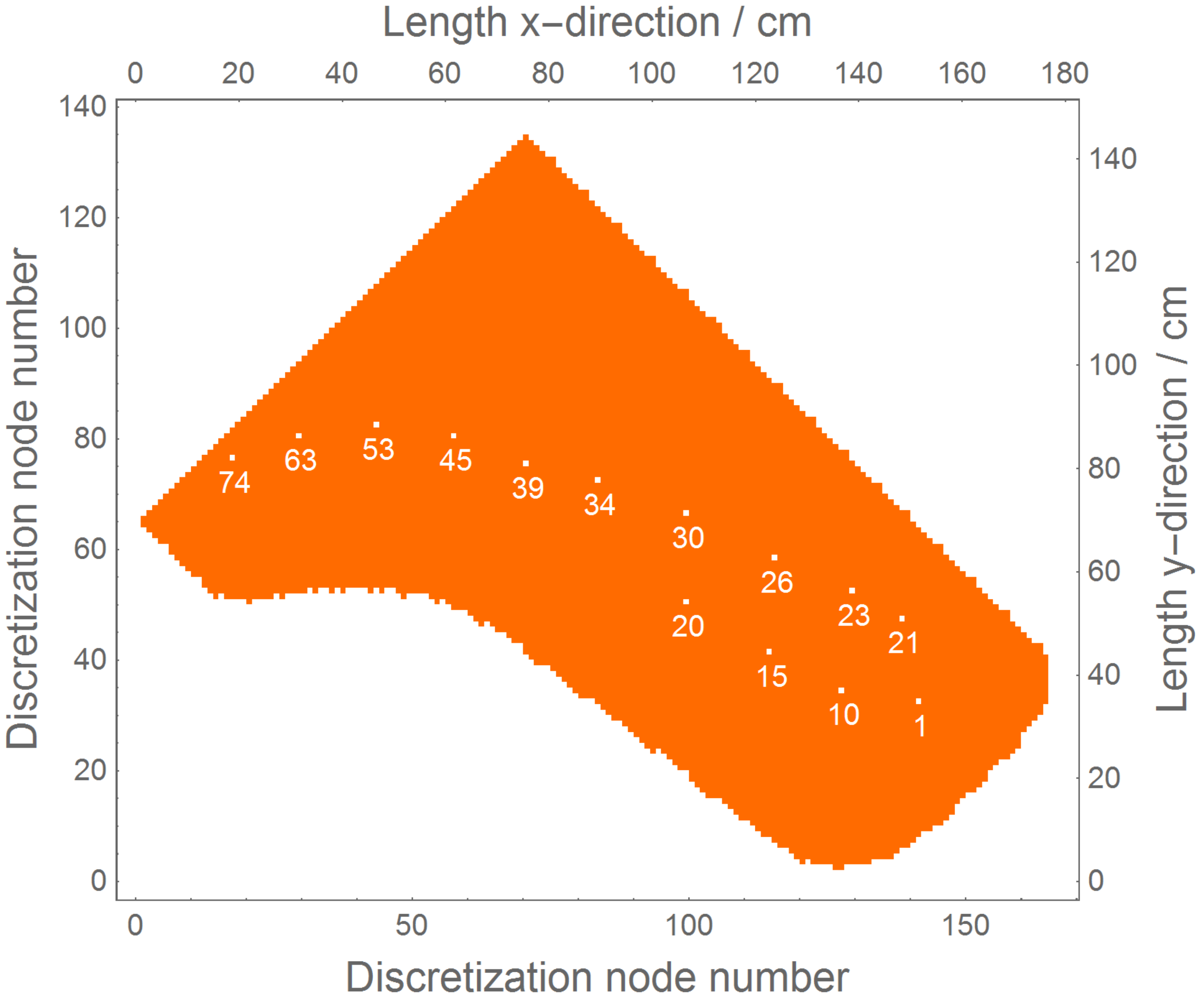
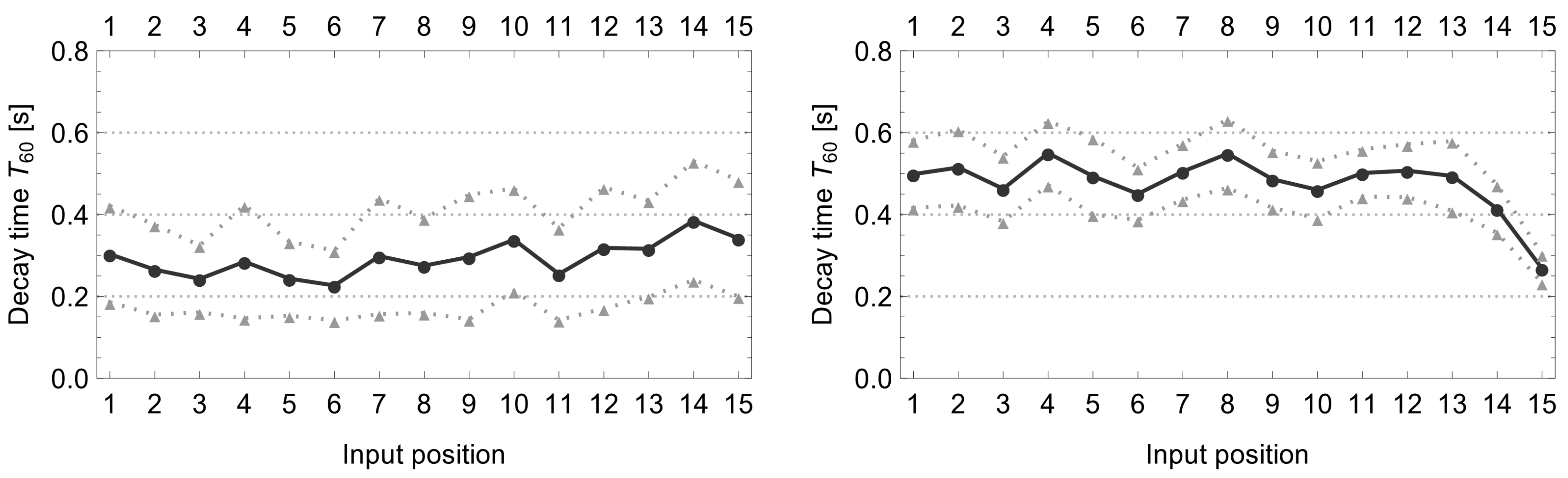
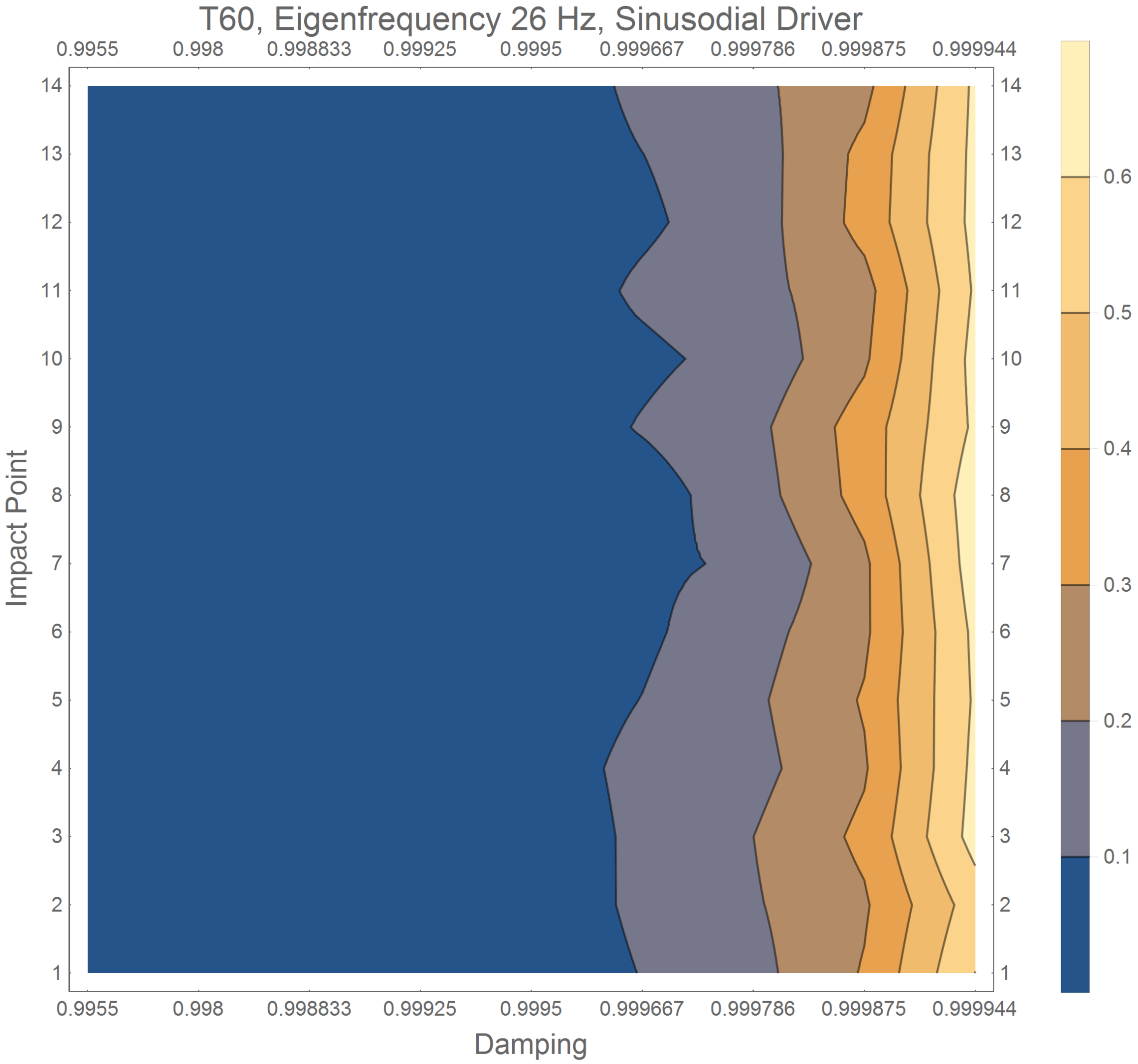
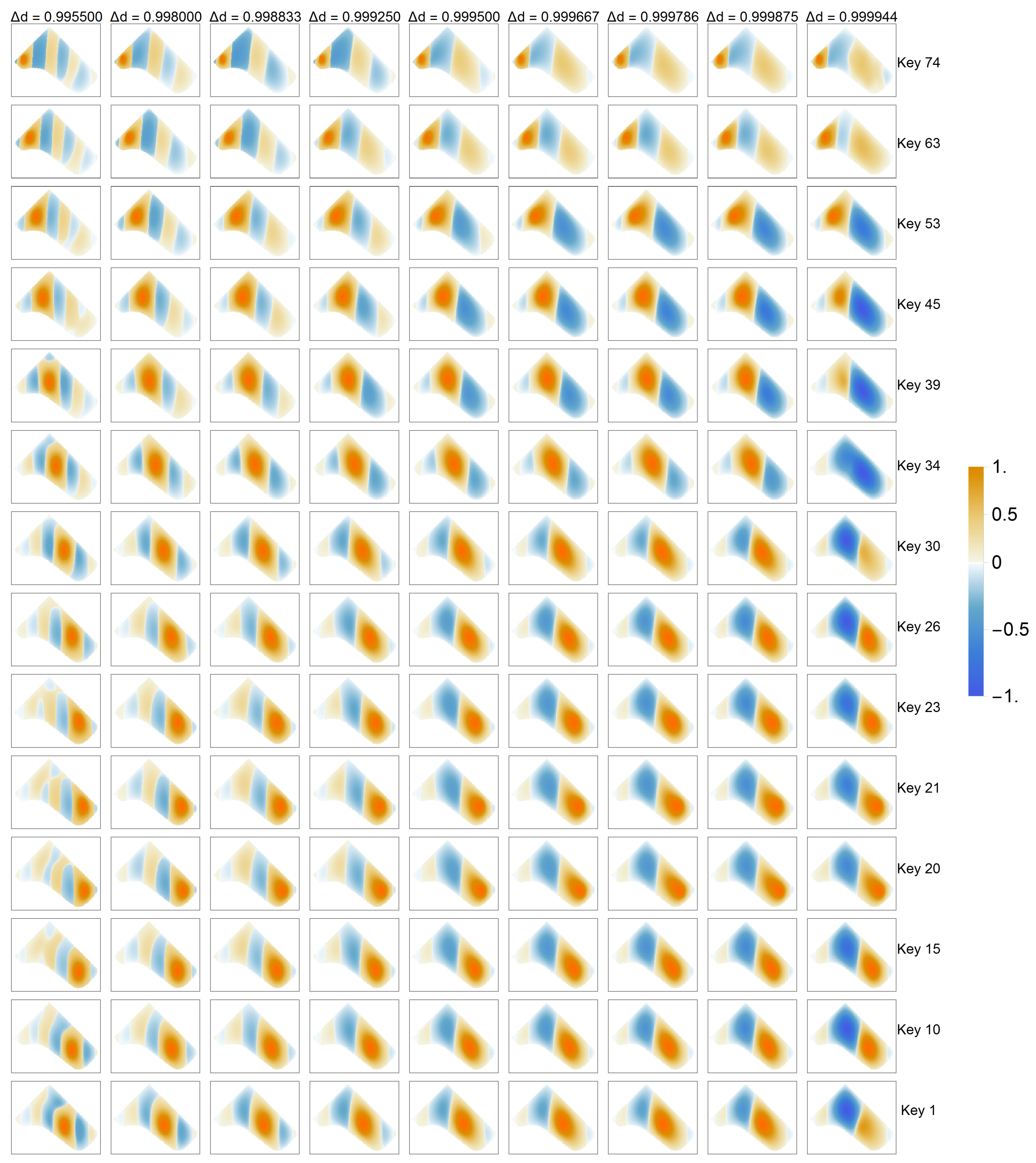
| Key | 1 | 10 | 15 | 20 | 21 | 23 | 26 | 30 | 34 | 39 | 45 | 53 | 63 | 74 |
| x-positon/mm | 395 | 530 | 590 | 645 | 270 | 320 | 400 | 485 | 591 | 680 | 780 | 895 | 1055 | 1220 |
| y-position/mm | 1730 | 1570 | 1375 | 1130 | 1560 | 1400 | 1200 | 965 | 735 | 560 | 375 | 225 | 95 | 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bader, R.; Plath, N. Impact of Damping on Oscillation Patterns on the Plain Piano Soundboard. Acoustics 2022, 4, 1013-1027. https://doi.org/10.3390/acoustics4040062
Bader R, Plath N. Impact of Damping on Oscillation Patterns on the Plain Piano Soundboard. Acoustics. 2022; 4(4):1013-1027. https://doi.org/10.3390/acoustics4040062
Chicago/Turabian StyleBader, Rolf, and Niko Plath. 2022. "Impact of Damping on Oscillation Patterns on the Plain Piano Soundboard" Acoustics 4, no. 4: 1013-1027. https://doi.org/10.3390/acoustics4040062
APA StyleBader, R., & Plath, N. (2022). Impact of Damping on Oscillation Patterns on the Plain Piano Soundboard. Acoustics, 4(4), 1013-1027. https://doi.org/10.3390/acoustics4040062






