Speech Enhancement Framework with Noise Suppression Using Block Principal Component Analysis
Abstract
1. Introduction
2. Background and Motivation
2.1. Principal Component Analysis
2.2. Motivation
3. Block Principal Component Analysis
4. Speech Enhancement Framework
- Let denote the time-domain noisy signal vector, be the clean speech signal, and represent noise. All signals at this step are real-valued and are related by:
- Using Hamming window of appropriate size, segment vector into multiple frames with appropriate level of overlap. The resulting segmented noisy signal is given by:where n represents the time point, and m represents the segment/frame number.
- Take the Fourier transform of the segmented noisy time-domain signal to get:where is the complex-valued truncated noisy spectrum with . Save , the phase of the noisy spectrum.
- Perform noise suppression on via Block-PCA with block size b, retaining q components per block, according to the steps provided in Section 3, to get:where the resulting is the real-valued magnitude of the approximated STFT.
- Apply speech enhancement algorithm to the noise-suppressed magnitude spectra to obtain the enhanced magnitude spectra .
- Generate the complex-valued spectra by combining the enhanced magnitude spectra with the phase of the noisy spectrum as follows:
- Take the inverse Fourier transform of to get , apply the general overlap, and add the (OLA) method to obtain the enhanced time-domain signal .
5. Experimental Evaluation
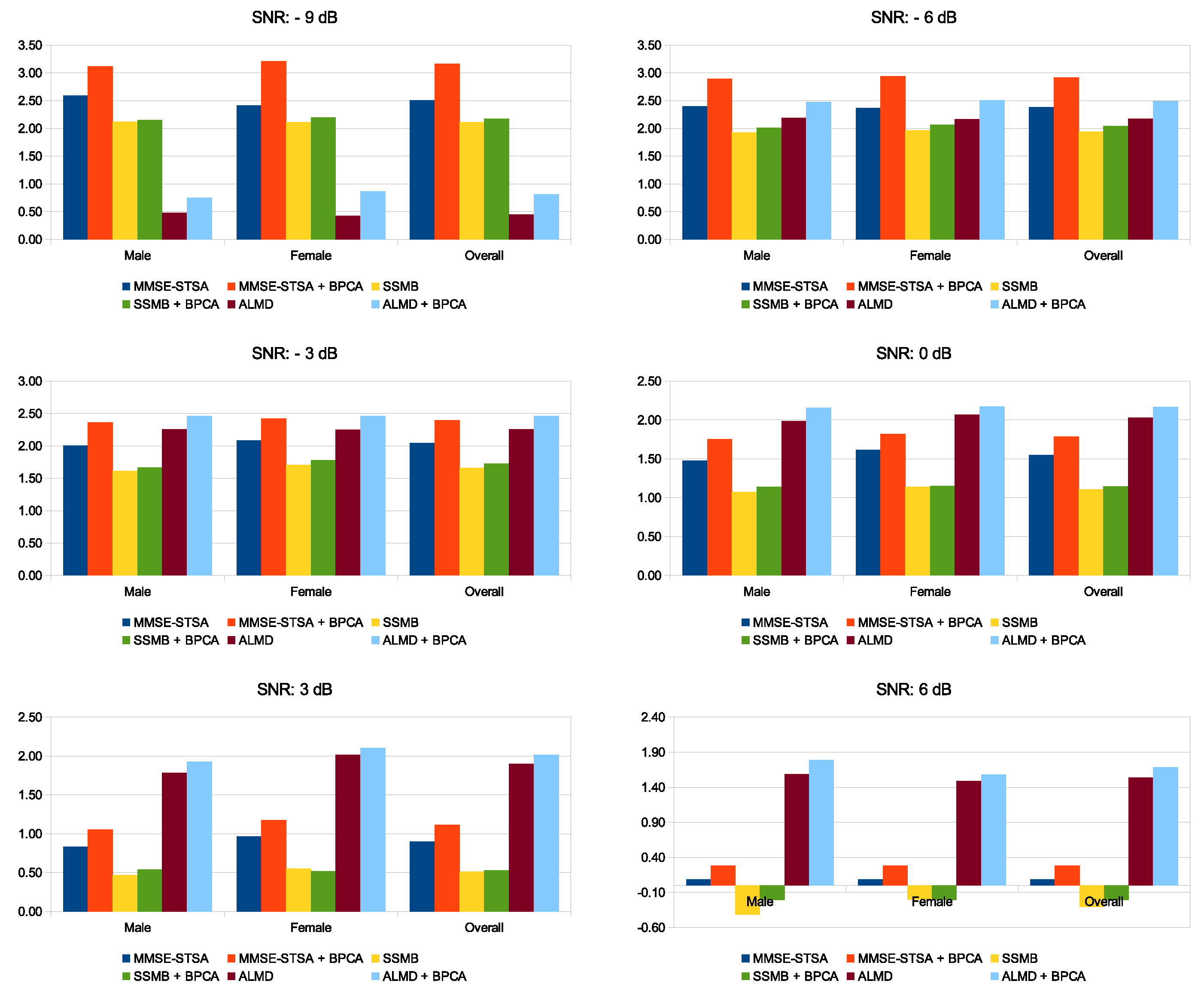
5.1. PESQ and SSNR Performance for Male and Female Speakers under Babble Noise Contamination
5.2. Performance Analysis under Different Noise Types Contamination with −6 dB SNR
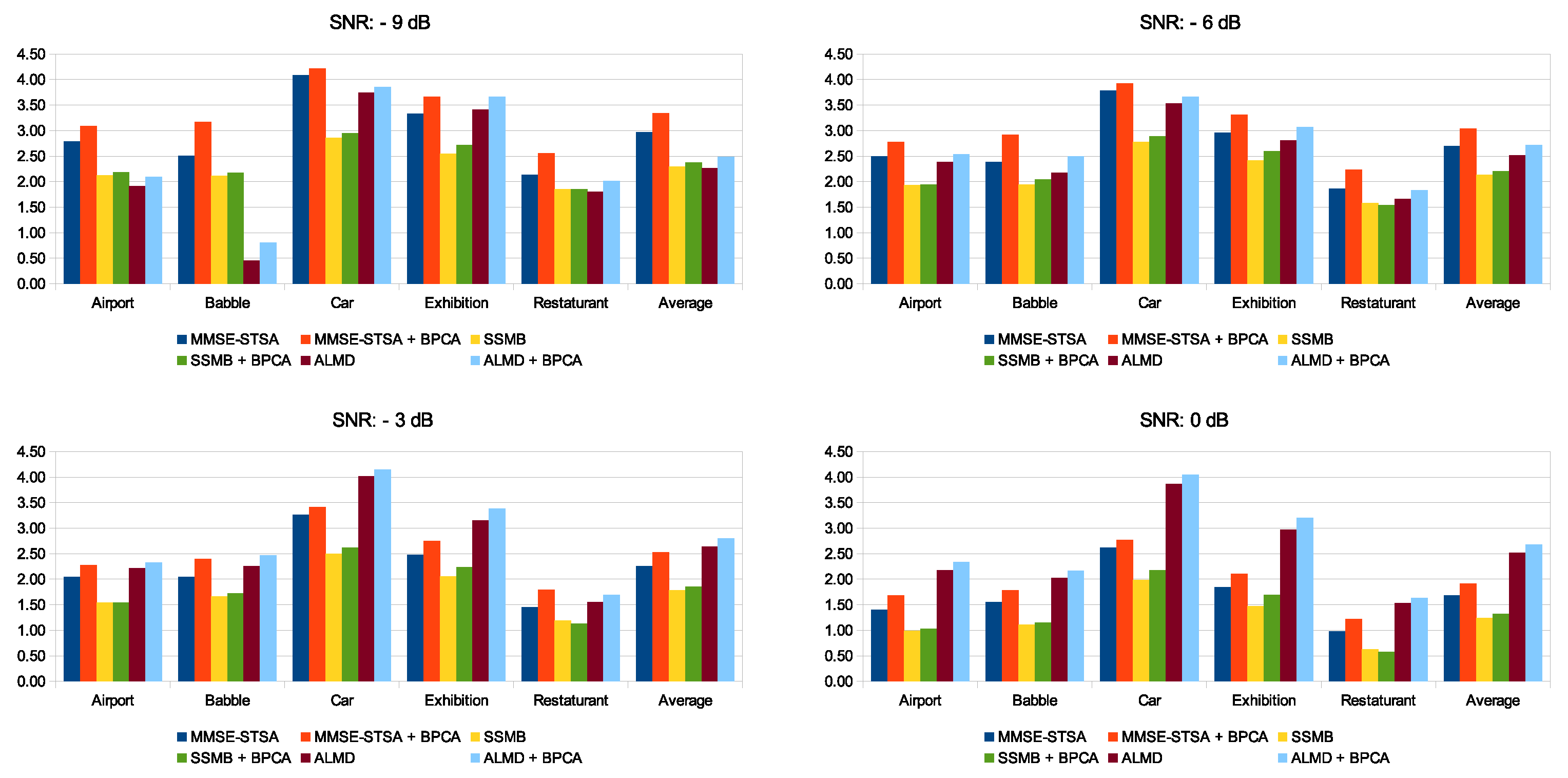
5.3. Performance Comparison for PESQ and SSNR over Multiple Noise Types and SNR Levels
5.4. Performance Comparison for Babble and Exhibition Noise Types over Multiple Metrics and SNR Levels
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Loizou, P.C. Speech Enhancement: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Veisi, H.; Sameti, H. Hidden-Markov-model-based voice activity detector with high speech detection rate for speech enhancement. IET Signal Process. 2012, 6, 54–63. [Google Scholar] [CrossRef]
- Wei, H.; Long, Y.; Mao, H. Improvements on self-adaptive voice activity detector for telephone data. Int. J. Speech Technol. 2016, 19, 623–630. [Google Scholar] [CrossRef]
- Sayoud, A.; Djendi, M. Efficient subband fast adaptive algorithm based-backward blind source separation for speech intelligibility enhancement. Int. J. Speech Technol. 2020, 23, 471–479. [Google Scholar] [CrossRef]
- Bahadur, I.N.; Kumar, S.; Agarwal, P. Performance measurement of a hybrid speech enhancement technique. Int. J. Speech Technol. 2021, 24, 665–677. [Google Scholar] [CrossRef]
- Sanam, T.F.; Shahnaz, C. A semisoft thresholding method based on Teager energy operation on wavelet packet coefficients for enhancing noisy speech. EURASIP J. Audio Speech Music. Process. 2013, 2013, 25. [Google Scholar] [CrossRef][Green Version]
- Boll, S. Suppression of acoustic noise in speech using spectral subtraction. IEEE Trans. Acoust. Speech Signal Process. 1979, 27, 113–120. [Google Scholar] [CrossRef]
- Kamath, S.; Loizou, P. A multi-band spectral subtraction method for enhancing speech corrupted by colored noise. In Proceedings of the 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, FL, USA, 13–17 May 2002; Volume 4, p. 44164. [Google Scholar]
- Yadava, T.G.; Jayanna, H.S. Speech enhancement by combining spectral subtraction and minimum mean square error-spectrum power estimator based on zero crossing. Int. J. Speech Technol. 2019, 22, 639–648. [Google Scholar] [CrossRef]
- Nahma, L.; Yong, P.C.; Dam, H.H.; Nordholm, S. An adaptive a priori SNR estimator for perceptual speech enhancement. Eurasip J. Audio Speech Music Process. 2019, 2019, 7. [Google Scholar] [CrossRef]
- Farahani, G. Autocorrelation-based noise subtraction method with smoothing, overestimation, energy, and cepstral mean and variance normalization for noisy speech recognition. EURASIP J. Audio Speech Music. Process. 2017, 2017, 13. [Google Scholar] [CrossRef]
- Abd El-Fattah, M.A.; Dessouky, M.I.; Abbas, A.M.; Diab, S.M.; El-Rabaie, E.S.M.; Al-Nuaimy, W.; Alshebeili, S.A.; Abd El-Samie, F.E. Speech enhancement with an adaptive Wiener filter. Int. J. Speech Technol. 2014, 17, 53–64. [Google Scholar] [CrossRef]
- Catic, J.; Dau, T.; Buchholz, J.; Gran, F. The Effect of a Voice Activity Detector on the Speech Enhancement Performance of the Binaural Multichannel Wiener Filter. EURASIP J. Audio Speech Music Process. 2010, 2010, 840294. [Google Scholar] [CrossRef]
- Ma, Y.; Nishihara, A. A modified Wiener filtering method combined with wavelet thresholding multitaper spectrum for speech enhancement. EURASIP J. Audio Speech Music Process. 2014, 2014, 32. [Google Scholar] [CrossRef]
- Ephraim, Y.; Malah, D. Speech enhancement using a minimum-mean square error short-time spectral amplitude estimator. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 1109–1121. [Google Scholar] [CrossRef]
- Ephraim, Y.; Malah, D. Speech enhancement using a minimum mean-square error log-spectral amplitude estimator. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 443–445. [Google Scholar] [CrossRef]
- You, C.H.; Koh, S.N.; Rahardja, S. /spl beta/-order MMSE spectral amplitude estimation for speech enhancement. IEEE Trans. Speech Audio Process. 2005, 13, 475–486. [Google Scholar]
- Bahrami, M.; Faraji, N. Minimum mean square error estimator for speech enhancement in additive noise assuming Weibull speech priors and speech presence uncertainty. Int. J. Speech Technol. 2021, 24, 97–108. [Google Scholar] [CrossRef]
- Sayoud, A.; Djendi, M.; Guessoum, A. A new speech enhancement adaptive algorithm based on fullband–subband MSE switching. Int. J. Speech Technol. 2019, 22, 993–1005. [Google Scholar] [CrossRef]
- Roy, S.K.; Paliwal, K.K. A noise PSD estimation algorithm using derivative-based high-pass filter in non-stationary noise conditions. EURASIP J. Audio Speech Music Process. 2021, 2021, 32. [Google Scholar] [CrossRef]
- Hu, Y. Subjective evaluation and comparison of speech enhancement algorithms. Speech Commun. 2007, 49, 588–601. [Google Scholar] [CrossRef]
- Kumar, B. Comparative performance evaluation of MMSE-based speech enhancement techniques through simulation and real-time implementation. Int. J. Speech Technol. 2018, 21, 1033–1044. [Google Scholar] [CrossRef]
- Ji, Y.; Zhu, W.P.; Champagne, B. Speech Enhancement Based on Dictionary Learning and Low-Rank Matrix Decomposition. IEEE Access 2018, 7, 4936–4947. [Google Scholar] [CrossRef]
- Sigg, C.D.; Dikk, T.; Buhmann, J.M. Speech enhancement using generative dictionary learning. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 1698–1712. [Google Scholar] [CrossRef]
- Li, C.; Jiang, T.; Wu, S.; Xie, J. Single-Channel Speech Enhancement Based on Adaptive Low-Rank Matrix Decomposition. IEEE Access 2020, 8, 37066–37076. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Koch, I. Analysis of Multivariate and High-Dimensional Data; Cambridge University Press: Cambridge, UK, 2013; Volume 32. [Google Scholar]
- Pyatykh, S.; Hesser, J.; Zheng, L. Image noise level estimation by principal component analysis. IEEE Trans. Image Process. 2012, 22, 687–699. [Google Scholar] [CrossRef]
- Zhang, L.; Lukac, R.; Wu, X.; Zhang, D. PCA-based spatially adaptive denoising of CFA images for single-sensor digital cameras. IEEE Trans. Image Process. 2009, 18, 797–812. [Google Scholar] [CrossRef]
- Srinivasarao, V.; Ghanekar, U. Speech enhancement—An enhanced principal component analysis (EPCA) filter approach. Comput. Electr. Eng. 2020, 85, 106657. [Google Scholar] [CrossRef]
- Sun, P.; Qin, J. Low-rank and sparsity analysis applied to speech enhancement via online estimated dictionary. IEEE Signal Process. Lett. 2016, 23, 1862–1866. [Google Scholar] [CrossRef]
- Khalilian, H.; Bajic, I.V. Video watermarking with empirical PCA-based decoding. IEEE Trans. Image Process. 2013, 22, 4825–4840. [Google Scholar] [CrossRef]
- Vaswani, N.; Chellappa, R. Principal components null space analysis for image and video classification. IEEE Trans. Image Process. 2006, 15, 1816–1830. [Google Scholar] [CrossRef]
- Seghouane, A.K.; Iqbal, A.; Desai, N.K. BSmCCA: A block sparse multiple-set canonical correlation analysis algorithm for multi-subject fMRI data sets. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 6324–6328. [Google Scholar]
- Seghouane, A.K.; Iqbal, A. The Adaptive Block Sparse PCA and its Application to Multi-Subject fMRI Data Analysis Using Sparse mCCA. Signal Process. 2018, 153, 311–320. [Google Scholar] [CrossRef]
- Caruso, G.; Battista, T.D.; Gattone, S.A. A micro-level analysis of regional economic activity through a PCA approach. In Proceedings of the International Conference on Decision Economics, Ávila, Spain, 26–28 June 2019; pp. 227–234. [Google Scholar]
- Yang, J.; Zhang, D.; Frangi, A.F.; Yang, J.Y. Two-dimensional PCA: A new approach to appearance-based face representation and recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 131–137. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Du, J.; Huo, Q. A speech enhancement approach using piecewise linear approximation of an explicit model of environmental distortions. In Proceedings of the Ninth Annual Conference of the International Speech Communication Association, Brisbane, QLD, Australia, 22–26 September 2008. [Google Scholar]
- Hu, Y.; Loizou, P.C. Evaluation of objective quality measures for speech enhancement. IEEE Trans. Audio Speech Lang. Process. 2007, 16, 229–238. [Google Scholar] [CrossRef]
- Quackenbush, S.R. Objective Measures of Speech Quality (Subjective). Ph.D. Dissertation, The University of Michigan, Ann Arbor, MI, USA, 1986. [Google Scholar]
- Klatt, D. Prediction of perceived phonetic distance from critical-band spectra: A first step. In Proceedings of the ICASSP’82 IEEE International Conference on Acoustics, Speech, and Signal Processing, Paris, France, 3–5 May 1982; Volume 7, pp. 1278–1281. [Google Scholar]





| Reference | Input SNR Range in dB |
|---|---|
| [3] | −3 dB onwards |
| [5] | −5 dB onwards |
| [6] | −15 dB onwards |
| [10] | 0 dB onwards |
| [11] | −5 dB onwards |
| [20] | −3 dB onwards |
| [22] | 1 dB onwards |
| [23] | 0 dB onwards |
| [24] | 0 dB onwards |
| [25] | 0 dB onwards |
| Babble | |||||||
|---|---|---|---|---|---|---|---|
| SNR dB | Method/Average Scores | PESQ | LLR | SSNR | Csig | Cbak | Covl |
| −6 | Noisy | 1.39 | 1.03 | −7.15 | 2.11 | 1.30 | 1.62 |
| MMSE-STSA | 1.30 | 1.16 | −4.77 | 1.77 | 1.26 | 1.37 | |
| MMSE-STSA + BPCA | 1.78 | 1.09 | −4.24 | 2.12 | 1.51 | 1.75 | |
| SSMB | 1.30 | 1.10 | −5.21 | 1.90 | 1.28 | 1.44 | |
| SSMB + BPCA | 1.62 | 1.05 | −5.11 | 2.11 | 1.41 | 1.68 | |
| ALMD | 1.13 | 1.21 | −4.97 | 1.69 | 1.19 | 1.29 | |
| ALMD + BPCA | 1.53 | 1.15 | −4.66 | 1.97 | 1.38 | 1.60 | |
| Exhibition | |||||||
| SNR dB | Method/Average Scores | PESQ | LLR | SSNR | Csig | Cbak | Covl |
| −6 | Noisy | 1.32 | 1.25 | −7.20 | 1.91 | 1.30 | 1.50 |
| MMSE-STSA | 1.26 | 1.25 | −4.24 | 1.76 | 1.35 | 1.36 | |
| MMSE-STSA + BPCA | 1.78 | 1.21 | −3.89 | 2.09 | 1.61 | 1.77 | |
| SSMB | 1.24 | 1.24 | −4.78 | 1.79 | 1.33 | 1.37 | |
| SSMB + BPCA | 1.42 | 1.22 | −4.61 | 1.93 | 1.44 | 1.53 | |
| ALMD | 1.14 | 1.28 | −4.39 | 1.69 | 1.31 | 1.31 | |
| ALMD + BPCA | 1.48 | 1.24 | −4.13 | 1.92 | 1.49 | 1.59 | |
| Car | |||||||
| SNR dB | Method/Average Scores | PESQ | LLR | SSNR | Csig | Cbak | Covl |
| −6 | Noisy | 1.40 | 1.12 | −7.43 | 2.06 | 1.30 | 1.58 |
| MMSE-STSA | 1.60 | 1.08 | −3.65 | 2.23 | 1.62 | 1.79 | |
| MMSE-STSA + BPCA | 2.42 | 1.05 | −3.51 | 2.74 | 2.01 | 2.44 | |
| SSMB | 1.36 | 1.11 | −4.66 | 2.03 | 1.56 | 1.56 | |
| SSMB + BPCA | 1.50 | 1.08 | −4.54 | 2.15 | 1.68 | 1.68 | |
| ALMD | 1.52 | 1.15 | −3.90 | 2.28 | 1.70 | 1.84 | |
| ALMD + BPCA | 2.00 | 1.13 | −3.77 | 2.60 | 1.96 | 2.23 | |
| Babble | |||||||
|---|---|---|---|---|---|---|---|
| SNR dB | Method/Noises | PESQ | LLR | SSNR | Csig | Cbak | Covl |
| −9 | Noisy | 1.30 | 1.11 | −8.23 | 1.92 | 1.20 | 1.49 |
| MMSE-STSA | 1.06 | 1.25 | −5.72 | 1.46 | 1.10 | 1.14 | |
| MMSE-STSA + BPCA | 1.86 | 1.17 | −5.06 | 1.99 | 1.45 | 1.72 | |
| SSMB | 1.18 | 1.17 | −6.11 | 1.69 | 1.18 | 1.29 | |
| SSMB + BPCA | 1.65 | 1.13 | −6.06 | 1.98 | 1.34 | 1.63 | |
| ALMD | 0.87 | 1.99 | −7.78 | 1.39 | 1.03 | 1.06 | |
| ALMD + BPCA | 1.50 | 1.93 | −7.42 | 1.80 | 1.29 | 1.52 | |
| −6 | Noisy | 1.40 | 1.03 | −7.15 | 2.11 | 1.30 | 1.62 |
| MMSE-STSA | 1.30 | 1.16 | −4.77 | 1.77 | 1.26 | 1.37 | |
| MMSE-STSA + BPCA | 1.78 | 1.09 | −4.24 | 2.12 | 1.51 | 1.75 | |
| SSMB | 1.30 | 1.10 | −5.21 | 1.90 | 1.28 | 1.44 | |
| SSMB + BPCA | 1.62 | 1.05 | −5.11 | 2.11 | 1.41 | 1.68 | |
| ALMD | 1.13 | 1.21 | −4.97 | 1.69 | 1.19 | 1.29 | |
| ALMD + BPCA | 1.53 | 1.15 | −4.66 | 1.97 | 1.38 | 1.60 | |
| −3 | Noisy | 1.54 | 0.95 | −5.85 | 2.35 | 1.46 | 1.80 |
| MMSE-STSA | 1.60 | 1.07 | −3.80 | 2.12 | 1.51 | 1.69 | |
| MMSE-STSA + BPCA | 1.80 | 1.02 | −3.45 | 2.31 | 1.65 | 1.89 | |
| SSMB | 1.59 | 1.01 | −4.19 | 2.24 | 1.53 | 1.75 | |
| SSMB + BPCA | 1.73 | 0.95 | −4.12 | 2.36 | 1.59 | 1.87 | |
| ALMD | 1.47 | 0.98 | −3.59 | 2.14 | 1.55 | 1.71 | |
| ALMD + BPCA | 1.64 | 0.92 | −3.39 | 2.30 | 1.64 | 1.87 | |
| 0 | Noisy | 1.74 | 0.86 | −4.35 | 2.64 | 1.71 | 2.08 |
| MMSE-STSA | 1.86 | 0.98 | -2.81 | 2.46 | 1.77 | 2.01 | |
| MMSE-STSA + BPCA | 1.95 | 0.93 | −2.57 | 2.57 | 1.84 | 2.11 | |
| SSMB | 1.80 | 0.92 | −3.25 | 2.53 | 1.74 | 2.03 | |
| SSMB + BPCA | 1.89 | 0.86 | −3.21 | 2.63 | 1.79 | 2.12 | |
| ALMD | 1.77 | 0.79 | −2.33 | 2.53 | 1.85 | 2.09 | |
| ALMD + BPCA | 1.86 | 0.74 | −2.19 | 2.64 | 1.91 | 2.19 | |
| 3 | Noisy | 1.92 | 0.76 | −2.70 | 2.93 | 1.96 | 2.33 |
| MMSE-STSA | 2.09 | 0.88 | −1.80 | 2.79 | 2.01 | 2.31 | |
| MMSE-STSA + BPCA | 2.14 | 0.84 | −1.59 | 2.88 | 2.06 | 2.39 | |
| SSMB | 2.02 | 0.81 | −2.19 | 2.85 | 1.97 | 2.32 | |
| SSMB + BPCA | 2.08 | 0.76 | −2.17 | 2.94 | 2.01 | 2.39 | |
| ALMD | 2.19 | 0.67 | −0.80 | 2.92 | 2.12 | 2.45 | |
| ALMD + BPCA | 2.25 | 0.62 | -0.68 | 3.01 | 2.17 | 2.53 | |
| 6 | Noisy | 2.11 | 0.65 | −0.91 | 3.22 | 2.22 | 2.59 |
| MMSE-STSA | 2.28 | 0.78 | −0.82 | 3.09 | 2.22 | 2.58 | |
| MMSE-STSA + BPCA | 2.33 | 0.74 | −0.63 | 3.17 | 2.27 | 2.65 | |
| SSMB | 2.22 | 0.71 | −1.22 | 3.14 | 2.18 | 2.58 | |
| SSMB + BPCA | 2.27 | 0.66 | −1.12 | 3.23 | 2.22 | 2.65 | |
| ALMD | 2.45 | 0.51 | 0.63 | 3.26 | 2.37 | 2.76 | |
| ALMD + BPCA | 2.50 | 0.47 | 0.77 | 3.34 | 2.42 | 2.83 | |
| Exhibition | |||||||
|---|---|---|---|---|---|---|---|
| −9 | Noisy | 1.17 | 1.32 | −8.27 | 1.71 | 1.18 | 1.35 |
| MMSE-STSA | 1.20 | 1.33 | −4.94 | 1.60 | 1.26 | 1.30 | |
| MMSE-STSA + BPCA | 1.99 | 1.30 | −4.61 | 2.05 | 1.61 | 1.84 | |
| SSMB | 1.13 | 1.31 | −5.73 | 1.60 | 1.22 | 1.27 | |
| SSMB + BPCA | 1.46 | 1.30 | −5.56 | 1.82 | 1.37 | 1.50 | |
| ALMD | 1.02 | 1.37 | −4.86 | 1.49 | 1.14 | 1.16 | |
| ALMD + BPCA | 1.58 | 1.36 | −4.61 | 1.82 | 1.39 | 1.54 | |
| −6 | Noisy | 1.32 | 1.25 | −7.20 | 1.91 | 1.30 | 1.50 |
| MMSE-STSA | 1.26 | 1.25 | −4.24 | 1.76 | 1.35 | 1.36 | |
| MMSE-STSA + BPCA | 1.78 | 1.21 | −3.89 | 2.09 | 1.61 | 1.77 | |
| SSMB | 1.24 | 1.24 | −4.78 | 1.79 | 1.33 | 1.37 | |
| SSMB + BPCA | 1.42 | 1.22 | −4.61 | 1.93 | 1.44 | 1.53 | |
| ALMD | 1.14 | 1.28 | −4.39 | 1.69 | 1.31 | 1.31 | |
| ALMD + BPCA | 1.48 | 1.24 | −4.13 | 1.92 | 1.49 | 1.59 | |
| −3 | Noisy | 1.47 | 1.17 | −5.89 | 2.15 | 1.48 | 1.70 |
| MMSE-STSA | 1.48 | 1.14 | −3.42 | 2.08 | 1.55 | 1.63 | |
| MMSE-STSA + BPCA | 1.73 | 1.11 | −3.14 | 2.24 | 1.69 | 1.84 | |
| SSMB | 1.42 | 1.15 | −3.84 | 2.06 | 1.52 | 1.60 | |
| SSMB + BPCA | 1.54 | 1.11 | −3.65 | 2.18 | 1.60 | 1.72 | |
| ALMD | 1.55 | 1.17 | −2.75 | 2.17 | 1.63 | 1.72 | |
| ALMD + BPCA | 1.73 | 1.13 | −2.52 | 2.31 | 1.74 | 1.88 | |
| 0 | Noisy | 1.61 | 1.07 | −4.39 | 2.41 | 1.69 | 1.91 |
| MMSE-STSA | 1.72 | 1.04 | −2.54 | 2.38 | 1.77 | 1.92 | |
| MMSE-STSA + BPCA | 1.81 | 1.01 | −2.28 | 2.45 | 1.83 | 2.00 | |
| SSMB | 1.66 | 1.04 | −2.91 | 2.38 | 1.74 | 1.90 | |
| SSMB + BPCA | 1.77 | 0.98 | −2.70 | 2.52 | 1.82 | 2.02 | |
| ALMD | 1.84 | 1.06 | −1.42 | 2.53 | 1.92 | 2.06 | |
| ALMD + BPCA | 1.94 | 1.01 | −1.18 | 2.64 | 1.99 | 2.17 | |
| 3 | Noisy | 1.78 | 0.96 | −2.72 | 2.69 | 1.93 | 2.15 |
| MMSE-STSA | 1.96 | 0.95 | −1.58 | 2.69 | 1.99 | 2.21 | |
| MMSE-STSA + BPCA | 2.02 | 0.91 | −1.33 | 2.75 | 2.03 | 2.27 | |
| SSMB | 1.89 | 0.92 | −1.98 | 2.70 | 1.96 | 2.19 | |
| SSMB + BPCA | 2.02 | 0.85 | −1.67 | 2.85 | 2.05 | 2.33 | |
| ALMD | 2.11 | 0.91 | 0.02 | 2.88 | 2.17 | 2.40 | |
| ALMD + BPCA | 2.20 | 0.85 | 0.30 | 2.99 | 2.24 | 2.50 | |
| 6 | Noisy | 1.97 | 0.84 | -0.92 | 2.98 | 2.18 | 2.41 |
| MMSE-STSA | 2.19 | 0.84 | −0.61 | 3.00 | 2.21 | 2.50 | |
| MMSE-STSA + BPCA | 2.23 | 0.82 | −0.39 | 3.04 | 2.25 | 2.54 | |
| SSMB | 2.11 | 0.80 | −1.01 | 3.01 | 2.17 | 2.47 | |
| SSMB + BPCA | 2.23 | 0.74 | −0.66 | 3.17 | 2.26 | 2.61 | |
| ALMD | 2.44 | 0.75 | 1.49 | 3.25 | 2.47 | 2.71 | |
| ALMD + BPCA | 2.52 | 0.71 | 1.78 | 3.34 | 2.53 | 2.80 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsheibi, A.Z.; Valavanis, K.P.; Iqbal, A.; Aman, M.N. Speech Enhancement Framework with Noise Suppression Using Block Principal Component Analysis. Acoustics 2022, 4, 441-459. https://doi.org/10.3390/acoustics4020027
Alsheibi AZ, Valavanis KP, Iqbal A, Aman MN. Speech Enhancement Framework with Noise Suppression Using Block Principal Component Analysis. Acoustics. 2022; 4(2):441-459. https://doi.org/10.3390/acoustics4020027
Chicago/Turabian StyleAlsheibi, Abdullah Zaini, Kimon P. Valavanis, Asif Iqbal, and Muhammad Naveed Aman. 2022. "Speech Enhancement Framework with Noise Suppression Using Block Principal Component Analysis" Acoustics 4, no. 2: 441-459. https://doi.org/10.3390/acoustics4020027
APA StyleAlsheibi, A. Z., Valavanis, K. P., Iqbal, A., & Aman, M. N. (2022). Speech Enhancement Framework with Noise Suppression Using Block Principal Component Analysis. Acoustics, 4(2), 441-459. https://doi.org/10.3390/acoustics4020027








