On the Incipient Indicial Lift of Thin Wings in Subsonic Flow: Acoustic Wave Theory with Unsteady Three-Dimensional Effects
Abstract
1. Introduction
2. Governing Physics: From Nonlinear Compressible to Linear Incompressible Flow
3. Incompressible Potential Flow: Lifting-Line Theory
3.1. Thin Aerofoils: Two-Dimensional Wake Inflow and Chordwise Gust Penetration
3.2. Thin Wings: Three-Dimensional Downwash Angle and Spanwise Gust Penetration
3.2.1. Elliptical Wings: Curved Taper
3.2.2. Trapezoidal Wings: Swept Taper
4. Compressible Potential Flow: Acoustic Wave Theory
4.1. Thin Aerofoils: Two-Dimensional Acoustic Waves Propagation and Chordwise Gust Penetration
4.2. Thin Wings: Three-Dimensional Downwash Angle, Spanwise Gust Penetration, and Mean Wing Section
4.2.1. Elliptical Wings: Curved Taper
4.2.2. Trapezoidal Wings: Swept Taper
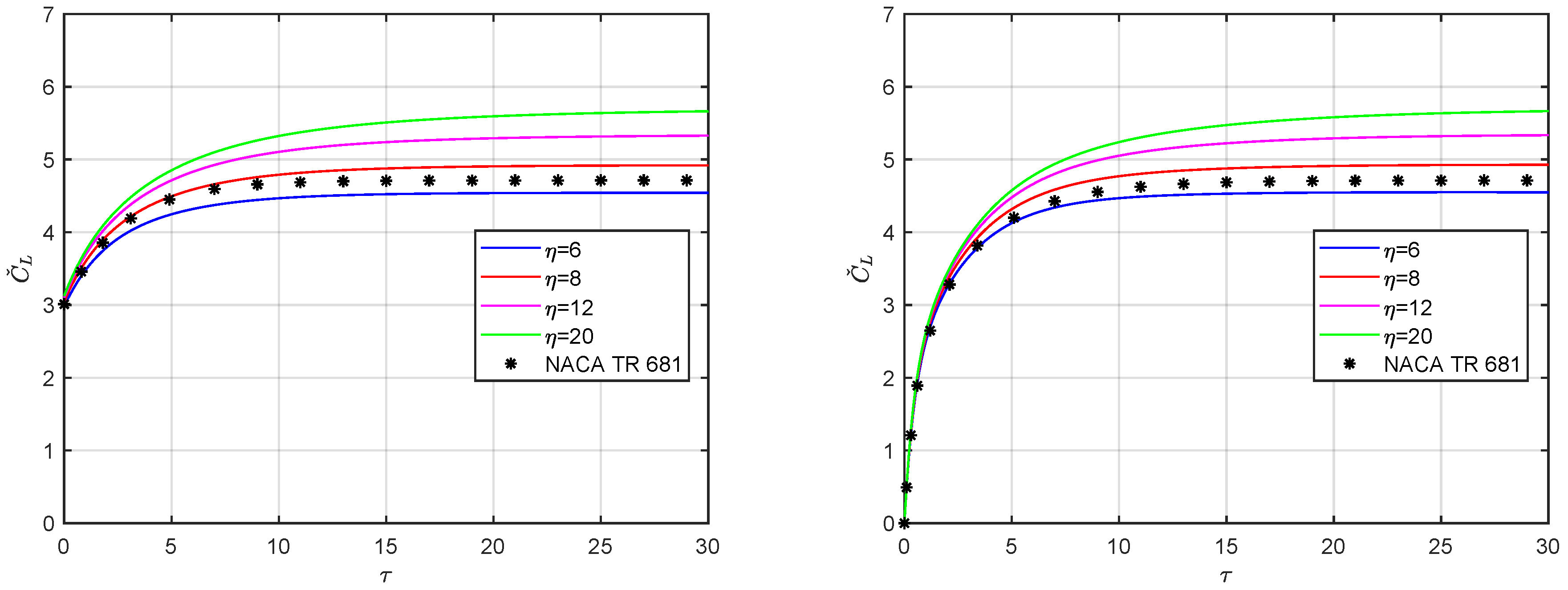
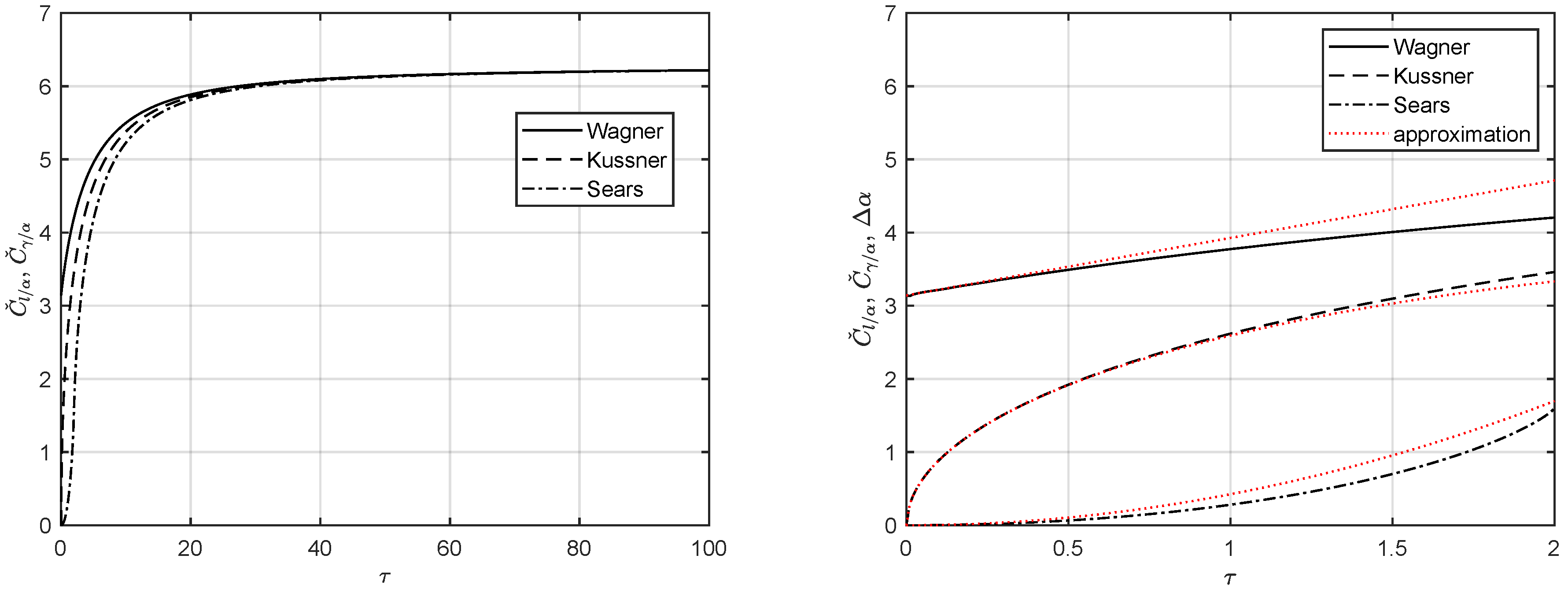
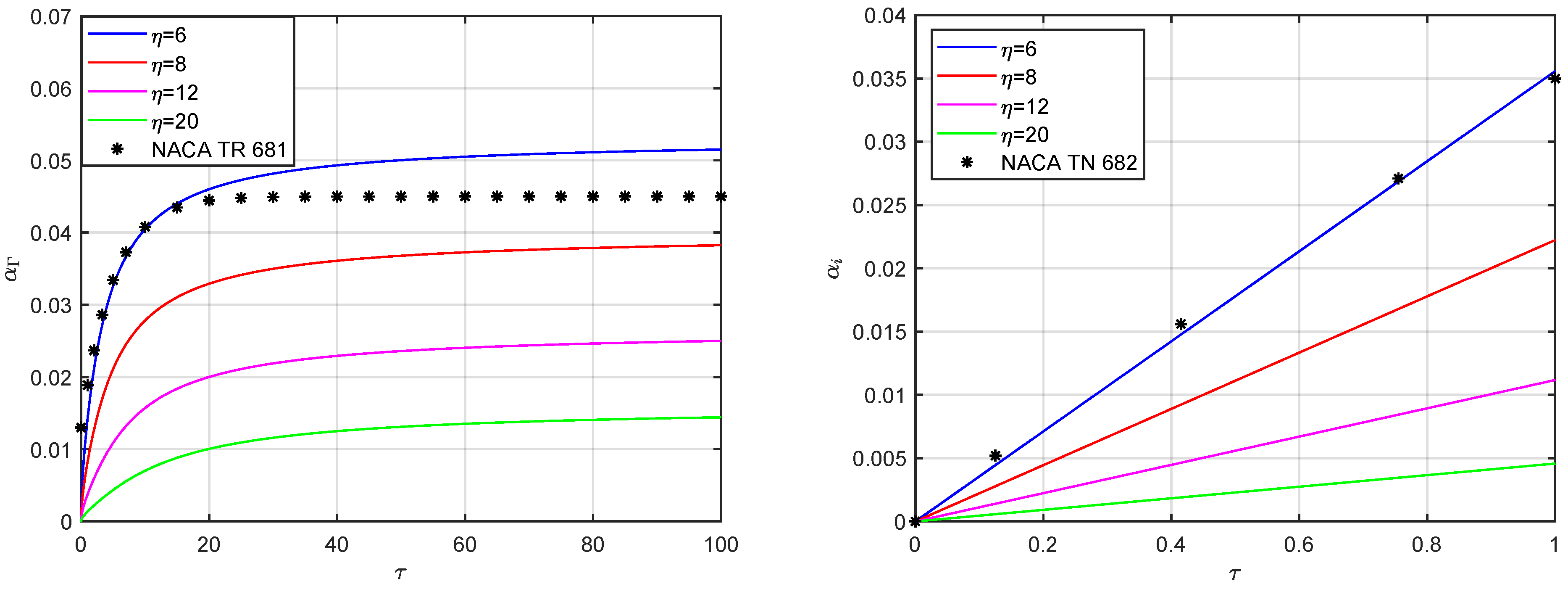
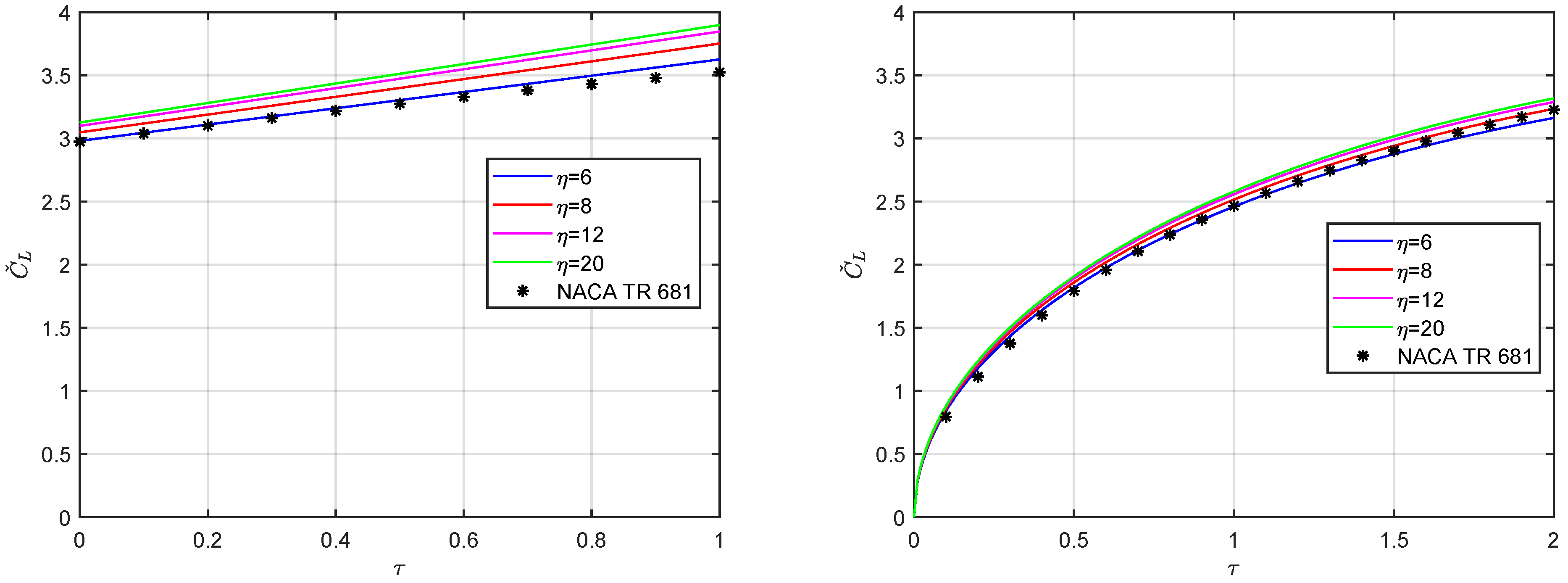
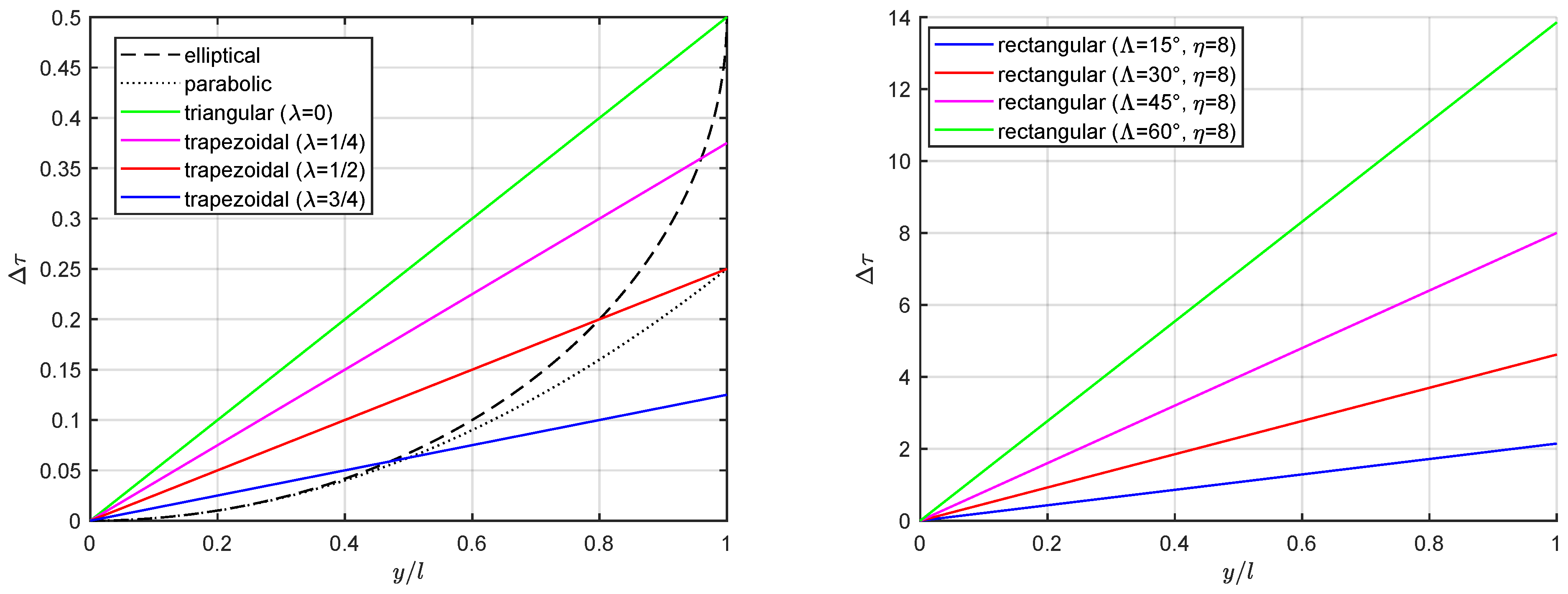
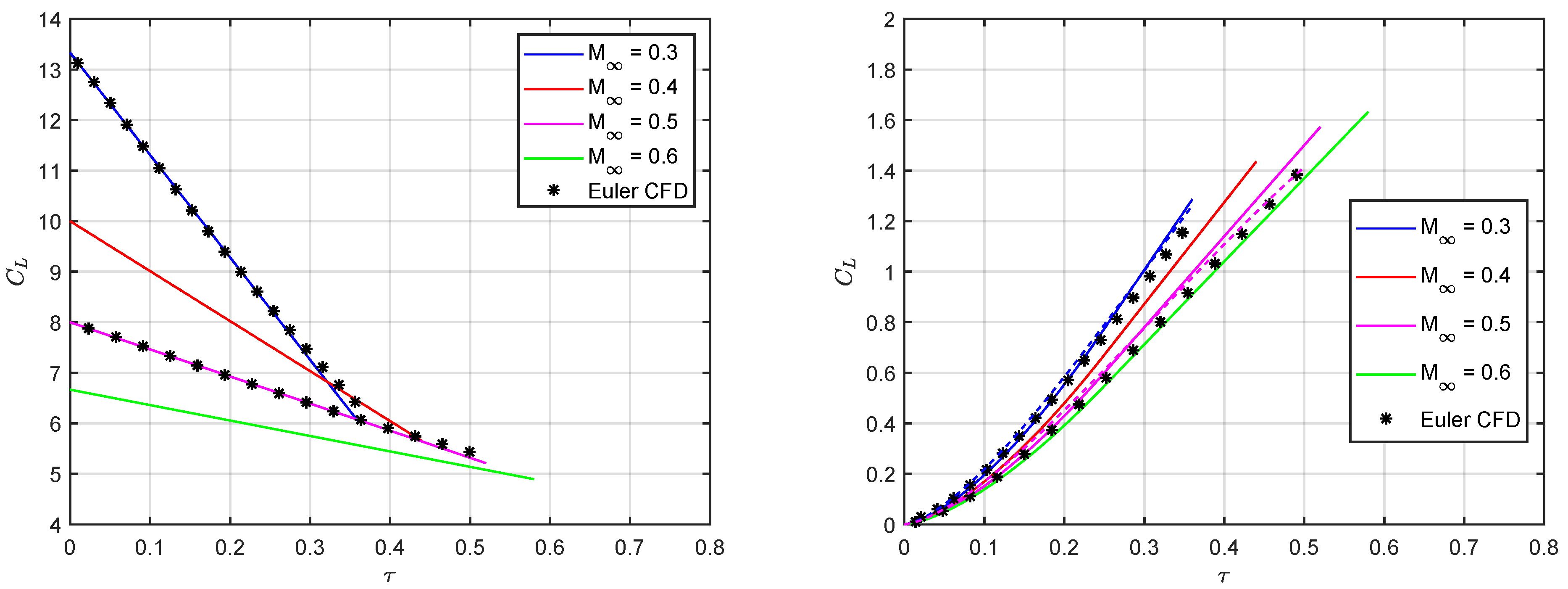
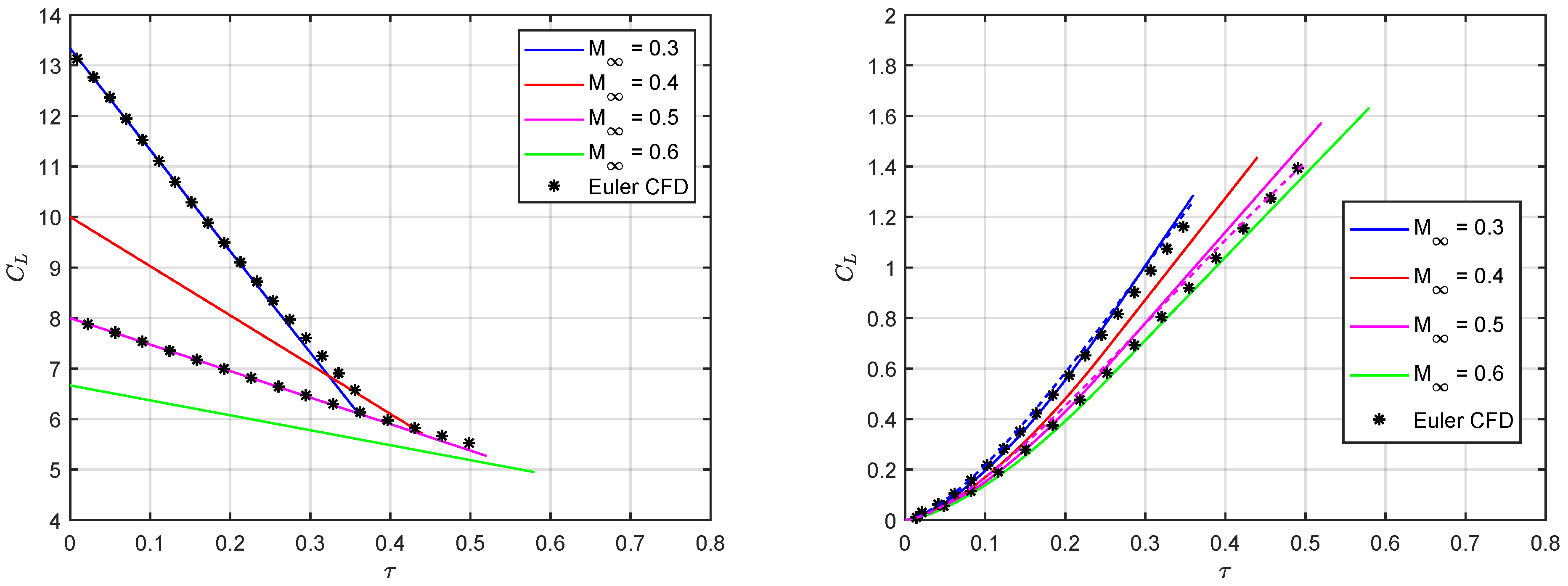
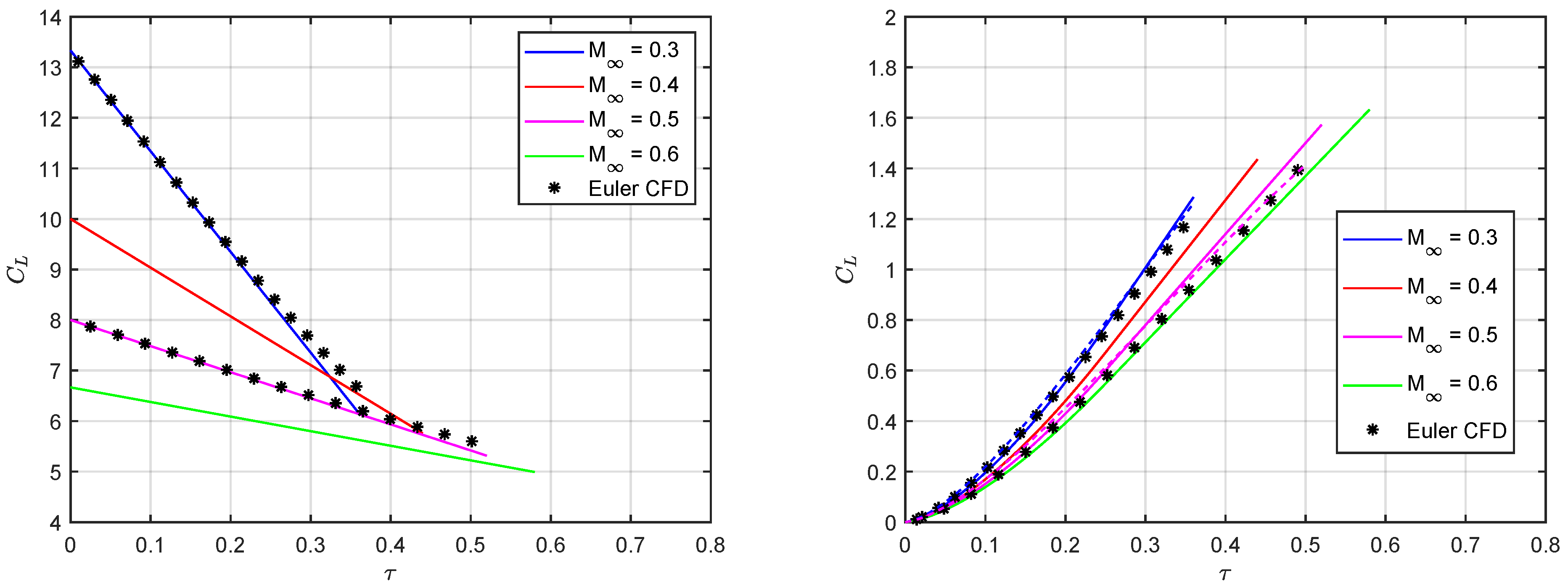
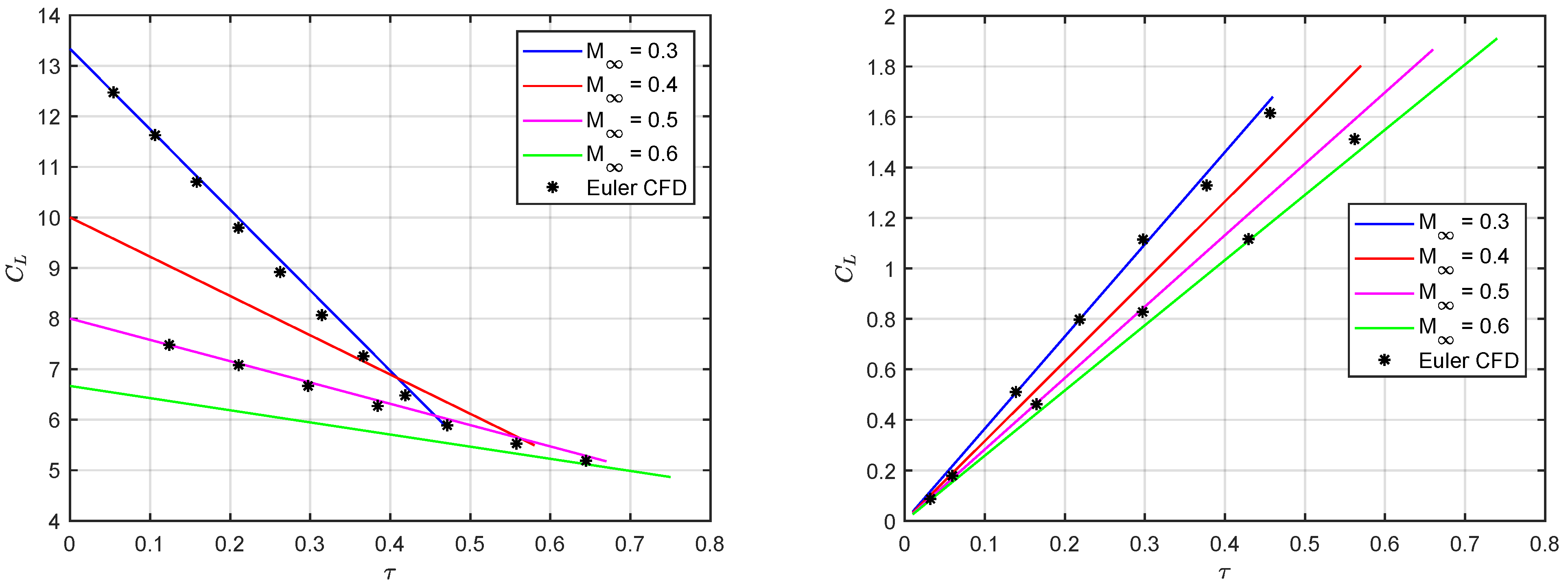
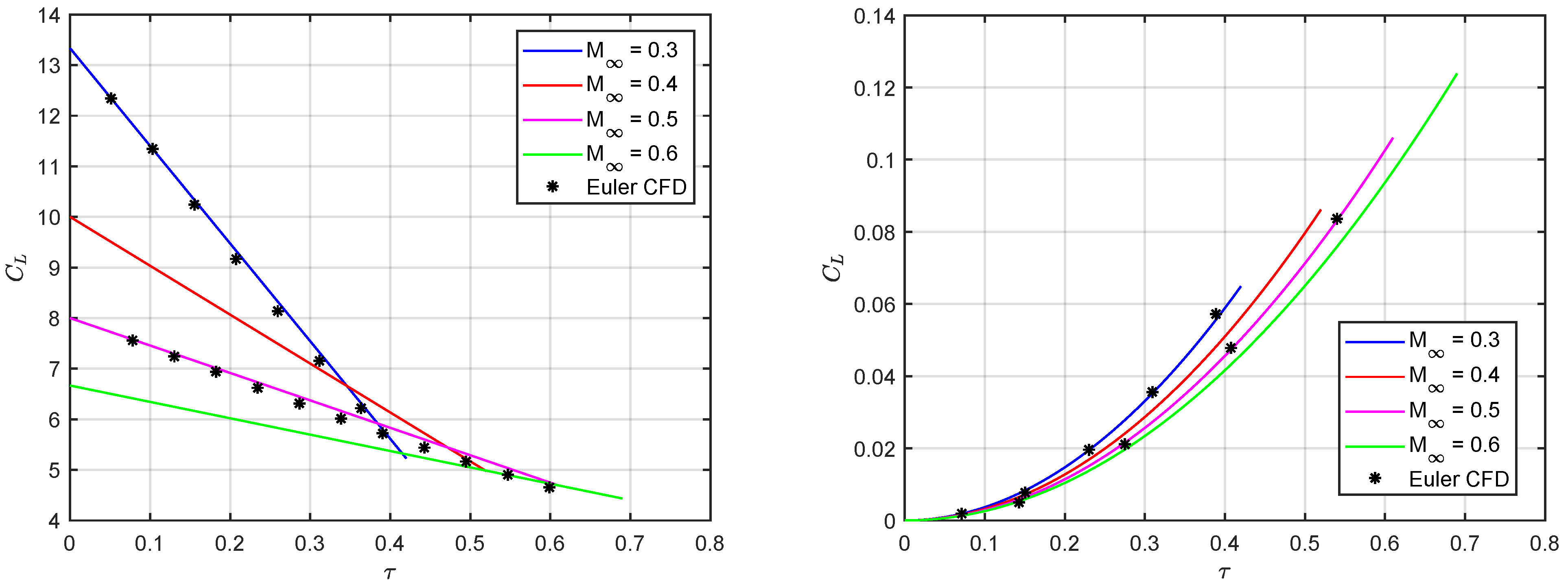
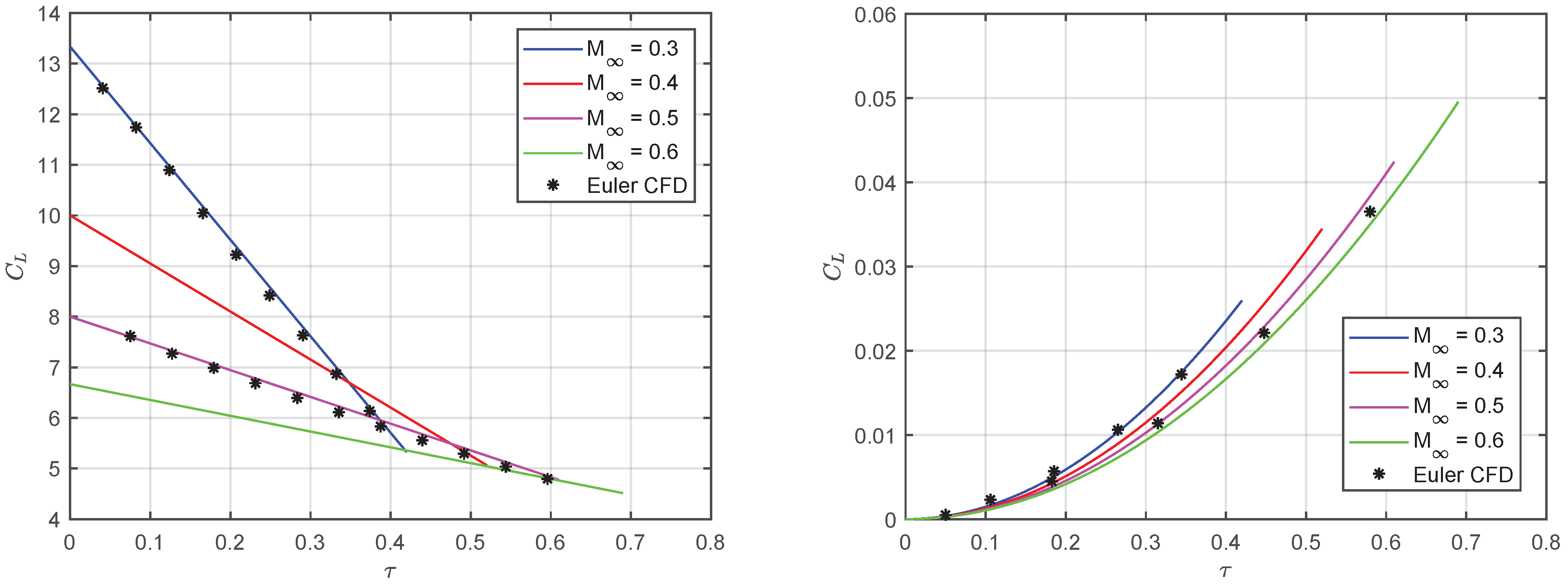
5. Results and Discussion
6. Conclusions
Funding
Conflicts of Interest
Acronyms
| AOA | Angle of Attack |
| CFD | Computational Fluid Dynamics |
| FSI | Fluid–Structure Interaction |
| MDO | Multidisciplinary Design Optimisation |
| PDE | Partial Differential Equation |
| ROM | Reduced-Order Model |
| SEG | Sharp-Edged Gust |
Symbols
| a | sound speed |
| A | wing area |
| Bessel’s functions of first type and n-th order | |
| c | wing section chord |
| isobaric heat capacity | |
| isochoric heat capacity | |
| wing section circulation coefficient | |
| wing section circulation derivative | |
| wing circulation coefficient | |
| wing circulation derivative | |
| wing section lift coefficient | |
| wing section lift derivative | |
| wing lift coefficient | |
| wing lift derivative | |
| pressure coefficient | |
| Sears’s circulation-deficiency function | |
| Sears’s lift-deficiency function | |
| Theodorsen’s lift-deficiency function | |
| e | edge-velocity factor |
| E | airflow internal energy |
| f | wing area impingement factor |
| g | downwash gradient factor |
| H | airflow enthalpy |
| Hankel’s functions of second type and n-th order | |
| I | complete elliptic integral of the second kind |
| k | reduced frequency |
| l | wing semi-span |
| M | Mach number |
| normal vector | |
| N | expansion terms |
| p | airflow pressure |
| r | mean chord ratio |
| R | gas constant |
| s | non-dimensional elliptic integral argument |
| space vector | |
| S | airflow entropy |
| t | time |
| T | airflow temperature |
| U | horizontal free-stream |
| x | chordwise coordinate |
| y | spanwise coordinate |
| z | vertical coordinate |
| Greek | |
| angle of attack | |
| airflow compressibility factor | |
| airflow disturbance potential | |
| airflow velocity potential | |
| wing aspect ratio | |
| shape factor (downwash tuning) | |
| airflow heat capacity ratio | |
| wing section circulation | |
| wing span impingement fraction | |
| wing taper ratio | |
| sweep angle | |
| airflow velocity vector | |
| spanwise angle | |
| airflow density | |
| sound-travelled distance | |
| reduced time | |
| non-dimensional wake development | |
| angular frequency | |
| airflow vorticity vector | |
| Superscripts | |
| angle of attack step | |
| gust front parallel to leading edge | |
| gust front normal to reference airspeed | |
| airflow normal to aerodynamic axis | |
| circulatory | |
| non-circulatory | |
| steady | |
| Subscripts | |
| average | |
| foremost cone | |
| gust | |
| induced | |
| leading edge | |
| root | |
| rearmost cone | |
| section | |
| tip | |
| trailing edge | |
| wing | |
| initial | |
| unperturbed | |
Appendix A
Appendix B
References
- Alexandrov, N.; Hussaini, M. Multidisciplinary Design Optimization: State of the Art; SIAM: Philadelphia, PA, USA, 1997. [Google Scholar]
- Martins, J.; Lambe, A. Multidisciplinary Design Optimization: A Survey of Architectures. AIAA J. 2013, 51, 2049–2075. [Google Scholar] [CrossRef]
- Tobak, M. On the Use of the Indicial-Function Concept in the Analysis of Unsteady Motions of Wings and Wing-Tail Combinations. In NACA-TR-1188; NACA: Washington, DC, USA, 1954. [Google Scholar]
- Lomax, H. Indicial Aerodynamics. In Manual on Aeroelasticity; AGARD-R-578-71; AGARD: London, UK, 1971. [Google Scholar]
- Quarteroni, A.; Rozza, G. Reduced Order Methods for Modeling and Computational Reduction; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Silva, W. AEROM: NASA’s Unsteady Aerodynamic and Aeroelastic Reduced-Order Modeling Software. Aerospace 2018, 5, 41. [Google Scholar] [CrossRef]
- Livne, E. Integrated Aeroservoelastic Optimization: Status and Direction. J. Aircr. 1999, 36, 122–145. [Google Scholar] [CrossRef]
- Livne, E. Future of Airplane Aeroelasticity. J. Aircr. 2003, 40, 1066–1092. [Google Scholar] [CrossRef]
- Stanford, B.K. Role of Unsteady Aerodynamics During Aeroelastic Optimization. AIAA J. 2015, 53, 3826–3831. [Google Scholar] [CrossRef]
- Katz, J.; Plotkin, A. Low Speed Aerodynamics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Anderson, J.D. Fundamentals of Aerodynamics; McGraw-Hill: New York, NY, USA, 2007. [Google Scholar]
- NOAA. U.S. Standard Atmosphere. In NOOA-S/T 76-1562; NASA: Washington, DC, USA, 1976. [Google Scholar]
- LeVeque, R.J. Numerical Methods for Conservation Laws; Springer: Basel, Switzerland, 1992. [Google Scholar]
- Karamcheti, K. Principles of Ideal-Fluid Aerodynamics; Wiley: New York, NY, USA, 1967. [Google Scholar]
- Thornhill, C.K. The Numerical Method of Characteristics for Hyperbolic Problems in Three Independent Variables. In ARC-RM-2615; ARC: London, UK, 1952. [Google Scholar]
- Lomax, H.; Heaslet, M.A. The Indicial Lift and Pitching Moment for a Sinking or Pitching Two-Dimensional Wing Flying at Subsonic or Supersonic Speeds. In NACA-TN-2403; NACA: Washington, DC, USA, 1951. [Google Scholar]
- Lomax, H.; Heaslet, M.A.; Fuller, F.D.; Sluder, L. Two- and Three-Dimensional Unsteady Lift Problems in High-Speed Flight. In NACA-TR-1077; NACA: Washington, DC, USA, 1952. [Google Scholar]
- Glauert, H. The Effect of Compressibility on the Lift of an Aerofoil. Proc. R. Soc. Lond. Ser. A 1928, 118, 113–119. [Google Scholar]
- Gothert, B.H. Plane and Three-Dimensional Flow at High Subsonic Speeds. In NACA-TM-1105; NACA: Washington, DC, USA, 1946. [Google Scholar]
- Leishman, J. Principles of Helicopter Aerodynamics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Heaslet, M.A.; Lomax, H.; Spreiter, J.R. Linearized Compressible-Flow Theory for Sonic Flight Speeds. In NACA-TR-956; NACA: Washington, DC, USA, 1950. [Google Scholar]
- Bendiksen, O.O. Review of Unsteady Transonic Aerodynamics: Theory and Applications. Prog. Aerosp. Sci. 2011, 47, 135–167. [Google Scholar] [CrossRef]
- Bisplinghoff, R.; Ashley, H.; Halfman, R. Aeroelasticity; Dover: Mineola, NY, USA, 1996. [Google Scholar]
- Bisplinghoff, R.; Ashley, H. Principles of Aeroelasticity; Dover: Mineola, NY, USA, 2013. [Google Scholar]
- Mazelsky, B. Numerical Determination of Indicial Lift of a Two-Dimensional Sinking Airfoil at Subsonic Mach Numbers from Oscillatory Lift Coefficients with Calculations for Mach Number 0.7. In NACA-TN-2562; NACA: Washington, DC, USA, 1951. [Google Scholar]
- Mazelsky, B. Determination of Indicial Lift and Moment of a Two-Dimensional Pitching Airfoil at Subsonic Mach Numbers from Oscillatory Coefficients with Numerical Calculations for a Mach Number of 0.7. In NACA-TN-2613; NACA: Washington, DC, USA, 1952. [Google Scholar]
- Mazelsky, B. Numerical Determination of Indicial Lift and Moment Functions for a Two-Dimensional Sinking and Pitching Airfoil at Mach Numbers 0.5 and 0.6. In NACA-TN-2739; NACA: Washington, DC, USA, 1952. [Google Scholar]
- Beddoes, T.S. Practical Computation of Unsteady Lift. Vertica 1984, 8, 55–71. [Google Scholar]
- Leishman, J.G. Indicial Lift Approximations for Two-Dimensional Subsonic Flow as Obtained from Oscillatory Measurements. J. Aircr. 1993, 30, 340–351. [Google Scholar] [CrossRef]
- Leishman, J.G. Subsonic Unsteady Aerodynamics Caused by Gusts Using the Indicial Method. J. Aircr. 1996, 33, 869–879. [Google Scholar] [CrossRef]
- Soviero, P.; Hernandes, F. Compressible Unsteady Vortex Lattice Method for Arbitrary Two-Dimensional Motion of Thin Profiles. J. Aircr. 2007, 44, 1494–1498. [Google Scholar] [CrossRef]
- Mateescu, D. Theoretical Solutions for Unsteady Compressible Subsonic Flows Past Oscillating Rigid and Flexible Airfoils. Math. Eng. Sci. Aerosp. 2011, 2, 1–27. [Google Scholar]
- Lomax, H. Lift Development on Unrestrained Rectangular Wings Entering Gusts at Subsonic and Supersonic Speeds. In NACA-TR-1162; NACA: Washington, DC, USA, 1953. [Google Scholar]
- Jones, W.P. Oscillating Wings in Compressible Subsonic Flow. In ARC-RM-2855; ARC: London, UK, 1957. [Google Scholar]
- Miranda, I.; Soviero, P. Indicial Response of Thin Wings in a Compressible Subsonic Flow. In Proceedings of the 18th International Congress of Mechanical Engineering, Ouro Preto, Brazil, 6–11 November 2005. [Google Scholar]
- Hernandes, F.; Soviero, P. Unsteady Aerodynamic Coefficients Obtained by a Compressible Vortex Lattice Method. J. Aircr. 2009, 46, 1291–1301. [Google Scholar] [CrossRef]
- Albano, E.; Rodden, W. A Doublet-Lattice Method for Calculating Lift Distributions on Oscillating Surfaces in Subsonic Flows. AIAA J. 1969, 7, 279–285. [Google Scholar] [CrossRef]
- Rodden, W.; Taylor, P.; McIntosh, S. Further Refinement of the Subsonic Doublet-Lattice Method. J. Aircr. 1998, 35, 720–727. [Google Scholar] [CrossRef]
- Morino, L. A General Theory of Unsteady Compressible Potential Aerodynamics. In NASA-CR-2464; NASA: Washington, DC, USA, 1974. [Google Scholar]
- Morino, L.; Chen, L.; Suciu, E. Steady and Oscillatory Subsonic and Supersonic Aerodynamics around Complex Configurations. AIAA J. 1975, 13, 368–374. [Google Scholar] [CrossRef]
- Bindolino, G.; Mantegazza, P. Improvements on a Green’s Function Method for the Solution of Linearized Unsteady Potential Flows. J. Aircr. 1987, 24, 355–361. [Google Scholar] [CrossRef]
- Marzocca, P.; Librescu, L.; Kim, D.H.; Lee, I.; Schober, S. Development of an Indicial Function Approach for the Two-Dimensional Incompressible/Compressible Aerodynamic Load Modelling. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2007, 221, 453–463. [Google Scholar] [CrossRef]
- Chung, T. Computational Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Parameswaran, V.; Baeder, J.D. Indicial Aerodynamics in Compressible Flow-Direct Computational Fluid Dynamic Calculations. J. Aircr. 1997, 34, 131–133. [Google Scholar] [CrossRef]
- Raveh, D.E. Reduced-Order Models for Nonlinear Unsteady Aerodynamics. AIAA J. 2001, 39, 1417–1429. [Google Scholar] [CrossRef]
- Gennaretti, M.; Mastroddi, F. Study of Reduced-Order Models for Gust-Response Analysis of Flexible Fixed Wings. J. Aircr. 2004, 41, 304–313. [Google Scholar] [CrossRef]
- Ghoreyshi, M.; Jirasek, A.; Cummings, R. Computational Investigation into the Use of Response Functions for Aerodynamic-Load Modeling. AIAA J. 2012, 50, 1314–1327. [Google Scholar] [CrossRef]
- Ghoreyshi, M.; Jirasek, A.; Cummings, R. Reduced Order Unsteady Aerodynamic Modeling for Stability and Control Analysis Using Computational Fluid Dynamics. Prog. Aerosp. Sci. 2014, 71, 167–217. [Google Scholar] [CrossRef]
- Farhat, C.; Lesoinne, M.; LeTallec, P. Load and Motion Transfer Algorithms for Fluid/Structure Interaction Problems with Non-Matching Discrete Interfaces: Momentum and Energy Conservation, Optimal Discretization and Application to Aeroelasticity. Comput. Methods Appl. Mech. Eng. 1998, 157, 95–114. [Google Scholar] [CrossRef]
- Cizmas, P.; Gargoloff, J. Mesh Generation and Deformation Algorithm for Aeroelasticity Simulations. J. Aircr. 2008, 45, 1062–1066. [Google Scholar] [CrossRef]
- Berci, M.; Cavallaro, R. A Hybrid Reduced-Order Model for the Aeroelastic Analysis of Flexible Subsonic Wings—A Parametric Assessment. Aerospace 2018, 5, 76. [Google Scholar] [CrossRef]
- Berci, M.; Torrigiani, F. A Multifidelity Sensitivity Study of Subsonic Wing Flutter for Hybrid Approaches in Aircraft Multidisciplinary Design and Optimisation. Aerospace 2020, 7, 161. [Google Scholar] [CrossRef]
- Berci, M.; Gaskell, P.H.; Hewson, R.W.; Toropov, V.V. Multifidelity Metamodel Building as a Route to Aeroelastic Optimization of Flexible Wings. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 2115–2137. [Google Scholar] [CrossRef]
- Berci, M.; Toropov, V.V.; Hewson, R.W.; Gaskell, P.H. Multidisciplinary Multifidelity Optimisation of a Flexible Wing Aerofoil with Reference to a Small UAV. Struct. Multidiscip. Optim. 2014, 50, 683–699. [Google Scholar] [CrossRef]
- Wieseman, C.D. Methodology for Matching Experimental and Computational Aerodynamic Data. In NASA-TM-100592; NASA: Washington, DC, USA, 1988. [Google Scholar]
- Brink-Spalink, J.; Bruns, J.M. Correction of Unsteady Aerodynamic Influence Coefficients Using Experimental or CFD Data. In Proceedings of the 41st Structures, Structural Dynamics, and Materials Conference and Exhibit, Atlanta, GA, USA, 3–6 April 2000. [Google Scholar]
- Sucipto, T.; Berci, M.; Krier, J. Gust Response of a Flexible Typical Section via High- and (Tuned) Low-Fidelity Simulations. Comput. Struct. 2013, 122, 202–216. [Google Scholar] [CrossRef]
- Berci, M.; Mascetti, S.; Incognito, A.; Gaskell, P.H.; Toropov, V.V. Dynamic Response of Typical Section Using Variable-Fidelity Fluid Dynamics and Gust-Modeling Approaches - with Correction Methods. J. Aerosp. Eng. 2014, 27, 1–20. [Google Scholar] [CrossRef]
- Whitham, G. Linear and Nonlinear Waves; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Jones, R.T. Classical Aerodynamic Theory. In NASA-RP-1050; NASA: Washington, DC, USA, 1979. [Google Scholar]
- Gulcat, U. Fundamentals of Modern Unsteady Aerodynamics; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Dowell, E. A Modern Course in Aeroelasticity; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Wright, J.; Cooper, J. Introduction to Aircraft Aeroelasticity and Loads; Wiley: Chichester, UK, 2014. [Google Scholar]
- Berci, M.; Righi, M. An Enhanced Analytical Method for the Subsonic Indicial Lift of Two-Dimensional Aerofoils—With Numerical Cross-Validation. Aerosp. Sci. Technol. 2017, 67, 354–365. [Google Scholar] [CrossRef]
- Righi, M.; Berci, M. On Elliptical Wings in Subsonic Flow: Indicial Lift Generation via CFD Simulations-with Parametric Analytical Approximations. ASD J. 2019, 7, 1–17. [Google Scholar]
- Da Ronch, A.; Ventura, A.; Righi, M.; Franciolini, M.; Berci, M.; Kharlamov, D. Extension of Analytical Indicial Aerodynamics to Generic Trapezoidal Wings in Subsonic Flow. Chin. J. Aeronaut. 2018, 31, 617–631. [Google Scholar] [CrossRef]
- Ames Research Staff. Equations, Tables and Charts for Compressible Flow. In NACA-TR-1135; NASA: Washington, DC, USA, 1953. [Google Scholar]
- Liepmann, H.W.; Roshko, A. Elements of Gasdynamics; Dover: Mineola, NY, USA, 2001. [Google Scholar]
- Bungartz, H.; Schafer, M. Fluid-Structure Interaction: Modelling, Simulation, Optimization; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Basu, B.C.; Hancock, G.J. The Unsteady Motion of a Two-Dimensional Aerofoil in Incompressible Inviscid Flow. J. Fluid Mech. 1978, 87, 159–178. [Google Scholar] [CrossRef]
- Hoblit, F.M. Gust Loads on Aircraft: Concepts and Applications; AIAA: Reston, VA, USA, 1988. [Google Scholar]
- Berci, M.; Vigevano, L. Sonic Boom Propagation Revisited: A Nonlinear Geometrical Acoustic Model. Aerosp. Sci. Technol. 2012, 23, 280–295. [Google Scholar] [CrossRef]
- Kussner, H.G. General Airfoil Theory. In NACA-TM-979; NACA: Washington, DC, USA, 1941. [Google Scholar]
- Reissner, E. On the General Theory of Thin Airfoil for Nonuniform Motion. In NACA-TN-946; NACA: Washington, DC, USA, 1944. [Google Scholar]
- Multhopp, H. Methods for Calculating the Lift Distribution of Wings (Subsonic Lifting-Surface Theory). In ARC-RM-2884; ARC: London, UK, 1950. [Google Scholar]
- Prandtl, L. Applications of Modern Hydrodynamics to Aeronautics. In NACA-TR-116; NASA: Washington, DC, USA, 1921. [Google Scholar]
- Peters, D.A. Two-Dimensional Incompressible Unsteady Airfoil Theory—An Overview. J. Fluids Struct. 2008, 24, 295–312. [Google Scholar] [CrossRef]
- Glauert, H. The Elements of Aerofoil and Airscrew Theory; Cambridge University Press: Cambridge, UK, 1926. [Google Scholar]
- Ahmadi, A.R.; Widnall, S.E. Unsteady Lifting-Line Theory as a Singular-Perturbation Problem. J. Fluid Mech. 1985, 153, 59–81. [Google Scholar] [CrossRef]
- Sclavounos, P.D. An Unsteady Lifting-Line Theory. J. Eng. Math. 1987, 21, 201–226. [Google Scholar] [CrossRef]
- Guermond, J.L.; Sellier, A. A Unified Unsteady Lifting-Line Theory. J. Fluid Mech. 1991, 229, 427–451. [Google Scholar] [CrossRef]
- Kutta, W.M. Auftriebskräfte in Strömenden Flüssigkeiten. Illus. Aeronaut. Mitt. 1902, 6, 133–135. [Google Scholar]
- Joukowski, N.E. Sur les Tourbillons Adjionts. Traraux Sect. Phys. Soc. Imp. Amis Sci. Nat. 1906, 13, 261–284. [Google Scholar]
- Newman, J.N. Marine Hydrodynamics; MIT Press: Cambridge, MA, USA, 1977. [Google Scholar]
- Jones, R.T. The Unsteady Lift of a Finite Wing. In NACA-TN-682; NACA: Washington, DC, USA, 1939. [Google Scholar]
- Jones, R.T. The Unsteady Lift of a Wing of Finite Aspect Ratio. In NACA-TR-681; NACA: Washington, DC, USA, 1940. [Google Scholar]
- Jones, R.T. Correction of the Lifting-Line Theory for the Effect of the Chord. In NACA-TN-817; NACA: Washington, DC, USA, 1941. [Google Scholar]
- Epps, B.P.; Roesler, B.T. Vortex Sheet Strength in the Sears, Küssner, Theodorsen, and Wagner Aerodynamics Problems. AIAA J. 2018, 56, 889–904. [Google Scholar] [CrossRef]
- Berci, M. On Aerodynamic Models for Flutter Analysis: A Systematic Overview and Comparative Assessment. Appl. Mech. 2021, 2, 29. [Google Scholar] [CrossRef]
- Berci, M. Lift-Deficiency Functions of Elliptical Wings in Incompressible Potential Flow: Jones’ Theory Revisited. J. Aircr. 2016, 53, 599–602, Erratum in 2017, 54, 1–2. [Google Scholar] [CrossRef]
- Wood, K.D. Aspect Ratio Corrections. J. Aeronaut. Sci. 1943, 10, 270–272. [Google Scholar] [CrossRef]
- Jones, R.T. Operational Treatment of the Nonuniform-Lift Theory in Airplane Dynamics. In NACA-TN-667; NACA: Washington, DC, USA, 1938. [Google Scholar]
- Sears, W.R. Operational Methods in the Theory of Airfoils in Non-Uniform Motion. J. Frankl. Inst. 1940, 230, 95–111. [Google Scholar] [CrossRef]
- Quarteroni, A.; Sacco, R.; Saleri, F. Numerical Mathematics; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Fung, Y. An Introduction to the Theory of Aeroelasticity; Dover: Mineola, NY, USA, 1993. [Google Scholar]
- Dimitriadis, G. Introduction to Nonlinear Aeroelasticity; Wiley: Chichester, UK, 2017. [Google Scholar]
- Jones, W.P. Theoretical Determination of the Aerodynamic Inertias of an Elliptic Plate in Still Air. In ARC-RM-1953; ARC: London, UK, 1942. [Google Scholar]
- Jones, W.P. Aerodynamic Forces on Wings in Non-Uniform Motion. In ARC-RM-2117; ARC: London, UK, 1945. [Google Scholar]
- Dore, B.D. The Unsteady Forces on Finite Wings in Transient Motion. In ARC-RM-3456; ARC: London, UK, 1964. [Google Scholar]
- James, E.C. Lifting-Line Theory for an Unsteady Wing as a Singular Perturbation Problem. J. Fluid Mech. 1975, 70, 753. [Google Scholar] [CrossRef]
- Queijo, M.J.; Wells, W.R.; Keskar, D.A. Approximate Indicial Lift Function for Tapered, Swept Wings in Incompressible Flow. In NACA-TP-1241; NASA: Washington, DC, USA, 1978. [Google Scholar]
- Devinant, P. An Approach for Unsteady Lifting-Line Time-Marching Numerical Computation. Int. J. Numer. Methods Fluids 1998, 26, 177–197. [Google Scholar] [CrossRef]
- Devinant, P.; Gallois, T. Swept and Curved Wings: A Numerical Approach based on Generalized Lifting-Line Theory. Comput. Mech. 2002, 29, 322–331. [Google Scholar] [CrossRef]
- Sugar-Gabor, O. A General Numerical Unsteady Non-Linear Lifting-Line Model for Engineering Aerodynamics Studies. Aeronaut. J. 1998, 122, 1199–1228. [Google Scholar] [CrossRef]
- Boutet, J.; Dimitriadis, G. Unsteady Lifting Line Theory Using the Wagner Function for the Aerodynamic and Aeroelastic Modeling of 3D Wings. Aerospace 2018, 5, 92. [Google Scholar] [CrossRef]
- Bird, H.J.A.; Ramesh, K. Unsteady Lifting-Line Theory and the Influence of Wake Vorticity on Aerodynamic Loads. Theor. Comput. Fluid Dyn. 2021, 35, 609–631. [Google Scholar] [CrossRef]
- Cicala, P. Comparison of Theory with Experiment in the Phenomenon of Wing Flutter. In NACA-TM-887; NACA: Washington, DC, USA, 1939. [Google Scholar]
- Jones, W.P.; Skan, S.W. Calculations of Derivatives for Rectangular Wings of Finite Span by Cicala’s Method. In ARC-RM-1920; ARC: London, UK, 1940. [Google Scholar]
- Jones, W.P. The Virtual Inertias of a Tapered Wing in Still Air. In ARC-RM-1946; ARC: London, UK, 1941. [Google Scholar]
- Jones, W.P. Calculation of Additional Mass and Inertia Coefficients for Rectangular Plates in Still Air. In ARC-RM-1947; ARC: London, UK, 1941. [Google Scholar]
- Jones, W.P. Theoretical Air-Load and Derivative Coefficients for Rectangular Wings. In ARC-RM-2142; ARC: London, UK, 1943. [Google Scholar]
- Jones, W.P. Aerodynamic Forces on Wings in Simple Harmonic Motion. In ARC-RM-2026; ARC: London, UK, 1945. [Google Scholar]
- Schade, T.; Krienes, K. The Oscillating Circular Airfoil on the Basis of Potential Theory. In NACA-TM-1098; NACA: Washington, DC, USA, 1947. [Google Scholar]
- Reissner, E. Effect of Finite Span on the Airload Distributions for Oscillating Wings I: Aerodynamic Theory of Oscillating Wings of Finite Span. In NACA-TN-1194; NACA: Washington, DC, USA, 1947. [Google Scholar]
- Reissner, E. Effect of Finite Span on the Airload Distributions for Oscillating Wings II: Methods of Calculation and Examples of Application. In NACA-TN-1195; NACA: Washington, DC, USA, 1947. [Google Scholar]
- Kochin, N.E. Steady Vibrations of Wing of Circular Planform. In NACA-TM-1324; NACA: Washington, DC, USA, 1953. [Google Scholar]
- Lehrian, D.E. Calculation of Stability Derivatives Oscillating Wings. In ARC-RM-2922; ARC: London, UK, 1953. [Google Scholar]
- Watkins, C.E.; Runyan, H.L.; Woolston, D.S. On the Kernel Function of the Integral Equation Relating the Lift and Downwash Distribution of Oscillating Finite Wings in Subsonic Flow. In NACA-TN-3131; NACA: Washington, DC, USA, 1954. [Google Scholar]
- Watkins, C.E.; Runyan, H.L.; Woolston, D.S. On the Kernel Function of the Integral Equation Relating the Lift and Downwash Distribution of Oscillating Finite Wings in Subsonic Flow. In NACA-TR-1234; NACA: Washington, DC, USA, 1955. [Google Scholar]
- Lehrian, D.E. Initial Lift of Finite Aspect-Ratio Wings due to a Sudden Change of Incidence. In ARC-RM-3023; ARC: London, UK, 1955. [Google Scholar]
- Lehrian, D.E. Calculating Derivatives for Rectangular Wings Oscillating in Compressible Subsonic Flow. In ARC-RM-3068; ARC: London, UK, 1956. [Google Scholar]
- Drischler, J.A. Approximate Indicial Lift Functions for Several Wings of Finite Span in Incompressible Flow as Obtained from Oscillatory Lift Coefficients. In NACA-TN-3639; NACA: Washington, DC, USA, 1956. [Google Scholar]
- Carson, Y.E. Calculation of Flutter Characteristics for Finite Span Swept or Unswept Wings at Subsonic and Supersonic Speeds by a Modified Strip Analysis. In NACA-RM-L57L10; NACA: Washington, DC, USA, 1958. [Google Scholar]
- Watkins, C.E.; Woolston, D.S.; Cunningham, H.J. A Systematic Kernel Function Procedure for Determining Aerodynamic Forces on Oscillating or Steady Finite Wings at Subsonic Speeds. In NACA-TR-R-48; NACA: Washington, DC, USA, 1960. [Google Scholar]
- Acum, W.E.A.; Garner, H.C. The Estimation of Oscillatory Wing and Control Derivatives. In ARC-CP-623; ARC: London, UK, 1964. [Google Scholar]
- Hauptman, A.; Miloh, T. Aerodynamic Coefficients of a Thin Elliptic Wing in Unsteady Motion. AIAA J. 1987, 25, 769–774. [Google Scholar] [CrossRef]
- Chiocchia, G.; Tordella, D.; Prössdorf, S. The Lifting Line Equation for a Curved Wing in Oscillatory Motion. ZAMM-J. Appl. Math. Mech. 1997, 77, 295–315. [Google Scholar] [CrossRef]
- Rodden, W. Theoretical and Computational Aeroelasticity; Crest Publishing: Los Angeles, CA, USA, 2011. [Google Scholar]
- Richardson, J.R. A Method for Calculating the Lifting Forces on Wings (Unsteady Subsonic and Supersonic Lifting Surface Theory). In ARC-RM-3157; ARC: London, UK, 1955. [Google Scholar]
- Van Holten, T. Some Notes on Unsteady Lifting-Line Theory. J. Fluid Mech. 1976, 77, 561. [Google Scholar] [CrossRef]
- Wagner, H. Uber die Entstehung des Dynamischen Auftriebes von Tragflugeln. ZAMM-J. Appl. Math. Mech. 1925, 5, 17–35. [Google Scholar] [CrossRef]
- Kussner, H.G. Zusammenfassender Bericht uber den Instationaren Auftrieb von Flugeln. Luftfahrtforschung 1936, 13, 410–424. [Google Scholar]
- Theodorsen, T. General Theory of Aerodynamic Instability and the Mechanism of Flutter. In NACA-TR-496; NACA: Washington, DC, USA, 1935. [Google Scholar]
- Von Karman, T.; Sears, W.R. Airfoil Theory for Non-Uniform Motion. J. Aeronaut. Sci. 1938, 5, 379–390. [Google Scholar] [CrossRef]
- Sears, W.R.; Kuethe, A.M. The Growth of the Circulation of an Airfoil Flying through a Gust. J. Aeronaut. Sci. 1939, 6, 376–378. [Google Scholar] [CrossRef]
- Garrick, L.E. On some Reciprocal Relations in the Theory of Nonstationary Flows. In NACA-TR-629; NACA: Washington, DC, USA, 1938. [Google Scholar]
- Heaslet, M.A.; Spreiter, J.R. Reciprocity Relations in Aerodynamics. In NACA-TR-1119; NACA: Washington, DC, USA, 1953. [Google Scholar]
- Weissinger, J. The Lift Distribution of Swept-Back Wings. In NACA-TM-1120; NACA: Washington, DC, USA, 1947. [Google Scholar]
- Peirce, B.O. A Short Table of Integrals; Ginn and Company: Boston, MA, USA, 1929. [Google Scholar]
- Diederich, F. A Plan-Form Parameter for Correlating Certain Aerodynamic Characteristics of Swept Wings. In NACA-TN-2335; NACA: Washington, DC, USA, 1951. [Google Scholar]
- Laitone, E.V. Lift-Curve Slope for Finite-Aspect-Ratio Wings. J. Aircr. 1989, 26, 789–790. [Google Scholar] [CrossRef]
- Kida, T. An Asymptotic Expression of Lift Slope of Elliptic Wing with High Aspect Ratio. ZAMM-J. Appl. Math. Mech. 1982, 62, 491–493. [Google Scholar] [CrossRef]
- Hauptman, A. Exact and Asymptotic Expressions of the Lift Slope Coefficient of an Elliptical Wing. AIAA J. 1987, 25, 1261–1262. [Google Scholar] [CrossRef]
- Hodges, D.H.; Pierce, G.A. Introduction to Structural Dynamics and Aeroelasticity; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Berci, M. Semi-Analytical Static Aeroelastic Analysis and Response of Flexible Subsonic Wings. Appl. Math. Comput. 2015, 267, 148–169. [Google Scholar] [CrossRef]
- Possio, C. L’Azione Aerodinamica sul Profilo Oscillante in un Fluido Compressibile a Velocità Iposonora. L’Aerotecnica 1938, 18, 441–458. [Google Scholar]
- Frazer, R. Possio’s Subsonic Derivative Theory and its Application to Flexural-Torsional Wing Flutter. In ARC-RM-2553; ARC: London, UK, 1951. [Google Scholar]
- Timman, R.A.; Van de Vooren, I.; Greidanus, J.H. Aerodynamics Coefficients of an Oscillating Airfoil in Two-Dimensional Subsonic Flow. J. Aeronaut. Sci. 1951, 18, 797–802. [Google Scholar] [CrossRef]
- Reissner, E. On the Application of Mathieu Functions in the Theory of Subsonic Compressible Flow Past Oscillating Airfoils. In NACA-TN-2363; NACA: Washington, DC, USA, 1951. [Google Scholar]
- Balakrishnan, A.V. Unsteady Aerodynamics - Subsonic Compressible Inviscid Case. In NASA-CR-1999-206583; NASA: Washington, DC, USA, 1999. [Google Scholar]
- Lin, J.; Iliff, K.W. Aerodynamic Lift and Moment Calculations Using a Closed-Form Solution of the Possio Equation. In NASA-TM-2000-209019; NASA: Washington, DC, USA, 2000. [Google Scholar]
- Balakrishnan, A. Possio Integral Equation of Aeroelasticity Theory. J. Aerosp. Eng. 2003, 16, 139–154. [Google Scholar] [CrossRef]
- Polyakov, P.L. Solvability of the Generalized Possio Equation in 2D Subsonic Aeroelasticity. Comput. Methods Funct. Theory 2007, 7, 55–76. [Google Scholar] [CrossRef]
- Tewari, A. Adaptive Aeroservoelastic Control; Wiley: Chichester, UK, 2016. [Google Scholar]
- Abbott, I.; von Doenhoff, A. Theory of Wing Sections: Including a Summary of Aerofoil Data; Dover: New York, NY, USA, 1945. [Google Scholar]
- Jordan, P.F. Exact Solutions for Lifting Surfaces. AIAA J. 1973, 11, 1123–1129. [Google Scholar] [CrossRef]
- Kellaway, W. A Lifting Surface Theory Method for Treating Swept or Slender Wings in Attached Subsonic Flow. In ARC-RM-3760; ARC: London, UK, 1973. [Google Scholar]
- Medan, R.T. Steady, Subsonic, Lifting Surface Theory For Wings With Swept, Partial Span, Trailing Edge Control Surfaces. In NASA-TN-D-7251; NASA: Washington, DC, USA, 1973. [Google Scholar]
- Medan, R.T. Improvements to the Kernel Function Method of Steady, Subsonic Lifting Surface Theory. In NASA-TM-X-62327; NASA: Washington, DC, USA, 1974. [Google Scholar]
- Helmbold, H.B. Der Unverwundene Ellipsenflügel als Tragende Fläche. Jahrbuch der Deutschen Luftfahrtforschung 1942, I, 111–113. [Google Scholar]
- Vanderplaats, G. Numerical Optimization Techniques for Engineering Design: With Applications; McGraw Hill: New York, NY, USA, 1984. [Google Scholar]
- Kida, T. A Theoretical Treatment of Lifting Surface Theory of an Elliptic Wing. ZAMM-J. Appl. Math. Mech. 1980, 60, 645–651. [Google Scholar] [CrossRef]
- Hauptman, A.; Miloh, T. On the Exact Solution of the Linearized Lifting-Surface Problem of an Elliptic Wing. Q. J. Mech. Appl. Math. 1986, 39, 41–66. [Google Scholar] [CrossRef]
- Theodorsen, T. Theory of Wing Sections of Arbitrary Shape. In NACA-TR-411; NACA: Washington, DC, USA, 1931. [Google Scholar]
- Schrenk, O. A Simple Approximation Method for Obtaining the Spanwise Lift Distribution. In NACA-TM-948; NACA: Washington, DC, USA, 1940. [Google Scholar]
- Falkner, H.C. The Calculation of Aerodynamic Loading on Surfaces of Any Shape. In ARC-RM-1910; ARC: London, UK, 1943. [Google Scholar]
- Jones, W.P. Theoretical Determination of the Pressure Distribution on a Finite Wing in Steady Motion. In ARC-RM-2145; ARC: London, UK, 1943. [Google Scholar]
- Swanson, R.S.; Crandall, S.M. Lifting-Surface-Theory Aspect-Ratio Corrections to the Lift and Hinge-Moment Parameters for Full-Span Elevators on Horizontal Tail Surfaces. In NACA-TN-1175; NACA: Washington, DC, USA, 1947. [Google Scholar]
- Garner, H.C. Methods of Approaching an Accurate Three-Dimensional Potential Solution for a Wing. In ARC-RM-2721; ARC: London, UK, 1948. [Google Scholar]
- Hancock, G.J. Method for the Determination of the Pressure Distribution over a Finite Thin Wing at a Steady Low Speed. In ARC-CP-128; ARC: London, UK, 1953. [Google Scholar]
- Van Dyke, M. Lifting-Line Theory as a Singular-Perturbation Problem. J. Appl. Math. Mech. 1964, 28, 90–102. [Google Scholar] [CrossRef]
- Kida, T.; Miyai, Y. An Alternative Treatment of Lifting-Line Theory as a Perturbation Problem. Z. Angew. Math. Phys. 1978, 29, 591–607. [Google Scholar] [CrossRef]
- Guermond, J.L. A Generalized Lifting-Line Theory for Curved and Swept Wings. J. Fluid Mech. 1990, 211, 497–513. [Google Scholar] [CrossRef]
- Prossdorf, S.; Tordella, D. On an Extension of Prandtl’s Lifting-Line Theory to Curved Wings. IMPACT Comput. Sci. Eng. 1991, 3, 192–212. [Google Scholar] [CrossRef]
- Rasmussen, M.; Smith, D. Lifting-Line Theory for Arbitrarily Shaped Wings. J. Aircr. 1999, 36, 340–348. [Google Scholar] [CrossRef]
- Phillips, W.; Snyder, D. Modern Adaptation of Prandtl’s Classic Lifting-Line Theory. J. Aircr. 2000, 37, 662–670. [Google Scholar] [CrossRef]
- Phillips, W.; Hunsaker, D.F.; Niewoehner, R.J. Estimating the Subsonic Aerodynamic Center and Moment Components for Swept Wings. J. Aircr. 2008, 45, 1033–1043. [Google Scholar] [CrossRef][Green Version]
- Phillips, W.; Hunsaker, D.F. Lifting-Line Predictions for Induced Drag and Lift in Ground Effect. J. Aircr. 2013, 50, 1226–1233. [Google Scholar] [CrossRef]
- Caprace, D.G.; Chatelain, P.; Winckelmans, G. Lifting Line with Various Mollifications: Theory and Application to an Elliptical Wing. AIAA J. 2019, 57, 17–28. [Google Scholar] [CrossRef]
- Reid, J.T.; Hunsaker, D.F. General Approach to Lifting-Line Theory, Applied to Wings with Sweep. J. Aircr. 2021, 58, 334–346. [Google Scholar] [CrossRef]
- Stewartson, K. A Note on Lifting Line Theory. Q. J. Mech. Appl. Math. 1960, 13, 49–56. [Google Scholar] [CrossRef]
- Glauert, H. The Force and Moment on an Oscillating Aerofoil. In ARC-RM-1242; ARC: London, UK, 1929. [Google Scholar]
- Jones, W.P. Aerodynamic Forces on an Oscillating Aerofoil Aileron-Tab Combination. In ARC-RM-1948; ARC: London, UK, 1941. [Google Scholar]
- Theodorsen, T.; Garrick, L.E. Nonstationary Flow About a Wing-Aileron-Tab Combination Including Aerodynamic Balance. In NACA-TR-736; NACA: Washington, DC, USA, 1942. [Google Scholar]
- Radok, J.R.M. The Theory of Aerofoils in Unsteady Motion. Aeronaut. Q. 1952, 3, 297–320. [Google Scholar] [CrossRef]
- Woods, L.C. The Lift and Moment Acting on a Thick Aerofoil in Unsteady Motion. Philos. Trans. R. Soc. Lond.-Ser. A. Math. Phys. Sci. 1954, 247, 131–162. [Google Scholar]
- Williams, D.E. On the Integral Equations of Two-Dimensional Subsonic Flutter Derivative Theory. In ARC-RM-3057; ARC: London, UK, 1955. [Google Scholar]
- Van De Vooren, A.I. Unsteady Aerofoil Theory. Adv. Appl. Mech. 1958, 5, 35–89. [Google Scholar]
- Hewson-Browne, R.C. The Oscillation of a Thick Aerofoil in an Incompressible Flow. Q. J. Mech. Appl. Math. 1963, 16, 79–92. [Google Scholar] [CrossRef]
- Giesing, J.P. Nonlinear Two-Dimensional Unsteady Potential Flow with Lift. J. Aircr. 1968, 5, 135–143. [Google Scholar] [CrossRef]
- Ericsson, L.E.; Reding, J.P. Unsteady Airfoil Stall, Review and Extension. J. Aircr. 1971, 8, 609–616. [Google Scholar] [CrossRef]
- Kemp, N.H.; Homicz, G. Approximate Unsteady Thin-Airfoil Theory for Subsonic Flow. AIAA J. 1976, 14, 1083–1089. [Google Scholar] [CrossRef]
- Zeiler, T.A. Results of Theodorsen and Garrick Revisited. J. Aircr. 2000, 37, 918–920. [Google Scholar] [CrossRef]
- Mateescu, D.; Abdo, M. Theoretical Solutions for Unsteady Flows Past Oscillating Flexible Airfoils Using Velocity Singularities. J. Aircr. 2003, 40, 153–163. [Google Scholar] [CrossRef]
- Kayran, A. Kussner’s Function in the Sharp Edged Gust Problem—A Correction. J. Aircr. 2006, 43, 1596–1599. [Google Scholar] [CrossRef]
- Johnston, C.O.; Mason, W.H.; Han, C. Unsteady Thin Airfoil Theory Revisited for a General Deforming Airfoil. J. Mech. Sci. Technol. 2010, 24, 2451–2460. [Google Scholar] [CrossRef]
- McGowan, G.Z.; Granlund, K.; Ol, M.V.; Gopalarathnam, A.; Edwards, J.R. Investigations of Lift-Based Pitch-Plunge Equivalence for Airfoils at Low Reynolds Numbers. AIAA J. 2011, 49, 1511–1524. [Google Scholar] [CrossRef]
- Ramesh, K.; Gopalarathnam, A.; Edwards, J.R.; Ol, M.V.; Granlund, K. An Unsteady Airfoil Theory Applied to Pitching Motions Validated against Experiment and Computation. Theor. Comput. Fluid Dyn. 2013, 27, 843–864. [Google Scholar] [CrossRef]
- Berci, M.; Gaskell, P.H.; Hewson, R.W.; Toropov, V.V. A Semi-Analytical Model for the Combined Aeroelastic Behaviour and Gust Response of a Flexible Aerofoil. J. Fluids Struct. 2013, 38, 3–21. [Google Scholar] [CrossRef]
- Liu, T.; Wang, S.; Zhang, X.; He, G. Unsteady Thin-Airfoil Theory Revisited: Application of a Simple Lift Formula. AIAA J. 2015, 53, 1492–1502. [Google Scholar] [CrossRef]
- Perry, B. Comparison of Theodorsen’s Unsteady Aerodynamic Forces with Doublet Lattice Generalized Aerodynamic Forces. In NACA-TM–2017-219667; NASA: Washington, DC, USA, 2017. [Google Scholar]
- Riso, C.; Riccardi, G.; Mastroddi, F. Semi-Analytical Unsteady Aerodynamic Model of a Flexible Thin Airfoil. J. Fluids Struct. 2018, 80, 288–315. [Google Scholar] [CrossRef]
- Jones, A.R.; Cetiner, O. Overview of Unsteady Aerodynamic Response of Rigid Wings in Gust Encounters. AIAA J. 2021, 59, 731–736. [Google Scholar] [CrossRef]
- Jones, W.P. Summary of Formulae and Notations Used in Two-Dimensional Derivative Theory. In ARC-RM-1958; ARC: London, UK, 1942. [Google Scholar]
- Duncan, W.J. Some Notes on Aerodynamic Derivatives. In ARC-RM-2115; ARC: London, UK, 1945. [Google Scholar]
- Temple, G. The Representation of Aerodynamic Derivatives. In ARC-RM-2114; ARC: London, UK, 1945. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berci, M. On the Incipient Indicial Lift of Thin Wings in Subsonic Flow: Acoustic Wave Theory with Unsteady Three-Dimensional Effects. Acoustics 2022, 4, 26-52. https://doi.org/10.3390/acoustics4010003
Berci M. On the Incipient Indicial Lift of Thin Wings in Subsonic Flow: Acoustic Wave Theory with Unsteady Three-Dimensional Effects. Acoustics. 2022; 4(1):26-52. https://doi.org/10.3390/acoustics4010003
Chicago/Turabian StyleBerci, Marco. 2022. "On the Incipient Indicial Lift of Thin Wings in Subsonic Flow: Acoustic Wave Theory with Unsteady Three-Dimensional Effects" Acoustics 4, no. 1: 26-52. https://doi.org/10.3390/acoustics4010003
APA StyleBerci, M. (2022). On the Incipient Indicial Lift of Thin Wings in Subsonic Flow: Acoustic Wave Theory with Unsteady Three-Dimensional Effects. Acoustics, 4(1), 26-52. https://doi.org/10.3390/acoustics4010003




