Molecular Dynamics Simulations of Shockwave Affected STMV Virus to Measure the Frequencies of the Oscillatory Response
Abstract
1. Introduction
2. Materials and Methods
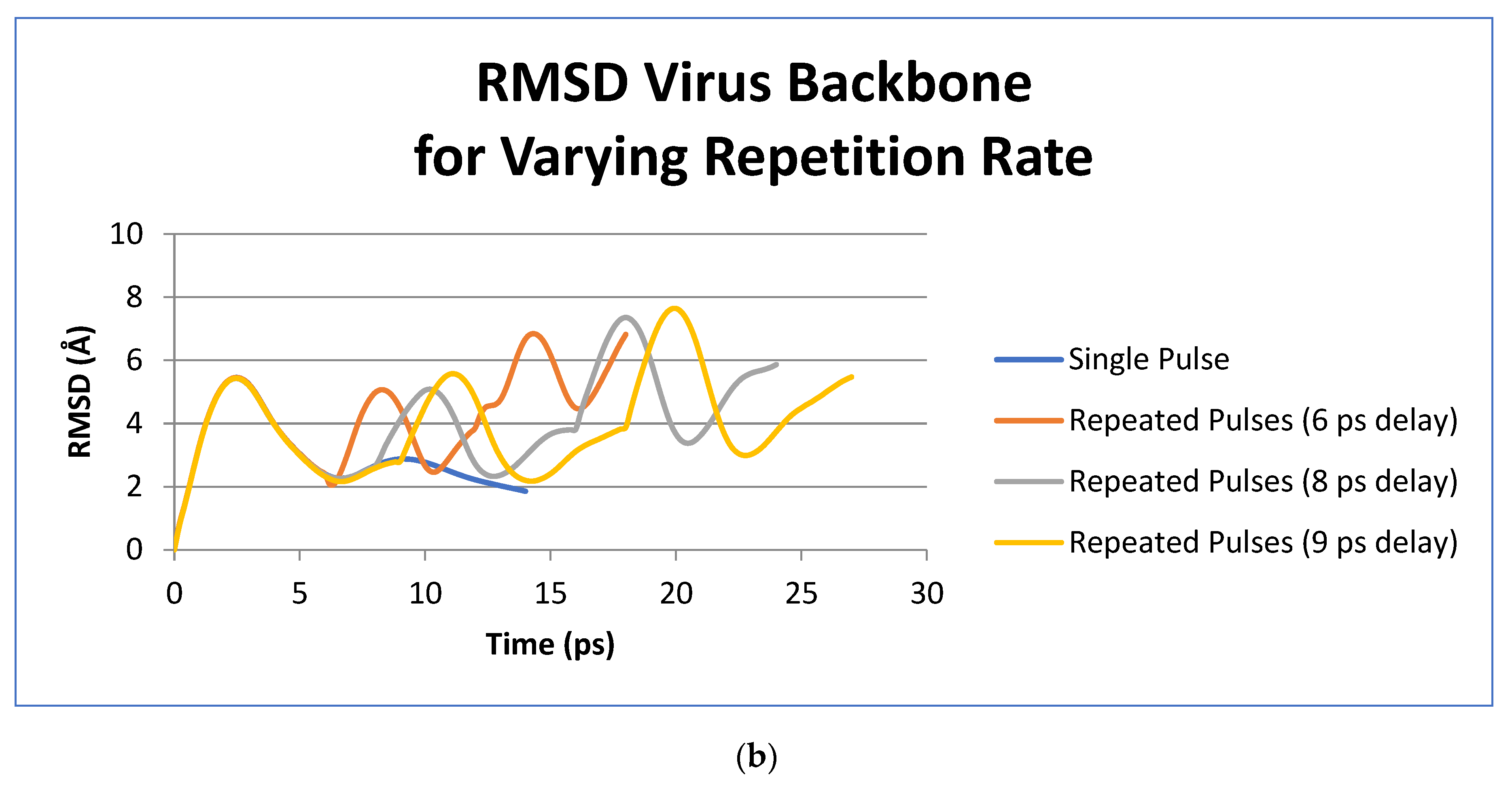
3. Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Spheroidal Mode Number | Frequency (GHz) |
|---|---|
| L0 | 92.47 |
| L1 | 60.60 |
| L2 | 44.67 |
| L3 | 66.57 |
References
- Hamrick, P.E.; Cleary, S.F. Laser-Induced Acoustic Breakage of Tobacco Mosaic Virus. Nature 1968, 220, 909–910. [Google Scholar] [CrossRef]
- Smith, R.J.; Cleary, S.F. Investigation of Structural Bonding Forces in Bacteriophage T2. J. Acoust. Soc. Am. 1974, 56, 1883–1889. [Google Scholar] [CrossRef]
- Tsen, S.-W.D.; Kingsley, D.H.; Poweleit, C.; Achilefu, S.; Soroka, D.S.; Wu, T.C.; Tsen, K.-T. Studies of Inactivation Mechanism of Non-Enveloped Icosahedral Virus by a Visible Ultrashort Pulsed Laser. Virol. J. 2014, 11, 20. [Google Scholar] [CrossRef]
- Nazari, M.; Xi, M.; Lerch, S.; Alizadeh, M.; Ettinger, C.; Akiyama, H.; Gillespie, C.; Gummuluru, S.; Erramilli, S.; Reinhard, B.M. Plasmonic Enhancement of Selective Photonic Virus Inactivation. Sci. Rep. 2017, 7, 11951. [Google Scholar] [CrossRef]
- Babincová, M.; Sourivong, P.; Babinec, P. Resonant absorption of ultrasound energy as a method of HIV destruction. Med. Hypotheses 2000, 55, 450. [Google Scholar] [CrossRef]
- Yang, S.-C.; Lin, H.-C.; Liu, T.-M.; Lu, J.-T.; Hung, W.-T.; Huang, Y.-R.; Tsai, Y.-C.; Kao, C.-L.; Chen, S.-Y.; Sun, C.-K. Efficient Structure Resonance Energy Transfer from Microwaves to Confined Acoustic Vibrations in Viruses. Sci. Rep. 2015, 5, 18030. [Google Scholar] [CrossRef]
- Hempel, E. Irradiation Device for Influencing a Biological Structure in a Subject with Electromagnetic Radiation 2010. U.S. Patent US7648498B2, 19 January 2010. [Google Scholar]
- Ford, L. Estimate of the Vibrational Frequencies of Spherical Virus Particles. Phys. Rev. E 2003, 67, 051924. [Google Scholar] [CrossRef]
- Saviot, L.; Murray, D.B.; Mermet, A.; Duval, E. Comment on “Estimate of the Vibrational Frequencies of Spherical Virus Particles”. Phys. Rev. E 2004, 69, 023901. [Google Scholar] [CrossRef]
- Fonoberov, V.A.; Balandin, A.A. Low-Frequency Vibrational Modes of Viruses Used for Nanoelectronic Self-Assemblies. Phys. Status Solidi (B) 2004, 241, R67–R69. [Google Scholar] [CrossRef]
- Talati, M.; Jha, P.K. Acoustic Phonon Quantization and Low-Frequency Raman Spectra of Spherical Viruses. Phys. Rev. E 2006, 73, 011901. [Google Scholar] [CrossRef]
- Yang, Z.; Bahar, I.; Widom, M. Vibrational Dynamics of Icosahedrally Symmetric Biomolecular Assemblies Compared with Predictions Based on Continuum Elasticity. Biophys. J. 2009, 96, 4438–4448. [Google Scholar] [CrossRef]
- Tama, F.; Brooks III, C.L. Diversity and Identity of Mechanical Properties of Icosahedral Viral Capsids Studied with Elastic Network Normal Mode Analysis. J. Mol. Biol. 2005, 345, 299–314. [Google Scholar] [CrossRef]
- Dykeman, E.C.; Sankey, O.F. Normal Mode Analysis and Applications in Biological Physics. J. Phys. Condens. Matter 2010, 22, 423202. [Google Scholar] [CrossRef]
- Lee, B.H.; Jo, S.; Choi, M.; Kim, M.H.; Choi, J.B.; Kim, M.K. Normal Mode Analysis of Zika Virus. Comput. Biol. Chem. 2018, 72, 53–61. [Google Scholar] [CrossRef]
- Dykeman, E.C.; Sankey, O.F. Atomistic Modeling of the Low-Frequency Mechanical Modes and Raman Spectra of Icosahedral Virus Capsids. Phys. Rev. E 2010, 81, 021918. [Google Scholar] [CrossRef] [PubMed]
- Tsen, K.-T.; Dykeman, E.C.; Sankey, O.F.; Tsen, S.-W.D.; Lin, N.-T.; Kiang, J.G. Raman Scattering Studies of the Low-Frequency Vibrational Modes of Bacteriophage M13 in Water—Observation of an Axial Torsion Mode. Nanotechnology 2006, 17, 5474. [Google Scholar] [CrossRef]
- Stephanidis, B.; Adichtchev, S.; Gouet, P.; McPherson, A.; Mermet, A. Elastic Properties of Viruses. Biophys. J. 2007, 93, 1354–1359. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Hartschuh, R.; Wargacki, S.; Xiong, H.; Neiswinger, J.; Kisliuk, A.; Sihn, S.; Ward, V.; Vaia, R.; Sokolov, A. How Rigid Are Viruses. Phys. Rev. E 2008, 78, 021907. [Google Scholar] [CrossRef]
- Tcherniega, N.; Pershin, S.; Bunkin, A.; Donchenko, E.; Karpova, O.; Kudryavtseva, A.; Lednev, V.; Mironova, T.; Shevchenko, M.; Strokov, M.; et al. Laser Excitation of Gigahertz Vibrations in Cauliflower Mosaic Viruses’ Suspension. Laser Phys. Lett. 2018, 15, 095603. [Google Scholar] [CrossRef]
- Sirotkin, S.; Mermet, A.; Bergoin, M.; Ward, V.; Van Etten, J.L. Viruses as Nanoparticles: Structure versus Collective Dynamics. Phys. Rev. E 2014, 90, 022718. [Google Scholar] [CrossRef]
- Burkhartsmeyer, J.; Wang, Y.; Wong, K.S.; Gordon, R. Optical Trapping, Sizing, and Probing Acoustic Modes of a Small Virus. Appl. Sci. 2020, 10, 394. [Google Scholar] [CrossRef]
- Mattarelli, M.; Vassalli, M.; Caponi, S. Relevant Length Scales in Brillouin Imaging of Biomaterials: The Interplay between Phonons Propagation and Light Focalization. ACS Photonics 2020, 7, 2319–2328. [Google Scholar] [CrossRef]
- Duval, E. Far-Infrared and Raman Vibrational Transitions of a Solid Sphere: Selection Rules. Phys. Rev. B 1992, 46, 5795. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Y.; Larson, S.B.; Heitsch, C.E.; McPherson, A.; Harvey, S.C. A Model for the Structure of Satellite Tobacco Mosaic Virus. J. Struct. Biol. 2012, 180, 110–116. [Google Scholar] [CrossRef] [PubMed]
- Freddolino, P.L.; Arkhipov, A.S.; Larson, S.B.; McPherson, A.; Schulten, K. Molecular Dynamics Simulations of the Complete Satellite Tobacco Mosaic Virus. Structure 2006, 14, 437–449. [Google Scholar] [CrossRef]
- Jung, J.; Mori, T.; Kobayashi, C.; Matsunaga, Y.; Yoda, T.; Feig, M.; Sugita, Y. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2015, 5, 310. [Google Scholar] [CrossRef]
- Kumar, S.; Sun, Y.; Kalé, L.V. Acceleration of an Asynchronous Message Driven Programming Paradigm on IBM Blue Gene/Q. In Proceedings of the 2013 IEEE 27th International Symposium on Parallel and Distributed Processing, Cambridge, MA, USA, 20–24 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 689–699. [Google Scholar]
- Solov’yov, A.V.; Surdutovich, E.; Scifoni, E.; Mishustin, I.; Greiner, W. Physics of Ion Beam Cancer Therapy: A Multiscale Approach. Phys. Rev. E 2009, 79, 011909. [Google Scholar] [CrossRef]
- Surdutovich, E.; Yakubovich, A.V.; Solov’yov, A.V. Biodamage via Shock Waves Initiated by Irradiation with Ions. Sci. Rep. 2013, 3, 1289. [Google Scholar] [CrossRef]
- Surdutovich, E.; Solov’yov, A. Multiscale Physics of Ion-Beam Cancer Therapy. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2012; Volume 373, p. 012001. [Google Scholar]
- Adhikari, U.; Goliaei, A.; Berkowitz, M.L. Mechanism of Membrane Poration by Shock Wave Induced Nanobubble Collapse: A Molecular Dynamics Study. J. Phys. Chem. B 2015, 119, 6225–6234. [Google Scholar] [CrossRef]
- Koshiyama, K.; Kodama, T.; Yano, T.; Fujikawa, S. Molecular Dynamics Simulation of Structural Changes of Lipid Bilayers Induced by Shock Waves: Effects of Incident Angles. Biochim. Biophys. Acta (BBA)-Biomembr. 2008, 1778, 1423–1428. [Google Scholar] [CrossRef]
- Phillips, J.C.; Hardy, D.J.; Maia, J.D.C.; Stone, J.E.; Ribeiro, J.V.; Bernardi, R.C.; Buch, R.; Fiorin, G.; Hénin, J.; Jiang, W.; et al. Scalable Molecular Dynamics on CPU and GPU Architectures with NAMD. J. Chem. Phys. 2020, 153, 044130. [Google Scholar] [CrossRef]
- Holian, B.L.; Lomdahl, P.S. Plasticity Induced by Shock Waves in Nonequilibrium Molecular-Dynamics Simulations. Science 1998, 280, 2085–2088. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD–Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Lamb, H. On the Vibrations of an Elastic Sphere. Proc. Lond. Math. Soc. 1881, 1, 189–212. [Google Scholar] [CrossRef]
- Murray, D.B.; Saviot, L. Phonons in an Inhomogeneous Continuum: Vibrations of an Embedded Nanoparticle. Phys. Rev. B 2004, 69, 094305. [Google Scholar] [CrossRef]
- MacKerell Jr, A.D.; Bashford, D.; Bellott, M.; Dunbrack Jr, R.L.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef]


| Initial Velocity | Period of Oscillation (ps) | Frequency (GHz) |
|---|---|---|
| Water Slice (Å/ps) | ||
| 99.999 | 15.2 | 65.79 |
| 89.999 | 16 | 62.5 |
| 79.999 | 16.4 | 60.98 |
| 69.999 | 16.4 | 60.98 |
| 59.999 | 16.8 | 59.52 |
| 49.999 | 14 | 71.43 |
| 39.999 | 14 | 71.43 |
| 29.999 | 14.8 | 67.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burkhartsmeyer, J.; Wong, K.S. Molecular Dynamics Simulations of Shockwave Affected STMV Virus to Measure the Frequencies of the Oscillatory Response. Acoustics 2022, 4, 268-275. https://doi.org/10.3390/acoustics4010016
Burkhartsmeyer J, Wong KS. Molecular Dynamics Simulations of Shockwave Affected STMV Virus to Measure the Frequencies of the Oscillatory Response. Acoustics. 2022; 4(1):268-275. https://doi.org/10.3390/acoustics4010016
Chicago/Turabian StyleBurkhartsmeyer, Jeffrey, and Kam Sing Wong. 2022. "Molecular Dynamics Simulations of Shockwave Affected STMV Virus to Measure the Frequencies of the Oscillatory Response" Acoustics 4, no. 1: 268-275. https://doi.org/10.3390/acoustics4010016
APA StyleBurkhartsmeyer, J., & Wong, K. S. (2022). Molecular Dynamics Simulations of Shockwave Affected STMV Virus to Measure the Frequencies of the Oscillatory Response. Acoustics, 4(1), 268-275. https://doi.org/10.3390/acoustics4010016






