Modelling of Microperforated Panel Absorbers with Circular and Slit Hole Geometries
Abstract
:1. Introduction
2. Single-Layer Microperforated or Microslit Panels
- viscous–thermal dissipation within the perforations, characterized by impedance Zhole for an MPP, and Zslit for an MSP;
- flow distortion in the perforation edges, characterized by impedance Zedge;
- resonances in the air cavity, with impedance ZD;
- structural vibrations of the panel impinged by the incident acoustic field, with impedance Zvib.
2.1. Maa Model
2.2. Randeberg–Vigran (RV) Model
2.3. Equivalent Fluid (F) Model
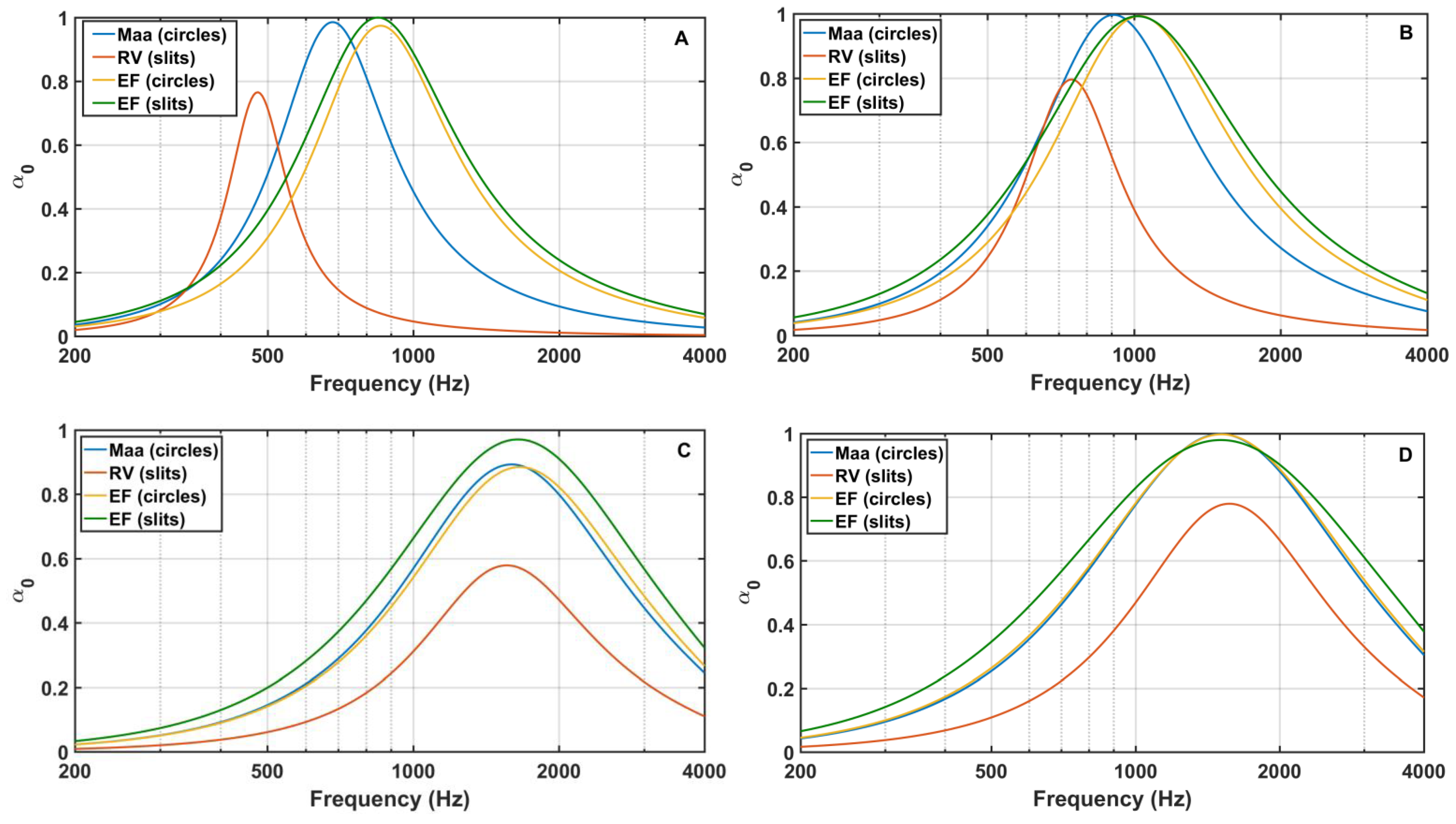
2.4. Comparison of Models
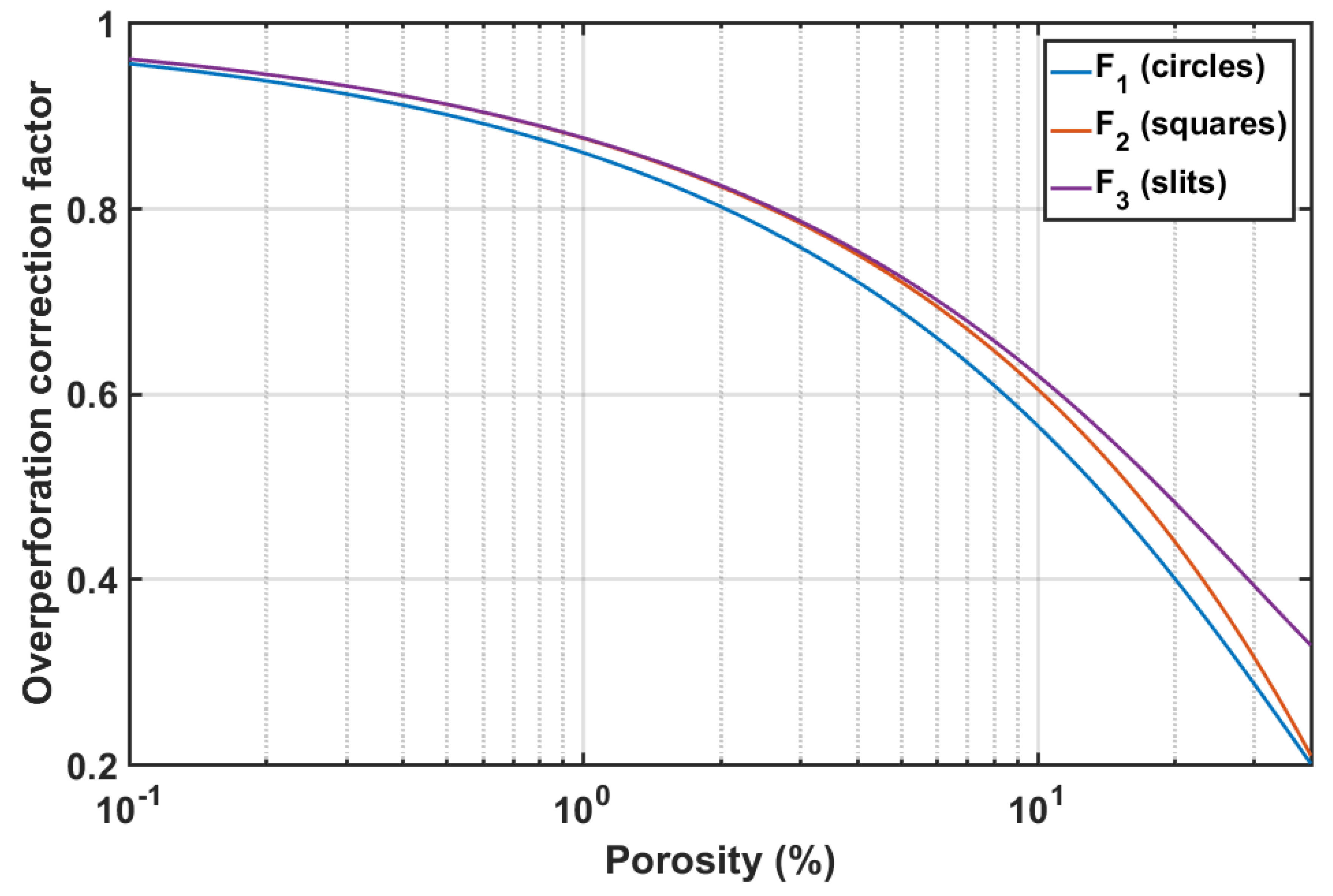
- When the perforation ratio increases (overperforation) and the perforation diameter decreases, the absorption peak moves towards higher frequencies and the absorption bandwidth becomes wider [6].
- It seems that the Maa model of MPP always provides more absorption than the RV model for the equivalent MSP. The absorption peaks may be displaced towards lower frequencies for low perforation ratios, although the bandwidth of the Maa curve is wider than that of the RV model for the equivalent MSP, for the considered combinations of parameters.
- There are discrepancies between the absorption curves provided by the Maa model and the EF model for circular holes at low perforation ratios (Figure 2A,B). In this case, the EF curve is slightly displaced towards higher frequencies with respect to the Maa curve. However, when the perforation ratio increases (Figure 2C,D), both curves tend to match each other.
- The discrepancies between the absorption curves provided by the RV and the EF models for slits are large for all combinations of parameters. For low perforation ratios (Figure 2A,B) the EF curve is displaced towards higher frequencies. For high perforation ratios (Figure 2C,D) the EF curve has a higher peak and wider bandwidth.
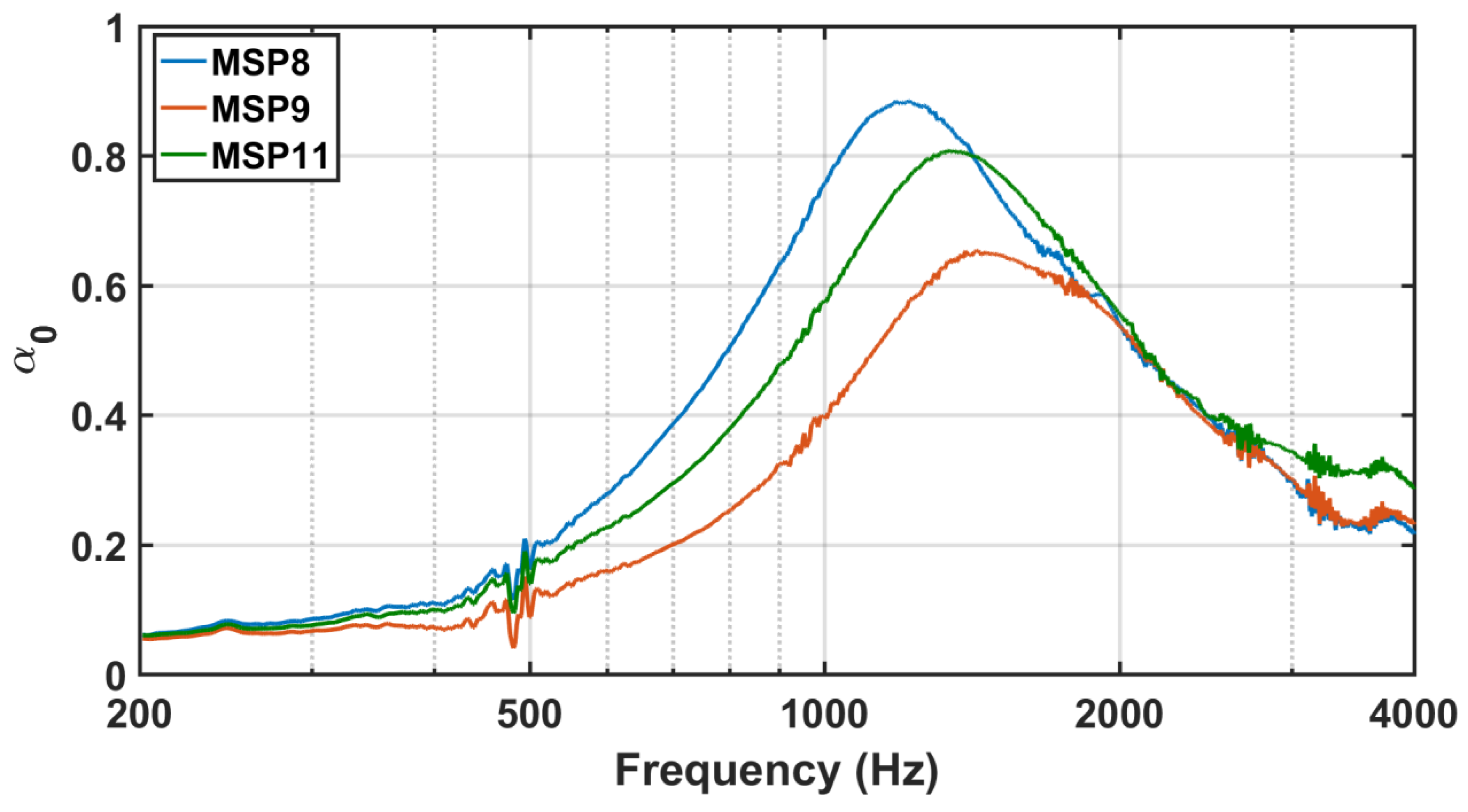
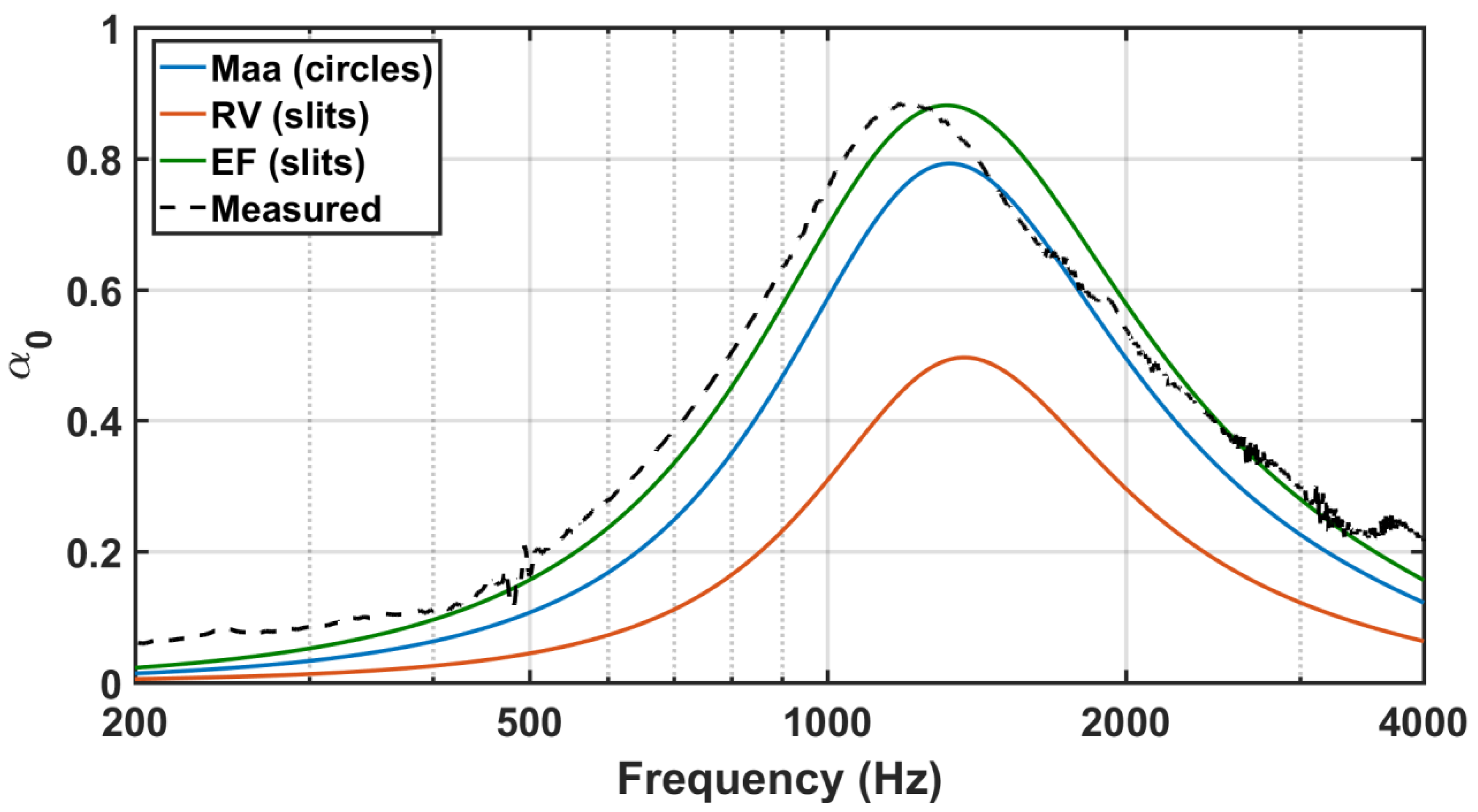
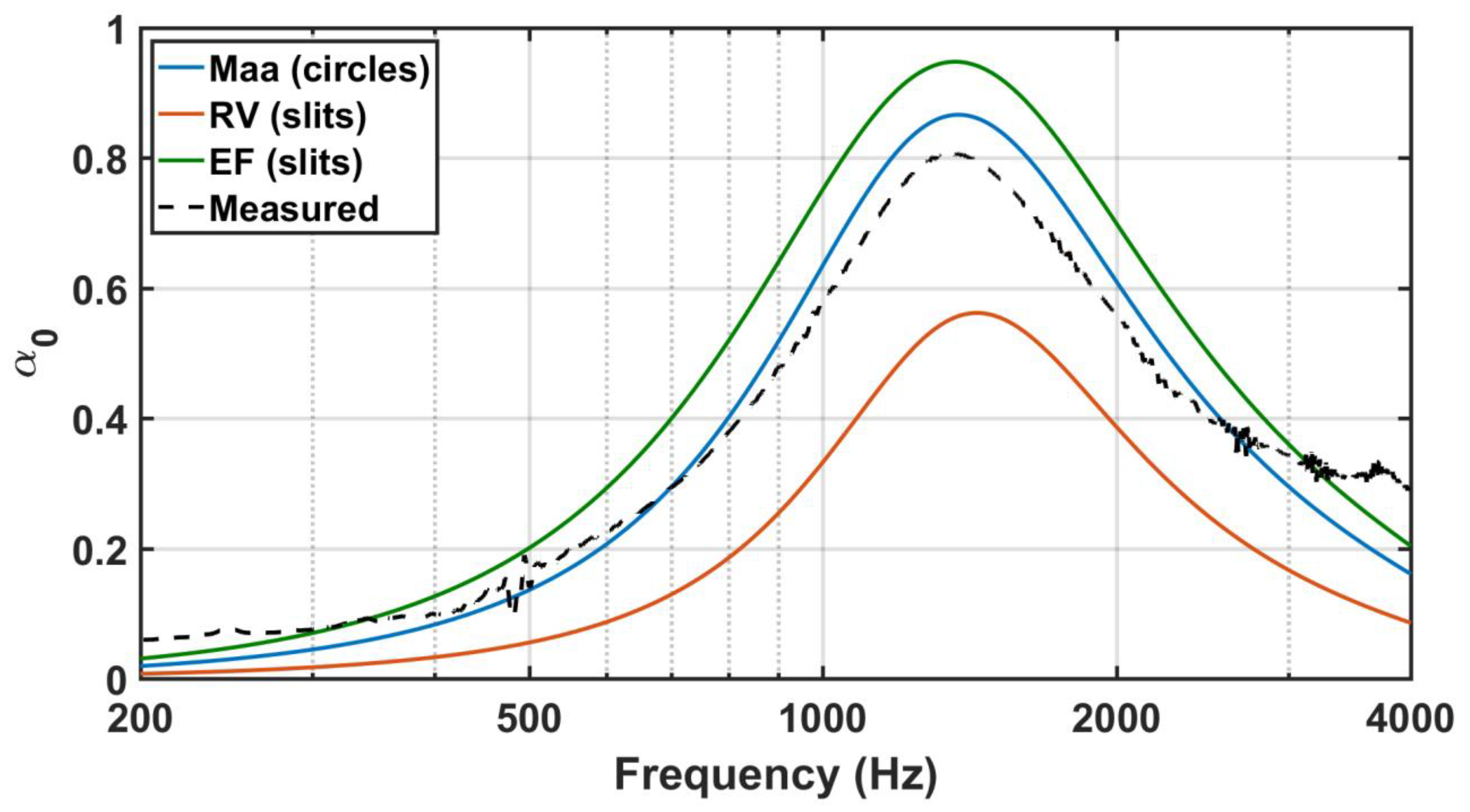
3. Results
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maa, D.Y. Microperforated-panel wideband absorbers. Noise Control. Engr. J. 1987, 29, 77–84. [Google Scholar] [CrossRef]
- Maa, D.Y. Potential of microperforated panel absorber. J. Acoust. Soc. Am. 1998, 104, 2861–2866. [Google Scholar] [CrossRef]
- Kang, J.; Fuchs, H.V. Predicting the sound absorption of open weave textiles and microperforated membranes backed by an air space. J. Sound Vib. 1999, 220, 905–920. [Google Scholar] [CrossRef]
- Herrin, D.W.; Liu, W.; Hua, X.; Liu, J. A guide to the application of microperforated panel absorbers. Sound Vib. 2017, 51, 12–18. [Google Scholar]
- Cobo, P.; Simón, F. Multiple-Layer Microperforated Panels as Sound Absorbers in Buildings: A Review. Buildings 2019, 9, 53. [Google Scholar] [CrossRef] [Green Version]
- Qian, J.Y.; Kong, D.Y.; Liu, S.M.; Sun, S.M.; Zhao, Z. Investigation on micro-perforated panel absorber with ultra-micro perforations. App. Acoust. 2013, 74, 931–935. [Google Scholar] [CrossRef]
- Liu, Z.; Zhan, J.; Fard, M.; Davy, J.L. Acoustic properties of multilayer sound absorbers with a 3D printed micro-perforated panel. Appl. Acoust. 2017, 121, 25–32. [Google Scholar] [CrossRef]
- Bucciarelli, F.; Malfense Fierro, G.P.; Meo, M. A multilayer microperforated panel prototype for broadband sound absorption at low frequencies. Appl. Acoust. 2019, 146, 134–144. [Google Scholar] [CrossRef]
- Yang, X.; Bai, P.; Sheng, X.; To, S.; Chen, L.; Zhang, X.; Yin, Q. Optimal design and experimental validation of sound absorbing multilayer microperforated panel with constraint conditions. Appl. Acoust. 2019, 146, 334–344. [Google Scholar] [CrossRef]
- Cobo, P.; de la Colina, C.; Roibás-Millán, E.; Chimeno, M.; Simón, F. A wideband triple-layer microperforated panel sound absorber. Comp. Struct. 2019, 226, 111226. [Google Scholar] [CrossRef]
- Huang, S.; Li, S.; Wang, X.; Mao, D. Micro-perforated absorbers with incompletely partitioned cavities. Appl. Acoust. 2017, 126, 114–119. [Google Scholar] [CrossRef]
- Cobo, P.; Ruiz, H.; Alvarez, J. Double-layer microperforated panel/porous absorber as liner for anechoic closing of the test section in wind tunnels. Acta Acust. United Acust. 2010, 96, 914–922. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Zhan, J.; Fard, M.; Davy, J.L. Acoustic measurement of a 3D printed micro-perforated panel combined with a porous material. Measurements 2017, 1041, 233–236. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Y.; Wen, J.; Lam, Y.W.; Umnova, O. A slim subwavelength absorber based on coupled microslits. App. Acoust. 2018, 142, 11–17. [Google Scholar] [CrossRef]
- Li, X.; Wu, Q.; Kang, L.; Liu, B. Design of Multiple Parallel-Arranged Perforated Panel Absorbers for Low Frequency Sound Absorption. Materials 2019, 12, 2099. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, S.H. Acoustic properties of micro-perforated panel absorbers backed by Helmholtz resonators for the improvement of low-frequency sound absorption. J. Sound Vib. 2013, 332, 4895–4911. [Google Scholar] [CrossRef]
- Peng, X.; Ji, J.; Jing, Y. Composite honeycomb metasurface panel for broadband sound absorption. J. Acoust. Soc. Am. 2018, 144, EL255–EL261. [Google Scholar] [CrossRef] [Green Version]
- Ingard, U. On the theory and design of acoustic resonators. J. Acoust. Soc. Am. 1953, 25, 1037–1061. [Google Scholar] [CrossRef]
- Atalla, N.; Sgard, J.F. Modeling of perforated plates and screens using rigid frame porous models. J. Sound Vib. 2007, 303, 195–208. [Google Scholar] [CrossRef]
- Allard, J.F.; Atalla, N. Propagation of Sound in Porous Media. Modelling Sound Absorbing Materials; Wiley: Chichester, UK, 2009. [Google Scholar]
- Maa, D.Y. Theory of microslit absorber. Chin. J. Acoust. 2001, 21, 1–10. [Google Scholar]
- Randeberg, R.T. A Helmholtz resonator with a lineal elongated orifice. Acta Acust. United Acust. 2000, 86, 77–82. [Google Scholar]
- Randeberg, R.T. Adjustable slitted panel absorber. Acta Acust. United Acust. 2002, 88, 507–512. [Google Scholar]
- Vigran, T.E. The acoustic properties of panels with rectangular apertures. J. Acoust. Soc. Am. 2014, 135, 2777–2784. [Google Scholar] [CrossRef] [PubMed]
- Vigran, T.E.; Haugen, T. Silencers for circular ducts–Application of plates with micro-slits. Acta Acust. United Acust. 2016, 102, 566–577. [Google Scholar] [CrossRef]
- Yang, W.; Bai, X.; Zhu, W.; Kiran, R.; An, J.; Chua, C.K.; Zhou, K. 3D Printing of Polymeric Multi-Layer Micro-Perforated Panels for Tunable Wideband Sound Absorption. Polymers 2020, 12, 360. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cobo, P.; de la Colina, C.; Simón, F. On the modelling of microslit panel absorbers. App. Acoust. 2020, 159, 107118. [Google Scholar] [CrossRef]
- Tayong, R.; Leclaire, P. Hole Interaction Effects under High and Medium Sound Intensities for Micro-Perforated Panels Design; 10éme Congress Francais d’Acoustique: Lyon, France, 2010. [Google Scholar]
- Jaouen, L.; Becot, F.X. Acoustical characterization of perforated facings. J. Acoust. Soc. Am. 2011, 129, 1400–1406. [Google Scholar] [CrossRef]
- Ning, J.F.; Ren, S.W.; Zhao, G.P. Acoustic properties of micro-perforated panel absorber having arbitrary cross-sectional perforations. App. Acoust. 2016, 111, 135–142. [Google Scholar] [CrossRef]
- Melling, T.H. The acoustic impedance of perforates at medium and high sound pressure levels. J. Sound Vib. 1973, 29, 1–65. [Google Scholar] [CrossRef]
- Rschevkin, S.N. A Course of Lectures on the Theory of Sound; Pergamon Press: Oxford, UK, 1963. [Google Scholar]
- Kristiansen, U.R.; Vigran, T.E. On the design of resonant absorbers using a slotted plate. App. Acoust. 1994, 43, 39–48. [Google Scholar] [CrossRef]
- Chevillotte, F. Controlling sound absorption by an upstream resistive layer. App. Acoust. 2012, 73, 56–60. [Google Scholar] [CrossRef]
- Jiang, C.; Li, X.; Xing, T.; Zhang, B. Additional length model for the impedance end correction of microperforated panels. J. Acoust. Soc. Am. 2020, 148, 566–574. [Google Scholar] [CrossRef] [PubMed]
- ISO 10534-2:1998. Acoustics—Determination of Sound Absorption Coefficient and Impedance in Impedance Tubes—Part 2: Transfer-Function Method; ISO: Geneva, Switzerland, 1998. [Google Scholar]
- Cobo, P.; Simón, F.; de la Colina, C. Comparison of multiple-layer versus multiple-cavity microperforated panels for sound absorption at low frequency. Noise Control Engr. J. 2021, 69, 341–350. [Google Scholar] [CrossRef]
- Li, X. End correction model for the transfer impedance of microperforated panels using viscothermal wave theory. J. Acoust. Soc. Am. 2017, 141, 1426–1436. [Google Scholar] [CrossRef] [PubMed]
- Naderyan, V.; Raspet, R.; Hickey, C.J.; Mohammadi, M. Acoustic end corrections for micro-perforated plates. J. Acoust. Soc. Am. Express Letters 2019, 146, EL399–EL404. [Google Scholar] [CrossRef] [Green Version]
- Aulitto, A.; Hirschberg, A.; Lopez-Arteaga, I. Influence of geometry on acoustic end-corrections of slits in microslit absorbers. J. Acoust. Soc. Am. 2021, 149, 3073–3085. [Google Scholar] [CrossRef] [PubMed]
- Ren, S.; Liu, X.; Gong, J.; Tang, Y.; Sin, F.; Huang, L.; Lu, T.J. Tunable acoustic absorbers with periodical micro-perforations having varying pore shapes. Europhys. Lett. 2017, 120, 44001. [Google Scholar] [CrossRef]
- Xu, Z.; He, W.; Peng, X.; Xin, F.; Lu, T.J. Sound absorption theory for micro-perforated panel with petal-shaped perforations. J. Acoust. Soc. Am. 2020, 148, 18–24. [Google Scholar] [CrossRef]
- Xu, Z.; Peng, X.; Liu, X.; Xin, F.; Lu, T.J. Modified theory of a microperforated panel with roughened perforations. Europhys. Lett. 2019, 125, 34004. [Google Scholar] [CrossRef]
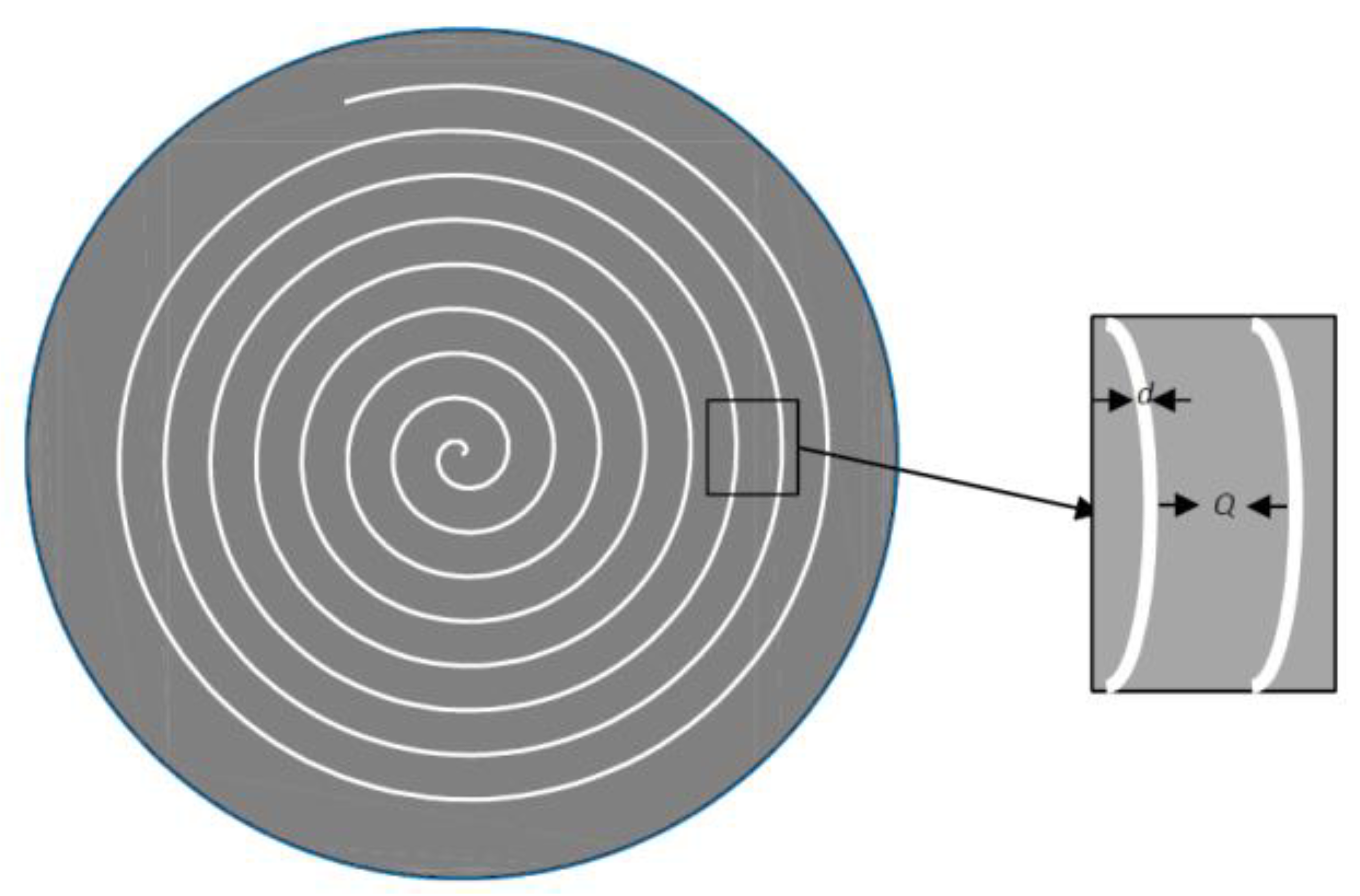

| Circle | Square | Equilateral Triangle | Slit | |
|---|---|---|---|---|
| C1 | 1 | 1.07 | 1.11 | 0.81 |
| C2 | 8 | 7 | 6.5 | 12 |
| MSP | d (mm) | N | φ (%) |
|---|---|---|---|
 | 0.44 | 6 | 16 |
 | 0.44 | 7 | 19 |
 | 0.35 | 8 | 18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cobo, P. Modelling of Microperforated Panel Absorbers with Circular and Slit Hole Geometries. Acoustics 2021, 3, 665-678. https://doi.org/10.3390/acoustics3040042
Cobo P. Modelling of Microperforated Panel Absorbers with Circular and Slit Hole Geometries. Acoustics. 2021; 3(4):665-678. https://doi.org/10.3390/acoustics3040042
Chicago/Turabian StyleCobo, Pedro. 2021. "Modelling of Microperforated Panel Absorbers with Circular and Slit Hole Geometries" Acoustics 3, no. 4: 665-678. https://doi.org/10.3390/acoustics3040042
APA StyleCobo, P. (2021). Modelling of Microperforated Panel Absorbers with Circular and Slit Hole Geometries. Acoustics, 3(4), 665-678. https://doi.org/10.3390/acoustics3040042






