Active Noise Control System Based on the Improved Equation Error Model
Abstract
1. Introduction
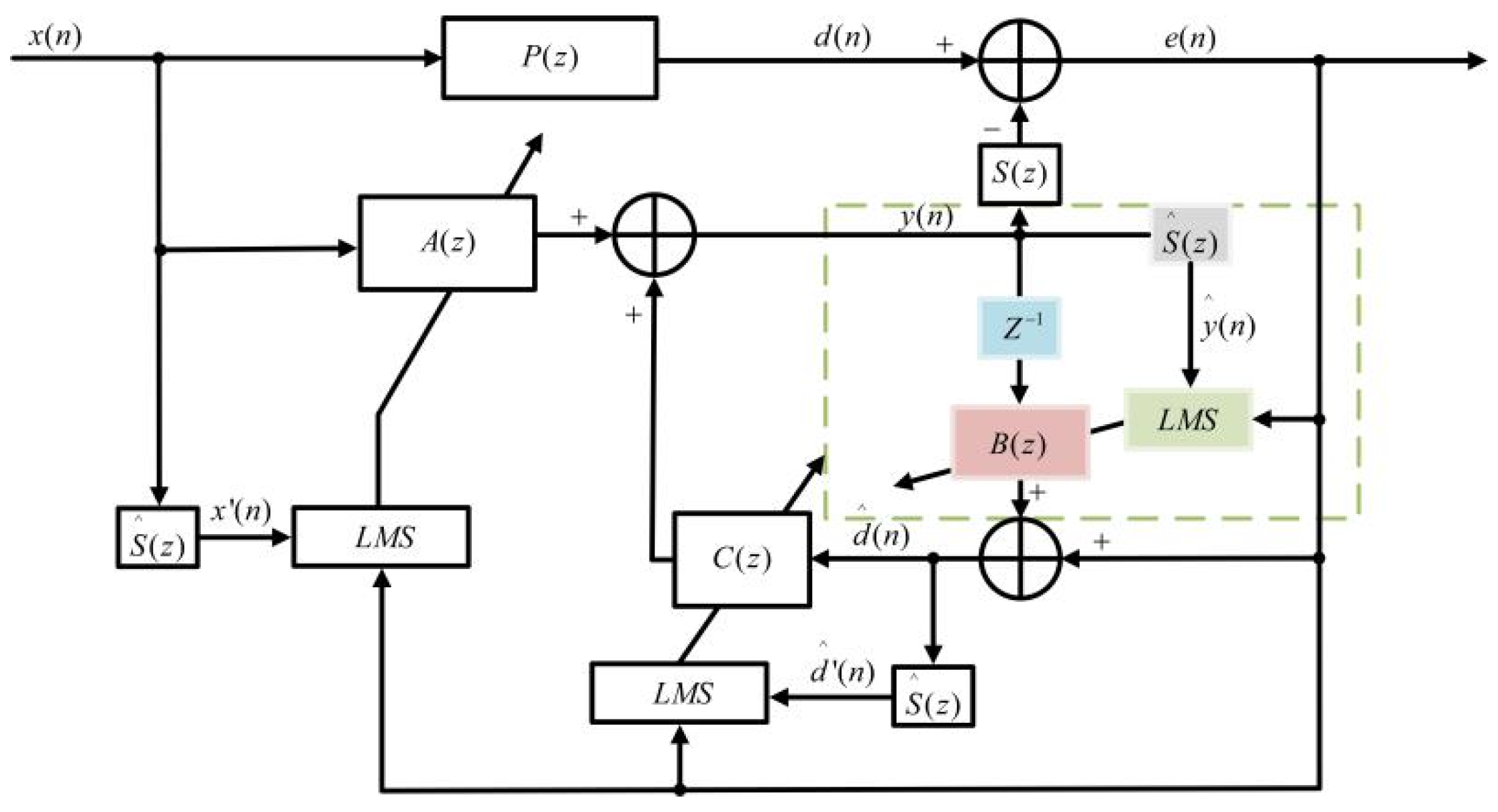
2. The OE-Model-Based ANC System
3. The EE Adaptive IIR-Filter-Based ANC Algorithm
4. The EE Adaptive IIR-Filter-Based ANC Algorithm
4.1. The Step-Size Constraint
4.2. Global Minimum Solutions
5. Computer Simulation
5.1. Test Environment and Noise Characteristics
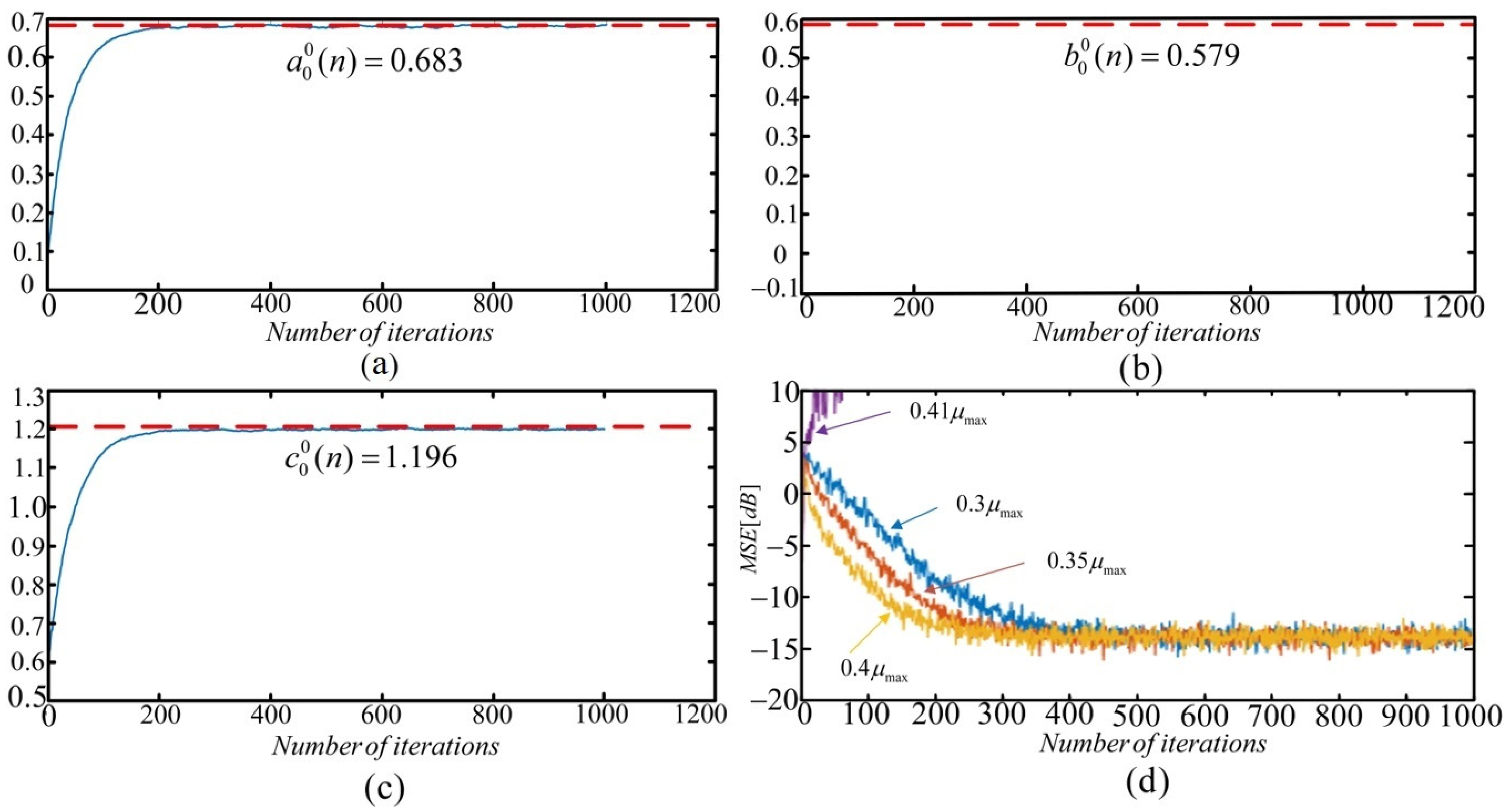
5.2. Simulation Results
5.3. Computational Complexity
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lasota, A.; Meller, M. Iterative Learning Approach to Active Noise Control of Highly Autocorrelated Signals with Applications to Machinery Noise. IET Signal Process. 2020, 14, 560–568. [Google Scholar] [CrossRef]
- Nelson, P.A.; Elliott, S.J.; John, E.W.F. Active control of sound basics of interferometry. Phys. Today 1993, 46, 75. [Google Scholar] [CrossRef]
- Fredianelli, L.; Del Pizzo, A.; Licitra, G. Recent developments in sonic crystals as barriers for road traffic noise mitigation. Environments 2019, 6, 14. [Google Scholar] [CrossRef]
- Koussa, F.; Defrance, J.; Jean, P.; Blanc-Benon, P. Acoustical efficiency of a sonic crystal assisted noise barrier. Acta Acust. United Acust. 2013, 99, 399–409. [Google Scholar] [CrossRef]
- Kuo, S.M.; Morgan, D.R. Active Noise Control Systems; Wiley: New York, NY, USA, 1996; Volume 4. [Google Scholar]
- Aggogeri, F.; Al-Bender, F.; Brunner, B.; Elsaid, M.; Mazzola, M.; Merlo, A.; Ricciardi, D.; De La ORodriguez, M.; Salvi, E. Design of piezo-based avc system for machine tool applications. Mech. Syst. Signal Process. 2013, 36, 53–65. [Google Scholar] [CrossRef]
- Guo, X.; Jiang, J.; Chen, J.; Du, S.; Tan, L. Bibo-stable implementation of adaptive function expansion bilinear filter for nonlinear active noise control. Appl. Acoust. 2020, 168, 107407. [Google Scholar] [CrossRef]
- Lam, B.; Shi, C.; Shi, D.; Gan, W.S. Active control of sound through full-sized open windows. Build. Environ. 2018, 141, 16–27. [Google Scholar] [CrossRef]
- Murao, T.; Shi, C.; Gan, W.S.; Nishimura, M. Mixed-error approach for multi-channel active noise control of open windows. Appl. Acoust. 2017, 127, 305–315. [Google Scholar] [CrossRef]
- Shi, C.; Jia, Z.; Xie, R.; Li, H. An active noise control casing using the multi-channel feedforward control system and the relative path based vir-tual sensing method. Mech. Syst. Signal Process. 2020, 144, 106878. [Google Scholar] [CrossRef]
- Carini, A.; Mathews, V.J.; Sicuranza, G.L. Sufficient stability bounds for slowly varying direct-form recursive linear filters and their applications in adaptive iir filters. IEEE Trans. Signal Process. 1999, 47, 2561–2567. [Google Scholar] [CrossRef]
- Feng, D.Z.; Zheng, W.X. Fast rls-type algorithm for unbiased equation-error adaptive iir filtering based on approximate inverse-power iteration. IEEE Trans. Signal Process. 2005, 53, 4169–4185. [Google Scholar] [CrossRef]
- Netto, S.L.; Diniz, P.S.; Agathoklis, P. Adaptive iir filtering algorithms for system identification: A general framework. IEEE Trans. Educ. 1995, 38, 54–66. [Google Scholar] [CrossRef]
- Regalia, P. Adaptive IIR Filtering in Signal Processing and Control; Rout-ledge: London, UK, 2018. [Google Scholar]
- Mandelbrot, B.B. The variation of certain speculative prices. In Fractals and Scaling in Finance; Springer: Berlin, Germany, 1997; pp. 371–418. [Google Scholar]
- Bouvet, M.; Schwartz, S.C. Comparison of adaptive and robust receivers for signal detection in ambient underwater noise. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 621–626. [Google Scholar] [CrossRef]
- Elliott, S.; Nelson, P. The active control of sound. Electron. Commun. Eng. J. 1990, 2, 127–136. [Google Scholar] [CrossRef]
- Ho, C.Y.; Shyu, K.K.; Chang, C.Y.; Kuo, S.M. Development of equation-error adaptive iir-filter-based active noise control system. Appl. Acoust. 2020, 163, 107226. [Google Scholar] [CrossRef]
- Zhao, T.; Liang, J.; Zou, L.; Zhang, L. A new fxlms algorithm with offline and online secondary-path modeling scheme for active noise control of power transformers. IEEE Trans. Ind. Electron. 2017, 64, 6432–6442. [Google Scholar] [CrossRef]
- Kim, I.S.; Na, H.S.; Kim, K.J.; Park, Y. Constraint filtered-x and filtered-u least-mean-square algorithms for the active control of noise in ducts. J. Acoust. Soc. Am. 1994, 95, 3379–3389. [Google Scholar] [CrossRef]
- Fraanje, R.; Verhaegen, M.; Doelman, N. Convergence analysis of the filtered-u lms algorithm for active noise control in case perfect cancellation is not possible. Signal Process. 2003, 83, 1239–1254. [Google Scholar] [CrossRef]





| Algorithm | Multplications | Additions |
|---|---|---|
| FxLMS | ||
| OE ANC | ||
| EE ANC | ||
| Proposed EE ANC |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, J.; Li, J.; Zhang, A.; Zhang, X.; Ran, J. Active Noise Control System Based on the Improved Equation Error Model. Acoustics 2021, 3, 354-363. https://doi.org/10.3390/acoustics3020024
Yuan J, Li J, Zhang A, Zhang X, Ran J. Active Noise Control System Based on the Improved Equation Error Model. Acoustics. 2021; 3(2):354-363. https://doi.org/10.3390/acoustics3020024
Chicago/Turabian StyleYuan, Jun, Jun Li, Anfu Zhang, Xiangdong Zhang, and Jia Ran. 2021. "Active Noise Control System Based on the Improved Equation Error Model" Acoustics 3, no. 2: 354-363. https://doi.org/10.3390/acoustics3020024
APA StyleYuan, J., Li, J., Zhang, A., Zhang, X., & Ran, J. (2021). Active Noise Control System Based on the Improved Equation Error Model. Acoustics, 3(2), 354-363. https://doi.org/10.3390/acoustics3020024





