Influence of Swept Blades on Low-Order Acoustic Prediction for Axial Fans
Abstract
1. Introduction
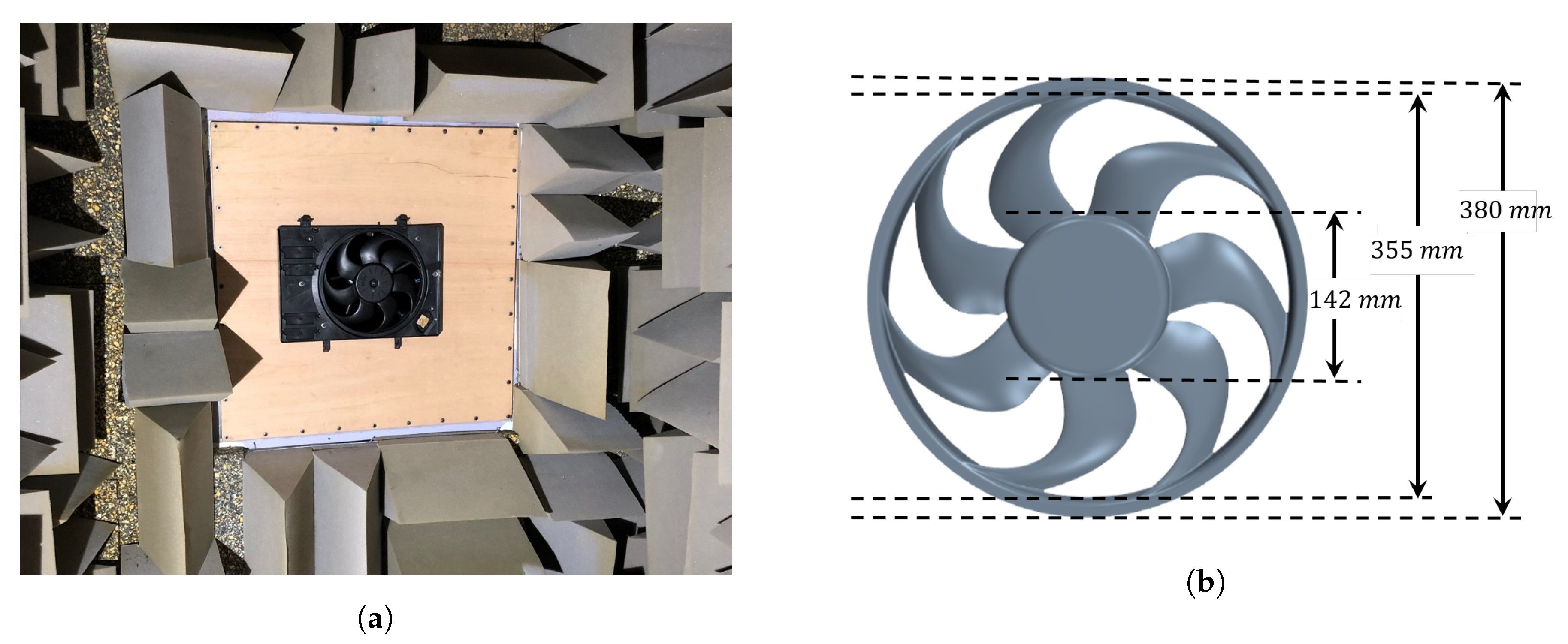
2. Experimental Setup
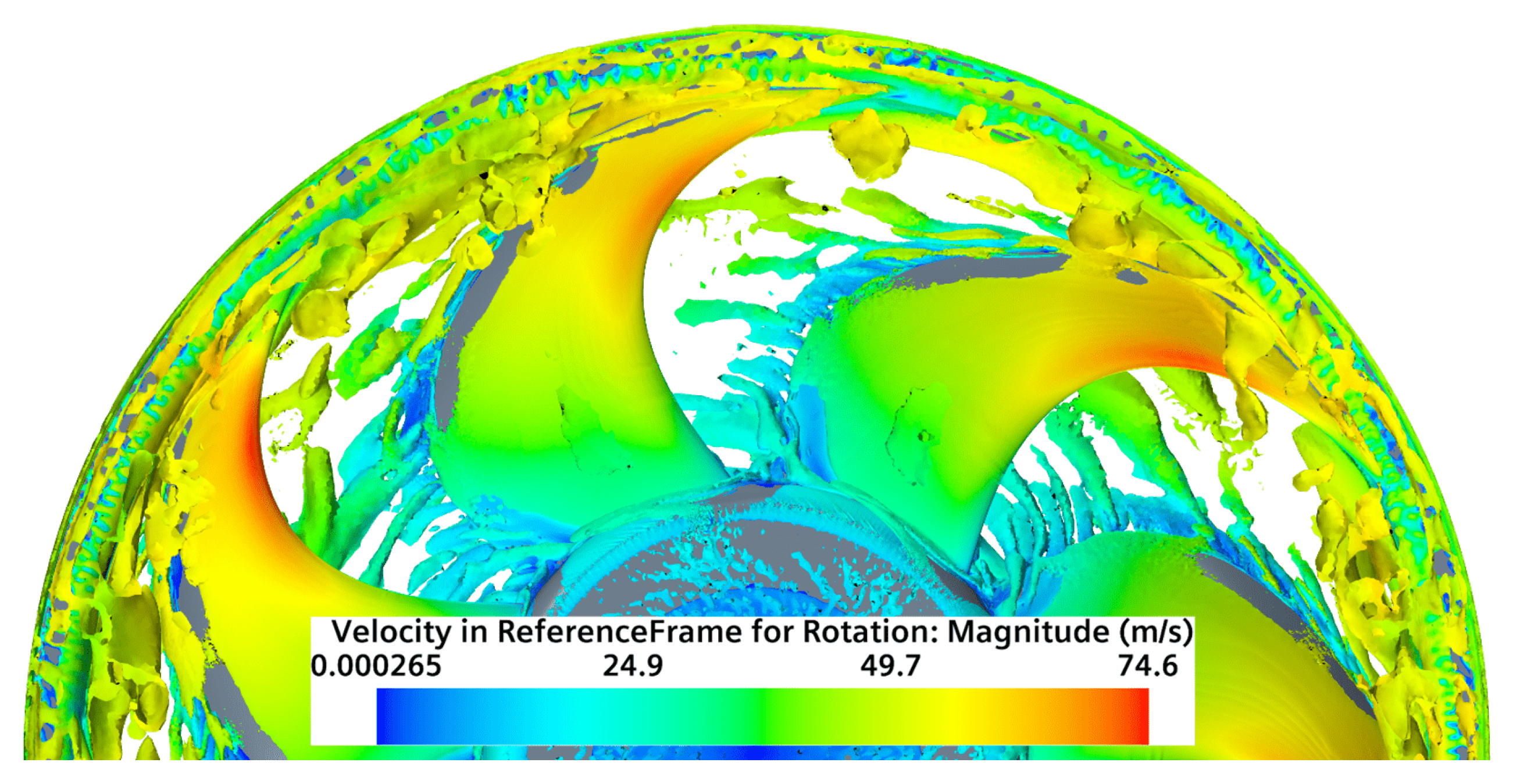
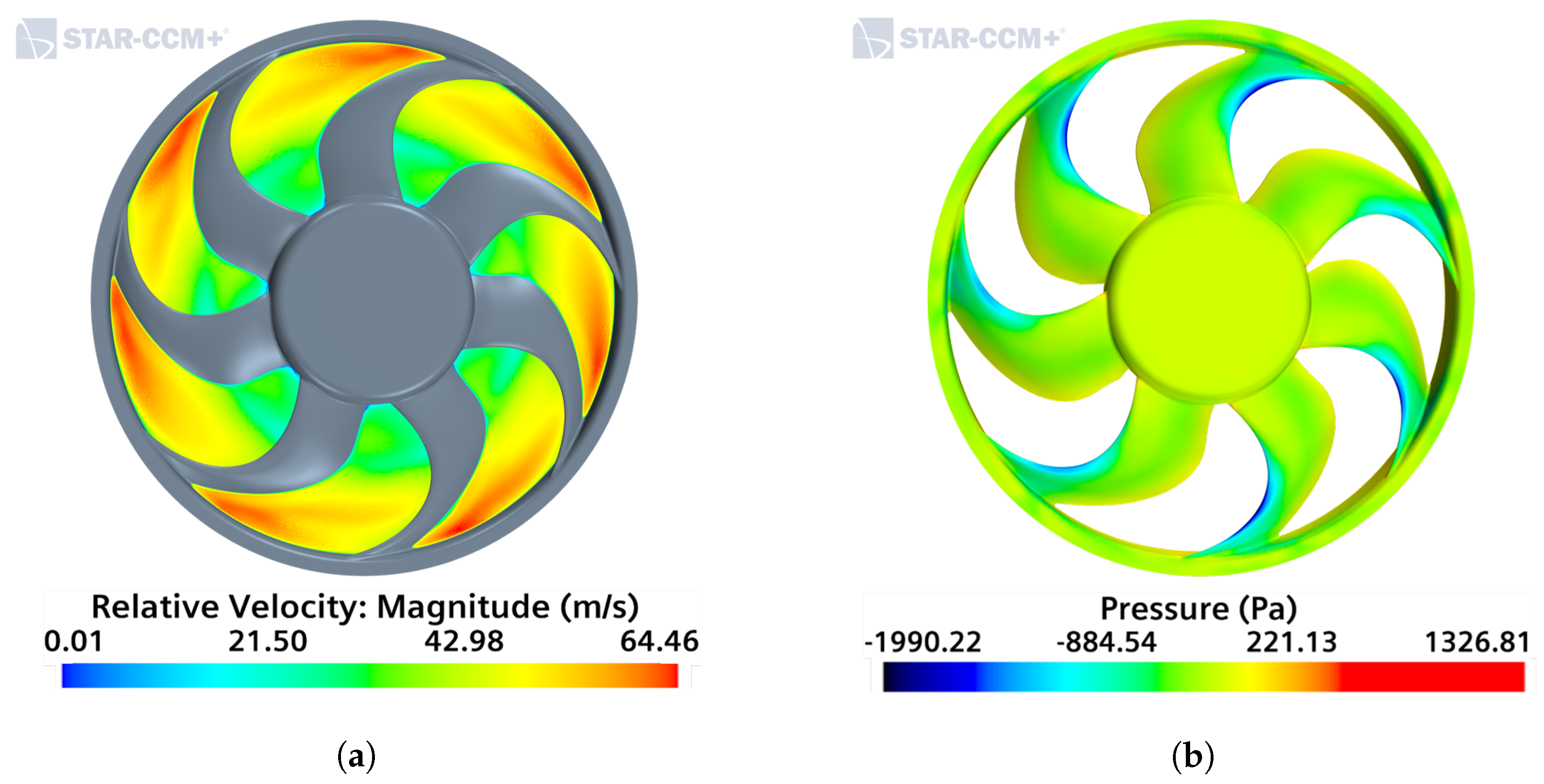
3. Numerical Simulation and RANS Extraction Procedure
3.1. Inlet Turbulence
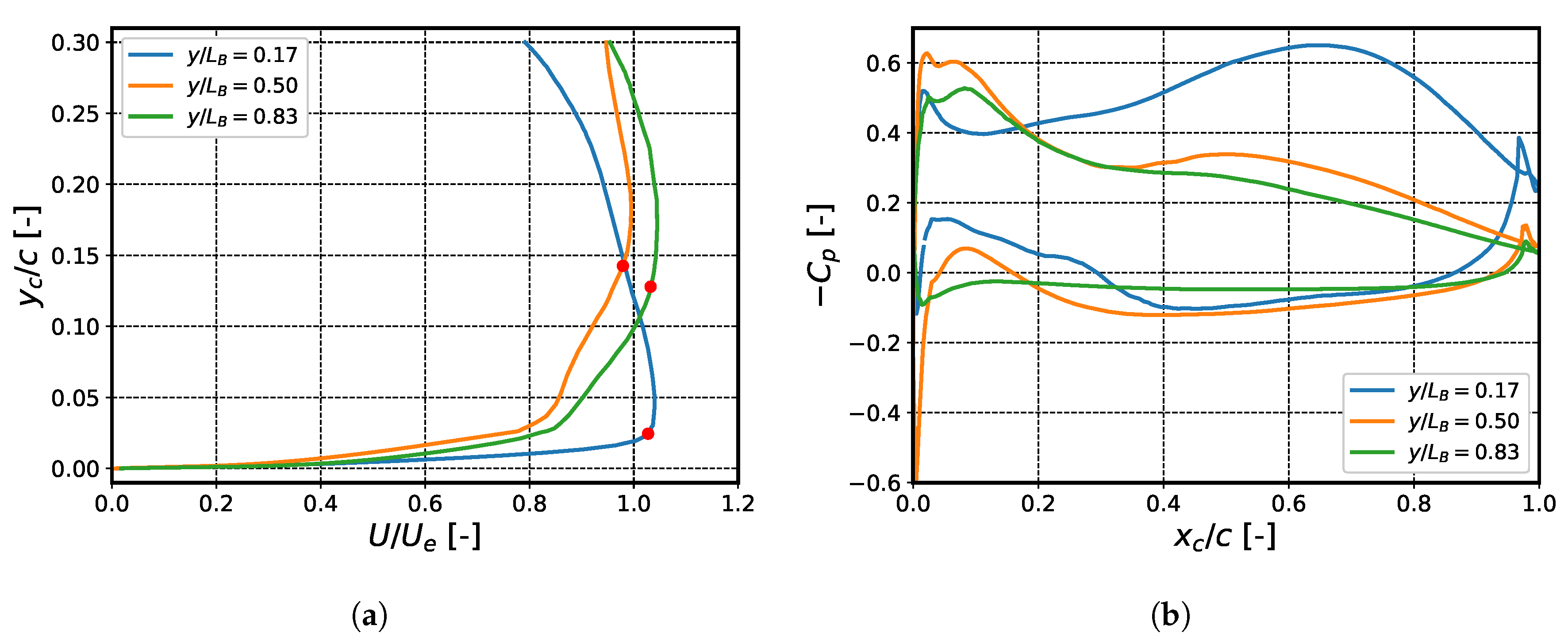
3.2. Boundary-Layer Parameters
4. Theoretical Background on Noise Prediction Methodology
4.1. Noise Emitted by Rotating Blades
4.2. Leading-Edge Noise Formulation
4.3. Trailing-Edge Noise Formulation
4.4. Generalized Corcos’ Model
4.5. Semiempirical Wall-Pressure Models
4.5.1. Goody’s Model
4.5.2. Rozenberg’s Model
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- .
4.5.3. Lee’s Model
5. Acoustic Far-Field Results
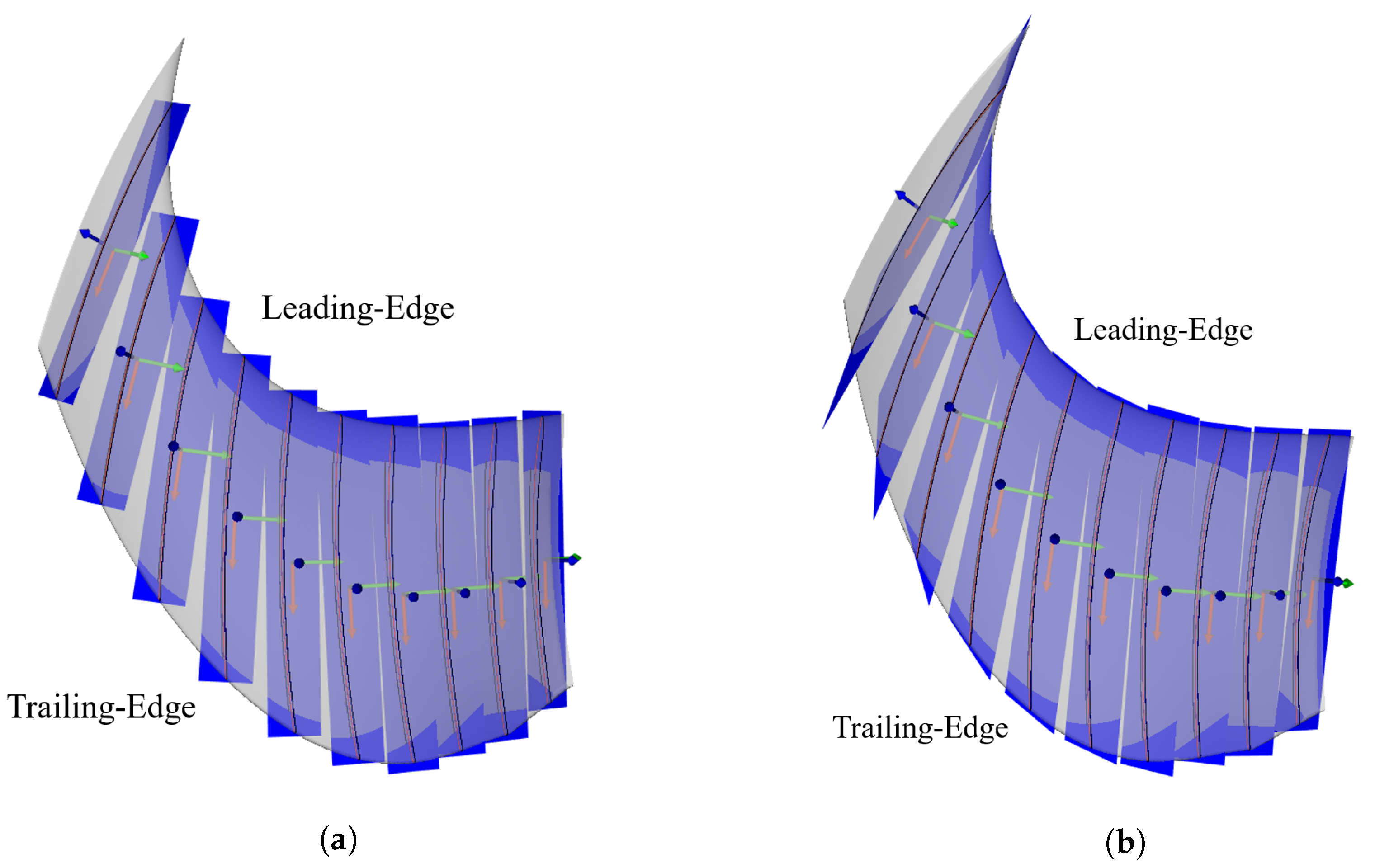
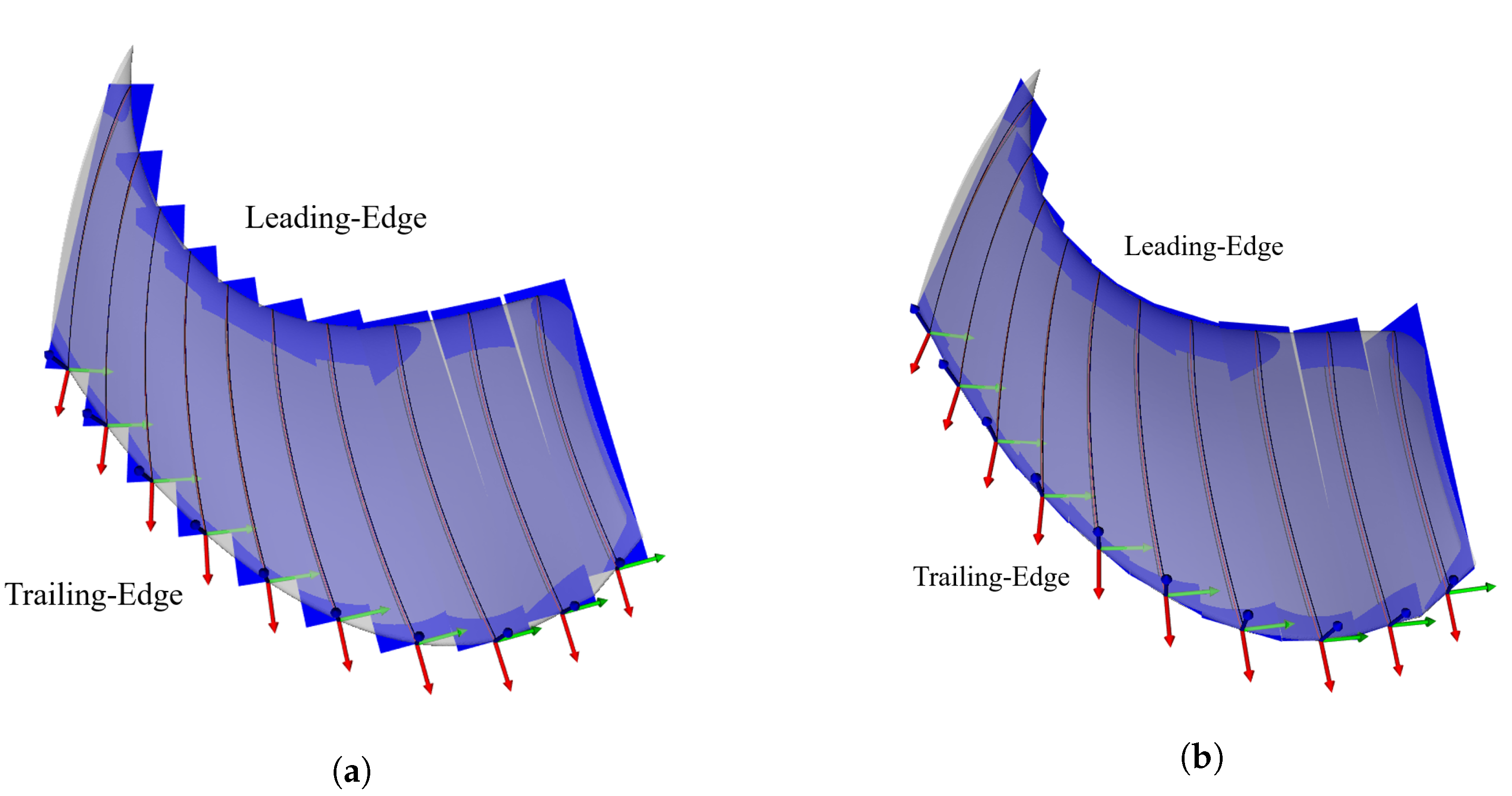
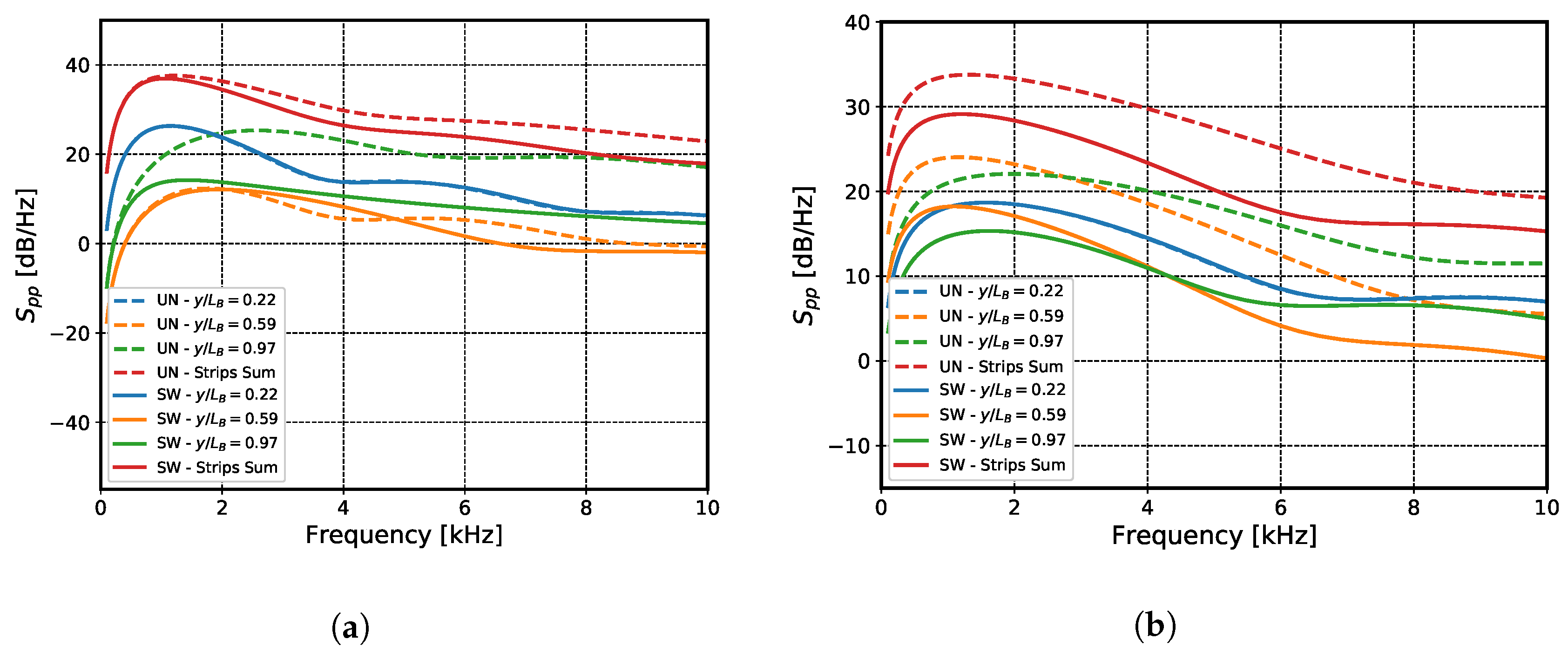
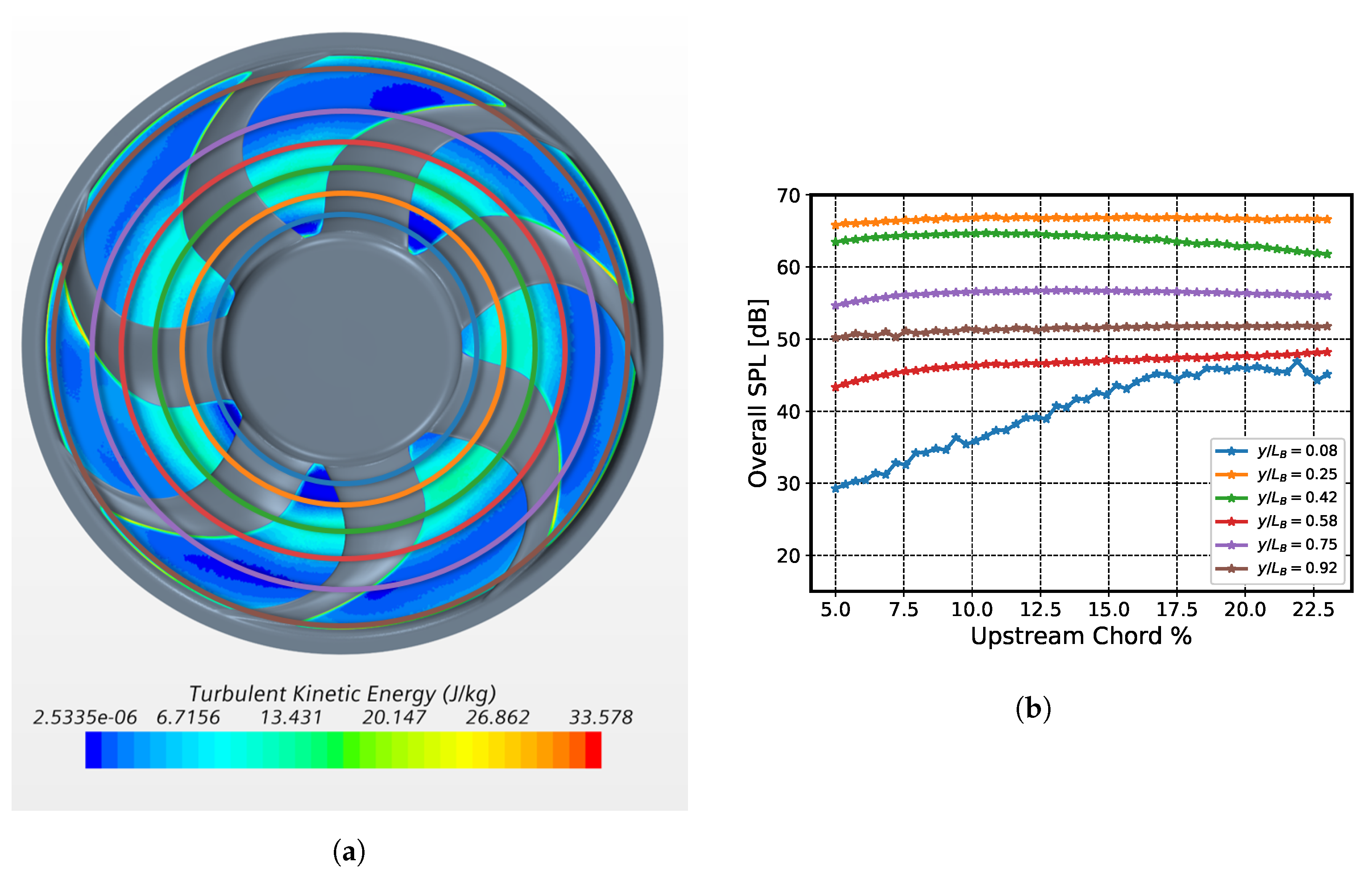
5.1. Noise Distribution over the Strips
5.2. Leading-Edge Upstream Extraction Location
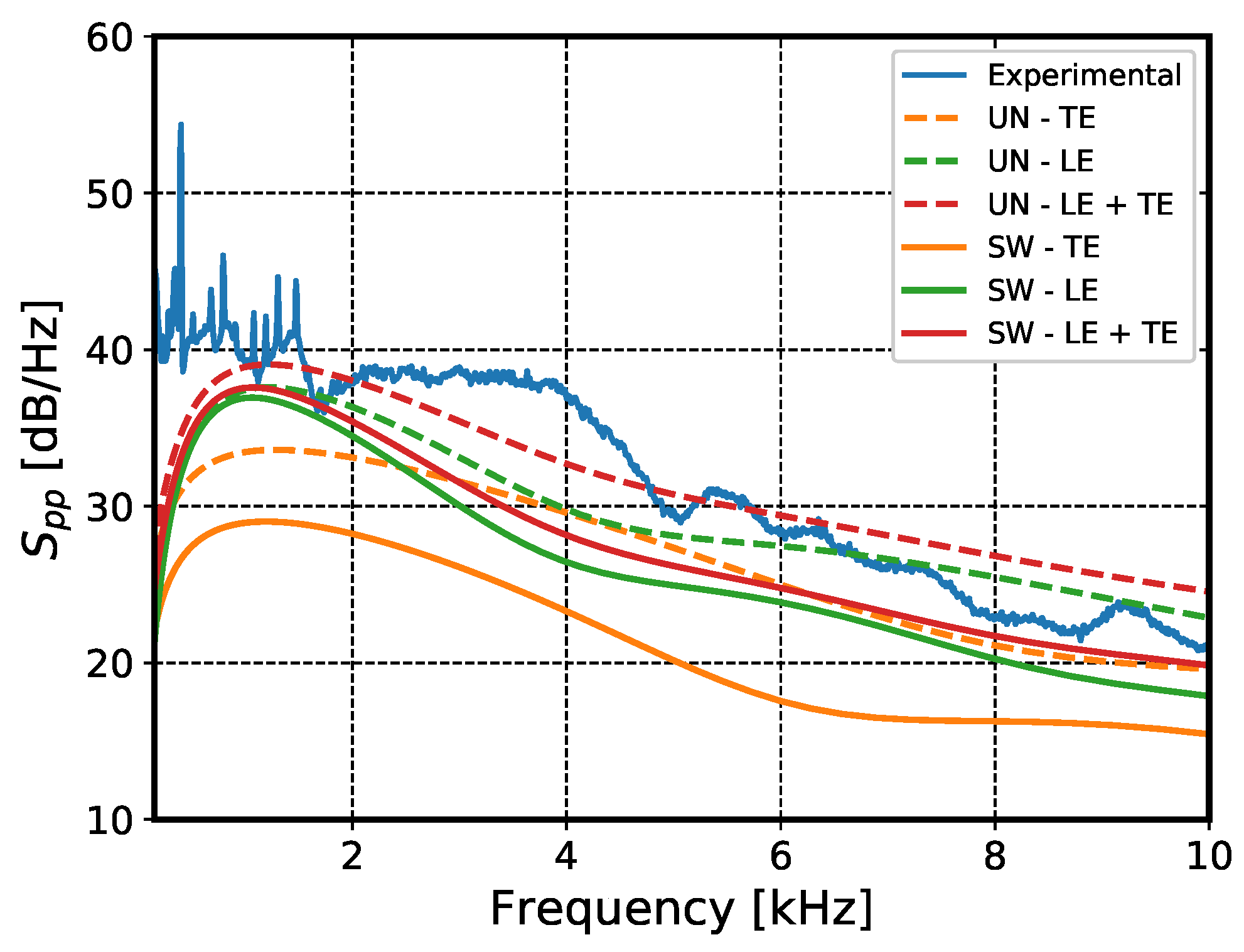
5.3. LE and TE Noise Comparison with Experimental PSD
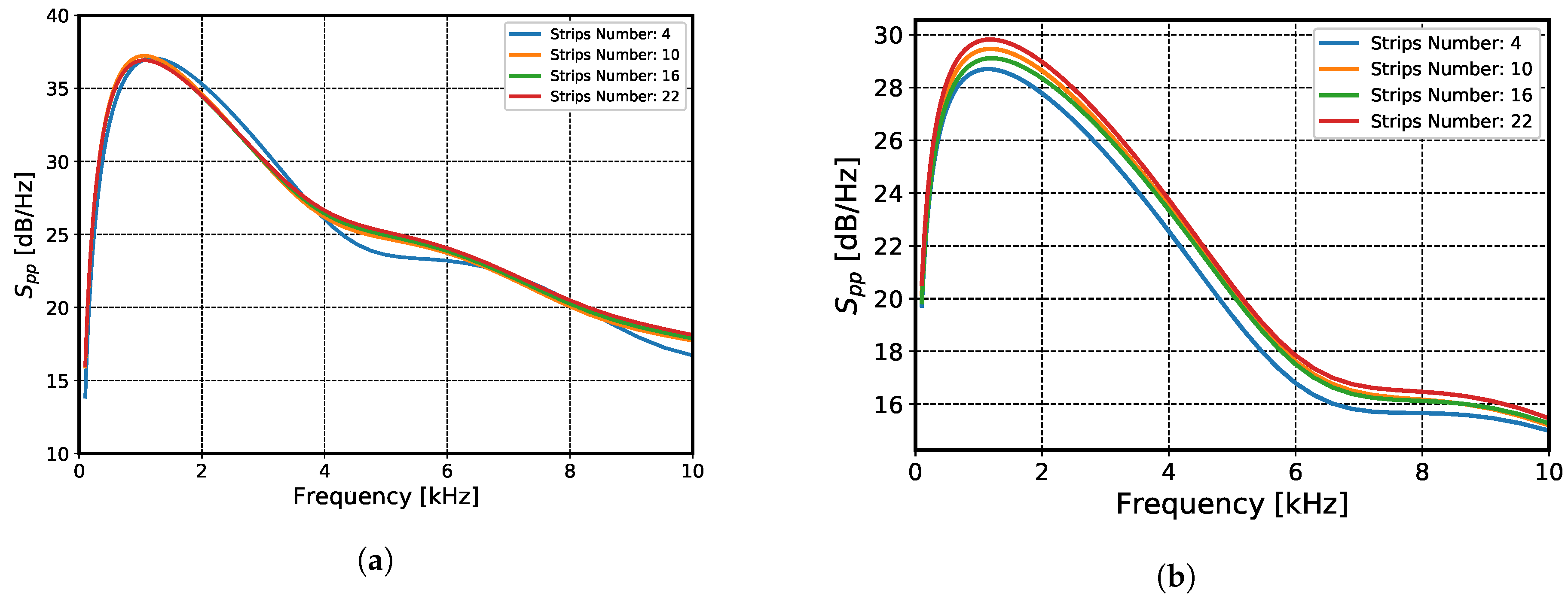
5.4. Sensitivity Study
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Latin letters: | |
| B | number of the blades |
| b | half-chord aligned with x and |
| rotated half-chord aligned with | |
| Corcos model constant | |
| c | chord aligned with |
| rotated chord aligned with | |
| speed of sound | |
| pressure coefficient | |
| Fresnel Integral | |
| wavenumber vector | |
| convective wavenumber parallel to | |
| aerodynamic wavenumber parallel to | |
| aerodynamic wavenumber parallel to | |
| acoustic wavenumber | |
| average wavenumber of the energy-containing eddies | |
| turbulent kinetic energy | |
| convective wavenumber | |
| leading-edge aeroacoustic transfer function | |
| trailing-edge aeroacoustic transfer function | |
| L | span of a strip aligned with the radius |
| rotated span of a strip aligned with | |
| radial blade length | |
| leading edge | |
| spanwise correlation length of wall-pressure fluctuations | |
| , Mach number based on the i-th mean velocity component | |
| Mach number of the source relative to the fluid | |
| Butterworth filter order coefficients | |
| laboratory pressure reference | |
| ratio of timescales of pressure | |
| r | fan radial distance |
| R | radius of the fan |
| listener’s corrected distance | |
| far-field sound PSD of the fan | |
| single-strip airfoil noise | |
| single-strip leading-edge airfoil noise | |
| single-strip trailing-edge airfoil noise | |
| trailing edge | |
| mean square of the velocity fluctuations | |
| U | boundary-layer velocity |
| local entrainment velocity | |
| convective velocity | |
| external boundary-layer velocity | |
| boundary-layer maximum velocity | |
| rotated velocity component parallel to | |
| rotated velocity component parallel to | |
| listener’s position | |
| local reference frame with x axis aligned with | |
| rotated local reference frame with parallel to the LE and TE edges | |
| strip-chord distance parallel to c | |
| vectorial location of the noise source | |
| boundary-layer dimensionless wall distance | |
| boundary-layer vertical distance | |
| Greek letters: | |
| compressibility factor | |
| compressibility factor based on i-th mean velocity component | |
| Gamma function | |
| boundary-layer thickness | |
| boundary-layer displacement thickness | |
| boundary-layer momentum thickness | |
| directivity angle in the X-Z plane | |
| turbulent integral length scale | |
| two-wavenumber velocity fluctuations spectrum | |
| single-point frequency spectrum of wall-pressure fluctuations | |
| two-wavenumber-frequency spectral density of wall-pressure fluctuations | |
| one-wavenumber-frequency spectral density of wall-pressure fluctuations | |
| fan azimuthal position | |
| sweep angle defined between x and | |
| laboratory density reference | |
| wall-shear stress across the boundary layer | |
| angular frequency | |
| source-emitted frequency | |
| turbulent kinetic energy specific dissipation rate | |
| fan velocity rotation | |
| Others: | |
| normalization by the rotated half chord, | |
| normalization by | |
| sweep-angle rotation |
References
- Moreau, S.; Roger, M. Advanced noise modeling for future propulsion systems. Int. J. Aeroacoust. 2018, 17, 576–599. [Google Scholar] [CrossRef]
- Allam, S.; Åbom, M. Noise reduction for automotive radiator cooling fans. In Proceedings of the FAN 2015, Lyon, France, 15–17 April 2015. [Google Scholar]
- Oerlemans, S. Reduction of wind turbine noise using blade trailing edge devices. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016. [Google Scholar]
- Schäfer, R.; Böhle, M. Validation of the Lattice Boltzmann Method for Simulation of Aerodynamics and Aeroacoustics in a Centrifugal Fan. Acoustics 2020, 2, 735–752. [Google Scholar] [CrossRef]
- Metzger, F.B.; Rohrbach, C. Benefits of blade sweep for advanced turboprops. J. Propuls. Power 1986, 2, 534–540. [Google Scholar] [CrossRef]
- Henner, M.; Demory, B.; Franquelin, F.; Beddadi, Y.; Zhang, Z. Test Rig Effect on Performance Measurement for Low Loaded Large Diameter Fan for Automotive Application. In Volume 1A: Aircraft Engine; Fans and Blowers; American Society of Mechanical Engineers: Düsseldorf, Germany, 2014. [Google Scholar]
- Henner, M.; Demory, B.; Alaoui, M.; Laurent, M.; Behey, B. Effect of Blade Curvature on Fan Integration in Engine Cooling Module. Acoustics 2020, 2, 776–790. [Google Scholar] [CrossRef]
- Moreau, S.; Roger, M. Competing Broadband Noise Mechanisms in Low-Speed Axial Fans. AIAA J. 2007, 45, 48–57. [Google Scholar] [CrossRef]
- Herold, G.; Zenger, F.; Sarradj, E. Influence of blade skew on axial fan component noise. Int. J. Aeroacoust. 2017, 16, 418–430. [Google Scholar] [CrossRef]
- Roger, M.; Moreau, S.; Guedel, A. Broadband fan noise prediction using single-airfoil theory. Noise Control Eng. J. 2006, 54, 5–14. [Google Scholar] [CrossRef]
- Moreau, S. Turbomachinery Noise Predictions: Present and Future. Acoustics 2019, 1, 92–116. [Google Scholar] [CrossRef]
- Sanjosé, M.; Moreau, S. Fast and accurate analytical modeling of broadband noise for a low-speed fan. J. Acoust. Soc. Am. 2018, 143, 3103–3113. [Google Scholar] [CrossRef]
- Grasso, G.; Roger, M.; Moreau, S. Effect of sweep angle and of wall-pressure statistics on the free-field directivity of airfoil trailing-edge noise. In Proceedings of the 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, 20–23 May 2019. [Google Scholar]
- Roger, M.; Schram, C.; Moreau, S. On vortex–airfoil interaction noise including span-end effects, with application to open-rotor aeroacoustics. J. Sound Vib. 2014, 333, 283–306. [Google Scholar] [CrossRef]
- Rozenberg, Y.; Roger, M.; Moreau, S. Rotating Blade Trailing-Edge Noise: Experimental Validation of Analytical Model. AIAA J. 2010, 48, 951–962. [Google Scholar] [CrossRef]
- Amiet, R. Acoustic radiation from an airfoil in a turbulent stream. J. Sound Vib. 1975, 41, 407–420. [Google Scholar] [CrossRef]
- Amiet, R. Noise due to turbulent flow past a trailing edge. J. Sound Vib. 1976, 47, 387–393. [Google Scholar] [CrossRef]
- Zarri, A.; Christophe, J.; Schram, C.F. Low-Order Aeroacoustic Prediction of Low-Speed Axial Fan Noise. In Proceedings of the 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, 20–23 May 2019; p. 2760. [Google Scholar]
- Lee, S. Empirical Wall-Pressure Spectral Modeling for Zero and Adverse Pressure Gradient Flows. AIAA J. 2018, 56, 1818–1829. [Google Scholar] [CrossRef]
- Corcos, G.M. The structure of the turbulent pressure field in boundary-layer flows. J. Fluid Mech. 1964, 18, 353–379. [Google Scholar] [CrossRef]
- Roger, M.; Moreau, S. Back-scattering correction and further extensions of Amiet’s trailing-edge noise model. Part 1: Theory. J. Sound Vib. 2005, 286, 477–506. [Google Scholar] [CrossRef]
- Caiazzo, A.; D’Amico, R.; Desmet, W. A Generalized Corcos model for modelling turbulent boundary layer wall pressure fluctuations. J. Sound Vib. 2016, 372, 192–210. [Google Scholar] [CrossRef]
- Magne, S.; Moreau, S.; Berry, A. Subharmonic tonal noise from backflow vortices radiated by a low-speed ring fan in uniform inlet flow. J. Acoust. Soc. Am. 2015, 137, 228–237. [Google Scholar] [CrossRef]
- Moreau, S.; Sanjose, M. Sub-harmonic broadband humps and tip noise in low-speed ring fans. J. Acoust. Soc. Am. 2016, 139, 118–127. [Google Scholar] [CrossRef]
- Sanjose, M.; Lallier-Daniels, D.; Moreau, S. Aeroacoustic Analysis of a Low-Subsonic Axial Fan. In Volume 1: Aircraft Engine; Fans and Blowers; Marine; ASME: Montreal, QC, Canada, 2015. [Google Scholar]
- Bilka, M.; Anthoine, J.; Schram, C. Design and evaluation of an aeroacoustic wind tunnel for measurement of axial flow fans. J. Acoust. Soc. Am. 2011, 130, 3788–3796. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Sreenivasan, K.R. On the universality of the Kolmogorov constant. Phys. Fluids 1995, 7, 2778–2784. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson Education Ltd.: Harlow, UK; New York, NY, USA, 2007. [Google Scholar]
- Schlinker, R.; Amiet, R. Helicopter rotor trailing edge noise. In Proceedings of the 7th Aeroacoustics Conference, Palo Alto, CA, USA, 5–7 October 1987; AIAA: Palo Alto, CA, USA, 1981. [Google Scholar]
- Sinayoko, S.; Kingan, M.; Agarwal, A. Trailing edge noise theory for rotating blades in uniform flow. Proc. R. Soc. A Math. Phys. Eng. Sci. 2013, 469, 20130065. [Google Scholar] [CrossRef]
- Giez, J.; Vion, L.; Roger, M.; Moreau, S. Effect of the Edge-and-Tip Vortex on Airfoil Selfnoise and Turbulence Impingement Noise. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016; AIAA: Lyon, France, 2016. [Google Scholar]
- Roger, M.; Carazo, A. Blade-Geometry Considerations in Analytical Gust-Airfoil Interaction Noise Models. In Proceedings of the 16th AIAA/CEAS Aeroacoustics Conference, Stockholm, Sweden, 7–9 June 2010. [Google Scholar]
- Rozenberg, Y. Modélisation Analytique du Bruit AéRodynamique à Large Bande des Machines Tournantes: Utilisation de Calculs MoyennéS de MéCanique des Fluides. Ph.D. Thesis, Ecole Centrale de Lyon, Ecully, France, 2007; p. 190. [Google Scholar]
- Christophe, J.; Anthoine, J.; Moreau, S. Amiet’s Theory in Spanwise-Varying Flow Conditions. AIAA J. 2009, 47, 788–790. [Google Scholar] [CrossRef]
- Christophe, J. Application of Hybrid Methods to High Frequency Aeroacoustics. Ph.D. Thesis, Universite Libre de Bruxelles, Brussels, Belgium, 2011. [Google Scholar]
- Volkmer, K.; Carolus, T. Correction: Aeroacoustic airfoil shape optimization utilizing semi-empirical models for trailing edge noise prediction. In Proceedings of the 2018 AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 25–29 June 2018; American Institute of Aeronautics and Astronautics: Atlanta, GA, USA, 2018. [Google Scholar] [CrossRef]
- Goody, M. Empirical Spectral Model of Surface Pressure Fluctuations. AIAA J. 2004, 42, 1788–1794. [Google Scholar] [CrossRef]
- Küçükosman, Y.C.; Christophe, J.; Schram, C. Trailing edge noise prediction based on wall pressure spectrum models for NACA0012 airfoil. J. Wind Eng. Ind. Aerodyn. 2018, 175, 305–316. [Google Scholar] [CrossRef]
- Chase, D.M. Turbulent Boundary Layer Wall Pressure. J. Sound Vib. 1980, 70, 29–67. [Google Scholar] [CrossRef]
- Howe, M.S. Acoustics of Fluid-Structure Interactions, 1st ed.; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Bradshaw, P.; Ferriss, D.H. Applications of a General Method of Calculating Turbulent Shear Layers. J. Basic Eng. 1972, 94, 345–351. [Google Scholar] [CrossRef]
- Rozenberg, Y.; Robert, G.; Moreau, S. Wall-Pressure Spectral Model Including the Adverse Pressure Gradient Effects. AIAA J. 2012, 50, 2168–2179. [Google Scholar] [CrossRef]
- Zagarola, M.V.; Smits, A.J. Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 1998, 373, 33–79. [Google Scholar] [CrossRef]
- Clauser, F.H. Turbulent Boundary Layers in Adverse Pressure Gradients. J. Aeronaut. Sci. 1954, 21, 91–108. [Google Scholar] [CrossRef]
- Coles, D. The law of the wake in the turbulent boundary layer. J. Fluid Mech. 1956, 1, 191–226. [Google Scholar] [CrossRef]
- Durbin, P.A.; Pettersson Reif, B.A. Statistical Theory and Modeling for Turbulent Flows; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Amoiridis, O.; Zarri, A.; Zamponi, R.; Christophe, J.; Schram, C.F.; Yakhina, G.; Moreau, S. Experimental Analysis of the Sound Radiated by an Automotive Cooling Module Working at Different Operational Conditions. In AIAA AVIATION 2020 FORUM; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2020. [Google Scholar] [CrossRef]
- Guérin, S.; Kissner, C.; Seeler, P.; Blázquez, R.; Carrasco Laraña, P.; de Laborderie, H.; Lewis, D.; Chaitanya, P.; Polacsek, C.; Thisse, J. ACAT1 Benchmark of RANS-Informed Analytical Methods for Fan Broadband Noise Prediction: Part II—Influence of the Acoustic Models. Acoustics 2020, 2, 617–649. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zarri, A.; Christophe, J.; Moreau, S.; Schram, C. Influence of Swept Blades on Low-Order Acoustic Prediction for Axial Fans. Acoustics 2020, 2, 812-832. https://doi.org/10.3390/acoustics2040046
Zarri A, Christophe J, Moreau S, Schram C. Influence of Swept Blades on Low-Order Acoustic Prediction for Axial Fans. Acoustics. 2020; 2(4):812-832. https://doi.org/10.3390/acoustics2040046
Chicago/Turabian StyleZarri, Alessandro, Julien Christophe, Stéphane Moreau, and Christophe Schram. 2020. "Influence of Swept Blades on Low-Order Acoustic Prediction for Axial Fans" Acoustics 2, no. 4: 812-832. https://doi.org/10.3390/acoustics2040046
APA StyleZarri, A., Christophe, J., Moreau, S., & Schram, C. (2020). Influence of Swept Blades on Low-Order Acoustic Prediction for Axial Fans. Acoustics, 2(4), 812-832. https://doi.org/10.3390/acoustics2040046






