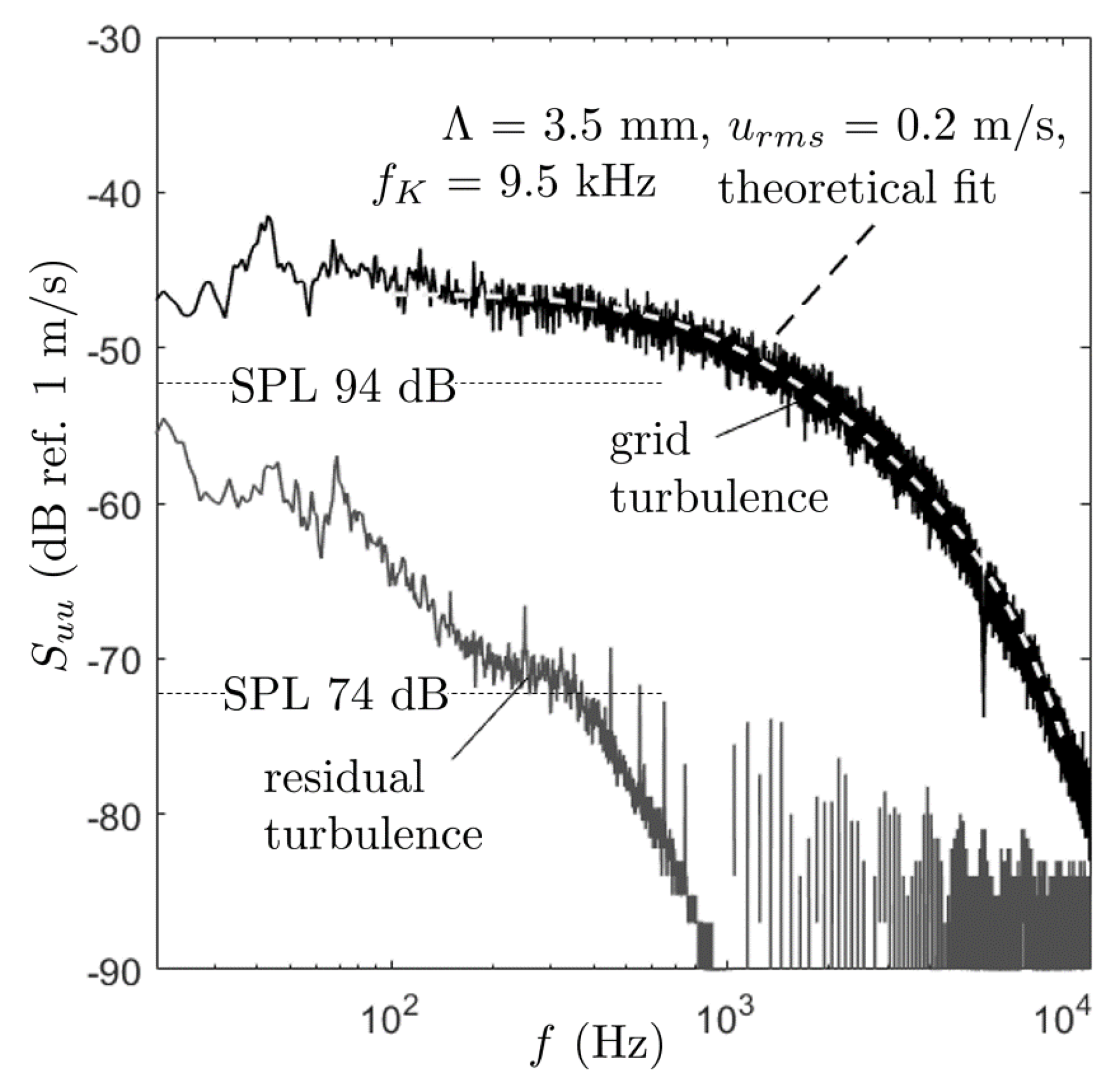
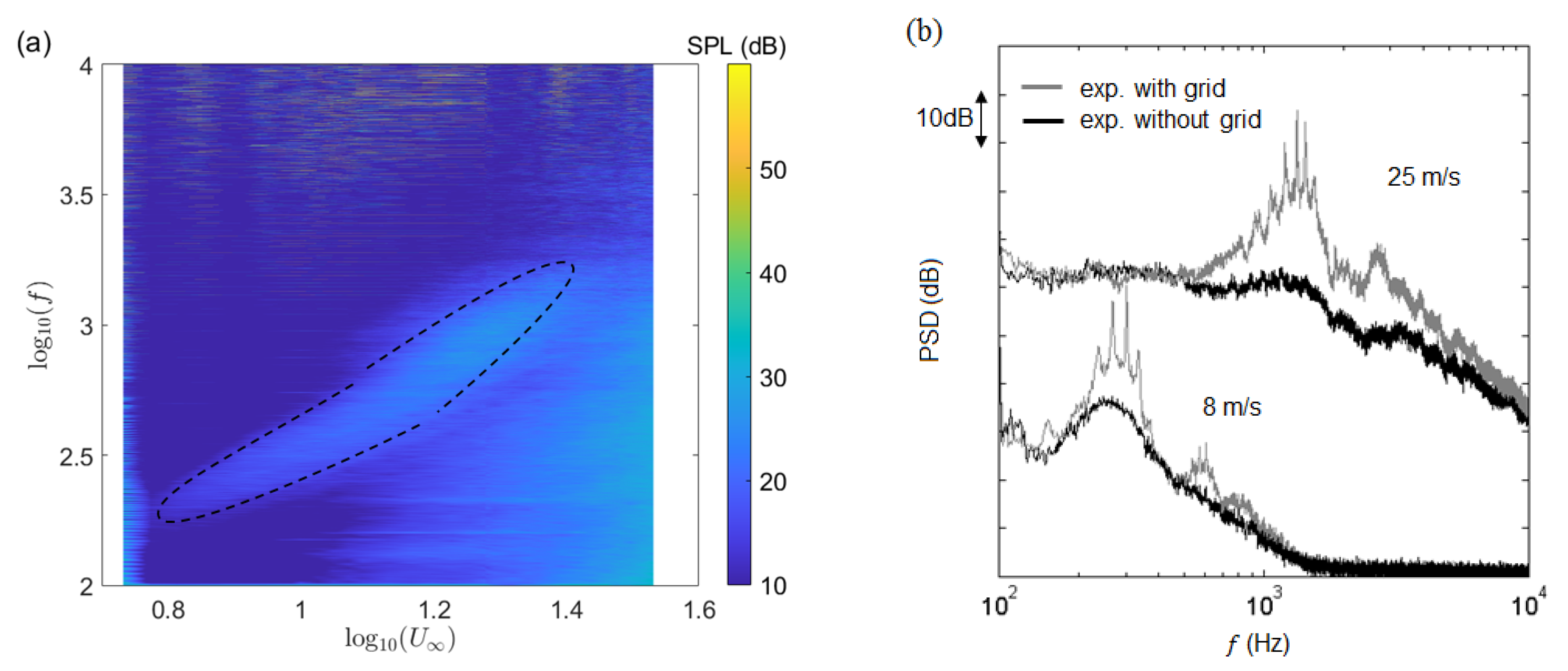
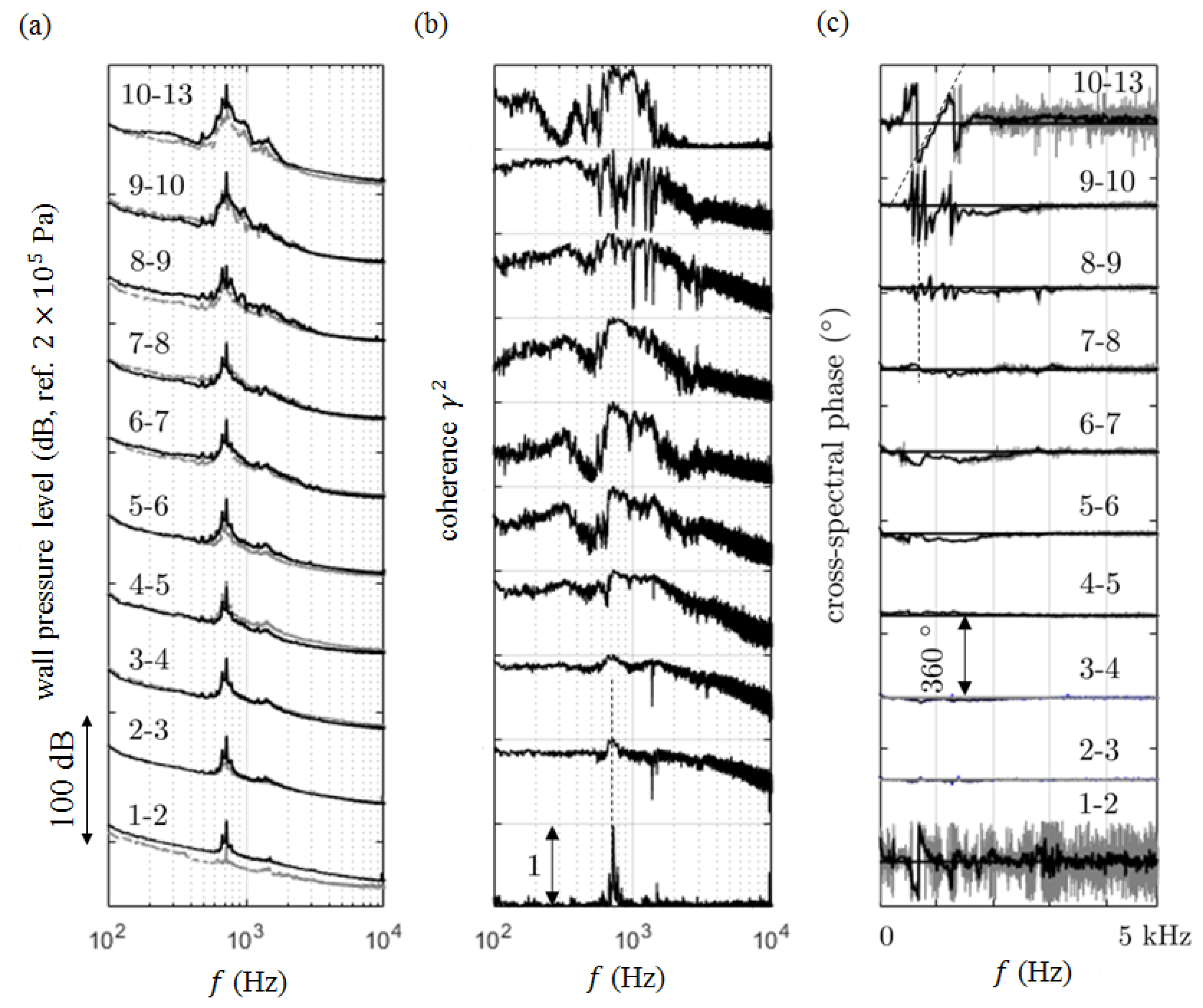
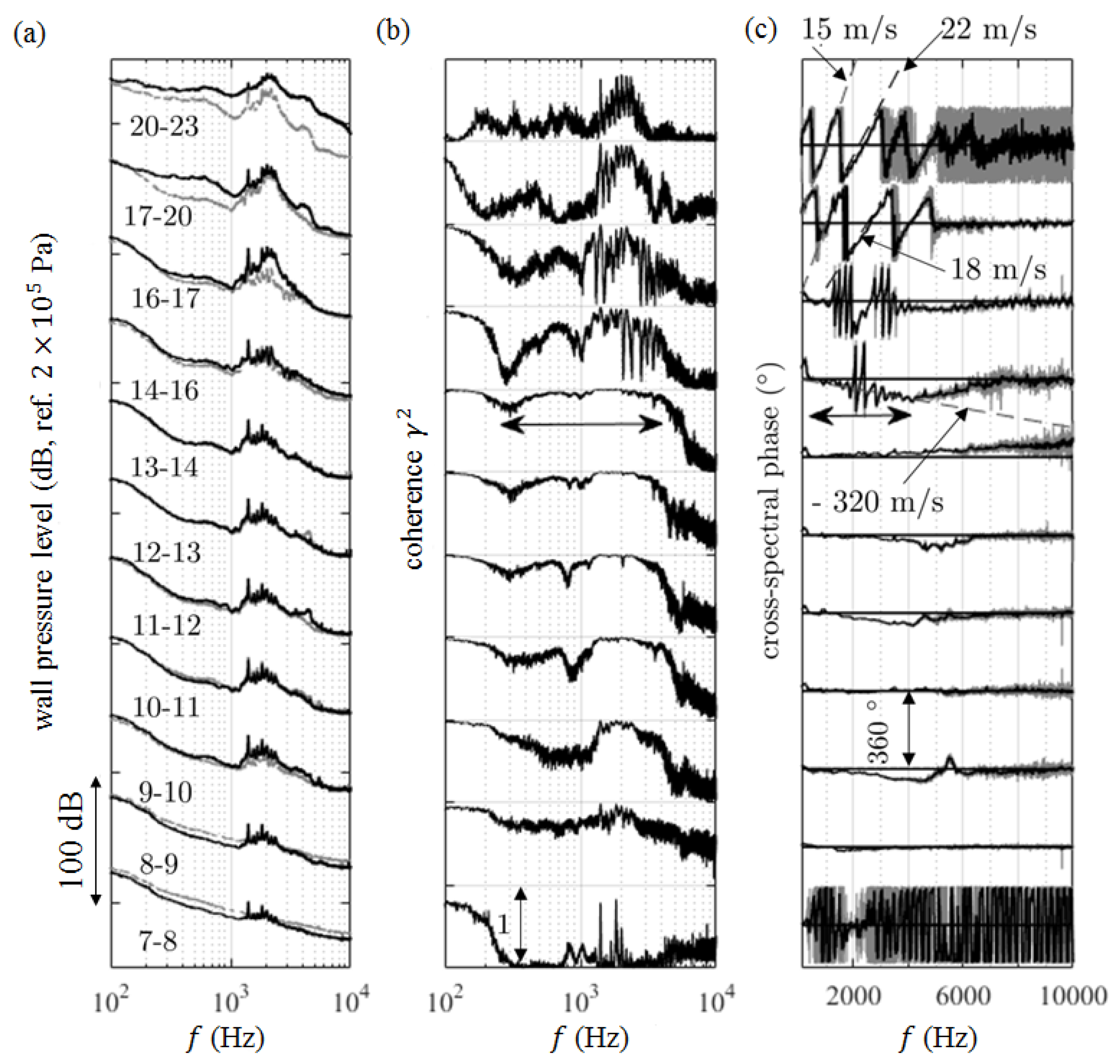
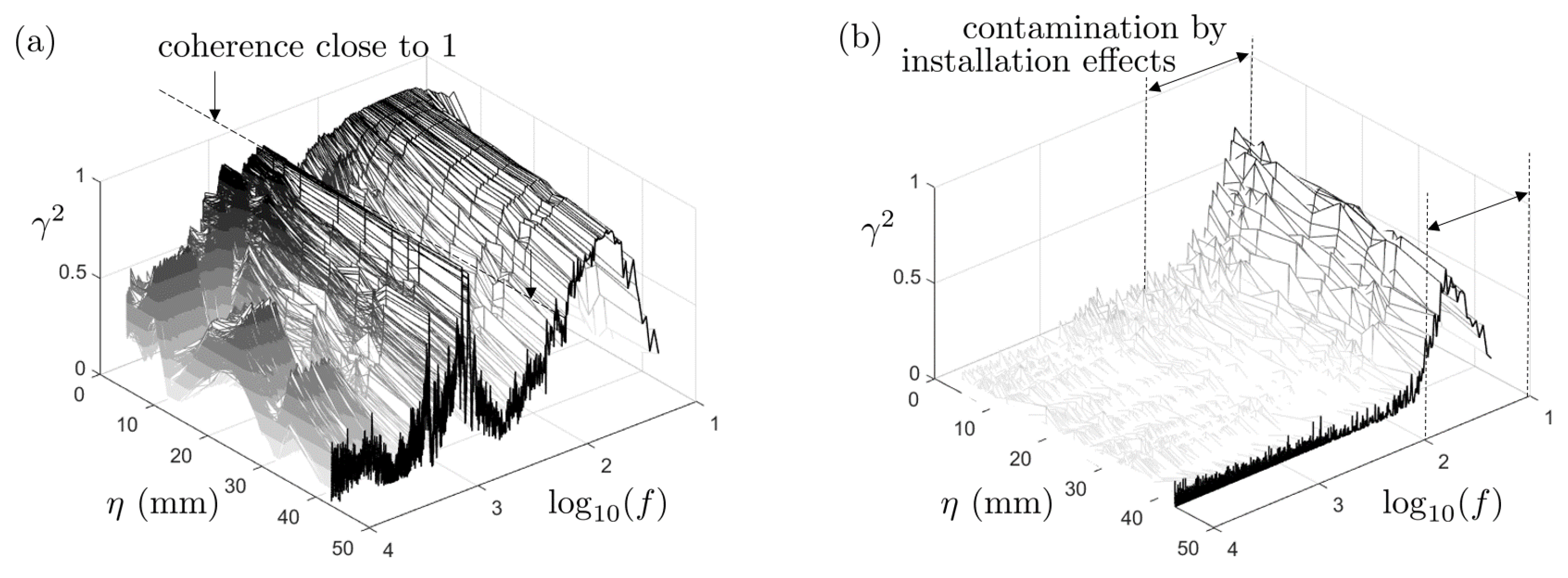
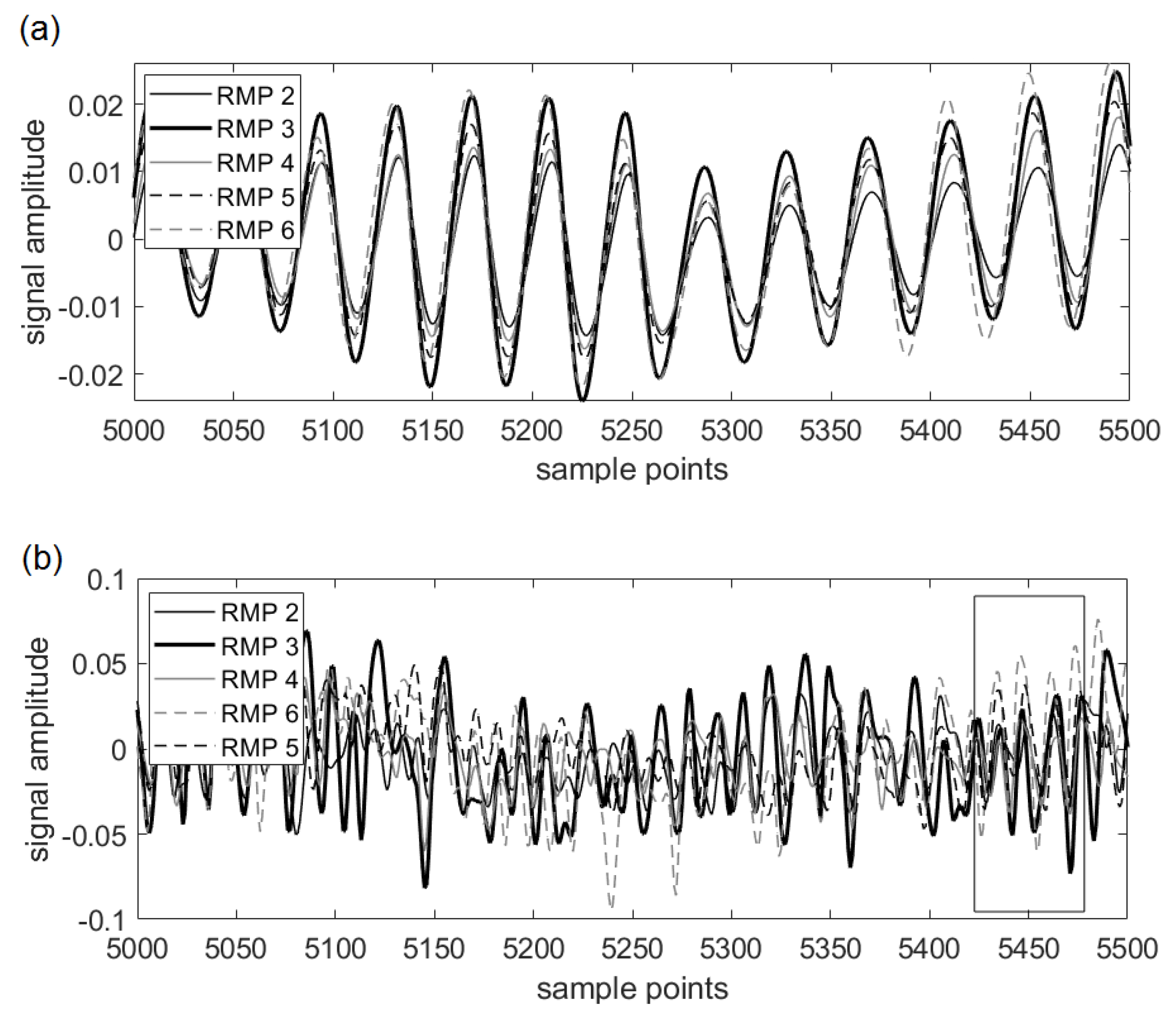
1. Introduction
Tonal trailing-edge noise refers to the loud, annoying whistling sometimes produced lifting surfaces at low Reynolds numbers and moderate angles of attack in a clean flow. It is heard not only in laboratory experiments involving aerofoils in controlled flow conditions, but also in rotating-blade engineering applications. Most often, true tones are identified in the first case, and a narrow-band spectral peak is emitted in the second case. This suggests that a well-defined tonal character
a priori requires spanwise-homogeneous conditions such as those ensured by the wind-tunnel mounting of rectangular aerofoils. Typically, glider wings emit tonal trailing-edge noise during some operations because the incident flow normal to the wing span is close to these conditions. In contrast, rotating-blade technologies make a more or less broadband or narrow-band signature instead of discrete frequencies because the flow conditions vary along the blade span. In fact, different acoustic signatures can be produced depending on blade design and on the portion of span actually involved in the generation of noise. For instance, a peak at much higher frequencies than the rotational noise has been reported for a low-speed fan by Longhouse [
1], whereas a signature very similar to those of rectangular isolated aerofoils with multiple tones has been observed during the wind-tunnel testing of model propellers by Grosche and Stiewitt [
2]. Both examples are discussed later on in the paper. Yet, for simplicity the wording ‘tonal noise’ is used in all cases throughout the paper.
The common necessary feature for the generation of tonal noise is the existence of an unstable, laminar/transitional boundary layer all over the aerofoil, or at least on one side. Indeed, forcing the transition to turbulence before the trailing edge by appropriate tripping suppresses the tones and produces low-level broadband trailing-edge noise. In that sense, tonal noise is characteristic of low Reynolds numbers. Instabilities in the boundary layers are a key factor for the emission of the sound by interaction with the trailing edge. For this reason the mechanism is referred to as Laminar-Boundary-Layer (LBL) wave radiation in this work, to be related to the LBL vortex-shedding noise according to the classification by Brooks et al. [
3]. The same mechanism is called vortex shedding by Longhouse [
1]. It has been thoroughly investigated over the last 50 years but some details of the underlying physics still remain points of controversy. Apart from its fundamental interest LBL-wave radiation is a matter of concern for all aerofoils and blades used in unmanned air vehicles (UAV) and micro air vehicles (MAV) that operate at low Reynolds numbers and that are promised to an intensive use in the near future.
After Fink [
4] and other works reviewed for instance by Longhouse [
1], Paterson et al. [
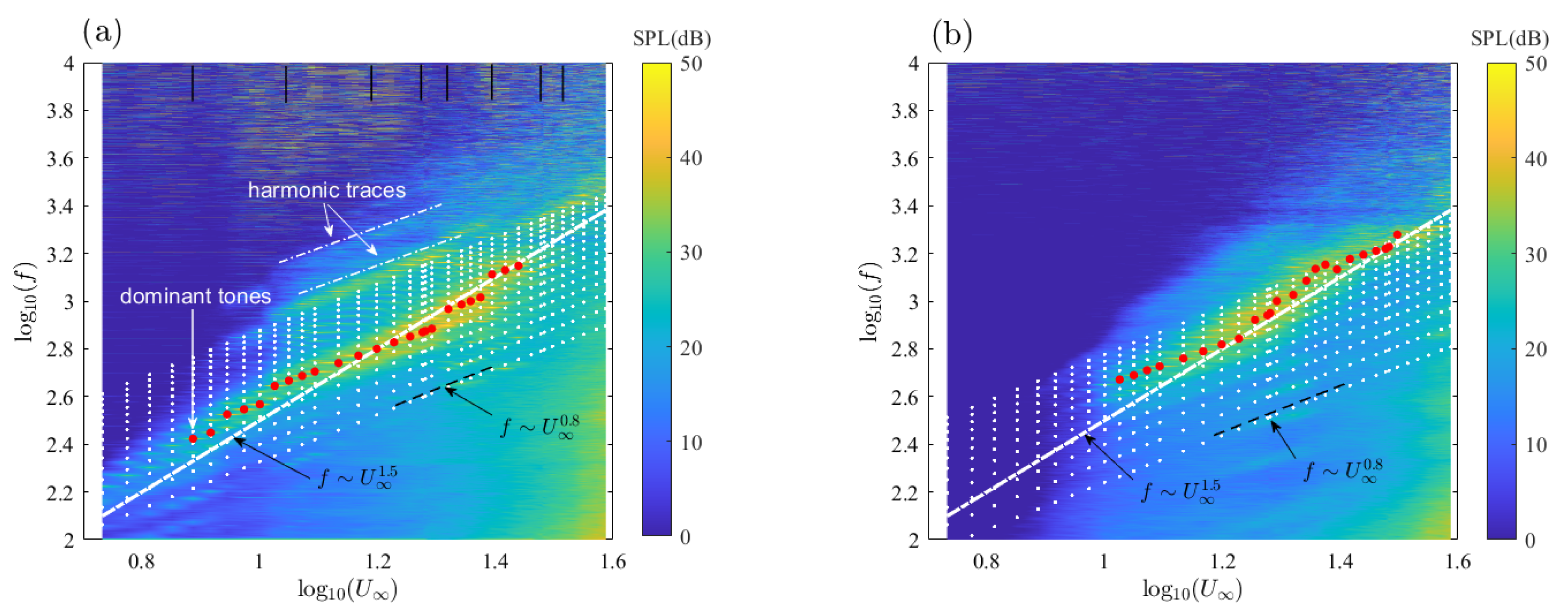
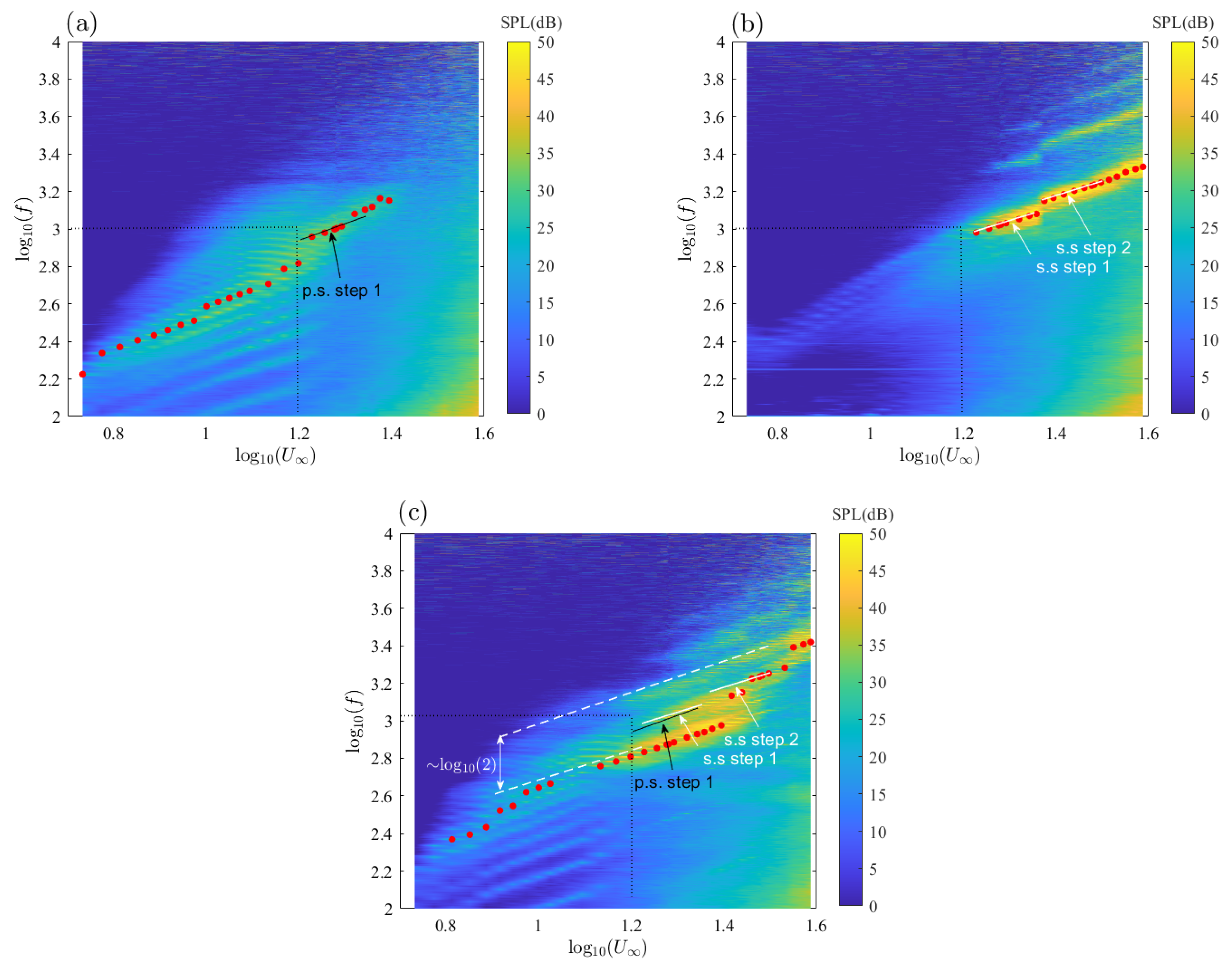
5] published a detailed study of the far-field tonal noise of the NACA-0012 aerofoil in an open-jet wind tunnel. A so-called ladder-type structure was observed when the frequency of the dominant tone was plotted as an increasing function of flow velocity. The global slope was found to approximately correspond to the law
, where
f was the frequency and
the incident flow speed, whereas the steps followed parallel lines scaling with a law close to
. Tam [
6] conjectured that an acoustic feedback loop took place between some source point in the wake and the trailing edge to explain the ladder-type structure. Longhouse later argued that the feedback rather took place between the trailing edge and an upstream point [
1]. He suggested that Tollmien–Schlichting (TS) waves generated at some initial point in the suction-side boundary layer of a cambered aerofoil were convected downstream toward the trailing edge where they scattered as sound. The acoustic waves propagating upstream were able to amplify the instabilities at some frequencies for which a favourable phase condition was fulfilled, yielding the emergence of discrete tones in the sound spectrum. The same interpretation was refined by Arbey and Bataille [
7] who stressed that the noise combined two components, namely a hump-like signature associated with the natural frequency range of the boundary-layer instabilities and discrete tones reinforced by the acoustic feedback loop identified by Longhouse. When simulating the NACA-0012 aerofoil at non-zero angle of attack, Desquesnes et al. pointed out that a primary feedback loop was set on the pressure side [
8]. They also assumed the existence of a second feedback loop on the suction side. The double feedback mechanism on a NACA-0012 aerofoil at non-zero angle of attack was also been assumed by Arcondoulis [
9] to explain multiple observed tones with high intensity.
Yet, this feature is not essential because only one laminar boundary layer, the opposite one being turbulent, is enough to ensure the emission of tones. It can therefore be guessed that several regimes of feedback take place depending on the flow conditions [
10]. Chong and Joseph [
11] inspected the relationships between the tones and confirmed that the lag between the frequency of maximum amplification for the instabilities and the multiple discrete tones caused the jumps of the dominant tonal frequency.
Some apparent contradiction was raised as the ladder-type structure was not found during measurements performed in a closed-section wind tunnel by Nash et al. [
12,
13]. The authors only observed a regular, monotonic frequency increase with flow speed. They suspected that previous studies in which the ladder-type structure was found were influenced by installation effects. Tests repeated in various open-jet installations including setups with narrow supports indicate that this should not be the case [
14]. Later, Tam and Ju [
15] showed on the basis of two-dimensional Direct Numerical Simulations (DNS) that only one tone was produced by the aerofoil and confirmed the assumption of Nash et al. [
12]. Yet, in the considered range of transitional Reynolds number based on the chord length
between 2 and 5 ×
, the 2D simulation might not yield a realistic turbulent flow. Some contributors also tried to bring out necessary and sufficient conditions for the effective emission of tones. Lowson et al. [
16] concluded that coherent instabilities in a laminar boundary layer, on the one hand, and the formation of a separation bubble, on the other hand, are not sufficient conditions [
12] if not associated. Other studies [
17,
18] evidenced that separation bubbles are involved in high-level tonal noise generation. Moreover, the location of the separation bubble strongly depends on the Reynolds number and on the angle of attack. Typically, this allows for suction-side dominated and pressure-side dominated regimes of tonal noise emission for the NACA-0012 aerofoil at low Reynolds numbers and at high Reynolds numbers, respectively. Acoustic measurements and particle image velocimetry (PIV) reported by Pröbsting et al. [
18,
19] indicate that the separation areas act as an amplifier for the instability waves. The authors also confirmed a ladder-type structure compatible with the aforementioned power laws identified by Paterson et al. [
5]. Furthermore, a time-resolved analysis showed that the tone frequencies were associated with vortical patterns at the trailing edge. Gerakopulos and Yarusevych [
20] used time-resolved wall-pressure measurements and hot-wire anemometry to investigate the separation bubbles on a NACA-0018 aerofoil. They observed a strong correlation between velocity fluctuations in the separated shear layer and wall-pressure fluctuations, and deduced values of the convection speed of the instabilities from measurements on pairs of wall microphones. A similar investigation will be detailed later on.
Except for the rotating-blade applications, most aforementioned isolated-aerofoil studies focused on the NACA-0012 aerofoil, which provides a reference configuration for comparing works by various teams. Padois et al. [
10,
21] also investigated another aerofoil geometry of engineering interest, namely a Controlled-Diffusion (CD) aerofoil used for low-speed fans and turboengine-compressor blades. They observed the same tonal-noise mechanisms with similar characteristics. In their anechoic wind tunnel with low turbulence intensity (less than 4%), they also detected both stationary tones and intermittent ones depending on the Reynolds number
and the angle of attack. A Lattice-Boltzmann (LBM) DNS of the CD aerofoil by Sanjosé et al. [
22] for an observed intermittent noise regime (
geometric angle of attack) led to the identification of two states of quiet and intense events yielding the intermittent tone. The state switched in time depending on whether or not the laminar separation bubble was shedding weak or strong vortices. The vortices were formed from strong Kelvin–Helmholtz instabilities, which broke down near the trailing edge and induced transition to turbulence. This has been later confirmed by tomographic particle image velocimetry [
23]. The synthesis of aforementioned observations makes the conjunction of a separation bubble and of large coherent structures a necessary condition to produce a significant tonal trailing-edge noise.
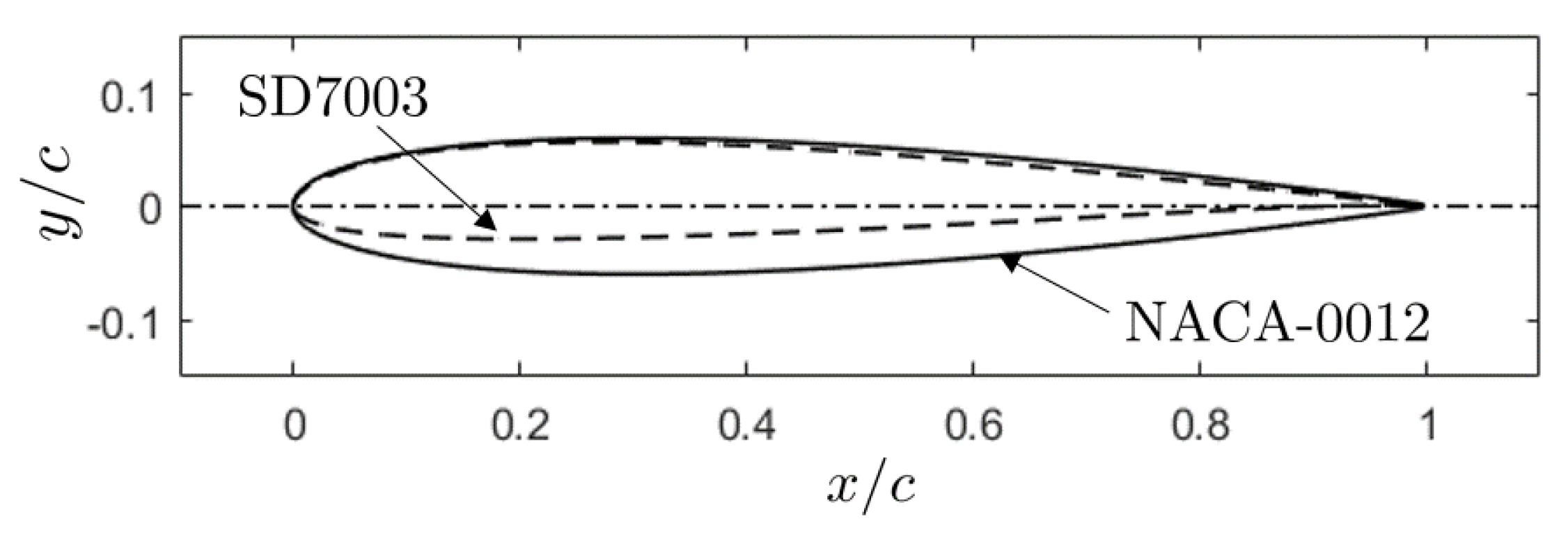
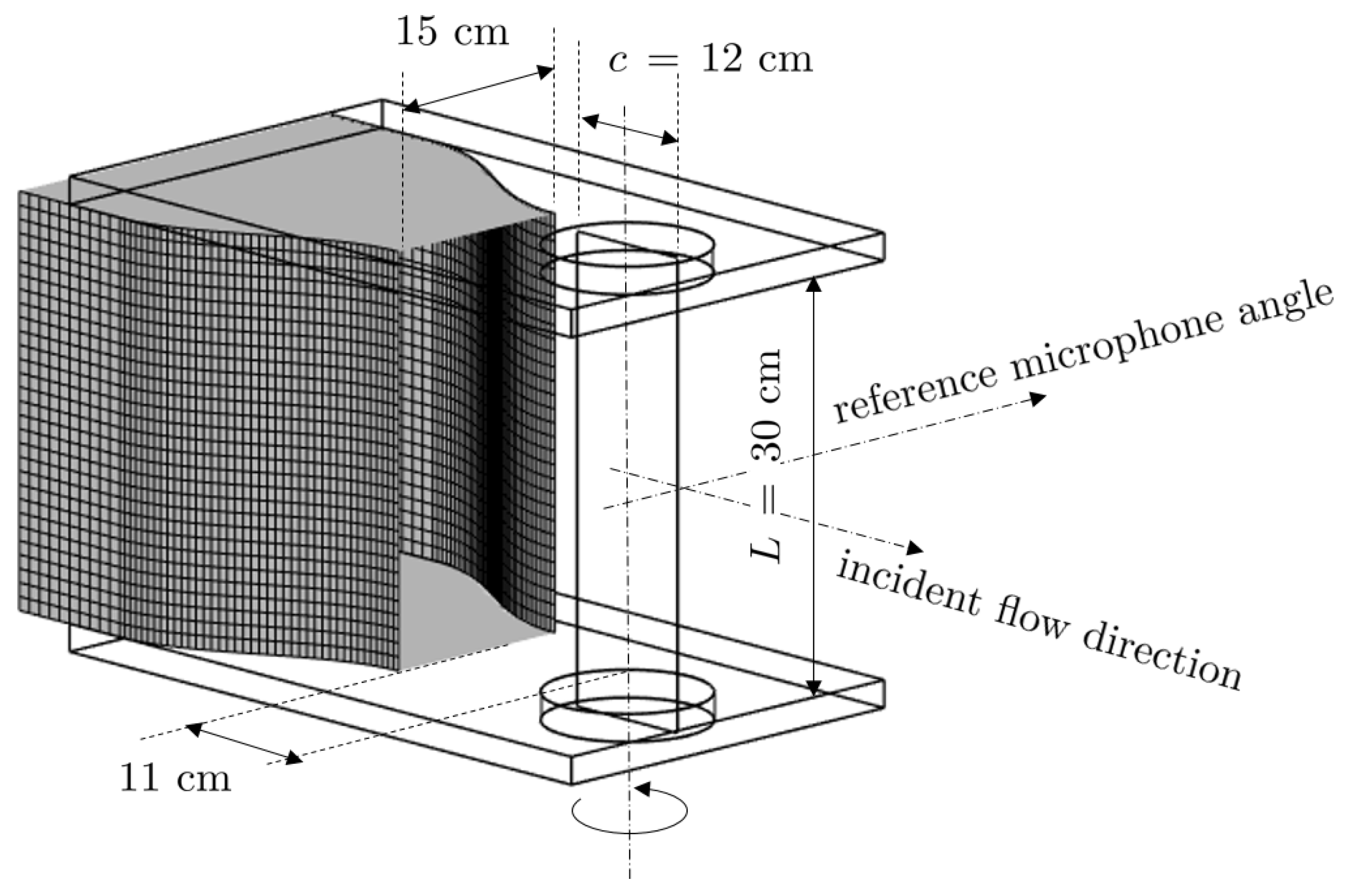
The present contribution is part of a collaborative research between Embry-Riddle Aeronautical University (ERAU) and Ecole Centrale de Lyon (ECL). It is aimed at completing the knowledge about tonal trailing-edge noise with experimental, analytical, and numerical investigations. The experimental study and the analytical modeling have been carried out at ECL [
24,
25] and the numerical simulations performed at ERAU [
26,
27,
28]. Two aerofoils have been selected, namely the symmetric NACA-0012 aerofoil and a slightly cambered SD7003 aerofoil. The former is again taken as a well documented reference aerofoil, which allows comparing with previously reported studies. The latter is widely used in MAV and UAV and is also considered as a way of addressing the effect of aerofoil design on the noise emission.
The article presents key results of the extended experimental work achieved during the project, not exhaustively detailed for the sake of conciseness. Analytical predictions of some aspects of the mechanism are also used to discuss cause-to-effect relationships. The experiment is mainly aimed at confirming or refuting controversial points, such as:
the possible reason of discrepancies in experimental and numerical studies,
the role of the separation bubble in tonal noise generation,
the experimental setup issues,
and at providing a complete database for the validation of the numerical simulations by ERAU. The database includes the measurements of both aerodynamic and acoustic quantities, such as far-field acoustic pressure, wall-pressure statistics, mean-pressure coefficient, mean and fluctuating velocities and flow visualization. The time-frequency and bicoherence analyses have also been used as in [
10]. Bicoherence is not discussed here because it could not help interpreting the mechanism, apart from confirming that the amplification of tones involves a significant nonlinearity. The experimental setup, aerofoil instrumentation and methodology are first described in
Section 2. The main results and their interpretation are presented in
Section 3. The noise emission regimes and the role of the separation bubble are highlighted during the discussion. The detailed analysis of the wall-pressure measurements with cross-spectral coherence and phase is presented to distinguish the aerodynamic and acoustic nature of recorded signals. The additional
Section 4 is dedicated to the analysis of several experiments performed on low-speed fans and propellers. It proves that the laminar-boundary-layer instabilities are also observed in rotating machines. Finally
Section 5 is dedicated to the analytical modeling of both near-field and far-field pressures associated with amplified tones.
4. Comparison with Rotating-Blade Configurations
Stating about the possible occurrence of aforementioned observed phenomena in true rotating-blade environments is a matter of practical interest. It is addressed in this section by inspection of previous works by Grosche and Stiewitt [
2] and Longhouse [
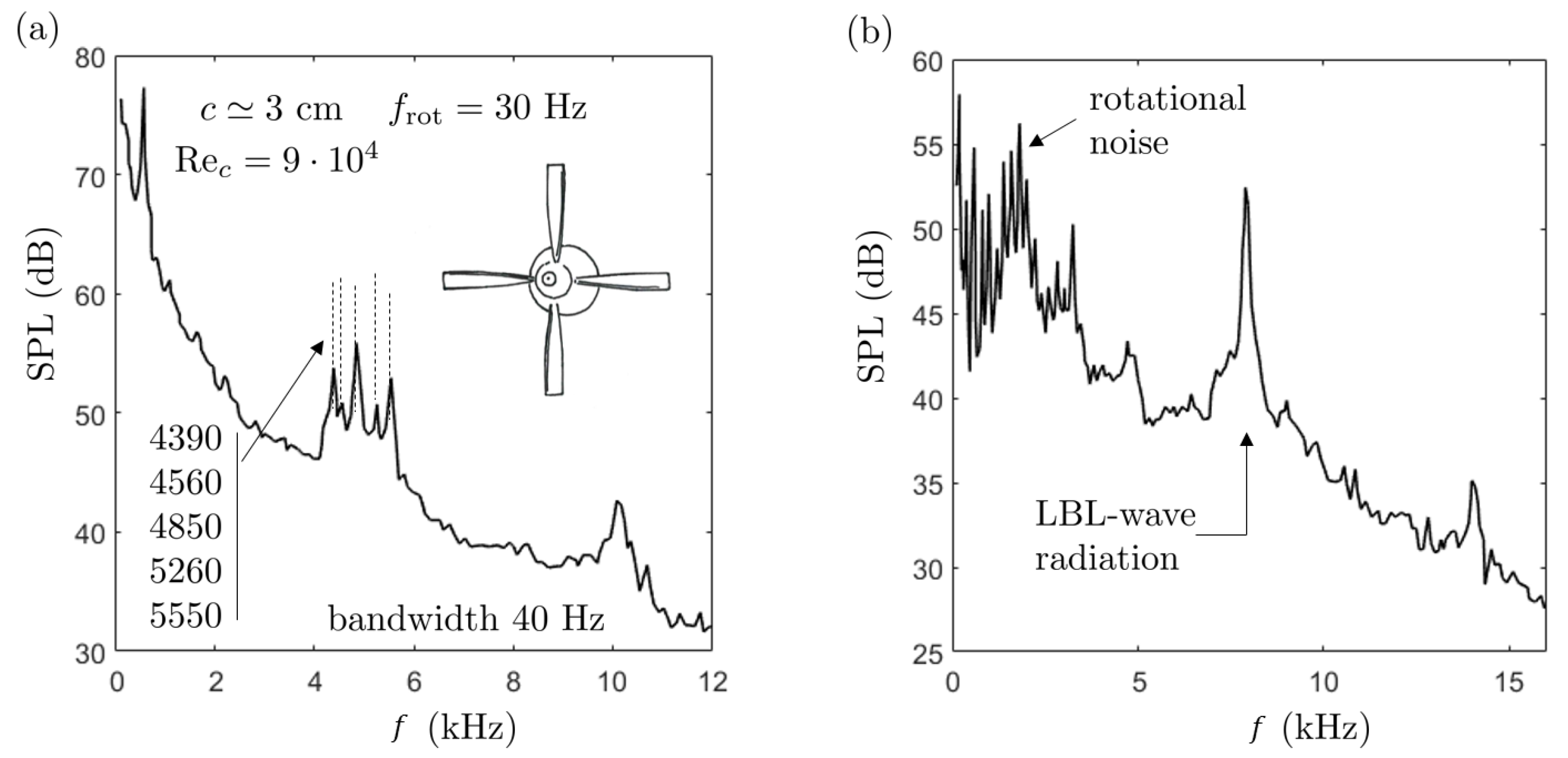
1], on the one hand, and of unpublished results for a small 9-bladed low-speed fan used for cooling electronic racks, on the other hand. Grosche and Stiewitt’s investigation refers to a four-bladed model propeller with a conventional blade design. The blades have a quite large aspect ratio. They are shown with the sound spectrum measured for some intermediate loading conditions of the blades using a mirror microphone in
Figure 21, reproduced from the reference. The microphone is in the rotation plane. The spectrum features a clear narrow-band hump with several superimposed tones centered around 5 kHz as well as a harmonic hump around 10 kHz. This behavior is very similar to the signature of both aerofoils investigated in the present work for some speeds. However, the rotating motion causes an additional modulation of the actually emitted frequencies, which must be taken into account.
Longhouse [
1] observed LBL-wave radiation in the experimental study of a low-speed four-bladed fan. Tests were performed with tripping to force transition to turbulence in the boundary layers on all blades, except for a small portion of span near the tip of a single blade. This ensured a laminar regime on this portion and highlighted the nearly-tonal signature. The quality of the flow was also checked visually with an acenaphthene mixture. A typical sound spectrum at reduced speed is shown in
Figure 21b. It exhibits a single peak frequency but up to three frequencies are reported by Longhouse at higher speeds. The microphone is on axis in this case so that no rotation-induced modulation occurs, as emphasized below. Longhouse’s interpretation is compatible with the assumption of a feedback according to Equation (
3) except that the term
is not considered. At the price of some adjustment it led to the orders
12, 13, and 14 for the measured tones. The fact that higher orders
n only can be identified is confirmed by matching theoretical lines in
Figure 6. Now in both aforementioned references there is no proof that the multiple tones are produced simultaneously. If they are, there is no clue of an underlying modulation mechanism other than the effect of rotation.
The aforementioned modulation effect can be assessed in both experiments. To this end, expressions for the Fourier transform of the far-field acoustic pressure for a rotating blade segment as provided in many handbooks, for instance [
49], are reliable. If a compact blade segment of mean radius
and coherent emission at the angular frequency
are assumed, this transform reads
being the acoustic wavenumber at angular frequency
,
the rotational speed,
the stagger angle of the blades as defined with respect to the rotational plane,
the dipole source strength, and
R the distance. The dipole character is strictly valid only at low frequencies but it is retained for simplicity in the present estimates. For an observer in the rotation plane, at 90
from the propeller axis as in Grosche and Stiewitt’s experiment the expression reduces to
which corresponds to the maximum amount of modulation, whereas for an on-axis observer, thus
as in Longhouse’s experiment it reduces to
because only the term
contributes. No modulation occurs in this case. Therefore, the discussion now focuses on Grosche and Stiewitt’s experiment.
It can be guessed that the LBL waves are not blade-to-blade correlated, so that the main trends of the formula are not questioned if all blades are taken into account. The Dirac comb of angular frequencies
is generated by the modulation but its envelope is determined by the function
in Equation (
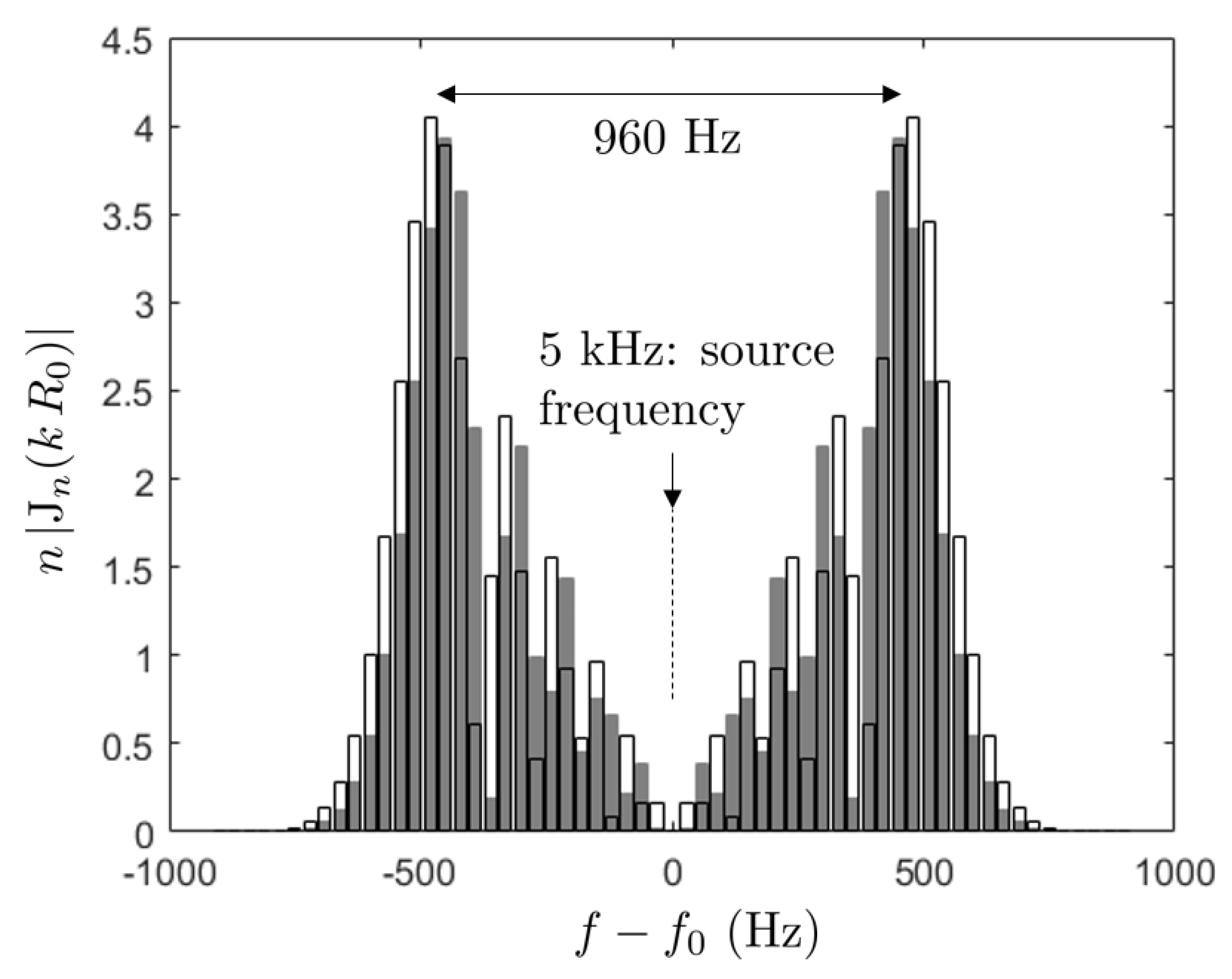
11). This function is plotted in
Figure 22 for values of
of 88% and 92% of the tip radius in Grosche and Stiewitt’s experiment and the same parameters as in
Figure 21a, in particular a source frequency
Hz. Arbitrarily selecting radii close to the blade-tip region is justified by the fact that the latter has low twist and is more likely to allow the onset of tonal noise. As a result that the frequency resolution of 40 Hz is higher than the modulating frequency of 30 Hz, it is expected to generate two peaks in the sound spectrum apart from the actually emitted frequency
. The fact that the source frequency is not theoretically captured is because the term
is zero in the sum. Probably this is not so in the experiment because the mirror averages sounds emitted also at angles different from 90
; in this case the more complete form of the expression, Equation (
10) should be used. Yet, five tones are observed, the frequencies of which are indicated in
Figure 21a. The theoretical peak-to-peak distance is around 960 Hz, which is smaller than the measured span of about 1160 Hz between the extreme tones in the figure. If only the first four or last four tones from the five are considered the value of 960 Hz is recovered. It is therefore concluded that more than just one tone is emitted by the blade segments responsible for the LBL-wave radiation. As a complement to the test illustrated in
Figure 3, these results confirm that the present observations on isolated aerofoils are representative of true rotating-blade features and not deteriorated by installation effects. The similarity of the results is even surprising in view of the spanwise-variable conditions encountered on the propeller. The design of the blades makes their outer part nearly rectangular with no sweep and moderate twist [
2]; therefore, only the tip region very likely experiences the favorable conditions for sustained LBL waves.
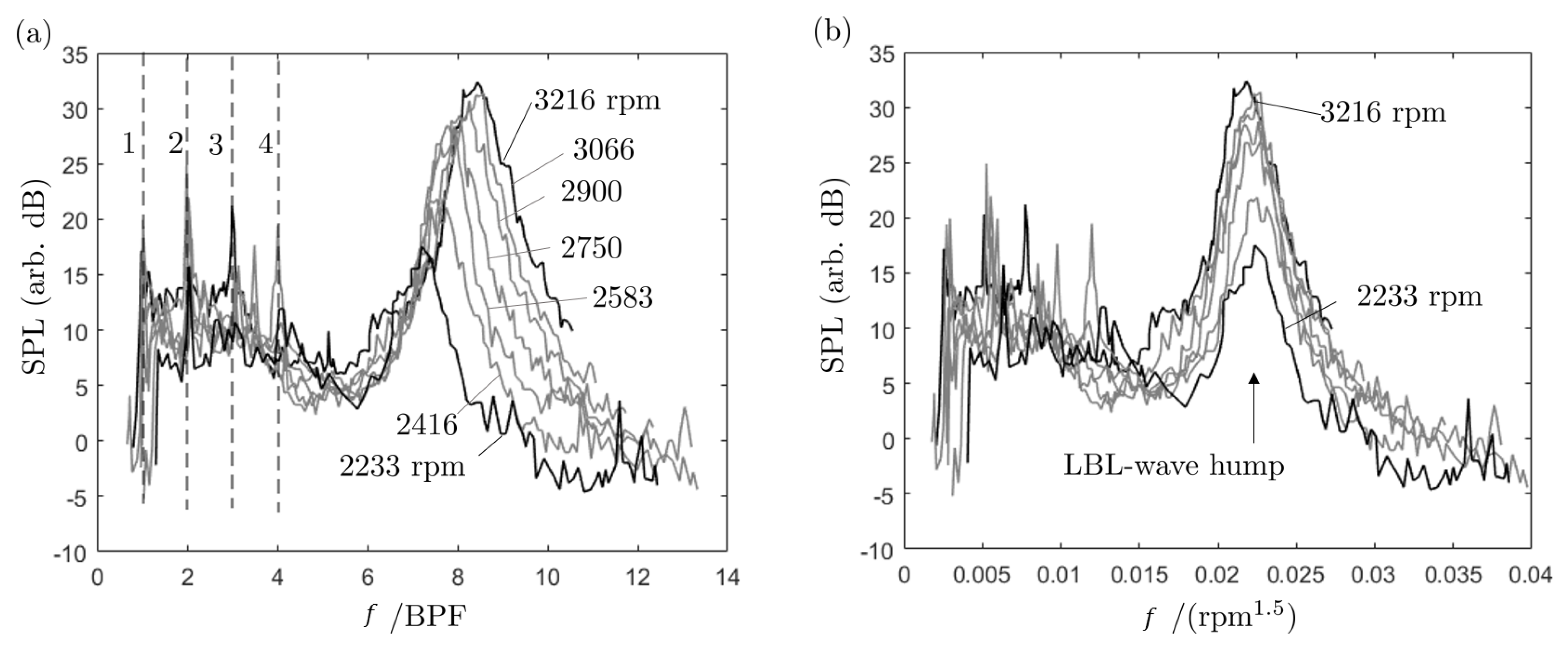
As a useful complement for the discussion, sound spectra of a small-size, axial-flow cooling fan for electronic equipments are reported in
Figure 23, after the processing of additional data from Bridelance [
50] by the authors. The measurements were made for a series of rotational speeds triggering nearly proportional relative speeds on the blades. The 9-bladed fan was mounted with an inlet bellmouth in a clean environment. It has a diameter of 145 mm and a hub-to-tip ratio of 0.6. In
Figure 23a, the frequency is made dimensionless by the blade passing frequency (BPF), which leads to a clear identification of the first four BPF harmonics. The feature of interest is the higher-frequency hump, obviously of higher amplitude and shifted to higher frequencies as the rotational speed increases. If attributed to some von Kármán vortex shedding due to blade thickness at the trailing edge the hump would have a constant center frequency. Now scaling the frequency with the power 1.5 of the rotational speed leads to the plot in
Figure 23b, where the hump is found at the same place for all speeds. Moreover, putting small tripping strips close to the suction-side leading edges of the blades has been found to suppress the spectral hump. This suggests that the hump is again produced by LBL-wave radiation. Yet, no tonal noise is observed. Reasons for that could be the non-homogeneous conditions along the quite short span of the blades, on the one hand, and sound scattering by the shroud of the fan and blade-to-blade proximity effects, on the other hand. The very small size of the blades might also be insufficient. The hump can be considered as the primary radiation of the instability waves, free of acoustic feedback, similar to the oblique trace in
Figure 16.
5. Analytical Prediction of the Tonal Noise Emission
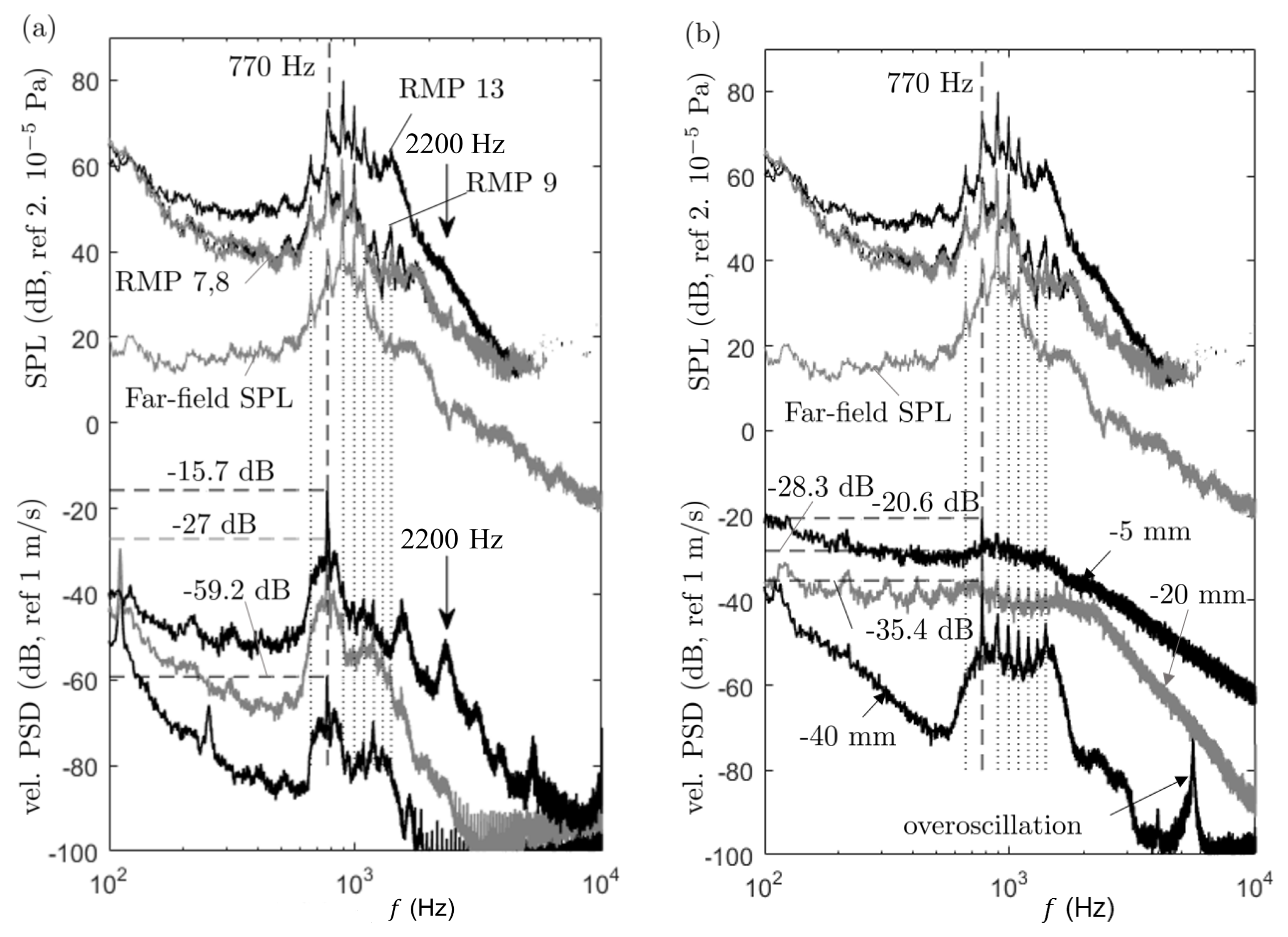
A two-dimensional analytical model of the trailing-edge scattering with acoustic feedback is justified by the inspection of signals delivered by the RMPs of the spanwise array discussed in
Section 3.6.2. In this section, compressible Amiet’s theory is selected for its ability to provide two key results, namely an explicit expression for the acoustic wall-pressure generated by the scattering and another expression for the three-dimensional far-field sound in the mid-span plane. This allows estimating the acoustic forcing of the boundary layers from microphone measurements. Only some outcomes of the theory are presented here and details can be found in [
38,
48,
51].
The accepted interpretation of the aerofoil tonal noise mechanism is that instability waves developing as an incompressible motion are driven by the acoustic waves they generate when interacting with the trailing edge. Now both the incompressible (hydrodynamic) and compressible (acoustic) motions have very different characteristic scales at the present low Mach numbers, typically below 0.12. The acoustic-to-hydrodynamic wavelength ratio is inversely proportional to the Mach number. As a result, the acoustic motion is nearly in phase over quite large portions of the aerofoil chord. Intuitively this is compatible with a feedback between some starting point A and the trailing edge only if the instabilities are receptive to acoustic forcing in the vicinity of A and not elsewhere. This condition is fulfilled as long as the instabilities grow exponentially to reach high amplitudes away from the point A and as the acoustic motion is at a somewhat intermediate level. In order to confirm the scenario, estimates of the orders of magnitude of the various involved motions are needed, resorting to relevant models and/or measured quantities. The instability growth and overall level can be inferred from wall-pressure measurements performed at various chordwise locations but such measurements are also including acoustic pressure. It can also be investigated from numerical simulations. The other measured quantity is the far-field sound at 90
from the streamwise direction in the mid-span plane. LBL-wave radiation is just a declination of trailing-edge noise, therefore any validated model of that noise can be used to quantify the source-to-sound relationship and therefore help to interpret various measurements [
48].
Amiet’s solution is in two steps. The first step provides an expression for the unsteady pressure distribution induced along the aerofoil surface by the scattering of a hydrodynamic pressure gust into sound at the trailing edge. This distribution is the trace of the acoustic motion at the wall that is actually forcing the developing hydrodynamic instability waves. In the second step, the far-field pressure is calculated from this wall-pressure distribution by a radiation integral.
The present use of Amiet’s model is to confirm the nature of the measured wall-pressure close to the trailing edge and its cause-to-effect relationship with the far-field sound by calculating the former from the latter. This is attempted only for the tones, the two-dimensionality of the instabilities being a crucial point. Now Amiet’s model is usually used to predict broadband trailing-edge noise within the scope of a statistical analysis in which the spanwise correlation length is smaller than the wetted span, leading to a closed-form expression of the far-field pressure PSD [
38]. In the present case of assumed perfect correlation a deterministic formulation is required, associating a single LBL wave at a given frequency to an isolated gust. If the back-scattering by the leading edge is ignored for simplicity, which is justified at high frequencies [
38,
48], the amplitude of the near-field wall pressure induced on the aft part of the aerofoil by trailing-edge scattering at the angular frequency
simply reads
for some amplitude
of the incident (hydrodynamic) pressure gust. In this expression
,
,
,
,
,
being the negative coordinate with origin at the trailing-edge made dimensionless by the half chord and
being the ratio of the external flow speed to the convection speed of the hydrodynamic disturbances.
is the Fresnel integral defined as
This first step defines the trace of a cylindrical wave at the wall acting as a forcing term for the developing instability. No transient is considered so that it is assumed that the instability has reached its saturation level.
The main concern with the practical application of Equation (
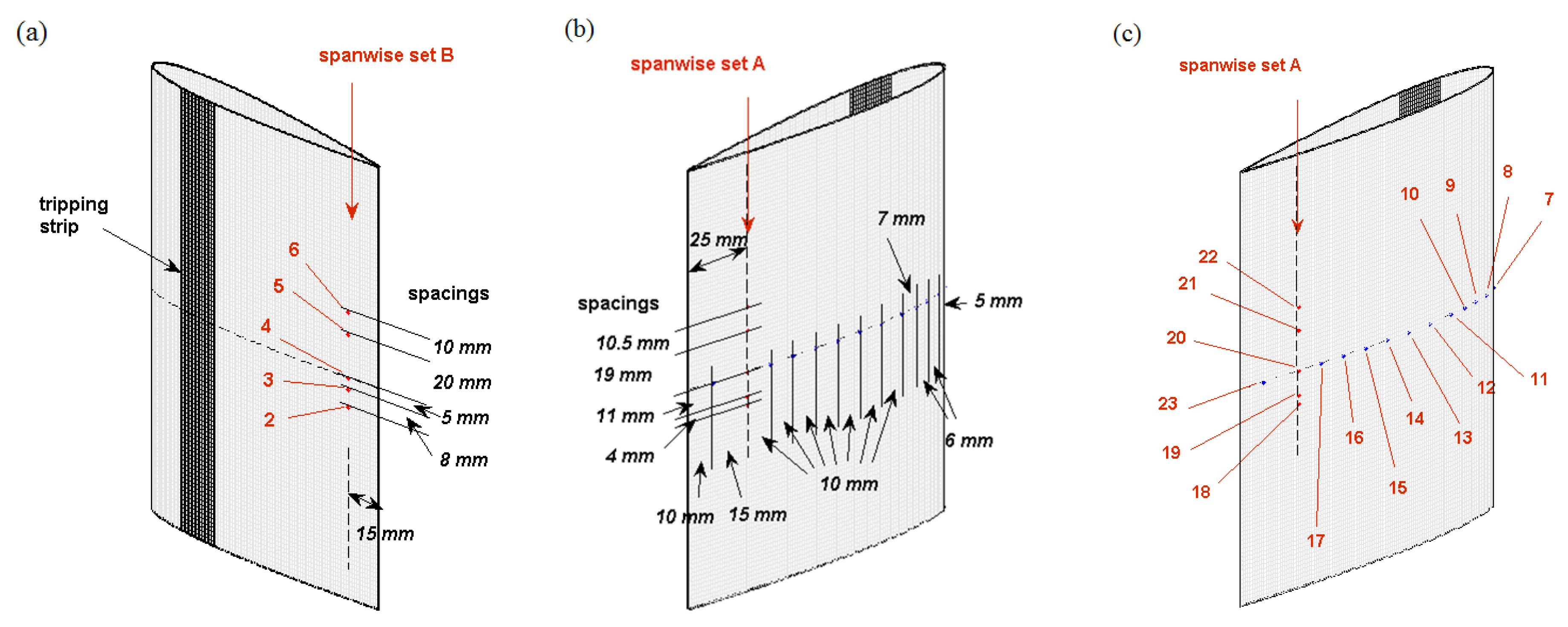
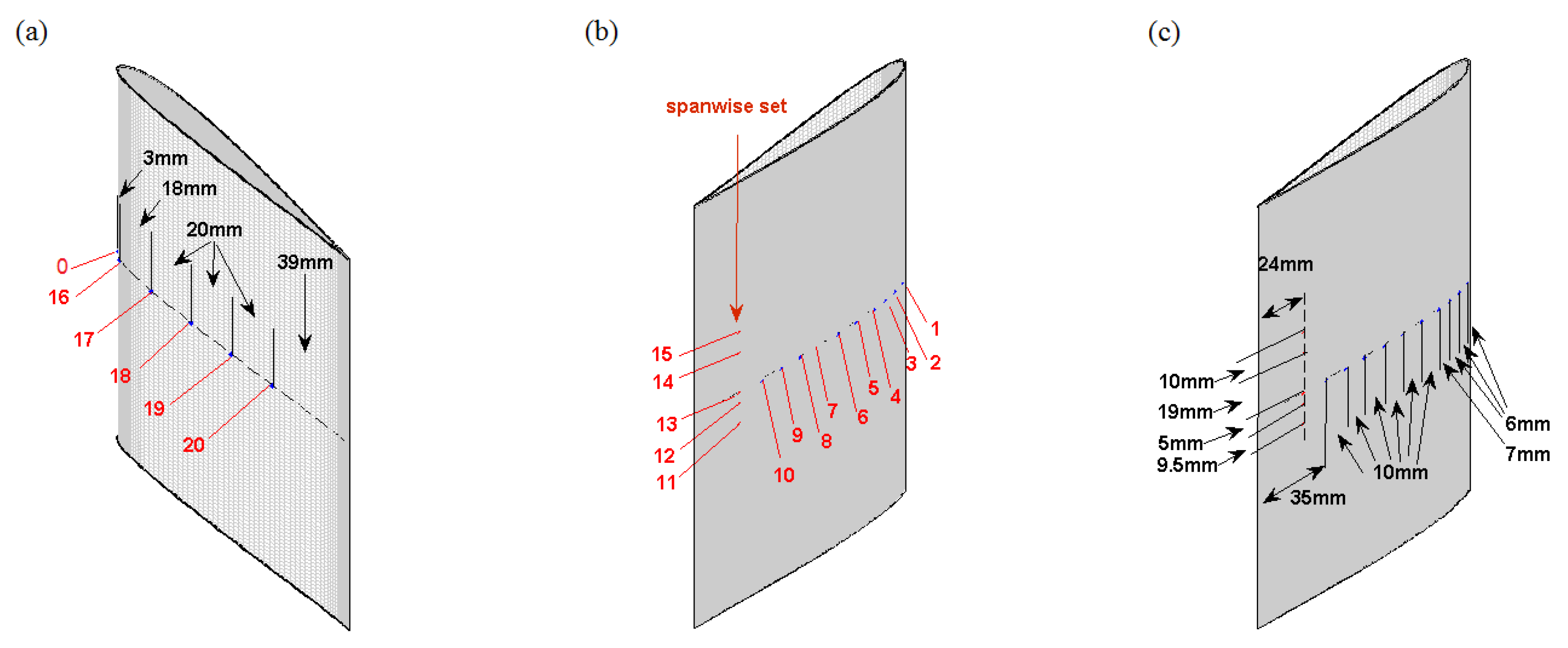
13) is that the amplitude
of the pressure gust that acts as an input should be taken just before the trailing edge whereas it is only measured 15 mm away from the trailing edge for the set B on the NACA-0012 aerofoil, thus at 87.5% of chord. The convection speed is also needed; it could be deduced with some approximation from the cross-spectrum phase calculated for the last chordwise RMP pair. Numerical simulations and computations based on the linear stability theory performed at 25 m/s by Nguyen et al. [
27] are used in the present work to assess the relevance of the analytical modeling. Key results are reproduced in
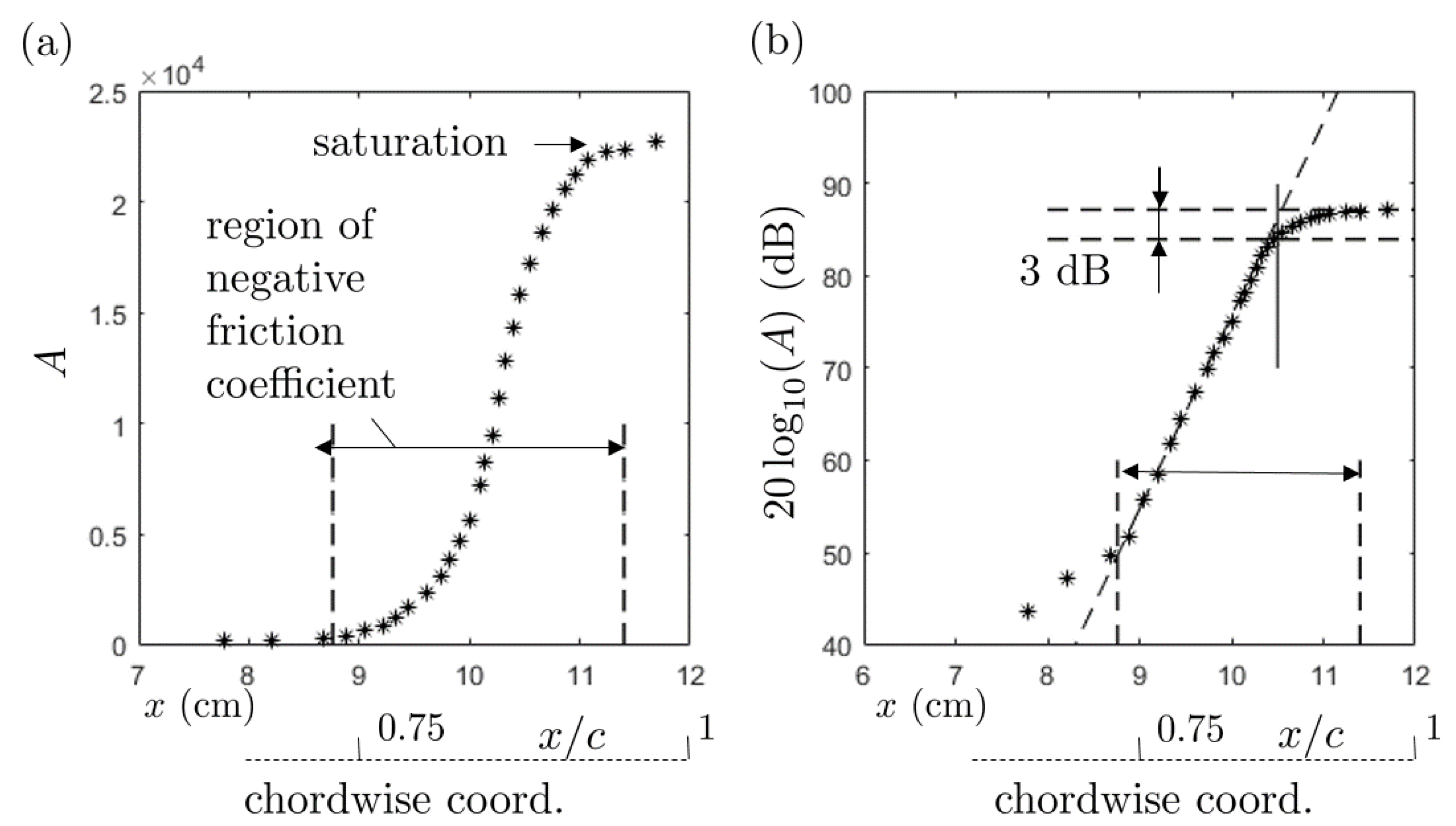
Figure 24 for the frequency of 1550 Hz corresponding to one of the emitted tones. The amplification of the oscillations as predicted with the linear stability theory is plotted in linear scale in
Figure 24a and in logarithmic scale in
Figure 24b. The amplitude unit is arbitrary because only relative variations are considered. The rapid growth takes place in the range of negative predicted friction coefficient thus in the separation area and leads to a saturation when approaching the trailing edge. Expressed in equivalent decibels the growth is approximately 21 dB per cm. The location of the last RMP is pointed out by the vertical line at
x = 10.5 cm where the saturation starts. The plot indicates that the amplitude measured by the RMP must be increased by 3 dB to get a correct estimate of the gust at the trailing edge where the scattering as sound occurs. This makes sense only if the measurement is of purely hydrodynamic nature so that it can be considered as the relevant input in the analytical model. It is therefore essential to state about the relative levels of the developing instability and of the upstream-propagating sound wave for a clear assessment of the feedback. Furthermore, the same computations lead to convection speeds of about 40% of the external flow speed
to be used in the analytical solution.
The second step of the model leads to an approximation of the far-field pressure amplitude in the mid-span plane as [
38]
where
,
H is the span length,
R the microphone distance, and
k the acoustic wavenumber. Forming the ratio
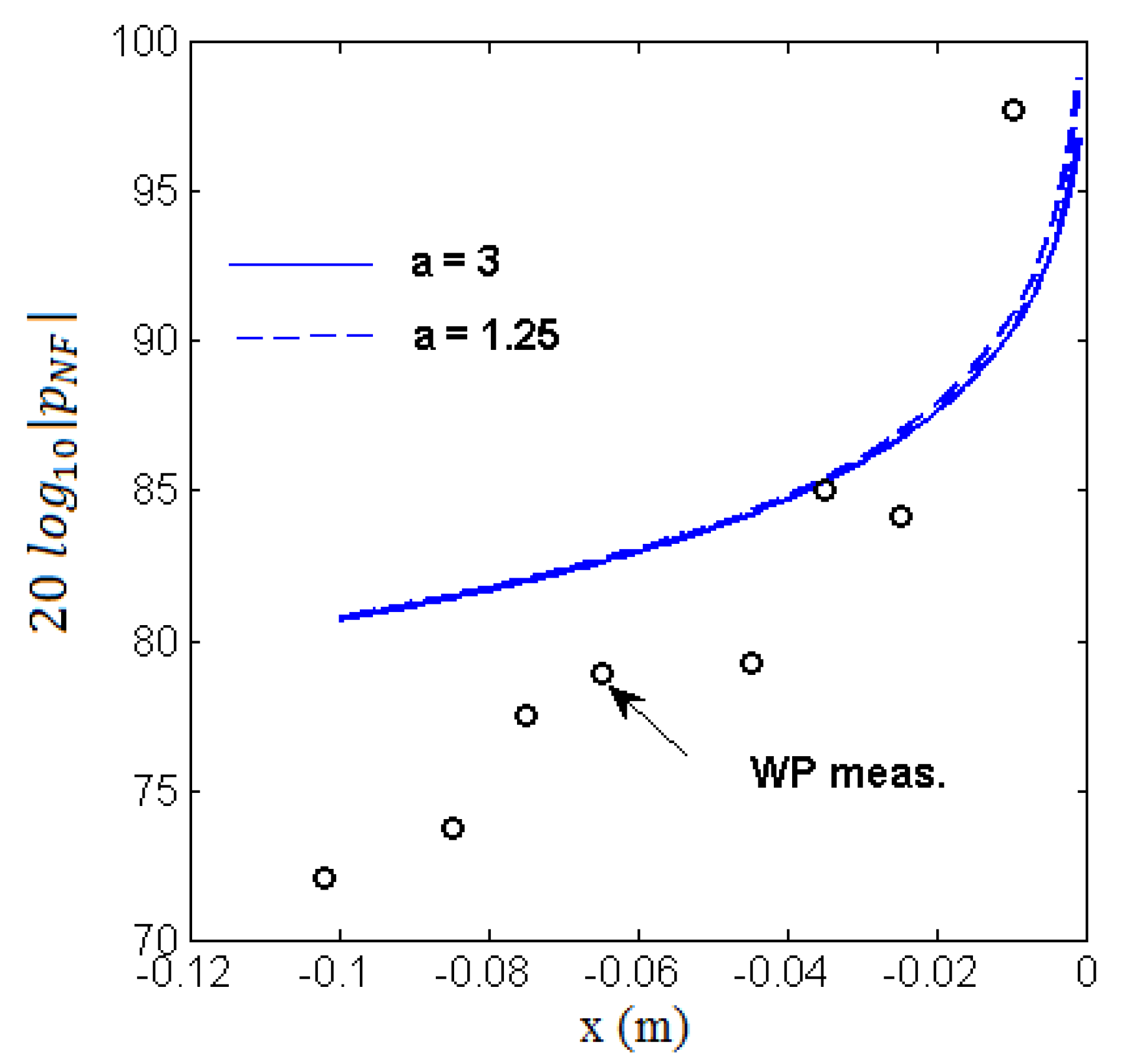
and multiplying by the amplitude of the measured far-field sound restores the needed acoustic trace on the wall as a function of the distance to the trailing edge (see
Figure 25). The parameter
a strongly determines the amplitude of trailing-edge noise generation but it has a negligible effect on the aforementioned ratio. Indeed, it is given two values here, namely 3 and 1.25, without producing significant changes. The acoustic near-field is expected close to 100 dB directly upstream of the trailing edge, corresponding to the dominant tone. The near-field acoustic pressure is expected slightly above 80 dB around the location of point A according to this prediction. Unexpectedly the measured peak level at the wall is well below this value except in the aft part of the aerofoil whereas the RMP presumably capture the total pressure field, combining acoustic and hydrodynamic pressures.
The estimate must be taken with care because of ignored effects that are expected to occur close to the wall. The mean-velocity gradient in the boundary layer is responsible for refraction of upstream-propagating sound waves away from the wall. This possibly explains the results of
Figure 25. Another point is that as the trailing-edge scattered pressure combines with the incident pressure, the phase shift of
presented in Equation (
3) tends to produce a cancelling of the total pressure. This could also explain the unexpected misfit. Anyway, in view of the results the growing instabilities are probably not receptive to acoustic forcing in the last 30% of chord. However, they could be forced farther upstream. This makes the hypothesis of a feedback loop physically acceptable.
When addressing quantitative sound predictions from a specified amplitude in the hydrodynamic field, the convection speed must be known with a reasonable accuracy. Facing the difficulty of determining it for tones by the usual examination of the phases of cross-spectra between chordwise distributed sensors, the aforementioned stability calculations performed at ERAU [
27,
28] have been used instead. The theoretical convection speed is found below 30% of the external flow speed in the trailing-edge area. Higher convection speeds of 50% and 70% more representative of attached turbulent boundary layers have also been tested, leading to a range of values that can be interpreted as an uncertainty in the input data. Moreover, the analytical prediction from the measured wall spectra is made difficult for various reasons. Firstly, both sides of the aerofoil contribute, therefore calculations are to be performed for each; but the way the contributions interfere is not elucidated. Secondly, the wall pressure is measured only at some distance upstream of the trailing edge, whereas the instability waves are continuously amplified (or possibly damped) down to the trailing edge where they are scattered as sound. This makes some underestimate (or overestimate) expected. Finally, the reattachment of the separated layers in the very vicinity of the trailing edge presumably modifies the properties of the noise emission. Despite these questionable points, tone-level prediction have been attempted for the NACA-0012 aerofoil at the two flow speeds of 16 and 25 m/s taking the wall-pressure tone levels measured at RMP 4 (right-bank) and 23 (left-bank) as input data. This provides estimated values of the far-field sound that must be compared to the microphone measurements.
At 16 m/s the results are reported in
Table 4. The tone at 556 Hz is only related to the right-bank side probe, as a result of the imbalance between both sides attributed to the installation. The dominant tone at 635 Hz is emitted from both sides with nearly equivalent source levels, though the overall wall-pressure level at probe 4 is lower than that at probe 23. This level difference is also possibly attributed to the larger distance of 15 mm (instead of 10 mm) to the edge at RMP location 4 (see
Figure 4). The associated measured sound levels are 49 and 61.5 dB for the lower and the higher frequencies, respectively. Amiet’s model predicts sound levels ranging from 47.2 to 51 dB at 556 Hz for the extreme values of convection speeds 0.29
and 0.7
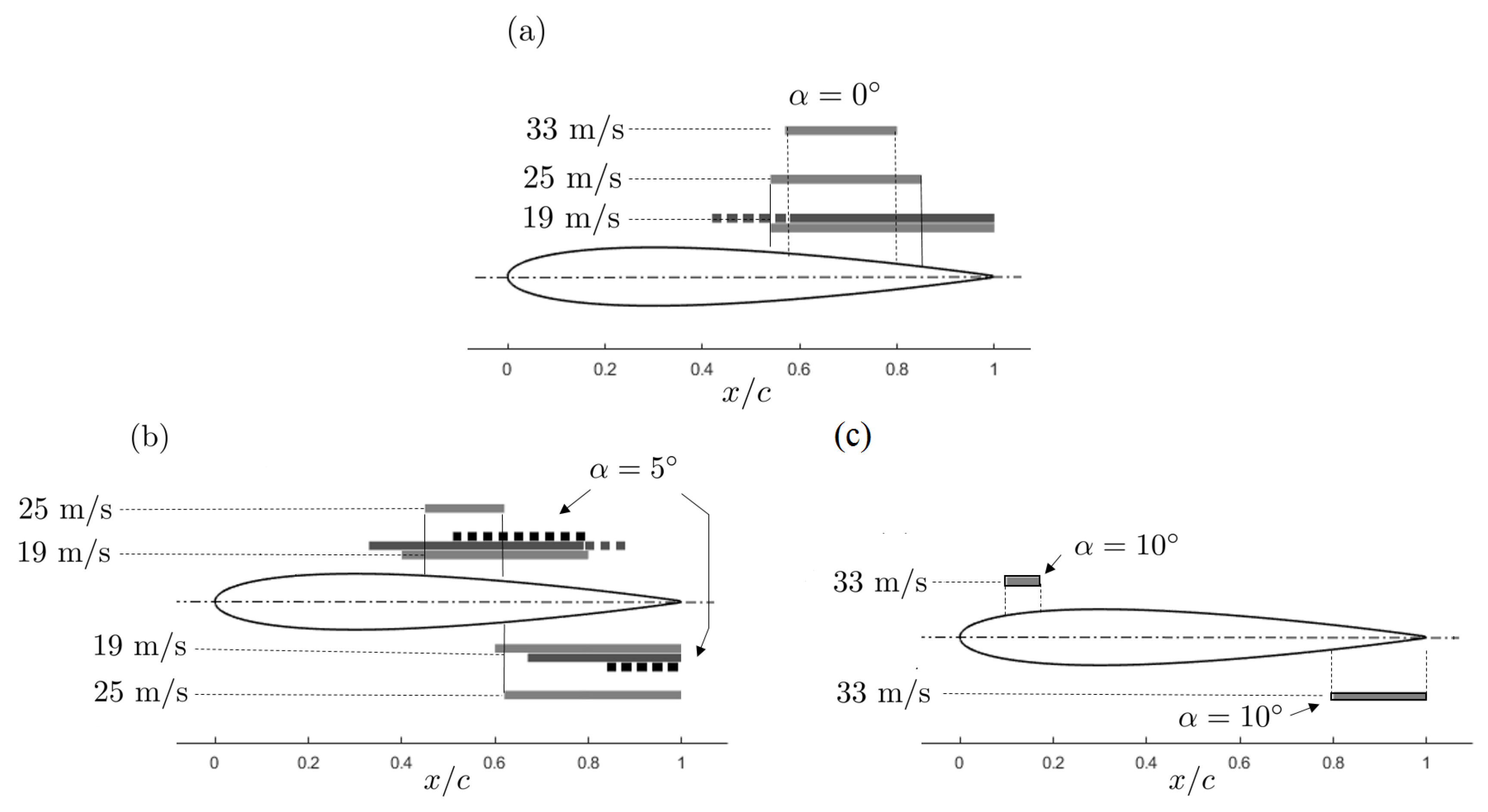
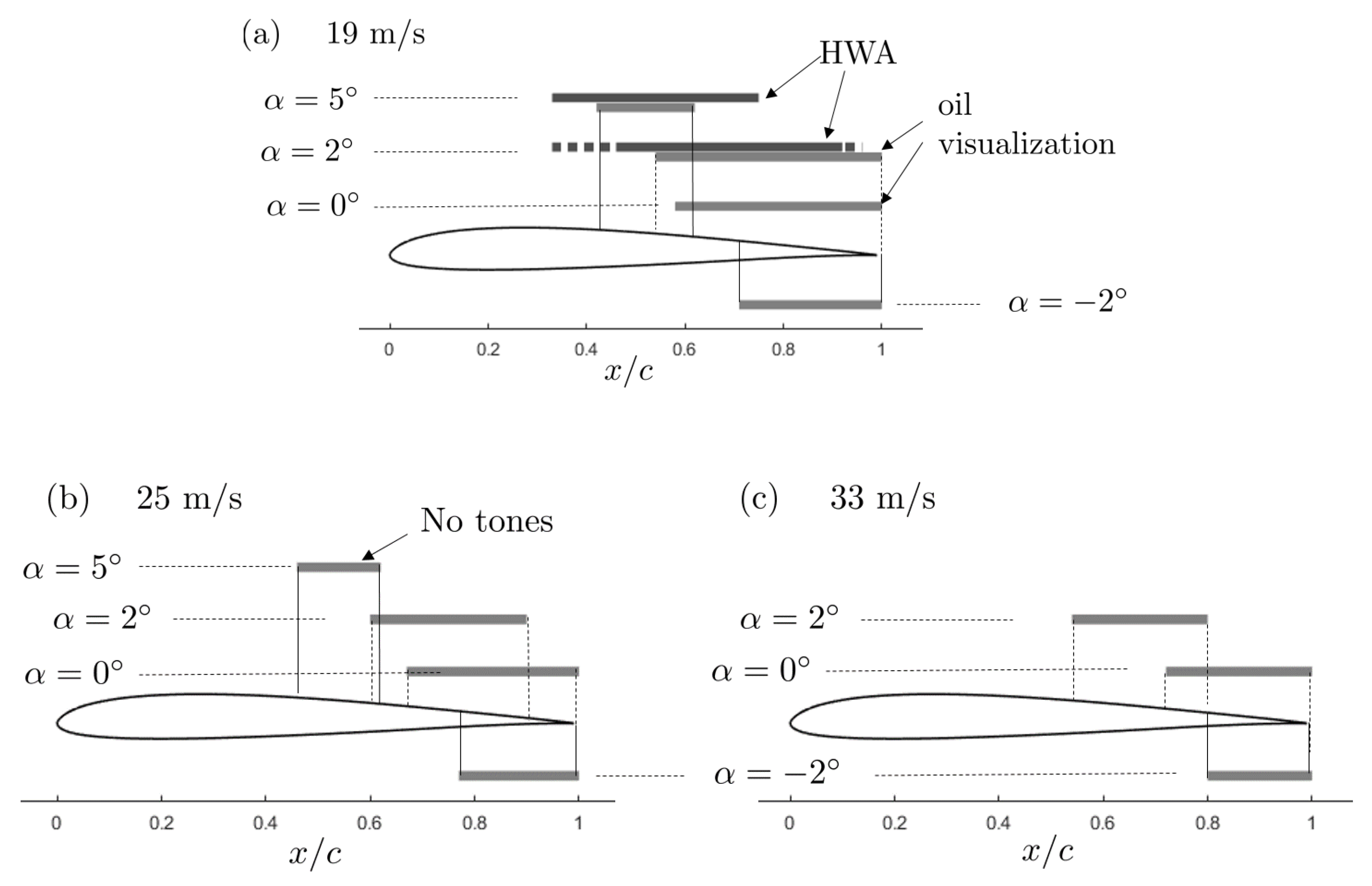
, higher convection speeds leading to higher sound predictions. At 635 Hz, the predictions range from 60.3 to 64 and from 62 to 66 dB depending on either the input data are considered at RMP 4 or RMP 23, respectively. In most cases, a slight over-prediction takes place. It is worth noting that both the developing boundary layers on the end plates and additional plate-aerofoil junction effects reduce the spanwise extent over which the laminar unstable regime takes place. Indeed the laminar instabilities are associated with the separation areas. This can be globally estimated from flow visualizations made with oil mixture as about 2.5 cm of attached flow at both junctions. The effective span length would be 25 cm instead of 30 cm according to this argument, which makes a sound-level reduction of about −16 dB expected. This makes the comparison quite satisfactory.
Surprisingly the same test repeated at 25 m/s (see
Table 5) leads to larger overestimates. Indeed, for the frequencies 1200 Hz and 1333 Hz the measured tone levels are 50 and 55.6 dB whereas the predictions produced by both probe inputs range from 55 to 59 dB and from 62 to 69 dB, respectively. As can be seen at this flow velocity the over-prediction is systematic. It is not excluded (though not proved) that between the wall-pressure measurement point and the trailing edge, some reduction of the amplitude of the laminar boundary layer waves operates in this case.
6. Conclusions
The present study was aimed at getting a deeper understanding of the underlying physics of aerofoil tonal trailing-edge noise, as a basis for noise reduction or analytical prediction. A complete experimental database has been built for the NACA-0012 aerofoil and for the cambered SD7003 aerofoil. Though numerical predictions were also included in the collaborative research project, the present paper is mostly focused on the experimental and analytical results.
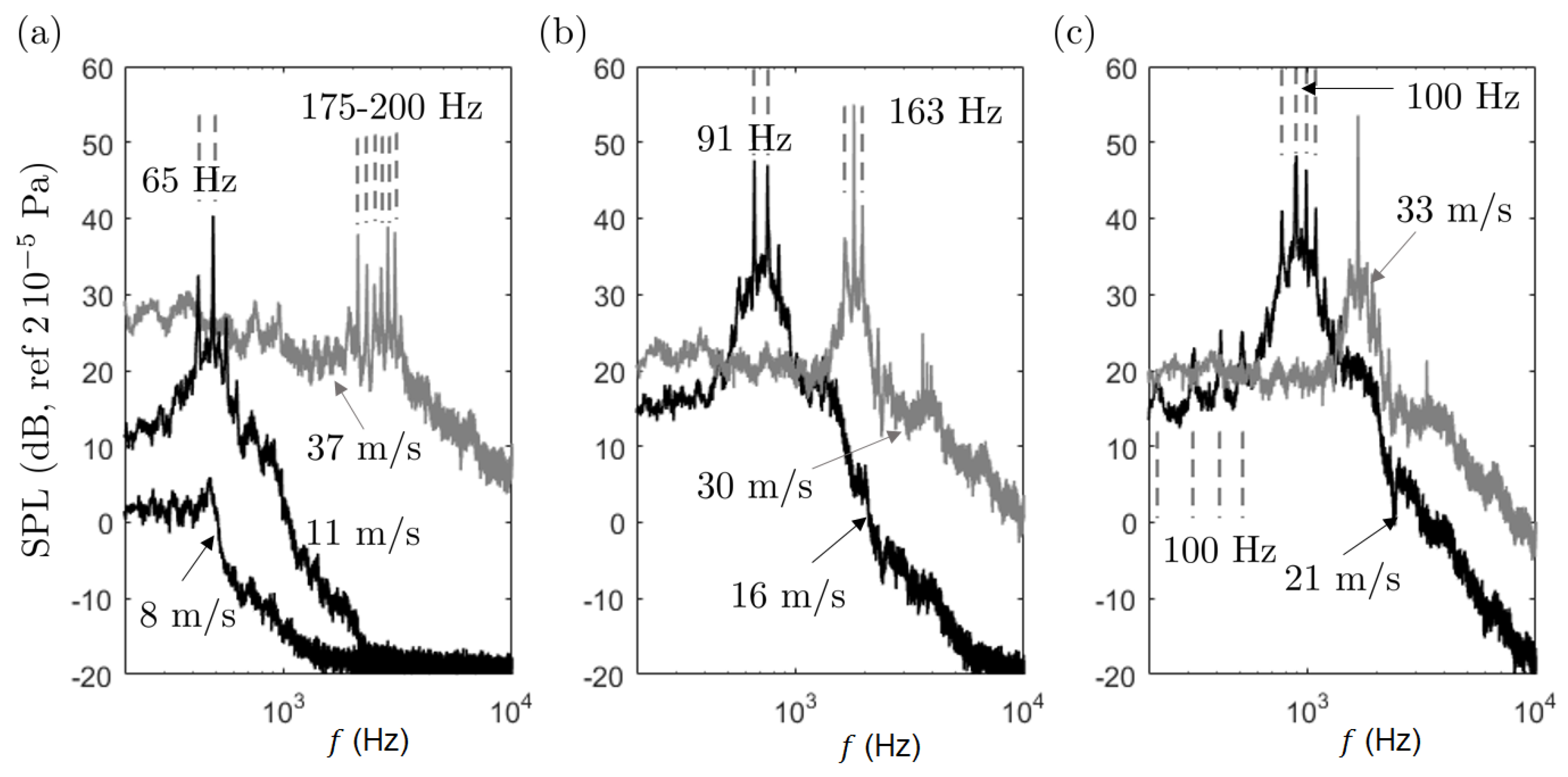
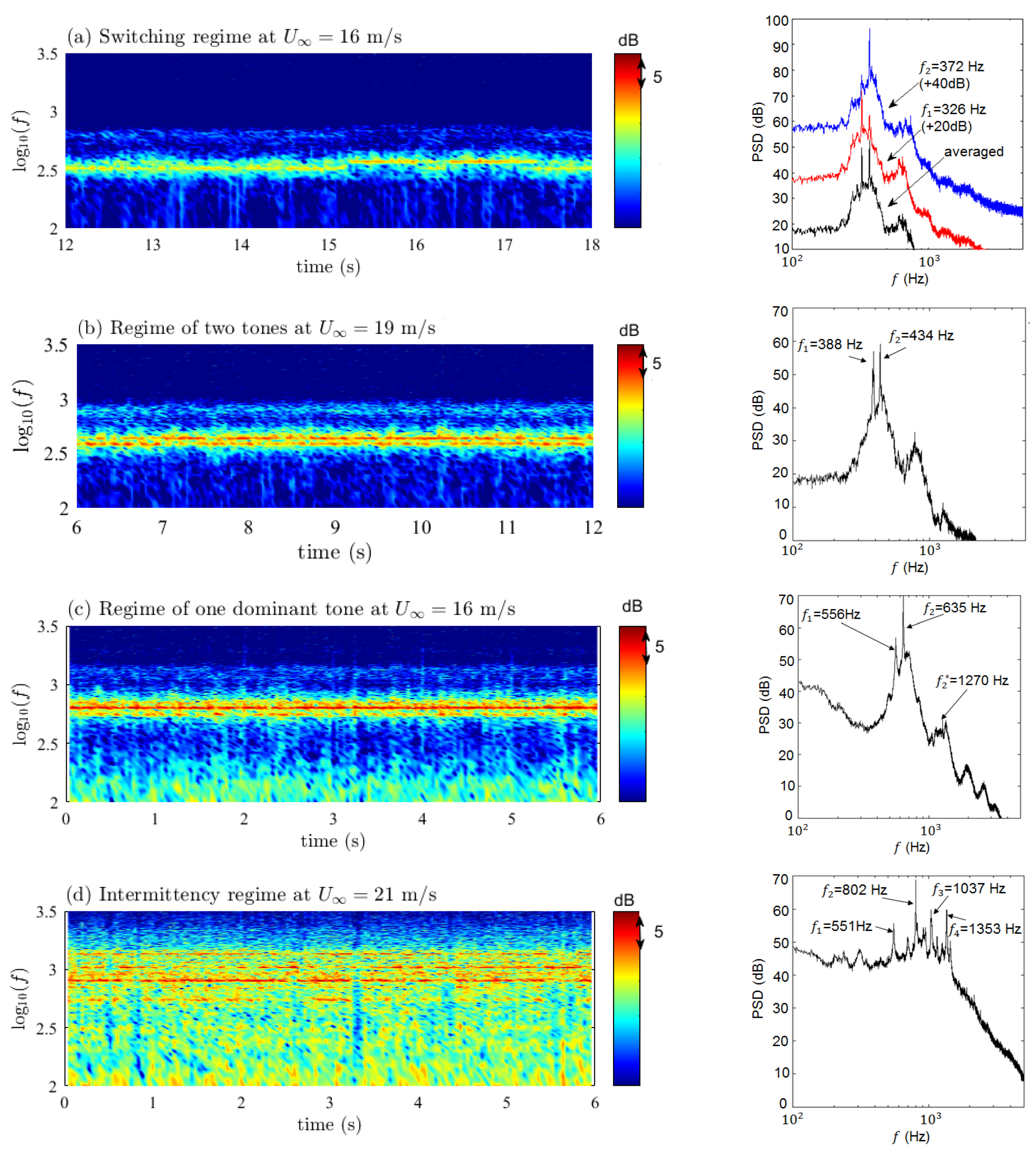
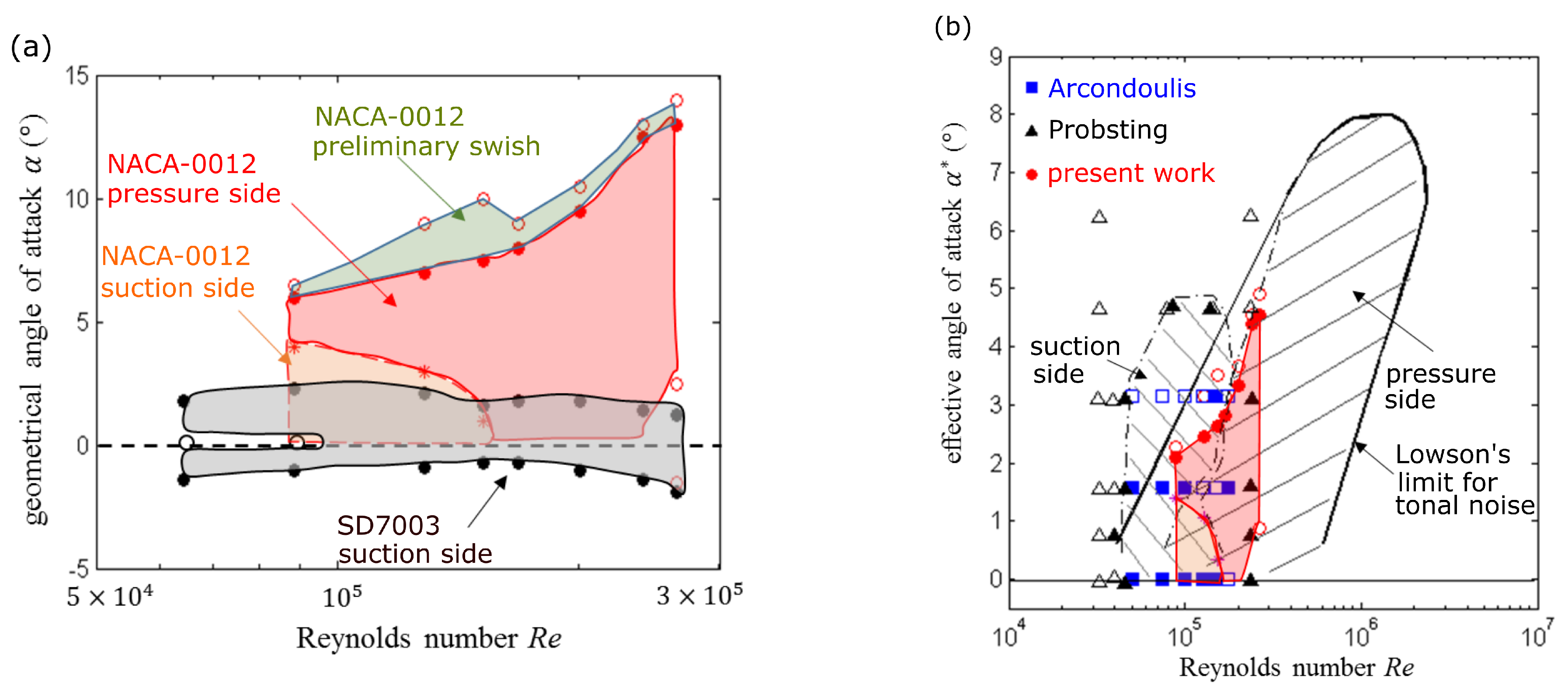
Far-field sound-pressure measurements performed at various flow speeds and geometrical angle of attack allowed pinpointing the limits of the tonal-noise emission area in the angle of attack and Reynolds number plane, showing both similarities and some differences with previously reported studies. This suggests the high sensitivity of the mechanism to experimental conditions. The SD7003 aerofoil is found to have a much narrower emission area than the NACA-0012. The measurements confirmed the “ladder-type” structure featured when plotting the variation of the dominant tone with increasing flow speed, for both aerofoils, explained by an acoustic feedback. Several regimes of tone emission were observed, namely a switching regime between two tones that are not observed simultaneously, a regime with a single tone or two simultaneous tones and a regime of intermittency with multiple unstable tones. Again, these regimes take place for both aerofoils depending on the flow parameters. This multiplicity could be more deeply addressed in the future as a possible explanation for the discrepancies sometimes found between numerical simulations and experiments. Keeping in mind that the former often run over very short times except in the recent LBM direct numerical simulations. Supplementary results obtained for the low-speed fans and propellers confirm that the laminar-boundary-layer instabilities can also be one of the noise sources in such rotating machines.
Special attention was paid to the role of each side of an aerofoil in the tonal noise generation, typically by resorting to one-side boundary-layer tripping. For the NACA-0012 aerofoil, the suction side boundary-layer has been found responsible for the tone generation only at low geometrical angles of attack and velocities, whereas for higher values of these parameters the sound can be attributed to the pressure-side boundary layer. In the case of the SD7003 aerofoil, only the suction-side boundary layer contributes, the pressure-side one remaining laminar and stable. This confirms that a single laminar and unstable boundary layer is sufficient for the onset of tonal noise. In addition, the combination of the unstable boundary-layer with a very thin separation bubble is essential to sustain high-amplitude tone emission. This was verified by both hot-wire anemometry scanning of the boundary-layer profiles and by oil flow visualization. The condition for efficient tonal noise generation is that the separation bubble extends down to the trailing edge or close to it. The separation bubble acts as an amplifier for the boundary layer instabilities. As shown by accompanying numerical simulations not detailed here, the receptivity point for the acoustic feedback is the attached-flow area where Tollmien–Schlichting waves develop just upstream of the separation point. The acoustic feedback and the tone emission have been simply suppressed and replaced by a hump-like primary narrow-band emission of much lower amplitude, by imposing upstream small-scale and small-amplitude turbulence in the incident flow, without changing the nature of the separation bubble. This proves that the separation bubble is a necessary but not sufficient condition for the mechanism. The acoustic feedback loop that amplifies the boundary layer instabilities at some frequencies is also required.
The cross-spectral analysis of chordwise located wall-pressure probes highlighted the highly coherent nature of the fluctuations at the frequencies of the tones. It also gave access to the convection speed of the instability waves used in analytical predictions. Furthermore, the analysis of the spanwise set of probes showed that the tones are associated with two-dimensional unstable motion. This is understood as a consequence of the acoustic feedback.
The analytical prediction of the tonal noise with an adapted Amiet’s model based on the measured surface pressure data acquired in the rear part of the aerofoil surface showed an overall satisfactory agreement with the measured tonal levels. It also confirms the cause-to-effect relationship between the wall pressure and the radiated sound. A possible cause of remaining discrepancies is the minimum distance of the last pressure probe to the trailing edge; indeed the instabilities can still evolve from that point to the trailing edge where they are scattered as sound.
Further analysis of the data base and/or additional investigations are needed to elucidate the physics underlying various emission regimes.