Ultrasounds Used as Promoters of Heat-Transfer Enhancement of Natural Convection in Dielectric Fluids for the Thermal Control of Electronic Equipment
Abstract
1. Introduction
2. The Use of Ultrasound for Heat Transfer Enhancement: Fundamental Physical Elements
- Acoustic streaming: consists in the alteration of the trajectories of the fluid flow, with its consequent mixing which alters heat transfer;
- Acoustic alteration of the boundary layer: the oscillation of the velocity component perpendicular to the portion of the wall affected by the exchange determines alternating compression and expansion phases of the thermal boundary layer which determines an overall increase of the heat transfer;
- Acoustic cavitation: the phenomenon causes temperature and pressure oscillations due to the propagation of the acoustic waves, which can be quite large, the fluid locally reaches, during the rarefaction phase, the steam condition. Steam bubbles then form: after a certain period of time, they implode violently, causing shock waves and jets of fluid. If the collapse of the bubbles occurs near the thermal boundary layer, it produces strong internal mixing, with consequent variation of the local heat-transfer coefficient.
2.1. Sound and Acoustic Cavitation
2.2. The Mechanisms of Action of Ultrasonic Waves for Heat-Transfer Enhancement
- -
- the fluid and its phase (gas, liquid or two-phase);
- -
- the operating conditions of the fluid (such as temperature and pressure);
- -
- the ultrasonic frequency of the generator, f;
- -
- the power of the ultrasound generator, Pgen;
- -
- the geometry of the system;
- -
- the characteristics of the surfaces;
- -
- the material of the surface and the possible formation of chemical substances.
3. Experimental Studies on Heat-Transfer Enhancement: General Elements
- Difficulty in modifying the acoustic parameters: the frequency is almost always fixed and often the power cannot be varied; geometry and fluid dynamics influence the actual power released by the generator. It would be useful to modify the generators in such a way that they always supply the set power;
- With the exception of some particular cases, the acoustic generation leads to high PUS/∆Pth ratios, where PUS is the total power given with the ultrasounds and ΔPth represents the heat-transfer enhancement. This occurs because a large part of the acoustic energy is dissipated in the fluid before reaching the exchange surface and before altering it. The possibility could be assessed case by case to switch to mechanical generation or to bring the exchange surface as close as possible to the generation area.
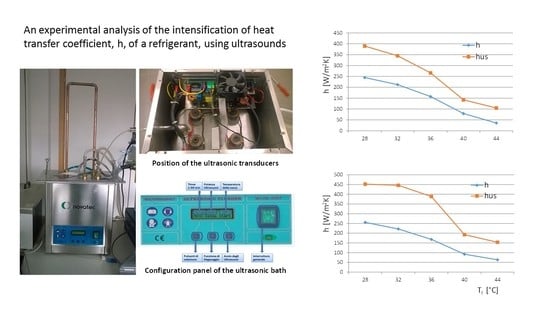
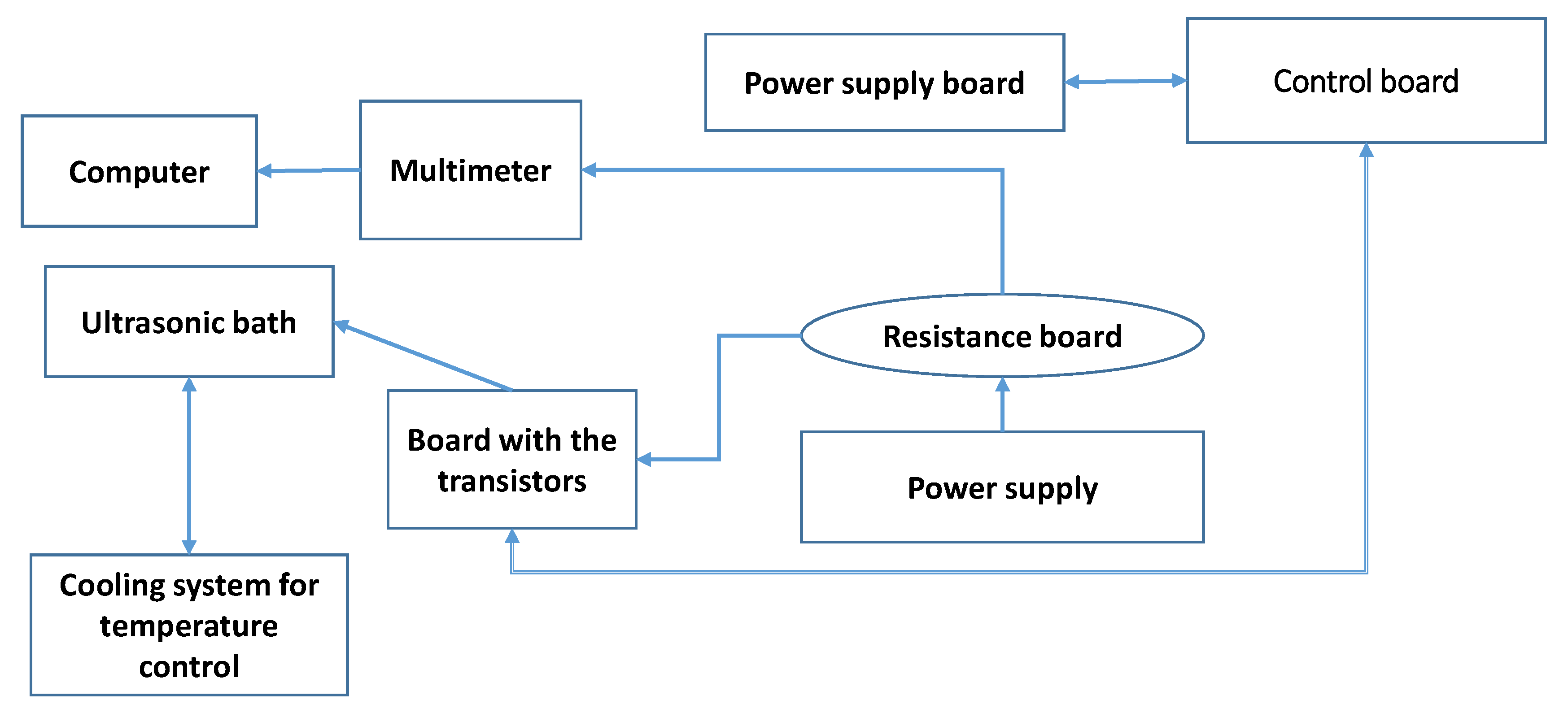
4. Definition of the Experimental Setup and Measurement System
4.1. Experimental Setup
4.2. Measurement Strategy and Control System
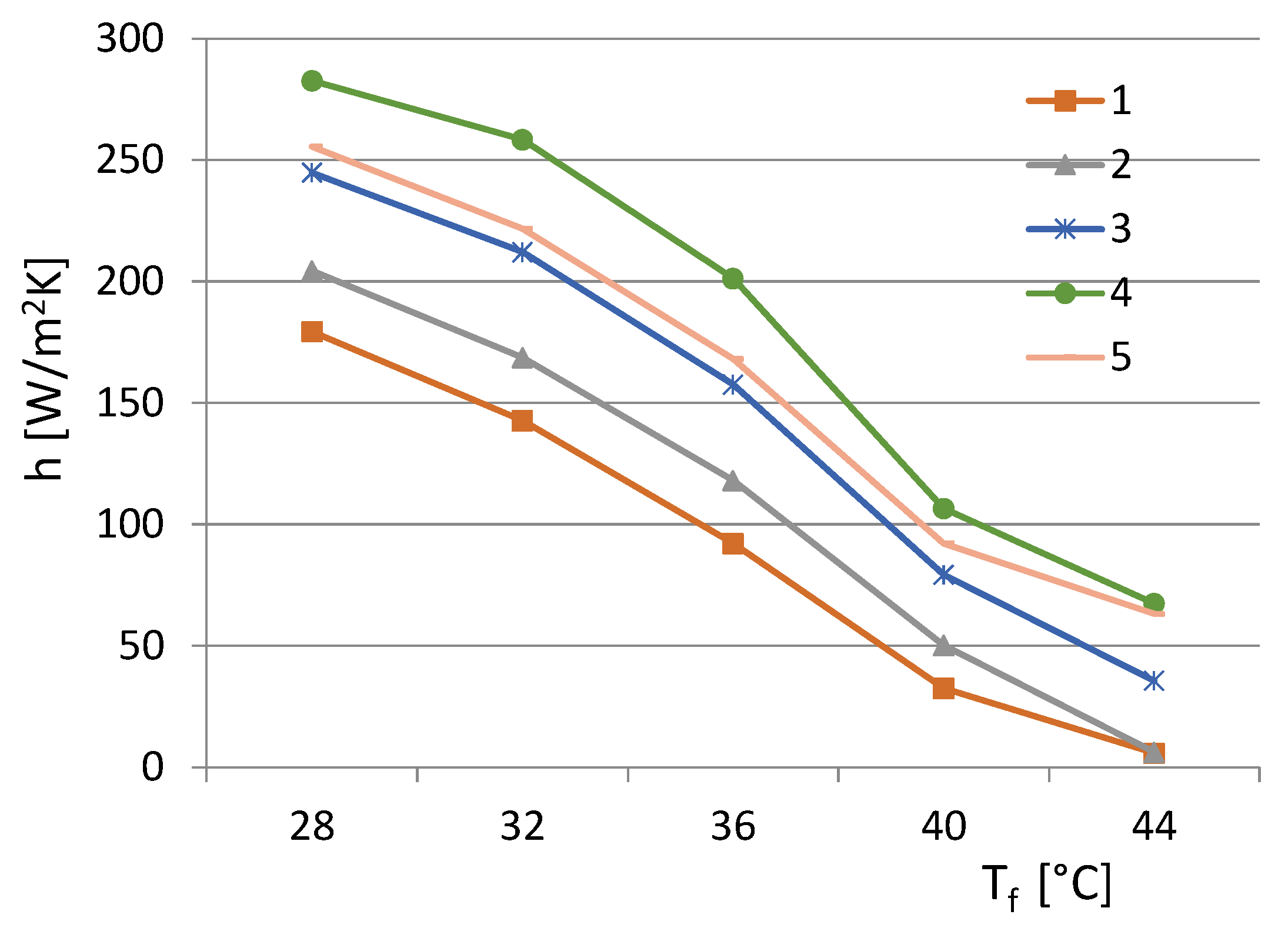
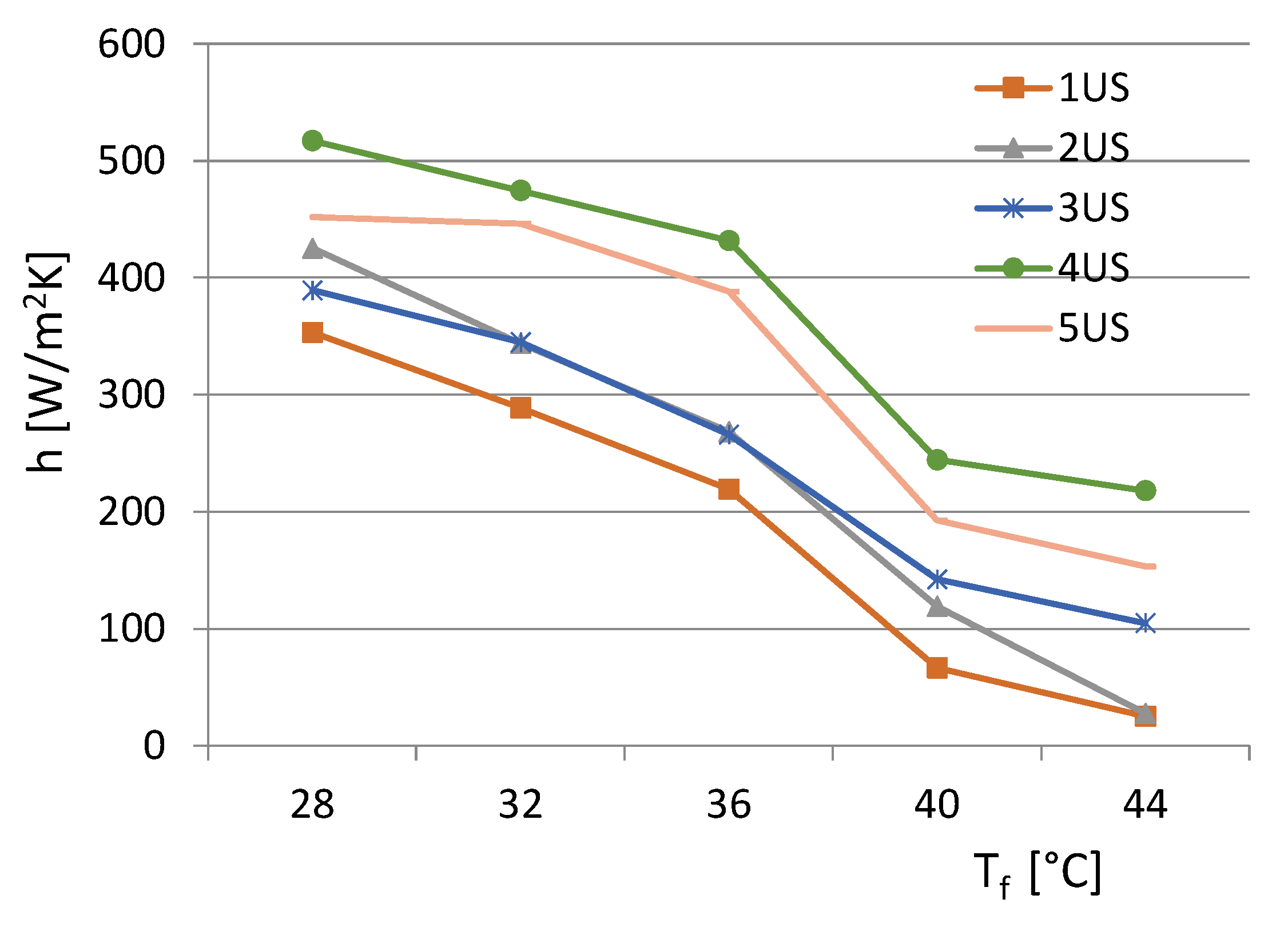
5. Measurements for the Electronic Equipment Validation and Heat-Transfer Analysis
5.1. Preliminary Operation
5.2. Thermal Measurements and Data Analysis
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Martinelli, R.C.; Boelter, L.M.K. The Effect of Vibration upon the Free Convection from a Horizontal Tube. In Proceedings of the 5th International Congress for Applied Mechanics, Cambridge, MA, USA, 12–16 September 1938; Volume 578. [Google Scholar]
- Fand, R.M.; Roos, J.; Cheng, P.; Kaye, J. The local heat-transfer coefficient around a heated horizontal cylinder in an intense sound field. J. Heat Transf. 1962, 84, 245–250. [Google Scholar] [CrossRef]
- Kubanskii, P.N. Currents around a heated solid in a standing acoustic wave. Trans. USSR Acad. Sci. 1952, 82, 585. [Google Scholar]
- Holman, J.P.; Mott-Smith, T.P. The effect of high constant pressure sound fields on free convection heat transfer from a horizontal cylinder. J. Aerosp. Sci. 1959, 20, 188. [Google Scholar] [CrossRef]
- Anantanarayanan, R.; Ramachandran, A. Effect of vibration on heat transfer from a wire to air in parallel flow. ASME J. Heat Transf. 1958, 80, 1426–1432. [Google Scholar]
- Jackson, T.W.; Harrison, W.B.; Boteler, W.C. Free convection, forced convection, and acoustic vibrations in a constant temperature vertical tube. ASME J. Heat Transf. 1959, 81, 68–74. [Google Scholar] [CrossRef]
- Lemlich, R.; Hwu, C.K. The effect of acoustic vibration on forced convective heat transfer. AIChE J. 1961, 71, 102–106. [Google Scholar] [CrossRef]
- Fand, R.M.; Cheng, P. The influence of sound on heat transfer from a cylinder in crossflow. Int. J. Heat Mass Transf. 1963, 6, 571–596. [Google Scholar] [CrossRef]
- Larson, M.B.; London, A.L. A study of the effect of ultimate vibrations on convective heat transfer to liquids. ASME 1962, 62, 62–68. [Google Scholar]
- Deaver, F.K.; Penney, W.R.; Jefferson, T.B. Heat transfer from an oscillating horizontal wire to water. J. Heat Transf. 1962, 84, 251–254. [Google Scholar] [CrossRef]
- Fand, R.M. The influence of acoustic vibrations on heat transfer by natural convection from a horizontal cylinder to water. J. Heat Transf. 1965, 87, 309–310. [Google Scholar] [CrossRef]
- West, F.B.; Taylor, A.T. The effect of pulsations on heat transfer-turbulent flow of water inside tubes. Chem. Eng. Prog. 1952, 48, 39–43. [Google Scholar]
- Scanlan, J.A. Effects of normal surface vibration on laminar forced convective heat transfer. Ind. Eng. Chem. 1958, 50, 1565–1568. [Google Scholar] [CrossRef]
- Raben, I. The use of acoustic vibrations to improve heat transfer. In Proceedings of the 1961 Heat Transfer and Fluid Mechanica Institute, Los Angeles, CA, USA, 19–21 June 1961; pp. 90–97. [Google Scholar]
- Bergles, A.E. The influence of flow vibrations on forced-convection heat transfer. J. Heat Transf. 1964, 86, 559–560. [Google Scholar] [CrossRef]
- Isakoff, S.E. Effect of an Ultrasonic Field on Boiling Heat Transfer-Exploratory Investigation; Heat Transfer and Fluid Mechanics Institute, Stanford University Press: Palo Alto, CA, USA, 1956; pp. 1–15. [Google Scholar]
- Nangia, K.K.; Chon, W.Y. Some observations on the effect of interfacial vibration on saturated boiling heat transfer. AIChE J. 1967, 13, 872–876. [Google Scholar] [CrossRef]
- Park, K.A.; Bergles, A.E. Ultrasonic enhancement of saturated and subcooled pool boiling. Int. J. Heat Mass Transf. 1988, 31, 664–667. [Google Scholar] [CrossRef]
- Baffigi, F.; Bartoli, C. Effects of ultrasounds on the heat transfer enhancement from a circular cylinder to distilled water in subcooled boiling. J. Therm. Sci. Eng. Appl. 2011, 3, 011001. [Google Scholar] [CrossRef]
- Bartoli, C.; Baffigi, F. Use of ultrasonic waves in subcooling boiling. Appl. Therm. Eng. 2012, 47, 95–110. [Google Scholar] [CrossRef]
- Duan, X.L.; Wang, X.Y.; Wang, G.; Chen, Y.Z.; Qiu, X.Q. Experimental study on the influence of ultrasonic vibration on heat transfer and pressure drop in heat exchanger tubes. Petro-Chem. Equip. 2004, 33, 1–4. [Google Scholar]
- Bulliard-Sauret, O.; Ferrouillat, S.; Vignal, L.; Memponteil, A.; Gondrexon, N. Heat transfer enhancement using 2 MHz ultrasound, Ultrason. Sonochem 2017, 39, 262–271. [Google Scholar] [CrossRef]
- Franco, A.; Bartoli, C. The ultrasounds as a mean for the enhancement of heat exchanger performances: An analysis of the available data. J. Phys. Conf. Ser. 2019, 1224, 012035. [Google Scholar] [CrossRef]
- Franco, A.; Bartoli, C. Heat transfer enhancement due to acoustic fields: A methodological analysis. Acoustics 2019, 1, 281–294. [Google Scholar] [CrossRef]
- Baffigi, F.; Bartoli, C. Heat Transfer Enhancement from a Circular Cylinder to Distilled Water by Ultrasonic Waves: Preliminary Remarks. In Proceedings of the 7-th Word Conference on Experimental Heat Transfer (ExHFT-7), Krakow, Poland, 28 June–3 July 2009. [Google Scholar]
- Baffigi, F.; Bartoli, C. Heat transfer enhancement from a circular cylinder to distilled water by ultrasonic waves in subcooled boiling conditions. In Proceedings of the Interdisciplinary Transport Phenomena VI: Fluid, Thermal; Biological, Materials and Space Sciences (ITP09), Volterra, Italy, 4–9 October 2009. [Google Scholar]



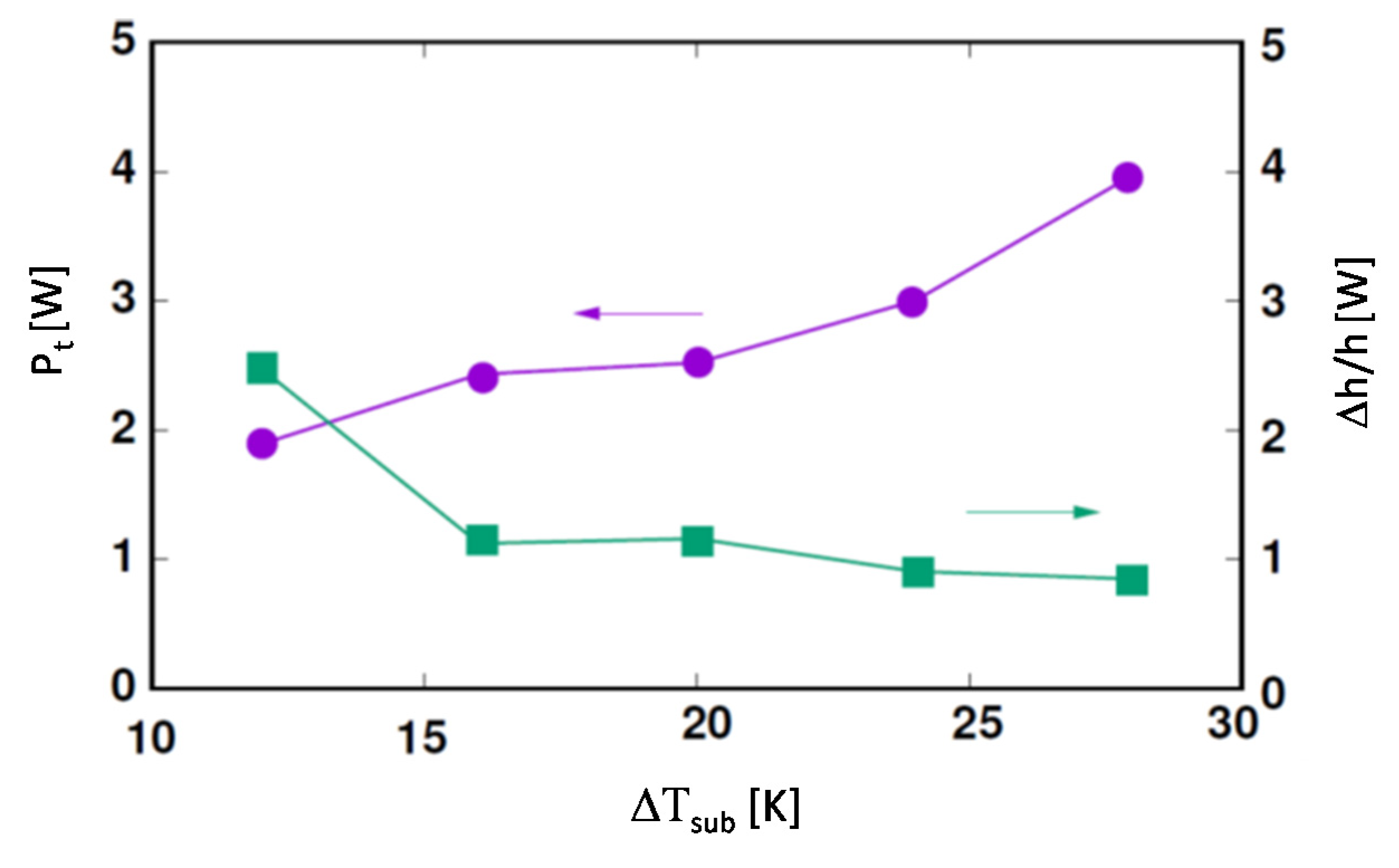
| ΔTsub [K] | Pt [W] | EF | Δh/h |
|---|---|---|---|
| 12 | 1.89 | 3.476 | 2.476 |
| 16 | 2.43 | 2.223 | 1.123 |
| 20 | 2.52 | 2.260 | 1.160 |
| 24 | 3.00 | 1.907 | 0.907 |
| 28 | 3.97 | 1.848 | 0.848 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bartoli, C.; Franco, A.; Macucci, M. Ultrasounds Used as Promoters of Heat-Transfer Enhancement of Natural Convection in Dielectric Fluids for the Thermal Control of Electronic Equipment. Acoustics 2020, 2, 279-292. https://doi.org/10.3390/acoustics2020017
Bartoli C, Franco A, Macucci M. Ultrasounds Used as Promoters of Heat-Transfer Enhancement of Natural Convection in Dielectric Fluids for the Thermal Control of Electronic Equipment. Acoustics. 2020; 2(2):279-292. https://doi.org/10.3390/acoustics2020017
Chicago/Turabian StyleBartoli, Carlo, Alessandro Franco, and Massimo Macucci. 2020. "Ultrasounds Used as Promoters of Heat-Transfer Enhancement of Natural Convection in Dielectric Fluids for the Thermal Control of Electronic Equipment" Acoustics 2, no. 2: 279-292. https://doi.org/10.3390/acoustics2020017
APA StyleBartoli, C., Franco, A., & Macucci, M. (2020). Ultrasounds Used as Promoters of Heat-Transfer Enhancement of Natural Convection in Dielectric Fluids for the Thermal Control of Electronic Equipment. Acoustics, 2(2), 279-292. https://doi.org/10.3390/acoustics2020017