Abstract
A novel effective vibrational mode was discovered in the conventional transducer with an array of orthogonal (square) regular piezoelectric rods in 1-3 piezocomposite, containing the damping backing and front matching layers. The operational resonance in the structure was determined as the Surface Acoustic Wave (SAW) on the backing boundary excited by the adjacent piezo-rods, with its frequency typically near 3 times lower the fundamental half-lambda conventional piezocomposite resonance. Pulse-echo sensitivity and transmitting sound pressure level (SPL) in air showed that the signal strength is roughly comparable to the industrial similar air transducers at the frequency range 100–700 kHz, where at these frequencies the lateral and longitudinal piezoelement dimensions in the conventional transducer design are typically close to each other causing interference with unwanted coupling modes. As was determined theoretically and proved in experiments, the backing SAW resonance effect in the transducer performance is inherent just to the regular periodic 1-3 piezocomposite structure and does occur neither with randomly located/oriented piezo-rods nor in the homogeneous piezo-plate at least with the same lateral cross-section as the connected to it backing. The purpose of the article is to investigate a newly discovered operational vibrational mode of a SAW type in 1-3 regular piezocomposite, other than piezoelectric resonance. The investigated phenomena can improve the transceiver sensitivity and bandwidth, providing lower drive voltage and smaller and lighter weight ultrasonic transducers. Based on the piezocomposites with thickness’ 1–1.5 mm (rod resonance near 2–3 MHz), pillar width 0.2–0.8 mm, kerf width 0.1–0.4 mm, the transceivers with an operating frequency from 140 kHz to 650 kHz were designed and fabricated with a conventional backing of a mixture of high-density tungsten powder and epoxy and a matching layer of a mixture of low-density glass bubbles and epoxy. Experimental evaluation of their acoustical performance showed expected characteristics suitable for practical applications.
1. Introduction
The 1-3 piezocomposite consists of an array of parallel piezoelectric rods embedded in a polymer matrix with electrode layers on the top and bottom surfaces and incorporates epoxy (‘ies) for bond-lines, backing, and matching layers. It improves mechanical and ultrasonic performance compared to a baseline traditional design with a homogeneous piezoelectric plate, for example, providing broader bandwidth, shorter pulse, lower Q-factor, and clear spectra with suppressed planar unwanted modes. In conventional piezocomposite applications, the height of the pillars normally is about one-half wavelength at the operating frequency. The piezoelectric layer in the structure is an active resonating transducing element, which converts electrical energy to acoustical energy and vice versa. The most common piezoelectric materials used in ultrasonic transducers are piezoceramics, such as lead zirconate titanate (Pb(Zr,Ti)O3, or PZT), and piezocomposites based on it, which possess relatively strong piezoelectric effect [1,2,3].
In the traditional operation, a voltage pulse is applied between the front and back surfaces of the piezoceramic rods of particularly a 1-3 piezocomposite to excite a mechanical expansion thickness resonance (rod length) of the piezoelectric plate.
The transducer generally works as a transceiver, generating and receiving the pressure and voltage pulses typically at the transducer half-lambda resonant frequency Fr evaluated [2,4] as:
where L is the thickness of piezoelectric layer and c is the speed of sound (SOS) for the thickness mode in piezoelectric material. For a thin homogeneous plate the latter parameter , and for a 1-3 piezocomposite , C33E and 1/S33E taken as elastic stiffness and Young modulus under short-circuit condition, is the material density. For a typical piezoelectric material, a 2 MHz array needs approximately 1.0 mm thick ceramic layer.
Conventionally, the planar (radial) modes are used for a low-frequency range below near 100 kHz, while for a high-frequency range above near 700 kHz a thickness vibrational mode of a monolithic, or piezocomposite, plate is exploited [5]. In the present research, a newly discovered operational vibrational mode of a SAW type in a 1-3 regular piezocomposite, other than piezoelectric resonance, was proposed and investigated for the 100–700 kHz applications.
Typically, a quarter-lambda wavelength thick matching layer is introduced to provide the acoustic matching between the ceramic and loading fluid. The impedance of air is as low as near 100 Rayls so that a light couplant is used to reduce this impedance mismatch. For a transducer with a single matching layer, its optimal acoustic impedance Zm value is a geometrical mean [4] , where Z0 and ZR is the acoustical impedance of piezoelectric material and fluid, respectively. The effect of perfectly matching layer is the energy transmission maximum efficient at the center frequency, providing relatively wide transducer bandwidth. Implementing typically light glass bubbles into epoxies is common practice to form matching material when the acoustic impedance can be adjusted by the percentage of loaded bubbles to meet the design requirements of transducers [6].
The energy generated in the transducer can radiate in both the forward direction and reverse direction. The purpose of the matching layer is to encourage energy to be propagated in the forward direction with low loss and reflections. On the contrary, the backing layer is designed to maximum attenuate the signal emanating from the back surface of the piezoelectric plate, as well as reduce ringing. If the attenuation of the backing material is sufficiently large, no reflections from the back surface of backing layer can be found [2].
To minimize the ringing, the acoustic impedance of backing can be matched to piezoelectric material. However, as a result, half of the energy will be transferred into the backing layer and then lost.
A very short pulse could be obtained, but with a relatively low amplitude. Thus, compromise is always taken between sensitivity and bandwidth of the transceiver. Therefore, the acoustic impedance of backing layer is usually slightly lower than the one of piezoelectric layer in order to improve sensitivity at the cost of slightly increased pulse length or ringing–for some particular applications a predetermined waveform, with a definite number of the sine peaks, should be provided. The epoxies loaded with fine dense powders and heavy chips such as tungsten are commonly used as backing materials [2]. The purpose of loading powder into epoxies is to change the acoustic impedance similarly to the technique used for matching layer design, but with the opposite effect of increased density, also creating multiple centers of energy dissipation.
The general benefits of the 1-3 piezocomposite structure are higher thickness mode piezoactivity (rods with vibration of k33-type), lower frequency transverse (planar) unwanted modes, lower acoustical impedance, and transducer Q-factor. Several unwanted higher frequency lateral resonances caused by the regular piezoceramic-epoxy structure in piezocomposites are found and described in References [7,8,9,10,11]. To damp the unwanted resonances, an irregular piezocomposite structure is recommended at this point as in References [12,13,14].
For the acoustical performance characterization of the conventional layered transceiver, the transmission line (one-dimensional 1-D approach) theory is typically considered [4]. For this reason, it directly suggests and relates to the averaged (effective) or homogeneous piezoelement and backing bodies of the same planar area. For a transversely structured design, more advanced 2-D and 3-D approaches and simulation methods are used in acoustical performance characterization [10].
In the case of a 1-3 piezocomposite element (Figure 1a), it is structured with typically periodic piezoelectric rods imbedded into softer and lighter epoxy. In the conventional approach, the effective acoustical impedance of such a structure is proportional to the structural effective (averaged) density, following to the kerf-to-pitch piezocomposite parameter. Typically, the effective acoustical impedance of a piezocomposite is near 2 times lower than that in piezoceramics.
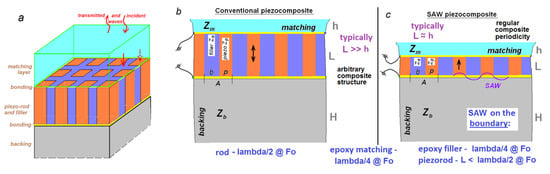
Figure 1.
1-3 epoxy-filled lead zirconate titanate (PZT) piezocomposite transceiver: (a) general view; (b) structure for the conventional thickness resonance mode; (c) structure for the novel Surface Acoustic Wave (SAW) resonance mode on backing of the same operation frequency.
To the contrary of the conventional approach for the total piezocomposite structure as a whole, a single piezoelectric rod attached to a transversely wider backing was considered here as a baseline to describe the multiple rods individual and collective behavior on the backing, based on the theory of vibrations and 2-D FEA simulation.
2. Boundary SAW Resonance Performance of the Piezoelectric 1-3 Composite Bonded to Backing
2.1. 1-3 Piezocomposites with Regular Structure for the Experiments
In the present research, a novel acoustically effective vibrational mode in the 1-3 piezoelectric transducer was discovered and investigated. Its resonance is based on the SAW-type wave on the backing bonding boundary and has frequency significantly lower the piezocomposite fundamental (λ/2 mode) thickness resonance. In this case, the typical operation transducer frequency (piezocomposite with backing and matching) is nearly 3 times lower than the conventional piezocomposite thickness resonance (Figure 1b,c).
As was found, there are two critical factors supporting the transducer SAW operation with that new condition: necessary regular periodic transverse structure in the 1-3 piezocomposite, and a solid layer of bonding material (hard epoxy) between 1-3 piezocomposite and backing. The transducer structure has a conventional damping backing with near 10–20 MRayls acoustical bulk impedance; conventional low impedance matching layer (glass bubbles with epoxy), with its quarter-lambda thickness at the SAW resonance frequency.
Practical realization of the frequency range with near 100–500 kHz operation frequency in a conventional transducer design is complicated due to the necessity to use a piezoelement with close lateral and transverse dimensions, causing complex transducer spectra and hence relatively lower acoustical efficiency.
In the present experiments, the 1-3 piezocomposites have nearly 65% volume of PZT-5A type (CeramTec GmbH, Germany) [3] piezoceramic, with effective acoustical impedance near 17 MRayl. They have typically 12 mm × 7 mm planar dimensions, with nearly 2.5 MHz piezoelement thickness resonance. Structural parameters of the piezocomposite samples used in the experiments are shown in Table 1. All values and formula further are presented in SI, if other is not specified.

Table 1.
Structural array piezocomposite parameters, used in experiments.
Relative ceramic volume (effective density) in piezocomposite is determined by the parameter p2/(p + b)2, and the effective density can be expressed as
The backing with a height H of a dozen wavelengths at the operation (SAW) frequency was a typical dense mixture of tungsten powder and chips with epoxy—it provides effective damping backing with acoustical impedance nearly 15 MRayls and Q-factor near 5 [15]. The quarter-lambda thickness matching layer was a mixture of glass bubbles with epoxy, providing relatively low acoustical impedance near 1 MRayl. Basic parameters of the materials used in the experiments are shown in Table 2.

Table 2.
Transceiver materials data.
For the acoustical tests, the distance ~2.5″ was used in pitch-catch testing, and with a reflective SS block as a target in pulse-echo tests, both locations are the transducer “far field” area.
An excitation spike of 300 V amplitude was applied to the transducer structure, so that with an output signal typically 100 mV, it provides nearly −70 dB pulse-echo sensitivity. In the basic characterization, together with the fundamental thickness resonance, typical higher frequency spurious resonances were noticed, related to a lateral Lamb wave in just a piezocomposite plate, with rods filled with epoxy [7,8,9,10,11].
2.2. SAW on the Backing Boundary—Acoustical Effect Prediction
A regular piezo-rod structure in the conventional 1-3 piezocomposite, under applied voltage or pressure, causes localized deformation of the backing boundary pre-surface with the same structural periodicity. When the excitation frequency coincides with that SAW resonance, the total transceiver structure and synchronized collective piezorods motion exhibit the resonance characteristics suitable for its ultrasonic operation and performance.
The effect is somewhat similar to how the piezoelectric SAW devices with interdigital electrodes (IDT) work [16]. One of the differences is that an in-phase voltage is applied to all piezo-rods in piezocomposite, while in a SAW device, the counter-phase voltage is applied to every other electrode strips in the electrode comb array structure. It is also known that in the SAW resonator with IDT on a piezo-substrate, the phase velocity of SAW is considerably reduced since the metal IDT implies the mass load on the substrate. As an FEA simulation showed, there is a similar effect for the propagating SAW, when an isolated loading mass shifts down the working frequency as well, from the “ideal” resonance determined by the SAW speed of sound.
The surface wave physically occurs in an effective pre-layer of backing, including a thin layer of hard bonding epoxy used to connect the backing to the piezocomposite rods and filler. The condition for a relatively low-frequency SAW resonance (caused by its low SOS), in the first approximation, requires for the two adjacent rods distance to be an integer multiple to the surface acoustical wavelength:
where N = 1, 2, 3… is a positive integer; A is the pitch of piezocomposite, as a sum of the kerf b and pillar width p. As an estimation for the SAW wavelength , the backing bulk SOS is roughly 1500 m/s, and the shear (SAW) SOS is estimated as csaw = ~0.45 cb ~ 600 m/s, then the backing SAW wavelength λ ≈ 1.5 mm is expected for 500 kHz frequency.
2.3. FEA Simulation of SAW Resonances on Backing with 1-3 Piezocomposite Rod Structure
COMSOL (Comsol Inc., Burlington, MA, USA) software was used to simulate the SAW propagation on the backing pre-surface, loaded with the periodic piezoceramic rod structure bonded on the backing boundary. In a simplified linear array of the axial and transverse 2D model, an elementary cell of a regular piezocomposite was considered, under continuous wave excitation (CW, applied voltage 100 VAC). It was supposed that a 3D model provides some shifted parameters of secondary significance. In the model design, soft type piezoceramic PZT-5A [3], with damping coefficient Q = 20, a piezoceramic rod with basic height (length) L in a range from 50 µm to 1.5 mm, and total width from 20 µm to 240 µm (minimum 10 µm kerf) in the fixed pitch 250 µm for certainty, were used in the simulation.
The backing parameters are presented in Table 2, so that for a total backing height H 4 mm, with periodicity (pitch) 250 µm, it provides a longitudinal backing resonance much lower of 100 kHz. Both the fundamental (lowest) backing SAW and longitudinal piezo-rod resonance frequencies are relatively stable versus piezo-rod width, as shown in Figure 2a. For the backing SAW resonance, it has a broader peak bandwidth for wider rods.
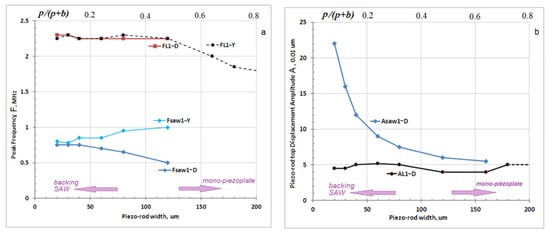
Figure 2.
Simulation resonance frequencies (a) and top piezo-rod displacement (b) dependences on the rod width (pillar) under constant pitch (p + b = 250 µm); the piezo-rod length 0.76 mm.
In Figure 2a, the data are presented for the saw1-Y and saw1-D fundamental (lowest) SAW resonance taken respectively from the piezocomposite electrical admittance (Y = 1/Z) and from the piezo-rod top displacement (D); and for L1-Y and L1-D, similarly for the fundamental (lowest) longitudinal resonance of the piezo-rod in piezocomposite, where L1 denotes the fundamental rod length vibrational mode. The respected displacement resonance amplitudes are presented in Figure 2b.
There are a number of SAW harmonics excited in the structure, and data for four lowest SAW modes were taken for analysis. For the baseline case of negligible piezo-rod’s mass, the resonance frequencies are just directly proportional to their consecutive orders (N = 1,2,3…). For some longer piezo-rods (Figure 3a), when their own rod’s longitudinal resonance coincides with one of the SAW resonances, a coupled modes vibration takes place. Under such conditions, the largest top piezo-rod displacement is provided at the lowest SAW resonance, as shown in Figure 3b.
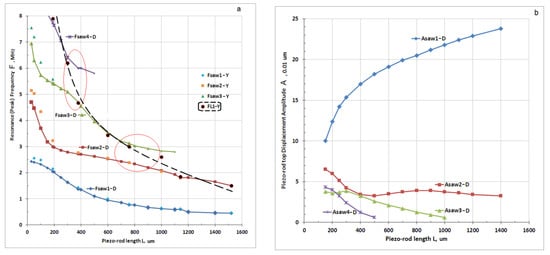
Figure 3.
Simulation results for the resonance frequencies (a) and top piezo-rod displacement (b) vs. rod length under constant pitch (p + b = 250 μm) and pillar width p (25 μm). The SAW and rod-length (piezocomposite thickness) resonance branches are shown inside the red circles where they are most acoustically coupled.
As follows from Figure 2b data, for the piezocomposite structure with a relatively narrow kerf, the top piezo-rod displacement is relatively low and close to that of a conventional homogeneous piezo-plate. For a larger kerf, the fundamental SAW mode shows a large and rapid increase in the top piezo-rod displacement at the backing SAW resonance—the effect directly determining the transducer higher vibrational sensitivity and efficiency.
The resonance characteristics variation under just the kerf width varying, with all other structural array parameters taken constant, is presented in Figure 4a. For a relatively wider kerf or the same larger pitch, the spectra effectively go from a mono-frequency resonance to the multi-resonance peaks of SAW harmonics.
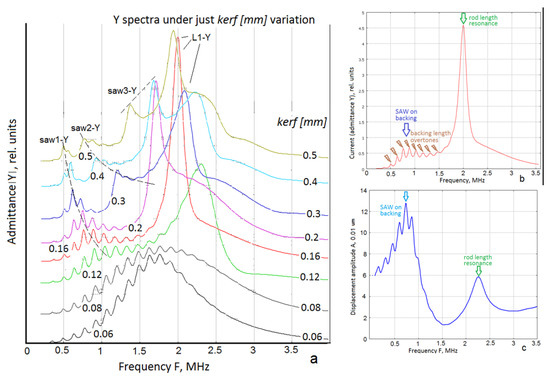
Figure 4.
Simulated spectra (admittance IYI, continuous wave (CW)) transformation under composite piezo-rod structural variation: (a) just kerf variation (pillar width 50 μm); (b,c) – comparative peak amplitudes admittance and top rod displacement (pitch 250 μm and pillar 50 μm), respectively; rod length 0.76 mm in the structure of just piezo-rods on backing.
On the admittance piezocomposite characteristic, the SAW resonance is hardly identified (Figure 4b); however, the piezo-rod top displacement amplitude is significantly higher than that at the piezocomposite plate fundamental mode (Figure 4c), making it obviously beneficial at least for more efficient energy transmission into load medium. Note that the fundamental SAW resonance on the backing boundary works also like a high-stop filter for the lower frequency longitudinal backing resonances, represented as a comb of peaks in Figure 4.
The waveform displacement and stress (von Mises) pattern in the resonating transducer structure at the fundamental SAW vibrational mode is shown in Figure 5. For a low (negligible) mass of tiny piezo-rods, the space SAW waveform is close to the ideal total sine period (Figure 5a). The effect of piezo-rod width variation on the stress distribution is demonstrated in Figure 5b–d. As seen from the simulation, the effective SAW in-depth into the backing equals to near same SAW wavelength, estimated as a motion intensity transition from the SAW to the bulk flat waves in the backing. For a narrower kerf (Figure 5d), the vibrational displacement is getting lower, so that in a limit of zero kerf (homogeneous piezo-plate) the SAW effect on backing disappears.
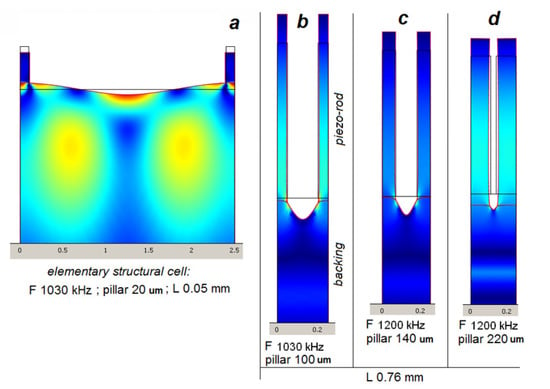
Figure 5.
Space waveform displacement and stress (CW) distribution at the SAW backing resonance under composite structure (a), and their transformation under variation of piezo-rod height and width (b–d). Backing length 4 mm; pitch 250 μm.
2.4. Basic Estimation for the 1-3 Piezocomposite Rod Structure with SAW Vibrational Mode on Backing
Various types of SAW devices such as filters, resonators, and sensors have been reported by researchers and are used in many industries and electronic equipment [16]. They basically consist of and are employing an electro-acoustic interdigital transducer (IDT) fabricated on a piezoelectric substrate [16,17] for transmitting and receiving acoustical waves. An IDT consists of metallic comb-shaped electrodes of sub-micron thickness normally placed over the surface. That IDT mass loading effect on the SAW resonance has close similarities to the SAW phenomenon on the backing under current consideration. In the literature, a reduction of SAW velocity was investigated caused by the mass loading of metal IDT, and also as an additional structured mass’ along the wave propagation on the surface.
Typically, metal IDTs fabricated over the substrate introduce secondary effects such as re-emission (reflection) the waves. Due to the IDT mass load effect, the SAW phase velocity reduces from the ideal (unloaded) velocity. The IDT fabricated over the substrate affects mostly the surface wave velocity and the bulk wave velocity is not much affected since the bulk waves propagate interior to the device substrate. The velocity (cb) of bulk acoustic wave (BAW) is normally two times as higher the SAW velocity (csaw) [3,18] in the same material (in the backing under current consideration).
The decrease in SAW phase velocity caused by mass load of IDT-like rod can be estimated using an elementary structural unit. For the lowest first fundamental SAW resonance, using a correction factor based on the spring-mass model, it can be written as
where A = p + b is equal to the SAW “natural” wavelength. As an estimate, typically in practice L ~ 2A, then , where FL is the piezo-rod λ/2 resonance frequency and cL is the longitudinal speed of sound in piezoceramic, so that typically in general Fsaw ≈ 0.4FL and lies close to the λ/4-type ineffective piezocomposite resonance (see Table 2). On the contrary, it is a SAW resonance on the backing boundary, sophisticated with an “appendant” mass of the piezo-rods.
For the rod extensional fundamental frequency higher than the lowest SAW resonance on backing (FL > Fsaw1), for simplicity considering the non-loaded condition as a reference, the rod influence on the actual SAW resonance is determined by the loading rod mass. Just note that in the opposite case, with the rod fundamental frequency lower the SAW resonance (FL < Fsaw1), the rod influence on the SAW resonance is determined by the loading rod elasticity, not its mass [19]. The resonance modes in the transitional frequency area have a dispersion character typical for modes’ coupling (Figure 3). As a reference point, the “ideal” (free surface) SAW harmonic resonances, tied to the composite basic structural configuration, are determined as , with N λ= A ≡ p + b as the periodic piezocomposite pitch integer multiple (harmonic order N = 1, 2, 3 …) to the SAW wavelength.
SAW fundamental resonance frequency variation for small loading masses (3D-configuration) can be described also as in [17,19].
where m is the rod mass per base square, Zb and cb are the cell acoustic impedance and bulk SOS of the backing. It particularly follows that the SAW resonance frequency vs. relative rod’s width is near constant, as supported by the simulation results presented in Figure 2.
The latter effect partly refers to the spring(k)–mass(M) model, where the resonance is determined as . Then, the frequency effect of mass variation (loading), with a parameter of loading mass (M) relative to the effective mass of moving unit cell in the SAW, can be estimated as
Extending expression (5), including larger connected mass, it can be expressed as:
There are several particular conclusions to be noticed. The rod length derivative of the resonance frequency (ΔF/F)/ΔL ~ N is proportional to the SAW harmonic order that agrees well with the simulation data of Figure 3. If the rod resonance is taken as , and the backing acoustical impedance Zb is some lower than that in piezoceramic, then the condition of maximum modes coupling with equal frequencies Fsaw,N = FL is as follows
If and , then , so that for high-order SAW harmonics with N >> 1, the condition is required for the high-order modes coupling.
Based on the estimation and simulation results, for the structure of piezo-rods connected to backing, several features of vibrational performance can be noticed related to the characteristic structural parameters:
The SAW resonance frequency(s) is inversely proportional to the composite pitch. Caused particularly by the kerf increase, with the fixed rod width and length, all SAW resonance branches are going down, with respect to the piezo-rod thickness mode frequency in piezocomposite. The strongest SAW modes are when located below the thickness (rod length) resonance and with descending SAW resonance intensities when above it.
When the rod width and kerf are varying simultaneously and in opposite directions, like a wider rod width under fixed pitch, then both (e.g., lowest) SAW and length rod resonance frequencies remain relatively constant.
When the kerf is getting much less than the rod width (or under the kerf-to-pitch ratio reaching zero), the SAW resonances disappear, mostly due to the mass loading effect—the total resonance spectra is getting closer to that of the elementary monolithic rod, or plate, connected to the backing of the same transverse cross-section.
When the rod height varies, with all other structural parameters fixed, the SAW resonances disappear with increased rods, mostly due to the mass loading effect.
2.5. Consecutive FEA Simulation of Air-Coupled 1-3 Piezocomposite Transducer with SAW Resonance on Backing
COMSOL FEA simulation was conducted to analyze the expected effects with SAW resonance on the transducer backing, with step-by-step adding structural elements into the total rods-epoxy-backing-matching transducer structure—a respective elementary cell in the 2D simulation model is shown in Figure 5.
The consecutive transformation of the electrical admittance spectra in the regular periodic piezocomposite assembly is shown in Figure 6. The matching-to-air boundary condition was set just through the air acoustical loading impedance.
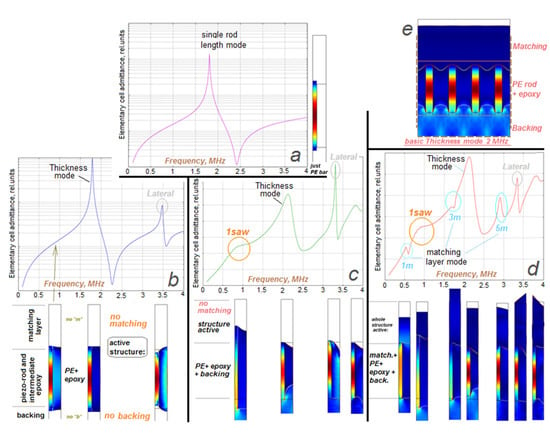
Figure 6.
FEA simulation of the electrical admittance and stress, with consecutive structural complexity of the piezocomposite transducer in 2D model with a periodic elementary cell containing: a single free rod (a); just 1-3 piezocomposite plate (b); piezocomposite connected to the backing (c); full assembly with matching layer (d). The spectra include the fundamental thickness mode (e), piezocomposite lateral, backing boundary SAW, and matching layer resonances at the different assembly stages. Backing 4 mm; rod L 0.76 mm; pitch 250 μm; pillar 70 μm.
A detailed description of the effects is based on the vibrational analysis of a rod connected (bonded) to the infinite boundary (backing). It determines specific features of the rod vibration, different from the case when the transverse cross-areas of the piezoelement and connected to its backing are finite and equal.
The basic stages and corresponding conclusions in the analysis of the data presented in Figure 6 are as follows. A free piezo-rod has its own length fundamental resonance (a). Then, in a piezoelement structured into a piezocomposite, additionally to that basic resonance, a higher frequency lateral mode appears (b) [10]. Then, most importantly, the piezocomposite plate just connected to the backing provides an extra low-frequency vibrational mode identified as a SAW resonance on the backing boundary with piezo-rods array (c). Finally, connecting the matching layer with its λ/4-resonance provides maximum transceiver efficiency when it coincides with particularly the SAW resonance (d). In that totally assembled piezocomposite transducer, the thickness resonance mode per se has a conventional character of motion of the parts (e).
3. Experimental Performance of a Transceiver with Piezoelectric 1-3 Composite Bonded to the Backing Layer—SAW Mode
3.1. Impedance Characteristics
For the SAW effect demonstration and performance comparison, two fully assembled transducers were built: one with a traditional monolithic piezo-plate and the second with a regular periodic 1-3 piezocomposite (see Table 1, sample #2), both with close overall dimensions and thickness resonances. The backing in both cases is a plate made of tungsten powder/chips mixed with epoxy; and the matching layer is a mixture of glass-bubbles with epoxy, with its thickness corresponding to the λ/4 resonance at 500 kHz, close to the expected SAW resonance on the backing boundary. As shown in Figure 7, the transducer with monolithic piezo-plate demonstrates a relatively smooth resistance characteristic, without any specific resonances at low frequencies up to the fundamental thickness mode. In the case of 1-3 piezocomposite, there is a characteristic peak at near 600…700 kHz identified as the backing SAW resonance, gained by the fundamental λ/4 matching layer resonance tuned to the same frequency, with its higher-order multiple overtones seen as well.
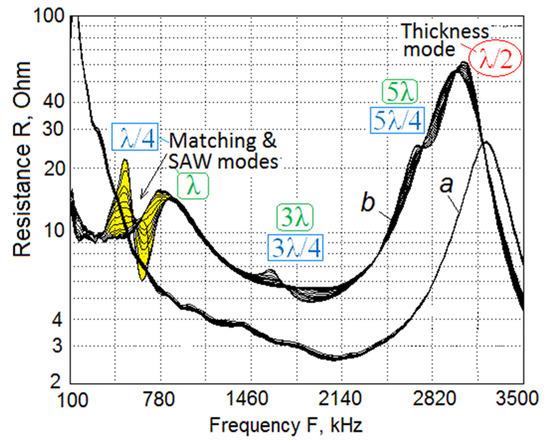
Figure 7.
Comparative characteristics of the resonance vibrational modes for a conventional homogenous piezoelement (a) and regular piezocomposite (b) with close overall dimensions, all are in the fully assembled transducers with backing and matching (at 500 kHz). The resonator OD 30 mm × H 0.72 mm, (b) piezocomposite sample 2 (Table 1), (a) same overall dimensions conventional piezoplate. Yellow area—most effective front surface sensitivity.
To preliminarily evaluate the transducer acoustical sensitivity, a simple express method was used with a rubber put on the front matching layer, and then the recorded resonance peak resistance variation was used as a measure of acoustical efficiency, as demonstrated in Figure 7 with multiple curves in the yellow area, reflecting different level of rubber damping. In the latter case, the most sensitive resonance is the λ/4 matching layer resonance located/coinciding with interpreted as a SAW resonance on the backing. The λ/4 matching layer resonance coupled to the backing SAW of the 1-3 piezocomposite plate bonded to the backing is deeply damped with quality factor near several units Q ~ 3…5 and demonstrates relatively strong sensitivity. Further experiments supported that conclusion with more details.
For the same sample #2 as in Figure 7, the full impedance loops of the basic thickness and SAW resonances are shown in Figure 8, demonstrating a deeply damped character of the λ/4 matching layer resonance coupled to the backing SAW. A specific of the SAW resonance is that its active resistance is close to the minimum transducer resistance (real part of the impedance), including its thickness resonance.
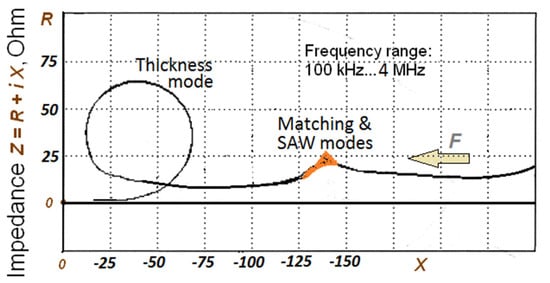
Figure 8.
Resonance characteristics in the frequency range 0.1–4 MHz including the low-frequency SAW and basic thickness vibrational modes for a regular periodic piezocomposite transducer with backing and matching layer (500 kHz). The resonator OD 30 mm × H 0.72 mm, sample #2.
3.2. Backing SAW Resonance Mode Strength in 1-3 Piezocomposite Transceiver
Three piezocomposites with different structural configurations were used in the experiments, as presented in Table 1. The impedance Z characteristics just of the free original piezocomposite plates are relatively smooth below the fundamental thickness resonance, which is proportional to the plate’s inverse thickness (1), and with some planar mode low-frequency weak “ripple”, as shown in Figure 9a. Being attached to the backing, the 1-3 regular periodic piezocomposites demonstrate complex spectra, with additional SAW fundamental mode at near 600 kHz (Figure 9b). The data are in a good agreement with the simulation results and theoretical interpretation given to the SAW resonance, including the mass loading effect.
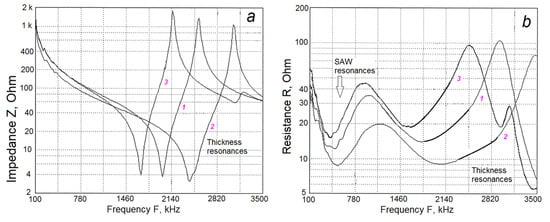
Figure 9.
Effects of the backing in piezocomposites with three different thicknesses: experimental electrical impedance Z for initial free piezocomposite plates (a) and resistance R for those piezocomposites just attached to the 4mm backing (b); all samples as in Table 1.
The resistance R of the complex impedance Z characteristic was chosen as a parameter better reflecting the SAW resonance behavior with deep damping. In the experiments, the backing with quality factor Q ~ 5 (a mixture of tungsten powder and chips with epoxy) was connected to the piezocomposite plate through a thin layer of hard epoxy—on this stage just before connecting a front matching layer.
As the acoustical strength of the SAW effect is highly sensitive to the mechanical bonding between 1-3 piezocomposite plate and backing, to demonstrate the transient resonance characteristics caused by the bonding conditions, a piezocomposite plate was put on the backing with freshly prepared glue (LOCTITE hard epoxy). Then, the resistance R characteristics transformation in the glue curing process was further under monitoring. As shown in Figure 10, initially the piezocomposite just exhibits some damping on its basic λ/2 thickness resonance (as it is loaded with a lower-impedance epoxy liquid), then upon the bonding epoxy getting harder and solid, its intensity is further going down, while to the contrary the new SAW resonance aroused and strengthened. A novel resonance with nearly 2 times lower frequency is getting stronger, reaching its maximum strength when the bonding epoxy is completely cured. This resonance is identified as a SAW vibrational type that occurred on the backing boundary in the regular 1-3 piezocomposite, being out of the piezoelectric rods resonance in the structure at that frequency.
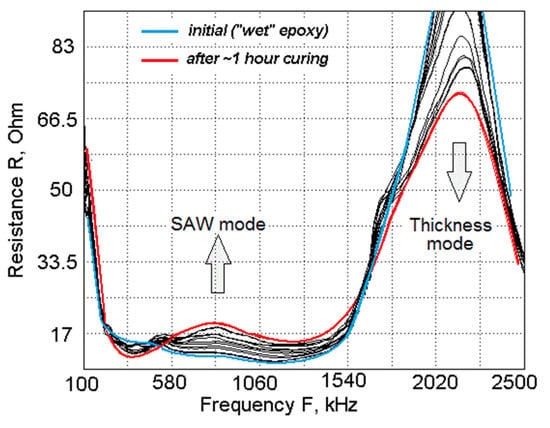
Figure 10.
Comparative transient transformation of the low-frequency SAW vibrational mode resonance under curing of epoxy (increased bonding strength) between piezocomposite element and backing. The resonator OD 30 mm × H 0.72 mm. Rising SAW mode is identified as an additional resonance in the structure.
Further extended experiments showed that the SAW resonance, and related effects, is provided only by a regular structure - the rods must be well arranged in the “dice and fill” 1-3 piezocomposite.
The SAW mode on the backing boundary neither occurs with irregularly oriented and distributed rods, when piezoelectric fibers (a bunch) are embedded randomly in a polymer matrix in the form of a 1-3 composite (e.g., [13,14]), nor with a homogeneous conventional piezoelectric monolithic plate/rod, specifically when the cross area for both piezoelement and backing are equal. The letter is demonstrated in Figure 7, where both comparative characteristics for 1-3 piezocomposite and conventional piezoelectric plates are presented. Note that, as was found, the strongest SAW resonance is provided with a relatively hard bonding epoxy between piezoelectric structure and backing supporting a collective character of motion in the multiple regular elementary cells.
3.3. Pulse-Echo Characteristics of 1-3 Piezocomposite Transceiver in Air operating at the SAW Mode on the Backing Boundary
Total transducer assembly was built with regular periodic 1-3 piezocomposites, backing, and a single front λ/4 matching layer. For generating and analyzing the acoustical waves, pulse/receiver P/R Panametrics 5077 (GE Panametrics, Lago Vista, TX, USA) was used as a basic device, with a general-purpose oscilloscope, such as Agilent 54622 (Agilent Technologies, Santa Clara, CA, USA), to provide pulse visualization. Impedance/Gain-Phase HP 4194A Analyzer (Hewlett-Packard, Palo Alto, CA, USA) was used for electrical immittance measurements, with 0.5 V max output. All measurements were performed in the presence of air under atmospheric pressure (air-coupled) at room temperature.
Acoustical signal strength measurements and Q-factor estimation were done with a transducer excited with a spike single cycle and 2% duty cycle tone burst. The SAW operational mode on the backing boundary, as excited in the experiments, showed expected promising results, specifically for the applications where a relatively low Q-factor ~3…10 is required for higher resolution.
The transducer has been tested in both pulse-echo and pitch-catch modes. For a typical pulse recorded (Figure 11), with a spike input 400 V0-p, the signal output was ~70 mVp-p, with a transfer level −75 dB for a full 4” pitch-catch transmitter–receiver path in atmospheric air. The pulse has relatively short rise- and decay-times, with near 2 to 3 periods each.
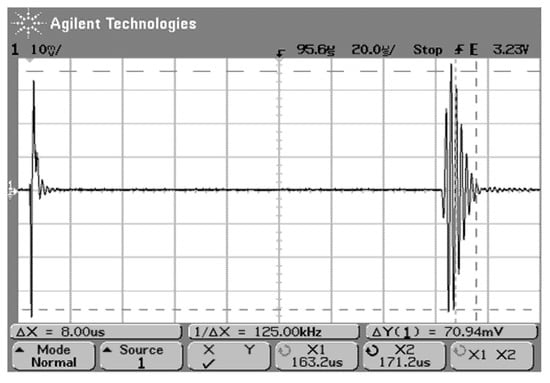
Figure 11.
Typical pulse waveform of the novel piezocomposite transducer with the SAW operational vibrational mode on the backing in 1-3 piezocomposite resonator at a relatively low frequency ~600 kHz. Sample #2 (Table 1), pitch-catch with 4″ distance.
In the SPL measurements with a calibrated microphone, a transmitter with SAW resonance on backing at near 150 kHz (sample D, Table 1) with similar input conditions demonstrated ~50 Pa effective acoustical pressure (pulse maximum), or SPL 128dB re 20μPa @4”@150kHz@400V0-p. Then, an estimated transceiver peak pressure sensitivity is roughly near -83dB re 1V @1μbar.
The performance of the proposed novel transducer is compared with that of conventional air-coupled transducers operating in a similar frequency range. Compared to one of the industrial prototypes such as Sonda 007CX; QMI AS400C [20] at 400 kHz, the piezocomposite transducer with SAW vibrational mode demonstrates similar acoustical performance suitable for practical applications, with usable sensitivity, efficiency, and short pulse duration, and being well-damped.
When the transducer was prepared in its full structure, the effectiveness of its sensitivity performance was first evaluated with a simple express method, applying some soft material (like a rubber) on the front transducer surface and recording its electrical impedance variations under that influence. It is supposed that the largest impedance variation is at the resonance frequency(-ies) of maximum transducer sensitivity of the acoustically active front surface. As shown in Figure 12, and supported by the data of Figure 7, the optimal transceiver operational frequency is near 500 kHz, with the sensitivity intensity dynamic range near ~2.4–4 times between the maximum-to-minimum peaks, with effective Q-factor ~3–5 [15].
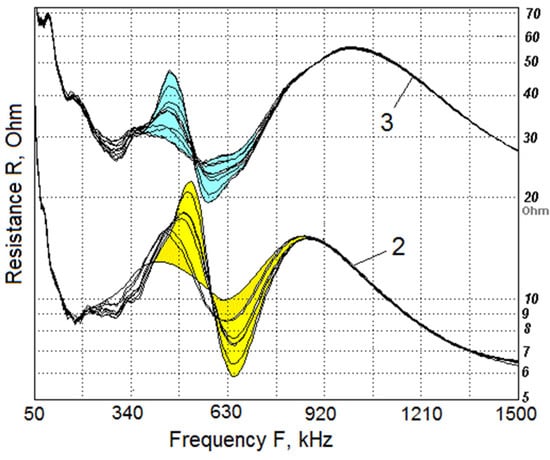
Figure 12.
Effectiveness of the front surface sensitivity characteristic of the low-frequency SAW vibrational mode resonance on backing for two regular periodic 1-3 piezocomposite elements (#2 and 3, Table 1), with the backing close to optimal and quarter-lambda matching layer. The area of highest sensitivity is shown in color.
The effect of matching layer thickness on the piezocomposite transducer performance during its operation based on the backing SAW has a typical resonance character; as was shown in an experiment, there is the optimal matching layer thickness providing maximum signal amplitude (Figure 13). It corresponds to the λ/4 matching layer thickness at the 500 kHz operation frequency of the backing SAW resonance.
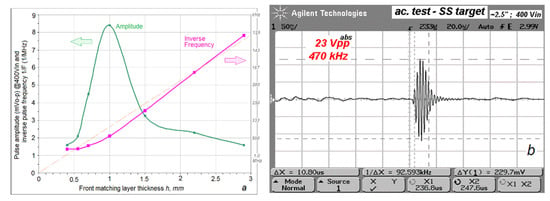
Figure 13.
Experimental data of the pulse strength under variation of the matching layer thickness in a piezocomposite transceiver with SAW operational mode on backing: (a) signal amplitude and effective frequency of the pulse; (b) pulse waveform with maximum output.
The experiment was made in the pulse-echo regime, with a 2.5″ SS target and the transducer using regular periodic 1-3 piezocomposite as presented in Table 1, sample 2.
4. Discussion
The Rayleigh SAW resonance discovered in the piezocomposite backing boundary is a powerful and promising tool for the air (gas) transducer operation. It requires, first of all, rigid piezo-rod-to-backing bonding and regular periodic structure array, at least with several adjacent piezo-rods.
The condition for the relatively low-frequency SAW resonance, in the first approximation, requires for the rods periodicity to be an integer multiple to the surface acoustical wavelength on the backing boundary, which is predominantly of a Rayleigh (Stoneley) type. The surface wave physically occurs in a layer of backing, involving bonding epoxy between the rods and backing, with an effective depth in the backing comparable to the SAW wavelength. As was found, just a hard epoxy for bonding provides maximum acoustical signal strength. Moreover, for a piezocomposite element, it also provides better bonding quality on the boundary between epoxy filler and backing, with its extra acoustical coupling.
For the described SAW resonance effect, a regular periodic 1-3 (or 2-2) structure is needed. Its acoustical performance is a collective effect between at least several adjacent piezo-rods with a regular space translation. In the latter case, a wider transducer bandwidth, or even a phase array, can be achieved under special structural apodization if needed.
As was predicted and experimentally verified, no effective (i.e., collective) backing SAW resonance effect exists with varying planar rod dimensions, and/or irregularly distributed rods, when the piezoelectric rods (or a fibers bunch) are embedded randomly in a polymer matrix in the form of a 1-3 composite (Figure 14). Note that the SAW effect does not exist also with a homogeneous conventional piezoelectric monolithic plate/rod, specifically when the overall cross area for both the piezoelement and backing are equal.

Figure 14.
An example of an irregular 1-3 piezocomposite structure that causes ineffective SAW behavior on the bonding boundary: piezo-rods of different cross-sections, and their irregular (random) relative planar disposition.
As a possible variant, a monolithic piezo-plate, with the bonding side grated, can be used instead of conventional rods, or alternatively such regular grating can be put on the backing boundary surface, as shown in Figure 15. The regular voids can be filled with a relatively soft material. The vibrational operation of that structure is very similar to the separated piezo-rods considered, just with larger effective mass for the “rods”.
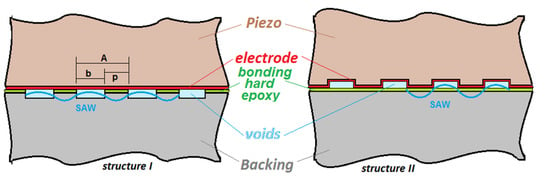
Figure 15.
Alternative structures with a boundary SAW resonance effect using monolithic bulk piezo-plate—with shallow regular grooves at least on one of the boundary surfaces, piezoceramic and/or backing, as shown in structure I and II.
5. Conclusions
Surface acoustical wave on the damping backing boundary of a piezocomposite transceiver is an effective resonating mechanism that was discovered and then specifically investigated for the air (gas) transducer application. As shown, the novel SAW vibrational mode with a significantly lower natural resonance in a regular periodic 1-3 piezocomposite transducer is an effective mechanism for the air-coupled ultrasonic applications. Collective SAW synchronized motion of the backing surface on the piezocomposite bonding boundary requires a regular (translational periodicity) rods’ structure to provide strong resonance efficiency of the transceiver, to the contrary of the conventional thickness mode approach with resonating piezoelectric rods.
Along with less transducer weight (a thinner piezocomposite required), the described SAW resonance effect on the backing effectively “bridges the gap” in the transitional intermediate frequency range 100–700 kHz, problematic for the conventional airborne transceiver designs typically with the unwanted strongly coupled thickness and planar resonances in a monolithic piezoelement with an aspect ratio close to 1. For practical evaluation, a typical piezocomposite structure (2–3 MHz thickness resonance) was used and it provided −64 dB pulse-echo signal strength at the backing SAW 500 kHz resonance in air with wide bandwidth and Q-factor near 5, being equipped with the backing and corresponding quarter-lambda conventional matching layer at that frequency.
The benefits of using relatively slow SAW waves are smaller volume and weight of the total transducer, clear well-damped spectra, with lower excitation voltage required because of a thinner piezoelement needed. It provides acceptable acoustical efficiency and sensitivity, along with low transducer Q-factor and consequently relatively wide BW. This is the case where a strong regular periodicity of the 1-3 piezocomposite greatly matters for successful transceiver operation.
Author Contributions
The author fully contributed to formal analysis, investigation, data curation, writing, and editing. The author has read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
Nomenclature
| pillar | piezoceramic rod (with length L and width p) in piezocomposite structure, with its length-to-width aspect ratio (L/p); |
| kerf | cut/dicing width (b), particularly for an orthogonal (square) array filled with epoxy; |
| pitch (kerf plus pillar width A ≡ b + p) | a shift between piezocomposite cuts, or structural periodicity; |
| CW | continuous wave; |
| SAW | surface acoustic wave; |
| BAW | bulk acoustic wave; |
| BW | frequency bandwidth; |
| PE | piezoelement; |
| SOS | speed of sound; |
| SPL | sound pressure level; |
| SS | metal stainless steel reflecting target in acoustic test; |
| IDT | interdigital transducer; |
| F | current frequency; |
| R | electrical resistance R = ReZ component of impedance Z; |
| saw1-Y and saw1-D | fundamental (lowest) SAW resonance determined from the piezocomposite electrical admittance (Y = 1/Z) and from the piezo-rod top displacement (D); |
| N | SAW harmonic order 1,2,3…; |
| L1-Y and L1-D | fundamental (lowest) longitudinal resonance of the piezo-rod in piezocomposite; |
| FsawN-Y and FsawN-D | SAW resonance harmonics (N = 1,2,3…) determined from the piezocomposite electrical admittance (Y = 1/Z) and from the piezo-rod top displacement (D); |
| λ | wave-length, used for SAW, matching layer, and piezorod longitudinal resonances; |
| FL | fundamental λ/2 rod resonance frequency; |
| nm | matching layer vibrational mode of the nm = 1,3,5… order; |
| Zac, Z0, ZR, Zm, Z | acoustical impedance, particularly of piezoelectric material, loading fluid, front matching, and backing layers, respectively; |
| c, cb, csaw, cL | speed of sound (SOS), particularly bulk and SAW on backing, and longitudinal SOS in piezo-rod; |
| density, particularly backing and piezoceramic density; | |
| E, σ, Q | Young module, Poisson coefficient, and material quality factor; |
| M, m | mass in the vibrational models. |
References
- Lee, H.J.; Zhang, S. Design of low-loss 1-3 piezoelectric composites for high-power transducer applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2012, 59, 1969–1975. [Google Scholar] [PubMed]
- Smith, W.; Auld, B. Modeling 1-3 composite piezoelectrics: Thickness-mode oscillations. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1991, 38, 40–47. [Google Scholar] [CrossRef] [PubMed]
- CeramTec GmbH. Piezo Ceramic Components. Materials; CeramTec GmbH: Ebersbach, Germany, 2019; Available online: https://www.ceramtec.com/ceramic-materials/soft-pzt/ (accessed on 16 February 2020).
- Hayward, G.; Gachagan, A. An evaluation of 1-3 connectivity composite transducers for air-coupled ultrasonic applications. J. Acoust. Soc. Am. 1996, 99, 2148–2157. [Google Scholar] [CrossRef]
- Mezheritsky, A.V. Invariants of coupling coefficients in piezoceramics. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2003, 50, 1742–1751. [Google Scholar] [CrossRef] [PubMed]
- Toda, M. New type of matching layer for air-coupled ultrasonic transducer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2002, 49, 972–976. [Google Scholar] [CrossRef] [PubMed]
- Certon, D.; Casula, O.; Patat, F.; Royer, D. Theoretical and experimental investigations of lateral modes in 1-3 piezocomposites. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1997, 44, 643–651. [Google Scholar] [CrossRef]
- Gururaja, T.; Schulze, W.; Cross, L.; Newnham, R.; Auld, B.; Wang, Y. Piezoelectric Composite Materials for Ultrasonic Transducer Applications. Part I: Resonant Modes of Vibration of PZT Rod-Polymer Composites. IEEE Trans. Sonics Ultrason. 1985, 32, 481–498. [Google Scholar] [CrossRef]
- Robertson, D.; Hayward, G.; Gachagan, A.; Murray, V. Comparison of the frequency and physical nature of the lowest order parasitic mode in single crystal and ceramic 2-2 and 1-3 piezoelectric composite transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2006, 53, 1503–1512. [Google Scholar] [CrossRef] [PubMed]
- Certon, D.; Patat, F.; Casula, O.; Tran Hu Hue, L.P. Two dimensional modeling of lateral modes in 1-3 piezocomposites. In Proceedings of the IEEE Ultrasonics Symposium, Cannes, France, 31 October–3 November 1994; pp. 991–994. [Google Scholar]
- Rouffaud, R.; Hladky-Hennion, A.-C.; Pham-Thi, M.; Bantignies, C.; Levassort, F. Influence of 1-3 piezocomposite fabrications on lateral modes. In Proceedings of the 2012 IEEE International Ultrasonics Symposium, Dresden, Germany, 7–10 October 2012; pp. 1–4. [Google Scholar]
- Smart Materials. 1-3 Random Fiber Piezocomposites; Smart Materials: Sarasota, FL, USA, 2019; Available online: https://www.smart-material.com/13Crand-product-main.html (accessed on 16 February 2020).
- Qi, W.; Cao, W. Finite element analysis of periodic and random 2-2 piezocomposite transducers with finite dimensions. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1997, 44, 1168–1171. [Google Scholar]
- Ruddle, J.; Cass, R.; Mohammadi, F. Advanced cerametrics harvests clean energy. Am. Ceram. Soc. Bull. 2007, 86, 24–27. [Google Scholar]
- Mezheritsky, A.V. A method of “weak resonance” for piezoelectrics quality factor and coupling coefficient measurements. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2005, 52, 2120–2130. [Google Scholar] [CrossRef] [PubMed]
- Ramakrisnan, N.; Nemade, H.B.; Palathinkal, R.P. Resonant frequency characteristics of a SAW device attached to resonating micropillars. Sensors 2012, 12, 3789–3797. [Google Scholar] [CrossRef] [PubMed]
- Pomorska, A.; Schukin, D.; Hammond, R.; Cooper, M.A.; Grundmeier, G.; Johannsmann, D. Positive frequency shift observed upon absorbing icro-sized solid objects to a quartz crystal microbalance from the liquid phase. Anal. Chem. 2010, 82, 2237–2242. [Google Scholar] [CrossRef] [PubMed]
- Alhazmi, H.; Guldiken, R. Quantification of Bolt Tension by Surface Acoustic Waves: An Experimentally Verified Simulation Study. Acoustics 2019, 1, 794–807. [Google Scholar] [CrossRef]
- Plessky, V.; Koskela, J. Coupling-of-modes analysis of SAW devices. Int. J. High Speed Electron. Syst. 2000, 10, 867–947. [Google Scholar] [CrossRef]
- Quality Material Inspection (QMI), Inc. Huntington Beach, CA, USA, 2019. Available online: https://www.qmi-inc.com/airscan.php (accessed on 16 February 2020).
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).