Estimation of Acoustic Power Output from Electrical Impedance Measurements

Abstract

A method is proposed for estimating the acoustic power output of ultrasound transducers using a two-port model with electrical impedance measurements made in three different propagation media. When evaluated for two high-intensity focused ultrasound transducers at centre frequencies between 0.50 and 3.19 MHz, the resulting power estimates exceeded acoustic estimates by 4.5–21.8%. The method was shown to be valid for drive levels producing up to 20 MPa in water and should therefore be appropriate for many HIFU (high-intensity focused ultrasound) applications, with the primary advantage of employing relatively low-cost, non-specialist materials and instrumentation.

1. Introduction

1.1. Motivation and Overview of Current Methods

The measurement of transducer acoustic output is necessary for deriving safety indices for diagnostic ultrasound transducers; for a review, see [1]. Acoustic power measurements are also critical for therapeutic treatment scenarios, especially those involving targeted hyperthermia [2]. In the current practice, parameters defining safety (peak rarefaction pressure, spatial-peak temporal-average intensity, temporal-average acoustic power) are determined usually by using either a hydrophone measurement system (for pressure and intensity measurement and sometimes also for acoustic power calculations) or a radiation force balance (for acoustic power measurement) [1,3]. However, there are several drawbacks for using hydrophone systems, such as the difficulty in measuring high pressures (they generally do not withstand high pressures and/or long pulses) and the time for the setup of field scans required for power calculation. Measurements using a radiation force balance are much more time efficient; however, the specific-purpose devices are relatively expensive (7–24k USD) and therefore unobtainable by many laboratories and institutes with a limited budget. A method of rapidly testing transducers in a cost-effective manner, using otherwise multi-purpose standard laboratory equipment, may be useful in several use cases. Custom-designed transducers may be quickly tested during production without requiring a full characterization. Moreover, during manufacturing, all manufactured items may be tested without the need for random sampling. Lastly, a clinician may test the performance of a transducer over time without requiring access to expensive equipment.

1.2. Equivalent Circuit Models for Transducers with Reference to the Current Work

The total power dissipation of a transducer is partially due to electrical losses. Calculating the total power dissipation from electrical impedance measurements may provide an upper limit to the acoustic power output, under the assumption that all electrical power going into the transducer is converted to acoustic power. Since such an assumption is too idealistic and leads to a significant overestimation of the acoustic power output of a transducer, more sophisticated methods are needed for a closer estimation of the electrical losses and acoustic output. There exist methods using equivalent circuit models of transducers for a full description of their electrical and acoustical behaviour [4,5], the most popular transducer model being the KLM model [6]. However, these methods require extensive knowledge of transducer parameters (such as physical dimensions, acoustic impedance, sound velocity, and the coupling factor of the piezoelectric ceramic) [7] that are not necessarily available when testing. There also exists work, broadly termed the electromechanical impedance technique, that seeks to characterize a material placed on a piezoelectric transducer by measuring the electrical impedance of the two; for a review, see [8]. However, the aim of such work is not to characterize the power output of the transducer itself, but to characterize the loading placed in front of it.

Here, we propose a method for acoustic output power estimation based on ultrasound transducer electrical impedance measurements only. The transducer is modelled as a two-port network loaded by the acoustic propagation medium, a generalization of the KLM model that retains the linearity and reciprocity assumptions of the latter [7]. Such a lumped two-port model has been used in the literature for electrical matching [9]. Here, the two-port network model parameters are derived by measuring the electrical impedance of the transducer as it is placed in different propagation media (similarly to [10], where the model parameters are used to characterize the properties of a material placed onto the front of the piezoelectric transducer). In the present case, the model parameters are used to estimate the acoustic power dissipation and subsequently compare with acoustic measurements for validation. To the knowledge of the authors, this is the first time that changing the exterior loading of a piezoelectric transducer has been used to estimate its output power.

2. Theory

In accordance with the KLM model, a piezoelectric transducer is interpreted as a system with three ports. One electrical port connects the transducer to the electrical pulser and signal receiver system. Two acoustic ports represent the connection to the mechanical fields in the front and back acoustic loads (see Figure 1). In such a model, $V_2$ and $I_2$ stand for the acoustic pressure and particle velocity of the front load, as electrical circuit equivalents. Treating the transducer as a system including the backing load, as well as optional electrical matching circuit as inner parts of the system, the model can be generalized to a two-port network (see Figure 2).

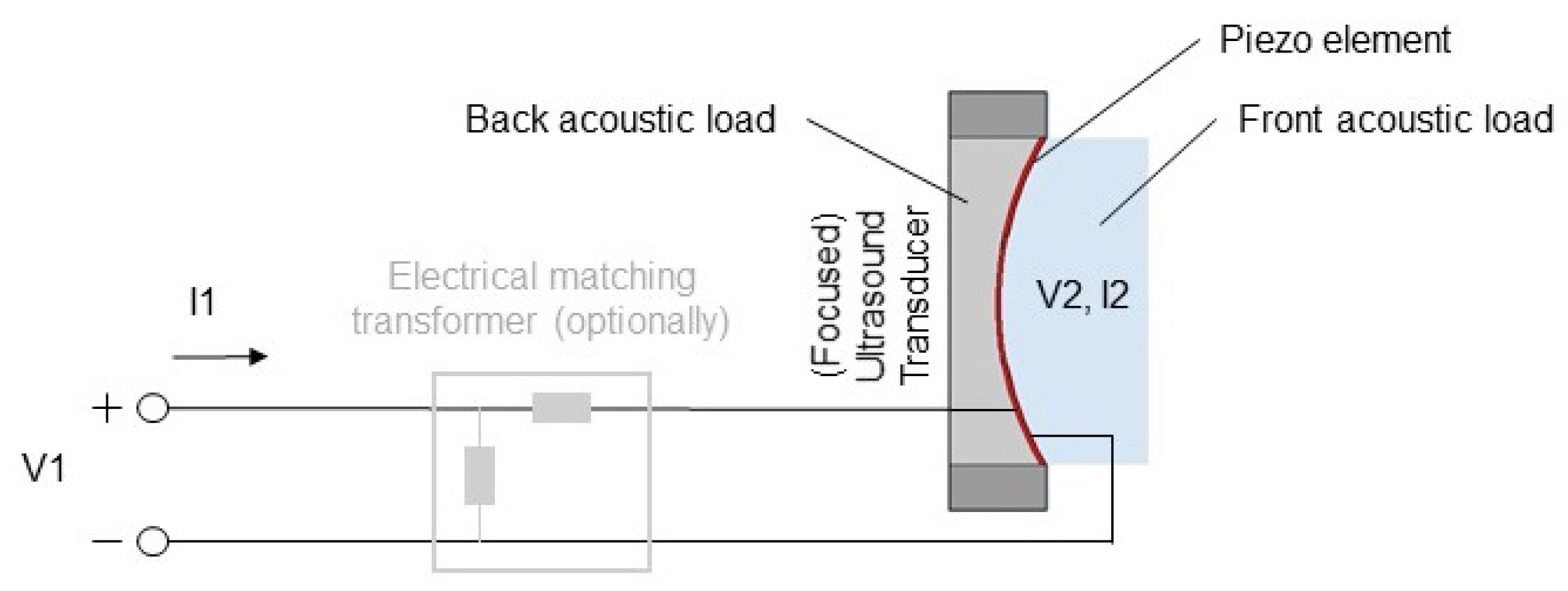
2.1. Two-Port Transducer Model

Defining an electrical port as a pair of terminals with equal currents flowing in and out, an electrical circuit with two ports may be treated as a two-port network (Figure 2) defined fully by four impedance parameters $Z_{11},Z_{12},Z_{21},Z_{22}$ [11,12], with state equations:

$$\begin{array}{ccc}\hfill V_1& =& Z_{11}{I}_1+Z_{12}{I}_2,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill V_2& =& Z_{21}{I}_1+Z_{22}{I}_2,\hfill \end{array}$$

(2)

where $V_n$, $I_n$ are the voltage at and current going into ports $n\in 1,2$, respectively (with $Z_{mn}$ ($m,n\in 1,2$) impedance parameters describing their interconnections). Placing an acoustic load $Z_L$ at port 2, the input impedance $Z_{in}=V_1/I_1$ “seen” from port 1 is [13]:

$$Z_{in}=Z_{11}-\frac{Z_{12}{Z}_{21}}{Z_{22}+Z_L}.$$

(3)

2.2. Estimation of Two-Port Parameters and Power

Rewriting Equation (3) as a linear combination of parameters,

$$\begin{array}{ccc}\hfill [Z_L,-Z_{in},1]\mathbf{x}& =& Z_{in}{Z}_L,\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill \mathbf{x}& =& {[Z_{11},Z_{22},Z_{11}{Z}_{22}-Z_{12}{Z}_{21}]}^{\prime }.\hfill \end{array}$$

(5)

The system of equations in Equation (4) is currently not unique for the four impedance parameters of x (Equation (5)). However, using the assumption of reciprocity, generally true for circuits containing passive elements only and shown to be true for the KLM model [7], $Z_{12}=Z_{21}$. During the calculation of the impedance parameters, the square root of $Z_{12}{Z}_{21}$ is taken, which gives a positive real impedance value for both $Z_{12}$ and $Z_{21}$. Since there are three unknown terms remaining in x, at any given frequency, measurements of the input impedance $Z_{in}$ using at least three different acoustic loads $Z_L$ allows an estimate of the parameter vector $\mathbf{x}$ to be obtained using matrix inversion. The equation system will have a unique solution as long as the impedance properties of the three loads are different.

Rearrangement of Equations (1) and (2), using also $V_2=-Z_L{I}_2$ (see Figure 2), yields (see Appendix A):

$$V_2={\left[\frac{Z_{11}}{Z_{21}}\left(1+\frac{Z_{22}}{Z_L}\right)-\frac{Z_{12}}{Z_L}\right]}^{-1}{V}_1.$$

(6)

Expressing all voltages in terms of their root mean squared (rms) value, the average power dissipated on the acoustic load is:

$$P_a=\frac{{\left|V_2\right|}^2}{Z_L}=V_1^2\frac{Z_L}{{\left|\frac{Z_{11}}{Z_{21}}\left(Z_L+Z_{22}\right)-Z_{12}\right|}^2}.$$

(7)

We note here that the acoustic load $Z_L$ in the electrical circuit encapsulates all the acoustic dissipation into the acoustic medium, while the purely electrical dissipation is contained in the two-port network. We further note that $Z_L$ can be defined as any multiple of the acoustic impedance, with the two-port network ensuring the appropriate conversion between electrical and acoustic impedance. For simplicity, the acoustic load used is simply the acoustic impedance. The above considerations are analogous to the ones made in the KLM model [7], although our proposed model has a more general and therefore simplified form.

3. Materials and Methods

In this section, we describe the experiments conducted to assess the validity of the proposed method. First, electrical impedance measurements were made with two high-intensity focused ultrasound (HIFU) transducers loaded in turn with three distinct fluid media. Data collected from these measurements were processed according to Section 2.2 to yield estimates of radiated power. Acoustic field measurements were then made in the focal planes of the HIFU transducers in order to gain independent estimates of radiated power. Finally, the pressure range of applicability was assessed through a series of additional acoustic and electrical measurements performed with drive levels producing pressures up to approximately 20 MPa. Details are provided in the following subsections.

3.1. Transducers Used for the Measurements

Two spherically-focused HIFU transducers (Sonic Concepts, Bothell, WA, USA) were used for measurements at both their fundamental and 3^rd harmonic frequencies: H-102, SN: B-022 (1.060/3.190 MHz) and H-107, SN: 031 (0.5/1.7 MHz). The fundamental and 3^rd harmonic bandwidths, as defined by the manufacturer, down to -3dB normalized to a perfect 50 $\mathsf{\Omega }$ match, were 640/700 kHz (H-102) and 340/80 kHz (H-107). The H-102 and H-107 transducers had a rectangular and circular cutout, respectively, modifying their surface areas from 32.2 to 26.5 cm${}^2$ and 32.2 to 30.8 cm${}^2$, respectively (Figures 4a and 5a).

For experimental validation of the theory presented in Section 2, the acoustic power dissipation was estimated from electrical impedance (“Z”) measurements and compared with the corresponding acoustic measurements (acoustic power dissipation calculated from measurements of pressure “p”) as a reference (Figure 3), as described in the following subsections. These measurements were performed for both transducers with both of their driving frequencies.

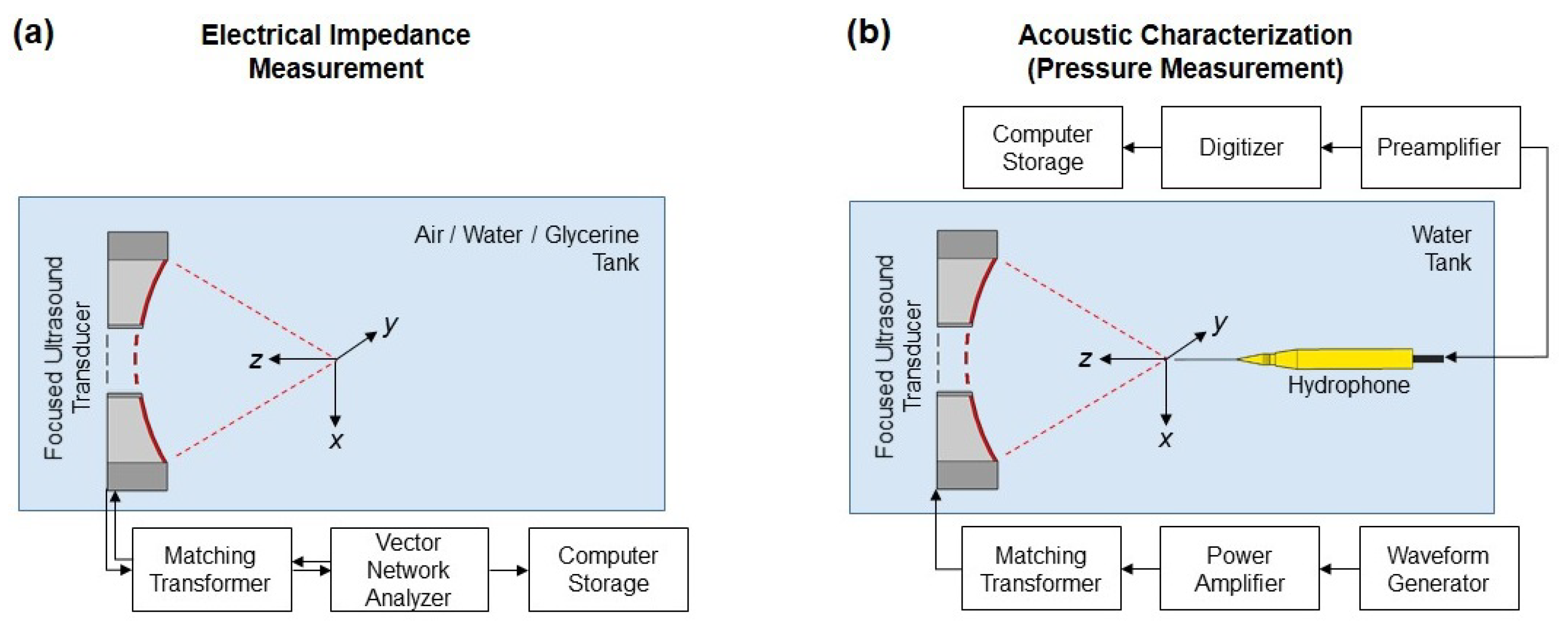
3.2. Electrical Impedance Measurements

Electrical impedance measurements were performed using a Bode 100 vector network analyser (Omicron Lab, Klaus, Austria), in the frequency range of 100 Hz–4 MHz. The input signal source for the impedance measurements was a continuous wave sinusoid, and a 1 kHz receiver bandwidth was used. Each HIFU transducer had a matching transformer; all electrical measurements were made at the transformer input (Figure 3a). During the measurements, the transducer was placed into three easily obtainable and safe media with known acoustic impedances: air, water, and 87.5% glycerine, with characteristic acoustic impedances of 0.4 $\times {10}^{-3}$, 1.50, and 2.06 MRayl ($2.06\times {10}^6$ Rayleigh) assuming linear mixing for glycerine [14]. Since inadvertent physical movement of the transducer cable could potentially change its impedance, care was taken to not move it while the propagation media was being changed.

The acoustic power output was estimated from the impedance measurements with MATLAB (MathWorks, Natick, MA) using the proposed method (Section 2). For more details on the calculations, see Appendix B. Since the two-port model automatically adapts to the conversion factor used, for simplicity, a conversion factor of 1 $\mathsf{\Omega }/\mathrm{Rayl}$ was used when defining the load impedances $Z_{L_m}$.

The estimated impedance coefficients were used to derive acoustic power consumption, as well as total power consumption for unit peak drive voltage ($V_1=1$ V) with water as the acoustic load. Total power consumption $P_t$ was calculated using the first part of Equation (7) for the root mean squared drive voltage $V_{1,rms}$ and for the impedance of the whole system with water load (as observed from port 1 of the network model) $Z_{i{n}_{water}}$, as follows: $P_t={\left|V_{1,rms}\right|}^2/Z_{i{n}_{water}}$. In a similar way, transmitted acoustic power $P_a$ was calculated from the root mean squared output voltage $V_{2,rms}$ of the two-port network model (see Equation (6)) and from the impedance of water as the load material ($Z_{L_{water}}$). The efficiency of the transducer at a given frequency was calculated as the ratio of the transmitted acoustic power ($P_a$) and the total power ($P_t$), in %.

3.3. Acoustic Characterization

Direct measurements of radiated acoustic pressure were carried out with the transducers submerged in a tank filled with filtered and degassed water. For each transducer/frequency combination, a drive signal was provided by a waveform generator (Agilent 33225A, Santa Clara, CA, USA) connected to a power amplifier (Model 1140LA, E&I limited, Rochester, NY, USA) as shown in Figure 3b. The drive signal consisted of two-cycle bursts having a centre frequency defined by the manufacturer at the fundamental or third harmonic resonance of the transducer, with the short burst typically providing at least 300 kHz of usable processing bandwidth. Note that due to the capture of both magnitude and phase spectra of the drive and receive waveforms, the output for an arbitrary pulse frequency (within the measurement bandwidth) and length can be reconstructed from these measurement results (see Appendix C), provided that the longer pulse length itself does not introduce additional nonlinearities (e.g., near a cavitation threshold). The focal plane pressure fields were measured with a calibrated needle hydrophone (HNC0400, (Onda Corp, Sunnyvale, CA, USA) for 500 kHz, or PA0200 (Precision Acoustics, Dorset, U.K.) for higher frequencies). Hydrophone positioning and data acquisition were coordinated by software control (UMS, Precision Acoustics). Spatial measurement ranges were chosen to capture at least three sidelobes, as verified by preliminary line scans. Additional measurements were made on the H-107 transducer at higher amplitudes and varying pulse lengths in order to assess the validity of the proposed power estimation method with respect to drive scaling and system linearity.

For estimates of radiated power, the point-by-point field measurements $h\left(t\right)$ were first Fourier transformed $F[ ]$ and normalized by the transform of the drive voltage $d\left(t\right)$ and the hydrophone calibration $M_h\left(t\right)$ to yield pressure spectra per unit drive voltage:

$$p\left(f\right)=\frac{F\left[h\left(t\right)\right]}{F\left[d\left(t\right)\right]M_h\left(f\right)}.$$

(8)

Radiated power was then found by numerically integrating the pressures under the assumption of locally planar propagation:

$$P\left(f\right)=\frac{1}{2\rho c}{\int \int }_A{\left|p\left(f\right)\right|}^{2}dA,$$

(9)

where the integration area $dA$ was taken from the scan step size (0.1 mm) and the ambient sound speed c was found from a temperature-speed relationship [15] and a thermocouple measurement made during the scan.

It should be noted that the H-107 measurements were repeated to expand the spatial scan for power computation. In the time between the initial and repeat experiments, it was found that the electrical impedance of the H107-matching transformer system changed. This was accounted for using the procedures in Appendix D.

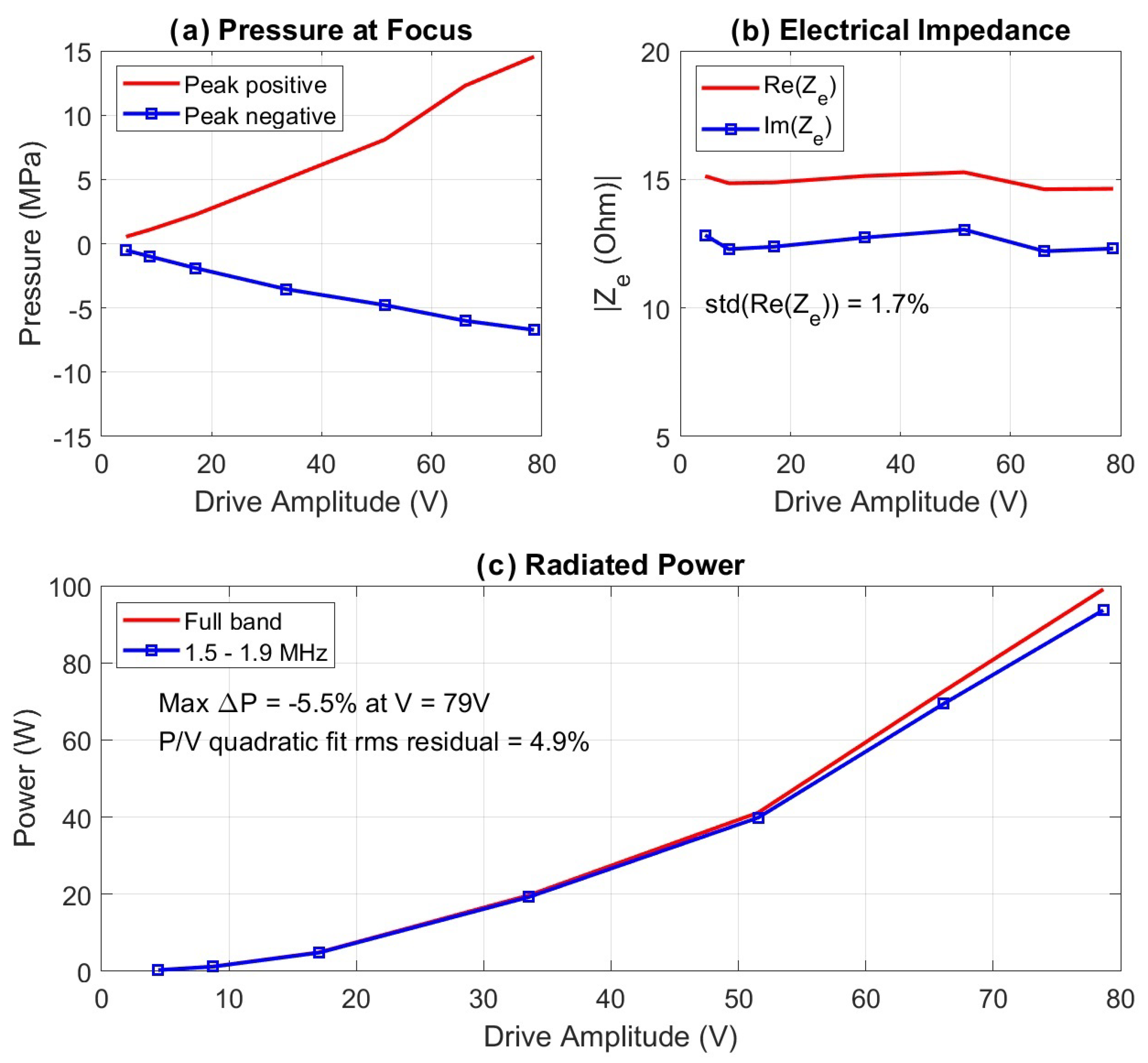
3.4. Measurements Validating the Range of Linearity for the Model

The estimate of acoustic power output from a given voltage input relied on a linear model. The electrical impedance measurements were done using a small current injection so their linear extrapolation should work as long as the acoustic output was in the linear range. To demonstrate the validity of linearity in terms of drive voltage, measurements were performed as follows.

The H-107 transducer was driven in its 3rd harmonic band over a range of amplitudes so that the final peak to peak pressure was just over 20 MPa. Fields were measured with a membrane hydrophone (D1602, Precision Acoustics, Dorset, U.K.) whose frequency response was flat within 1–2% over the 1–20 MHz range allowing determination of calibrated pressure as harmonics appeared in the received waveforms. The hydrophone was scanned through a radial line spanning ±6 mm about the focus for each drive level, and the scan data were processed to yield acoustic power estimates as described above (Equation (9)). Electrical impedance was also measured, using a current probe (4100, Pearson Electronics, Palo Alto, CA, USA) and a voltage probe (PP017, LeCroy, Geneva, Switzerland) connected to the amplifier output.

4. Results

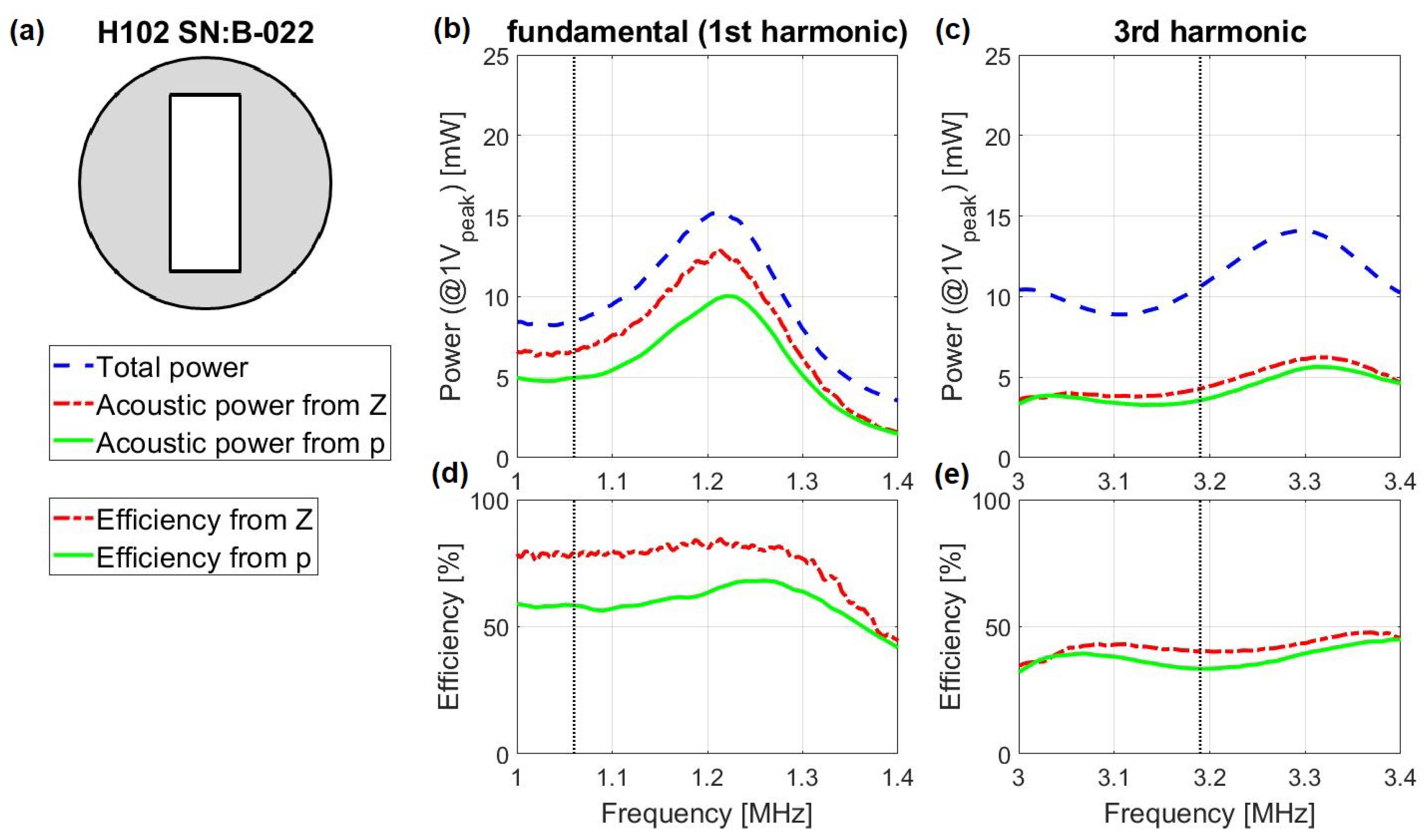
4.1. Comparison of Estimated and Measured Acoustic Powers

Results are shown here in terms of power and efficiency. As an example, in Figure 4, the estimated (from impedance “Z”) and measured (from pressure “p”) acoustic powers were compared in relation to the total (electric and acoustic) power calculated from impedance measurements (Section 3.2). The lower plots (d,e) show the efficiency calculated for both estimation and measurement of acoustic power, using the data of the plots at the top (b,c).

The results for four cases of transducer and driving frequency combinations (see Figure 4 and Figure 5) indicated that the method presented in this paper gave an estimation in between the total power and the measured acoustic power values. A good agreement was found in the frequency dependency of these three values, with estimations being closer to the measured acoustic power for frequencies near the third harmonic, coupled with a lower efficiency. At the nominal transducer resonance frequencies, the estimated/measured powers were 6.7/5.0 mW (H-102, 1.06 MHz) 4.3/3.6 mW (H-102, 3.19 MHz), 8.1/6.2 mW (H-107, 0.5 MHz), and 5.2/4.4 mW (H-107, 1.7 MHz). The mean absolute difference between estimated and measured power, in % of the average measured power, was 17.0% and 4.5% for the H-102 fundamental and third harmonic; 21.8% and 7.8% for the H-107 fundamental and third harmonic. The impedance-based power predictions were consistently above the acoustic measurements. The acoustic measurements themselves had an uncertainty of around 32% (in accordance with 15% hydrophone calibration uncertainty for pressure). The uncertainty of the impedance-based method was estimated to be between 0.7 and 7.1% depending on the device and its drive band (Appendix E).

4.2. Linearity of the Model

The linearity of the transducer response, in terms of pressure-voltage correlation, was assumed when suggesting that the small-signal impedance measurements used to estimate the power output of the transducer were valid over a higher voltage range, as well as for a broad frequency range.

A wide range of linearity was verified for the proposed model by measurements performed as described in Section 3.4. Results are shown in Figure 6.

Figure 6a shows the peak positive and negative pressures measured at the focus of the H-107 transducer and includes all frequency content up to 20 MHz. From the asymmetry of the values, the waveform clearly exhibited nonlinear behaviour even at low drive levels (“drive amplitude” is the amplifier output).

Figure 6b shows the values of electrical impedance $Z_e$ at 1.7 MHz as determined from voltage and current probes at the amplifier output terminal. The datasets had standard deviations of <2% over the drive range. At the higher drive levels, small nonlinearities did show up in the drive spectrum (not shown on the figure), but they were no larger than 1/20th of the 1.7 MHz amplitude. All this suggested that the nonlinearities were primarily in the water, not in the drive chain (as expected). Because the electrical impedance was essentially invariant with driving amplitude, this further validated the use of the proposed model for higher driving voltages.

In Figure 6c, the computed radiated powers are shown in two forms: using the full bandwidth of the data and only keeping the part that was in the 1.5–1.9 MHz band. The latter presumably was what would come from the electrical impedance-based predictions. At the highest drive level, the band-limited power estimate was only 5.5% lower than the full band. This was largely as expected when the nonlinearity was occurring locally in the focus due to elevated pressures. The main lobe peak had a minimal contribution to the total power because there was very little corresponding area through which energy flowed at the peak intensity. For pressures in the range reported here, similar observations were made regarding heating of tissues with focused beams: nonlinearity may produce a waveform distortion, but it did not necessarily impact spatially cumulative outputs that were quadratic in pressure (e.g., power, heat deposition). Finally, the power–voltage curves followed the expected quadratic dependence, with a residual difference of about 5%.

In summary, the proposed method did not appear to be limited by deviations from linearity (or voltage scaling as presented above) for this transducer for up to 20 MPa peak-peak pressure. This pressure range is relevant to many therapeutic scenarios, and therefore, the association with “HIFU” is appropriate based on these findings.

5. Discussion

5.1. Interpretation of Transducer-Specific Phenomena Affecting Measurements

As shown in Figure 4 and Figure 5, efficiency values at the fundamental frequency were significantly lower for measured acoustic power than for electrical impedance-based estimations, in all four cases. The efficiency estimates were also lower than the values reported by the manufacturer for a representative transducer (with different SN). However, the representative transducer did not have a cutout, and having cutouts of any shape (and the resulting boundary conditions and vibration shapes) could impact the power estimates via the input energy going into subsonic vibrations (such as bending or surface wave motion) near the edges of the ceramic, rather than deformation that produces volume change and efficient radiation. In this way, some energy may be dissipated in ceramic losses and kinetic energy of the loading fluid (water), near the edges. Assuming that the edge “losses” scale with the wavelength may explain the larger difference between estimated and measured acoustic power for the fundamental frequency than that for the third harmonic.

Conceivably, a larger transducer with a greater surface area to edge length would be less susceptible to the proposed loss mechanism. To the authors’ knowledge, all clinical HIFU transducers (unless array based) would fit this description. Another potential loss mechanism at lower frequencies would be coupling into the transducer body (side walls). In a transducer without a cutout, we would expect even closer correspondence of our impedance-based estimates of the acoustic power dissipation with the real dissipation shown by reference acoustic measurements.

The acoustic resonance frequencies, as measured using electrical impedance and acoustic measurements, are seen to be in close agreement in Figure 4 and Figure 5. However, there were discrepancies with the values provided by the manufacturer. This could be due to several factors, including changes of transducer properties with time and handling.

5.2. Scaling of the Results

The results presented in Section 4.1 were measured and calculated for unit voltage amplitude. Projections to a given drive voltage amplitude should consider both the electrical and acoustic linearity of a specific transducer for a drive voltage and frequency range. Note that, with the assumption of linearity, the power output increased as the square of voltage (meaning that a 32 V drive would scale the plots of Figure 4 and Figure 5 from mW to W), and for HIFU applications, even higher voltages (e.g., 50 V and higher) were typically used. As long as the model was applied in its linear range, the relative (%) errors (Section 4.1) remained valid.

The effect of drive level on the scaling of model results was evaluated with the H-107 transducer, with measurements made of the drive voltage, drive current, and focal plane acoustic pressure (Section 4.2). For drive amplitudes between 4 and 79 V, the electrical impedance in the “drive band” (1.6–1.8 MHz) exhibited negligible variation (1.7% standard deviation). At the highest drive amplitude, the focal pressure waveform was highly nonlinear, with a peak-to-peak value of approximately 20 MPa. Still, the estimated radiated power followed a simple quadratic relationship with drive voltage over the range tested. This presumably was because the amplifier-transducer system behaved linearly, and the nonlinear response of the medium (water) was not strong enough to cause meaningful thermo-viscous losses that would appear as a loss of beam power. Further study would be required to evaluate other transducer systems and drive conditions. However, the data in this study confirmed that the proposed method was valid even when the response of the medium yielded strongly nonlinear waveforms.

5.3. Potential Advantages of the Proposed Method

The primary advantage of the proposed method is its cost effectiveness. The liquids used for the presented measurements are commonly available lab supplies, and the electrical impedance measurement could be done with probes or simple circuits if an impedance analyser were not available. Another advantage is its simplicity. It only requires changing the media in which the transducer is placed and performing quick impedance measurements in each. There is no need for precise setting of the orientation of the transducer if the tank is large enough. A further advantage is time effectiveness. An electrical impedance measurement only takes about a few seconds for a frequency range of tens of MHz. Including the changes of propagation media, the three measurements can be done within 15 min, approximately.

Future work could investigate the use of media with an even higher acoustic impedance than glycerine to ensure a higher contrast in electrical impedance values, the expected effect being to reduce sensitivity to measurement errors.

6. Conclusions

A method for acoustic power output estimation of ultrasound transducers was proposed in this paper, based on simple electrical impedance measurements in three different propagation media and requiring knowledge only of the relative characteristic acoustic impedances of these media. Results showed agreement of estimated acoustic power outputs (based on electrical measurements) with relevant reference acoustic measurements, for four cases of transducer and driving frequency combinations. Since the estimates were consistently above the measured acoustic values, they may potentially be useful for providing an upper bound for ultrasound exposure safety analyses. Quantitatively, a 21.8% overestimate as seen with the H-107 fundamental would translate to a 10.4% overestimate in pressure, which is similar to the maximum uncertainty in a direct measurement with a hydrophone. Drive scaling analyses indicated that the proposed method could yield valid power estimates even when the output waveform was highly nonlinear, making it suitable for many HIFU calibration scenarios.

Although estimates of acoustic power dissipation may be used to estimate acoustic intensity and pressure output, this was left out of the scope of the current paper as the calculations involved considerable deliberation [2]. However, with future work, the proposed time-, complexity-, and cost-effective method may be elaborated to give predictions on the mechanical index (MI) and thermal index (TI) used to characterize ultrasound transducer safety for diagnostic and therapeutic applications. Such a method would be of great benefit for making quick and simple independent measurements both in industrial and clinical environments, filling a gap for laboratories and institutes with a limited budget.