Sound Pressure Level Analysis of a Liquid-Fueled Lean Premixed Swirl Burner with Various Quarls
Abstract
1. Introduction
2. Materials and Methods
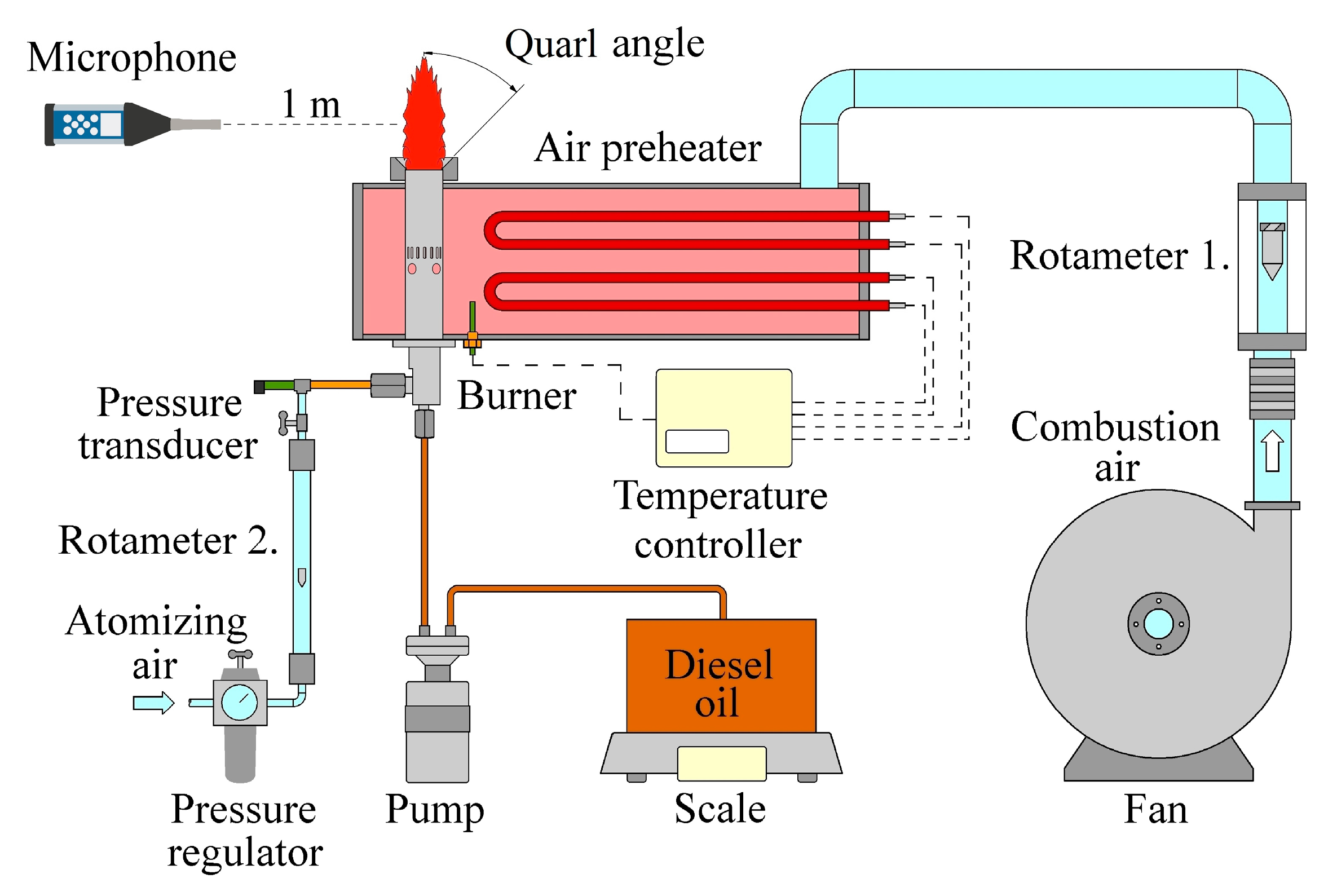
2.1. Experimental Setup
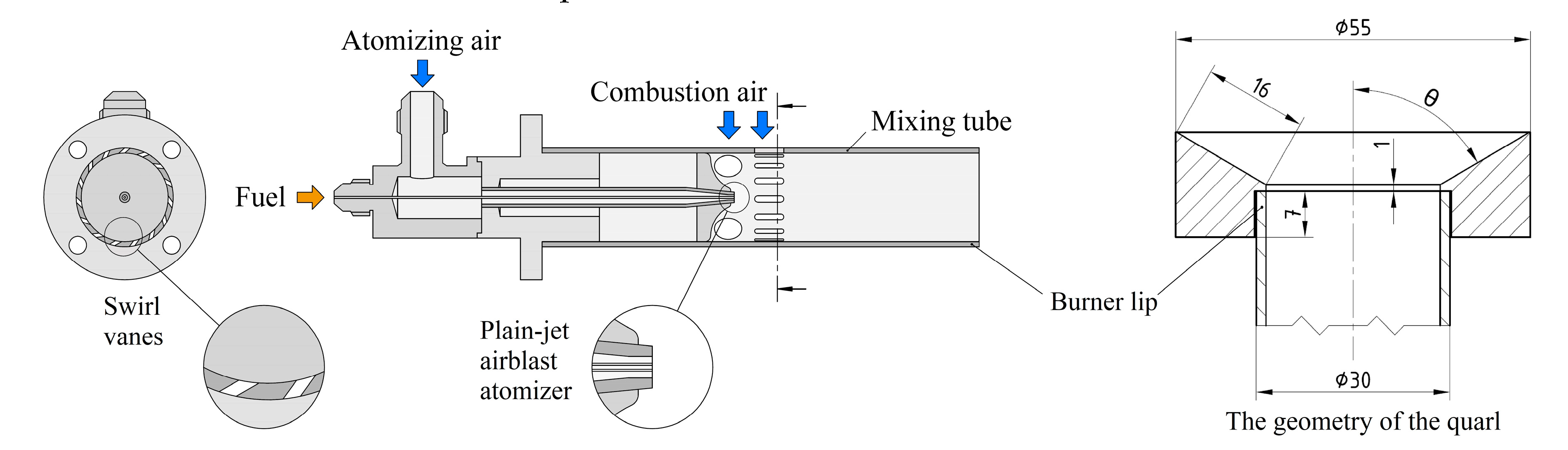
2.2. Burner Design and Atomization
2.3. Swirl Characterization and Observed Flames
3. Results and Discussion
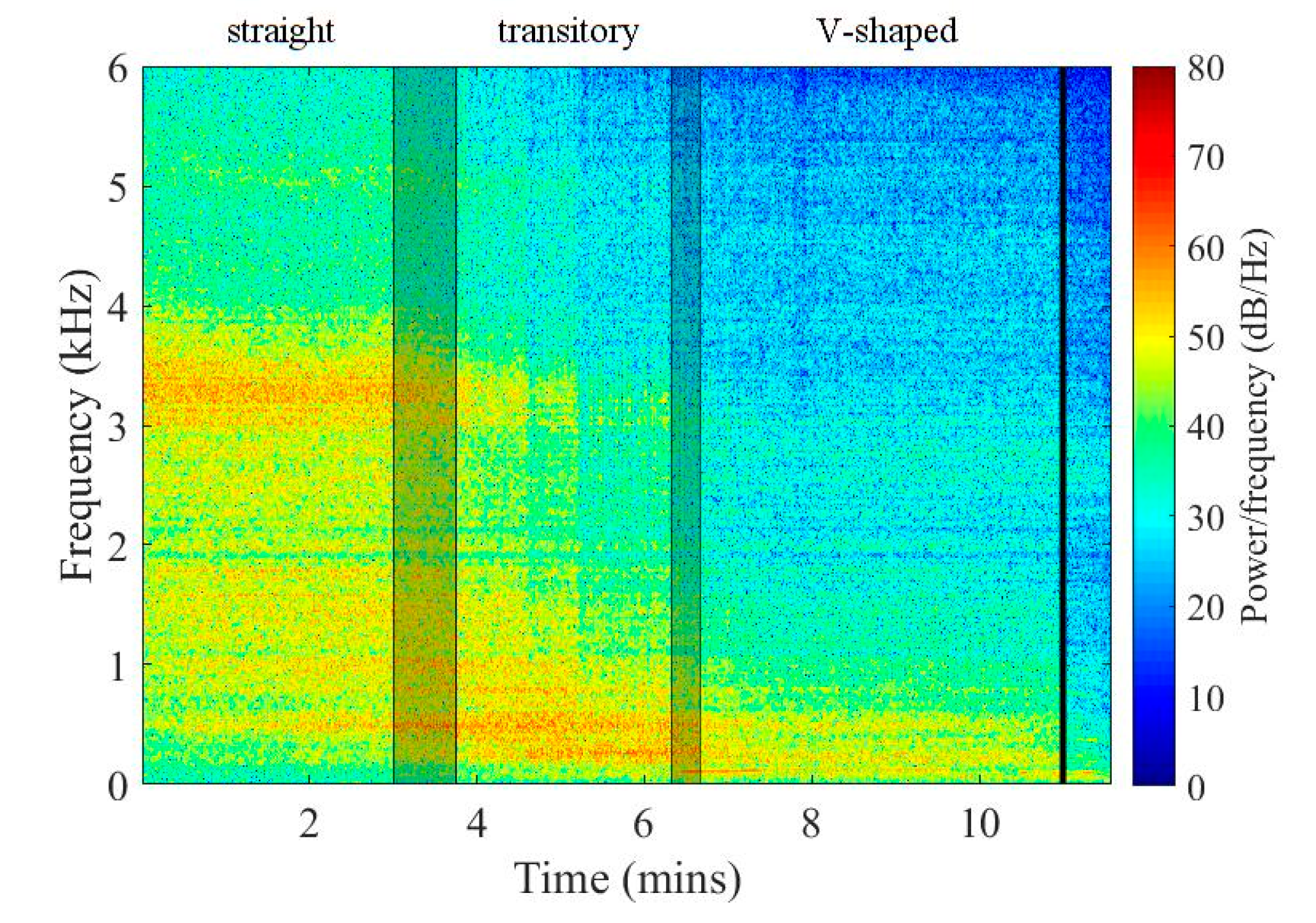
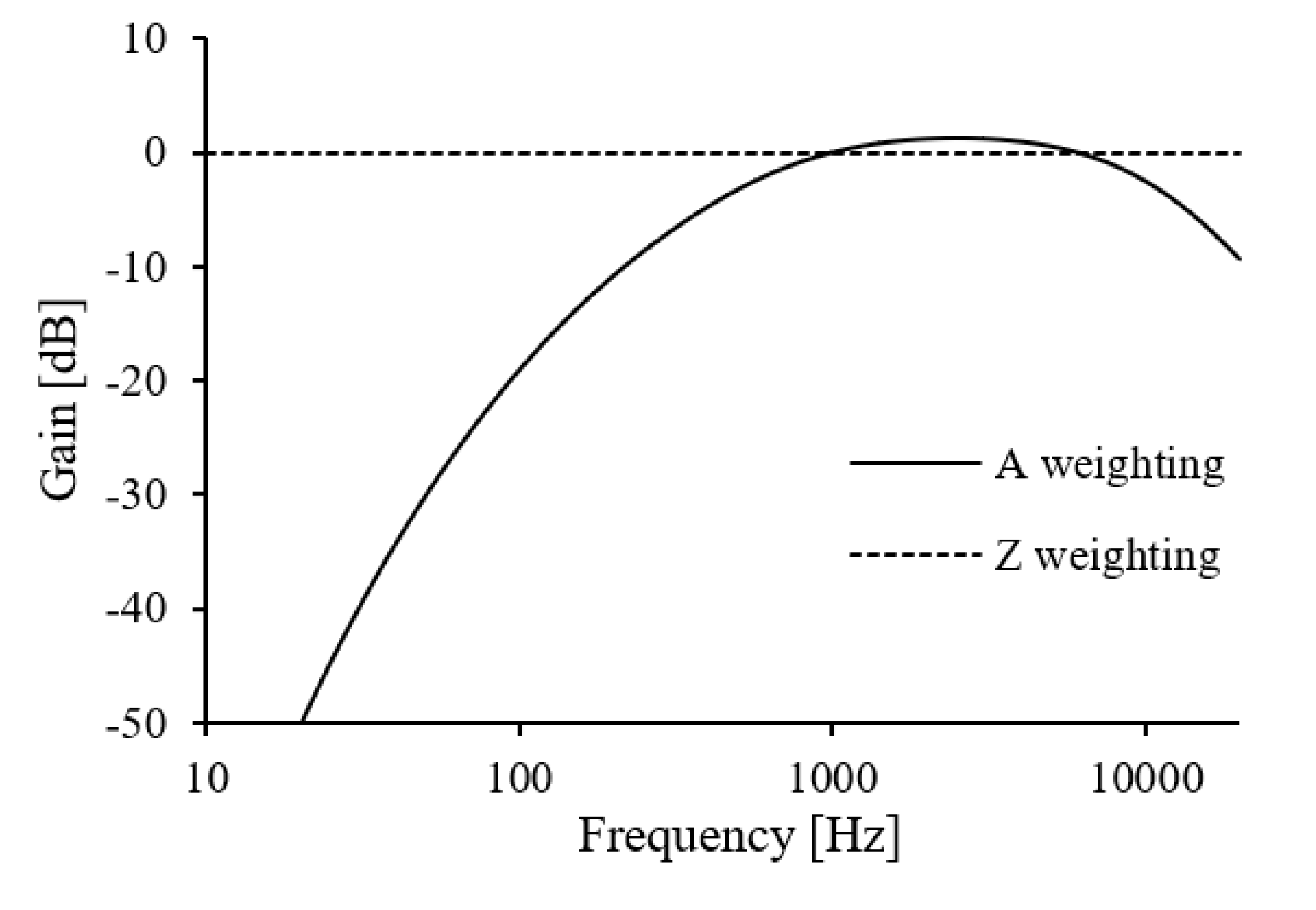
3.1. Spectral Analysis of the Flame
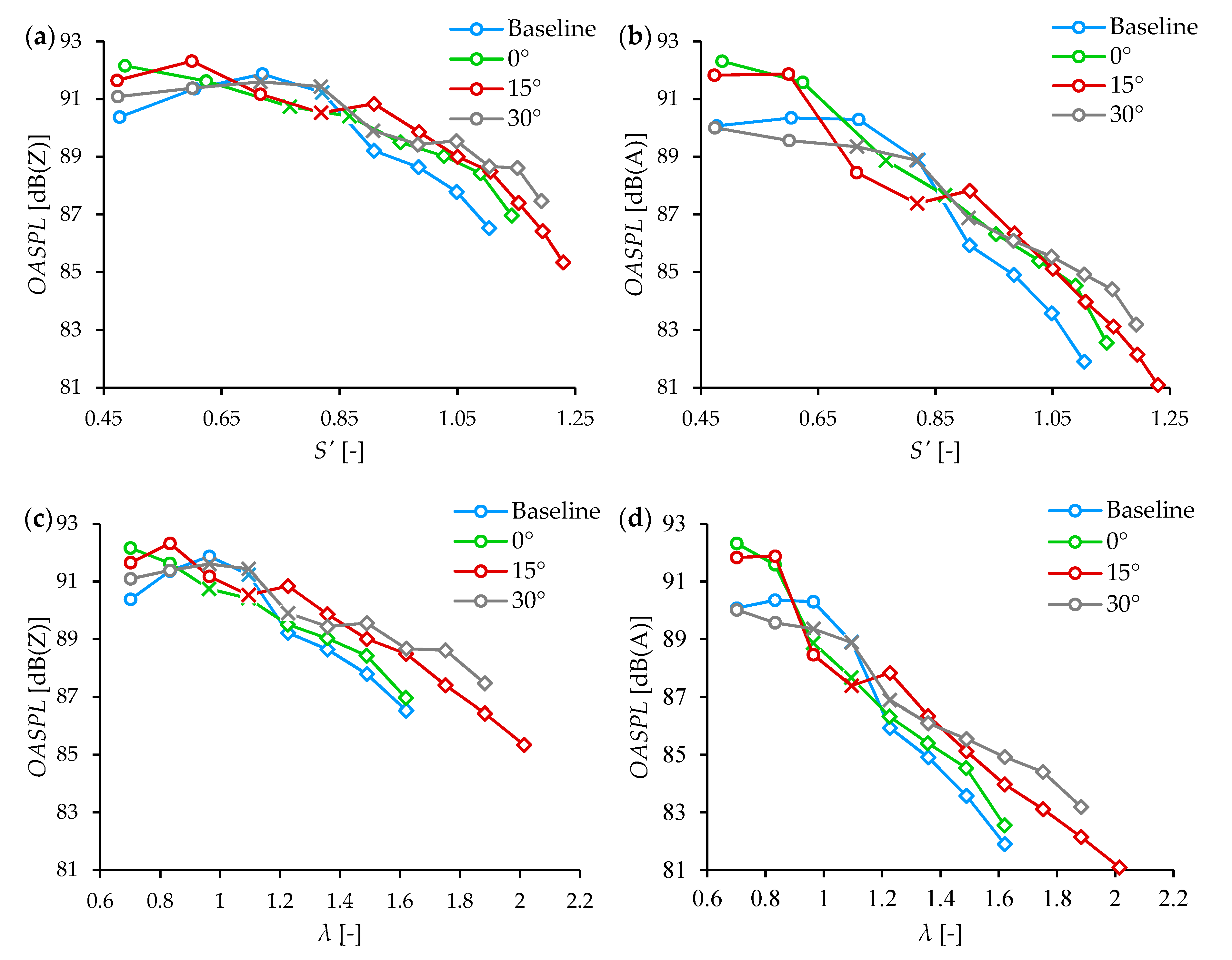
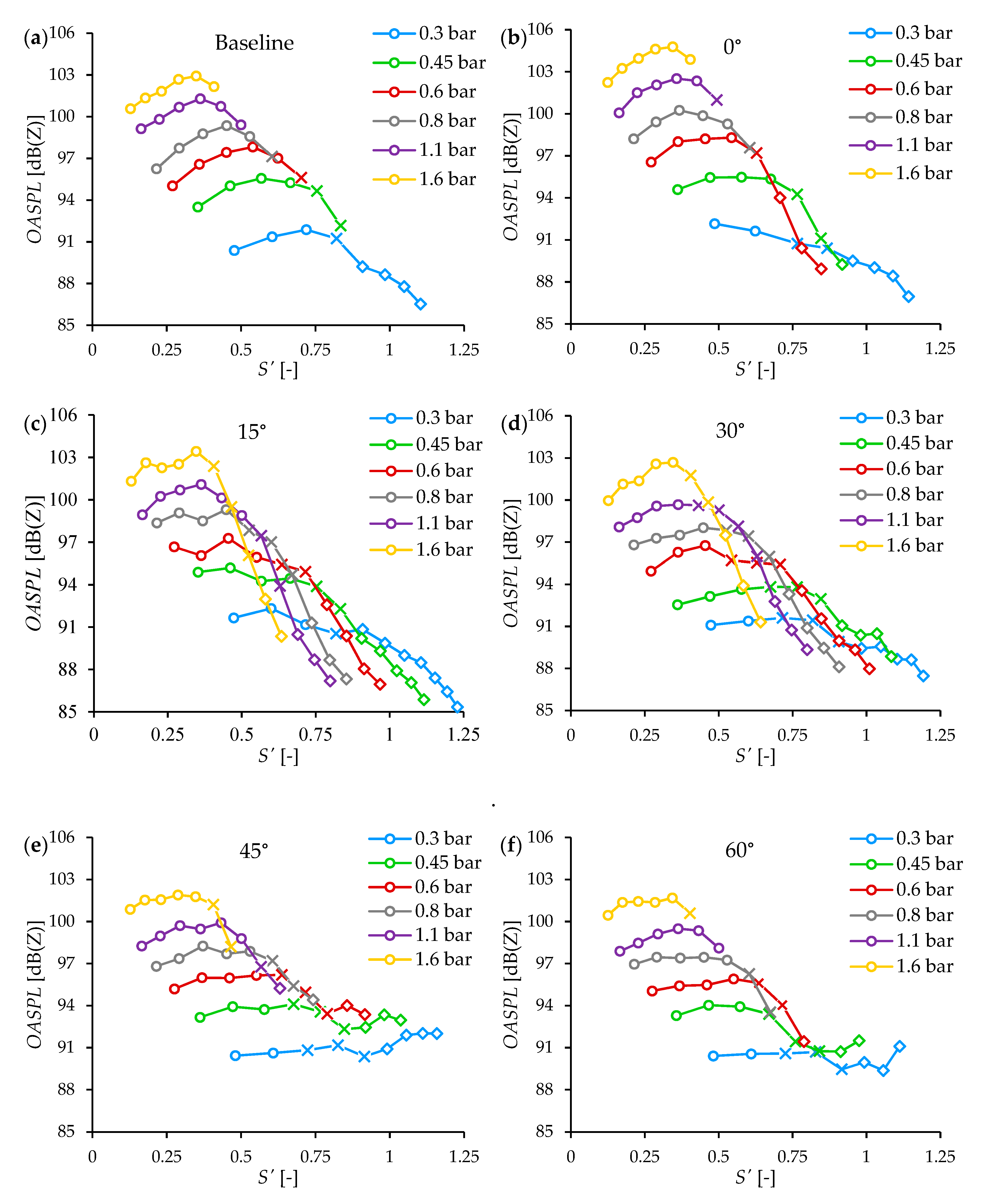
3.2. OASPL at pg = 0.3 bar
3.3. Effect of Quarls
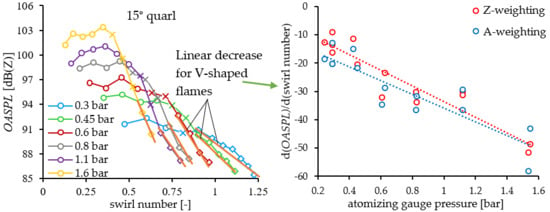
3.4. Linearity Analysis of the OASPL trends of V-shaped Flames
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Latin letters | ||
| a | (m/s) | Speed of sound |
| AFR | (–) | Air-to-fuel mass flow ratio |
| B | (mm) | Height of the swirl slots |
| D | (mm) | Diameter of the circular slots |
| d0 | (mm) | Fuel pipe inner diameter |
| Gφ | (Nm) | Axial flux of the angular momentum |
| Gx | (N) | Axial thrust |
| G’x | (N) | Axial thrust for the geometric swirl number calculation |
| h | (mm) | Width of the swirl slots |
| (kg/s) | Mass flow rate | |
| Ma | (–) | Mach number |
| pg | (bar) | Atomizing gauge pressure |
| R | (m) | Mixing tube inner radius |
| Re | (–) | Reynolds number |
| S | (–) | Swirl number |
| S’ | (–) | Geometric (estimated) swirl number |
| s | (mm) | Slot-to-slot distance in the circumference of the mixing tube |
| SMD | (µm) | Sauter Mean Diameter |
| OASPL | (dB) | Overall Sound Pressure Level |
| T | (K) | Temperature |
| w | (m/s) | Velocity |
| We | (–) | Weber number |
| y | (piece) | Number of circular slots in the cylindrical surface of the mixing tube |
| z | (piece) | Number of swirl slots in the cylindrical surface of the mixing tube |
| Greek letters | ||
| α | (°) | Swirl vane angle |
| λ | (–) | Air-to-fuel equivalence ratio |
| µ | (Pa·s) | Dynamic viscosity |
| ψ | (–) | Blockage factor |
| ρ | (kg/m3) | Density |
| σ | (N/m) | Surface tension |
| Subscripts | ||
| A | Atomizing air | |
| air | Sum of air | |
| C | Combustion air | |
| F | Fuel | |
| S | Air passing through the swirl vanes | |
| sto | Stoichiometric | |
| x | Mixture |
References
- Liu, Y.; Sun, X.; Sethi, V.; Nalianda, D.; Li, Y.G.; Wang, L. Review of modern low emissions combustion technologies for aero gas turbine engines. Prog. Aerosp. Sci. 2017, 94, 12–45. [Google Scholar] [CrossRef]
- Chanphavong, L.; Zainal, Z.A. Characterization and challenge of development of producer gas fuel combustor: A review. J. Energy Inst. 2018. [Google Scholar] [CrossRef]
- Lefebvre, A.H.; Ballal, D.R. Gas Turbine Combustion, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar] [CrossRef]
- Shen, J.; Li, F.; Li, Z.; Wang, H.; Shen, Y.; Liu, Z. Numerical investigation of air-staged combustion to reduce NOXemissions from biodiesel combustion in industrial furnaces. J. Energy Inst. 2018, 1–13. [Google Scholar] [CrossRef]
- Deshmukh, N.N.; Sharma, S.D. Suppression of thermo-acoustic instability using air injection in horizontal Rijke tube. J. Energy Inst. 2017, 90, 485–495. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, V. Dynamics and stability of lean-premixed swirl-stabilized combustion. Prog. Energy Combust. Sci. 2009, 35, 293–364. [Google Scholar] [CrossRef]
- Noiray, N.; Denisov, A. A method to identify thermoacoustic growth rates in combustion chambers from dynamic pressure time series. Proc. Combust. Inst. 2017, 36, 3843–3850. [Google Scholar] [CrossRef]
- Kabiraj, L.; Sujith, R.I. Nonlinear self-excited thermoacoustic oscillations: Intermittency and flame blowout. J. Fluid Mech. 2012, 1–22. [Google Scholar] [CrossRef]
- Durox, D.; Moeck, J.P.; Bourgouin, J.F.; Morenton, P.; Viallon, M.; Schuller, T.; Candel, S. Flame dynamics of a variable swirl number system and instability control. Combust. Flame 2013, 160, 1729–1742. [Google Scholar] [CrossRef]
- Ballester, J.; García-Armingol, T. Diagnostic techniques for the monitoring and control of practical flames. Prog. Energy Combust. Sci. 2010, 36, 375–411. [Google Scholar] [CrossRef]
- Shen, Y.; Li, F.; Liu, Z.; Wang, H.; Shen, J. Study on the characteristics of evaporation–atomization–combustion of biodiesel. J. Energy Inst. 2018, 92, 1458–1467. [Google Scholar] [CrossRef]
- Józsa, V.; Kun-Balog, A. Effect of quarls on the blowout stability and emission of pollutants of a liquid-fueled swirl burner. J. Eng. Gas Turbines Power 2018. [Google Scholar] [CrossRef]
- Rodríguez-Díaz, A.; Adenso-Díaz, B.; González-Torre, P.L. A review of the impact of noise restrictions at airports. Transp. Res. Part D Transp. Environ. 2017, 50, 144–153. [Google Scholar] [CrossRef]
- International Civil Aviation Organization. Guidance on the Balanced Approach to Aircraft Noise Management; International Civil Aviation Organization: Montreal, QC, Canada, 2008. [Google Scholar] [CrossRef]
- Ganic, E.M.; Netjasov, F.; Babic, O. Analysis of noise abatement measures on European airports. Appl. Acoust. 2015, 92, 115–123. [Google Scholar] [CrossRef]
- Laurenzo, R. Hushing the roar. Aerosp. Am. 2006, 44, 38–42. [Google Scholar]
- Smith, T.J.B.; KIlham, J.K. Noise Generation by Open Turbulent Flames. J. Acoust. Soc. Am. 1963, 35, 715–724. [Google Scholar] [CrossRef]
- Rolls-Royce. The Jet Engine, 5th ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2015. [Google Scholar]
- Férand, M.; Livebardon, T.; Moreau, S.; Sanjosé, M. Numerical Prediction of Far-Field Combustion Noise from Aeronautical Engines. Acoustics 2019, 1, 12. [Google Scholar] [CrossRef]
- Geyer, T.F.; Sarradj, E. Self Noise Reduction and Aerodynamics of Airfoils With Porous Trailing Edges. Acoustics 2019, 1, 22. [Google Scholar] [CrossRef]
- Moreau, S. Turbomachinery Noise Predictions: Present and Future. Acoustics 2019, 1, 8. [Google Scholar] [CrossRef]
- Clavin, P.; Siggia, E.D. Turbulent Premixed Flames and Sound Generation. Combust. Sci. Technol. 1991, 78, 147–155. [Google Scholar] [CrossRef]
- IEC 61672. International Standard for Sound Level Meters (Electroacoustics); IEC: Geneva, Switzerland, 2013. [Google Scholar]
- Everest, F.A. Master Handbook of Acoustics, 4th ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Noise Control Act, Public Law 92-574, 27 October 1972; 86 Stat. 1234; 42 USC; Federal Government of the United States: Washington, DC, USA, 1972.
- Canada Labour Code, Part II; R.S.C. 1985, c. L-2; Parliament of Canada: Ottawa, ON, Canada, 1985.
- Ministry of the Environment, Government of Japan. Law No. 98 of 1968; Amended by Law No. 91 of 2000; Ministry of the Environment, Government of Japan: Tokyo, Japan, 2000.
- EN. Directive 2003/10/EC of the European Parliament and of the Council. Off. J. Eur. Union 2003, 42, 38–44. [Google Scholar]
- Freund, J.B. Noise sources in a low-Reynolds-number turbulent jet at Mach 0.9. J. Fluid Mech. 2001, 438, 277–305. [Google Scholar] [CrossRef]
- Bailly, C.; Lafon, P.; Candel, S. Subsonic and supersonic jet noise predictions from statistical source models. AIAA J. 1997, 35, 1688–1696. [Google Scholar] [CrossRef][Green Version]
- Candel, S.; Durox, D.; Ducruix, S.; Birbaud, A.-L.; Noiray, N.; Schuller, T. Flame Dynamics and Combustion Noise: Progress and Challenges. Int. J. Aeroacoustics 2009, 8, 1–56. [Google Scholar] [CrossRef]
- Swaminathan, N.; Balachandran, R.; Xu, G.; Dowling, A.P. On the correlation of heat release rate in turbulent premixed flames. Proc. Combust. Inst. 2011, 33, 1533–1541. [Google Scholar] [CrossRef]
- Pillai, A.L.; Kurose, R. Numerical investigation of combustion noise in an open turbulent spray flame. Appl. Acoust. 2018, 133, 16–27. [Google Scholar] [CrossRef]
- Speth, R.L.; Ghoniem, A.F. Using a strained flame model to collapse dynamic mode data in a swirl-stabilized syngas combustor. Proc. Combust. Inst. 2009, 32, 2993–3000. [Google Scholar] [CrossRef]
- Singh, K.K.; Zhang, C.; Gore, J.P.; Mongeau, L.; Frankel, S.H. An experimental study of partially premixed flame sound. Proc. Combust. Inst. 2005, 30, 1707–1716. [Google Scholar] [CrossRef]
- Kilham, J.K.; Kirmani, N. The effect of turbulence on premixed flame noise. Symp. Combust. 1979, 17, 327–336. [Google Scholar] [CrossRef]
- Balakrishnan, P.; Srinivasan, K. Influence of swirl number on jet noise reduction using flat vane swirlers. Aerosp. Sci. Technol. 2018, 73, 256–268. [Google Scholar] [CrossRef]
- Balakrishnan, P.; Srinivasan, K. Jet noise reduction using co-axial swirl flow with curved vanes. Appl. Acoust. 2017, 126, 149–161. [Google Scholar] [CrossRef]
- Shanbhogue, S.J.; Sanusi, Y.S.; Taamallah, S.; Habib, M.A.; Mokheimer, E.M.A. Flame macrostructures, combustion instability and extinction strain. Combust. Flame 2015, 1–14. [Google Scholar] [CrossRef]
- Hong, S.; Shanbhogue, S.J.; Ghoniem, A.F. Impact of fuel composition on the recirculation zone structure and its role in lean premixed flame anchoring. Proc. Combust. Inst. 2015, 35, 1493–1500. [Google Scholar] [CrossRef]
- Choi, B.C.; Ghoniem, A.F. Stabilization and blowout characteristics of lean premixed turbulent flames behind a backward-facing step in a rectangular combustor with heated propane-air mixtures. Fuel 2018, 222, 627–637. [Google Scholar] [CrossRef]
- Lefebvre, A.H.; Miller, D. The Development of an Air Blast Atomizer for Gas Turbine Application; CoA. Report Aero No. 193; College of Aeronautics Cranfield: Cranfield, UK, 1966. [Google Scholar]
- Csemány, D.; Józsa, V. Fuel Evaporation in an Atmospheric Premixed Burner: Sensitivity Analysis and Spray Vaporization. Processes 2017, 5, 80. [Google Scholar] [CrossRef]
- Singh, A.V.; Yu, M.; Gupta, A.K.; Bryden, K.M. Investigation of noise radiation from a swirl stabilized diffusion flame with an array of microphones. Appl. Energy 2013, 112, 313–324. [Google Scholar] [CrossRef]
- Hadef, R.; Merkle, K.; Lenze, B.; Leuckel, W. An experimental study of airblast atomizer spray flames. J. Inst. Energy 2000, 73, 50–55. [Google Scholar]
- Lefebvre, A.H.; McDonell, V.G.; Arthur, H.; Lefebvre, V.G.M. Atomization and Sprays, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Lefebvre, A.H.; Arthur, H. Lefebvre. Airblast atomization. Prog. Energy Combust. Sci. 1980, 6, 233–261. [Google Scholar] [CrossRef]
- Urbán, A.; Zaremba, M.; Malý, M.; Józsa, V.; Jedelský, J. Droplet dynamics and size characterization of high-velocity airblast atomization. Int. J. Multiph. Flow. 2017, 95, 1–11. [Google Scholar] [CrossRef]
- Beér, J.M.; Chigier, N.A. Combustion Aerodynamics; Robert, E., Ed.; Krieger Publishing Company, Inc.: London, UK, 1972. [Google Scholar]
- Galley, D.; Ducruix, S.; Lacas, F.; Veynante, D. Mixing and stabilization study of a partially premixed swirling flame using laser induced fluorescence. Combust. Flame 2011, 158, 155–171. [Google Scholar] [CrossRef]
- Singh, A.V.; Yu, M.; Gupta, A.K.; Bryden, K.M. Thermo-acoustic behavior of a swirl stabilized diffusion flame with heterogeneous sensors. Appl. Energy 2013, 106, 1–16. [Google Scholar] [CrossRef]



| pg (bar) | SMD (µm) | WeA (–) | AFR (–) | ρA (kg/m3) | TA (K) | Ma (–) |
|---|---|---|---|---|---|---|
| 0.3 | 21.6 | 779 | 0.778 | 1.27 | 277 | 0.62 |
| 0.45 | 16.2 | 1121 | 0.948 | 1.31 | 268 | 0.75 |
| 0.6 | 13.4 | 1438 | 1.089 | 1.34 | 261 | 0.85 |
| 0.8 | 11.1 | 1830 | 1.249 | 1.39 | 252 | 0.95 |
| 1.1 | 9.17 | 2363 | 1.451 | 1.45 | 241 | 1.08 |
| 1.6 | 7.44 | 3143 | 1.725 | 1.54 | 227 | 1.25 |
| Property | Value |
|---|---|
| Thermal power | 15 kW |
| Lower heating value | 43 MJ/kg |
| Fuel flow rate | 0.35 g/s |
| Dynamic viscosity | 3.45 mPa·s |
| Density | 830 kg/m3 |
| Surface tension | 28 mN/m |
| Quarl | pg (bar) | R2 (S’, dB(Z)) | R2 (S’, dB(A)) | R2 (λ, (dBZ)) | R2 (λ, (dBA)) |
|---|---|---|---|---|---|
| Baseline | 0.3 | 0.944 | 0.970 | 0.971 | 0.988 |
| 0° | 0.3 | 0.885 | 0.924 | 0.926 | 0.955 |
| 15° | 0.3 | 0.963 | 0.996 | 0.993 | 0.993 |
| 0.45 | 0.989 | 0.997 | 0.995 | 0.987 | |
| 0.6 | 0.988 | 0.965 | 0.979 | 0.947 | |
| 0.8 | 0.974 | 0.964 | 0.966 | 0.955 | |
| 1.1 | 0.999 | 0.999 | 0.998 | 0.998 | |
| 1.5 | 1.000 | 1.000 | 1.000 | 1.000 | |
| 30° | 0.3 | 0.802 | 0.934 | 0.853 | 0.967 |
| 0.45 | 0.763 | 0.722 | 0.793 | 0.739 | |
| 0.6 | 0.983 | 0.980 | 0.970 | 0.966 | |
| 0.8 | 0.987 | 0.994 | 0.978 | 0.989 | |
| 1.1 | 0.993 | 0.998 | 0.989 | 0.995 | |
| 1.5 | 0.994 | 0.990 | 0.992 | 0.987 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Novotni, G.I.; Józsa, V. Sound Pressure Level Analysis of a Liquid-Fueled Lean Premixed Swirl Burner with Various Quarls. Acoustics 2020, 2, 131-146. https://doi.org/10.3390/acoustics2010010
Novotni GI, Józsa V. Sound Pressure Level Analysis of a Liquid-Fueled Lean Premixed Swirl Burner with Various Quarls. Acoustics. 2020; 2(1):131-146. https://doi.org/10.3390/acoustics2010010
Chicago/Turabian StyleNovotni, Gergely I., and Viktor Józsa. 2020. "Sound Pressure Level Analysis of a Liquid-Fueled Lean Premixed Swirl Burner with Various Quarls" Acoustics 2, no. 1: 131-146. https://doi.org/10.3390/acoustics2010010
APA StyleNovotni, G. I., & Józsa, V. (2020). Sound Pressure Level Analysis of a Liquid-Fueled Lean Premixed Swirl Burner with Various Quarls. Acoustics, 2(1), 131-146. https://doi.org/10.3390/acoustics2010010