Abstract
The nonlinear energy harvester has become a hot topic due to its broad bandwidth and lower resonant frequency. Based on the preliminary test and analyses in our previous work, further analyses and tests on the influence of parameters, including the nonlinear magnetic force of the hybrid energy harvesting structure on its output performance under harmonic excitation, are performed in this paper, which will provide powerful support for structural optimization. For designing a nonlinear piezoelectric-electromagnetic hybrid energy harvester, the state equation of electromechanical coupling, the harmonic response and average output power, voltage, and current of a nonlinear hybrid energy harvester under harmonic excitation are derived by the harmonic balance method. The effects of the excitation acceleration and the external load on the output performance of the nonlinear hybrid energy harvester are verified through experimental tests. The results showed that the output power of the nonlinear hybrid energy harvester increases with the increase in the acceleration of harmonic excitation, and the increase is affected by external load. When the piezoelectric-electromagnetic hybrid harvester operates at the optimal load and the resonant frequency, the average output power reaches its maximum value and the increase of the load of the piezoelectric unit makes the resonant frequency of the energy harvesting system increase. Compared with linear harvesting structures, the nonlinear hybrid harvester has better flexibility of environmental adaptability and is more suitable for harvesting energy in low-frequency environments.
1. Introduction
Vibration energy harvesters can convert vibration energy into electrical energy by piezoelectric, electromagnetic, and electrostatic mechanisms. This process has been improved significantly with the use of low-power electronic devices [1,2,3,4,5,6]. Broader bandwidth and lower resonant frequency are two main challenges when the harvester is used in practice [7,8,9,10]. Therefore, researchers have proposed many methods to solve these problems. Many researchers have introduced nonlinearity into energy harvesting to widen frequency bandwidth and improve performance, for example, adding stoppers to the structure, adopting active tuning structure, utilizing material nonlinearity or introducing nonlinear force. Of these, the nonlinear energy harvesting technique is one of the most feasible solutions [11,12,13,14].
Mann [15] and Foisal et al. [16] designed a nonlinear magnetic spring electromagnetic energy harvester. By analyzing the size of the magnets and the distance between the magnets, the frequency bandwidth of the harvester can be optimized. Luigi and Maryam [17] proposed a vibration energy harvesting model based on nonlinear vibration-damping. The output power and harvesting frequency bandwidth of this model are better than those of linear energy harvester. Waleed [18] designed a piezoelectric harvester with adjustable resonant frequency by changing the force between the magnets. The experiment results showed that the resonant frequency of the harvester can be adjusted up by 70%. Marcin [19] designed a MEMS piezoelectric energy harvester with adjustable stiffness, with which the harvesting frequency bandwidth can be increased by 36%. In addition, Challa [5] designed a nonlinear piezoelectric harvester with adjustable resonant frequency by changing the system’s effective stiffness. The experimental tests demonstrated that the natural frequency of the linear energy harvester can be adjusted by ±20%.
In order to improve the energy conversion efficiency and broaden the application bandwidth of the vibration energy harvester, a hybrid energy harvesting technique of combining piezoelectric (PE) and electromagnetic (EM) mechanisms was proposed, which benefits from the advantages of the two techniques simultaneously [20,21,22,23]. Karami and Inman [24] established a unified approximation method for linear, softly nonlinear, and bi-stable nonlinear energy harvesters. The method quantifies equivalent changes in the damping and excitation frequency of the mechanical subsystem that resembles the backward coupling from energy harvesting. Hamdi and Belhaq [25] introduced time delay in the mechanical component of the delayed hybrid energy harvester, consisting of a nonlinear mono-stable harvester device. The results show that the powers output performance of the harvester is significantly improved at certain ranges of time delay and delay amplitude. In this paper, a nonlinear PE-EM hybrid energy harvester with adjustable stiffness is proposed and its governing equations are established. By means of the harmonic balance method, expressions of the vibration amplitude, output voltage, current, and average power of hybrid harvester under the harmonic excitation are derived. The effects of excitation acceleration, load resistance to vibration amplitude, output power, and the resonant frequency of nonlinear hybrid energy harvesters are investigated experimentally and the results are compared with the output performances of linear energy harvesters.
2. Nonlinear Hybrid Energy Harvester Structure
An illustration of the nonlinear hybrid PE-EM energy harvester is shown in Figure 1. The central movable magnet is supported by two identical clamped hybrid beams on both sides, and two coils are placed above and below the movable magnet, respectively. Besides this, two magnets are mounted inside the two coils, and forces between the movable magnets and fixed magnets are an attractive force, so the forces decrease the natural frequency of harvester by reducing the effective spring constant. In addition, piezoelectric layers (PZT) mounted on the top of the movable magnet are polarized in the beam thickness direction (vertical direction, shown in Figure 1), and based on piezoelectric effect and electromagnetic induction law, PZT layers and coils will output electrical energy under external excitation.
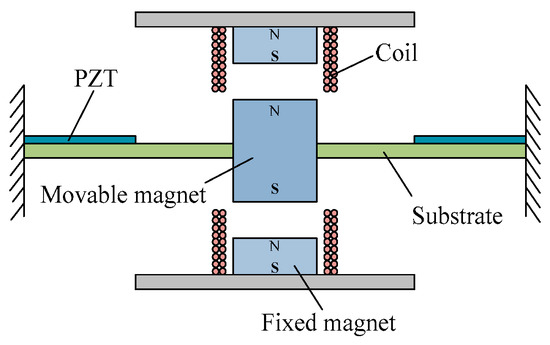
Figure 1.
Illustration of a nonlinear energy harvester structure.
Cylindrical magnets are used in the design to apply the desired magnetic force, and the magnetic force between any two cylindrical magnets is given by Equation (1) [26],
where H/m is magnetic permeability, and are volumes of two cylindrical magnets, and are magnetization of the two magnets, respectively, and is the static distance between the magnets. For the designed nonlinear hybrid energy harvester shown above, the total force generated between the top fixed magnet and the movable magnet, and that between the bottom fixed magnet and the movable magnet is given by Equation (2),
where is the equilibrium distance between the top (or bottom) magnet and the movable magnet; is the vertical displacement of the movable magnet under the external excitation; and are the magnetization and volume of the central magnet, respectively; and are the magnetization and volume of the top magnet respectively; and and are the magnetization and volume of the bottom magnet respectively. To avoid the irreversible plastic deformation of the beams, the nonlinear force should be less than the elastic restoring force of the beams, which means
where is the stiffness of the beam.
For the designed nonlinear hybrid energy harvester, the top and bottom magnets are the same, and their equilibrium distances from the central magnet are equal. By the method of Taylor expansion [27], when neglecting high-order terms and , Equation (2) can be expressed as:
where:
According to Figure 2, and combining the former study for linear hybrid energy harvesters [28], the governing equations of a nonlinear hybrid PE and EM energy harvester can be illustrated as:
where is the excitation acceleration; is the equivalent mass of the vibration system; and are the damping coefficient and linear stiffness of the vibration system, respectively; and are the load resistance of the PE and EM energy harvesting unit, respectively; is the equivalent capacitance of the PE layer; is the output voltage of the PE energy harvesting unit; is the output current of the EM energy harvesting unit; and refers to the resistance and inductance of coils; and and are the PE and EM transfer factors, respectively. These parameters are dependent on the material constants and the design of the energy harvester, which can be derived by standard model analysis.
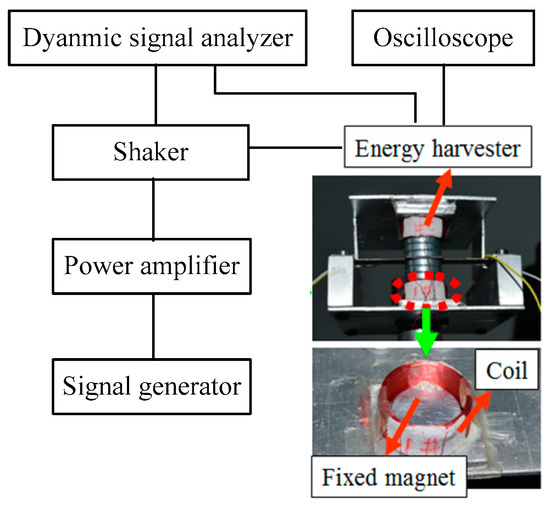
Figure 2.
Experimental setup and a hybrid structure.
3. Vibration Responses and Output of Nonlinear Energy Harvester under Harmonic Excitation
Substituting Equation (4) into Equation (7), Equation (7) becomes the typical Duffing equation, if the external excitation is harmonic excitation, and the inductance effect of the coil is ignored in the low frequency vibration. When the excitation acceleration input to the energy harvester is , let , , , , . According to the harmonic balance method [29,30], considering the weak nonlinear condition, and assuming that the response of the energy harvesting system is mainly the single harmonic frequency, the vibration response of the energy harvester, the output voltage of the piezoelectric energy harvesting unit, and the electromagnetic energy harvesting unit are shown in Equations (10)–(12), respectively:
Substituting Equations (10)–(12) into Equation (7), according to
and ignoring high-order harmonic terms, the following equation can be obtained:
By making the coefficients of the two sides of the equation equal, we obtain:
and the six-order nonlinear expression of vibration amplitude as:
In the actual calculation, the vibration amplitude can be calculated using Equation (17), according to the designed characteristic parameters. The output voltage of the piezoelectric energy harvesting unit is:
Similarly, the output current of the electromagnetic energy harvesting unit is:
The output powers of the PE and EM energy harvesting units are:
Therefore, the total output power of the designed nonlinear PE-EM hybrid energy harvester is:
4. Experimental Tests
In order to test and study the output characteristics of the nonlinear PE-EM hybrid energy harvester, the designed energy harvester structure and the experimental test system are shown in Figure 2.
4.1. Influence of Magnetic Force on the Output of Nonlinear Hybrid Harvesting Structure
The magnetic force in the harvesting energy structure can change the vibration state of the cantilever beam, and can improve the environmental adaptability of the harvesting energy structure.
Figure 3 shows that under the action of magnet attractive force, as the distance between the fixed magnet and movable magnet, d, increases, the peak frequency of the nonlinear energy harvester increases and the total output power increases. The dots are the experimental mean values of three tests, the solid lines are the best fits of the data.
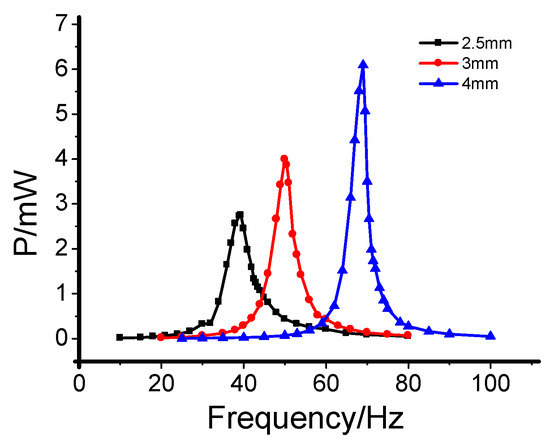
Figure 3.
Output of harvester under the attractive force.
When the magnetic force is a repulsive force, the relationship between the total output power of nonlinear energy harvester and the peak frequency at different distance is as shown in Figure 4. As the distance between the magnets increases, the repulsive force decreases, the peak frequency of the harvesting structure decreases, and the 3db bandwidth decreases. However, when the distance between magnets increases to a certain extent, the change of the output power is no longer obvious.
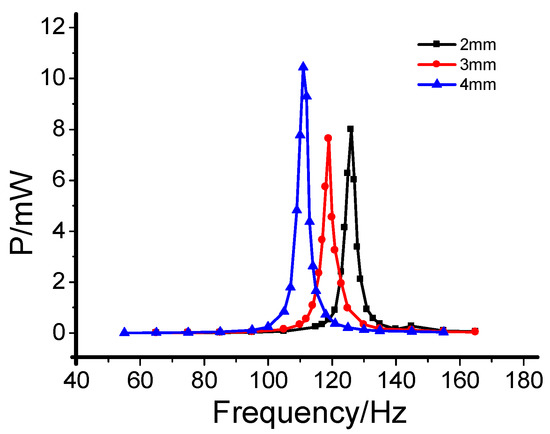
Figure 4.
Output of harvester under the repulsive force.
From the above analyses, the influence of the distance between the magnets on the bandwidth and output power should be considered when designing a nonlinear hybrid energy harvester. Under the same environmental conditions, selecting the magnetic attractive force is more conducive to reducing the peak frequency of the harvesting structure, increasing the bandwidth, and improving the environmental adaptability of the harvesting structure.
4.2. Effects of Excitation Acceleration on Energy Harvesting Characteristics
When the external acceleration from the shaker is 0.3, 0.45, and 0.6 g, the total output power of the nonlinear hybrid energy harvester changes with the excitation frequency, as shown in Figure 5, where g is the gravitational acceleration.
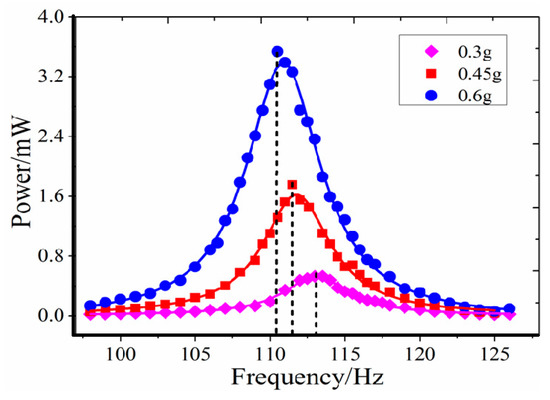
Figure 5.
Output power of a nonlinear hybrid energy harvester under different excitation accelerations.
According to the test results shown in Figure 3, both the output power and the bandwidth of the energy harvester increase with the increase in the excitation acceleration. When the external acceleration is 0.3, 0.45, and 0.6 g, the maximum output power of the energy harvester is 0.52, 1.76, and 3.54 mW, respectively. At the same time, the resonant frequency of the energy harvester decreases with the increase in the excitation acceleration. As shown in in Figure 3, when the excitation acceleration increases from 0.3 to 0.6 g, the resonant frequency decreases from 113.2 to 110.5 Hz. This tells us the stiffness of this system is softening as amplitude increases.
Since the peak frequency of the nonlinear hybrid energy harvester changes with the excitation acceleration, the optimal load of the energy harvester also changes. At the resonant frequency, when the acceleration is 0.2 and 0.45 g, the change of the output peak voltage and power of the piezoelectric energy harvesting unit with the piezoelectric load is as shown in Figure 6, and the electromagnetic energy harvesting unit is the optimal load at this time. The data shown in Figure 6 are averaged over several tests.
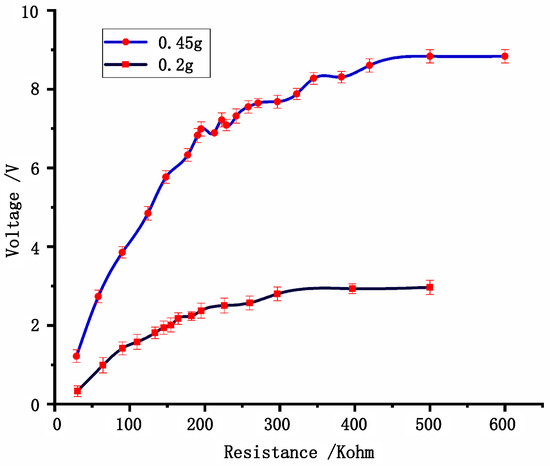
Figure 6.
Piezoelectric energy harvesting unit output varies with piezoelectric load.
According to the results shown in Figure 6, the higher the acceleration, the higher the output voltage of the piezoelectric unit. When the excitation accelerations are 0.2 and 0.45 g, the maximum output powers of the piezoelectric unit are 0.085 and 0.5 mW and the corresponding optimal loads are 140 and 190 kΩ, respectively. Therefore, the peak load of the piezoelectric unit increases as the acceleration increases.
At the resonant frequency point of the system, when the excitation accelerations are 0.2 and 0.45 g, the changes in the output voltage and power of the electromagnetic energy harvesting unit with the electromagnetic load are as shown in Figure 7, wherein the piezoelectric energy harvesting unit is connected with the optimal load. When the excitation accelerations are 0.2 and 0.45 g, the maximum output powers of the electromagnetic unit are 0.14 and 1.19 mW and the corresponding optimal loads are 17.5 and 21 Ω, respectively, that is, the optimal load of the electromagnetic unit also increases with the increasing of excitation acceleration. The data shown in Figure 7 are averaged over several tests.
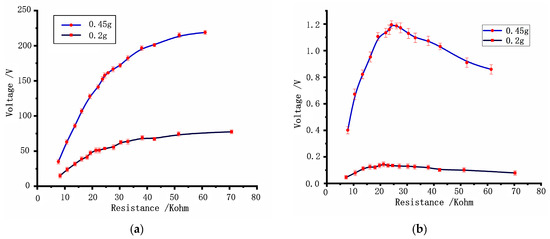
Figure 7.
Electromagnetic unit output varies with electromagnetic load. (a) Voltage, (b) Power.
4.3. Effect of Load on Energy Harvesting Characteristics
When the excitation acceleration is 0.45 g and the loads of the piezoelectric unit are 50 and 170 kΩ, the output power of the PE energy harvester unit is as shown in Figure 8. In addition, when the loads of the electromagnetic unit are 5 and 15 Ω, the output power of the EM energy harvester unit is as shown in Figure 9.
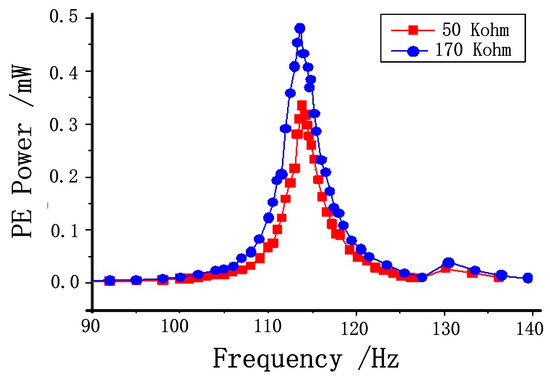
Figure 8.
Effect of piezoelectric load on the PE energy harvesting unit.
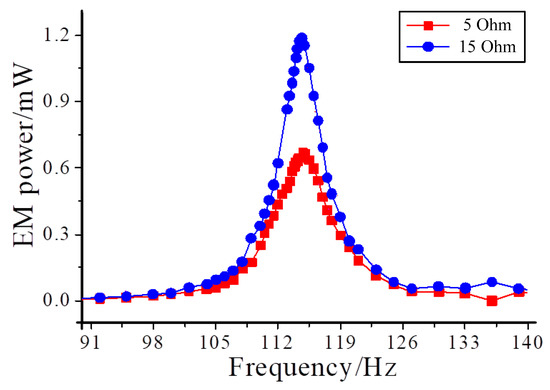
Figure 9.
Effect of electromagnetic load on the EM energy capture harvesting unit.
According to the test results shown in Figure 8 and Figure 9, the loads of the piezoelectric and electromagnetic unit can affect the output power of the energy harvester, and they also affect the energy harvesting frequency bandwidth. When the electromagnetic load remains unchanged, the energy harvesting frequency bandwidth of the piezoelectric unit at the load of 170 KΩ is larger than that at 50 KΩ; at the same time, when the piezoelectric load remains unchanged, the electromagnetic energy harvesting frequency bandwidth at the load of 15 Ω is larger than that at 5 Ω. In addition, the resonant frequency of the energy harvester is increased by 0.5 Hz, but the electromagnetic load hardly affects the resonant frequency of the energy harvester.
In addition, the effects of piezoelectric and electromagnetic loads on the output power of the electromagnetic unit and the piezoelectric unit are shown in Figure 10 and Figure 11. The data shown in Figure 10 and Figure 11 are averaged over several tests. The output power of the piezoelectric unit increases with the increase in the electromagnetic load, and the output power of the electromagnetic unit decreases first and then increases with the increase in the piezoelectric load, and up to the minimum value at the optimal load of the piezoelectric unit. The reason for this is that the coupling effect of the electromagnetic unit to the energy harvesting system is mainly represented by the damping effect. Therefore, the vibration amplitude of the energy harvesting system is increased, and the output power of the piezoelectric unit is increased. The output power of the piezoelectric unit is up to the maximum value when the load is the optimal load. At this time, the stiffness feedback to the energy harvesting system is maximized.
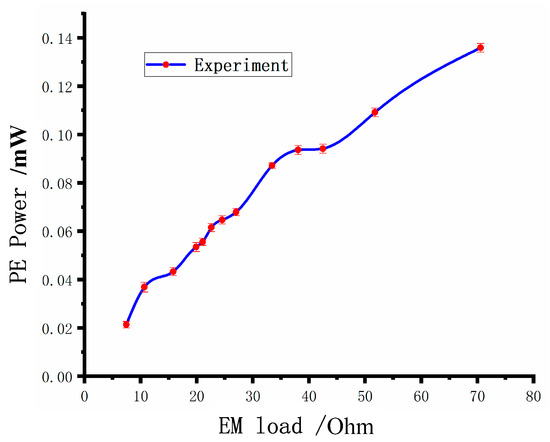
Figure 10.
Effect of electromagnetic load on maximum piezoelectric power.
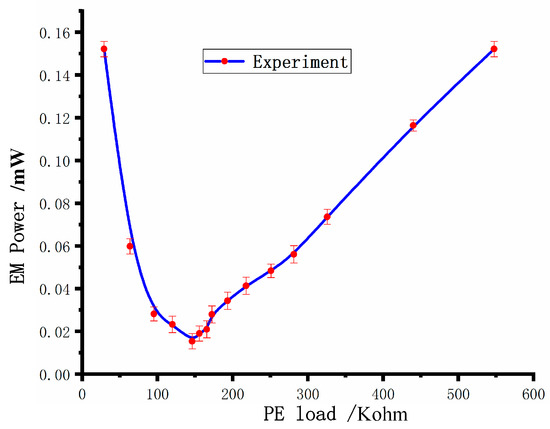
Figure 11.
Effect of piezoelectric load on maximum electromagnetic power.
When the excitation acceleration is 0.2 g and the force between the magnets is the attraction force, through the experimental tests, the optimal loads of the PE and EM units of nonlinear energy harvester are 152.5 kΩ and 17.3 Ω. The optimal loads of the PE and EM units of the corresponding linear energy harvester (without fixed magnets and the nonlinear magnetic forces is free) are 133 kΩ and 15.5 Ω, respectively. At the same time, the output powers at the optimal load of the nonlinear hybrid energy harvester and the corresponding linear energy harvester are shown in Figure 12.
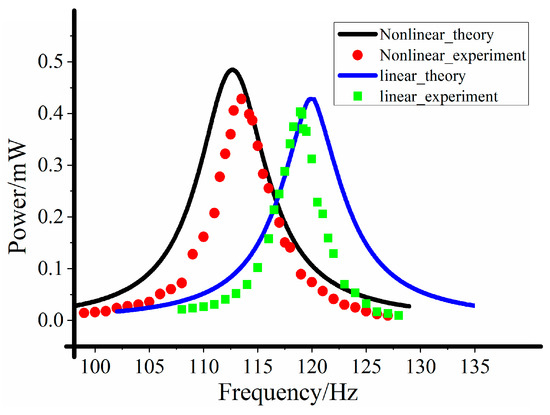
Figure 12.
Comparison between output of linear and nonlinear hybrid energy harvester.
According to the results shown in Figure 10, the output power of the nonlinear energy harvester is larger than that of the corresponding linear energy harvester. Under the same excitation acceleration, the output powers are 0.44 and 0.4 mW, respectively. Due to the nonlinear magnetic force, the resonant frequency of the nonlinear energy harvester decreased, and the resonant frequency of the linear energy harvester and the nonlinear energy harvester are measured to be 119 Hz and 113.5 Hz, respectively. Therefore, the nonlinear energy harvester can increase the output power and reduce the resonant frequency, and it is more suitable for low-frequency vibration energy harvesting.
5. Conclusions
According to the electromechanical coupling equation of the PE-EM hybrid harvester, the expressions of the vibration response, output voltage, current, and power of the nonlinear hybrid energy harvester under harmonic excitation were derived. The output characteristics of the nonlinear hybrid harvester under harmonic excitation were also studied by the experimental testing. From the results of theoretical analysis and experimental tests, it was observed that: (1) The average power, output voltage, and output current of a nonlinear hybrid energy harvester increases with the increase in excitation acceleration under harmonic excitation, and the output power increases linearly with the acceleration, and is also affected by the load. (2) When the PE-EM hybrid energy harvester operates at the optimal load and the peak frequency, the average output power can reach the maximum value, and the increase in the load of the piezoelectric unit makes the peak frequency of the energy harvesting system increase. (3) Compared with linear structures, the designed nonlinear PE-EM hybrid energy harvesting has better environmental adaptability and is more suitable for harvesting energy in low-frequency environments.
Author Contributions
H.L., S.G., P.L. did experiments and data analyses, J.W. helped editing and revised the manuscript. H.L. and J.W. discussed the concept of the article.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Erturk, A.; Inman, D. Broadband piezoelectric power generation on high-energy orbits of the bistable Duffing oscillator with electromechanical coupling. J. Sound Vib. 2011, 330, 2339–2353. [Google Scholar] [CrossRef]
- Tiwari, R.; Buch, N.; Garcia, E. Energy balance for peak detection method in piezoelectric energy harvester. J. Intell. Mater. Syst. Struct. 2014, 25, 1024–1035. [Google Scholar] [CrossRef]
- Ferrari, M.; Ferrari, V.; Guizzetti, M. Improved energy harvesting from wideband vibrations by nonlinear piezoelectric converters. Sens. Actuators A Phys. 2010, 162, 425–431. [Google Scholar] [CrossRef]
- Marzencki, M.; Defosseux, M.; Basrour, S. MEMS Vibration Energy Harvesting Devices with Passive Resonance Frequency Adaptation Capability. J. Microelectromech. Syst. 2009, 18, 1444–1453. [Google Scholar] [CrossRef]
- Challa, V.R.; Prasad, M.G.; Shi, Y. A vibration energy harvester with bidirectional resonance frequency tunability. Smart Mater. Struct. 2008, 17, 015035. [Google Scholar] [CrossRef]
- Kang, J.; Kim, I.; Kim, D. Wireless Information and Power Transfer: Rate-Energy Tradeoff for Nonlinear Energy Harvesting. IEEE Trans. Wirel. Commun. 2017, 7, 2787569. [Google Scholar] [CrossRef]
- Cammarano, A.; Neild, S.; Burrow, S.; Wagg, D.; Inman, D.; Wagg, D. Optimum resistive loads for vibration-based electromagnetic energy harvesters with a stiffening nonlinearity. J. Intell. Mater. Syst. Struct. 2014, 25, 1757–1770. [Google Scholar] [CrossRef]
- Li, P.; Gao, S.; Cai, H.; Wang, H. Coupling effect analysis for hybrid piezoelectric and electromagnetic energy harvesting from random vibrations. Int. J. Precis. Eng. Manuf. 2014, 15, 1915–1924. [Google Scholar] [CrossRef]
- Li, P.; Gao, S.; Cai, H. Modeling and analysis of hybrid piezoelectric and electromagnetic energy harvesting from random vibrations. Microsyst. Technol. 2015, 21, 401–414. [Google Scholar] [CrossRef]
- Lallart, M. Nonlinear technique and self-powered circuit for efficient piezoelectric energy harvesting under unloaded cases. Energy Convers. Manag. 2017, 133, 444–457. [Google Scholar] [CrossRef]
- Zhou, X.; Gao, S.; Liu, H.; Jin, L. Nonlinear Hybrid Piezoelectric and Electromagnetic Energy Harvesting Driven by Colored Excitation. Energies 2018, 11, 498. [Google Scholar] [CrossRef]
- Harne, R.; Sun, A.; Wang, K. Leveraging nonlinear saturation-based phenomena in an L-shaped vibration energy harvesting system. J. Sound Vib. 2016, 363, 517–531. [Google Scholar] [CrossRef]
- Jiang, W.A.; Chen, L.Q. An equivalent linearization technique for nonlinear piezoelectric energy harvesters under Gaussian white noise. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2897–2904. [Google Scholar] [CrossRef]
- Green, P.L.; Worden, K.; Atallah, K.; Sims, N.D. The benefits of Duffing-type nonlinearities and electrical optimization of a mono-stable energy harvester under white Gaussian excitations. J. Sound Vib. 2012, 20, 4504–4517. [Google Scholar] [CrossRef]
- Mann, B.P.; Owens, B.A. Investigations of a nonlinear energy harvester with a bistable potential well. J. Sound Vib. 2010, 329, 1215–1226. [Google Scholar] [CrossRef]
- Foisal, A.R.M.; Hong, C.; Chung, G.S. Multi-frequency electromagnetic energy harvester using a magnetic spring cantilever. Sens. Actuators A Phys. 2012, 182, 106–113. [Google Scholar] [CrossRef]
- Simeone, L.; Tehrani, M.G.; Elliott, S.J.; Hendijanizadeh, M. Nonlinear Damping in an Energy Harvesting Device. In Proceedings of the International Conference of Noise and Vibration Engineering, Leuven, Belgium, 15–17 September 2014; pp. 1–12. [Google Scholar]
- Al-Ashtari, W.; Hunstig, M.; Hemsel, T.; Sextro, W. Frequency tuning of piezoelectric energy harvesters by magnetic force. Smart Mater. Struct. 2012, 21, 35019. [Google Scholar] [CrossRef]
- Marzencki, M.; Basrour, S.; Charlot, B.; Spirkovich, S.; Colin, M. A MEMS piezoelectric vibration energy harvesting device. In Proceedings of the Fifth International Workshop on Micro and Nanotechnology for Power Generation and Energy Conversion Applications (PowerMEMS’05), Tokyo, Japan, 28–30 November 2005; pp. 45–48. [Google Scholar]
- Challa, V.R.; Prasad, M.G.; Fisher, F.T. A coupled piezoelectric–electromagnetic energy harvesting technique for achieving increased power output through damping matching. Smart Mater. Struct. 2009, 18, 1–11. [Google Scholar] [CrossRef]
- Torsten, R.; Armaghan, S. Analysis and Modelling towards Hybrid Piezo-Electromagnetic Vibrating Energy Harvesters. AIP Conf. Proc. 2010, 81, 81–85. [Google Scholar]
- Shan, X.-B.; Guan, S.-W.; Liu, Z.-S.; Xu, Z.-L.; Xie, T. A new energy harvester using a piezoelectric and suspension electromagnetic mechanism. J. Zhejiang Univ. Sci. A 2013, 14, 890–897. [Google Scholar] [CrossRef]
- Yang, X.; Wang, Y.; Cao, Y.; Liu, S.; Zhao, Z.; Dong, G. A New Hybrid Piezoelectric-Electromagnetic Vibration-Powered Generator and Its Model and Experiment Research. IEEE Trans. Appl. Supercond. 2014, 24. [Google Scholar] [CrossRef]
- Karami, M.A.; Inman, D.J. Equivalent damping and frequency change for linear and nonlinear hybrid vibrational energy harvesting systems. J. Sound Vib. 2011, 330, 5583–5597. [Google Scholar] [CrossRef]
- Hamdi, M.; Belhaq, M. Energy Harvesting in a Hybrid Piezoelectric-Electromagnetic Harvester with Time Delay, Recent Trends in Applied Nonlinear Mechanics and Physics. Springer Proc. Phys. 2017, 199, 69–83. [Google Scholar]
- Owens, B.A.M.; Mann, B.P. Linear and nonlinear electromagnetic coupling models in vibration-based energy harvesting. J. Sound Vib. 2012, 331, 922–937. [Google Scholar] [CrossRef]
- Department of Mathematics, Tongji University. Higher Mathematics; High Education Press: Beijing, China, 2007. [Google Scholar]
- Spreemann, D.; Manoli, Y. Electromagnetic Vibration Energy Harvesters; Springer: Berlin, Germany, 2012. [Google Scholar]
- Liu, Y.; Chen, L. Nonlinear Vibration; Higher Education Press: Beijing, China, 2001. [Google Scholar]
- Chen, Y. Nonlinear Vibration; Tianjin Science and Technology Press: Tianjin, China, 1983. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).