A Semi-Automated Image-Based Method for Interfacial Roughness Measurement Applied to Metal/Oxide Interfaces
Abstract
1. Introduction
2. Materials and Methods
2.1. Manual Method
2.2. Semi-Automated Method (Algorithm)
3. Results and Discussion
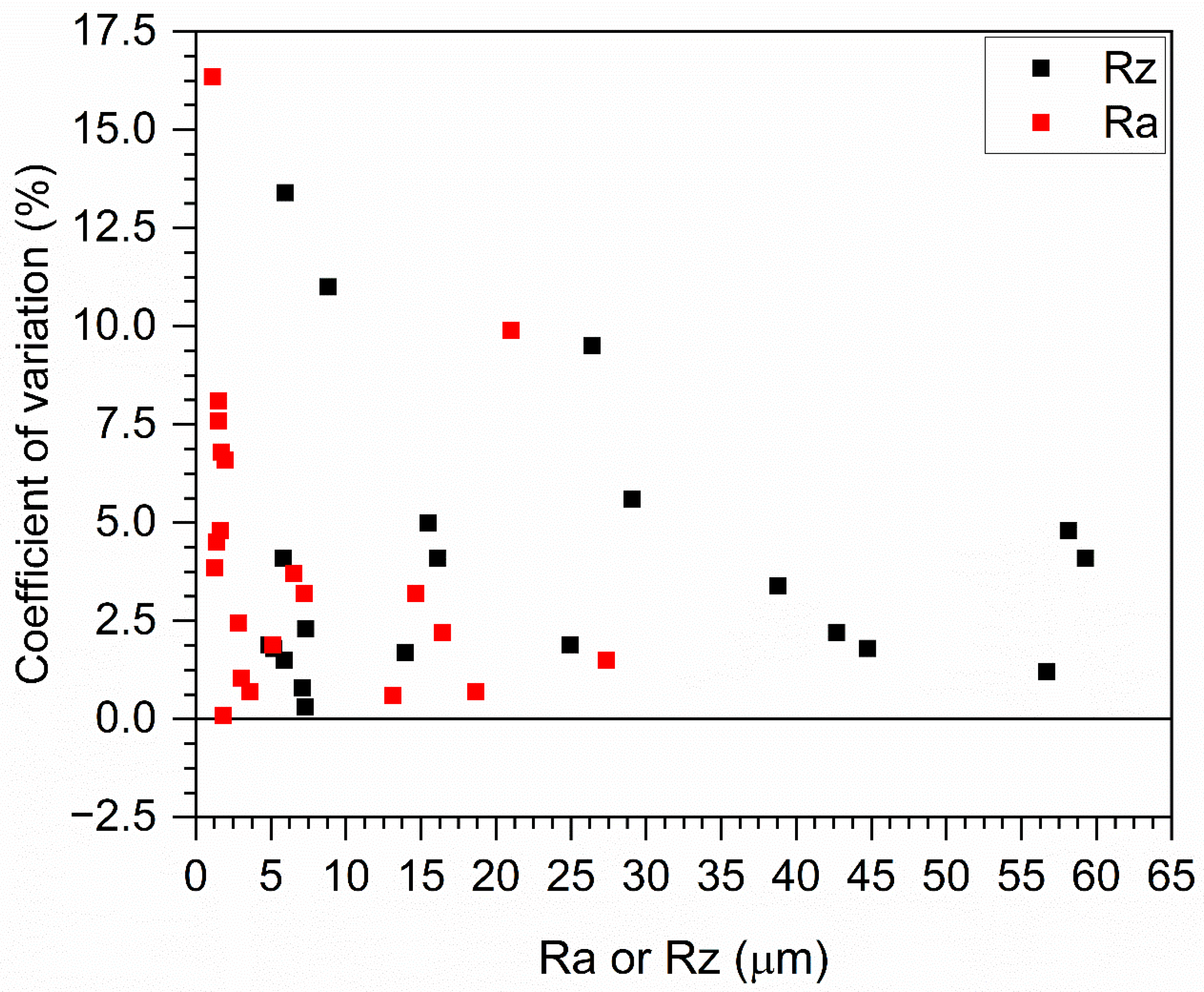
3.1. Roughness Measurements
3.2. Influence of Threshold Value on Algorithm Measurements
3.3. Main Sources of Variance in Measurements
3.3.1. Gray Value Differences in the Interface and in the Selected Region
3.3.2. Peaks and Valleys with Complex Shapes
3.4. Error Propagation and Traceability in the Measurement Workflow
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Whitesides, D.J. Handbook of Surface and Nanometrology; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Galedari, S.A.; Mahdavi, A.; Azarmi, F.; Huang, Y.; McDonald, A. A Comprehensive Review of Corrosion Resistance of Thermally-Sprayed and Thermally-Diffused Protective Coatings on Steel Structures. J. Therm. Spray Technol. 2019, 28, 645–677. [Google Scholar] [CrossRef]
- Nazeer, A.A.; Madkour, M. Potential Use of Smart Coatings for Corrosion Protection of Metals and Alloys: A Review. J. Mol. Liq. 2018, 253, 11–22. [Google Scholar] [CrossRef]
- Mah, J.C.W.; Muchtar, A.; Somalu, M.R.; Ghazali, M.J. Metallic Interconnects for Solid Oxide Fuel Cell: A Review on Protective Coating and Deposition Techniques. Int. J. Hydrogen Energy 2017, 42, 9219–9229. [Google Scholar] [CrossRef]
- Rizwan, M.; Alias, R.; Zaidi, U.Z.; Mahmoodian, R.; Hamdi, M. Surface Modification of Valve Metals Using Plasma Electrolytic Oxidation for Antibacterial Applications: A Review. J. Biomed. Mater. Res. Part A 2018, 106, 590–605. [Google Scholar] [CrossRef] [PubMed]
- Nicholls, J.R.; Bennett, M.J. Cyclic Oxidation—Guidelines for Test Standardisation, Aimed at the Assessment of Service Behaviour†. Mater. High Temp. 2000, 17, 413–428. [Google Scholar] [CrossRef]
- Silva, R.; Vacchi, G.S.; Santos, I.G.R.; Malafaia, A.d.S.; Kugelmeier, C.L.; Filho, A.A.M.; Pascal, C.; Sordi, V.L.; Rovere, C.A.D. Insights into High-Temperature Oxidation of Fe-Mn-Si-Cr-Ni Shape Memory Stainless Steels and Its Relationship to Alloy Chemical Composition. Corros. Sci. 2020, 163, 108269. [Google Scholar] [CrossRef]
- Zhang, X.; Mo, J.; Si, Y.; Guo, Z. How Does Substrate Roughness Affect the Service Life of a Superhydrophobic Coating? Appl. Surf. Sci. 2018, 441, 491–499. [Google Scholar] [CrossRef]
- Hagen, C.M.H.; Hognestad, A.; Knudsen, O.Ø.; Sørby, K. The Effect of Surface Roughness on Corrosion Resistance of Machined and Epoxy Coated Steel. Prog. Org. Coat. 2019, 130, 17–23. [Google Scholar] [CrossRef]
- Croll, S.G. Surface Roughness Profile and Its Effect on Coating Adhesion and Corrosion Protection: A Review. Prog. Org. Coat. 2020, 148, 105847. [Google Scholar] [CrossRef]
- Ostwald, C.; Grabke, H.J. Initial Oxidation and Chromium Diffusion. I. Effects of Surface Working on 9–20% Cr Steels. Corros. Sci. 2004, 46, 1113–1127. [Google Scholar] [CrossRef]
- Guttmann, V.; Hukelmann, F.; Griffin, D.; Daadbin, A.; Datta, S. Studies of the Influence of Surface Pre-Treatment on the Integrity of Alumina Scales on MA 956. Surf. Coat. Technol. 2003, 166, 72–83. [Google Scholar] [CrossRef]
- Sudbrack, C.K.; Beckett, D.L.; Mackay, R.A. Effect of Surface Preparation on the 815 °C Oxidation of Single-Crystal Nickel-Based Superalloys. J. Miner. Met. Mater. Soc. 2015, 67, 2589–2598. [Google Scholar] [CrossRef]
- Platt, P.; Allen, V.; Fenwick, M.; Gass, M.; Preuss, M. Observation of the Effect of Surface Roughness on the Oxidation of Zircaloy-4. Corros. Sci. 2015, 98, 1–5. [Google Scholar] [CrossRef]
- Malafaia, A.M.d.S.; Nascimento, V.R.D.; Sousa, L.M.; Silveira, M.E.; de Oliveira, M.F. Anomalous Cyclic Oxidation Behaviour of an Fe-Mn-Si-Cr-Ni Alloy—A Finite Element Analysis. Corros. Sci. 2019, 147, 223–230. [Google Scholar] [CrossRef]
- Malafaia, A.M.d.S.; de Oliveira, M.F. Anomalous Cyclic Oxidation Behaviour of a Fe–Mn–Si–Cr–Ni Shape Memory Alloy. Corros. Sci. 2017, 119, 112–117. [Google Scholar] [CrossRef]
- Rabelo, L.; Silva, R.; Della Rovere, C.; Malafaia, A.d.S. Metal/Oxide Interface Roughness Evolution Mechanism of an FeMnSiCrNiCe Shape Memory Stainless Steel under High Temperature Oxidation. Corros. Sci. 2020, 163, 108228. [Google Scholar] [CrossRef]
- Pindera, M.-J.; Aboudi, J.; Arnold, S.M. The Effect of Interface Roughness and Oxide Film Thickness on the Inelastic Response of Thermal Barrier Coatings to Thermal Cycling. Mater. Sci. Eng. A 2000, 284, 158–175. [Google Scholar] [CrossRef]
- Ahrens, M.; Vaßen, R.; Stöver, D. Stress Distributions in Plasma-Sprayed Thermal Barrier Coatings as a Function of Interface Roughness and Oxide Scale Thickness. Surf. Coat. Technol. 2002, 161, 26–35. [Google Scholar] [CrossRef]
- Li, Y.; Gao, H.; Wang, L.; Sun, Y.; Zhang, J. Discrete Element Modeling of Effect of Interfacial Roughness and Pre-Crack on Crack Propagation in Thermal Barrier Coatings. Comp. Part. Mech. 2025, 12, 31–39. [Google Scholar] [CrossRef]
- Ferguen, N.; Leclerc, W.; Lamini, E.-S. Numerical Investigation of Thermal Stresses Induced Interface Delamination in Plasma-Sprayed Thermal Barrier Coatings. Surf. Coat. Technol. 2023, 461, 129449. [Google Scholar] [CrossRef]
- Carim, A.H.; Sinclair, R. The Evolution of Si/SiO2 Interface Roughness. J. Electrochem. Soc. 1987, 134, 741–746. [Google Scholar] [CrossRef]
- Bossis, P.; Lefebvre, F.; Barbéris, P.; Galerie, A. Corrosion of Zirconium Alloys: Link between the Metal/Oxide Interface Roughness, the Degradation of the Protective Oxide Layer and the Corrosion Kinetics. Mater. Sci. Forum 2001, 369–372, 255–262. [Google Scholar] [CrossRef]
- Platt, P.; Wedge, S.; Frankel, P.; Gass, M.; Howells, R.; Preuss, M. A Study into the Impact of Interface Roughness Development on Mechanical Degradation of Oxides Formed on Zirconium Alloys. J. Nucl. Mater. 2015, 459, 166–174. [Google Scholar] [CrossRef]
- Roux, S.L.; Deschaux-Beaume, F.; Cutard, T.; Lours, P. Quantitative Assessment of the Interfacial Roughness in Multi-Layered Materials Using Image Analysis: Application to Oxidation in Ceramic-Based Materials. J. Eur. Ceram. Soc. 2015, 35, 1063–1079. [Google Scholar] [CrossRef]
- Ridley, M.; Garcia, E.; Kane, K.; Sampath, S.; Pint, B. Environmental Barrier Coatings on Enhanced Roughness SiC: Effect of Plasma Spraying Conditions on Properties and Performance. J. Eur. Ceram. Soc. 2023, 43, 6473–6481. [Google Scholar] [CrossRef]
- Chikhalikar, A.S.; Godbole, E.P.; Poerschke, D.L. Approach for Statistical Analysis of Oxide- and Sulfate-Induced Hot Corrosion of Advanced Alloys. Corros. Sci. 2023, 211, 110892. [Google Scholar] [CrossRef]
- Paksoy, A.H.; Scotson, D.; Yilmaz, E.; Xiao, P. Interfacial Characteristics and Adhesion Behaviour of Ytterbium Silicate Environmental Barrier Coatings Exposed to Steam Oxidation. Corros. Sci. 2025, 251, 112879. [Google Scholar] [CrossRef]
- Stegmueller, M.J.R.; Grant, R.J.; Schindele, P. Quantification of the Interfacial Roughness When Coating Stainless Steel onto Aluminium by Friction Surfacing. Surf. Coat. Technol. 2019, 375, 22–33. [Google Scholar] [CrossRef]
- Balachandran, S.; Smathers, D.B.; Kim, J.; Sim, K.; Lee, P.J. A Method for Measuring Interface Roughness from Cross-Sectional Micrographs. IEEE Trans. Appl. Supercond. 2023, 33, 1–5. [Google Scholar] [CrossRef]
- Gadelmawla, E.S.; Koura, M.M.; Maksoud, T.M.A.; Elewa, I.M.; Soliman, H.H. Roughness Parameters. J. Mater. Process. Technol. 2002, 123, 133–145. [Google Scholar] [CrossRef]
- O’Donnell, K.A. Effects of Finite Stylus Width in Surface Contact Profilometry. Appl. Opt. 1993, 32, 4922. [Google Scholar] [CrossRef] [PubMed]














| User-Measured Values | ||||||
|---|---|---|---|---|---|---|
| Rz (μm) | Ra (μm) | |||||
| Image | Average | Standard Deviation (s) | 100 × CV | Average | Standard Deviation (s) | 100 × CV |
| 1 | 26.42 | 2.5095 | 9.5 | 5.102 | 0.0974 | 1.9 |
| 2 | 29.04 | 1.6308 | 5.6 | 7.201 | 0.2306 | 3.2 |
| 3 | 24.95 | 0.4812 | 1.9 | 6.536 | 0.2429 | 3.7 |
| 4 | 44.73 | 0.807 | 1.8 | 13.106 | 0.0773 | 0.6 |
| 5 | 42.68 | 0.951 | 2.2 | 18.63 | 0.135 | 0.7 |
| 6 | 38.78 | 1.311 | 3.4 | 14.63 | 0.465 | 3.2 |
| 7 | 7.29 | 0.023 | 0.3 | 1.95 | 0.129 | 6.6 |
| 8 | 7.11 | 0.055 | 0.8 | 1.61 | 0.078 | 4.8 |
| 9 | 5.89 | 0.090 | 1.5 | 1.48 | 0.121 | 8.1 |
| 10 | 56.67 | 0.703 | 1.2 | 16.44 | 0.359 | 2.2 |
| 11 | 59.26 | 2.458 | 4.1 | 27.37 | 0.413 | 1.5 |
| 12 | 58.11 | 2.812 | 4.8 | 21.00 | 2.084 | 9.9 |
| 13 | 4.87 | 0.095 | 1.9 | 1.40 | 0.064 | 4.5 |
| 14 | 5.20 | 0.096 | 1.8 | 1.81 | 0.003 | 0.1 |
| 15 | 5.97 | 0.803 | 13.4 | 1.67 | 0.114 | 6.8 |
| 16 | 7.32 | 0.168 | 2.3 | 1.24 | 0.048 | 3.85 |
| 17 | 5.81 | 0.237 | 4.1 | 1.10 | 0.179 | 16.35 |
| 18 | 8.82 | 0.970 | 11.0 | 1.52 | 0.116 | 7.6 |
| 19 | 15.49 | 0.777 | 5.0 | 3.05 | 0.032 | 1.05 |
| 20 | 16.08 | 0.659 | 4.1 | 3.50 | 0.026 | 0.7 |
| 21 | 13.97 | 0.240 | 1.7 | 2.81 | 0.068 | 2.45 |
| Algorithm | 99% Confidence Interval (User Measurements) (Min; Max) | |||
|---|---|---|---|---|
| Image | Rz (μm) | Ra (μm) | Rz (μm) | Ra (μm) |
| 1 | 20.93 | 4.81 | (12.04; 40.79) | (4.54; 5.66) |
| 2 | 24.11 | 5.84 | (19.70; 38.39) | (5.88; 8.52) |
| 3 | 22.32 | 6.39 | (22.19; 27.70) | (5.15; 7.93) |
| 4 | 41.06 | 11.99 | (40.10; 49.35) | (12.66; 13.55) |
| 5 | 44.30 | 18.45 | (37.23; 48.13) | (17.86; 19.41) |
| 6 | 36.62 | 14.00 | (31.27; 46.29) | (11.97; 17.29) |
| 7 | 6.49 | 1.55 | (7.15; 7.42) | (1.21; 2.69) |
| 8 | 6.29 | 1.32 | (6.80; 7.43) | (1.17; 2.06) |
| 9 | 5.70 | 1.07 | (5.38; 6.41) | (0.79; 2.18) |
| 10 | 49.27 | 15.99 | (52.65; 60.70) | (14.38; 18.50) |
| 11 | 50.46 | 27.31 | (45.17; 73.34) | (25.00; 29.73) |
| 12 | 45.56 | 17.58 | (41.99; 74.22) | (9.06; 32.94) |
| 13 | 4.37 | 1.24 | (3.94; 5.64) | (1.03; 1.76) |
| 14 | 5.10 | 1.61 | (3.11; 6.92) | (1.80; 1.83) |
| 15 | 5.63 | 1.35 | (2.32; 9.35) | (1.02; 2.32) |
| 16 | 6.42 | 1.02 | (6.35; 8.28) | (0.96; 1.51) |
| 17 | 5.23 | 0.81 | (4.45; 7.17) | (0.07; 2.12) |
| 18 | 7.68 | 1.33 | (3.27; 14.38) | (0.86; 2.19) |
| 19 | 14.24 | 2.73 | (11.04; 19.95) | (2.86; 3.23) |
| 20 | 12.19 | 3.27 | (12.30; 19.86) | (3.44; 3.74) |
| 21 | 12.19 | 2.53 | (12.60; 15.35) | (2.42; 3.20) |
| Rz (μm) | Ra (μm) | |||||||
|---|---|---|---|---|---|---|---|---|
| User | Algorithm | User | Algorithm | |||||
| Sample | Average | Ranking | Average | Ranking | Average | Ranking | Average | Ranking |
| 1 (1–3) | 26.80 | 3 | 22.45 | 3 | 6.28 | 3 | 5.68 | 3 |
| 2 (4–6) | 42.06 | 2 | 40.66 | 2 | 15.46 | 2 | 14.81 | 2 |
| 3 (7–9) | 6.76 | 6 | 6.16 | 6 | 1.68 | 5 | 1.31 | 6 |
| 4 (10–12) | 58.01 | 1 | 48.43 | 1 | 21.60 | 1 | 20.29 | 1 |
| 5 (13–15) | 5.34 | 7 | 5.03 | 7 | 1.63 | 6 | 1.40 | 5 |
| 6 (16–18) | 7.32 | 5 | 6.44 | 5 | 1.29 | 7 | 1.05 | 7 |
| 7 (19–21) | 15.18 | 4 | 12.87 | 4 | 3.15 | 4 | 2.84 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Passos, J.G.d.C.; Rabelo, L.F.P.; Rovere, C.A.D.; de Sousa Malafaia, A.M. A Semi-Automated Image-Based Method for Interfacial Roughness Measurement Applied to Metal/Oxide Interfaces. Corros. Mater. Degrad. 2025, 6, 31. https://doi.org/10.3390/cmd6030031
Passos JGdC, Rabelo LFP, Rovere CAD, de Sousa Malafaia AM. A Semi-Automated Image-Based Method for Interfacial Roughness Measurement Applied to Metal/Oxide Interfaces. Corrosion and Materials Degradation. 2025; 6(3):31. https://doi.org/10.3390/cmd6030031
Chicago/Turabian StylePassos, João Gabriel da Cruz, Luis Fernando Pedrosa Rabelo, Carlos Alberto Della Rovere, and Artur Mariano de Sousa Malafaia. 2025. "A Semi-Automated Image-Based Method for Interfacial Roughness Measurement Applied to Metal/Oxide Interfaces" Corrosion and Materials Degradation 6, no. 3: 31. https://doi.org/10.3390/cmd6030031
APA StylePassos, J. G. d. C., Rabelo, L. F. P., Rovere, C. A. D., & de Sousa Malafaia, A. M. (2025). A Semi-Automated Image-Based Method for Interfacial Roughness Measurement Applied to Metal/Oxide Interfaces. Corrosion and Materials Degradation, 6(3), 31. https://doi.org/10.3390/cmd6030031








