Validation of Water Radiolysis Models Against Experimental Data in Support of the Prediction of the Radiation-Induced Corrosion of Copper-Coated Used Fuel Containers

Abstract

Copper has been proposed as a container material for the disposal of used nuclear fuel in a number of countries worldwide. The container materials will be subject to various corrosion processes in a deep geological repository, including radiation-induced corrosion (RIC) resulting from the γ-irradiation of the near-field environment. A comprehensive model is being developed to predict the extent of RIC by coupling a radiolysis model to the interfacial electrochemical reactions on the container surface. An important component of the overall model is a radiolysis model to predict the time-dependent concentration of oxidizing and reducing radiolysis products. As a first step in the model development, various radiolysis models have been validated against experimental measurements of the concentrations of dissolved and gaseous radiolysis products. Experimental data are available for pure H₂O- and Cl⁻-containing solutions, with and without a gas headspace. The results from these experiments have been compared with predictions from corresponding radiolysis models, including the effects of the partitioning of gaseous species (O₂ and H₂) at the gas–solution interface. Different reaction schemes for the Cl⁻ radiolysis models are also compared. The validated radiolysis model will then be coupled with interfacial reactions on the copper surface and additional processes related to the presence of bentonite clay in Steps 2 and 3 of the overall model, respectively.

1. Introduction

The Nuclear Waste Management Organization (NWMO) is responsible for developing a design for a deep geological repository (DGR) for the safe, long-term management of used nuclear fuels in Canada [1]. NWMO has recently selected a site in Northwest Ontario as the potential host for a DGR. The repository would be excavated in suitable rock at a depth range of 650–800 m in the crystalline rock of the Revell Batholith [2]. Groundwaters at repository depth are expected to be anoxic and saline comprising a Ca-Na-based chloride (Cl⁻) solution with a Cl⁻ concentration of approximately 0.1 mol/L [3]. The copper-coated used fuel containers (UFC) would be surrounded by compacted bentonite buffer using prefabricated buffer boxes, with any remaining spaces in the repository filled with a granular bentonite gapfill material [4]. A modest γ-radiation field will be present at the surface of the copper-coated UFC due to the decay of radionuclides in the used fuel (also referred to as spent fuel in some national waste management programs), with a maximum absorbed dose rate at the time of emplacement of approximately 1 Gy/h decaying with a half-life of ~30 y (equivalent to the half-life of Cs-137, the predominant γ-emitting fission product) [5]. As a consequence of the in-growth of γ-emitting long-lived radionuclides, the long-term dose rate is of the order of 0.01–0.1 mGy/h resulting in a total absorbed dose of around 2 MGy in one million years [6].

As for all other corrosion processes to which the UFC will be subject, it is necessary to estimate the extent of corrosion due to radiation-induced corrosion (RIC) [7]. Since the dose rate is insufficient to ennoble the corrosion potential (E_CORR) of the UFC to induce localized corrosion or stress corrosion cracking mechanisms that are contingent on exceeding a threshold potential [8], the only radiation-induced corrosion mechanism of concern is uniform corrosion supported by the production of oxidizing radiolysis products. A mixed-potential model is being developed to predict the extent of RIC of containers in a DGR based on fully coupling a radiolysis model to a set of interfacial electrochemical reactions (plus other homogeneous reactions) [6]. The model, referred to as the Copper Corrosion Model for Radiation-induced Corrosion (CCM-RIC), is being developed in a stepwise fashion, with Step 1 being the development of a validated radiolysis model [6]. We have previously validated the Step 1 model against experimental measurements of the concentrations of H₂O₂ and dissolved H₂ from the radiolysis of pure H₂O in the absence of a headspace [6]. We also performed model-to-model validations to demonstrate that the finite element software used for the CCM-RIC is capable of solving the stiff numerical problems associated with radiolysis modeling [9].

In this paper, we present further model-to-experiment and model-to-model validations of the Step 1 radiolysis model. The model development is extended to include mass-transfer at the gas–solution interface, in order to simulate experiments with a gas headspace [10]. In addition, to investigate the effects of Cl⁻, the implementation was extended by using two different radiolytic reaction schemes proposed in the literature. In both cases, the results of the Step 1 model are compared to both experimental measurements of the concentrations of various radiolytic species as well as to earlier model predictions based on the use of the FACSIMILE code [11].

2. Background

2.1. Overview of CCM-RIC

The CCM-RIC is a fully coupled radiolysis and mixed-potential model for the prediction of the effects of irradiation on the corrosion of copper UFC [6]. The code couples a mixed-potential model for the corrosion of copper in Cl⁻ solutions to a radiolysis model for the estimation of the yield of radiolytic species. The consumption of radiolytic oxidants (and reductants) at the corroding interface may impact the corresponding yields, as demonstrated by Macdonald and Urquidi-Macdonald [12]. Therefore, the direct coupling is considered to be a more rigorous approach than the use of uncoupled radiolysis corrosion models in which the production of radiolytic oxidants (and reductants) is treated as being independent of their rate of consumption at the corroding interface [8].

As noted above, the CCM-RIC is being developed in a stepwise fashion. The Step 1 model, described here and by Behazin et al. [6], involves the validation of a bulk radiolysis model to predict the yield of the different radiolysis products in the absence of any reactions involving the corroding interface. Following successful validation, the Step 2 model will couple the radiolysis model to a mixed-potential model for the corrosion of copper in Cl⁻ environments [13]. This mixed-potential model has been separately validated against the results of experiments in O₂-containing environments [13,14]. The combined radiolysis–mixed-potential model will be validated against the results of irradiation corrosion experiments on copper in Cl⁻ solutions. Finally, the validated coupled radiolysis-corrosion model will be further extended (Step 3) to include the effects of processes within the repository, such as the interaction between radiolysis products and the compacted bentonite buffer material, the enhanced yield of primary radiolysis species due to energy transfer across oxide (aluminosilicate)–water interfaces [15], and the long-term temporal and spatial variation in the dose rate at the UFC surface.

Behazin et al. [6] describe the results of the initial validation of the Step 1 radiolysis model against experimental data and other model simulations. The H₂O radiolysis model used by Behazin et al. was based on that described by Joseph et al. [16] suitably modified to conform to the requirements of the commercial software package used for the CCM-RIC (see Section 3.1). This model accounts for the primary radiolytic species formed on the picosecond timescale and the subsequent production of secondary species by chemical reactions on timescales up to microseconds [15]. This Step 1 H₂O radiolysis model was validated against experimental measurements of the radiolytic yield of H₂O₂ and of dissolved H₂ in systems with no headspace, i.e., in which O₂ and H₂ could not partition into a gas phase above the solution. The Step 1 model results were also compared with predictions from Joseph et al. [16] for the same H₂O radiolysis reaction scheme but implemented using the FACSIMILE software package. Radiolysis models involve the solution of so-called “stiff” numerical problems for which specialized codes, designed to handle the wide range of reaction rate constants, are considered to be required [9]. Lastly, Behazin et al. [6] demonstrated that the Step 1 model could be run to a total simulated time of 1 million years, a timespan that will be required to simulate the long-term performance of the UFC for the repository-focused Step 3 model.

2.2. Treatment of Mass Transfer at the Gas–Solution Interface

In many of the experimental radiolysis studies used for validation of the Step 1 model, the irradiated vessel was partially filled with solution and partially with a gas phase (typically either air or Ar). Volatile radiolysis products, principally O₂ and H₂, can then partition between the gas and solution phases. Even if no radiolysis reactions occur in the (humid) gas phase, the escape of O₂ and/or H₂ from the aqueous phase will reduce the respective concentrations of dissolved species and impact the rates of subsequent aqueous radiolytic reactions and ultimate yields. To simulate such experiments, it is therefore necessary to account for mass transfer at the gas–solution interface.

Yakabuskie et al. [17] developed an expression for the partitioning of species at the gas–solution interface based on the concept of a mass-transfer resistance between two boundary layer regions assumed to exist in the gas and solution phases. These boundary layer thicknesses are not known a priori and were treated by Yakabuskie et al. [17] as adjustable model parameters that necessitated fitting of their data to the model to obtain best-fit estimates.

Here, a simpler approach is used that does not require the calibration of the model to the experimental data. The experimental vessel is simulated by a 1-dimensional model domain divided between gas and solution phases with equilibrium (as described by Henry’s law) applied at the interface. The total length of the 1D model is given by the volume:cross-sectional area ratio of the irradiated vessel with the lengths of the gas and solution phases proportional to their respective volumes. Since mass transfer at the interface is infinitely fast (due to the assumption of equilibrium), the (relatively) slow rate of diffusive transport of species may result in concentration gradients within the layers, especially that representing the solution phase. Therefore, the entire length of the 1D model is sub-divided into a sufficient number of elements to permit accurate estimation of the distribution of radiolysis species in each layer.

2.3. Comparison of Different Chloride Radiolysis Models

In addition to further validation simulations with the H₂O radiolysis model described earlier by Behazin et al. [6], simulations have also been performed to investigate the effect of Cl⁻. Morco [10] describes a groundwater radiolysis model based on the Cl⁻-related reaction scheme proposed by Kelm and Bohnert [18] and Sunder and Christensen [19] which itself was based on an earlier reaction scheme proposed by Bjergbakke et al. [20]. This reaction scheme comprises a set of 45 first- and second-order reactions in addition to the set of 39 kinetic and equilibrium reactions previously used for the radiolysis of pure H₂O [6]. The set of 45 additional Cl⁻-related reactions as implemented here are given in

Table A1. Reaction scheme and associated rate constants for the Morco Cl⁻ model [10].

Reactants	Products	k (dm3 mol−1 s−1) or (s−1)
•OH + Cl−	•ClOH−	4.3 × 109
•OH + HClO	•ClO + H2O	9.0 × 109
•OH + HClO2	•ClO2 + H2O	6.3 × 109
eaq− + •Cl	Cl− + H2O	1.0 × 1010
eaq− + •Cl2−	2Cl− + H2O	1.0 × 1010
eaq− + •ClOH−	Cl− + OH− + H2O	1.0 × 1010
eaq− + HClO	•ClOH− + H2O	5.3 × 1010
eaq− + Cl2	•Cl2−	1.0 × 1010
eaq− + Cl3−	•Cl− + Cl2− + H2O	1.0 × 1010
eaq− + HClO2	•ClO + OH− + H2O	4.5 × 1010
eaq− + HClO3	•ClO2 + OH− + H2O	4.0 × 106
•H + Cl−	Cl− + H+	1.0 × 1010
•H + •Cl2−	2Cl− + H+	8.0 × 109
•H + •ClOH−	Cl− + H2O	1.0 × 1010
•H + Cl2	•Cl2− + H+	7.0 × 109
•H + HClO	•ClOH− + H+	1.0 × 1010
•H + •Cl3−	•Cl2− + Cl− + H+	1.0 × 1010
•HO2 + •Cl2−	2Cl− + O2 + H+	4.0 × 109
•HO2 + Cl2	•Cl2− + O2 + H+	1.0 × 109
•HO2 + Cl3−	•Cl2− + Cl− + O2 + H+	1.0 × 109
•O2− + •Cl2−	2Cl− + O2	2.0 × 1010
•O2− + HClO	•ClOH− + O2	7.5 × 106
H2O2 + •Cl2−	2Cl− + •O2− + 2H+	1.4 × 105
H2O2 + Cl2	•Cl2− + •HO2 + H+	1.9 × 102
H2O2 + HClO	Cl− + O2 + H+ + H2O	1.7 × 105
•Cl2− + OH−	•ClOH− + Cl−	7.3 × 106
Cl2 + OH−	HClO + Cl−	3.88 × 1011
•ClOH− + H+	•Cl + H2O	2.1 × 1010
Cl2O2 (H2O)	HClO + HClO2	2.0 × 102
Cl2O2 (H2O)	HClO + H+ + Cl− + O2	1.0 × 102
Cl2O (H2O)	2HClO	1.0 × 102
Cl2O4 (H2O)	HClO2 + HClO3	1.0 × 102
Cl2O4 (H2O)	HClO + Cl− + H+ + O4	1.0 × 102
O4	O2+ O2	1.0 × 105
Cl− + •Cl	•Cl2−	2.1 × 1010
Cl− + •ClOH−	•Cl2− + OH−	9.0 × 104
Cl− + HClO	Cl2 + OH−	1.0 × 1010
Cl− + Cl2	Cl3−	1.0 × 104
•ClOH−	•OH + Cl−	6.1 × 109
•Cl2−	Cl + Cl−	1.1 × 105
•Cl2− + •Cl2−	Cl− + Cl3−	7.0 × 109
Cl3−	Cl2 + Cl−	5.0 × 104
•ClO + •ClO	Cl2O2	1.5 × 1010
•ClO2 + •ClO2	Cl2O4	1.0 × 102
Cl2O2 + HClO2	HClO3 + Cl2O	1.0 × 102

, along with the corresponding rate constants. When simulating the effect of Cl⁻ using this reaction set, the entire radiolysis model consisted of a total of 84 kinetic and equilibrium reactions. The Cl⁻-based reactions introduce three new primary radiolysis species (^•Cl₂⁻, Cl₃⁻, and ^•ClOH⁻, and corresponding [Cl⁻]-dependent g-values) as well as 15 new secondary species (Cl⁻, ^•ClO, ^•ClOH⁻, HClO, ^•ClO₂, ^•Cl, ^•Cl₂⁻, Cl₃⁻, Cl₂, HClO₂, HClO₃, Cl₂O₂, Cl₂O, Cl₂O₄, O₄) in addition to those for the H₂O radiolysis model.

Jonsson [21] has criticized the use of the Kelm and Bohnert/Sunder and Christensen reaction scheme on the basis that approximately 25% of the reactions were annotated by Bjerbakke et al. [20] with the description “reaction not known, arbitrary rate constant”. Instead, Jonsson [21] proposed a simpler 15-reaction Cl⁻ radiolysis model based on a review of the available radiolysis literature and associated rate constants. Jonsson’s Cl⁻ reaction scheme, as implemented here, is given in

Table A2. Reaction scheme and associated rate constants for the Jonsson Cl⁻ model [21].

Reactants	Products	k (dm3 mol−1 s−1) or (s−1)
•OH+ Cl−	•ClOH−	4.3 × 109/6.1 × 109
•ClOH−	•Cl + OH−	2.3 × 101/1.8 × 1010
H+ + •ClOH−	•Cl + OH−	2.1 × 1010
•Cl + Cl−	•Cl2−	8.5 × 109/6.0 × 104
•Cl2− + •Cl2−	Cl3− + Cl−	2.0 × 109
•Cl + •Cl2−	Cl3−	6.3 × 108
Cl− + Cl2	Cl3−	1.0 × 104/5.0 × 104
•Cl + •Cl	Cl2	8.8 × 107
eaq− + •Cl	Cl−	1.0 × 1010
eaq− + •Cl2−	2Cl−	1.0 × 1010
eaq− + Cl3−	Cl− + •Cl2−	3.0 × 1010
•H + •Cl	H+ + Cl−	1.0 × 1010
•H + •Cl2−	H+ + 2Cl−	8.0 × 109
•H + Cl3−	H+ + Cl− + •Cl2−	1.0 × 1010
•HO2 + •Cl2−	2Cl− + O2 + H+	1.0 × 109

. Jonsson [21] did not define g-values for any Cl⁻-containing species, implying that there are no primary radiolysis products (other than those for H₂O), at least for the [Cl⁻] typical of deep groundwaters (of the order of 0.1–1 mol/L Cl⁻).

3. Software and Description of Validation Simulations

3.1. Software

COMSOL Multiphysics (www.comsol.com/comsol-multiphysics) is a general finite-element software package for the solution of a wide range of physicochemical problems (as well as other types of processes). Since other software packages for radiolysis models, such as MAKSIMA-CHEMIST [9] and FACSIMILE [11] have been specifically developed with stiff numerical problems in mind, close attention was paid to the ability of COMSOL to similarly accurately solve such numerical problems. COMSOL offers various explicit and implicit numerical integration methods, with the Reaction Engineering Module defaulting to an implicit backwards differentiation formula (BDF) method [22]. Implicit BDF algorithms are linear multi-step methods that use the solution from one or more preceding timesteps to calculate the subsequent timestep [23]. This can numerically dampen the rate of change of the system due to the look-back approach, making it less suitable for systems with rapidly changing solutions without careful application. However, the advantage of BDF methods, like other implicit methods, is their effectiveness in solving stiff systems of equations without requiring prohibitively small timesteps, as might be necessary with explicit methods [24].

The Step 1 CCM-RIC radiolysis model was implemented using COMSOL Multiphysics Version 6.3 with the Reaction Engineering Module. When using the Reaction Engineering Module to input the various radiolysis reactions, the software interprets each species on the left-hand side of the reaction as rate-determining. Thus, if the reaction involves two reactants, the software requires the use of a second-order rate constant, three reactants require a third-order rate constant, and so on. Since some of the reactions of the original radiolysis schemes used here were written with non-rate-determining species on the left-hand side (especially in the case of H₂O), some of the reactions had to be re-arranged in order to ensure that only rate-determining species appeared on the left-hand side. As a consequence, some of the reactions and rate constants in Table A1 and Table A2 differ from those defined in the original publications from which they were taken. In COMSOL, equilibrium reactions were inputted using forward and reverse rate constants.

3.2. Validation Simulations

Table 1. Summary of validation simulations performed and the corresponding experimental data.

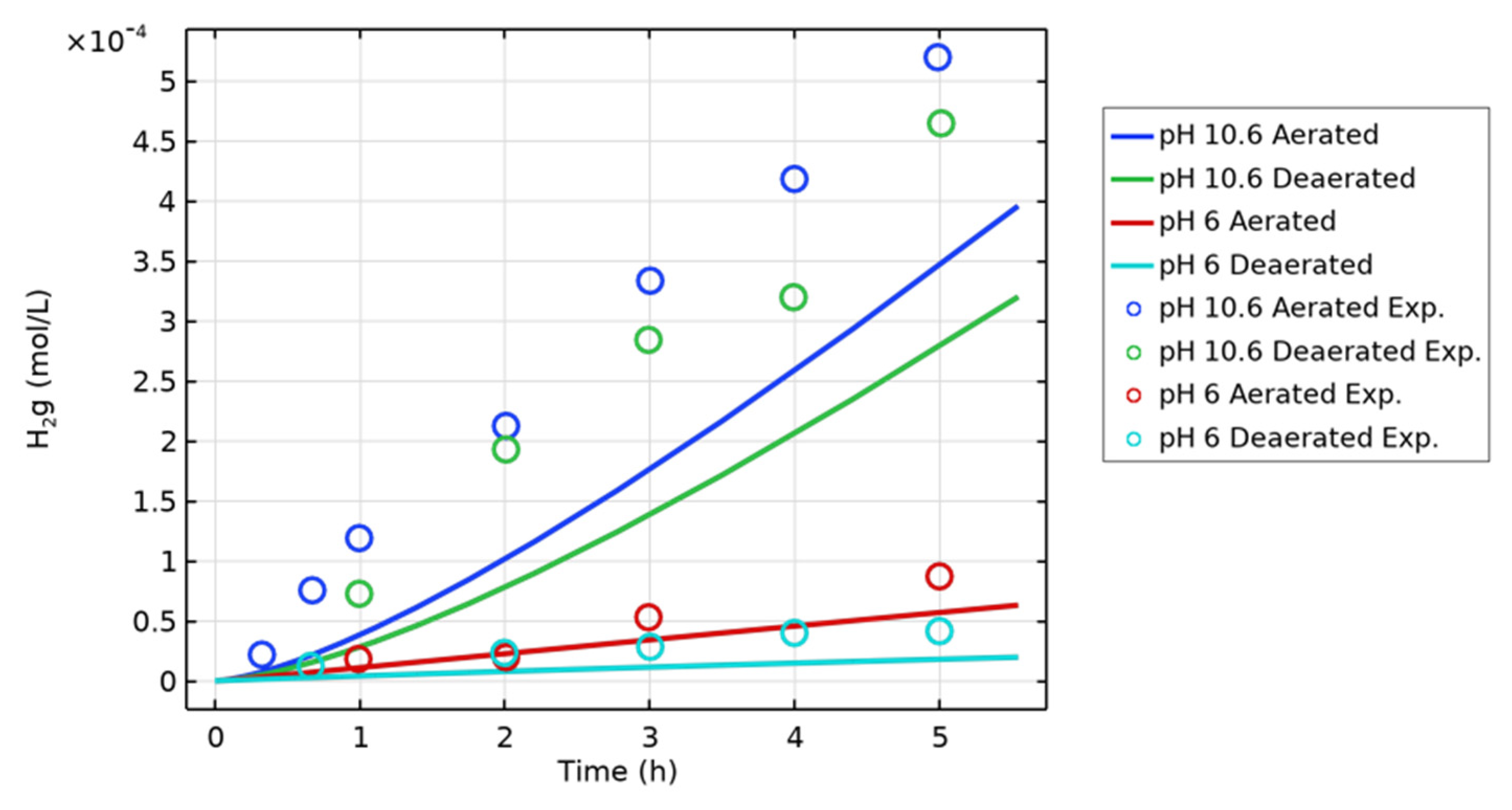
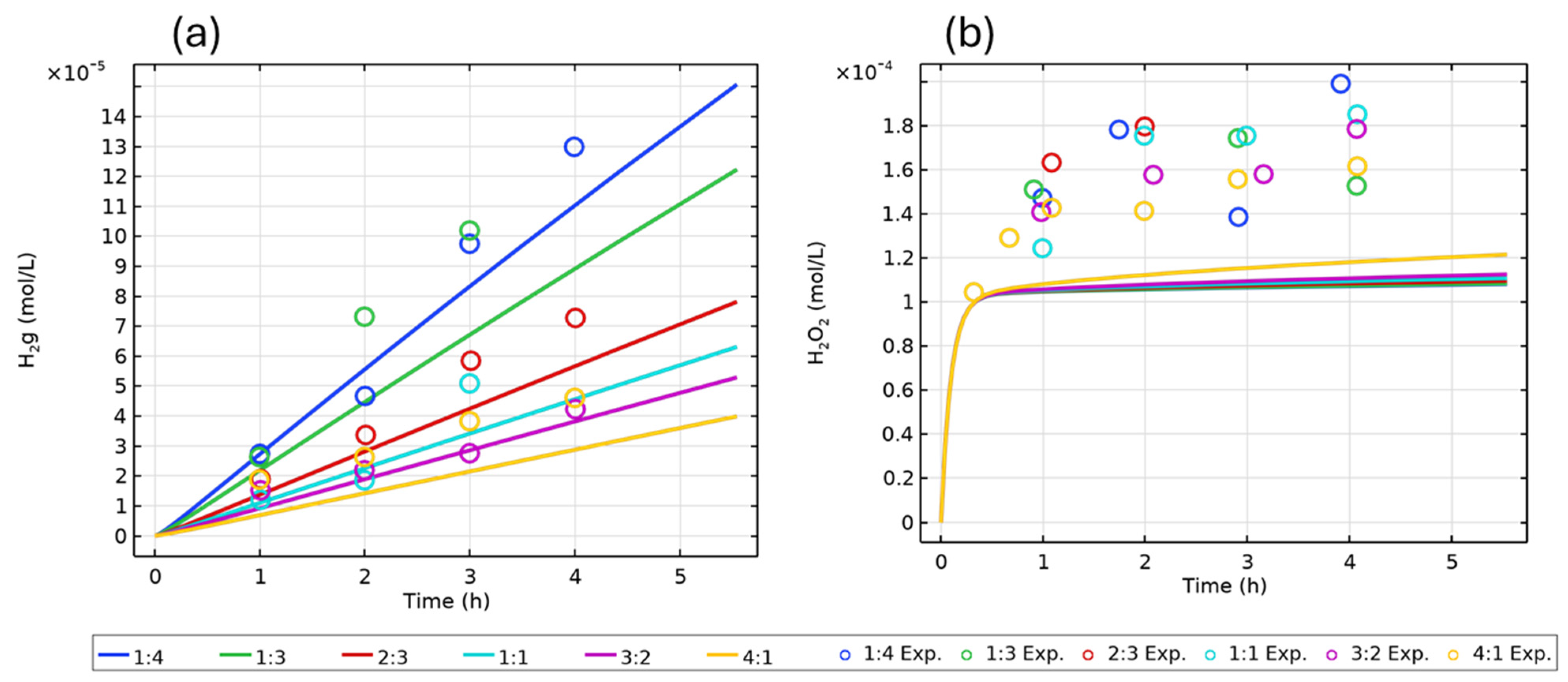
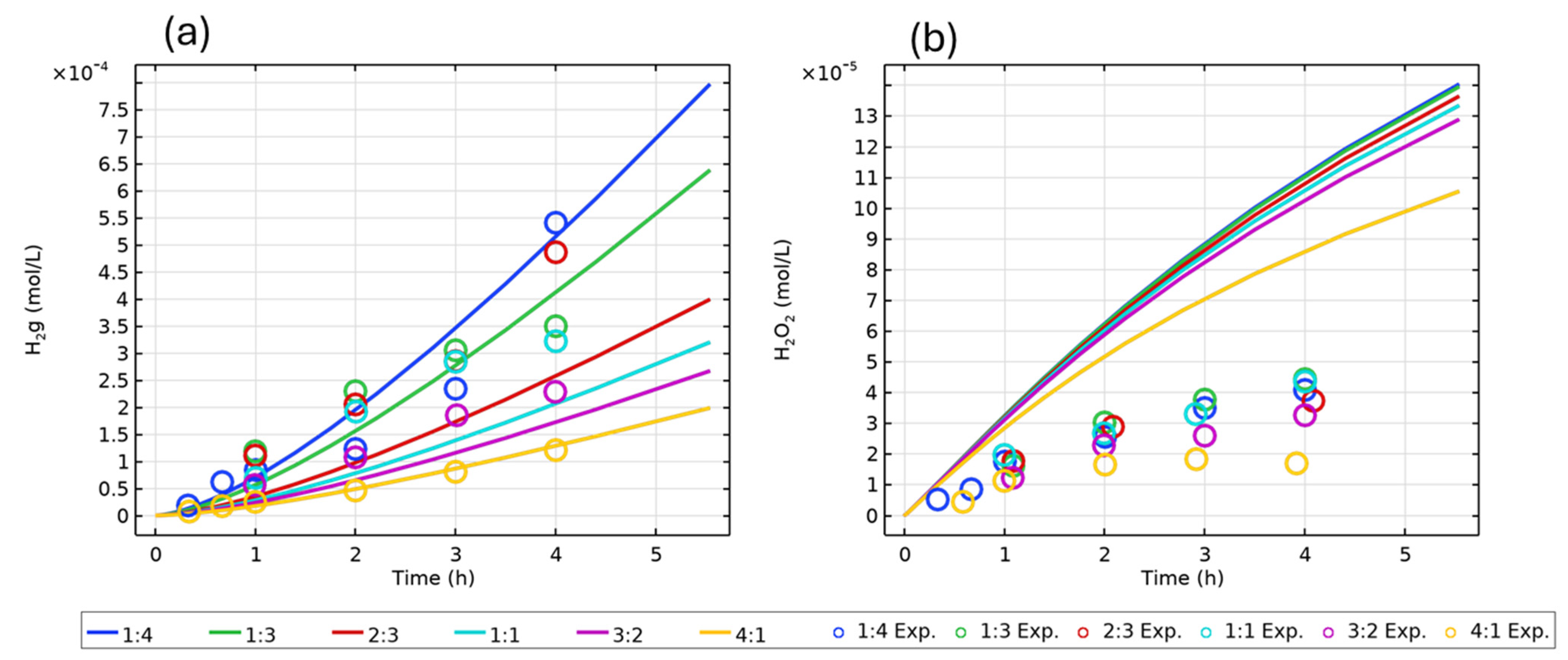
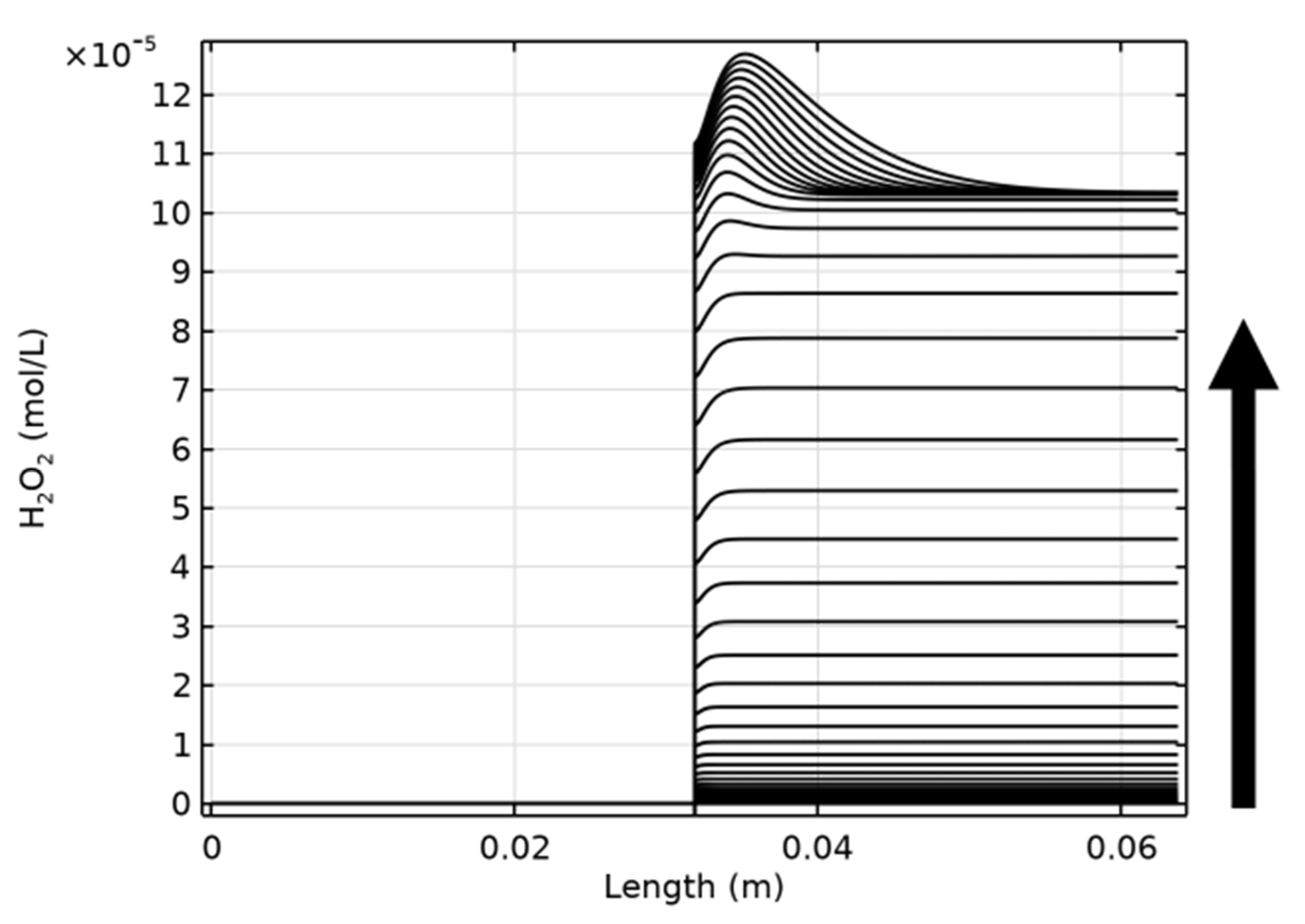
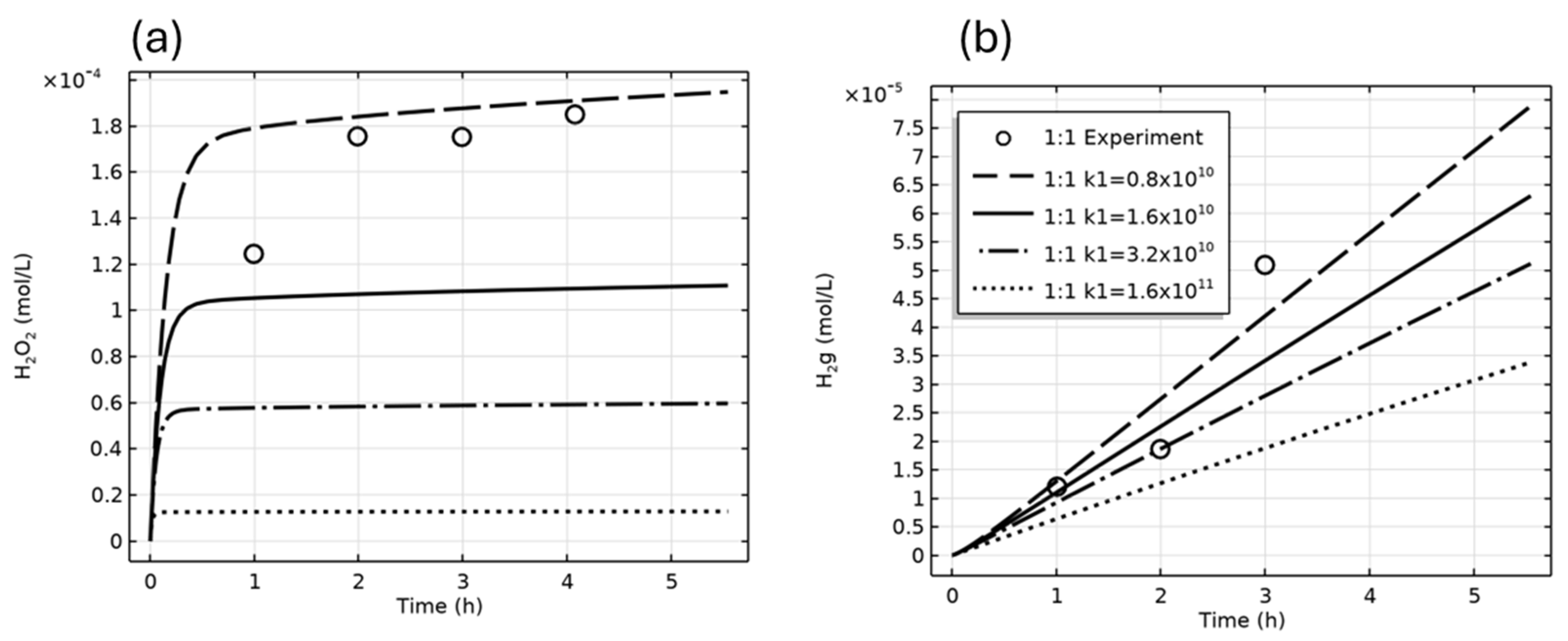
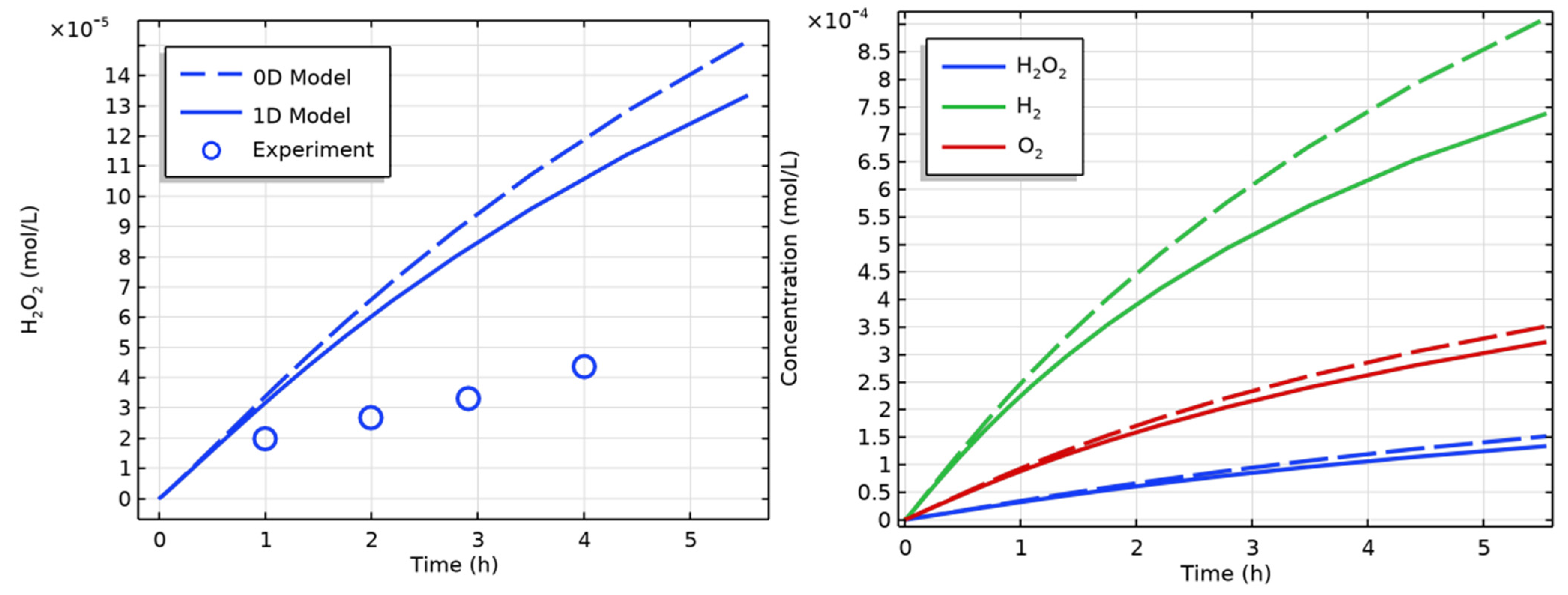
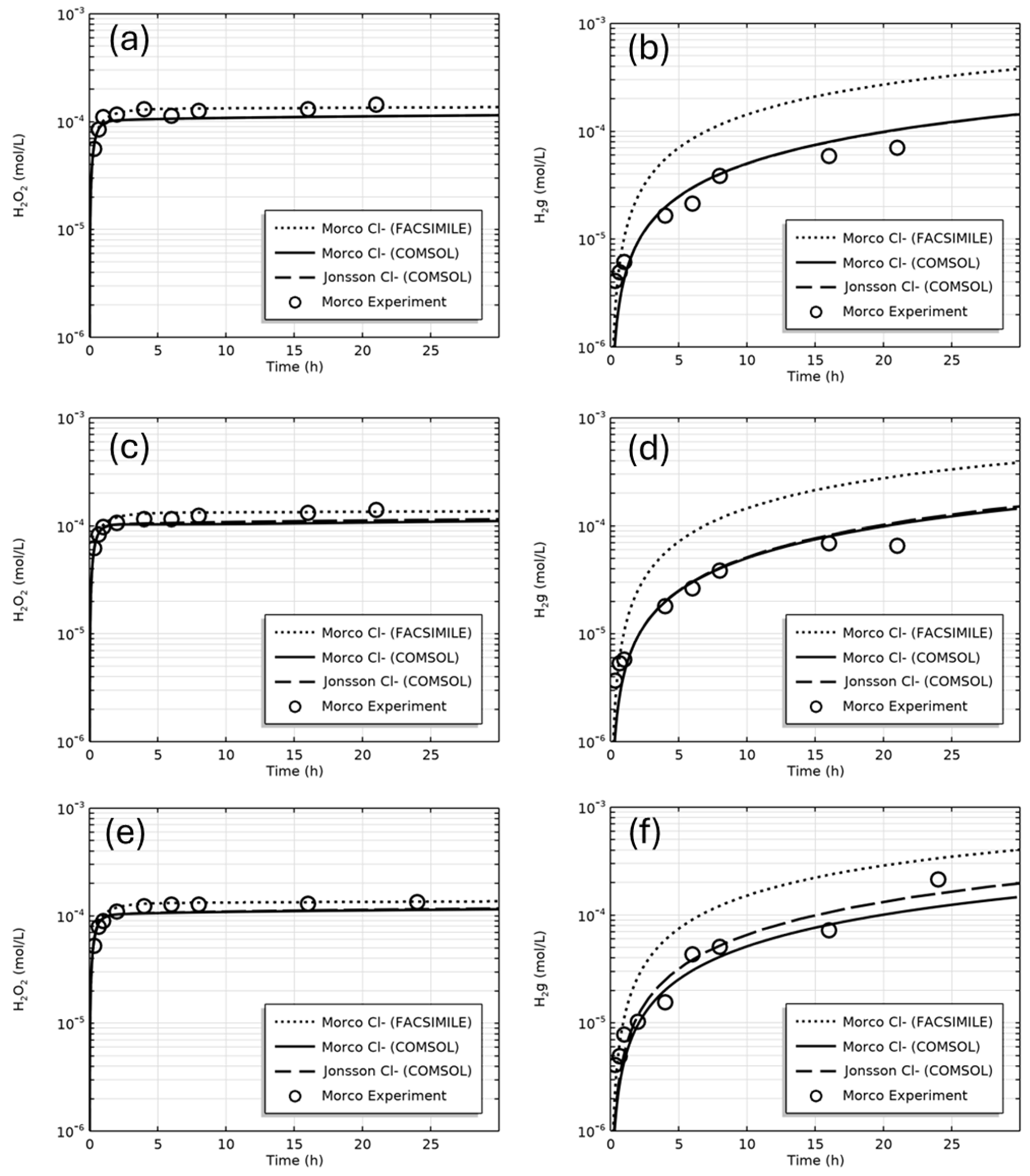
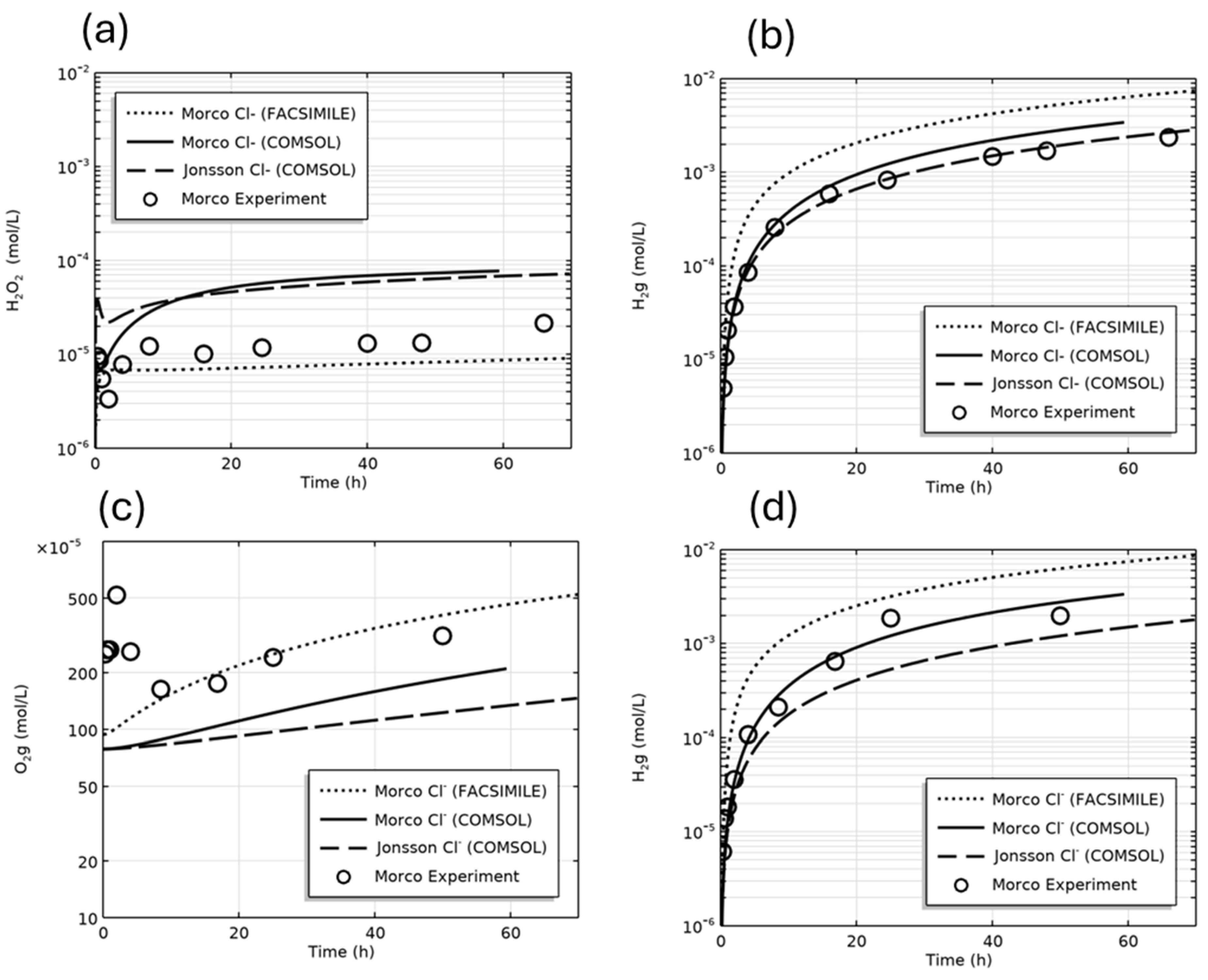
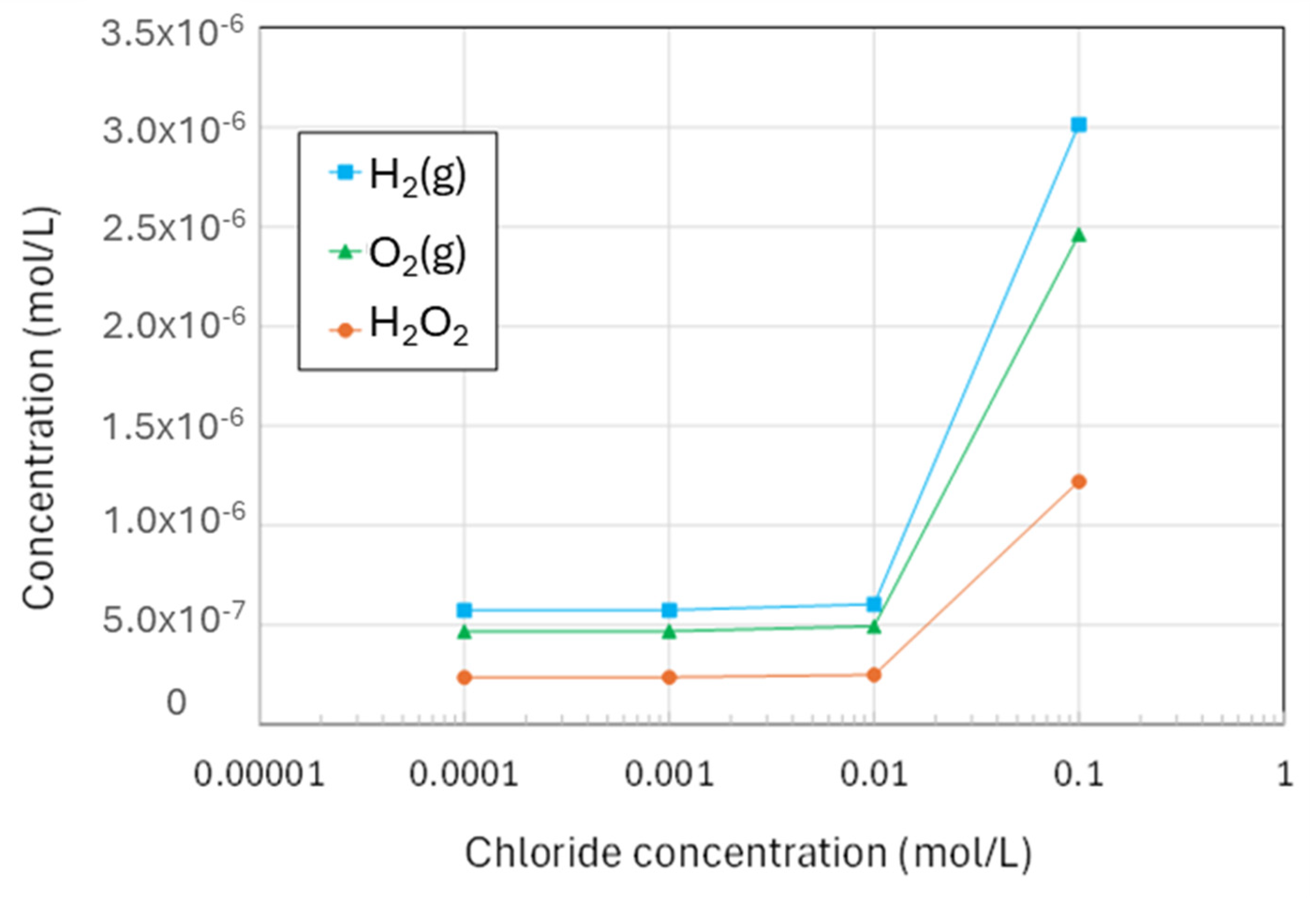
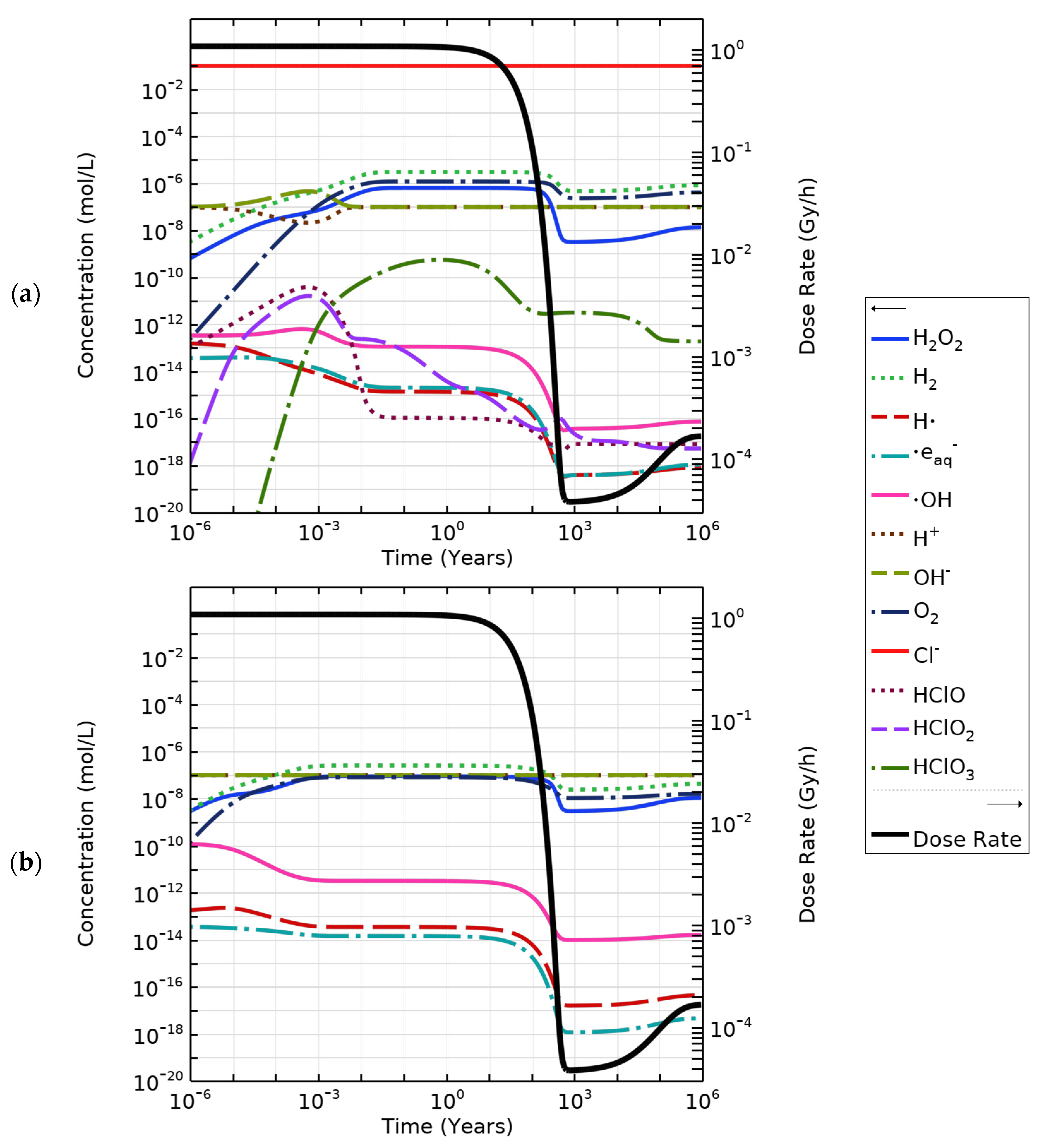
Figure	Radiolysis Model	[Cl−] (mol/L)	pH, Initial [O2]	Vg:Vaq	Dose Rate (kGy/h)	Experimental Data and Source
1	H2O (COMSOL)	-	pH 6 and 10.6, aerated and deaerated	1:1	9	H2(g) [16]
2	H2O (COMSOL)	-	pH 6, aerated	Various	9	H2(g), H2O2(aq) [16]
3	H2O (COMSOL)	-	pH 10.6, deaerated	Various	9	H2(g), H2O2(aq) [16]
5	Morco Cl− (COMSOL) Jonsson Cl− (COMSOL) Morco Cl− (FACSIMILE)	0, 0.001, 0.01	pH 6, aerated	1:1	2.3	H2(g), H2O2(aq) [10]
6	Morco Cl− (COMSOL) Jonsson Cl− (COMSOL) Morco Cl− (FACSIMILE)	2	pH 7, aerated and “low [O2]”	1:1	3	H2(g), H2O2(aq) [10]

summarizes the validation simulations that have been performed as part of the current study. We have validated various COMSOL-based models against experimental measurements of the [H₂(g)] and [H₂O₂(aq)] given by [10,16], including the model for H₂O previously described (referred to here as the H₂O (COMSOL) model) [6] and two H₂O-Cl⁻ models based on reaction schemes from either Morco [10] (Morco Cl⁻ (COMSOL)) (which itself is based on the original model of Christen and Sunder [19] and Bjergbakke et al. [20]) or Jonsson [21] (Jonsson Cl⁻ (COMSOL)) described in Table A1 and Table A2, respectively. We also compare our COMSOL implementation of the Morco Cl⁻ reactions with the original FACSIMILE implementation described in [10] (Morco Cl⁻ (FACSIMILE)). In all cases, partitioning of O₂ and H₂ between the solution phase and gas headspace is simulated, either using the assumption of equilibrium at the gas–solution interface for the COMSOL models or the mass-transfer resistance model of Yakabuskie et al. [17] in the case of the FACSIMILE model. Various gas:solution volume ratios (V_g:V_aq) have been simulated. Radiolysis is assumed to be limited to the solution phase only with no radiolysis reactions in the headspace. For the simulations involving Cl⁻ solutions, primary g-values for H₂O-derived species only were used for [Cl⁻] up to and including 0.1 mol/L [6], with a separate set of g-values (including values for three additional primary species ^•Cl₂⁻, Cl₃⁻, and ^•ClOH⁻) for 2 mol/L Cl⁻ (

Table A3. Primary g-values for H₂O and Cl⁻ radiolysis models [10,16].

Primary Species	H2O g-Values (μmol/J)	Cl− g-Values (2 mol/L Cl−) (μmol/J)
•eaq−	0.27	0.38
H+	0.27	0.13
•H	0.062	0
•OH	0.28	0.086
H2	0.047	0.047
H2O2	0.073	0.028
OH−	0	0
•Cl2−	-	0.14
Cl3−	-	0.054
•ClOH−	-	0.079

). Finally, various initial pH and [O₂] were assumed as defined by the experimental studies [10,16]. In the case of the “low [O₂]” solution in Table 1, the initial [O₂] was defined as being a factor of 10 lower than that in aerated solution based on the experimental description in [10].

4. Results and Discussions of Validation Simulations

4.1. Pure H₂O, Mass Transfer at the Gas–Solution Interface

The first series of simulations is focused on the validation of the treatment of the mass transfer of O₂ and H₂ across the gas–solution interface. Yakabuskie [17] measured the concentration of gaseous H₂ in the headspace and of dissolved H₂O₂ in the solution as a function of the time of irradiation. Studies were conducted in H₂O with the pH adjusted to either pH 6 or 10.6 and either initially aerated or deaerated. The effect of the V_g:V_aq ratio was also investigated by adjusting the volume of H₂O in the test vials.

Figure 1 shows a comparison between the time dependence of the measured concentrations of H₂(g) in the headspace with those predicted using the H₂O (COMSOL) model for different pH values and degrees of aeration. There is reasonable agreement between measured and predicted concentrations with the difference being less than a factor of two and, in many cases, much lower. The model tends to predict lower values than those found experimentally, but it does correctly predict that the concentration of H₂ increases with increasing pH and is higher in aerated solution than in deaerated solution.

Yakabuskie et al. [17] show similar model–experiment comparisons for their FACSIMILE-based H₂O radiolysis model with a mass-transfer resistance treatment of the interface. Based on a visual comparison, the current COMSOL model predictions for pH 6 solutions are similar to those for the FACSIMILE model, although the latter gives better agreement to the experiment at pH 10.6.

It is also interesting to note that the model accurately represents the time dependence of the measured values. In contrast to the relatively rapid attainment of steady-state concentrations in the absence of a headspace (in less than 1 h at pH 6 and about 6 h at pH 10.6 [6]), steady-state is not reached within the experimental timeframe of 6 h when a headspace is present, with both experimental and predicted values continuing to increase with exposure time.

While these simulations were for a V_g:V_aq ratio of 1:1 with the assumption of equilibrium at the interface for the COMSOL model, Figure 2 and Figure 3 show similar experimental and modeling results for various V_g:V_aq ratios between 1:4 and 4:1. Agreement between model and experiment is excellent in the case of the gaseous H₂ concentrations, both in terms of the absolute values and in the observed and predicted time dependencies (Figure 2a and Figure 3a). Poorer agreement between model and experiment is found in the case of the dissolved H₂O₂ concentrations (Figure 2b and Figure 3b). The difference in the influence of headspace on [H₂(aq)] vs. [H₂O₂] is due to the fact that [H₂(aq)] is affected by the interfacial transfer of H₂ alone while [H₂O₂] is affected by the transfer of both O₂ and H₂.

There is a significant amount of scatter in the experimental H₂O₂ measurements, with no consistent trend with the V_g:V_aq. Similarly, apart from the ratio of 4:1, the model predicts relatively little variation in the dissolved [H₂O₂] on the V_g:V_aq ratio. Yakabuskie et al. [17] also compared their H₂O (FACSIMILE) model to the experimental data in Figure 2 and Figure 3 and predicted good agreement between measured and predicted H₂ concentrations at pH 6, although their agreement at pH 10.6 appears qualitatively to not be as good as that shown in Figure 3a. However, the H₂O (FACSIMILE) model predictions for H₂O₂ were superior to those found for the H₂O (COMSOL) model at both pH values.

Since the H₂O (COMSOL) model is based on a 1D geometry, the gas and solution phases are represented in the model by layers with a length given by the volume:cross-sectional area of the vial used in the experiments. In principle, therefore, the concentrations of the different radiolysis products may vary spatially as well as temporally, even though the entire system is uniformly irradiated. In reality, the times being simulated are long compared with the rate of diffusion of gaseous species so that the concentrations of O₂ and H₂ in the gas phase are found to be uniform. However, this is not the case for dissolved species and non-uniform concentration profiles are predicted in the solution layer. For example, Figure 4 shows the predicted [H₂O₂] profiles in the solution layer for one of the simulations shown in Figure 2b. Since H₂O₂ does not partition into the gas phase, there is inevitably a discontinuity at the gas–solution interface (located at a length of 0.03185 m), but the [H₂O₂] varies with distance from the interface, with the non-uniform distribution increasing with increasing simulation time. The mean concentration of H₂O₂ over the entire solution layer was used for the purposes of comparison with the experimental data.

A number of sensitivity analyses were conducted to investigate the discrepancy between the H₂O (COMSOL) model predictions and the experimentally measured H₂O₂ concentrations in Figure 2b and Figure 3b. Of the ten reactions in the H₂O radiolysis reaction scheme in which H₂O₂ is either a reactant or a product [6], the following reactions are known to be the main removal pathways for H₂O₂ and H₂ [16].

e_aq⁻ + H₂O₂ → OH⁻ + ^•OH         k₁ = 1.6 × 10¹⁰ dm³ mol⁻¹ s⁻¹

(1)

^•OH + H₂O₂ → OH⁻ + ^•OH      k₂ = 2.7 × 10⁷ dm³ mol⁻¹ s⁻¹

(2)

^•OH + H₂ → ^•H + H₂O             k₃ = 4.2 × 10⁷ dm³ mol⁻¹ s⁻¹

(3)

where k is the second-order rate constant for these reactions. The rate constant k₁ was selected for sensitivity analysis due to its larger value compared with k₂. One of the simulations with a gas:solution volume ratio of 1:1 was repeated with values of k₁ that were ½, 2 times, and 10 times the default value. Figure 5 shows the results of the sensitivity analyses for the case of initially aerated H₂O at pH 6. As would be expected, the predicted [H₂O₂] is inversely related to the value of k₁ although the dependence is not directly proportional to the value of the rate constant (Figure 5a). This sub-linear dependence indicates that while Reaction (1) plays a significant role in H₂O₂ decomposition, Reaction (2) and some of the other reactions in which peroxide is involved also play a role. Similar sensitivity analysis was conducted for [H₂] by varying values of k₁. It is worth noting that although H₂ is neither a reactant nor a product in Reaction (1), the concentration of gaseous H₂ also depends on the value of k₁ (Figure 5a), since the ^•OH, the product of Reaction (1) is involved in Reaction (3) that does consume H₂ and, therefore, impacts the [H₂(g)] in this highly coupled reaction scheme.

Based on this limited sensitivity analysis, a better fit between the H₂O (COMSOL) model and the experimental [H₂(g)] and [H₂O₂] is obtained with a value of k₁ that is one half of the default value. Although the values of the rate and equilibrium constants for many of the 39 reactions involved in the H₂O radiolysis scheme are known with some certainty, it is noteworthy that relatively minor variations in the value of just one of the rate constants can have such significant effects on the predicted concentrations. It is evident that the model predictions are less sensitive to uncertainty in the values of rate constants for reactions that are not the main removal pathways of certain species in the overall radiolysis scheme as shown in Figure 5b. However, this sensitivity of the model predictions to the values of key input parameters does suggest that caution should be exercised when using the results of such models as they may not be as accurate as sometimes represented. In addition, this sensitivity suggests that perfect agreement between model and experiment should not be expected when validating radiolysis models and that agreement within an order of magnitude or better may be all that can be reasonably expected.

4.2. Comparison of Models with and Without a Headspace

Although the experimental studies used here to validate the models were conducted in vials with a gas headspace, the repository near-field is expected to be fully saturated within a period of a few decades to a few hundred years following the closure of the repository [25]. If gaseous species cannot partition into the gas phase, then the concentrations of dissolved O₂ and/or H₂ will be higher which impact the rate of subsequent radiolysis reactions involving these species. To investigate the effect of the presence of the headspace, 0-dimensional (0D) and 1-dimensional (1D) simulations were carried out with the pure H₂O radiolysis model at pH 10.6. At pH ≥ 8, the production of volatile species H₂ and O₂ is considerable [16,25]; therefore, to better observe the effect of the headspace, pH 10.6 was chosen for the simulation.

Figure 6 shows the time dependence of the predicted concentrations of H₂O₂, O₂, and H₂ in initially deaerated H₂O with and without a headspace. The predicted concentrations of all the species are higher without the headspace. In the presence of the headspace, the partitioning of gaseous species (O₂ and H₂) from the aqueous phase to the gas phase results in the decrease in the concentrations of these species in the solution. While H₂O₂ is not a volatile species and remains in the solution, the interfacial transfer of O₂ and H₂ affects the concentration of H₂O₂. Any effect of the headspace on the [H₂O₂] is due to the impact of a gas phase on solution radical concentrations (Reaction 1 and 2) [17].

4.3. Comparison of Chloride Radiolysis Models

Chloride is ubiquitous in deep groundwaters in crystalline host rock in Canada [2,3] and the bentonite pore water in contact with the UFC will inevitably contain Cl⁻. Two H₂O-Cl⁻ radiolysis models have been validated against experimental measurements of the gaseous H₂ and O₂ and dissolved H₂O₂ in solutions with [Cl⁻] ranging from 0.001 mol/L to 2 mol/L [10]. At sufficiently high [Cl⁻], stable Cl⁻-containing radiolysis products may be formed, such as ClO₃⁻, but generally at concentrations that make it difficult to measure reliably.

Figure 7 shows the comparison between measured and predicted concentrations of dissolved H₂O₂ and gaseous H₂ for H₂O and for dilute Cl⁻ solutions. Predictions are shown for three different models: the Morco Cl⁻ reaction scheme implemented in COMSOL (Morco Cl⁻ (COMSOL)), the Jonsson Cl⁻ reaction scheme implemented in COMSOL (Jonsson Cl⁻ (COMSOL)), and the original FACSIMILE-based Cl⁻ model of Morco [10] (Morco Cl⁻ (FACSIMILE)). The Morco Cl⁻ (COMSOL) and Jonsson Cl⁻ (COMSOL) models are based on the H₂O model described in [6] with the addition of the Cl⁻ reactions described in Table A1 and Table A2, respectively. All three models give good agreement with the measured H₂O₂ concentrations in H₂O, 0.001 mol/L Cl⁻, and 0.01 mol/L Cl⁻ solutions. Not only is there good agreement between the absolute values, but the models also reproduce the measured time dependence of the concentrations very well. The choice of Cl⁻ reaction scheme has little influence on the predicted [H₂O₂] in these dilute Cl⁻ solutions and the curves for the two COMSOL models are virtually identical in all cases.

The two COMSOL models also give close agreement with the measured [H₂(g)], with the Morco FACSIMILE model predicting slightly higher concentrations than those measured. As in the case of the H₂O₂ concentrations, the two COMSOL models are not only in good agreement with the absolute values but also accurately reproduce the observed time dependence of the experimental values. It is interesting to note that, in the case of gaseous H₂, the selected Cl⁻ reaction scheme does have an influence on the predicted values and there is a slight difference between the predictions of the two COMSOL models at a [Cl⁻] of 0.01 mol/L (Figure 7f).

Since differences between the different Cl⁻ models are most likely to be observed at higher [Cl⁻], simulations were also performed for a Cl⁻ concentration of 2 mol/L (Figure 8). At this higher concentration, there is a clear difference between the predictions from the two COMSOL Cl⁻ models, as well as between the two Morco Cl⁻ models implemented using different software (COMSOL and FACSIMILE). The simpler reaction scheme of the Jonsson Cl⁻ model (Table A2) predicts lower concentrations of gaseous O₂ (Figure 8c), and gaseous H₂ than the more extensive reaction scheme of the Morco model (Table A1), but slightly higher concentrations of H₂O₂ (Figure 8a). In the case of H₂O₂, the two Cl⁻ models predict different time dependencies, with an early peak in [H₂O₂] for the Jonsson model as opposed to an early minimum for the Morco model, as observed experimentally.

In terms of the absolute agreement between measured and predicted concentrations, the best overall match of the three models is found for the Morco Cl⁻ (COMSOL) model. The Morco Cl⁻ (FACSIMILE) model gives the best agreement between predicted and measured gaseous O₂ concentrations. In light of the sensitivity of the predicted H₂O₂ and H₂(g) concentrations to the value of a single rate constant (Figure 5), the apparently better agreement between predicted and measured concentrations for the Morco Cl⁻ (COMSOL) model should not be over-interpreted. Nevertheless, this quantitative agreement does provide some basis on which to select a Cl⁻ radiolysis model for further development of the Step 2 and Step 3 CCM-RIC models.

It is also interesting that the two Morco Cl⁻ models produce different predicted concentrations despite being based on nominally the same reaction schemes and same rate constants. Part of the reason for these differences may result from how the two reaction schemes are implemented in the respective codes. As noted in Section 3.1, some of the reactions were re-written in order to make them compatible with the requirements of the COMSOL Reaction Engineering Module. Perhaps a more significant difference between the two models is the treatment of mass transfer at the gas–solution interface. The FACSIMILE model is based on the mass-transfer resistance approach of [10,16], whereas the COMSOL model is based on the assumption of equilibrium at the interface. This difference in approach also appears to result in differences between predicted H₂O₂ and H₂(g) concentrations in pure H₂O in the absence of Cl⁻ (cf. Figure 1, Figure 2 and Figure 3 and the corresponding predictions in [10,16]).

4.4. Effect of Chloride on the Production of Molecular Radiolysis Products

The presence of Cl⁻ is reported to increase the concentration of radiolytic oxidants, such as O₂ and H₂O₂ [10]. Since Cl⁻ ions will be present in the bentonite pore water in contact with the UFC, simulations were performed at various [Cl⁻] to determine the impact of the pore-water salinity on the production of stable (molecular) oxidizing (O₂ and H₂O₂) and reducing (H₂) species.

Figure 9 shows the results of simulations with the Morco Cl⁻ (COMSOL) model and [Cl⁻] between 10⁻⁴ mol/L and 0.1 mol/L. The concentrations of the various molecular radiolysis products are relatively insensitive to [Cl⁻] for concentrations of <0.01 mol/L, but increasing amounts of H₂O₂, gaseous O₂ and H₂ are formed at higher [Cl⁻] due to depletion of ^•OH via reaction with Cl⁻:

^•OH + Cl⁻ → ^•ClOH⁻           k₄ = 4.3 × 10⁹ dm³ mol⁻¹ s⁻¹

(4)

Thus, the presence of saline pore fluids in the repository will lead to increased production of H₂O₂, H₂, and O₂.

4.5. Concentrations of Radiolysis Products Under Repository Conditions

While the validation simulations described in the previous section only considered the concentrations of molecular species such as gaseous H₂ and O₂ and dissolved H₂O₂ (since these were the species measured experimentally), the models also predict the time-dependent concentrations of the entire range of radiolysis products.

Most of the validation simulations performed here have involved dose rates much higher than those to which the external surface of the container will be exposed. Experimental studies typically involve dose rates of the order of kGy/h in order to produce radiolysis products in measurable concentrations. In contrast, the container will be exposed to a maximum dose rate of ~1 Gy/h, which will diminish to <0.1–1 mGy/h in the long term [5]. The resulting concentrations of molecular and radical radiolysis products will be much lower than those reported above.

Figure 10 shows the predicted concentrations of various molecular and radical radiolysis products based on the time-dependent dose rate for a copper-coated UFC. As expected, the concentrations of the various species are much lower than those considered above for simulations at much higher dose rates. Even the most important species are only present at concentrations of the order of 10⁻⁶–10⁻⁹ mol/L. The steady-state concentration of many molecular and radical species is proportional to the square root of the dose rate [16]. Thus, as the dose rate decreases by four orders of magnitude at times longer than 1000 years, the predicted concentrations of the various radiolysis products only decrease by approximately two orders of magnitude. Consistent with previous studies [16,17], the simulation results also show that the concentrations of molecular species are higher than those of radical radiolysis products.

5. Conclusions

In this paper, we described the validation of various radiolysis models against experimental measurements of the concentrations of dissolved and gaseous radiolysis products. In general, the model accurately represents the time dependence of the measured values. The sensitivity analysis conducted by varying the rate constants showcases the complexity of the radiolysis modeling and suggests that perfect agreement between model and experiment should not be expected when validating radiolysis models and that agreement within an order of magnitude or better may be all that can be reasonably expected. In addition to validation and verification steps for the water radiolysis model, progress has been made in understanding the effect of chloride on the time-dependent concentrations of water radiolysis products as a function of dose rate. In this study, two H₂O-Cl⁻ radiolysis models have also been compared against experimental measurements of the gaseous H₂ and O₂ and dissolved H₂O₂ in solutions with [Cl⁻] ranging from 0.001 mol/L to 2 mol/L. The simulation results showed the choice of Cl⁻ reaction scheme has little influence on the predicted [H₂O₂] in dilute Cl⁻ solutions. As the Cl⁻ concentration increases, the concentration of H₂O₂, H₂, and O₂ increases due to depletion of OH via reaction with Cl⁻.

These simulations were performed in a so-called “uncoupled” fashion without the presence of a corroding copper interface. It is implicitly assumed, therefore, that the consumption of radiolysis products (principally oxidizing species) on the copper surface does not influence the predicted concentrations. This may or may not be a valid assumption, but a more rigorous approach to the prediction of the effect of irradiation on corrosion is to couple the interfacial reactions with the homogenous radiolysis reactions. This is the approach being used for the Step 2 and Step 3 CCM-RIC which will be the subject of future publications.