Stress Corrosion Cracking in Amorphous Phase Separated Oxide Glasses: A Holistic Review of Their Structures, Physical, Mechanical and Fracture Properties
Abstract
1. Introduction
2. APS Glasses: Their Uses in Industry
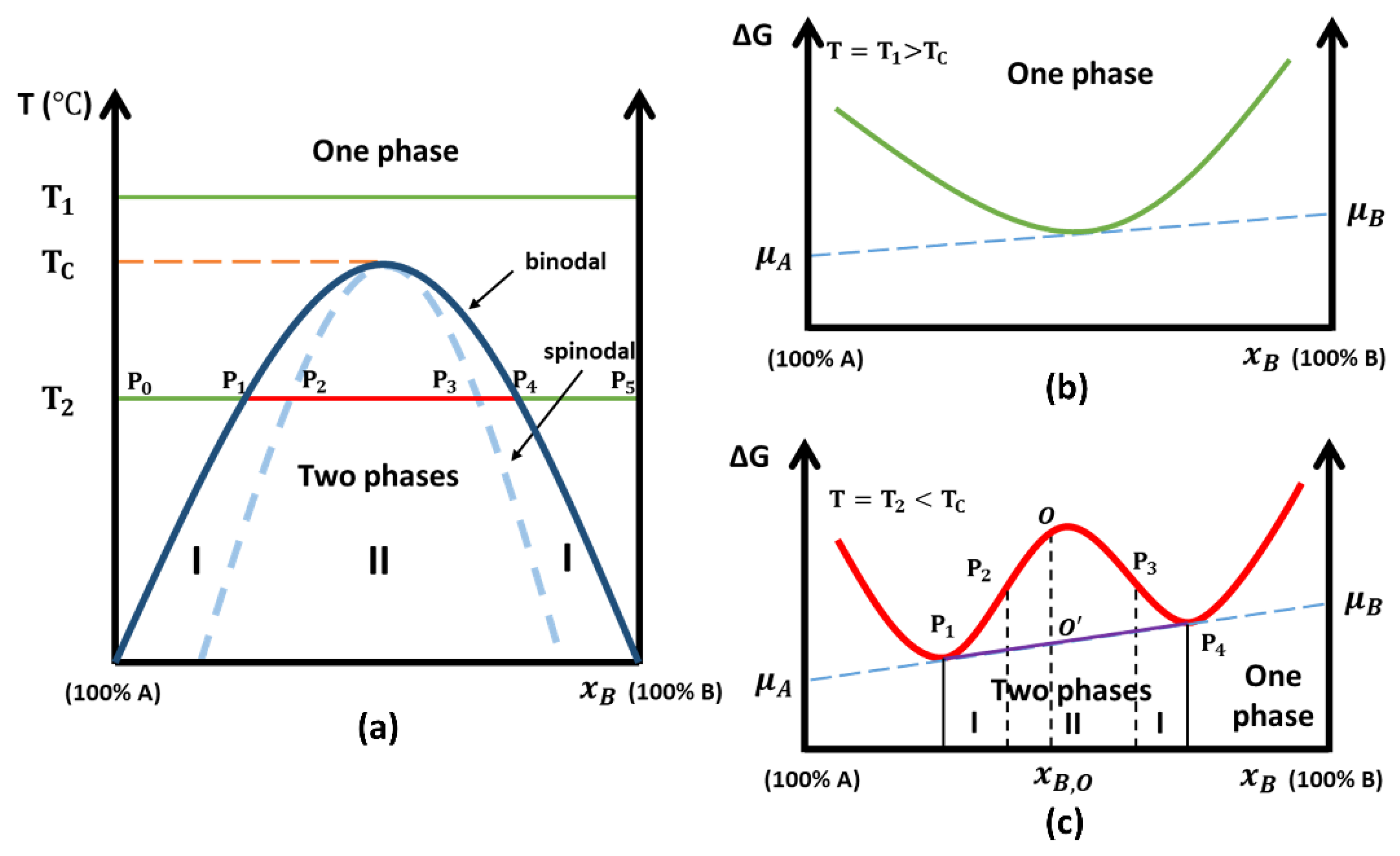
3. Thermodynamic Interpretations of Phase Separation
3.1. Binary Amorphous Phase Separation: A Two-Atom Theoretical Viewpoint
3.2. Beyond the Two-Atom Approximation
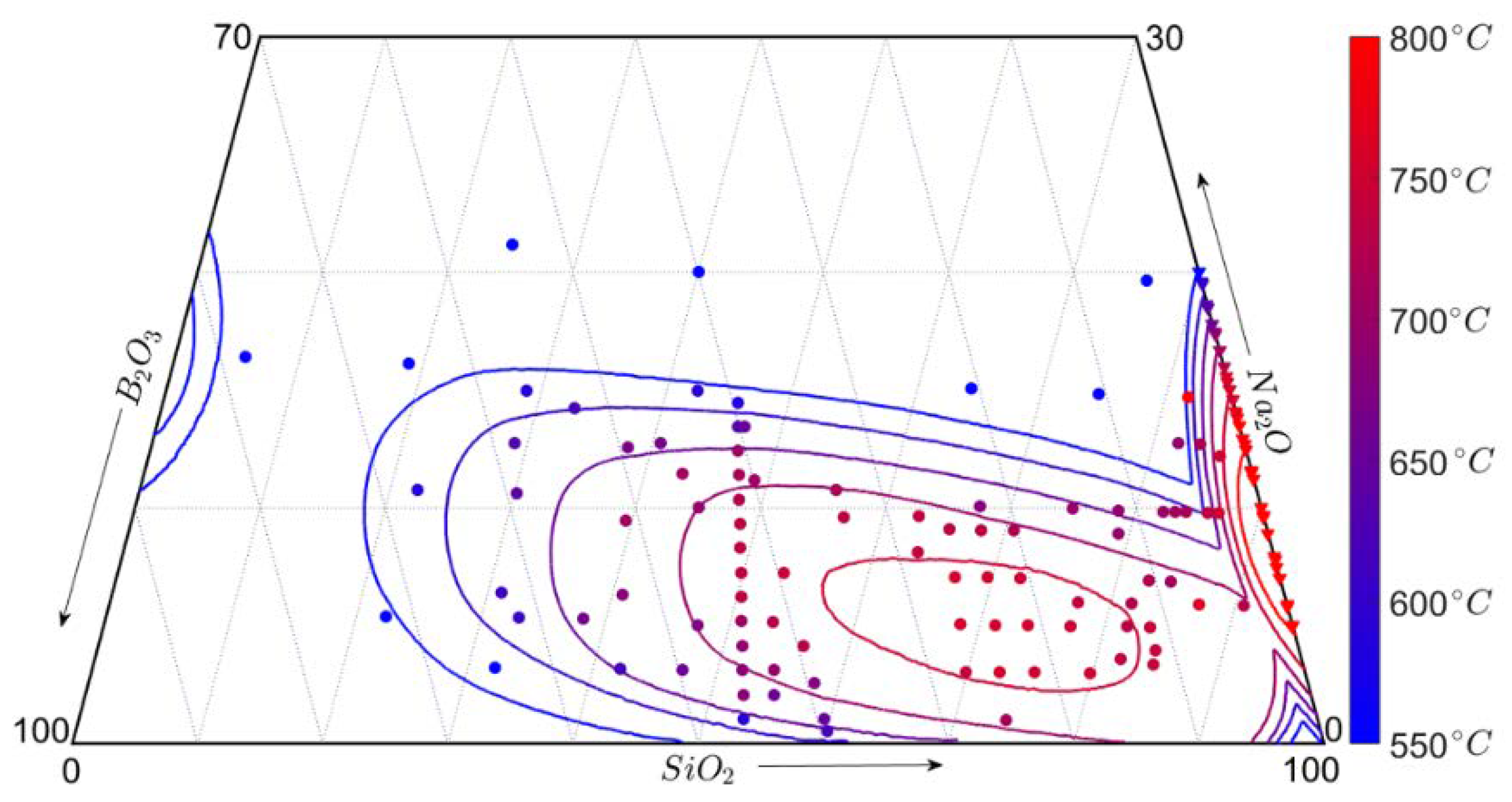
3.3. Phase Diagram of the SBN System
4. The Medium-Range Structure of APS-SBN Glasses
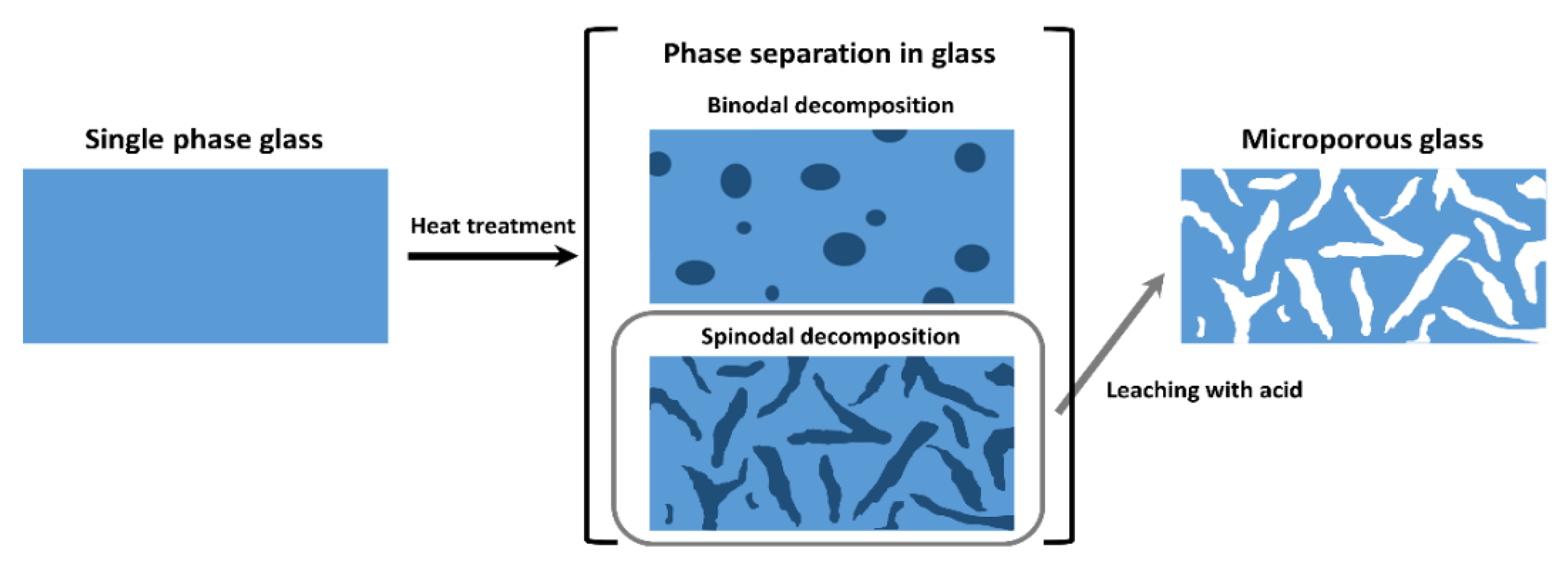
4.1. Sub-µm Amorphous Phase Separation in Glasses
4.1.1. Binodal Decomposition in SBN Glasses
4.1.2. Spinodal Decomposition in SBN Glasses
4.2. Secondary Phase Separation
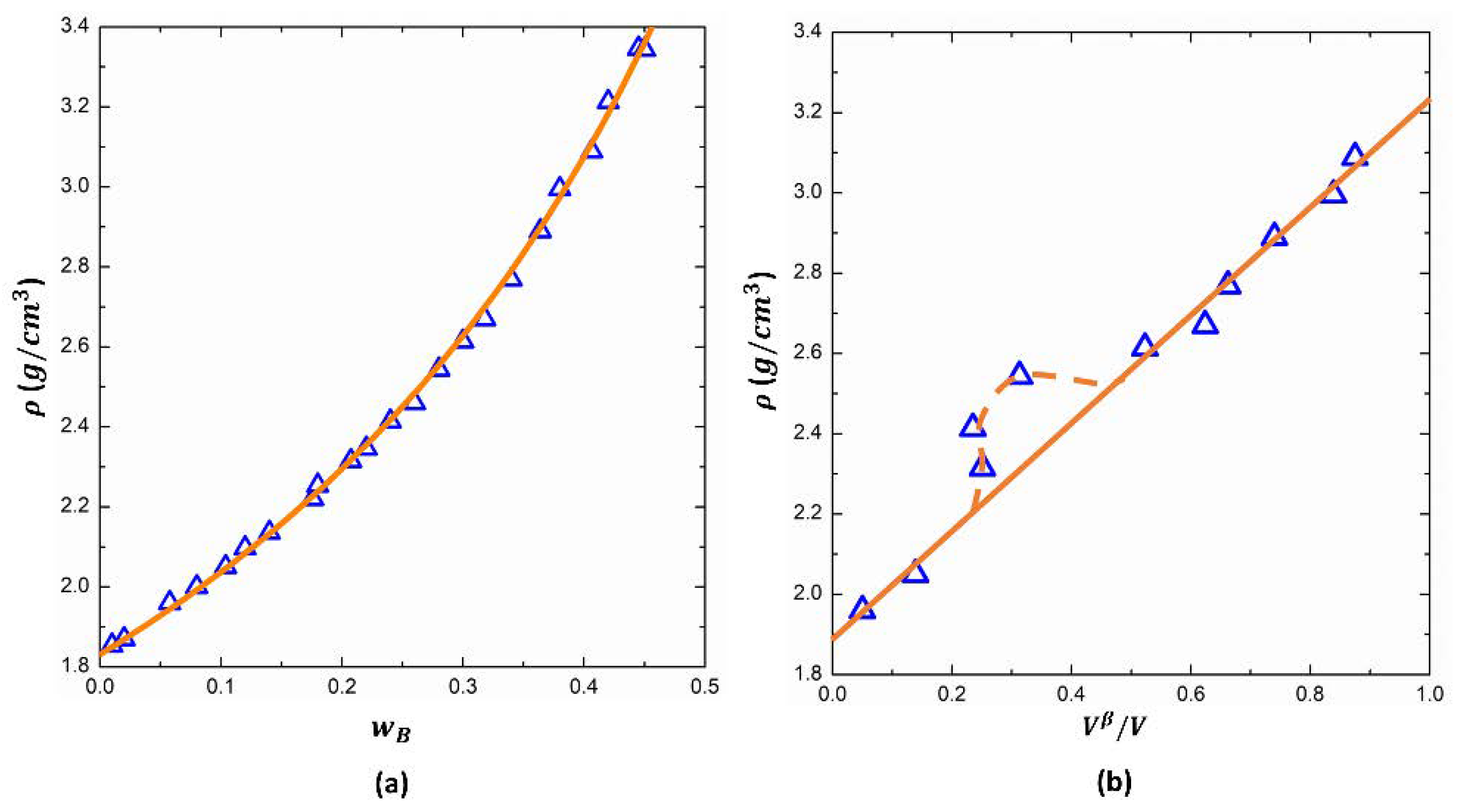
5. Physical Properties of APS Glasses
6. Mechanical/Fracture Properties of APS Glasses
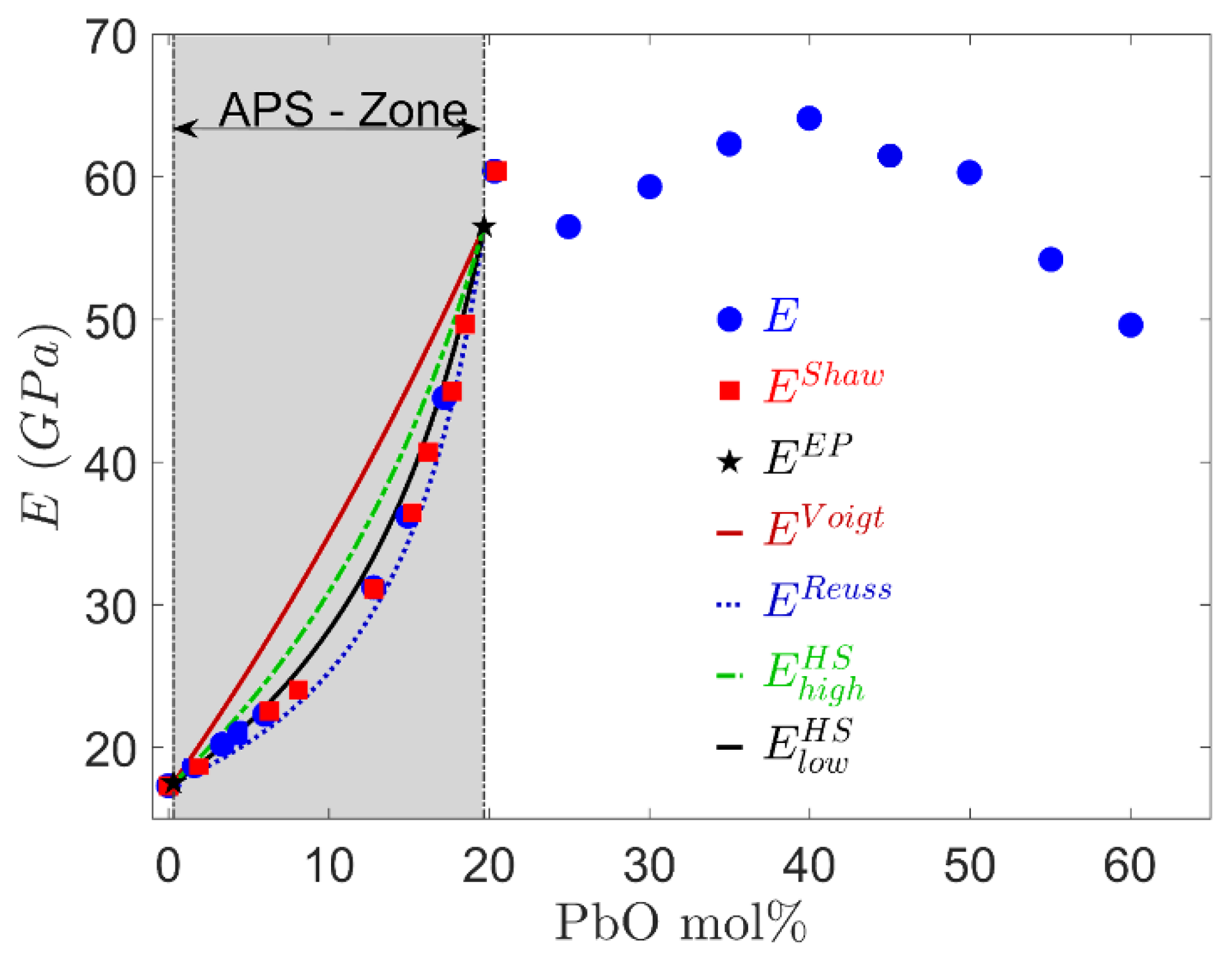
6.1. Young’s Modulus in Two-Phase Glasses
6.2. Fracture Properties of APS Glasses
6.2.1. Dynamic Fracture in Multi-Phase Microstructure
6.2.2. Effects of APS Structure on Fracture Toughness
- Fracture Toughness from Indentation Tests
- b.
- Fracture Toughness from Three-Point or Four-Point Bending Tests
- c.
- Comparison between Results Obtained by Indentation and Three-Point Bending Tests
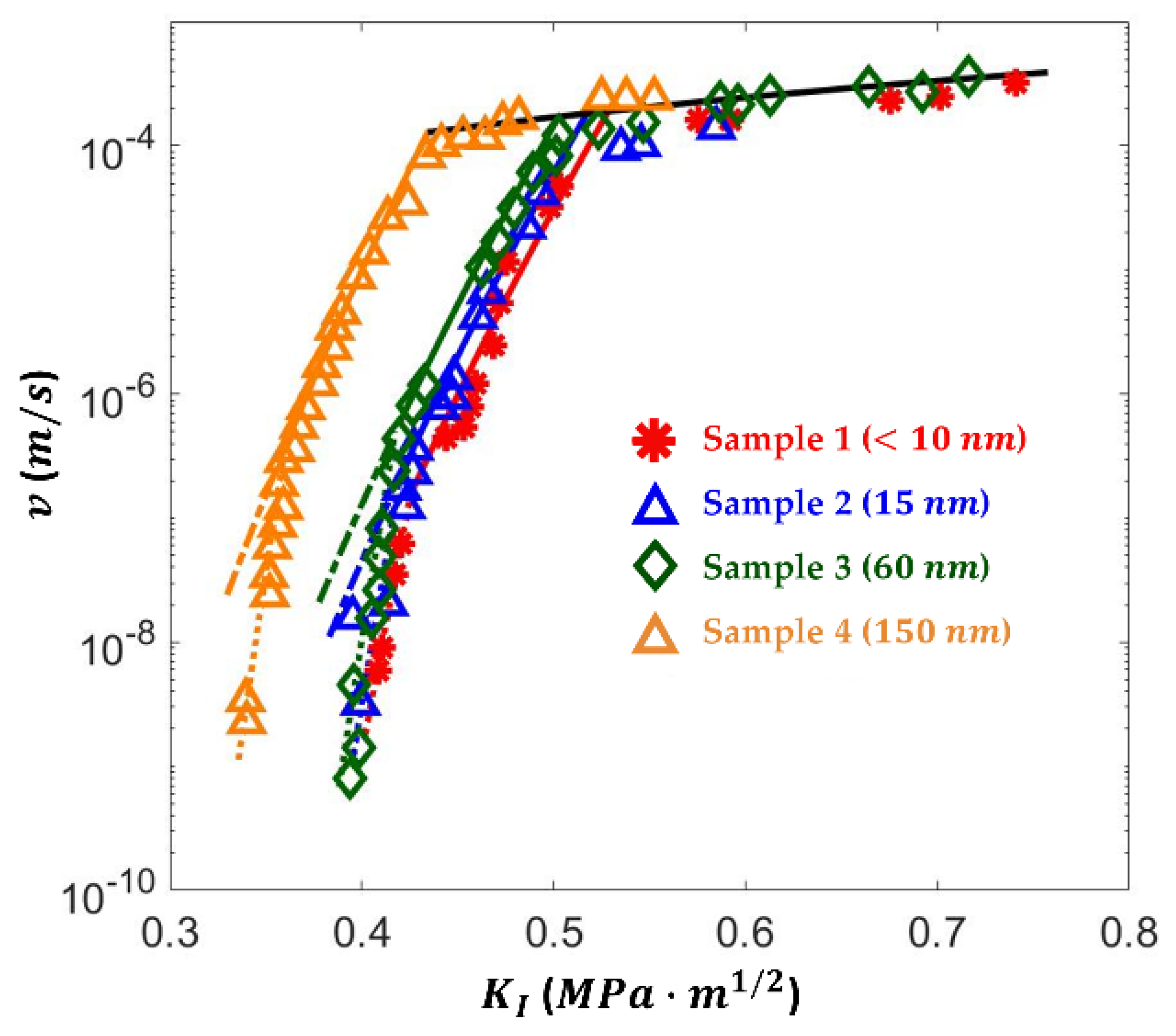
6.2.3. Sub-Critical Cracking of APS Glasses
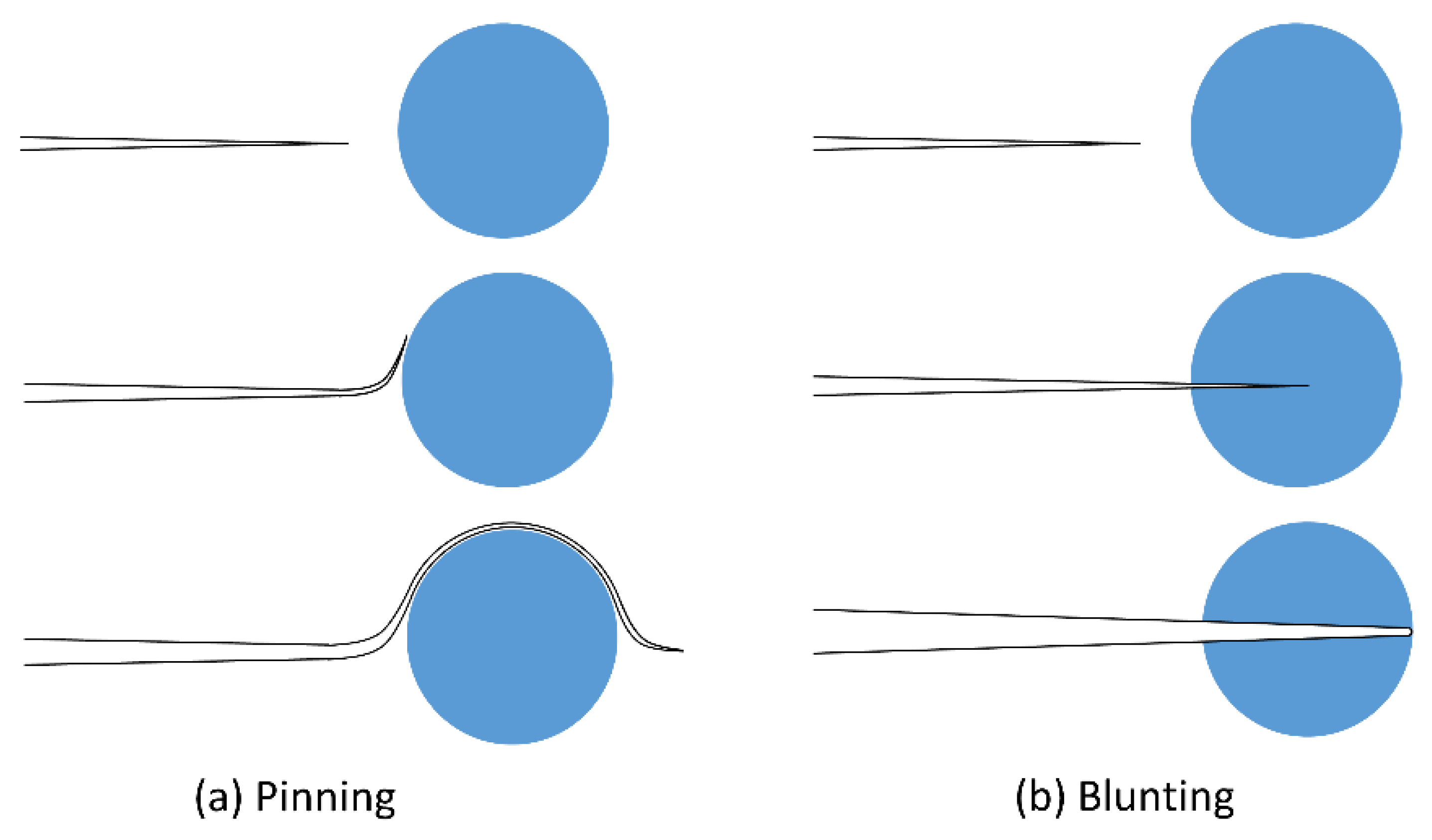
- Crack Front Interaction with Secondary Particulate Phase
- b.
- Effects of APS Structure on SCC Curve
6.2.4. Fracture Surface Toughness Investigation
7. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Hashin and Shtrikman Model for Predicting the Range of Moduli for Two-Phase Materials
Appendix B. Table with Mechanical/Fracture Properties for - Glass System
| References | ||||||
|---|---|---|---|---|---|---|
| 3-Points Bending | ||||||
| 0 | - | - | 17.3 | 24.5 | [141,143] | |
| APS glasses | Non-APS glasses | |||||
| 0.31 | 0.947 | 17.5 | 23.9 | [141] | ||
| 1.62 | 0.05 | - | 18.7 | 21.4 | [141,143] | |
| 3.35 | 0.13 | - | 20.2 | 16.9 | [141,143] | |
| 4.45 | 0.18 | 21.0 | 15.2 | [141,143] | ||
| 6.01 | 0.25 | 22.3 | 14.5 | [141,143] | ||
| -rich spherical particles in-rich matrix | -rich spherical particles in-rich matrix | |||||
| 12.80 | 0.59 | 31.2 | 37.6 | [141,143] | ||
| 14.38 | - | - | 34.5 | - | [141,143] | |
| 14.93 | 0.71 | 36.2 | 24.4 | [141,143] | ||
| 17.22 | 0.84 | 44.5 | 18.4 | [141,143] | ||
| 19.68 | 0.960 | 56.5 | 7.56 | [141] | ||
| APS glasses | Non-APS glasses | |||||
| 20.33 | - | 60.4 | 6.30 | [142] | ||
| 25 | - | - | 56.5 | 3.94 | [142] | |
| 30 | - | - | 59.3 | 3.62 | [142] | |
| 35 | - | - | 62.3 | 3.66 | [142] | |
| 40 | - | - | 64.1 | 3.46 | [142] | |
| 45 | - | - | 61.4 | 3.38 | [142] | |
| 50 | - | - | 60.3 | 2.82 | [142] | |
| 55 | - | - | 54.2 | 2.83 | [142] | |
| 60 | - | - | 49.6 | 2.28 | [142] | |
Appendix C. Nomenclature
| Symbol | Meaning | Equation | |
| Number of moles of component A | |||
| Number of moles of component B | |||
| Mole fraction of component A | (A4) | ||
| Mole fraction of component B | (A5) | ||
| Chemical potential of component A | |||
| Chemical potential of component B | |||
| Chemical potential of component A in phase | |||
| Chemical potential of component A in phase | |||
| Chemical potential of component B in phase | |||
| Chemical potential of component B in phase | |||
| Mass of component A | (A6) | ||
| Mass of component B | (A7) | ||
| Mass of phase | (A8) | ||
| Mass of phase | (A9) | ||
| Mass system assuming conservation of mass | (A10) | ||
| Mass of component B in phase | (A11) | ||
| Mass of component A in phase | (A12) | ||
| Mass of component B in phase | (A13) | ||
| Mass of component A in phase | (A14) | ||
| Mass fraction of component A in phase | (A15) | ||
| Mass fraction of component A in phase | (A16) | ||
| Mass fraction of component B in phase | (A17) | ||
| Mass fraction of component B in phase | (A18) | ||
| Mass fraction in phase | (A19) | ||
| Mass fraction in phase | (A20) | ||
| Mass fraction of component A | (A21) | ||
| Mass fraction of component B | (A22) | ||
| Fracture surface energy for matrix | |||
| Fracture surface energy for particles | |||
| Coefficient of thermal expansion for matrix | |||
| Coefficient of thermal expansion for particles | |||
| Shear modulus for matrix |
References
- Charleston, R.J.; Fisher, J.E.; Michael, J. Masterpieces of Glass: A World History from the Corning Museum of Glass; HN Abrams: New York, NY, USA, 1990; ISBN 0810924641. [Google Scholar]
- Barlet, M. Evolution of Mechanical Properties of Silicate Glasses: Impact of the Chemical Composition and Effects of Irradiation. Ph.D. Thesis, École Polytechnique, Palaiseau, France, 2014. [Google Scholar]
- Barlet, M.; Delaye, J.-M.; Boizot, B.; Caraballo, R.; Peuget, S.; Rountree, C.L. From network polymerization to stress corrosion cracking in sodium-borosilicate glasses: Effect of the chemical composition. J. Non-Cryst. Solids 2016, 450, 174–184. [Google Scholar] [CrossRef]
- Rountree, C.L. Recent progress to understand stress corrosion cracking in sodium borosilicate glasses: Linking the chemical composition to structural, physical and fracture properties. J. Phys. D Appl. Phys. 2017, 50, 343002. [Google Scholar] [CrossRef]
- Koike, A.; Tomozawa, M.; Ito, S. Sub-critical crack growth rate of soda-lime-silicate glass and less brittle glass as a function of fictive temperature. J. Non-Cryst. Solids 2007, 353, 2675–2680. [Google Scholar] [CrossRef]
- Koike, A.; Tomozawa, M. Fictive temperature dependence of subcritical crack growth rate of normal glass and anomalous glass. J. Non-Cryst. Solids 2006, 352, 5522–5530. [Google Scholar] [CrossRef]
- Ciccotti, M. Stress-corrosion mechanisms in silicate glasses. J. Phys. D Appl. Phys. 2009, 42, 214006. [Google Scholar] [CrossRef]
- Wiederhorn, S.M. Influence of water vapor on crack propagation in soda-lime glass. J. Am. Ceram. Soc. 1967, 50, 407–414. [Google Scholar] [CrossRef]
- Wiederhorn, S.M.; Freiman, S.W.; Fuller, E.R.; Simmons, C.J. Effects of water and other dielectrics on crack-growth. J. Mater. Sci. 1982, 17, 3460–3478. [Google Scholar] [CrossRef]
- Wiederhorn, S.M.; Johnson, H.; Diness, A.M.; Heuer, A.H. Fracture of glass in vacuum. J. Am. Ceram. Soc. 1974, 57, 336–341. [Google Scholar] [CrossRef]
- Célarié, F. Dynamique de Fissuration a Basse Vitesse des Matériaux Vitreux. Ph.D. Thesis, Université Montpellier II-Sciences et Techniques du Languedoc, Montpellier, France, 2004. [Google Scholar]
- Barlet, M.; Kerrache, A.; Delaye, J.-M.; Rountree, C.L. SiO2-Na2O-B2O3 density: A comparison of experiments, simulations, and theory. J. Non-Cryst. Solids 2013, 382, 32–44. [Google Scholar] [CrossRef]
- Bray, P.J.; Geissberger, A.E.; Bucholtz, F.; Harris, I.A. Glass structure. J. Non-Cryst. Solids 1982, 52, 45–66. [Google Scholar] [CrossRef]
- Rouxel, T. Elastic properties and short-to medium-range order in glasses. J. Am. Ceram. Soc. 2007, 10, 3019–3039. [Google Scholar] [CrossRef]
- Soules, T.F. A molecular dynamic calculation of the structure of sodium silicate glasses. J. Chem. Phys. 1979, 71, 4570–4578. [Google Scholar] [CrossRef]
- Zachariasen, W.H. The atomic arrangement in glass. J. Am. Chem. Soc. 1932, 54, 3841–3851. [Google Scholar] [CrossRef]
- Grandjean, A.; Malki, M.; Simonnet, C.; Manara, D.; Penelon, B. Correlation between electrical conductivity, viscosity, and structure in borosilicate glass-forming melts. Phys. Rev. B 2007, 75, 054112. [Google Scholar] [CrossRef]
- Ritland, H.N. Relation between refractive index and density of a glass at constant temperature. J. Am. Ceram. Soc. 1955, 38, 86–88. [Google Scholar] [CrossRef]
- Barlet, M.; Delaye, J.-M.; Gennisson, M.; Caraballo, R.; Boizot, B.; Bonamy, B.; Rountree, C.L. Influence of electronic irradiation on failure and hardness properties of pure silica glasses. Procedia Mater. Sci. 2014, 7, 286–293. [Google Scholar] [CrossRef]
- Barlet, M.; Delaye, J.-M.; Charpentier, T.; Gennisson, M.; Bonamy, D.; Rouxel, T.; Rountree, C.L. Hardness and toughness of sodium borosilicate glasses via Vicker’s indentations. J. Non-Cryst. Solids 2015, 417–418, 66–79. [Google Scholar] [CrossRef]
- Makishima, A.; Mackenzie, J.D. Calculation of bulk modulus, shear modulus and Poisson’s ratio of glass. J. Non-Cryst. Solids 1975, 17, 147–157. [Google Scholar] [CrossRef]
- Overend, M.; Parke, G.A.; Buhagiar, D. Predicting failure in glass—A general crack growth model. J. Struct. Eng. 2007, 133, 1146–1155. [Google Scholar] [CrossRef]
- Beason, W.L.; Morgan, J.R. Glass failure prediction model. J. Struct. Eng. 1984, 110, 197–212. [Google Scholar] [CrossRef]
- Rouxel, T.; Yoshida, S. The fracture toughness of inorganic glasses. J. Am. Chem. Soc. 2017, 100, 4374–4396. [Google Scholar] [CrossRef]
- Sih, G.C. Fracture toughness concept. In Properties Related to Fracture Toughness; ASTM International: West Conshohocken, PA, USA, 1976. [Google Scholar]
- Calabrese, L.; Proverbio, E. A review on the applications of acoustic emission technique in the study of stress corrosion cracking. Corros. Mater. Degrad. 2021, 2, 1–30. [Google Scholar] [CrossRef]
- Raja, V.S.; Shoji, T. Stress Corrosion Cracking: Theory and Practice; Elsevier: Amsterdam, The Netherlands, 2011; ISBN 978-1-84569-673-3. [Google Scholar]
- Sih, G.C. Mechanics of subcritical crack growth. In Fracture Mechanics Technology Applied to Material Evaluation and Structure Design; Sih, G.C., Ryan, N.E., Jones, R., Eds.; Springer: Dordrecht, The Netherlands, 1983; pp. 3–18. ISBN 978-94-009-6914-8. [Google Scholar]
- Wiederhorn, S.M.; Bolz, L.H. Stress corrosion and static fatigue of glass. J. Am. Ceram. Soc. 1970, 53, 543–548. [Google Scholar] [CrossRef]
- Bernstein, J. Polymorphism in Molecular Crystals 2e; International Union of Crystal: Chester, England, 2020; Volume 30, ISBN 9780199655441. [Google Scholar]
- Findlay, A. The Phase Rule and Its Applications; Longmans, Green: Harlow, UK, 1904. [Google Scholar]
- Glasstone, S. Text-Book of Physical Chemistry; Van Nostrand Co.: New York, NY, USA, 1940. [Google Scholar]
- Möbus, G.; Ojovan, M.; Cook, S.; Tsai, J.; Yang, G. Nano-scale quasi-melting of alkali-borosilicate glasses under electron irradiation. J. Nucl. Mater. 2010, 396, 264–271. [Google Scholar] [CrossRef]
- Cahn, J.W. Phase separation by spinodal decomposition in isotropic systems. J. Chem. Phys. 1965, 42, 93–99. [Google Scholar] [CrossRef]
- James, P.F. Liquid-phase separation in glass-forming systems. J. Mater. Sci. 1975, 10, 1802–1825. [Google Scholar] [CrossRef]
- Charles, R.J. Metastable immiscibility in BaO-Li2O-SiO2 system. Phys. Chem. Glasses 1967, 8, 185. [Google Scholar]
- Kim, S.S.; Sanders, T.H., Jr. Thermodynamic modeling of phase diagrams in binary alkali silicate systems. J. Am. Ceram. Soc. 1991, 74, 1833–1840. [Google Scholar] [CrossRef]
- Mazurin, O.V.; Porai-Koshits, E.A. Phase Separation in Glass; Elsevier: Amsterdam, The Netherlands, 1984; ISBN 9780080983653. [Google Scholar]
- Ghanbari-Ahari, K.; Cameron, A.M. Phase diagram of Na2O-B2O3-SiO2 system. J. Am. Ceram. Soc. 1993, 76, 2017–2022. [Google Scholar] [CrossRef]
- Kim, S.S.; Sanders, T.H., Jr. Calculation of subliquidus miscibility gaps in the Li2O-B2O3-SiO2 system. Ceram. Int. 2000, 26, 769–778. [Google Scholar] [CrossRef]
- Polyakova, I.G. Alkali borosilicate systems: Phase diagrams and properties of glasses. Phys. Chem. Glasses 2000, 41, 247–258. [Google Scholar]
- Bouttes, D. Micro-Tomographie d’un Borosilicate de Baryum Démixé: Du Mûrissement à la Fragmentation. Ph.D. Thesis, ParisTech, Paris, France, 2014. [Google Scholar]
- Bouttes, D.; Gouillart, E.; Boller, E.; Dalmas, D.; Vandembroucq, D. Fragmentation and limits to dynamical scaling in viscous coarsening: An interrupted in situ X-ray tomographic study. Phys. Rev. Lett. 2014, 112, 245701. [Google Scholar] [CrossRef] [PubMed]
- Bouttes, D.; Lambert, O.; Claireaux, C.; Woelffel, W.; Dalmas, D.; Gouillart, E.; Lhuissier, P.; Salvo, L.; Boller, E.; Vandembroucq, D. Hydrodynamic coarsening in phase-separated silicate melts. Acta Mater. 2015, 92, 233–242. [Google Scholar] [CrossRef]
- Bouttes, D.; Gouillart, E.; Vandembroucq, D. Topological symmetry breaking in viscous coarsening. Phys. Rev. Lett. 2016, 117, 145702. [Google Scholar] [CrossRef]
- Mazurin, O.V.; Roskova, G.P.; Kluyev, V.P. Properties of phase-separated soda-silica glasses as a means of investigation of their structure. Discuss. Faraday Soc. 1970, 50, 191–199. [Google Scholar] [CrossRef]
- Oliveira, J.M.; Correia, R.N.; Fernandes, M.H. Effect of SiO2 on amorphous phase separation of CaO-P2O5-SiO2-MgO glasses. J. Non-Cryst. Solids 2000, 273, 59–63. [Google Scholar] [CrossRef]
- Gueguen, Y.; Houizot, P.; Célarié, F.; Chen, M.; Hirata, A.; Tan, Y.; Allix, M.; Chenu, S.; Roux-Langlois, C.; Rouxel, T. Structure and viscosity of phase-separated BaO-SiO2 glasses. J. Am. Ceram. Soc. 2017, 100, 1982–1993. [Google Scholar] [CrossRef]
- Pye, L.D.; Ploetz, L.; Manfredo, L. Physical properties of phase separated soda-silica glasses. J. Non-Cryst. Solids 1974, 14, 310–321. [Google Scholar] [CrossRef]
- Hammel, J.; Allersma, T. Method of Making Thermally Stable and Crush Resistant Microporous Glass Catalyst Supports. U.S. Patent 3843341A, 22 October 1974. [Google Scholar]
- Enke, D.; Janowski, F.; Schwieger, W. Porous glasses in the 21st century—A short review. Microporous Mesoporous Mater. 2003, 60, 19–30. [Google Scholar] [CrossRef]
- Ramsden, A.H.; James, P.F. The effects of amorphous phase separation on crystal nucleation kinetics in BaO-SiO2 glasses. J. Mater. Sci. 1984, 19, 1406–1419. [Google Scholar] [CrossRef]
- Suzuki, M.; Tanaka, T. Materials design for the fabrication of porous glass using phase separation in multi-component borosilicate glass. ISIJ Int. 2008, 48, 1524–1532. [Google Scholar] [CrossRef][Green Version]
- Deubener, J.; Allix, M.; Davis, M.J.; Duran, A.; Höche, T.; Honma, T.; Komatsu, T.; Krüger, S.; Mitra, I.; Müller, R.; et al. Updated definition of glass-ceramics. J. Non-Cryst. Solids 2018, 501, 3–10. [Google Scholar] [CrossRef]
- Zhong, J.; Chen, D.; Peng, Y.; Lu, Y.; Chen, X.; Li, X.; Ji, Z. A review on nanostructured glass ceramics for promising application in optical thermometry. J. Alloys Compd. 2018, 763, 34–48. [Google Scholar] [CrossRef]
- Fafet, G.P.; Fredholm, A.M. Glass-Ceramic Cooking Plate for Gas Cookers, and Method for Making Same. U.S. Patent 5931152A, 3 August 1999. [Google Scholar]
- Höland, W.; Ritzberger, C.; Rheinberger, V.; Apel, E. Dental Glass Ceramics. U.S. Patent 7846857B2, 7 December 2010. [Google Scholar]
- Höland, W.; Rheinberger, V.; Schweiger, M. Control of nucleation in glass ceramics. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2003, 361, 575–589. [Google Scholar] [CrossRef]
- Tomozawa, M. Liquid-phase separation and crystal nucleation in Li2O-SiO2 glasses. Phys. Chem. Glasses 1972, 13, 161. [Google Scholar]
- Kleebusch, E.; Patzig, C.; Krause, M.; Hu, Y.; Höche, T.; Rüssel, C. The effect of TiO2 on nucleation and crystallization of a Li2O-Al2O3-SiO2 glass investigated by XANES and STEM. Sci. Rep. 2018, 8, 2929. [Google Scholar] [CrossRef] [PubMed]
- Uhlmann, D.R.; Goldstein, M.; Scholes, S.; Barry, T.I.; Zarzycki, J.; Tomozawa, M.; MacCrone, R.K.; Porai-Koshits, E.A.; Andreev, N.S.; Mazurin, O.V.; et al. General discussion. Discuss. Faraday Soc. 1970, 50, 222–240. [Google Scholar] [CrossRef]
- Gangopadhyay, A.K.; Croat, T.K.; Kelton, K.F. The effect of phase separation on subsequent crystallization in Al88Gd6La2Ni4. Acta Mater. 2000, 48, 4035–4043. [Google Scholar] [CrossRef]
- Höche, T.; Mäder, M.; Bhattacharyya, S.; Henderson, G.S.; Gemming, T.; Wurth, R.; Rüssel, C.; Avramov, I. ZrTiO4 crystallisation in nanosized liquid–liquid phase-separation droplets in glass–a quantitative XANES study. CrystEngComm 2011, 13, 2550–2556. [Google Scholar] [CrossRef]
- Pannhorst, W. Glass ceramics: State-of-the-art. J. Non-Cryst. Solids 1997, 219, 198–204. [Google Scholar] [CrossRef]
- Suzuki, M.; Tanaka, T. Thermodynamic prediction of spinodal decomposition in multi-component silicate glass for design of functional porous glass materials. High Temp. Mater. Processes 2012, 31, 323–328. [Google Scholar] [CrossRef]
- Koketsu, N.; Zhang, Z.; Kotani, Y.; Sugiyama, A.; Takashima, K. Method for Manufacturing Porous Glass, and Method for Manufacturing Optical Element. U.S. Patent 9162920B2, 20 October 2015. [Google Scholar]
- Hosono, H.; Abe, Y. Silver ion selective porous lithium titanium phosphate glass-ceramics cation exchanger and its application to bacteriostatic materials. Mater. Res. Bull. 1994, 29, 1157–1162. [Google Scholar] [CrossRef]
- Kuraoka, K.; Chujo, Y.; Yazawa, T. Hydrocarbon separation via porous glass membranes surface-modified using organosilane compounds. J. Membr. Sci. 2001, 182, 139–149. [Google Scholar] [CrossRef]
- Safronsky, E.D.; Roizin, Y.O.; Rysiakiewicz-Pasek, E. Application of porous glasses for humidity control. Opt. Mater. 1996, 5, 217–220. [Google Scholar] [CrossRef]
- Hermann, M.; Gottschalk, U. Large-scale immobilization of antibodies on porous glass carriers. Bioforum 2000, 3, 172. [Google Scholar]
- Hoffmann, M.; Kreft, S.; Georgi, G.; Fulda, G.; Pohl, M.-M.; Seeburg, D.; Berger-Karin, C.; Kondratenko, E.V.; Wohlrab, S. Improved catalytic methane combustion of Pd/CeO2 catalysts via porous glass integration. Appl. Catal. B 2015, 179, 313–320. [Google Scholar] [CrossRef]
- Dong, W.-Y.; Long, Y.-C. Preparation and characterization of preferentially oriented continuous MFI-type zeolite membranes from porous glass. Microporous Mesoporous Mater. 2004, 76, 9–15. [Google Scholar] [CrossRef]
- Lopez-Orozco, S.; Inayat, A.; Schwab, A.; Selvam, T.; Schwieger, W. Zeolitic materials with hierarchical porous structures. Adv. Mater. 2011, 23, 2602–2615. [Google Scholar] [CrossRef]
- Cui, Z.; Huang, Y.; Liu, H. Predicting the mechanical properties of brittle porous materials with various porosity and pore sizes. J. Mech. Behav. Biomed. Mater. 2017, 71, 10–22. [Google Scholar] [CrossRef]
- Takamori, T.; Tomozawa, M. HCl leaching rate and microstructure of phase-separated borosilicate glasses. J. Am. Ceram. Soc. 1978, 61, 509–512. [Google Scholar] [CrossRef]
- Marshall, W.P.; Hammel, J.J.; Barch, H.W.; Hegedus, R.D.; Robertson, W.J. Silica-Rich Porous Substrates with Reduced Tendencies for Breaking or Cracking. U.S. Patent 4933307A, 12 June 1990. [Google Scholar]
- Burnett, D.G.; Douglas, R.W. Liquid-liquid phase separation in soda-lime-silica system. Phys. Chem. Glasses 1970, 11, 125. [Google Scholar]
- Cottrell, A.H. Theoretical Structural Metallurgy; Edward Arnold: London, UK, 1960. [Google Scholar]
- Campbell, F.C. Phase Diagrams: Understanding the Basics; ASM International: Almere, The Netherlands, 2012; ISBN 9781615039869. [Google Scholar]
- Varshneya, A.K. Fundamentals of Inorganic Glasses; Elsevier: Amsterdam, The Netherlands, 2013; ISBN 9780128162262. [Google Scholar]
- Haller, W.; Blackburn, D.H.; Simmons, J.H. Miscibility gaps in alkali-silicate binaries—Data and thermodynamic interpretation. J. Am. Ceram. Soc. 1974, 57, 120–126. [Google Scholar] [CrossRef]
- Mazurin, O.V. Physical properties of phase separated glasses. J. Non-Cryst. Solids 1987, 95, 71–82. [Google Scholar] [CrossRef]
- Haller, W.; BlackBurn, D.H.; Wagstaff, F.E.; Charles, R.J. Metastable immiscibility surface in the system Na2O-B2O3-SiO2. J. Am. Ceram. Soc. 1970, 53, 34–39. [Google Scholar] [CrossRef]
- Shaw, R.R.; Uhlmann, D.R. Subliquidus immiscibility in binary alkali borates. J. Am. Ceram. Soc. 1968, 51, 377–382. [Google Scholar] [CrossRef]
- Charles, R.J. Origin of immiscibility in silicate solutions. Phys. Chem. Glasses 1969, 10, 169. [Google Scholar]
- Hudon, P.; Baker, D.R. The nature of phase separation in binary oxide melts and glasses. I. Silicate systems. J. Non-Cryst. Solids 2002, 303, 299–345. [Google Scholar] [CrossRef]
- McGahay, V.; Tomozawa, M. The origin of phase separation in silicate melts and glasses. J. Non-Cryst. Solids 1989, 109, 27–34. [Google Scholar] [CrossRef]
- Budhwani, K.; Feller, S. A density model for the lithium, sodium and potassium borosilicate glass systems. Phys. Chem. Glasses 1995, 36, 183–190. [Google Scholar]
- Dell, W.J.; Bray, P.J.; Xiao, S.Z. 11B NMR-studies and structural modeling of Na2O-B2O3-SiO2 glasses of high soda content. J. Non-Cryst. Solids 1983, 58, 1–16. [Google Scholar] [CrossRef]
- Feil, D.; Feller, S. The density of sodium borosilicate glasses related to atomic arrangements. J. Non-Cryst. Solids 1990, 119, 103–111. [Google Scholar] [CrossRef]
- Inoue, H.; Masuno, A.; Watanabe, Y.; Suzuki, K.; Iseda, T. Direct calculation of the physical properties of sodium borosilicate glass from its chemical composition using the concept of structural units. J. Am. Ceram. Soc. 2012, 95, 211–216. [Google Scholar] [CrossRef]
- Mazurin, O.V.; Streltsina, M.V. Determination of tie-line directions in the metastable phase-separation regions of ternary systems. J. Non-Cryst. Solids 1972, 11, 199–218. [Google Scholar] [CrossRef]
- Taylor, P.; Ashmore, S.D.; Owen, D.G. Chemical durability of some sodium borosilicate glasses improved by phase separation. J. Am. Ceram. Soc. 1987, 70, 333–338. [Google Scholar] [CrossRef]
- Häßler, J.; Rüssel, C. Self-organized growth of sodium borate-rich droplets in a phase-separated sodium borosilicate glass. Int. J. Appl. Glass Sci. 2017, 8, 124–131. [Google Scholar] [CrossRef]
- Kawamoto, Y.; Tomozawa, M. Prediction of immiscibility boundaries of the systems K2O-SiO2, K2O-Li2O-SiO2, K2O-Na2O-SiO2, and K2O-BaO-SiO2. J. Am. Ceram. Soc. 1981, 64, 289–292. [Google Scholar] [CrossRef]
- Bormann, R.; Gärtner, F.; Zöltzer, K. Application of the CALPHAD method for the prediction of amorphous phase formation. J. Less Common Met. 1988, 145, 19–29. [Google Scholar] [CrossRef]
- Gossé, S.; Guéneau, C.; Bordier, S.; Schuller, S.; Laplace, A.; Rogez, J. A thermodynamic approach to predict the metallic and oxide phases precipitations in nuclear waste glass melts. Procedia Mater. Sci. 2014, 7, 79–86, ISSN 2211-8128. [Google Scholar] [CrossRef]
- Strnad, Z.; Strnad, P. Calculation of metastable two-liquid tie lines in ternary glass-forming systems. J. Am. Ceram. Soc. 1978, 61, 283–286. [Google Scholar] [CrossRef]
- Saunders, N.; Miodownik, A.P. CALPHAD (Calculation of Phase Diagrams): A Comprehensive Guide; Elsevier: Amsterdam, The Netherlands, 1998; ISBN 9780080528434. [Google Scholar]
- Strnad, Z.; McMillan, P.W. Metastable two-liquid tie lines in the soda-lime-silica system. Phys. Chem. Glasses 1983, 24, 57–64. [Google Scholar]
- Benigni, P. CALPHAD modeling of the glass transition for a pure substance, coupling thermodynamics and relaxation kinetics. Calphad 2021, 72, 102238. [Google Scholar] [CrossRef]
- Hammel, J.J. Direct measurements of homogeneous nucleation rates in a glass-forming system. J. Chem. Phys. 1967, 46, 2234–2244. [Google Scholar] [CrossRef]
- Brequel, H.; Parmentier, J.; Sorar, G.D.; Schiffini, L.; Enzo, S. Study of the phase separation in amorphous silicon oxycarbide glasses under heat treatment. Nanostruct. Mater. 1999, 11, 721–731. [Google Scholar] [CrossRef]
- Wheaton, B.R.; Clare, A.G. Evaluation of phase separation in glasses with the use of atomic force microscopy. J. Non-Cryst. Solids 2007, 353, 4767–4778. [Google Scholar] [CrossRef]
- Kaspar, T.C.; Ryan, J.V.; Pantano, C.G.; Rice, J.; Trivelpiece, C.; Hyatt, N.C.; Corkhill, C.L.; Mann, C.; Hand, R.J.; Kirkham, M.A.; et al. Physical and optical properties of the international simple glass. Npj Mater. Degrad. 2019, 3, 15. [Google Scholar] [CrossRef]
- To, T. Fracture Toughness and Fracture Surface Energy of Inorganic and Non-Metallic Glasses. Ph.D. Thesis, Université de Rennes 1, Rennes, France, 2019. [Google Scholar]
- Gin, S.; Beaudoux, X.; Angéli, F.; Jégou, C.; Godon, N. Effect of composition on the short-term and long-term dissolution rates of ten borosilicate glasses of increasing complexity from 3 to 30 oxides. J. Non-Cryst. Solids 2012, 358, 2559–2570. [Google Scholar] [CrossRef]
- Jan, A.; Delaye, J.-M.; Gin, S.; Kerisit, S. Molecular dynamics simulation of ballistic effects in simplified nuclear waste glasses. J. Non-Cryst. Solids 2019, 505, 188–201. [Google Scholar] [CrossRef]
- Ojovan, M.I. The modified random network (MRN) model within the configuron percolation theory (CPT) of glass transition. Ceramics 2021, 4, 121–134. [Google Scholar] [CrossRef]
- Sitarz, M.; Mozgawa, W.; Handke, M. Rings in the structure of silicate glasses. J. Mol. Struct. 1999, 511, 281–285. [Google Scholar] [CrossRef]
- Ferlat, G.; Charpentier, T.; Seitsonen, A.P.; Takada, A.; Lazzeri, M.; Cormier, L.; Calas, G.; Mauri, F. Boroxol rings in liquid and vitreous B2O3 from first principles. Phys. Rev. Lett. 2008, 101, 065504. [Google Scholar] [CrossRef] [PubMed]
- Kieu, L.-H.; Delaye, J.-M.; Stolz, C. Modeling the effect of composition and thermal quenching on the fracture behavior of borosilicate glass. J. Non-Cryst. Solids 2012, 358, 3268–3279. [Google Scholar] [CrossRef]
- Boiko, G.G.; Bokov, N.A. Small-angle scattering and scattering of visible light by sodium-silicate glasses at phase separation. J. Non-Cryst. Solids 1970, 5, 41–54. [Google Scholar] [CrossRef]
- Du, L.S.; Stebbins, J.F. Nature of silicon-boron mixing in sodium borosilicate glasses: A high-resolution 11B and 17O NMR study. J. Phys. Chem. B 2003, 107, 10063–10076. [Google Scholar] [CrossRef]
- Furukawa, T.; Fox, K.E.; White, W.B. Raman spectroscopic investigation of the structure of silicate glasses. III. Raman intensities and structural units in sodium silicate glasses. J. Chem. Phys. 1981, 75, 3226–3237. [Google Scholar] [CrossRef]
- White, W.B. Investigation of phase separation by Raman spectroscopy. J. Non-Cryst. Solids 1982, 49, 321–329. [Google Scholar] [CrossRef]
- Cahn, J.W.; Charles, R.J. Initial stages of phase separation in glasses. Phys. Chem. Glasses 1965, 6, 181. [Google Scholar]
- Uhlmann, D.R.; Kolbeck, A.G. Phase separation and the revolution in concept of glass structure. Phys. Chem. Glasses 1976, 17, 146–158. [Google Scholar]
- Scholes, S.; Wilkinson, F.C.F. Glassy phase separation in sodium borosilicate glasses. Discuss. Faraday Soc. 1970, 50, 175–181. [Google Scholar] [CrossRef]
- Shepilov, M.P.; Kalmykov, A.E.; Sycheva, G.A. Liquid–liquid phase separation in sodium borosilicate glass: Ordering phenomena in particle arrangement. J. Non-Cryst. Solids 2007, 353, 2415–2430. [Google Scholar] [CrossRef]
- Dalmas, D.; Lelarge, A.; Vandembroucq, D. Quantitative AFM analysis of phase separated borosilicate glass surfaces. J. Non-Cryst. Solids 2007, 353, 4672–4680. [Google Scholar] [CrossRef]
- Elmer, T.H.; Nordberg, M.E.; Carrier, G.B.; Korda, E.J. Phase separation in borosilicate glasses as seen by electron microscopy and scanning electron microscopy. J. Am. Ceram. Soc. 1970, 53, 171–175. [Google Scholar] [CrossRef]
- Salvo, L.; Cloetens, P.; Maire, E.; Zabler, S.; Blandin, J.J.; Buffiere, J.Y.; Ludwig, W.; Boller, E.; Bellet, D.; Josserond, C. X-ray micro-tomography an attractive characterisation technique in materials science. Nucl. Instrum. Methods Phys. Res. Sect. B 2003, 200, 273–286. [Google Scholar] [CrossRef]
- Lacondemine, T. Initiation et Propagation d’une Fissure dans un Composite Particulaire à Matrice Verre: Expérimentation et Analyse Numérique. Ph.D. Thesis, Université de Rennes 1, Rennes, France, 2019. [Google Scholar]
- Yang, Z.; Ren, W.; Sharma, R.; McDonald, S.; Mostafavi, M.; Vertyagina, Y.; Marrow, T.J. In-situ X-ray computed tomography characterisation of 3D fracture evolution and image-based numerical homogenisation of concrete. Cem. Concr. Compos. 2017, 75, 74–83. [Google Scholar] [CrossRef]
- Buffiere, J.-Y.; Maire, E.; Adrien, J.; Masse, J.-P.; Boller, E. In situ experiments with X-ray tomography: An attractive tool for experimental mechanics. Exp. Mech. 2010, 50, 289–305. [Google Scholar] [CrossRef]
- Tanaka, H.; Araki, T. Spontaneous double phase separation induced by rapid hydrodynamic coarsening in two-dimensional fluid mixtures. Phys. Rev. Lett. 1998, 81, 389. [Google Scholar] [CrossRef]
- Han, J.H.; Mattern, N.; Kim, D.H.; Eckert, J. Phase separation and microstructure evolution of rapidly quenched Gd-Hf-Co-Al alloys. J. Alloys Compd. 2011, 509, S42–S45. [Google Scholar] [CrossRef]
- Seward, T.P., III; Uhlmann, D.R.; Turnbull, D. Phase separation in the system BaO-SiO2. J. Am. Ceram. Soc. 1968, 51, 278–285. [Google Scholar] [CrossRef]
- Shaw, R.R.; Breedis, J.F. Secondary phase separation in lead borate glasses. J. Am. Ceram. Soc. 1972, 55, 422–425. [Google Scholar] [CrossRef]
- Filipovich, V.N. Some aspects of the formation of new phases in melt and glasses. Struct. Glass 1965, 5, 39. [Google Scholar]
- Galakhov, F.Y.; Konovalova, S.F. Liquation phenomena in the system alumina-silica. Communication 1. Experimental data and their discussion. Izv. Akad. Nauk. SSSR Seriya Khimicheskaya 1964, 8, 1373. [Google Scholar]
- Porai-Koshits, E.A.; Averjanov, V.I. Primary and secondary phase separation of sodium silicate glasses. J. Non-Cryst. Solids 1968, 1, 29–38. [Google Scholar] [CrossRef]
- Shaw, R.R.; Uhlmann, D.R. Effect of phase separation on the properties of simple glasses. I. Density and molar volume. J. Non-Cryst. Solids 1969, 1, 474–498. [Google Scholar] [CrossRef]
- Shaw, R.R.; Uhlmann, D.R. Effect of phase separation on the properties of simple glasses. II. Elastic properties. J. Non-Cryst. Solids 1971, 5, 237–263. [Google Scholar] [CrossRef]
- Hood, H.P.; Stookey, S.D. Method of Making a Glass Article of High Mechanical Strength and Article Made Thereby. U.S. Patent 2779136A, 29 January 1957. [Google Scholar]
- Mirkhalaf, M.; Dastjerdi, A.K.; Barthelat, F. Overcoming the brittleness of glass through bio-inspiration and micro-architecture. Nat. Commun. 2014, 5, 3166. [Google Scholar] [CrossRef] [PubMed]
- Sehgal, J.; Ito, S. A new low-brittleness glass in the soda-lime-silica glass family. J. Am. Ceram. Soc. 1998, 81, 2485–2488. [Google Scholar] [CrossRef]
- Wondraczek, L.; Mauro, J.C.; Eckert, J.; Kühn, U.; Horbach, J.; Deubener, J.; Rouxel, T. Towards ultrastrong glasses. Adv. Mater. 2011, 23, 4578–4586. [Google Scholar] [CrossRef] [PubMed]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Miyata, N.; Jinno, H. Strength and fracture surface energy of phase-separated glasses. J. Mater. Sci. 1981, 16, 2205–2217. [Google Scholar] [CrossRef]
- Osaka, A.; Soga, N.; Kunugi, M. Elastic constants and Vickers hardness of lead borate glasses. J. Soc. Mater. Sci. Jpn. 1974, 23, 128–131. [Google Scholar] [CrossRef]
- Miyata, N.; Jinno, H. Use of Vickers indentation method for evaluation of fracture toughness of phase-separated glasses. J. Non-Cryst. Solids 1980, 38, 391–396. [Google Scholar] [CrossRef]
- Miyata, N.; Jinno, H. Fracture toughness and fracture surface energy of lead borate glasses. J. Mater. Sci. Lett. 1982, 1, 156–158. [Google Scholar] [CrossRef]
- Lange, F.F. The interaction of a crack front with a second-phase dispersion. Philos. Mag. 1970, 22, 0983–0992. [Google Scholar] [CrossRef]
- Simmons, C.J.; Freiman, S.W. Effects of phase separation on crack growth in borosilicate glass. J. Non-Cryst. Solids 1980, 38, 503–508. [Google Scholar] [CrossRef]
- Evans, A.G. Perspective on the development of high-toughness ceramics. J. Am. Ceram. Soc. 1990, 73, 187–206. [Google Scholar] [CrossRef]
- Bao, G.; Suo, Z. Remarks on crack-bridging concepts. Appl. Mech. Rev. 1992, 45, 355–366. [Google Scholar] [CrossRef]
- Budiansky, B.; Amazigo, J.C.; Evans, A.G. Small-scale crack bridging and the fracture toughness of particulate-reinforced ceramics. J. Mech. Phys. Solids 1988, 36, 167–187. [Google Scholar] [CrossRef]
- Bonamy, D.; Prades, S.; Rountree, C.L.; Ponson, L.; Dalmas, D.; Bouchaud, E.; Ravi-Chandar, K.; Guillot, C. Nanoscale damage during fracture in silica glass. Int. J. Fract. 2006, 140, 3–14, ISSN 0376-9429. [Google Scholar] [CrossRef]
- Gjerden, K.S.; Stormo, A.; Hansen, A. Local dynamics of a randomly pinned crack front: A numerical study. Front. Phys. 2014, 2, 66. [Google Scholar] [CrossRef]
- Bower, A.F.; Ortiz, M. A three-dimensional analysis of crack trapping and bridging by tough particles. J. Mech. Phys. Solids 1991, 39, 815–858. [Google Scholar] [CrossRef]
- Gao, H.; Rice, J.R. A first-order perturbation analysis of crack trapping by arrays of obstacles. J. Appl. Mech. 1989, 56, 828–836. [Google Scholar] [CrossRef]
- Mower, T.M.; Argon, A.S. Experimental investigations of crack trapping in brittle heterogeneous solids. Mech. Mater. 1995, 19, 343–364. [Google Scholar] [CrossRef][Green Version]
- Faber, K.T.; Evans, A.G. Crack deflection processes–I. Theory. Acta Metall. 1983, 31, 565–576. [Google Scholar] [CrossRef]
- Faber, K.T.; Evans, A.G. Crack deflection processes–II. Experiment. Acta Metall. 1983, 31, 577–584, ISSN 0001-6160. [Google Scholar] [CrossRef]
- Lebihain, M.; Leblond, J.-B.; Ponson, L. Effective toughness of periodic heterogeneous materials: The effect of out-of-plane excursions of cracks. J. Mech. Phys. Solids 2020, 137, 103876. [Google Scholar] [CrossRef]
- Laurson, L.; Santucci, S.; Zapperi, S. Avalanches and clusters in planar crack front propagation. Phys. Rev. E 2010, 81, 046116. [Google Scholar] [CrossRef] [PubMed]
- Måløy, K.J.; Santucci, S.; Schmittbuhl, J.; Toussaint, R. Local waiting time fluctuations along a randomly pinned crack front. Phys. Rev. Lett. 2006, 96, 045501. [Google Scholar] [CrossRef]
- Evans, A.G. A method for evaluating the time-dependent failure characteristics of brittle materials and its application to polycrystalline alumina. J. Mater. Sci. 1972, 7, 1137–1146, ISSN 1573-4803. [Google Scholar] [CrossRef]
- Ahlquist, C.N. On the interaction of cleavage cracks with second phase particles. Acta Metall. 1975, 23, 239–243. [Google Scholar] [CrossRef]
- Green, D.J.; Nicholson, P.S.; Embury, J.D. Fracture of a brittle particulate composite. J. Mater. Sci. 1979, 14, 1413–1420. [Google Scholar] [CrossRef]
- Selsing, J. Internal stresses in ceramics. J. Am. Ceram. Soc. 1961, 44, 419. [Google Scholar] [CrossRef]
- Miyata, N.; Takeda, S.; Jinno, H. Slow crack growth in phase-separated glasses. J. Non-Cryst. Solids 1987, 95, 1047–1054. [Google Scholar] [CrossRef]
- Kleebe, H.-J.; Pezzotti, G.; Ziegler, G. Microstructure and fracture toughness of Si3N4 ceramics: Combined roles of grain morphology and secondary phase chemistry. J. Am. Ceram. Soc. 1999, 82, 1857–1867. [Google Scholar] [CrossRef]
- Seal, A.K.; Chakraborti, P.; Roy, N.R.; Mukerjee, S.; Mitra, M.K.; Das, G.C. Effect of phase separation on the fracture toughness of SiO2-B2O3-Na2O glass. Bull. Mater. Sci. 2005, 28, 457–460. [Google Scholar] [CrossRef]
- Lane, M. Interface fracture. Annu. Rev. Mater. Res. 2003, 33, 29–54. [Google Scholar] [CrossRef]
- Raghava, R.S. Role of matrix-particle interface adhesion on fracture toughness of dual phase epoxy-polyethersulfone blend. J. Polym. Sci. Part B Polym. Phys. 1987, 25, 1017–1031. [Google Scholar] [CrossRef]
- Mecholsky, J.J. Toughening in glass ceramic through microstructural design. Fract. Mech. Ceram. 1983, 6, 165. [Google Scholar]
- Tang, L.; Krishnan, N.M.A.; Berjikian, J.; Rivera, J.; Smedskjaer, M.M.; Mauro, J.C.; Zhou, W.; Bauchy, M. Effect of nanoscale phase separation on the fracture behavior of glasses: Toward tough, yet transparent glasses. Phys. Rev. Mater. 2018, 2, 113602. [Google Scholar] [CrossRef]
- Kermouche, G.; Barthel, E.; Vandembroucq, D.; Dubujet, P. Mechanical modelling of indentation-induced densification in amorphous silica. Acta Mater. 2008, 56, 3222–3228. [Google Scholar] [CrossRef]
- Perriot, A.; Vandembroucq, D.; Barthel, E.; Martinez, V.; Grosvalet, L.; Martinet, C.; Champagnon, B. Raman microspectroscopic characterization of amorphous silica plastic behavior. J. Am. Ceram. Soc. 2006, 89, 596–601. [Google Scholar] [CrossRef]
- Cheng, S.; Song, C.; Ercius, P. Indentation cracking behaviour and structures of nanophase separation of glasses. Phys. Chem. Glasses-Eur. J. Glass Sci. Technol. Part B 2017, 58, 237–242. [Google Scholar] [CrossRef][Green Version]
- Evans, A.G.; Wilshaw, T.R. Quasi-static solid particle damage in brittle solids—I. Observations, analysis and implications. Acta Metall. 1976, 24, 939–956, ISSN 0001-6160. [Google Scholar] [CrossRef]
- Quinn, G.D.; Bradt, R.C. On the Vickers indentation fracture toughness test. J. Am. Ceram. Soc. 2007, 90, 673–680. [Google Scholar] [CrossRef]
- To, T.; Stabler, C.; Ionescu, E.; Riedel, R.; Célarié, F.; Rouxel, T. Elastic properties and fracture toughness of SiOC-based glass-ceramic nanocomposites. J. Am. Ceram. Soc. 2020, 103, 491–499. [Google Scholar] [CrossRef]
- Ostojic, P.; Mcpherson, R. A review of indentation fracture theory—Its development, principles and limitations. Int. J. Fract. 1987, 33, 297–312. [Google Scholar] [CrossRef]
- Fu, S.-Y.; Feng, X.-Q.; Lauke, B.; Mai, Y.-W. Effects of particle size, particle/matrix interface adhesion and particle loading on mechanical properties of particulate–Polymer composites. Compos. Part B Eng. 2008, 39, 933–961. [Google Scholar] [CrossRef]
- Bonamy, D.; Bouchaud, E. Failure of heterogeneous materials: A dynamic phase transition? Phys. Rep. 2010, 498, 1–44. [Google Scholar] [CrossRef]
- Bouchaud, E.; Lapasset, G.; Planes, J.; Naveos, S. Statistics of branched fracture surfaces. Phys. Rev. B 1993, 48, 2917–2928, ISSN 0163-1829. [Google Scholar] [CrossRef]
- Daguier, P.; Nghiem, B.; Bouchaud, E.; Creuzet, F. Pinning and depinning of crack fronts in heterogeneous materials. Phys. Rev. Lett. 1997, 78, 1062. [Google Scholar] [CrossRef]
- Bonamy, D.; Ponson, L.; Prades, S.; Bouchaud, E.; Guillot, C. Scaling exponents for fracture surfaces in homogeneous glass and glassy ceramics. Phys. Rev. Lett. 2006, 97, 135504, ISSN 0031-9007. [Google Scholar] [CrossRef] [PubMed]
- Ramanathan, S.; Ertas, D.; Fisher, D.S. Quasistatic crack propagation in heterogeneous media. Phys. Rev. Lett. 1997, 79, 873. [Google Scholar] [CrossRef]
- Rountree, C.L.; Feng, W. SILICA and its process zone. Int. J. Appl. Glass Sci. 2020, 11, 385–395. [Google Scholar] [CrossRef]
- Guerra, C.; Scheibert, J.; Bonamy, D.; Dalmas, D. Understanding fast macroscale fracture from microcrack post mortem patterns. Proc. Natl. Acad. Sci. USA 2012, 109, 390–394. [Google Scholar] [CrossRef] [PubMed]
- Ciccotti, M.; George, M. In Situ AFM investigations and fracture mechanics modeling of slow fracture propagation in oxide and polymer glasses. In Handbook of Materials Modeling: Applications: Current and Emerging Materials; Springer: New York, NY, USA, 2018; pp. 1–37. [Google Scholar] [CrossRef]
- Dalmas, D.; Lelarge, A.; Vandembroucq, D. Crack propagation through phase-separated glasses: Effect of the characteristic size of disorder. Phys. Rev. Lett. 2008, 101, 255501. [Google Scholar] [CrossRef] [PubMed]
- Pallares, G.; Lechenault, F.; George, M.; Bouchaud, E.; Ottina, C.; Rountree, C.L.; Ciccotti, M. Roughness of oxide glass subcritical fracture surfaces. J. Am. Ceram. Soc. 2018, 101, 1279–1288. [Google Scholar] [CrossRef]
- Wünsche, C.; Rädlein, E.; Frischat, G.H. Glass fracture surfaces seen with an atomic force microscope. Fresenius J. Anal. Chem. 1997, 358, 349–351. [Google Scholar] [CrossRef]
- Lechenault, F.; Pallares, G.; George, M.; Rountree, C.L.; Bouchaud, E.; Ciccotti, M. Effects of finite probe size on self-affine roughness measurements. Phys. Rev. Lett. 2010, 104, 025502. [Google Scholar] [CrossRef]
- Barés, J.; Barlet, M.; Rountree, C.L.; Barbier, L.; Bonamy, D. Nominally brittle cracks in inhomogeneous solids: From microstructural disorder to continuum-level scale. Front. Phys. 2014, 2, 70, ISSN 2296-424X. [Google Scholar] [CrossRef]
- Guin, J.P.; Wiederhorn, S.M.; Fett, T. Crack-tip structure in soda-lime-silicate glass. J. Am. Ceram. Soc. 2005, 88, 652–659, ISSN 0002-7820. [Google Scholar] [CrossRef]
- Tetelman, A.S.; McEvily, A.J. Fracture of Structural Materials; Wiley: Hoboken, NJ, USA, 1967. [Google Scholar]







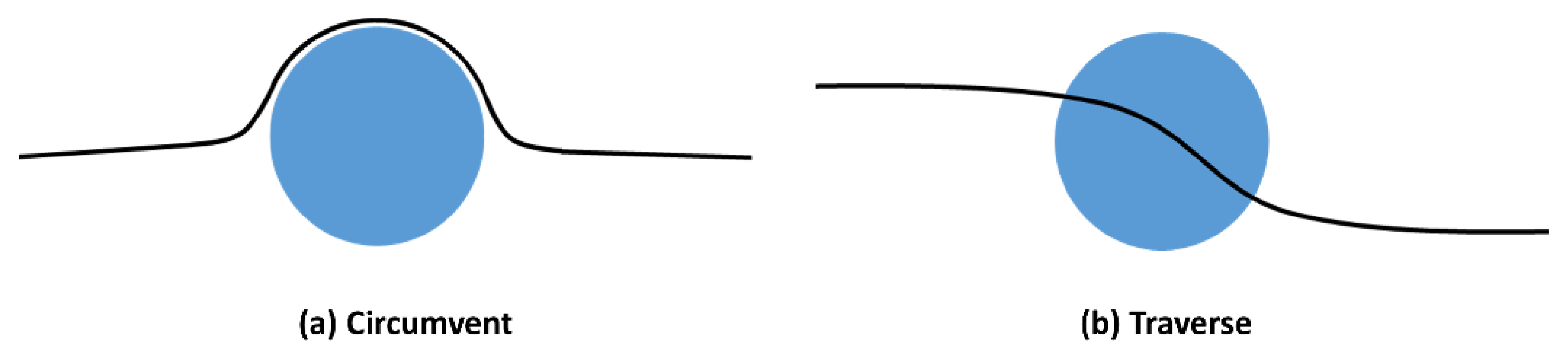




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, W.; Bonamy, D.; Célarié, F.; Fossati, P.C.M.; Gossé, S.; Houizot, P.; Rountree, C.L. Stress Corrosion Cracking in Amorphous Phase Separated Oxide Glasses: A Holistic Review of Their Structures, Physical, Mechanical and Fracture Properties. Corros. Mater. Degrad. 2021, 2, 412-446. https://doi.org/10.3390/cmd2030022
Feng W, Bonamy D, Célarié F, Fossati PCM, Gossé S, Houizot P, Rountree CL. Stress Corrosion Cracking in Amorphous Phase Separated Oxide Glasses: A Holistic Review of Their Structures, Physical, Mechanical and Fracture Properties. Corrosion and Materials Degradation. 2021; 2(3):412-446. https://doi.org/10.3390/cmd2030022
Chicago/Turabian StyleFeng, Weiying, Daniel Bonamy, Fabrice Célarié, Paul C. M. Fossati, Stéphane Gossé, Patrick Houizot, and Cindy L. Rountree. 2021. "Stress Corrosion Cracking in Amorphous Phase Separated Oxide Glasses: A Holistic Review of Their Structures, Physical, Mechanical and Fracture Properties" Corrosion and Materials Degradation 2, no. 3: 412-446. https://doi.org/10.3390/cmd2030022
APA StyleFeng, W., Bonamy, D., Célarié, F., Fossati, P. C. M., Gossé, S., Houizot, P., & Rountree, C. L. (2021). Stress Corrosion Cracking in Amorphous Phase Separated Oxide Glasses: A Holistic Review of Their Structures, Physical, Mechanical and Fracture Properties. Corrosion and Materials Degradation, 2(3), 412-446. https://doi.org/10.3390/cmd2030022






