Theoretical Study of the Adsorption of Li2S and Li2S2 Molecules on Multivacancy Defected Graphene
Abstract
1. Introduction
2. Materials and Methods
2.1. Methodology
2.2. Model
3. Results and Discussion
3.1. Adsorption Energies, Stability, and Geometry
3.2. Electronic Structure
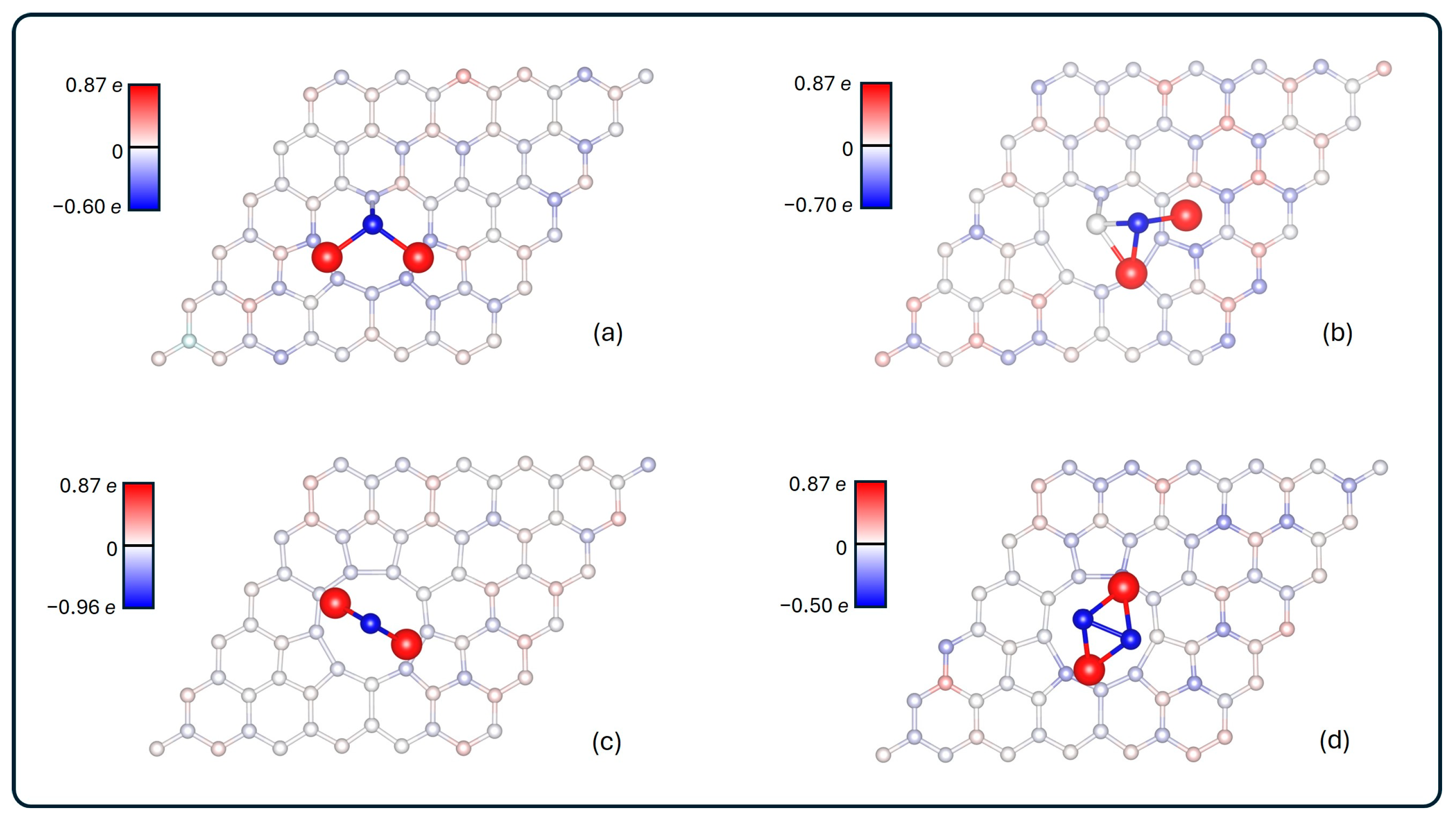
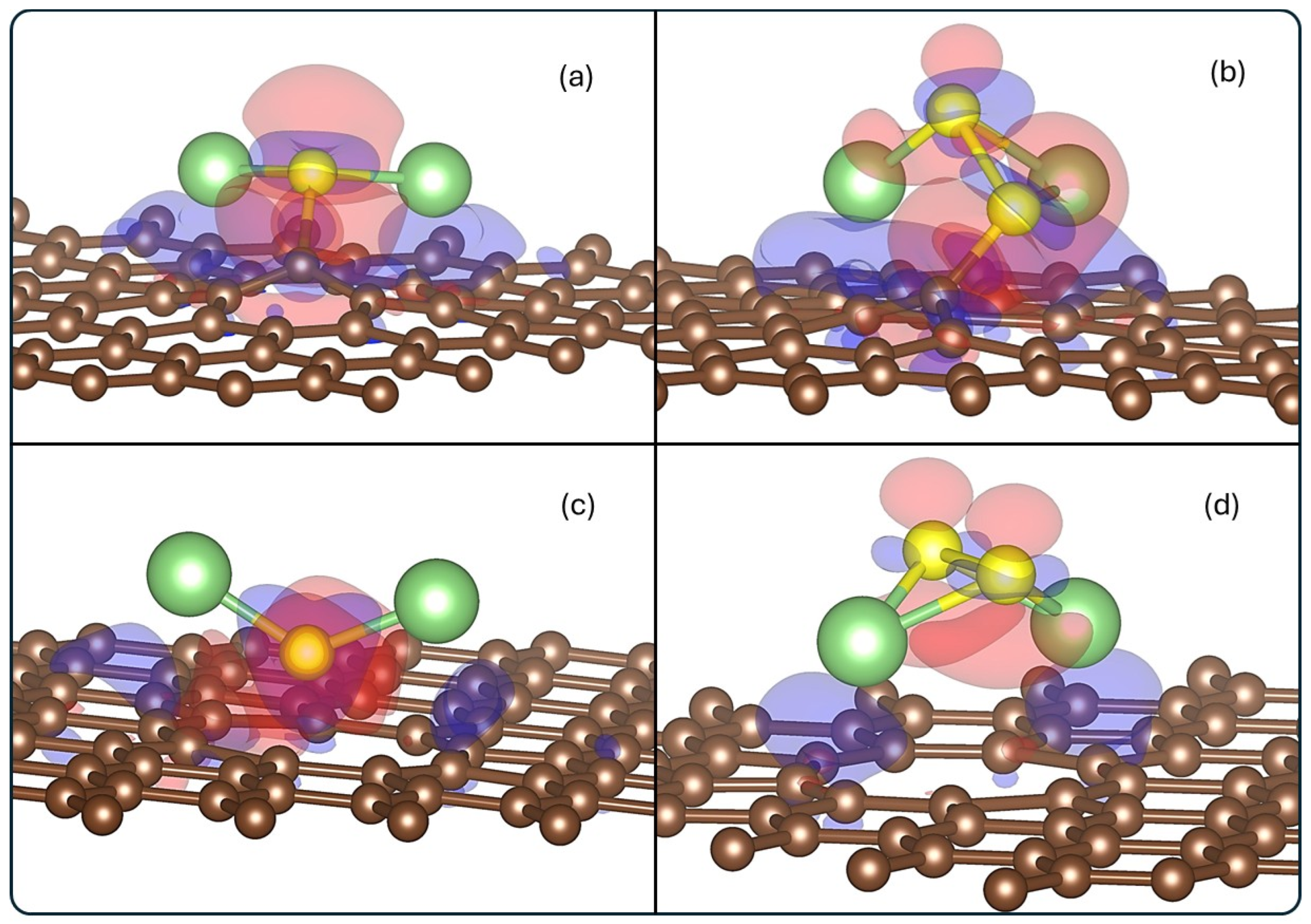
3.2.1. Charge Transfer Analysis and ELF Analysis
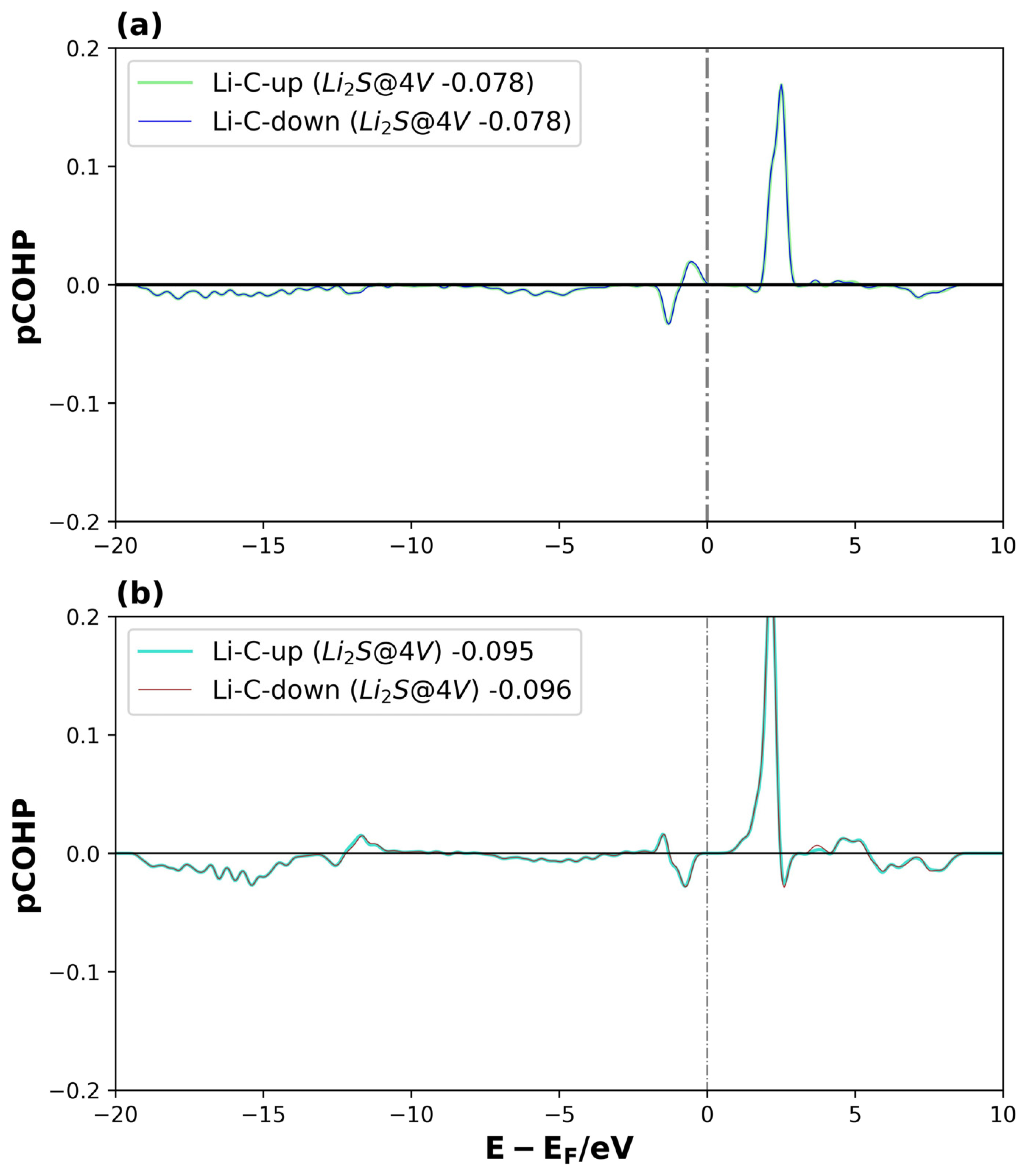
3.2.2. Density of States and COPH Analysis
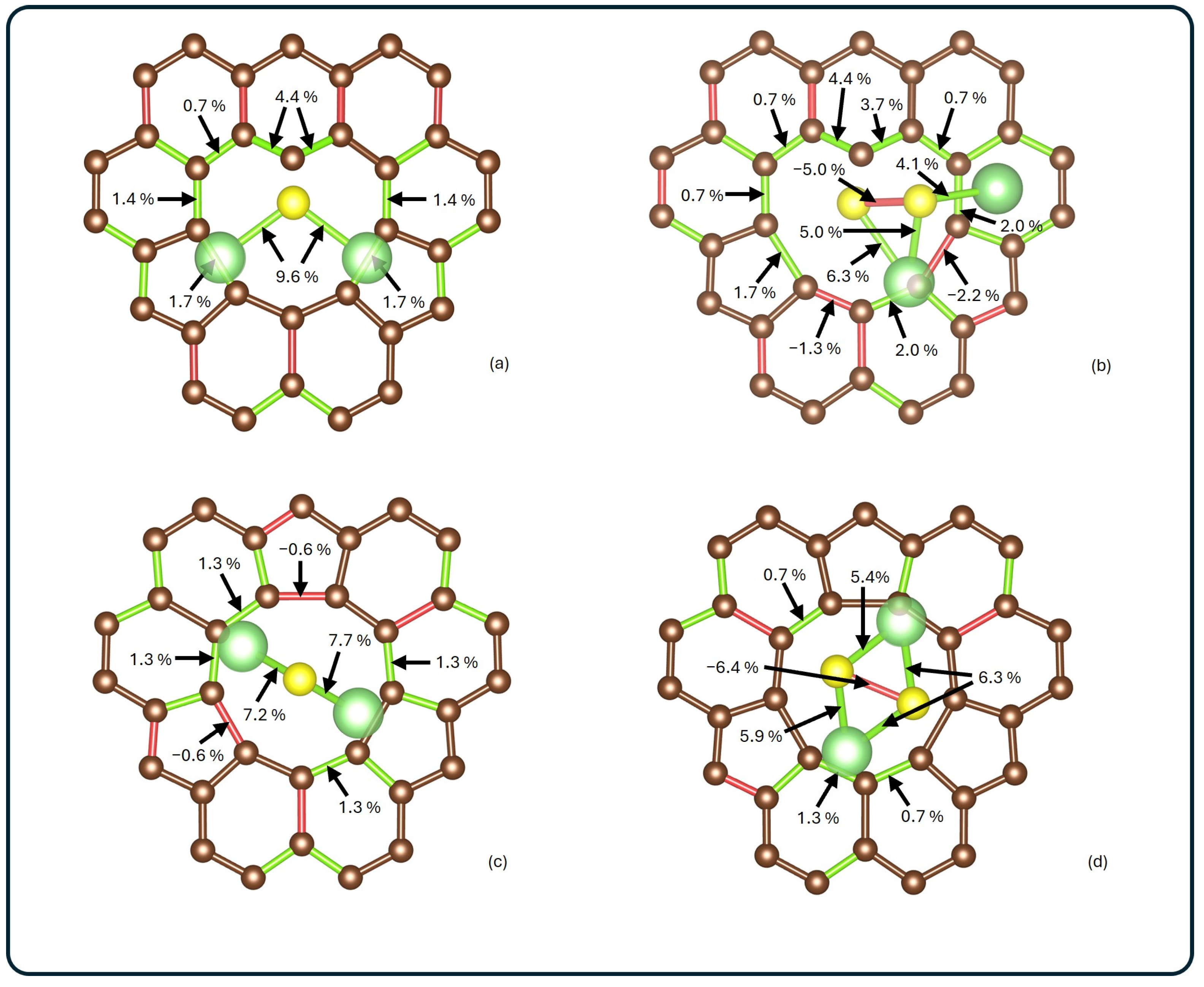
3.3. Bond Order and Interaction Strength
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANPCyT | Agencia Nacional de Promoción de Científica y Tecnológica |
| CONICET | Consejo Nacional de Investigaciones Científicas y Técnicas |
References
- Ji, X.; Nazar, L.F. Advances in Li–S Batteries. J. Mater. Chem. 2010, 20, 9821–9826. [Google Scholar] [CrossRef]
- Bruce, P.G.; Freunberger, S.A.; Hardwick, L.J.; Tarascon, J.-M. Li–O2 and Li–S Batteries with High Energy Storage. Nat. Mater. 2012, 11, 19–29. [Google Scholar] [CrossRef]
- Manthiram, A.; Fu, Y.; Su, Y.-S. Challenges and Prospects of Lithium–Sulfur Batteries. Acc. Chem. Res. 2013, 46, 1125–1134. [Google Scholar] [CrossRef] [PubMed]
- Ding, B.; Wang, J.; Fan, Z.; Chen, S.; Lin, Q.; Lu, X.; Dou, H.; Kumar Nanjundan, A.; Yushin, G.; Zhang, X.; et al. Solid-State Lithium–Sulfur Batteries: Advances, Challenges and Perspectives. Mater. Today 2020, 40, 114–131. [Google Scholar] [CrossRef]
- Zhao, M.; Li, B.; Peng, H.; Yuan, H.; Wei, J.; Huang, J. Lithium–Sulfur Batteries under Lean Electrolyte Conditions: Challenges and Opportunities. Angew. Chem. Int. Ed. 2020, 59, 12636–12652. [Google Scholar] [CrossRef] [PubMed]
- Hou, L.-P.; Zhang, X.-Q.; Li, B.-Q.; Zhang, Q. Challenges and Promises of Lithium Metal Anode by Soluble Polysulfides in Practical Lithium–Sulfur Batteries. Mater. Today 2021, 45, 62–76. [Google Scholar] [CrossRef]
- Deshmukh, A.; Thripuranthaka, M.; Chaturvedi, V.; Das, A.K.; Shelke, V.; Shelke, M.V. A Review on Recent Advancements in Solid State Lithium–Sulfur Batteries: Fundamentals, Challenges, and Perspectives. Prog. Energy 2022, 4, 042001. [Google Scholar] [CrossRef]
- Raza, H.; Bai, S.; Cheng, J.; Majumder, S.; Zhu, H.; Liu, Q.; Zheng, G.; Li, X.; Chen, G. Li-S Batteries: Challenges, Achievements and Opportunities. Electrochem. Energy Rev. 2023, 6, 29. [Google Scholar] [CrossRef]
- Lv, Z.-C.; Wang, P.-F.; Wang, J.-C.; Tian, S.-H.; Yi, T.-F. Key Challenges, Recent Advances and Future Perspectives of Rechargeable Lithium-Sulfur Batteries. J. Ind. Eng. Chem. 2023, 124, 68–88. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, T.; Wang, P.; Yuan, M.; Li, Q.; Feng, S. Challenges and Solutions for Low-Temperature Lithium–Sulfur Batteries: A Review. Materials 2023, 16, 4359. [Google Scholar] [CrossRef]
- Shao, Q.; Zhu, S.; Chen, J. A Review on Lithium-Sulfur Batteries: Challenge, Development, and Perspective. Nano Res. 2023, 16, 8097–8138. [Google Scholar] [CrossRef]
- Jiao, Y.; Wang, F.; Ma, Y.; Luo, S.; Li, Y.; Hu, A.; He, M.; Li, F.; Chen, D.; Chen, W.; et al. Challenges and Advances on Low-Temperature Rechargeable Lithium-Sulfur Batteries. Nano Res. 2023, 16, 8082–8096. [Google Scholar] [CrossRef]
- Shi, H.; Sun, W.; Cao, J.; Han, S.; Lu, G.; Ghazi, Z.A.; Zhu, X.; Lan, H.; Lv, W. Challenges and Solutions for Lithium–Sulfur Batteries with Lean Electrolyte. Adv. Funct. Mater. 2023, 33, 2306933. [Google Scholar] [CrossRef]
- Pathak, A.D.; Cha, E.; Choi, W. Towards the Commercialization of Li-S Battery: From Lab to Industry. Energy Storage Mater. 2024, 72, 103711. [Google Scholar] [CrossRef]
- Qian, W.; Guo, Y.; Zuo, W.; Wu, X.; Zhang, L. Toward Practical Lithium–Sulfur Batteries. Mater. Chem. Front. 2024, 8, 2556–2577. [Google Scholar] [CrossRef]
- Sawangphruk, M. New Materials for Lithium–Sulfur Batteries: Challenges and Future Directions. Chem. Commun. 2025, 61, 7770–7794. [Google Scholar] [CrossRef]
- Sharma, R.; Kumar, H.; Kumar, G.; Sharma, S.; Aneja, R.; Sharma, A.K.; Kumar, R.; Kumar, P. Progress and Challenges in Electrochemical Energy Storage Devices: Fabrication, Electrode Material, and Economic Aspects. Chem. Eng. J. 2023, 468, 143706. [Google Scholar] [CrossRef]
- Wang, H.; Yang, Y.; Liang, Y.; Robinson, J.T.; Li, Y.; Jackson, A.; Cui, Y.; Dai, H. Graphene-Wrapped Sulfur Particles as a Rechargeable Lithium–Sulfur Battery Cathode Material with High Capacity and Cycling Stability. Nano Lett. 2011, 11, 2644–2647. [Google Scholar] [CrossRef]
- Zhou, G.; Pei, S.; Li, L.; Wang, D.; Wang, S.; Huang, K.; Yin, L.; Li, F.; Cheng, H. A Graphene–Pure-Sulfur Sandwich Structure for Ultrafast, Long-Life Lithium–Sulfur Batteries. Adv. Mater. 2014, 26, 625–631. [Google Scholar] [CrossRef]
- Xu, G.; Ding, B.; Pan, J.; Nie, P.; Shen, L.; Zhang, X. High-Performance Lithium–Sulfur Batteries: Advances and Challenges. Small 2015, 11, 4321–4347. [Google Scholar] [CrossRef]
- Ji, X.; Lee, K.T.; Nazar, L.F. A Highly Ordered Nanostructured Carbon–Sulphur Cathode for Lithium–Sulphur Batteries. Nat. Mater. 2009, 8, 500–506. [Google Scholar] [CrossRef]
- Seh, Z.W.; Sun, Y.; Zhang, Q.; Cui, Y. Designing High-Energy Lithium–Sulfur Batteries. Chem. Soc. Rev. 2016, 45, 5605–5634. [Google Scholar] [CrossRef]
- Wang, S.; Qu, C.; Wen, J.; Wang, C.; Ma, X.; Yang, Y.; Huang, G.; Sun, H.; Xu, S. Progress of Transition Metal Sulfides Used as Lithium-Ion Battery Anodes. Mater. Chem. Front. 2023, 7, 2779–2808. [Google Scholar] [CrossRef]
- Liang, X.; Garsuch, A.; Nazar, L.F. Sulfur Cathodes Based on Conductive MXene Nanosheets for High-Performance Lithium–Sulfur Batteries. Angew. Chem. 2015, 127, 3979–3983. [Google Scholar] [CrossRef]
- Suzanowicz, A.; Mei, C.; Mandal, B. Approaches to Combat the Polysulfide Shuttle Phenomenon in Li–S Battery Technology. Batteries 2022, 8, 45. [Google Scholar] [CrossRef]
- Wang, J.; Wang, H.; Jia, S.; Zhao, Q.; Zheng, Q.; Ma, Y.; Ma, T.; Li, X. Recent Advances in Inhibiting Shuttle Effect of Polysulfide in Lithium-Sulfur Batteries. J. Energy Storage 2023, 72, 108372. [Google Scholar] [CrossRef]
- Rao, X.-Y.; Xiang, S.-F.; Zhou, J.; Zhang, Z.; Xu, X.-Y.; Xu, Y.-Y.; Zhou, X.-C.; Pan, Z.-D.; Tan, S.-C.; Dong, S.-X.; et al. Recent Progress and Strategies of Cathodes toward Polysulfides Shuttle Restriction for Lithium-Sulfur Batteries. Rare Met. 2024, 43, 4132–4161. [Google Scholar] [CrossRef]
- Evers, S.; Nazar, L.F. New Approaches for High Energy Density Lithium–Sulfur Battery Cathodes. Acc. Chem. Res. 2013, 46, 1135–1143. [Google Scholar] [CrossRef] [PubMed]
- Pan, H.; Cheng, Z.; He, P.; Zhou, H. A Review of Solid-State Lithium–Sulfur Battery: Ion Transport and Polysulfide Chemistry. Energy Fuels 2020, 34, 11942–11961. [Google Scholar] [CrossRef]
- Yu, M.; Li, R.; Wu, M.; Shi, G. Graphene Materials for Lithium–Sulfur Batteries. Energy Storage Mater. 2015, 1, 51–73. [Google Scholar] [CrossRef]
- Chadha, U.; Bhardwaj, P.; Padmanaban, S.; Suneel, R.M.; Milton, K.; Subair, N.; Pandey, A.; Khanna, M.; Srivastava, D.; Mathew, R.M.; et al. Review—Contemporary Progresses in Carbon-Based Electrode Material in Li-S Batteries. J. Electrochem. Soc. 2022, 169, 020530. [Google Scholar] [CrossRef]
- Liu, Y.; Wei, H.; Zhai, X.; Wang, F.; Ren, X.; Xiong, Y.; Akiyoshi, O.; Pan, K.; Ren, F.; Wei, S. Graphene-Based Interlayer for High-Performance Lithium–Sulfur Batteries: A Review. Mater. Des. 2021, 211, 110171. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, R.; Tang, R.; Cheng, X.; He, Z.; Meng, T. Insight into the Polysulfides Conversion Kinetics and Its Activation Energy Relationship on Ultrafine V8C7 in Li-S Batteries. Chem. Eng. J. 2024, 500, 156970. [Google Scholar] [CrossRef]
- Rao, D.; Wang, Y.; Zhang, L.; Yao, S.; Qian, X.; Xi, X.; Xiao, K.; Deng, K.; Shen, X.; Lu, R. Mechanism of Polysulfide Immobilization on Defective Graphene Sheets with N-Substitution. Carbon 2016, 110, 207–214. [Google Scholar] [CrossRef]
- Song, J.; Xu, T.; Gordin, M.L.; Zhu, P.; Lv, D.; Jiang, Y.; Chen, Y.; Duan, Y.; Wang, D. Nitrogen-Doped Mesoporous Carbon Promoted Chemical Adsorption of Sulfur and Fabrication of High-Areal-Capacity Sulfur Cathode with Exceptional Cycling Stability for Lithium-Sulfur Batteries. Adv. Funct. Mater. 2014, 24, 1243–1250. [Google Scholar] [CrossRef]
- Zhang, J.; Shi, Y.; Ding, Y.; Zhang, W.; Yu, G. In Situ Reactive Synthesis of Polypyrrole-MnO2 Coaxial Nanotubes as Sulfur Hosts for High-Performance Lithium–Sulfur Battery. Nano Lett. 2016, 16, 7276–7281. [Google Scholar] [CrossRef]
- Zhang, S.; Ueno, K.; Dokko, K.; Watanabe, M. Recent Advances in Electrolytes for Lithium–Sulfur Batteries. Adv. Energy Mater. 2015, 5, 1500117. [Google Scholar] [CrossRef]
- Li, J.; Qu, Y.; Chen, C.; Zhang, X.; Shao, M. Theoretical Investigation on Lithium Polysulfide Adsorption and Conversion for High-Performance Li–S Batteries. Nanoscale 2021, 13, 15–35. [Google Scholar] [CrossRef]
- Yang, X.; Luo, J.; Sun, X. Towards High-Performance Solid-State Li–S Batteries: From Fundamental Understanding to Engineering Design. Chem. Soc. Rev. 2020, 49, 2140–2195. [Google Scholar] [CrossRef]
- Chen, R.; Zhou, Y.; He, J.; Li, X. Advanced Computational Methods in Lithium–Sulfur Batteries. Adv. Funct. Mater. 2024, 34, 2407986. [Google Scholar] [CrossRef]
- Zhang, X.; Li, S.; Wang, Z.; Yan, J.; Liu, J.; Wu, Y. Review on the First-Principles Calculation in Lithium-Sulfur Battery. Prog. Chem. 2023, 35, 375–389. [Google Scholar] [CrossRef]
- Banhart, F.; Kotakoski, J.; Krasheninnikov, A.V. Structural Defects in Graphene. ACS Nano 2011, 5, 26–41. [Google Scholar] [CrossRef]
- Ambrusi, R.E.; Luna, C.R.; Juan, A.; Pronsato, M.E. DFT Study of Rh-Decorated Pristine, B-Doped and Vacancy Defected Graphene for Hydrogen Adsorption. RSC Adv. 2016, 6, 83926–83941. [Google Scholar] [CrossRef]
- Ambrusi, R.E.; Orazi, V.; Morelli, A.; Marchetti, J.M.; Juan, A. Theoretical Study of a Ti4 Cluster Interacting with B-Doped and Non-Doped Multivacancy Graphene. Phys. B Condens. Matter 2024, 683, 415875. [Google Scholar] [CrossRef]
- Ambrusi, R.E.; Orazi, V.; Marchetti, J.M.; Pronsato, M.E. Ni Clusters Embedded in Multivacancy Graphene Substrates. J. Phys. Chem. Solids 2020, 138, 109258. [Google Scholar] [CrossRef]
- Orazi, V.; Ambrusi, R.E.; Marchetti, J.M.; Pronsato, M.E. DFT Study of the Hydrogen Adsorption and Storage on Ni4 Cluster Embedded in Multivacancy Graphene. Int. J. Hydrogen Energy 2020, 45, 30805–30817. [Google Scholar] [CrossRef]
- Ambrusi, R.E.; Orazi, V.; Marchetti, J.M.; Juan, A.; Pronsato, M.E. Hydrogen Storage by Spillover on Ni4 Cluster Embedded in Three Vacancy Graphene. A DFT and Dynamics Study. J. Phys. Chem. Solids 2022, 167, 110706. [Google Scholar] [CrossRef]
- Faccio, R.; Fernández-Werner, L.; Pardo, H.; Goyenola, C.; Ventura, O.N.; Mombrú, A.W. Electronic and Structural Distortions in Graphene Induced by Carbon Vacancies and Boron Doping. J. Phys. Chem. C 2010, 114, 18961–18971. [Google Scholar] [CrossRef]
- Faccio, R.; Mombrú, A.W. Magnetism in Multivacancy Graphene Systems. J. Phys. Condens. Matter 2012, 24, 375304. [Google Scholar] [CrossRef]
- Faccio, R.; Mombrú, A.W. Influence of the Structural Configuration on the Stability and Magnetism in Multivacancy Graphene Systems. Comput. Mater. Sci. 2015, 97, 193–200. [Google Scholar] [CrossRef]
- Mombrú, D.; Faccio, R.; Mombrú, A.W. First Row Transition Metal Atoms Embedded in Multivacancies in a Rippled Graphene System. Appl. Surf. Sci. 2018, 435, 102–107. [Google Scholar] [CrossRef]
- Mombrú, D.; Faccio, R.; Mombrú, A.W. Sulfur Doping in Multivacancy Graphene Systems. Appl. Surf. Sci. 2018, 459, 336–344. [Google Scholar] [CrossRef]
- Rao, D.; Yang, H.; Shen, X.; Yan, X.; Qiao, G. Immobilisation of Sulphur on Cathodes of Lithium–Sulphur Batteries via B-Doped Atomic-Layer Carbon Materials. Phys. Chem. Chem. Phys. 2019, 21, 10895–10901. [Google Scholar] [CrossRef]
- Jyothirmai, M.V.; Ravva, M.K. Changes in Structure and Stability of Lithium Polysulfides Encapsulated in Carbon Nanotubes: A DFT Study. J. Mol. Liq. 2022, 359, 119287. [Google Scholar] [CrossRef]
- Yi, Z.; Su, F.; Huo, L.; Cui, G.; Zhang, C.; Han, P.; Dong, N.; Chen, C. New Insights into Li2S2/Li2S Adsorption on the Graphene Bearing Single Vacancy: A DFT Study. Appl. Surf. Sci. 2020, 503, 144446. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Dronskowski, R.; Bloechl, P.E. Crystal Orbital Hamilton Populations (COHP): Energy-Resolved Visualization of Chemical Bonding in Solids Based on Density-Functional Calculations. J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
- Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. Crystal Orbital Hamilton Population (COHP) Analysis as Projected from Plane-Wave Basis Sets. J. Phys. Chem. A 2011, 115, 5461–5466. [Google Scholar] [CrossRef] [PubMed]
- Nelson, R.; Ertural, C.; George, J.; Deringer, V.L.; Hautier, G.; Dronskowski, R. LOBSTER: Local Orbital Projections, Atomic Charges, and Chemical-bonding Analysis from Projector-augmented-wave-based Density-functional Theory. J. Comput. Chem. 2020, 41, 1931–1940. [Google Scholar] [CrossRef] [PubMed]
- Maintz, S.; Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. Analytic Projection from Plane-Wave and PAW Wavefunctions and Application to Chemical-Bonding Analysis in Solids. J. Comput. Chem. 2013, 34, 2557–2567. [Google Scholar] [CrossRef] [PubMed]
- Lehtinen, O.; Tsai, I.-L.; Jalil, R.; Nair, R.R.; Keinonen, J.; Kaiser, U.; Grigorieva, I.V. Non-Invasive Transmission Electron Microscopy of Vacancy Defects in Graphene Produced by Ion Irradiation. Nanoscale 2014, 6, 6569–6576. [Google Scholar] [CrossRef]
- Yan, R.; Zhao, Z.; Cheng, M.; Yang, Z.; Cheng, C.; Liu, X.; Yin, B.; Li, S. Origin and Acceleration of Insoluble Li2S2−Li2S Reduction Catalysis in Ferromagnetic Atoms-based Lithium-Sulfur Battery Cathodes. Angew. Chem. 2023, 62, e202215414. [Google Scholar] [CrossRef]
- Zhou, G.; Tian, H.; Jin, Y.; Tao, X.; Liu, B.; Zhang, R.; Seh, Z.W.; Zhuo, D.; Liu, Y.; Sun, J.; et al. Catalytic Oxidation of Li2S on the Surface of Metal Sulfides for Li−S Batteries. Proc. Natl. Acad. Sci. USA 2017, 114, 840–845. [Google Scholar] [CrossRef]
- Yang, G.; Shi, S.; Yang, J.; Ma, Y. Insight into the Role of Li2S2 in Li–S Batteries: A First-Principles Study. J. Mater. Chem. A Mater. 2015, 3, 8865–8869. [Google Scholar] [CrossRef]

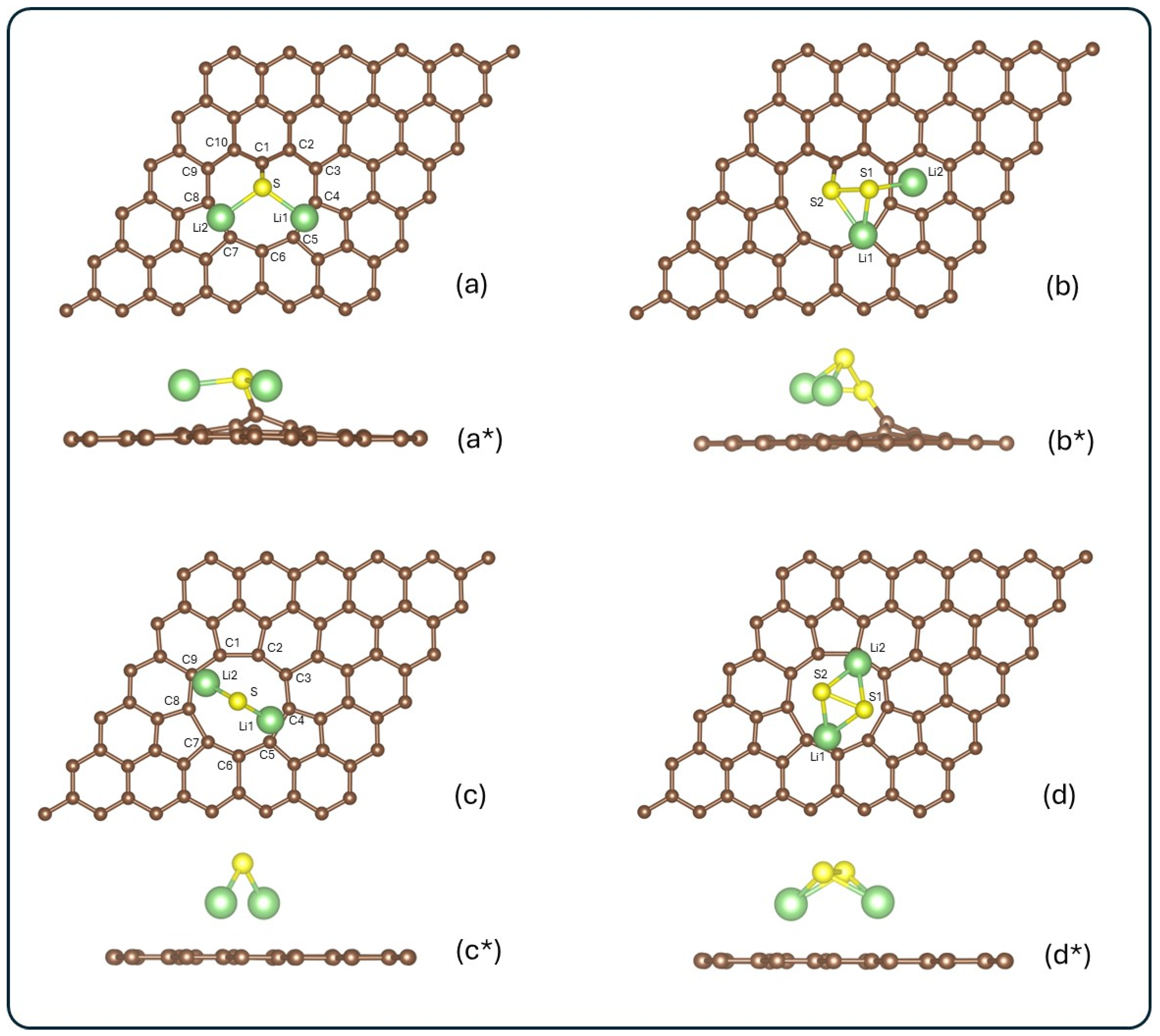
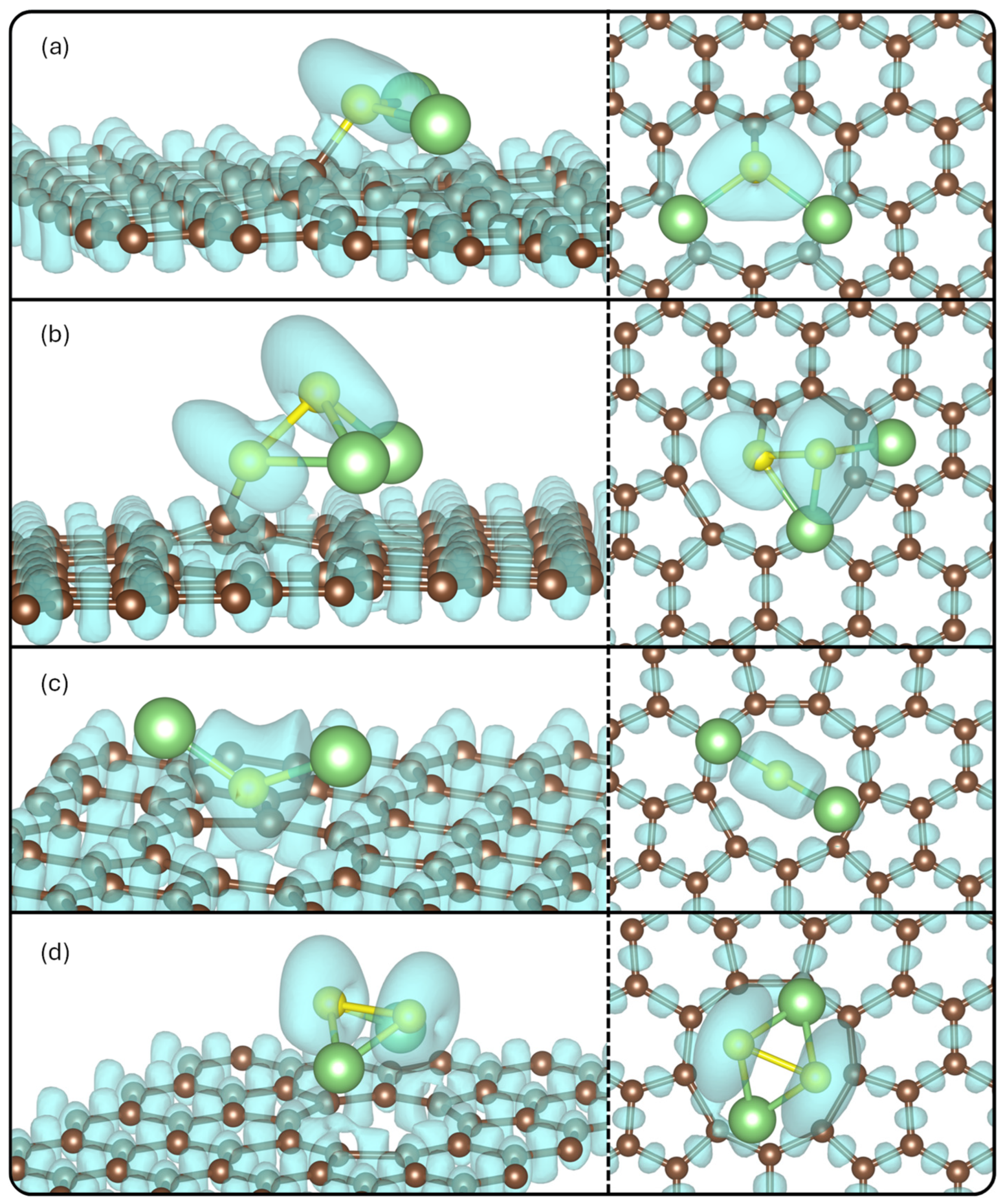

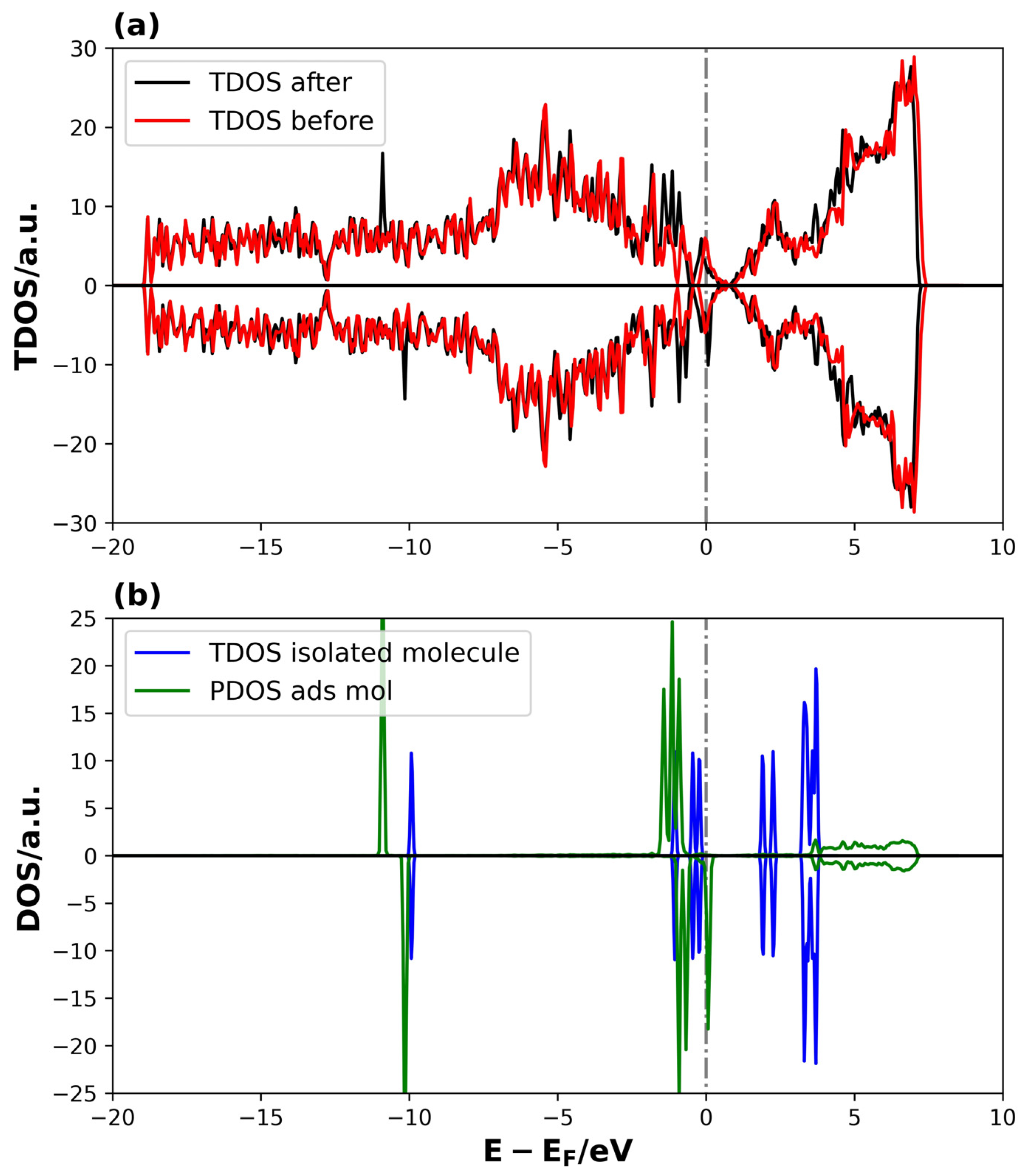
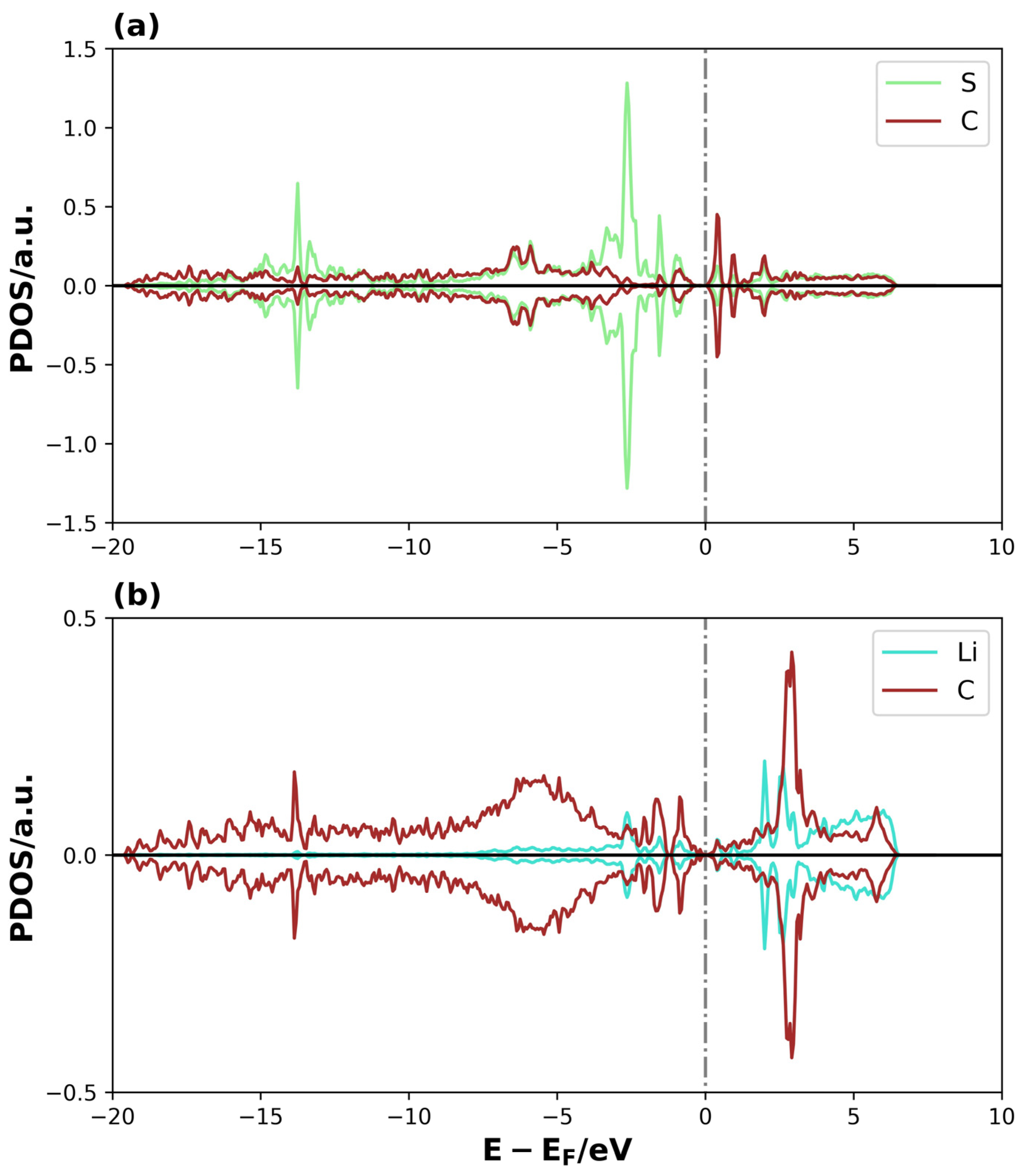

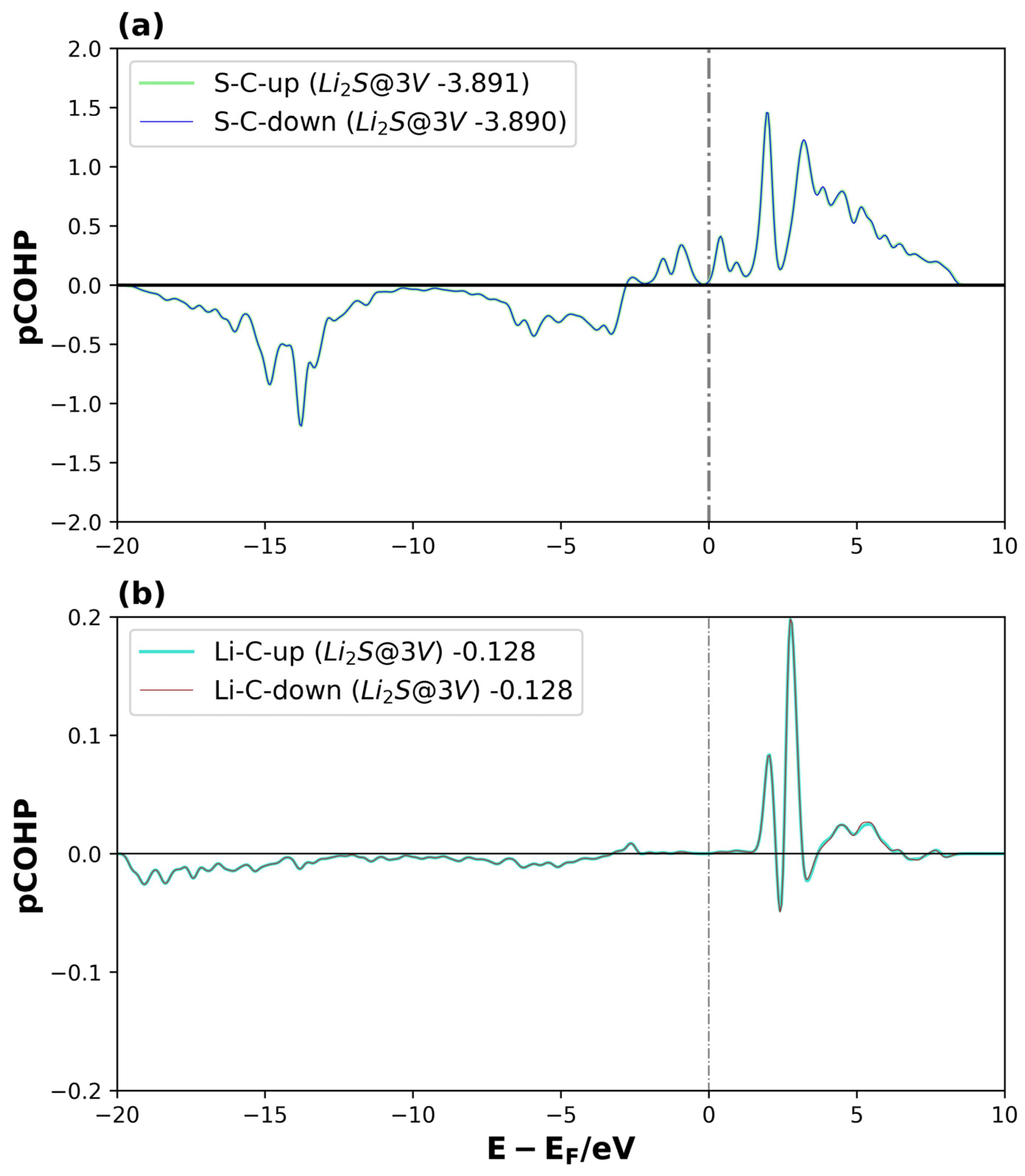
| System | Eads (eV) | |
|---|---|---|
| Li2S@3V-graphene | −3.84 | 0 |
| Li2S2@3V-graphene | −2.83 | 0 |
| Li2S@4V-graphene | −1.63 | 0.878 |
| Li2S2@4V-graphene | −1.51 | 0.944 |
| System | Carbon Ring Charge (e) | Graphene Charge (e) | Adsorbate Charge (e) |
|---|---|---|---|
| Li2S@3V-graphene | −0.80 | −1.01 | 1.13 |
| Li2S2@3V-graphene | −0.63 | −0.92 | 1.04 |
| Li2S@4V-graphene | −0.71 | −0.64 | 0.77 |
| Li2S2@4V-graphene | −0.60 | −0.63 | 0.75 |
| System | Bond | Before | After | % Δ |
|---|---|---|---|---|
| Li2S@3V-graphene | Li1–C5 | - | 0.084 | - |
| Li1–C4 | - | 0.091 | - | |
| Li2–C8 | - | 0.093 | - | |
| Li2–C7 | - | 0.084 | - | |
| S–C1 | - | 1.244 | - | |
| Li1–S | 0.440 | 0.205 | −53% | |
| Li2–S | 0.440 | 0.208 | −53% | |
| C1–C10 | 1.472 | 1.160 | −21% | |
| C1–C2 | 1.471 | 1.162 | −21% | |
| Li2S2@3V-graphene | S2–C1 | - | 1.077 | - |
| Li2–C3 | - | 0.070 | - | |
| Li1–C5 | - | 0.113 | - | |
| S2–Li1 | 0.223 | 0.118 | −47% | |
| S2–Li2 | 0.223 | 0.003 | −98% | |
| S1–Li1 | 0.223 | 0.202 | −9% | |
| S1–S2 | 1.546 | 1.402 | −9% | |
| C1–C10 | 1.472 | 1.221 | −17% | |
| C1–C2 | 1.471 | 1.224 | −17% | |
| C5–C4 | 0.695 | 0.770 | 11% | |
| C5–C6 | 1.240 | 1.180 | −5% | |
| C3–C4 | 1.219 | 1.169 | −4% |
| System | Bond | Before | After | % Δ |
|---|---|---|---|---|
| Li2S@4V-graphene | Li1–C5 | - | 0.082 | - |
| Li1–C4 | - | 0.082 | - | |
| Li2–C9 | - | 0.091 | - | |
| Li1–S | 0.440 | 0.309 | −31% | |
| Li2–S | 0.440 | 0.316 | −28% | |
| C5–C4 | 0.797 | 0.837 | 5% | |
| Li2S2@4V-graphene | Li1–C7 | - | 0.078 | - |
| Li1–C6 | - | 0.068 | - | |
| Li2–C2 | - | 0.092 | - | |
| S1–Li1 | 0.223 | 0.150 | −33% | |
| S1–Li2 | 0.223 | 0.152 | −32% | |
| S2–Li2 | 0.223 | 0.161 | −28% | |
| S2–Li1 | 0.223 | 0.158 | −29% | |
| S1–S2 | 1.546 | 1.664 | 8% | |
| C2–C1 | 0.797 | 0.835 | 5% | |
| C7–C8 | 0.797 | 0.831 | 4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaztañaga, F.; Ambrusi, R.E.; Juan, A.; Brizuela, G.P. Theoretical Study of the Adsorption of Li2S and Li2S2 Molecules on Multivacancy Defected Graphene. Surfaces 2025, 8, 76. https://doi.org/10.3390/surfaces8040076
Gaztañaga F, Ambrusi RE, Juan A, Brizuela GP. Theoretical Study of the Adsorption of Li2S and Li2S2 Molecules on Multivacancy Defected Graphene. Surfaces. 2025; 8(4):76. https://doi.org/10.3390/surfaces8040076
Chicago/Turabian StyleGaztañaga, Francisco, Rubén E. Ambrusi, Alfredo Juan, and Graciela P. Brizuela. 2025. "Theoretical Study of the Adsorption of Li2S and Li2S2 Molecules on Multivacancy Defected Graphene" Surfaces 8, no. 4: 76. https://doi.org/10.3390/surfaces8040076
APA StyleGaztañaga, F., Ambrusi, R. E., Juan, A., & Brizuela, G. P. (2025). Theoretical Study of the Adsorption of Li2S and Li2S2 Molecules on Multivacancy Defected Graphene. Surfaces, 8(4), 76. https://doi.org/10.3390/surfaces8040076






