Abstract
The main goal of the present study was to verify in detail whether the use of a cluster model for Stone–Wales (SW) defect-containing graphene (SWG) to study the adsorption of Ln atoms yields results similar to those previously obtained by employing a periodic model. We addressed this question by analyzing the optimized geometries of SWG + Ln complexes, their formation energies, and selected electronic parameters (in particular, the frontier orbital energies and atomic charges and spins). Within the frame of density functional theory, we used the computational methodology of the PBE-D2/DNP theoretical level using ECP pseudopotentials. The most important conclusion is that the use of a cluster model gives qualitatively similar results to those of the periodic model. While the corresponding plots of the dihedral angles θ versus the Ln atoms differ considerably, the two models have many common features in the trends of the bonding strength despite the use of two very different theoretical tools, namely periodic (plane waves) versus cluster calculations (localized basis sets). In comparing the results for SW defect-free and SW defect-containing cluster models, it is evident that SW defects serve as much more preferential adsorption sites compared to the conditions in the defect-free graphene model.
1. Introduction
Among the variety of structural imperfections that can exist in graphene sheets, those called Stone–Wales (SW) defects (often referred to as Stone–Thrower–Wales defects) deserve, and indeed have received, special attention [1,2,3,4,5,6]. One of the main reasons for this is that these types of defects do not require the removal of carbon atoms (as with vacancies) from or the addition of other atoms (heteroatoms) to the graphene backbone. Instead, the mechanism of SW defect generation implies 90° C-C bond rotation in the plane of the hexagonal network, which alters the nature of the sp2 backbone to a minimal degree.
On the other hand, the introduction of SW defects can have tangible effects on the physical and chemical properties of graphene compared to those of the pristine material, and this is the second main reason why they have been the subject of numerous studies (see, for example, refs. [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39]). In particular, it has been shown that the electronic [22,23,31,33,35,37], magnetic [8], and mechanical characteristics of graphene can be modified [16,17,19,25]. Among chemistry-oriented papers, those related to lithium doping and hydrogen storage [14,15,20,27] and the adsorption and/or chemisorption of main-group and transition metal atoms [9,12,13,18,28,34], lanthanide atoms [24,39], and simple ambient and organic molecules [7,9,10,11,12,21,26,28,36,38], as well as such large and complex molecules, such as transition metal monophthalocyanines [29] and rare-earth bisphthalocyanines [30,32], are worthy of mention.
Due to the evident and understandable difficulties in (or simply the principal impossibility of) direct experimental studies of the adsorption of various chemical species, the main source of information remains quantum-chemical calculations using density functional theory (DFT). Our reports [24,30,32,39] can serve as examples of such calculations; furthermore, they illustrate one of the most challenging tasks in treating highly degenerate systems containing 4f elements, that is, lanthanides (Ln). When considering such extended (or quasi-infinite) 2D systems as graphene sheets, two types of general theoretical modeling approaches can be employed: cluster-type or periodic. Depending on the particular goal, each of these models has its advantages and disadvantages, and it is impossible to know in advance which model will provide more trustworthy and realistic data. The optimal (but not always feasible) solution is to carry out both series of computations, then compare the results obtained. We followed this strategy when analyzing the interaction of single Ln atoms with a defect-free graphene sheet by using a 4 × 4 supercell (32 carbon atoms) for periodic calculations [40] and a supercoronene model (C54H18) for cluster calculations [41]. Even though we employed the same combination of functional and dispersion correction, we found considerable differences in the results. The most notable of these was a strong bending distortion in the supercoronene model, whereas the periodic model remained essentially planar.
In the present context, we were initially interested in the differences between the adsorption of Ln atoms onto pristine [40] and SW defect-containing [39] periodic graphene models, where an identical set of computation parameters was employed. We observed that the adsorption of lanthanide atoms induces considerable distortions in the SW defect-containing model, as is the case for a defect-free supercoronene cluster model [41]. Now, the question of how a cluster model of Stone–Wales defect-containing graphene (hereafter referred to as SWG) would behave upon the adsorption of Ln atoms, compared to the periodic model [39], arises. In the present study, we addressed this question by analyzing the optimized geometries of SWG + Ln complexes, their formation energies and selected electronic parameters (in particular, the frontier orbital energies and atomic charges and spins).
2. Computational Methodology
In the present work, we employed the DMol3 numerical-based DFT module [42,43,44,45] incorporated within the Materials Studio package. To facilitate a comparison with the previous related results [39,40,41], we maintained the use of the Perdew–Burke–Ernzerhof (PBE) general gradient approximation (GGA) functional [46] complemented by the empirical dispersion correction developed by Grimme [47]. This combination is usually referred to as PBE-D2. The basis set of choice was the DNP double-numerical basis set, which has a polarization d-function added to all non-hydrogen atoms plus a polarization p-function added to H atoms; this is approximately equivalent to the 6-31G(d,p) Pople-type basis set.
To make calculations involving lanthanide (as well as any other heavy element) species affordable, it is necessary to apply pseudopotentials. Within the DMol3 module, two types are available: DFT semi-core pseudopotentials (DSPPs; more recent and specially developed for use within this module), which implement relativistic effects and spin–orbit coupling, and quasi-relativistic effective core potentials (ECPs) [48,49]. As a recent comparative analysis [50] showed, both of these types exhibit certain imperfections. In particular, the use of DSPPs gives rise to very strong inversion of the frontier orbitals (with six empty orbitals between them) for Gd atoms, with a negative HOMO-LUMO gap value of −0.690 eV; calculations with ECPs do not exhibit such a flaw, but instead fail to reach self-consistent field (SCF) convergence for Tb [41,50]. In the present work, we decided to use ECPs, as in the previous reports [41,51].
The presence of 4f orbitals in lanthanide species results in the existence of a series of very close degenerate states near the Fermi level, which makes achieving SCF convergence almost always impossible without applying a thermal (or Fermi) smearing procedure. The correct way to apply it was illustrated in previous publications [32,39,40,41,51]; in particular, setting the smearing value as low as 0.0001 Ha (equivalent to a temperature of 31.6 K) produces stable and consistent results for most Ln-containing systems. The data reported here were obtained at the same smearing value.
The full geometry optimization and calculations of electronic parameters were completed with the convergence criteria set to ‘fine’, that is, to the following values: energy gradient, 10−5 Ha/Å; maximum force, 0.002 Ha/Å; maximum displacement, 0.005 Å; SCF tolerance, 10−6 Ha. The global orbital cutoff, defined by the presence of lanthanide atoms, was as high as 5.8 Å.
3. Results and Discussion
The cluster model for graphene containing the Stone–Wales defect at the center (SWG) is shown in Figure 1. One should note that its general formula C66H20 is somewhat larger than supercoronene model formula (C54H18) that was proposed for a defect-free graphene sheet [41]. The latter had a hexagonal symmetry, which cannot be conserved for a model with (at least) one SW defect. Furthermore, generating a SW defect within the supercoronene cluster would produce a low-symmetry C2v structure in which the defect would be displaced toward one edge; this would place it too close to its H atoms, and the two pentagonal rings would occupy non-equivalent positions. Instead, the C66H20 model has a higher D2h symmetry, where the SW defect is found at its center and has two equivalent pentagons.
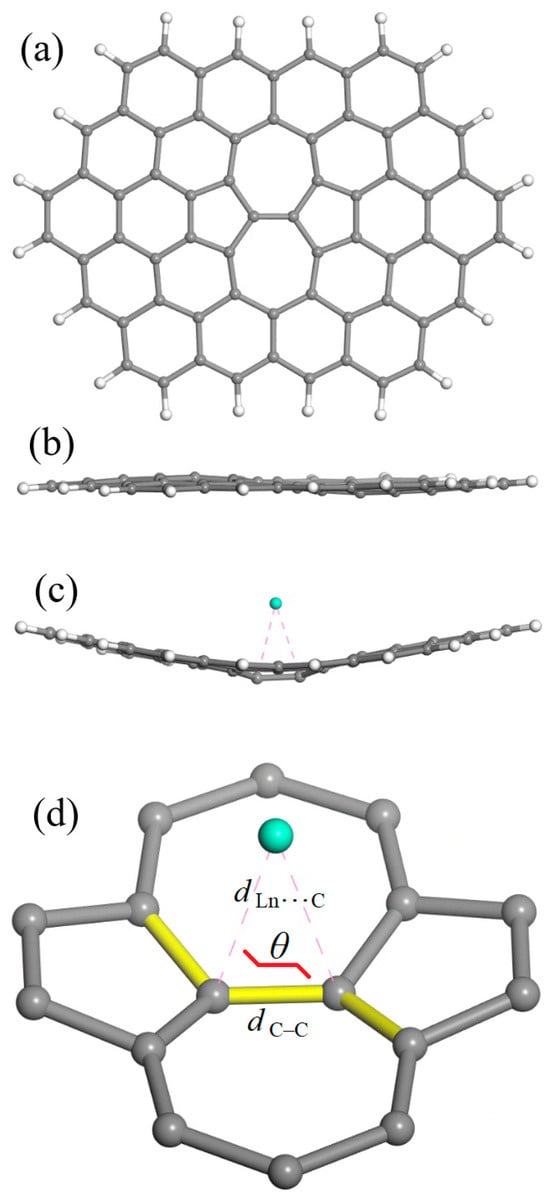
Figure 1.
The cluster model for graphene containing a Stone–Wales defect at the center (denoted as SWG; general formula C66H20): (a) top view and (b) side view. (c) A typical bent geometry (side view) for the SWG + Ln complexes. (d) Isolated SW defect with an adsorbed Ln atom, explaining the parameters employed for the geometry characterization: the C–C bond length (dC–C) in the (7,7) junction, the closest Ln⋯C approaches (dLn⋯C), and the dihedral angle θ (highlighted in yellow). Atom colors: carbon, gray; hydrogen, white; lanthanide, turquoise blue.
The choice of graphene models (cluster versus periodic) should be specifically addressed. The periodic models [39,40,51] can be a better match for the quasi-infinite structure of graphene sheet. A particular advantage of such calculations (which employ substantially different physical concepts and involve other types of parameters, such as plane waves, k-points, among others) is that they can provide information on band structure and density of states, which is crucial to characterize the material’s electronic properties. Cluster models, however, could be considered more general and versatile since they can account for a changeable chemical environment [52], such as oxidized functionalities at the graphene sheet edges [53,54,55,56]. Furthermore, introducing some defects gives rise to a symmetry that is impossible to implement in a periodic model, such as pentagonal symmetry due to the presence of one pentagonal ring [29,30,32,57].
Figure 1b shows that the SWG model is not totally planar, contrary to the common defect-free graphene models. Nevertheless, the degree of distortion is minor compared to the one observed for all SWG + Ln complexes (Figure 1c). Figure 1d shows what numeric characteristics were employed for the characterization of SWG + Ln complex geometry, namely, the C–C bond length (dC–C), the closest Ln⋯C approaches (dLn⋯C), and the dihedral angle θ.
As a matter of fact, the most important parameter describing the interaction between two chemical species is the bonding energy. As was demonstrated in our previous reports [39,41,57], the interaction between lanthanide species and graphene models is a very special (and somewhat ambiguous) case, in which the distortion of the normally planar polycyclic aromatic network of hexagonal rings inevitably and dramatically increases its energy. Due to elongation/shortening of C–C bonds and C–C–C angle bending, this increase (which we usually denote as ∆Edist) can be quantified by calculating the difference between the entire energy of the fully optimized isolated graphene model (either defect-free [39,52] or SW defect-containing [41]) and the single-point energy of the graphene model retrieved from the optimized graphene + Ln complex (in other words, after removing the Ln atom). Within the present context and terminology, the full formation energy ∆Efull for the SWG + Ln complexes can be calculated as
and it is a sum of two components, namely:
where ∆Ebond is the energy contribution specifically responsible for bonding between the Ln atom and SWG graphene model. It can be calculated as:
∆Efull = ESWG + Ln − (ELn + ESWG)
∆Efull = ∆Edist + ∆Ebond
∆Ebond = ∆Efull − ∆Edist
The ∆Efull, ∆Edist and ∆Ebond values obtained for all SWG + Ln complexes are specified in Table 1, with the corresponding plots presented in Figure 2a. The value attracting immediate attention is the positive formation energy ΔEfull of 7.8 kcal/mol calculated for SWG + Er, which could lead to the illogical conclusion that the interaction between SWG cluster and Er atom is repulsive. We previously addressed a similar situation for the complex of Gd atom with the supercoronene model, for which the ΔEfull was calculated to be 16.4 kcal/mol [41]. Nevertheless, the analysis based on the above equations provides a reasonable negative ∆Ebond value of −14.5 kcal/mol. As a whole, with some degree of oversimplification, one can say that the values of ∆Efull and ∆Ebond first increase from La to Sm and Eu, then decrease, then increase again from Dy to Er–Yb, and finally fall for Lu. Unfortunately, the central part of the two curves remains incognita due to the absence of data for Tb. The ΔEfull values span from −116.3 for La to 7.8 kcal/mol for Er, and the ΔEbond values, from −140.7 to −14.5 kcal/mol, for the same elements, respectively; in other words, by roughly one order of magnitude. Figure S1 compares the ΔEbond values calculated for the cluster (present work) and periodic SWG models [39] which shows that the general trends are rather similar.

Table 1.
The ∆Efull, ∆Edist, and ∆Ebond, along with HOMO, LUMO, and HOMO-LUMO gap energies for the SWG + Ln complexes.
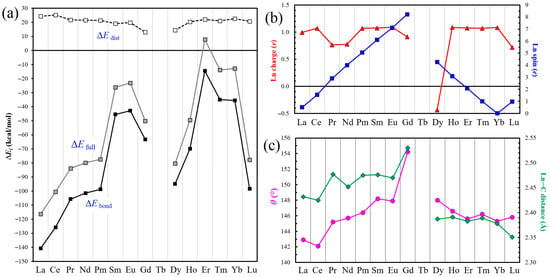
Figure 2.
(a) Changes in the ΔEfull, ΔEdist and ΔEbond energies (in kcal/mol) for the SWG + Ln complexes, from La to Lu. (b) Changes in charge (red) and spin (blue; absolute values) of the Ln atoms in SWG + Ln complexes, according to the Mulliken population analysis. (c) Changes in the dihedral angles θ for SWG + Ln complexes (dataset in pink) and in the corresponding Ln⋯C distances (green).
The values of ∆Edist, at the same time, change less significantly throughout the entire lanthanide series, not more than by a factor of two, from 13.0 kcal/mol for SWG + Gd to 25.2 kcal/mol for SWG + Ce. None of the energy parameters analyzed above correlate with the lanthanide contraction phenomenon.
When analyzing the geometric parameters (Figure 1d and Table 2), one can see that the shortest C–C bond (dC–C), 1.381 Å in the (7,7) junction, corresponds to SWG + Dy (central lanthanides), and the longest one, 1.428 Å, corresponds to the SWG complex with Yb, which does not have any unpaired electrons (in particular, its 4f shell is full). For comparison, the value of dC–C for the isolated optimized SWG model is 1.344 Å. For most SWG + Ln complexes, this bond length slightly fluctuates around 1.42 Å (Table 2). The SWG distortion can be most adequately characterized by the dihedral angle θ, which is 180° in the absence of Ln atoms. In the complexes, it varies from 142.1° for SWG + Ce to 154.2° for SWG + Gd (Table 2 and Figure 2c). It is important to note that the behavior of the dihedral angle θ qualitatively (ascending and descending branches of the plots) correlates with the closest Ln⋯C approaches (dLn⋯C). In particular, the longest dLn⋯C distances, 2.530 and 2.533 Å, were calculated for SWG + Gd. At the same time, the shortest ones, 2.351 Å for both, form in the case of Lu (and not Ce) complex; this is apparently caused by a manifestation of the lanthanide contraction.

Table 2.
The geometric parameters (Figure 1d), including the shortest distances dLn⋯C, the length of C–C bond in the (7,7) junction, the dihedral angle θ, along with the charge and spin of Ln species in SWG + Ln complexes, according to the Mulliken population analysis.
The charge and spin of Ln species in SWG + Ln complexes were retrieved from the Mulliken population analysis [58,59]. It was natural to expect that lanthanide atoms acquire some positive charge upon the interaction with a hyperconjugated aromatic system. Indeed, this is the case for all except for Dy, which becomes negatively charged (−0.434 e) (Figure 2b and Table 2). We made several attempts to recalculate SWG + Dy complex, but the value always remained negative. This appears to be an artifact of the Mulliken scheme because the Hirshfeld charge became positive (0.082 e), but was still too small. Unfortunately, it is not possible to obtain the related data for Tb, which is the ‘neighbor’ of Dy. For the remaining SWG + Ln complexes, the smallest positive charge on the lanthanide component was obtained for Lu (0.718 e), and the largest one, for Yb (1.090 e). This interesting observation was not expected. The Yb atom is a closed-shell species (note its close-to-zero spin of 0.003 e in SWG + Yb; Table 2), which should complicate the charge transfer. As the same time, the value for Lu could be expected to be higher due to the presence of one 5d electron, which is more easily transferrable to a graphene-like structure: that is, closer to the values of 0.995 e and 1.071 e found for La and Ce, respectively, both of which also contain one 5d electron.
Regarding the spin of adsorbed Ln atoms, they behave rather ‘smoothly’ (Figure 2b), correlating closely with the values of the isolated lanthanide atoms in their ground state. From Table 2, one can see that the calculated spin values tend to be positive (spin-up orientation), with a few exceptions of Ce, Gd, and Dy exhibiting negative values (spin-down). When analyzing their absolute values, one can see that, compared to the ground state, a spin gain takes place in most cases, with the exception of La, Ce, Pr, and Lu (spin depletion). The spin depletion varies from 0.010 e for Lu to as much as 0.496 e for La; the spin gain can be as negligible as 0.003 e for Yb, and reaches the maximum value of 0.276 e for Dy.
Another interesting related aspect is how exactly the unpaired electrons are distributed within SWG + Ln complexes, which can be visualized as spin density plots. In the isosurfaces at 0.02 a.u. (Figure 3), for the complexes with a low degree of spin gain or depletion (which form the majority of cases), only the lobes due to Ln atoms can be seen. The picture becomes more complicated for La (depletion of 0.496 e), Ce (depletion of 0.459 e), Gd (gain of 0.229 e) and Dy (gain of 0.276 e). In the latter two cases, minor spin-up lobes can be detected on the two carbon atoms of the (7,7) junction plus on the additional four C atoms adjacent to this bond. In the extreme cases of La and Ce, additional medium-sized lobes appear on the farthest C atoms of the heptagonal rings. Naturally, no lobes can be seen in the plot for SWG + Yb.
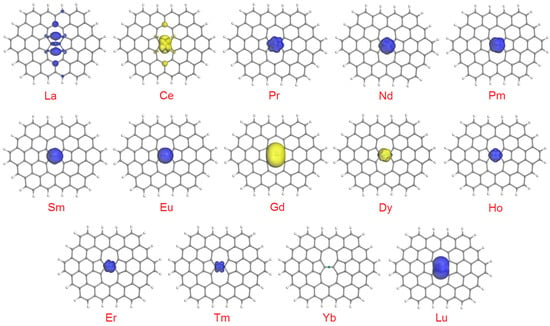
Figure 3.
Spin density plots (isosurfaces at 0.02 a.u.) for the SWG + Ln complexes. Blue lobes correspond to spin-up, and yellow lobes to spin-down unpaired electrons.
The last set of parameters we analyzed is the energies and distribution of the frontier orbitals. The HOMO, LUMO, and HOMO-LUMO gap energies for the SWG + Ln complexes are summarized in Table 1; for comparison, the corresponding values for the isolated components, that is, Ln atoms and SWG model, can be found in Table S1 in the Supplementary Materials. We focus on the HOMO-LUMO gap values, as the characteristics most important from the practical point of view. For the graphene model, we obtained the value of 0.893 eV. For the isolated Ln atoms, the gap energy spans from 0.203 eV for Ce to 2.867 eV for the closed-shell Yb. We discarded the negative value of −0.190 eV due to HOMO/LUMO inversion, as was observed for Sm [50]. In the case of SWG + Ln complexes, the variations in HOMO-LUMO gap energies were much less significant, from 0.225 eV for SWG + La to 0.995 eV for SWG + Eu. One can say, therefore, that this characteristic better correlates with the gap energy of the graphene model than with the one of isolated lanthanide atoms, with SWG + Yb (0.730 eV) as the most notable example.
The variability of the HOMO-LUMO plots presented in Figure 4 reflect the complexity in the behavior of the corresponding numerical values. All of the plots exhibit their own individual features. We attempted to classify them into categories, which are as follows:
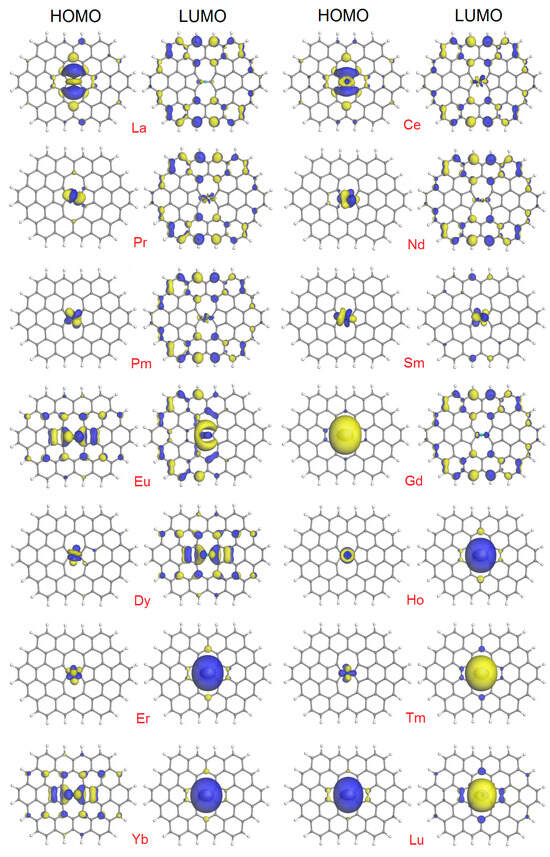
Figure 4.
HOMO and LUMO plots (isosurfaces at 0.03 a.u.) for the SWG + Ln complexes.
- (1)
- HOMO is localized (completely or mainly) on the Ln atom, and LUMO is distributed throughout heavy atoms of the complex. This is the case with Pr, Nd, Pm, Gd, and Dy.
- (2)
- HOMO expands from the Ln atom to the adjacent C atoms, and LUMO is distributed throughout most atoms of the complex. This is the case with La and Ce.
- (3)
- HOMO and LUMO are distributed to a similar degree but with a different pattern throughout heavy atoms of the complex. This is the case with Eu.
- (4)
- Both HOMO and LUMO are centered on the Ln atom, with a limited extension to the (mostly adjacent) C atoms. This is the case with Sm, Ho, Er, Tm, and Lu.
- (5)
- HOMO is distributed throughout heavy atoms of the complex (similar to SWG + Eu), with dominating LUMO lobes on Ln (as with the Ho, Er, Tm, and Lu complexes). This is the case with Yb.
4. Conclusions
The most important conclusion of the present study is that the use of a cluster model (general formula C66H20) for Stone–Wales defect-containing graphene to simulate the adsorption of Ln atoms gives qualitatively similar results compared to the periodic model [39]. There is a strong distortion of the adsorption site (SW defect), with the dihedral angle θ varying from 142.1° for SWG + Ce to 154.2° for SWG + Gd. In the case of the periodic model [39], the dihedral angle θ comprised the values from 140.9° for SWG + Tb to 149.7° for SWG + Sm. While the corresponding plots of θ versus Ln atom differ considerably, the trends in bonding strength (in terms of the ∆Efull and ∆Ebond energies) have many common features between the two models, despite the use of two very different theoretical tools, namely, periodic (plane waves) versus cluster models (localized basis sets).
When comparing the results for the defect-free (general formula C54H18 [41]) and SW defect-containing cluster models, it is evident that the presence of the SW defect in graphene produces energetically more favorable adsorption sites for Ln compared to pristine graphene. While the ∆Ebond values spanned from −72.4 to −4.6 kcal/mol for the defect-free cluster, in the present case, the bonding energy interval comprised from −140.7 to −14.5 kcal/mol, that is, the absolute values increased by roughly two times. The correlation between the ∆Ebond values for these two sets (Figure S2 in the Supplementary Materials) is much less evident compared to the one between the cluster (present work) and periodic SWG models [39] (Figure S1).
At the same time, at least two aspects need further clarification: (1) the behavior of Tb-containing systems (whose calculations fail when using the ECP pseudopotentials), and (2) why the Dy atom acquires a negative charge in SWG + Dy complex?
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/surfaces8020032/s1, Table S1: The total energies E, HOMO, LUMO, and HOMO-LUMO gap energies for the isolated components (Ln atoms and SWG model) and their SWG + Ln complexes, as well as single-point energies of the distorted SWG clusters after removing the Ln atom (SWG + Ln − Ln); Figure S1: Comparison between the ΔEbond values calculated for the cluster (present work) and periodic SWG models [39]; Figure S2: Comparison between the ΔEbond values calculated for the SWG (present work) and supercoronene cluster models [41].
Author Contributions
Conceptualization, E.V.B.; methodology, V.A.B.; validation, V.A.B.; formal analysis, V.A.B.; investigation, V.A.B.; resources, E.V.B.; data curation, V.A.B.; writing—original draft preparation, V.A.B.; writing—review and editing, E.V.B. and V.A.B.; funding acquisition, E.V.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Autonomous University of Mexico (UNAM), grant DGAPA-IG100125.
Data Availability Statement
Data is contained within the article or Supplementary Materials.
Conflicts of Interest
The authors have no competing interests to declare.
References
- Thrower, P.A. The study of defects in graphite by transmission electron microscopy. Chem. Phys. Carbon 1969, 5, 217–319. [Google Scholar]
- Stone, A.J.; Wales, D.J. Theoretical studies of icosahedral C60 and some related structures. Chem. Phys. Lett. 1986, 128, 501–503. [Google Scholar] [CrossRef]
- Leyssale, J.-M.; Vignoles, G.L. A large-scale molecular dynamics study of the divacancy defect in graphene. J. Phys. Chem. C 2014, 118, 8200–8216. [Google Scholar]
- Liao, Y.; Li, Z.; Chen, L.; Croll, A.B.; Xia, W. Crumpling defective graphene sheets. Nano Lett. 2023, 23, 3637–3644. [Google Scholar] [CrossRef]
- Dietrich, F.; Guevara, U.J.; Tiutiunnyk, A.; Laroze, D.; Cisternas, E. Vacancies and Stone–Wales defects in twisted bilayer graphene—A comparative theoretical study. FlatChem 2023, 41, 100541. [Google Scholar] [CrossRef]
- Chen, M.; Han, X.; Tang, K. Topological regulations of Stone-Wales graphene. Carbon 2024, 226, 119163. [Google Scholar] [CrossRef]
- Yang, F.O.; Huang, B.; Li, Z.; Xiao, J.; Wang, H.; Xu, H. Chemical functionalization of graphene nanoribbons by carboxyl groups on Stone-Wales defects. J. Phys. Chem. C 2008, 112, 12003–12007. [Google Scholar] [CrossRef]
- Chen, L.; Ouyang, Y.; Wang, Y.; Sun, Y.; Pan, H. The influence of Stone–Wales defects on magnetic properties in graphene. Phys. E Low-Dimens. Syst. Nanostruct. 2010, 43, 593–597. [Google Scholar] [CrossRef]
- Qin, X.; Meng, Q.; Zhao, W. Effects of Stone–Wales defect upon adsorption of formaldehyde on graphene sheet with or without Al dopant: A first principle study. Surf. Sci. 2011, 605, 930–933. [Google Scholar]
- Chen, L.; Li, J.; Li, D.; Wei, M.; Wang, X. Chemical functionalization of graphene by H adsorption on Stone-Thrower-Wales defects. Solid State Commun. 2012, 152, 1985–1989. [Google Scholar] [CrossRef]
- Guang, H.; Aoki, M.; Tanaka, S.; Kohyama, M. Hole doping by adsorption of oxygen on a Stone–Thrower–Wales defect in graphene. Solid State Commun. 2013, 174, 10–15. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, C.; Fu, Z.; Tang, Y.; Zhang, H. Adsorption of formaldehyde molecule on Stone–Wales defected graphene doped with Cr, Mn, and Co: A theoretical study. Comp. Mater. Sci. 2014, 83, 398–402. [Google Scholar] [CrossRef]
- Harman, A.J.; Raelynn, L. Density functional theory study of metal adatoms at or near a Stone-Wales defect in graphene. Procedia Eng. 2014, 93, 2–7. [Google Scholar] [CrossRef]
- Kim, D.; Lee, S.; Hwang, Y.; Yun, K.-H.; Chung, Y.-C. Hydrogen storage in Li dispersed graphene with Stone–Wales defects: A first-principles study. Int. J. Hydrogen Energy 2014, 39, 13189–13194. [Google Scholar] [CrossRef]
- Yildirim, H.; Kinaci, A.; Zhao, Z.-J.; Chan, M.K.Y.; Greeley, J.P. First-principles analysis of defect-mediated Li adsorption on graphene. ACS Appl. Mater. Interfaces 2014, 6, 21141–21150. [Google Scholar] [CrossRef]
- Long, X.J.; Zhao, F.P.; Liu, H.K.; Huang, J.Y.; Lin, Y.; Zhu, J.; Luo, S.N. Anisotropic shock response of Stone–Wales defects in graphene. J. Phys. Chem. C 2015, 119, 7453–7460. [Google Scholar] [CrossRef]
- Ebrahimi, S. Influence of Stone–Wales defects orientations on stability of graphene nanoribbons under a uniaxial compression strain. Solid State Commun. 2015, 220, 17–20. [Google Scholar] [CrossRef]
- Zhou, Q.; Fu, Z.; Wang, C.; Tang, Y.; Zhang, H.; Yuan, L.; Yang, X. The electronic and magnetic properties of B-doping Stone–Wales defected graphene decorated with transition-metal atoms. Phys. E Low-Dimens. Syst. Nanostruct. 2015, 73, 257–261. [Google Scholar] [CrossRef]
- Fu, Y.; Ragab, T.; Basaran, C. The effect of Stone-Wales defects on the mechanical behavior of graphene nano-ribbons. Comp. Mater. Sci. 2016, 124, 142–150. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, C.; Jiang, Q. Electric field induced enhancement of hydrogen storage capacity for Li atom decorated graphene with Stone-Wales defects. Int. J. Hydrogen Energy 2016, 41, 10776–10785. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, X.; He, F.; Li, K.; Wu, Z. Haeckelite and N-doped haeckelite as catalysts for oxygen reduction reaction: Theoretical studies. J. Phys. Chem. C 2017, 121, 28339–28347. [Google Scholar] [CrossRef]
- Zaminpayma, E.; Razavi, M.E.; Nayebi, P. Electronic properties of graphene with single vacancy and Stone-Wales defects. Appl Surf. Sci. 2017, 414, 101–106. [Google Scholar] [CrossRef]
- Rudi, S.G.; Faez, R.; Moravvej-Farshi, M.K.; Saghafi, K. Effect of Stone-Wales defect on an armchair graphene nanoribbon-based photodetector. Superlattices Microstruct. 2019, 130, 127–138. [Google Scholar] [CrossRef]
- Basiuk, V.A.; Kakazey, M.; Vlasova, M.; Basiuk, E.V. Effect of structural defects on the strength of adsorption of La and Lu species on graphene. Diam. Relat. Mater. 2019, 100, 107597. [Google Scholar] [CrossRef]
- Sadeghzadeh, S.; Ghojavand, M.; Mahmoudi, J. Influence of Stone-Wales defects on the mechanical properties of graphene-like polyaniline (PANI) C3N nanosheets. Diam. Relat. Mater. 2020, 101, 107555. [Google Scholar] [CrossRef]
- Kumar, J.; Ansh; Shrivastava, M. Stone–Wales defect and vacancy-assisted enhanced atomic orbital interactions between graphene and ambient gases: A first-principles insight. ACS Omega 2020, 5, 31281–31288. [Google Scholar] [CrossRef]
- Arokiyanathan, A.L.; Panjulingam, N.; Lakshmipathi, S. Chemical properties of lithium cluster (Lix, x = 2–8) on Stone–Wales defect graphene sheet: A DFT study. J. Phys. Chem. C 2020, 124, 7229–7237. [Google Scholar] [CrossRef]
- Yang, S.; Qian, X.; Xu, H.; Xiong, J.; Wang, Z.; Gu, H. The improved CO adsorption/sensing performance of Stone-Wales defected graphene doped with Fe: A DFT study. Phys. E Low-Dimens. Syst. Nanostruct. 2021, 128, 114603. [Google Scholar] [CrossRef]
- Mendoza-Domínguez, C.U.; Basiuk, V.A. Distortion and bonding strength of phthalocyanine molecules adsorbed on topological defects in graphene. Mater. Chem. Phys. 2021, 271, 124963. [Google Scholar] [CrossRef]
- Mendoza-Domínguez, C.U.; Basiuk, V.A. Adsorption of yttrium bisphthalocyanine on pristine and defect-contaning graphene models: A DFT study. Diam. Relat. Mater. 2022, 126, 109051. [Google Scholar] [CrossRef]
- Rudi, S.G.; Soleimani-Amiri, S. Bilayer armchair graphene nanoribbon photodetector with Stone-Wales defect: A computational study. Mater. Sci. Semicond. Proc. 2022, 150, 106918. [Google Scholar] [CrossRef]
- Mendoza-Domínguez, C.U.; Bolivar-Pineda, L.M.; Basiuk, V.A. Effect of structural defects in graphene on the geometry and electronic properties of adsorbed lanthanide bisphthalocyanines: A DFT analysis. Comp. Theor. Chem. 2023, 1225, 114152. [Google Scholar] [CrossRef]
- Oliveira, T.A.; Silva, P.V.; Meunier, V.; Girão, E.C. Tuning the carrier mobility and electronic structure of graphene nanoribbons using Stone–Wales defects. Carbon 2023, 201, 222–233. [Google Scholar] [CrossRef]
- Jovanović, A.Z.; Dobrota, A.S.; Skorodumova, N.V.; Pašti, I.A. Reactivity of Stone-Wales defect in graphene lattice—DFT study. FlatChem 2023, 42, 100573. [Google Scholar] [CrossRef]
- Wang, S.F.; Xue, D.; Liang, J.; Chen, L.Y.; Xie, Y.; Zhang, J.M. The synergistic regulation effect on the structure and electronic properties of graphene by methane plasma, Stone-Wales defect and equibiaxial strain. Diam. Relat. Mater. 2023, 140, 110426. [Google Scholar] [CrossRef]
- An, Y. Barrier height breakpoint in employing the Arrhenius equation to proton isotope permeation through Stone–Wales graphene. J. Phys. Chem. Lett. 2023, 14, 10779–10783. [Google Scholar] [CrossRef]
- Ghosh, M.; Chowdhury, S.; Majumdar, A.; Jana, D. Stone–Wales decorated phagraphene: A potential candidate for supercapacitor electrodes and thermal transport. ACS Appl. Electr. Mater. 2023, 5, 6725–6737. [Google Scholar] [CrossRef]
- Yuan, P.; Li, C.; Zhang, J.; Wang, F.; Chen, X. The special activity of Stone–Wales defect graphene for the oxygen reduction reaction: A comparison study between the charge-neutral model and the constant potential model calculated by density functional theory. J. Phys. Chem. C 2024, 128, 3250–3259. [Google Scholar] [CrossRef]
- Basiuk, V.A.; Wu, Y.; Prezhdo, O.V.; Basiuk, E.V. Lanthanide atoms induce strong graphene sheet distortion when adsorbed on Stone-Wales defects. J. Phys. Chem. Lett. 2024, 15, 9706–9713. [Google Scholar] [CrossRef]
- Basiuk, V.A.; Prezhdo, O.V.; Basiuk, E.V. Adsorption of lanthanide atoms on graphene: Similar, yet different. J. Phys. Chem. Lett. 2022, 13, 6042–6047. [Google Scholar] [CrossRef]
- Basiuk, E.V.; Prezhdo, O.V.; Basiuk, V.A. Strong bending distortion of supercoronene graphene model upon adsorption of lanthanide atoms. J. Phys. Chem. Lett. 2023, 14, 2910–2916. [Google Scholar] [CrossRef] [PubMed]
- Delley, B. An all-electron numerical method for solving the local density functional for polyatomic molecules. J. Chem. Phys. 1990, 92, 508–517. [Google Scholar] [CrossRef]
- Delley, B. Fast calculation of electrostatics in crystals and large molecules. J. Phys. Chem. 1996, 100, 6107–6110. [Google Scholar] [CrossRef]
- Delley, B. From molecules to solids with the DMol3 approach. J. Chem. Phys. 2000, 113, 7756–7764. [Google Scholar] [CrossRef]
- Delley, B.; Ellis, D.; Freeman, A.; Baerends, E.; Post, D. Binding energy and electronic structure of small copper particles. Phys. Rev. B 1983, 27, 2132–2144. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Dolg, M.; Wedig, U.; Stoll, H.; Preuss, H. Energy-adjusted ab initio pseudopotentials for the first row transition elements. J. Chem. Phys. 1987, 86, 866. [Google Scholar] [CrossRef]
- Bergner, A.; Dolg, M.; Kuechle, W.; Stoll, H.; Preuss, H. Ab initio energy-adjusted pseudopotentials for elements of groups 13–17. Mol. Phys. 1993, 80, 1431–1441. [Google Scholar] [CrossRef]
- Basiuk, V.A. DFT calculations on single lanthanide atoms: Is the task as simple as it seems? Comp. Theor. Chem. 2025, 1248, 115170. [Google Scholar] [CrossRef]
- Basiuk, V.A.; Prezhdo, O.V.; Basiuk, E.V. Thermal smearing in DFT calculations: How small is really small? A case of La and Lu atoms adsorbed on graphene. Mater. Today Commun. 2020, 25, 101595. [Google Scholar] [CrossRef]
- Colherinhas, G.; Fileti, E.E.; Chaban, V.V. The band gap of graphene is efficiently tuned by monovalent ions. J. Phys. Chem. Lett. 2015, 6, 302–307. [Google Scholar] [CrossRef]
- Basiuk, E.V.; Martínez-Herrera, M.; Álvarez-Zauco, E.; Henao-Holguín, L.V.; Puente-Lee, I.; Basiuk, V.A. Noncovalent functionalization of graphene with a Ni(II) tetraaza[14]annulene complex. Dalton Trans. 2014, 43, 7413–7428. [Google Scholar] [CrossRef]
- Basiuk, V.A.; Alzate-Carvajal, N.; Henao-Holguín, L.V.; Rybak-Akimova, E.V.; Basiuk, E.V. Coordination functionalization of graphene oxide with tetraazamacrocyclic complexes of nickel(II): Generation of paramagnetic centers. Appl. Surf. Sci. 2016, 371, 16–27. [Google Scholar] [CrossRef]
- Basiuk, V.A.; Rybak-Akimova, E.V.; Basiuk, E.V. Graphene oxide and nanodiamond: Same carboxylic groups, different complexation properties. RSC Adv. 2017, 7, 17442–17450. [Google Scholar] [CrossRef]
- Rodríguez-Otamendi, D.I.; Meza-Laguna, V.; Acosta, D.; Álvarez-Zauco, E.; Huerta, L.; Basiuk, V.A.; Basiuk, E.V. Eco-friendly synthesis of graphene oxide–silver nanoparticles hybrids: The effect of amine derivatization. Diamond Relat. Mater. 2020, 111, 108208. [Google Scholar] [CrossRef]
- Basiuk, V.A.; Acevedo-Guzmán, D.A.; Meza-Laguna, V.; Álvarez-Zauco, E.; Huerta, L.; Serrano, M.; Kakazey, M.; Basiuk, E.V. High-energy ball-milling preparation and characterization of Ln2O3−graphite nanocomposites. Mater. Today Commun. 2021, 26, 102030. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Akasaka, T.; Lu, X.; Adamowicz, L. Computational modeling of the Ce@C82 metallofullerene isomeric composition. ECS J. Solid State Sci. Technol. 2019, 8, M118–M121. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Akasaka, T.; Lu, X.; Adamowicz, L. Calculated relative thermodynamic stabilities of the Gd@C82 isomers. ECS J. Solid State Sci. Technol. 2021, 10, 071013. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).