Abstract
Density-functional theory calculations on P-rich InP(001):H surfaces are presented. Depending on temperature, pressure and substrate doping, hydrogen desorption or adsorption will occur and influence the surface electronic properties. For p-doped samples, the charge transition levels of the P dangling bond defects resulting from H desorption will lead to Fermi level pinning in the lower half of the band gap. This explains recent experimental data. For n-doped substrates, H-deficient surfaces are the ground-state structure. This will lead to Fermi level pinning below the bulk conduction band minimum. Surface defects resulting from the adsorption of additional hydrogen can be expected as well, but affect the surface electronic properties less than H desorption.
1. Introduction
Indium phosphide is frequently used for various applications, in particular in optoelectronics, high-speed electronics, and photovoltaics [1,2,3,4,5]. The structural and electronic properties of its growth plane have, therefore, been investigated for a long time, see, e.g., Ref. [6]. Typically, (i) the surface atoms form dimers in order to reduce the number of unsaturated surface dangling bonds and (ii) the electron counting principle [7] holds, i.e., the surfaces are uncharged and semiconducting, with empty cation dangling bonds and filled anion dangling bonds. In the case of clean surfaces, this leads to vacant dimer sites, i.e., surface reconstructions due to missing dimers.
Phosphorus-rich InP(001) surfaces grown by metal organic vapor phase epitaxy (MOVPE), or chemical beam epitaxy (CBE) are terminated by a monolayer of buckled P dimers. Hydrogen atoms adsorb on the dimer down P atoms and give rise to the formation of the so-called InP(001)(2 × 2)-2D-2H structure [8,9,10,11], see Figure 1 lhs. Depending on the H arrangement in adjacent P-dimer rows, in addition to the p(2 × 2) reconstruction also c(4 × 2) symmetries may be observed [12]. This disorder effect explains the (2 × 1)-like pattern typically observed in low energy electron diffraction (LEED). Due to the hydrogen saturation, no surface states occur in the energy region of the InP bulk band gap [13]. Interestingly, however, recent measurements [14] on MOVPE-grown P-rich InP (001) surfaces detected the Fermi level position slightly below the InP mid-gap energy.
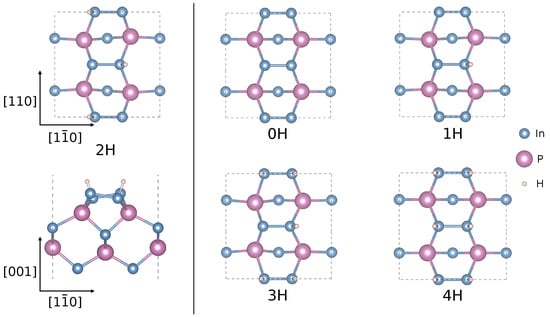
Figure 1.
Left: Top and side view of relaxed InP(001)(2 × 2)-2D-2H surface. Right: Top views of defective InP(001):H surfaces resulting from the 2H structure by H desorption (0H, 1H) and adsorption (3H, 4H). Pink (blue, gray) spheres represent In (P, H) atoms. The surface unit cells are indicated.
This finding motivates the present study. Surface defects appear as a plausible explanation for the appearance of surface states within the band gap [15,16,17,18,19]. Therefore, ab initio thermodynamics is used to determine the dominant defect species on InP(001):H surfaces. The present study goes beyond preliminary theoretical work [14] by (i) studying a variety of defects, (ii) accounting for substrate doping and defect charging, (iii) including spin polarization, and (iv) performing hybrid density-functional theory (DFT) calculations. The calculations study the energetics and charge transition levels of surface structures derived from the InP(001)(2 × 2)-2D-2H surface by considering H desorption and H adsorption. The structures considered in the present work are shown in Figure 1.
2. Method
Here spin-polarized density-functional theory (DFT) calculations are performed using the Vienna Ab-Initio Simulation Package (VASP) [20]. The electron exchange and correlation effects are treated within the generalized gradient approximation (GGA) using the PBE functional [21] for structural relaxation and band structure calculations. Hybrid DFT using the HSE functional [22] is employed to determine the defect energies and charge transition levels. The projector-augmented wave (PAW) scheme [23,24] describes the electron-ion interaction. The surfaces are modeled using periodic supercells that contain 12 atomic layers. A vacuum region of about 15 Å is used to decouple the material slab from its periodic image. The wave functions are expanded into plane waves up to an energy cutoff of 350 eV. The surface Brillouin zone is sampled using a -centered 4 × 4 k-point mesh. All interfaces are structurally relaxed until the forces acting on the atoms are below . Band structure calculations for defect-containing 2 × 2 surface unit cells were performed within 4 × 4 translational symmetry, in order to reduce spurious defect-defect interactions.
The Gibbs energy of formation for a surface defect D in charge state q in dependence on temperature T and pressure p is given by (see, e.g., Ref. [25])
where and are the Gibbs energies for surfaces with and without the defect, respectively, is the difference in the number of surface hydrogen referenced to the 2H surface, and is the hydrogen chemical potential. is the Fermi level, referenced to the InP bulk valence-band maximum. For surface calculations, we neglect the defect formation volume term and replace the Gibbs energy difference by the difference of the surface free energies calculated for the respective supercells. They are calculated here including vibrational and electronic entropy [26,27] as well as zero-point corrections in the harmonic approximation. In order to avoid comparing total energies of differently charged supercells, the Slater-Janak transition state model [28,29,30] is used, i.e., energy differences between N and electron systems are obtained from
assuming that the Kohn-Sham eigenvalue of the respective highest occupied state varies linearly with its occupation number. Hybrid DFT calculations result in an InP bulk band gap of 1.35 eV. We obtain the same value using quasiparticle calculations on the level of theory with three iterations in the Green’s function G. It is reasonably close to the measured value of 1.42 eV [31]. Generally, the technical accuracy in the calculation of excited state energies is of the order of 0.1 eV: Depending on the treatment of the electron screening and the level of self-consistency, InP bulk calculations result in a band gap between 1.32 and 1.56 eV [32,33,34].
The difference of the hydrogen chemical potential with respect to an isolated molecule, , is calculated in the approximation of a two-atomic ideal gas in dependence on partial pressure p and temperature T according to
where and are the rotational and vibrational partition functions, respectively, and the de Broglie thermal wavelength of the H2 molecule,
The density of some specific surface defect D is then finally obtained from the Boltzmann distribution according to
where N is the total number of potential defect sites.
3. Results
Figure 2 compares the calculated surface energies of the various defect structures considered here with the InP(001)(2 × 2)-2D-2H surface energy. Here, a hydrogen chemical potential eV is assumed. This value corresponds to typical InP growth conditions, see, e.g., Ref. [13]. In accordance with the experimental findings [8,14], the neutral charge state of the 2H structure is stable at these conditions for a wide range of Fermi level positions. This can be explained by the fact that this structure obeys the electron counting rule [7]. The charge state of the 2H surface changes from neutral to for Fermi levels below about 0.25 eV. This defines the lower limit of the band bending that can be expected upon p-doping. In reality, the band bending will be larger due to the desorption of hydrogen, as explained below.
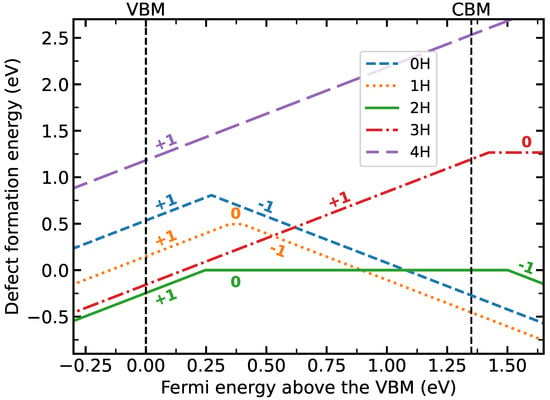
Figure 2.
Defect formation energies (with respect to the neutral 2H surface and assuming eV) for hydrogen-related InP(001):H surface defects calculated with the Slater-Janak transition state model as a function of Fermi energy.
The negatively charged 1H surface is lower in energy than the 2H surface for Fermi level positions above about 0.9 eV. This can be explained by the strong electron affinity of the partially filled P dangling bond. At the surface of n-doped samples, the P dangling bond is two-fold occupied and does not provide an adsorption site for hydrogen anymore. The strong electron affinity of the partially filled P dangling bond explains as well the strong preference of the negative charge state of the 0H defect structure.
The transition between the 2H and 1H surface structures depends on the hydrogen chemical potential, i.e., pressure and temperature, as well as on the Fermi level position. The latter dependence results from the charge term in Equation (1) and the electronic entropy contribution to the surface free energy. The thus calculated surface phase diagram is shown in Figure 3. As expected, high pressure in combination with low temperature and small Fermi energies stabilize the 2H with respect to the 1H surface. However, the transition between the 2H and the 1H structure will itself influence the Fermi level, due to the high density of surface P dangling bonds that have the potential to accept surface charge. Thus, no flat band conditions will occur for n-doped samples.
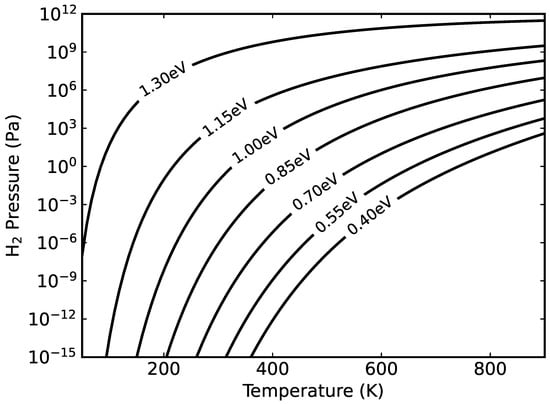
Figure 3.
The phase transition for the negatively charged 1H structure and the neutral 2H structure vs. temperature and pressure. Each curve is labeled with the corresponding Fermi level pinning energy. To the left (right) of each curve the 2H (1H) structure is the most stable.
We mention that concerning Figure 3 some caution is advised. It has to be kept in mind that further morphology changes, beyond the models shown in Figure 1, may occur. In particular, a transition from the P-rich InP surface to more cation-rich structures at temperatures above around 630 K has been observed [12,35]. Such structural transformations, that also depend sensitively on the hydrogen availability, are beyond the scope of the present work that focusses on P-dimer structures.
Adsorption of additional hydrogen, realized in the 3H and 4H defect structures, reduces the number of P surface dangling bonds. Accordingly, these structures are not stable in the negative charge state. Rather, the defects act as electron donors and are positively charged irrespective of the Fermi level position. Thus, they have no influence on the Fermi level position. Moreover, the adsorption of additional H in the form of the 3H and 4H defect structures is energetically not preferred, leading to a low density of the respective defects.
The detailed analysis of the defect formation probability requires the evaluation of Equation (5) in dependence on the hydrogen chemical potential, i.e., partial pressure and temperature as well as the Fermi level position. For n type material, the 1H surface is the most stable structure and will dominate (see Figure 3).
The total defect density in dependence on temperature and partial pressure for p type material is shown in the top panel of Figure 4. The parameter space can be divided into three regions. Low temperatures and high pressure make the 3H the most frequently occurring defect, whereas 0H is preferred for high temperatures. The 1H defect becomes dominant in between.
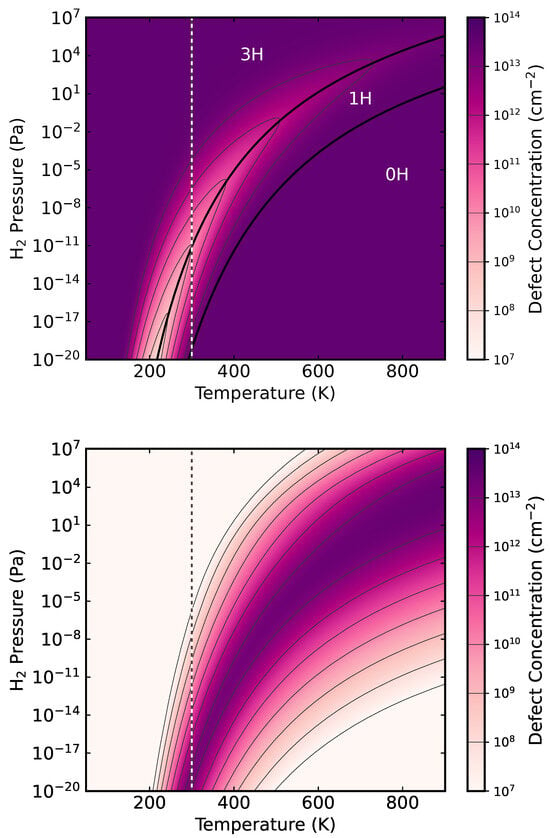
Figure 4.
Top: Total defect concentration on InP(001):H surfaces as a function of pressure and temperature for the p-type material. The respective most dominant defect species in dependence on temperature and pressure is indicated. Bottom: Density of the one H vacancy defect 1H. The vertical dashed lines depict room temperature.
The 1H defect is characterized by a charge transition state at about 0.37 eV above the bulk VBM. This is higher than the charge transition level of the 2H surface. Provided the defect density is sufficiently high, this could possibly explain the surface Fermi-level pinning in the lower half of the band gap observed experimentally for p-doped samples in Ref. [14]. The calculated 1H defect density for p-doped substrates is shown in the lower panel of Figure 4. The desorption of single hydrogens is the predominant defect type for in the range of to eV. This corresponds to MOVPE growth conditions [13]. A defect concentration range of to cm−2 is calculated for room temperature. This agrees nicely with the surface charge density of cm−2 concluded from the measured band bending [14] and supports the interpretation of the Fermi-level pinning in terms of H desorption related surface defects.
Here, again a word of caution is in order. On the one hand, we are aware of only a single measurement for the defect density. On the other hand, the seemingly good agreement between this measured value and the calculated defect density may be fortuitous to some extent: Already small uncertainties of the order of 0.1 eV in the Gibbs energy of defect formation cause a deviation in defect concentration of about cm−2. In addition, surface defects not considered in our work will occur as well [12,35]. Apart from hydrogen related defects also substrate related defects as well as domain boundaries can be expected. They will contribute as well to the measured surface electronic properties. This should be kept in mind when considering the numbers predicted in the present study.
The influence of the energetically most relevant 1H defect on the InP(001):H surface band structure and the electron density of states (DOS) is shown in Figure 5. For numerical reasons, the calculations are done on the DFT-GGA level of theory and suffer, therefore, from the DFT band gap problem [32,33]. The ideal InP(001)(2 × 2)-2D-2H surface is characterized by completely filled and empty surface states close to the InP valence and conduction band edges, respectively, see Ref. [13]. In contrast, the H vacancy gives rise to bound surface states in the band gap region. The atom-resolved DOS demonstrates that these states are of p character and primarily related to the partially filled P dangling bond. Spin polarization leads to an appreciable splitting of the P dangling bond related surface state. The occupied spin state moves close to the VBM and the unoccupied spin state is situated close to the conduction band. As expected, the effect of spin-polarization is essentially restricted to the defect state and does not play a role for the InP substrate states.
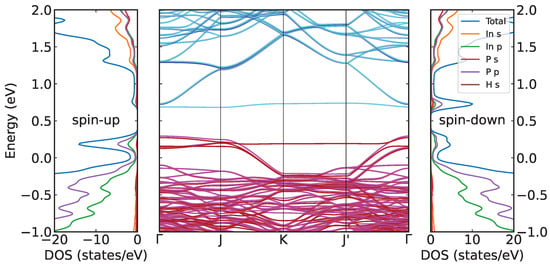
Figure 5.
Spin-polarized band structure and atom- as well as orbital-resolved electronic density of states of the InP(001):H-2D-1H surface calculated in a (4 × 4) surface unit cell. Magenta indicates occupied states with spin-down, red occupied with spin-up, cyan unoccupied with spin-down, and blue unoccupied with spin-up. The energy zero corresponds to the InP bulk valence band maximum.
4. Discussion
The results presented above show that the surface properties of gas-phase epitaxy grown InP surfaces depend sensitively not only on the surface preparation conditions, but also on the substrate doping. Depending on temperature and hydrogen partial pressure, adsorption of additional hydrogen or hydrogen desorption will occur. Desorption of hydrogen exposes P dangling bonds.
Electron donation by these bonds will pin the Fermi level on p-doped samples in the lower half of the band gap. This mechanism is somewhat complementary to the interpretation of recent experimental findings for hydrogen etched and hydrogen adsorbed GaAs(110) surfaces [18,19]: Here it has been argued that Ga-H bridge bonds and double-occupied Ga dangling bonds lead to a surface Fermi level pinning 0.25 to 0.3 eV above the valence band edge.
In case of of n-doped InP samples, even the ground-state structure of the surface can be expected to change. Rather than the neutral 2D-2H structure, negatively charged hydrogen deficient surfaces are stabilized. The exact cross-over between the 2D-2H surface and less H-rich surfaces depends on the surface preparation conditions as we as on the doping concentration. It will in any event, however, lead to a Fermi level pinning below the bulk conduction band minimum.
5. Conclusions
In the present work it is shown that the ideal 2D-2H InP surface structure derived previously from electron counting heuristics [7] is not sufficient to fully explain the measured electronic properties of gas-phase epitaxy grown P-rich InP(001):H surfaces. In particular the desorption of hydrogen, to be expected at elevated temperatures and in particular for n-doped samples, will give rise to an appreciable density of surface states that pin the Fermi level within the InP band gap. Our work underlines the importance of realistic surface models as well as the necessity of accounting for thermodynamic effects for a meaningful experiment-theory comparison.
Author Contributions
Conceptualization, I.A.R.A. and W.G.S.; Methodology, R.S. and I.A.R.A.; Software, R.S. and I.A.R.A.; Validation, R.S.; Formal Analysis, R.S. and I.A.R.A.; Investigation, R.S. and I.A.R.A.; Resources, W.G.S.; Data Curation, R.S. and I.A.R.A.; Writing—Original Draft Preparation, R.S.; Writing—Review & Editing, R.S., I.A.R.A. and W.G.S.; Visualization, R.S. and I.A.R.A.; Supervision, I.A.R.A. and W.G.S.; Project Administration, W.G.S.; Funding Acquisition, W.G.S. All authors have read and agreed to the published version of the manuscript.
Funding
Financial support by DFG (PAK981—SCHM1361/26) is gratefully acknowledged. The authors thank the Paderborn Center for Parallel Computing (PC2) and the Höchstleistungs-Rechenzentrum Stuttgart (HLRS) for grants of high-performance computer time.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yan, Z.; Han, Y.; Lin, L.; Xue, Y.; Ma, C.; Ng, W.K.; Wong, K.S.; Lau, K.M. A monolithic InP/SOI platform for integrated photonics. Light Sci. Appl. 2021, 10, 200. [Google Scholar] [CrossRef]
- Mukherjee, C.; Deng, M.; Nodjiadjim, V.; Riet, M.; Mismer, C.; Guendouz, D.; Caillaud, C.; Bertin, H.; Vaissiere, N.; Luisier, M.; et al. Towards Monolithic Indium Phosphide (InP)-Based Electronic Photonic Technologies for beyond 5G Communication Systems. Appl. Sci. 2021, 11, 2393. [Google Scholar] [CrossRef]
- Raj, V.; dos Santos, T.S.; Rougieux, F.; Vora, K.; Lysevych, M.; Fu, L.; Mokkapati, S.; Tan, H.H.; Jagadish, C. Indium phosphide based solar cell using ultra-thin ZnO as an electron selective layer. J. Phys. D Appl. Phys. 2018, 51, 395301. [Google Scholar] [CrossRef]
- Cheng, W.H.; Richter, M.H.; May, M.M.; Ohlmann, J.; Lackner, D.; Dimroth, F.; Hannappel, T.; Atwater, H.A.; Lewerenz, H.J. Monolithic Photoelectrochemical Device for Direct Water Splitting with 19% Efficiency. ACS Energy Lett. 2018, 3, 1795–1800. [Google Scholar] [CrossRef]
- Gao, L.; Cui, Y.; Vervuurt, R.H.J.; van Dam, D.; van Veldhoven, R.P.J.; Hofmann, J.P.; Bol, A.A.; Haverkort, J.E.M.; Notten, P.H.L.; Bakkers, E.P.A.M.; et al. High-Efficiency InP-Based Photocathode for Hydrogen Production by Interface Energetics Design and Photon Management. Adv. Funct. Mater. 2016, 26, 679–686. [Google Scholar] [CrossRef]
- Schmidt, W.G. III–V compound semiconductor (001) surfaces. Appl. Phys. A 2002, 75, 89. [Google Scholar] [CrossRef]
- Pashley, M.D. Electron counting model and its application to island structures on molecular-beam epitaxy grown GaAs(001) and ZnSe(001). Phys. Rev. B 1989, 40, 10481–10487. [Google Scholar] [CrossRef]
- Schmidt, W.G.; Hahn, P.H.; Bechstedt, F.; Esser, N.; Vogt, P.; Wange, A.; Richter, W. InP(001)-(2 × 1) Surface: A Hydrogen Stabilized Structure. Phys. Rev. Lett. 2003, 90, 126101. [Google Scholar] [CrossRef]
- Chen, G.; Cheng, S.F.; Tobin, D.J.; Li, L.; Raghavachari, K.; Hicks, R.F. Indium phosphide (001)-(2 × 1): Direct evidence for a hydrogen-stabilized surface reconstruction. Phys. Rev. B 2003, 68, 121303(R). [Google Scholar] [CrossRef]
- Hannappel, T.; Visbeck, S.; Töben, L.; Willig, F. Apparatus for investigating metalorganic chemical vapor deposition-grown semiconductors with ultrahigh-vacuum based techniques. Rev. Sci. Instruments 2004, 75, 1297. [Google Scholar] [CrossRef]
- Letzig, T.; Schimper, H.-J.; Hannappel, T.; Willig, F. P-H bonds in the surface unit cell of P-rich ordered InP(001) grown by metalorganic chemical vapor deposition. Phys. Rev. B 2005, 71, 033308. [Google Scholar] [CrossRef]
- Vogt, P.; Hannappel, T.; Visbeck, S.; Knorr, K.; Esser, N.; Richter, W. Atomic surface structure of the phosphorous-terminated InP(001) grown by MOVPE. Phys. Rev. B 1999, 60, R5117. [Google Scholar] [CrossRef]
- Hahn, P.H.; Schmidt, W.G. Surface Ordering of P-rich InP(001): Hydrogen Stabilization vs Electron Correlation. Surf. Rev. Lett. 2003, 10, 163–167. [Google Scholar] [CrossRef]
- Moritz, D.C.; Ruiz Alvarado, I.A.; Zare Pour, M.A.; Paszuk, A.; Frieß, T.; Runge, E.; Hofmann, J.P.; Hannappel, T.; Schmidt, W.G.; Jaegermann, W. P-Terminated InP (001) Surfaces: Surface Band Bending and Reactivity to Water. ACS Appl. Mater. Interfaces 2022, 14, 47255–47261. [Google Scholar] [CrossRef]
- Ebert, P.; Urban, K.; Aballe, L.; Chen, C.H.; Horn, K.; Schwarz, G.; Neugebauer, J.; Scheffler, M. Symmetric Versus Nonsymmetric Structure of the Phosphorus Vacancy on InP(110). Phys. Rev. Lett. 2000, 84, 5816–5819. [Google Scholar] [CrossRef] [PubMed]
- Qian, M.C.; Göthelid, M.; Johansson, B.; Mirbt, S. Atomic and electronic properties of anion vacancies on the (110) surfaces of InP, InAs, and InSb. Phys. Rev. B 2002, 66, 155326. [Google Scholar] [CrossRef]
- Hedström, M.; Schindlmayr, A.; Schwarz, G.; Scheffler, M. Quasiparticle Corrections to the Electronic Properties of Anion Vacancies at GaAs(110) and InP(110). Phys. Rev. Lett. 2006, 97, 226401. [Google Scholar] [CrossRef]
- Rosenzweig, D.S.; Hansemann, M.N.L.; Schnedler, M.; Ebert, P.; Eisele, H. Atomically resolved study of initial stages of hydrogen etching and adsorption on GaAs(110). Phys. Rev. Mater. 2022, 6, 124603. [Google Scholar] [CrossRef]
- Rosenzweig, D.S.; Schnedler, M.; Dunin-Borkowski, R.E.; Ebert, P.; Eisele, H. Morphologic and electronic changes induced by thermally supported hydrogen cleaning of GaAs (110) facets. J. Vac. Sci. Technol. B 2023, 41, 044202. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mat. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Freysoldt, C.; Grabowski, B.; Hickel, T.; Neugebauer, J.; Kresse, G.; Janotti, A.; Van de Walle, C.G. First-principles calculations for point defects in solids. Rev. Mod. Phys. 2014, 86, 253–305. [Google Scholar] [CrossRef]
- Valtiner, M.; Todorova, M.; Grundmeier, G.; Neugebauer, J. Temperature Stabilized Surface Reconstructions at Polar ZnO(0001). Phys. Rev. Lett. 2009, 103, 065502(R). [Google Scholar] [CrossRef]
- Zhang, X.; Grabowski, B.; Körmann, F.; Freysoldt, C.; Neugebauer, J. Accurate electronic free energies of the 3d,4d, and 5d transition metals at high temperatures. Phys. Rev. B 2017, 95, 165126. [Google Scholar] [CrossRef]
- Janak, J.F. Proof that = ϵ in density-functional theory. Phys. Rev. B 1978, 18, 7165–7168. [Google Scholar] [CrossRef]
- Sanna, S.; Frauenheim, T.; Gerstmann, U. Validity of the Slater-Janak transition-state model within the LDA+U approach. Phys. Rev. B 2008, 78, 085201. [Google Scholar] [CrossRef]
- Gallino, F.; Pacchioni, G.; Di Valentin, C. Transition levels of defect centers in ZnO by hybrid functionals and localized basis set approach. J. Chem. Phys. 2010, 133, 144512. [Google Scholar] [CrossRef]
- Madelung, O. Semiconductors: Group IV Elements and III-V Compounds (Data in Science and Technology); Springer: Berlin, Germany, 2013. [Google Scholar]
- Kim, Y.S.; Hummer, K.; Kresse, G. Accurate band structures and effective masses for InP, InAs, and InSb using hybrid functionals. Phys. Rev. B 2009, 80, 035203. [Google Scholar] [CrossRef]
- Schmidt, W.G.; Esser, N.; Frisch, A.M.; Vogt, P.; Bernholc, J.; Bechstedt, F.; Zorn, M.; Hannappel, T.; Visbeck, S.; Willig, F.; et al. Understanding reflectance anisotropy: Surface-state signatures and bulk-related features in the optical spectrum of InP(001)(2 × 4). Phys. Rev. B 2000, 61, R16335. [Google Scholar] [CrossRef]
- Chantis, A.N.; van Schilfgaarde, M.; Kotani, T. Ab Initio Prediction of Conduction Band Spin Splitting in Zinc Blende Semiconductors. Phys. Rev. B 2006, 96, 086405. [Google Scholar] [CrossRef]
- Hannappel, T.; Töben, L.; Möller, K.; Willig, F. In-Situ Monitoring of InP(100) and GaP(100) Interfaces and Characterization with RDS at 20 K. J. Electron. Mater. 2001, 30, 1425. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
