Long-Range ACEO Phenomena in Microfluidic Channel

Abstract

Microfluidic devices are increasingly utilized in numerous industries, including that of medicine, for their abilities to pump and mix fluid at a microscale. Within these devices, microchannels paired with microelectrodes enable the mixing and transportation of ionized fluid. The ionization process charges the microchannel and manipulates the fluid with an electric field. Although complex in operation at the microscale, microchannels within microfluidic devices are easy to produce and economical. This paper uses simulations to convey helpful insights into the analysis of electrokinetic microfluidic device phenomena. The simulations in this paper use the Navier–Stokes and Poisson Nernst–Planck equations solved using COMSOL to determine the maximum attainable fluid velocity with an electric potential applied to the microchannel and the most suitable frequency or voltage to use for transporting the fluid. Alternating current electroosmosis (ACEO) directs and provides velocity to the ionized fluid. ACEO can also mix the fluid at low frequencies for the purpose of dispersing particles. DC electroosmosis (DCEO) applies voltage along the microchannel to create an electric field that ionizes fluid within the microchannel, making it a cost-effective method for transporting fluid. This paper explores a method for an alternate efficient utilization of microfluidic devices for efficient mixing and transportation of ionized fluid and analyzes the electrokinetic phenomena through simulations using the Navier–Stokes and Poisson Nernst–Planck equations. The results provide insights into the parameters at play for transporting the fluid using alternating current electroosmosis (ACEO) and DC electroosmosis (DCEO).

1. Introduction

Microfluidics is a field that explores the movement, control, and modification of ionized fluids under various forces in a miniature environment. Crucial to this is electroosmosis, which is utilized for fluid transport and flow generation [1]. Microfluidics has been applied across various scientific fields, particularly in the biological and health sciences, as it offers an effective solution delivery system. Furthermore, it enables the rapid conduct of experiments in a cost-efficient manner at scale. Multiple common examples exist. One path is through medical diagnostics through the analysis of proteins or DNA, to indicate a health state via point-of-care testing. Another is through environmental monitoring, through which environmental pollutants can be rapidly scanned for, including heavy metals, toxic chemicals, or invasive species biomarkers, in water or air samples. Another is through food and beverage analysis for consumer product quality control, allowing for contaminate, poison, toxin, or unexpected metabolite identification. One of the core functionalities of microfluidic devices is pumping [2]. Microfluidics is the study of fluids in the micro- to nanoscale and is characterized by the use of thin and short channels for simulations. Numerous analytical solutions to boost specific uses have been described [3,4,5,6].

Microfluidic systems use microscopic channels to transport fluids through varied processes with modifiable parameters. One such process is called alternating current electroosmosis (ACEO), where an external electric field is applied to move the fluid through the microchannel. Another method is pressure-driven flow, which also moves fluid through the channel. These processes are essential for understanding how fluid flows through microchannels. In ACEO, the electric field created by the applied voltage generates a surface charge, which helps to drive the fluid flow, unlike a natural surface charge [7]. Using the ACEO process in microfluidic systems can create a stronger force to move fluid through the microchannel. This force is much stronger than other methods such as DCEO, but it requires a challenging design process. One drawback is that there is little space for pressure to build up, but this design provides excellent control in a small and precise context. To achieve this process, one needs to create electrodes that are both inexpensive and effective. These electrodes will generate the electric field necessary for the ACEO process to occur. An alternating potential difference is applied to each pair of asymmetric electrodes, creating a nonuniform electric field [8]. This field will then create two vortical flow patterns between each electrode that spans across the microchannel. Some advantages of using ACEO can be the sorting the particles undergo as they are filtered through the microchannel. ACEO can also be operated at low voltages, which is ideal and cost effective. Another advantage is the ability to manipulate the shape of the electrode. This advantage allows for fluid movement to flow in different patterns. For the sake of this study, a flat ended electrode will be used. In this process, a double-layer forms on the surface of the electrodes and channel. This induced charge is subjected to the action of the tangential component of the electric field, giving rise to a force directed from the center of the gap onto the electrode surface [9]. This layer allows for constant motion and movement of the ions in the fluid. This fluid movement then drives the bulk fluid through the entirety of the microchannel. Alternating current electroosmosis can also be used as a micromixing process. Dutta and Beskok introduced the new concept of time periodic electroosmosis [10], which has been expanded on since by using new geometries of the channel [11,12,13] and non-Newtonian fluids [14,15,16]. This technique is used primarily for mixing [17], more so than fluid transportation. As electric fields switch direction, localized flow also, switches and the double layer created does not change [9,18]. Further authors reported similar findings despite changing microchannel parameters, and this observation has been reported with the use of multiple different fluids within the microchannel. There are many different categories for micromixing. Some micromixing is due to an external force such as pressure [19], acoustics [20], electric field [21], and magnetic field [3]. Additionally, influentially reported through various approaches concerning parallel plates, ideal operating parameters, the viscoelastic nature of fluids, analytical modeling, and hydrodynamic dispersion involve modifying the Péclet number [4,5], ion partitioning [6], and concentration of ions in the electrolyte solution and EDL thickness [22]. Aside from acoustics and magnetic fields, this study focuses heavily on the other micromixers, along with passive micromixers such as the geometry of the microchannel. Electroosmotic flow (EOF) depends upon many factors that can be manipulated in microfluidics. The electric field created by the alternating current performs much of the mixing, which can be enhanced by additional pressure-driven flow.

Another process to take into consideration is DC electroosmosis. This process is typically known as electroosmotic flow (EOF) as well. DCEO dates back to the 19th Century when Reuss showed fluid motion between a cathode and anode in clay diaphragms, and these findings allowed a means for researchers to investigate microscale fluid flow [23]. Wiedemann expanded upon this concept and was among the first to provide an explanation for this phenomenon and find a way to create an experiment to study it [24]. In the early 1990s, most electroosmotic flow was used in rectangular channels [8] and circular channels [25]. Previous research on DCEO was limited by the technology available at the time, but advancements in micro-imagery in the 21st century allowed for deeper insights. Researchers discovered that DCEO can be created by using symmetrical electrodes with different charges across a microchannel. This setup creates an electric field that generates a vortical flow pattern between the electrodes, with the highest velocity near the electrode surface. The fluid in the microchannel contains many ions that flow in the direction of the electric field, creating an electric double layer. Due to the attractive forces between ions, the fluid is driven through the microchannel. The electric field polarizes the particles and moves them through the liquid or electrolyte. Dutta et al. [26] present the ability to build pressure using DC electroosmotic flow within a microchannel of different surface electrical properties. Similar findings were made by Herr et al. [27]. In mixed pressure-driven and electroosmotic flow [18], the use of pressure is important. There may also be an electrokinetic force that stems from an electric field [28]. One advantage of this process is that it is highly efficient and results in fast fluid flow. It only requires low voltages, which are easy to produce, yet it yields great results. It is a highly efficient process that requires very little energy input to achieve a high output. What follows this section is the mathematical method used to demonstrate electrokinetic phenomena and simulations to demonstrate them.

2. Mathematical Method

2.1. Alternating Current Electroosmosis

Alternating current electroosmosis (ACEO) is the electroosmotic flow due to an AC electric field created within a geometrical microchannel. This process involves creating an electric field with neighboring electrodes to generate fluid flow. The applied frequency to the electrodes tends to make the ions move in a vortex through the microchannel. ACEO will drive the fluid through a bulk diffuse layer and the double layer formed within the channel. Gonzalez et al. [29] presented their model for the electric double layer and their linear double theory. Kilic et al. [30] expanded upon their concept and claimed the potential difference across the electric double layer was greater than the thermal potential. In the microchannel, this process yields the ability for the ions to flow in two directions. In this process, there are two electrodes in the microchannel, one positively charged, and the other negatively charged. The positively charged ions will flow towards our negatively charged electrode, and vice versa. Due to ACEO, the charge of each electrode will constantly change. This will make the ions flow in their appropriate directions because of the conductive surface having and electric field of alternating current. Naturally, this phenomenon gives this process the name alternating current electroosmosis. ACEO is the process in which there is a double layer formed right above the surface of the channel and electrodes. Typically, it is a negatively charged surface, so the positive ions will form the first layer. The negative ions will then form the next layer. In ACEO, the surface charges are induced by some external voltage applied by the electrode [31]. Above this, there is a diffuse layer where any free ions will move in their electrical attraction direction. Most of the fluid is unaffected in the bulk layer and is quickly guided through the channel via ACEO. It is still possible to manipulate neutral particles using the DEP process [10].

2.2. Governing Equations

The equations can be derived for AC electroosmosis, coming from the Navier–Stokes and continuity equations. After some simplifying, the equation appears to be:

$$∆p=\mu ∆V+\overrightarrow{F}\left(\overrightarrow{r},t\right)$$

(1)

$$\nabla ·\overrightarrow{V}=0$$

(2)

The $p$ represents the pressure, $V$ is the flow velocity, and $\overrightarrow{F}$ is body force per unit volume.

For AC electroosmosis, another set of equations can be derived pertaining to slip velocity, Laplace, Poisson, and Nernst–Planck, respectively:

$$u_t=-\frac{\epsilon }{\mu }\left[\left(\tilde{\varphi }-\tilde{\psi }\right)\widetilde{\overrightarrow{E_t}}\right]$$

(3)

$$-{\epsilon }_f{\nabla }^2\psi =0$$

(4)

$$-{\epsilon }_f{\nabla }^2\varnothing =F\left(c_1-c_2\right)$$

(5)

$$\nabla ·\left(u{c}_i-D_i\nabla c_i-z_i\frac{D_i}{RT}F{c}_i\nabla \varnothing \right)=0,i=1,2$$

(6)

From Equation (3), the $\tilde{\varphi }$ is the complex electric potential at the inner side of the diffuse layer, and the $\widetilde{\overrightarrow{E_t}}$ is the tangential (complex) electric field. From Equations (4)–(6), ${\epsilon }_f$ is the permittivity of the electrolyte solution; $z_i$, $D_i$, and $c_i$ are the valence, diffusivity and ionic concentration of ionic species K⁺ (i = 1) and Cl⁻ (i = 2), respectively; and $F$, R, and T are the Faraday constant, gas constant, and the absolute temperature, respectively [32].

2.3. Boundary Conditions

To solve Equations (1) and (2), in this study we used different inlet velocities, the outlet boundary condition was atmosphere pressure and channel walls used electroosmotic velocity. For electric current, we use Equations (4) and (5), where the applied electric potentials were V₀sin(ωt) and −V₀sin(ωt) in electrodes. For transport diluted species, we used Equation (6) and inlet boundary used C₀ (1 mol/m³).

Due to low Reynolds number, the inertial term was neglected from the Navier–Stokes equation. Electroosmotic velocity boundary conditions were used on top and bottom walls in the microchannel. Zero pressure was used in the outlet boundary and different inlet velocities were used in the inlet boundary. Navier–Stokes and continuity equations were coupled in this simulation. The electric field was governed by the Laplace equation, and electric insulation was used for the inlet and outlet boundaries in the microchannel. Electric potential was V₀sin(ωt) and −V₀sin(ωt) applied in electrodes. Nernst–Planck equation was used for ions transportation. Bulk concentration was used for the inlet boundary and outflow boundary. No flux was used in the top and bottom boundaries. Navier–Stokes, Continuity, Laplace, Poisson, and Nernst–Planck equations along with boundary conditions (Equations from (1) to (6)) were solved using COMSOL Multiphysics.

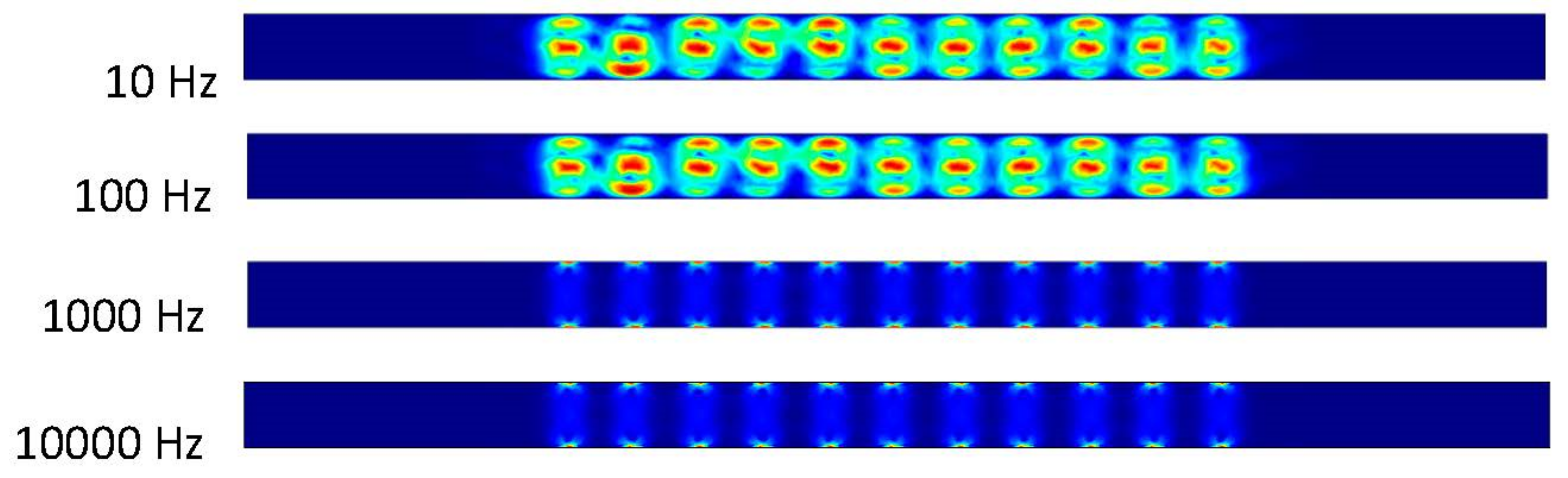
Typically, ACEO requires a lower voltage as well. ACEO will also tend to occur between 10–100 Hz, as observed in our simulations. As ions flow in the vortical pattern, it also drives the rest of the fluid through the bulk of the microchannel. Ramos et al. [33] describe the electrode pattern for fluid flow in a preferred direction. Since this process typically occurs at lower frequencies and voltages, the direction of flow is determined by the pressure-driven flow due to inlet velocity. To improve pumping due to ACEO, Huang et al. [34] presented the idea of stepping the electrodes and comparing them to the typical micropump. In this study, the arrangement for the electrodes will be similar to the typical micropump build.

2.4. Direct Current Electroosmosis

Electroosmotic flow is the liquid motion due to an externally applied electric field that directs the flow of ions. This process is the movement of fluid due to electrodes having a set charge. Electroosmosis is the motion of ionized liquid relative to the stationary charged surface under the action of an applied electric field. With these set charges, an electric field form can be observed. The ions will move in the direction of our electric field and will assist in the drive of our fluid. The surface will be negatively charged, which will attract our positive ions. This will create base layers and an electric field. These base layers typically form into electric double layers. The electric double layer is rich in cations, which will create an electric field. This electric double layer will drive positive ions in the same direction as the electric field it created. Negative ions will flow in the opposite direction of the electric field. The bulk layer of fluid will be driven in the same direction as the positive ions and electric field. In this process, we do not have any pressure-driven flow, strictly just the DCEO movement. We can derive an equation for flow velocity in our channel. Our equation is:

$$u\left(y\right)=-\frac{\zeta \epsilon }{\mu }{E}_x\left(1-\frac{\psi \left(y\right)}{\zeta }\right)$$

(7)

The $\psi$ represents the electric potential in the fluid, $E_x$ represents the tangential electric field, $y$ represents the distance away from our channel centerline, and $\zeta$ is the zeta potential.

At the channel surface, the electric potential approaches the zeta potential [1]. We can also use the Helmholtz–Smoluchowski velocity equation when the electric potential drops to zero. The approximated equation is:

$$u_{HS}=-\frac{\zeta \epsilon }{\mu }{E}_x$$

(8)

The unchanged parameters are called constants. The parameters are set as Diffusivity (D) = 1 × 10⁻¹¹ m²/s, Density $(\rho )$ = 1000 kg/m³, Zeta Potential $(\zeta )$ = −0.1 V, Electric Permittivity $(\epsilon )$ = 80.2 F/m, Conductivity $(\sigma )$ = 0.11845 S/m, T= 298K, R = 8.314 J·mol⁻¹K⁻¹, and Bulk concentration c0 = 1 mol/m³, V₀ = 2V.

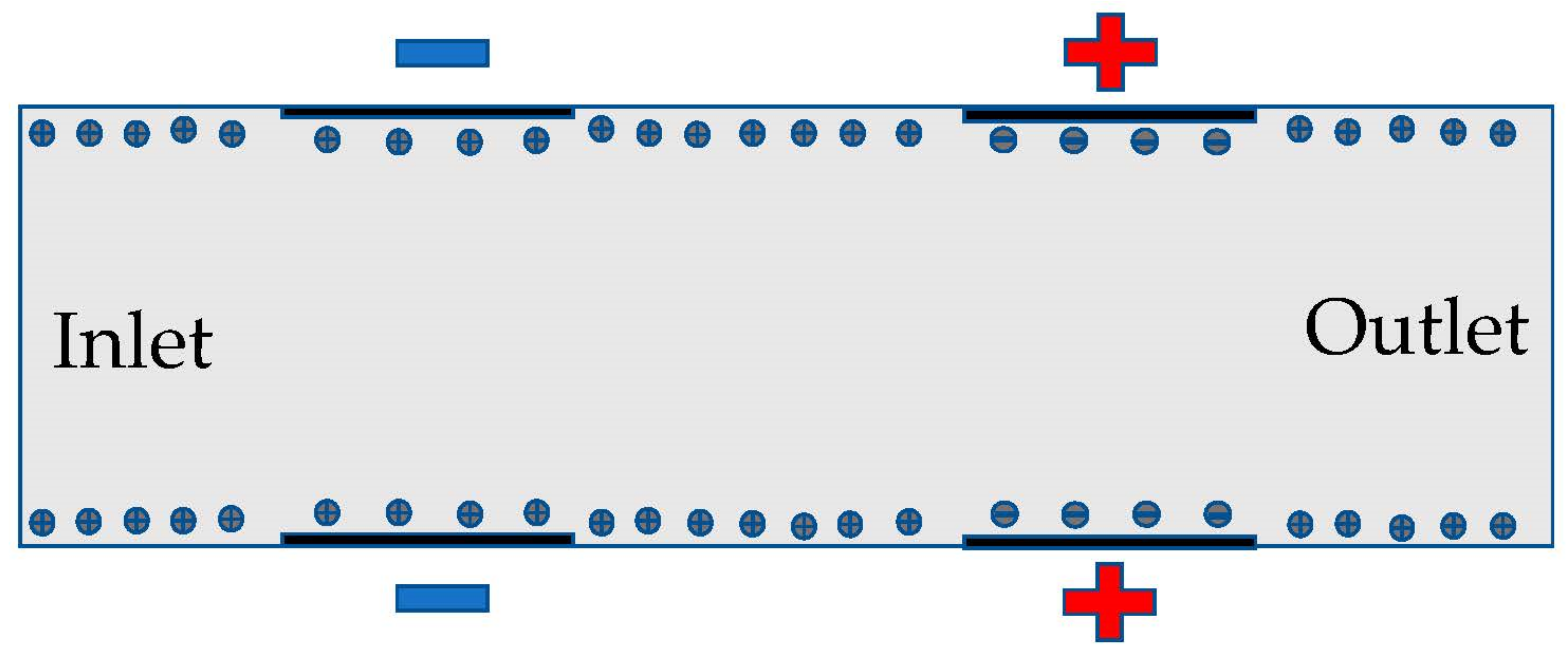
The electrodes are directly across from one another in the microchannel in Figure 1. The layer of ions forms at the surface of the channel, allowing for the electric field to drive the fluid. The geometry of the microchannel determines the electroosmotic flow and the mixing capabilities of the fluid. Figure 1 is zoomed in and not to scale for purposes of showing more details and only shows 4 sets of electrodes instead of all sets of electrodes.

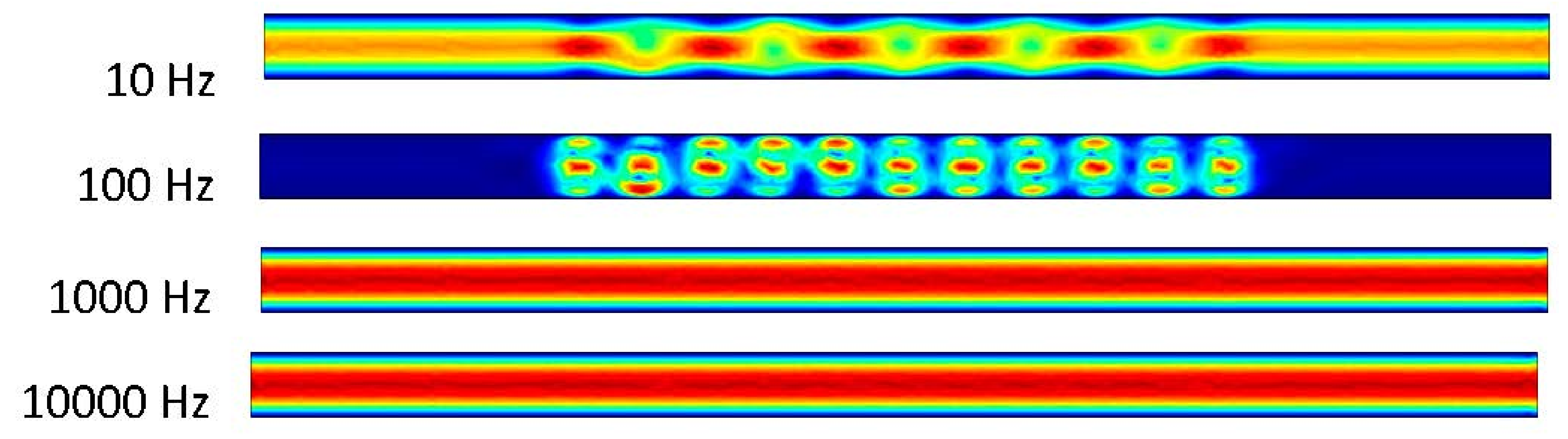
The full microchannel picture is shown in the left image before the applied mesh on microchannel, and the same size scale image is shown in the right after the applied mesh on the device (Figure 2). The length of the microchannel is 2000 microns and has a height of 100 microns. In this study, the channel length to height ratio was 20:1. We investigated long-range ACEO phenomena in microchannels. Our simulation results show long-range fluid induced by ACEO at 10 Hz. Strong vortices were observed on the top and bottom electrodes of the microchannel at low frequency. Lu et al. [35] observed centimeter scale vortices when channel height changes. There are 6 sets of electrodes on the top and bottom of the microchannel. Each set contains a positive and negative electrode. The electrodes are set symmetrically across channels. Each electrode has a width of 90 microns with a spacing of 10 microns. The first electrode from the inlet is 400 microns away. Similarly, there are 400 microns between the last electrode and the outlet.

2.5. Mesh

A physics-controlled mesh was used in the entire domain. The element quality was skewness, and 1947 mesh vertices were used in the entire geometry. Mesh generation was implemented in the simulation region. In this work, we used 2292 triangles, 632 quads, 336 edge elements and 52 vertex elements. The number of elements was 2924, the element area ratio was 0.088 and the average element quality was 0.833.

3. Simulations and Results

The focus of the study is to understand the electroosmotic flow of fluids when put under various circumstances. The simulation results of the microchannel vary when they undergo increasing velocities and frequencies that increase by a factor of ten. Throughout the simulation, the changing frequency that is induced upon the electrodes can be observed to play a huge role in the vortical flow of ions in the channel. The simulation begins with an alternating current, which changes the directional flow along with the magnitude of the velocity constantly, producing an electric double layer along the walls of the microchannel. Ramos et al. [7] studied the ACEO where the fluid flow is always in one direction, but when the experiment was carried out by the same group, the theory was inconclusive [36]. The use of a direct current that flows continuously in one direction produces similar results in the transportation of the ionic fluid, such as the process of dielectrophoresis [37]. There are findings that show the particle movement of a densely populated system can produce a fluid flow and become a pump in DEP [38,39]. The same concept should work for DCEO. The ionized fluid used in the study is sodium chloride (NaCl). When using this fluid, the ions contained within the fluid will have either a positive or negative charge, which will determine the flow through the microchannel. We can do this through several processes such as alternating current electroosmosis (ACEO) or direct current electroosmosis (DCEO). ACEO is a process in which the flow of the fluid occurs between the conductive surfaces of our electrodes, producing a vortical flow of ions. DCEO is the motion of the particles due to fixed charged electrodes. This process should be inexpensive to create, quickly produced, and use minimal materials [40,41,42,43,44,45], which produce successful results.

3.1. AC Electroosmosis

Our first step was to run the simulation using COMSOL. The initial inlet velocity is zero. The data taken start at zero seconds with every data point taken after occurring one tenth of a second until two seconds are reached. The frequency applied to the electrodes begins at ten followed by one-hundred, one-thousand, and ten-thousand Hertz (Figure 3, Figure 4 and Figure 5).

3.2. AC Electroosmosis with Pressure Driven Flow

3.2.1. 100 nm/s

For the remaining trials, there are various values for inlet velocity driving the fluid through the microchannel. The first data set will include trials of 100 nm/s inlet velocity. Despite this velocity being a very small value, it produces great results in transportation and mixing of the fluids. However, since the scale is small, this inlet velocity is driving a considerable amount of fluid through the microchannel. The effects this inlet velocity has on the microfluidic device channels and the fluid flowing through them vary from each frequency value.

Figure 6 shows that the frequency exerted upon the electrodes has a resulting effect upon the fluid at 10 and 100 Hz. At 1000 and 10,000 Hz, it can be determined from the ACEO definition that the frequency is too much for the process to occur compared to the pressure-driven flow having the greater effect on the fluid. These results are from the 100 nm/s inlet velocity after one second. The detailed imagery gives a sense of directional flow during the ACEO process. It can be determined from the imagery that the ACEO occurs in the 10 Hz microchannel trial. The fluid velocity at one second in the 10 Hz microchannel is 0.408 μm/s. This time there is a helical flow pattern when the bulk of the ions flow in the vortical pattern throughout the charged section of the microchannel in the 10 Hz trial. The ions go from electrode to electrode diagonally, causing the fluid to flow in this pattern as well. In the 100 Hz trial, there is a slight mixture of ACEO and pressure-driven flow occurring. Towards the center of the microchannel, the velocity vectors and their magnitude have maximum values. The flow is 0.277 μm/s, and it decreases towards the sidewalls of the channel before it increases again. It can be observed there is an interesting symmetry in the flow pattern throughout the microchannel. As well as with the other 1000 and 10,000 Hz trials, the pressure-driven flow takes over. The flow velocity in both of those microchannels is 0.155 μm/s.

3.2.2. 300 nm/s

The next trials have an inlet velocity of 300 nm/s exerted upon them. This is a 200 nm/s increase from the last data set, which is a substantial amount in the microchannels. The differences this will have on the microchannels vary from trial to trial through the simulation imagery.

It can be observed that the ACEO process takes place in the 10 and 100 Hz trials in Figure 7. In the 10 Hz trial, there is an interesting movement of the fluid occurring in the microchannel. There is an increase in velocity through the center of the channel. This velocity is 0.71 μm/s. This comes from the increase in the inlet velocity and pressure-driven flow. Similar results can be observed between the 100 Hz trial and the previous results. The velocity in the 100 Hz trial at 1 s is 27.7 μm/s. The final two trials of 1000 and 10,000 Hz are identical to previous trials where the pressure-driven flow is the main component in the microchannel, with the velocity of the flow being 0.464 μm/s. The imagery above shows the helical flow pattern throughout the mixture, as mentioned before in the 10 Hz trial. The flow moves from top to bottom of the microchannel as it also flows circularly through the microchannel. The ACEO process may be occurring, but it is not as strong as the pressure-driven flow. A closer look at the velocity arrows will indicate the pressure-driven flow beginning to take over. The inlet is on the left side of the simulation imagery, so the pressure-driven flow is pushing the fluid to the right, which agrees with the velocity arrows. In the 100 Hz trial, the velocity arrows oppose the inlet velocity, but they are not as big in size. This indicates the flow is not very strong in that direction.

In Figure 6 and Figure 7, the flow patterns inside the channel were different when the applied frequency at the electrodes was 10 Hz. In both cases, pressure-driven flow and ACEO played important roles for fluid motion. Based on incompressible Navier–Stokes and continuity equations, fluid motion surged inside the channel when the inlet velocity increased, which was observed in this study. Though the fluid flow pattern was similar in Figure 6 and Figure 7 when the frequency was 100 Hz, their maximum velocity magnitudes were different in both cases. At 100 Hz, ACEO played a dominating role compared to pressure-driven flow for fluid motion. The fluid flow pattern was similar in Figure 6 and Figure 7 when applied at a high frequency such as 1000 and 10,000 Hz in electrodes. In both cases, pressure-driven flow played a more important role than the ACEO process.

3.2.3. 500 nm/s

The next set of data demonstrates the flow at 500 nm/s inlet velocity. Yet again, the inlet velocity is increasing by 200 nm/s. As can be determined from the imagery below, the results are similar to the earlier trials. The flow is almost identical throughout the whole microchannel.

Figure 8 shows an interesting phenomenon in the 10 Hz trial. The pressure-driven flow appears to take over and the ACEO is not strong enough to compete with the inlet velocity. This results in a velocity of 1.01 μm/s. In the 100 Hz trial, the ACEO occurring in the microchannel can be observed. It appears to be concentrated at this frequency, which is reasonable from the ACEO definition, thus resulting in a flow velocity of 27.9 μm/s in the 100 Hz frequency microchannel. It appears that in the 1000 and 10,000 Hz trials, the pressure-driven flow and ACEO are driving the fluid at an increased rate. In these microchannels, the flow velocity is 0.773 μm/s.

3.3. AC Simulated Mixing

3.3.1. AC Mixing with Pressure Driven Flow

In these trials, the dispersion of separate particles is studied as micromixing occurs within the microchannels (Figure 9 and Figure 10). They are subjected to various elements that alter their results such as frequency changes, inlet velocity applied, and time. Mei et al. [46] investigate the electroosmotic micromixing of non-Newtonian fluid in a microchannel.

10 μm/s

Moving on to the simulated concentration at 10 μm/s, the results become interesting. Figure 11 and Figure 12 are the results from zero to 0.5 s. The microchannel is subjected to flow from the head end, spreading down the entire length of the tube. As mixing occurs for 0.5 s, there is a mix of the fluid at the electrode ends in the 10 and 100 Hz trials. The flow velocity in the 10 Hz concentration microchannel is 0.116 μm/s. In the 100 Hz microchannel, the velocity is 0.189 μm/s. The results from the 1000 and 10,000 Hz trials stay relatively the same with a possibility of minimal mixture. The flow velocity at 0.5 s is 0.107 μm/s. The first data set is at zero seconds and the final set is at 0.5 s. Figure 11 shows the separation that occurs in the microchannel after exerting an inlet velocity that is much greater than previous trials. Figure 12 shows the mixture of the two fluids as the ACEO and pressure-driven flow act within the microchannel.

The ACEO phenomenon depends on positive ion dominated electrical double layer (EDL), negative ion dominated EDL, frequency, time and potentials. In Figure 11, the results were taken when the time was zero seconds. Fluids flow from the inlet to outlet due to the pressure-driven flow, and the inlet velocity was 10 μm/s. ACEO did not play any role when time was 0 s, hence two fluids were separated, and no mixing occurred. In Figure 12, two fluids were mixed at low frequency (10 and 100 Hz) when the time was 0.5 s. ACEO plays the important role of mixing the two fluids inside the channel. However, at high frequencies such as 1000 and 10,000 Hz, the two fluids were separated. In this study, we observed that the ACEO phenomenon was negligible at high frequencies. Consequently, Figure 11 and Figure 12 have similar types of results.

50 μm/s

The next data set is the concentration at 50 μm/s inlet velocity. This is a noticeable difference from the last set of data. These results are also from zero to 0.5 s. As with before, the first set is at zero seconds and the last set is at 0.5 s.

It was observed that the mixture and separation of the fluids as they are acted upon by the ACEO process and the inlet velocity produce interesting results. In the first four trials (Figure 13), there is separation between the two fluids. The results are congruent throughout each trial. This is due to the inlet velocity being a large value. This pressure-driven flow is pushing the fluid through at an increased rate and there is no room for the fluid to separate more. The next four trials (Figure 14) show the mixture between the fluids. The results are similar to previous results. In the area of the electrodes, more mixing occurs due to the ACEO process at that point. In the 10 Hz microchannel, the flow velocity is 0.114 μm/s. In the 100 Hz microchannel, the flow velocity is 0.18 μm/s. In the 1000 and 10,000 Hz microchannels, the ACEO definition stands as the better results happen at lower frequencies and it is possible to visualize what is truly happening in the microchannel at the lower frequency. In these two microchannels, the flow velocity is 0.105 μm/s.

3.3.2. AC Graphs

We can now look at trends in our solution through our graphs. These graphs show the paths our solution takes throughout all of our inlet velocities ranging from 0 to 200 μm/s. They also show the conductivity, concentration, and frequencies.

In Figure 15, we can see the trend of velocity at each frequency set. In our first trial of 0 inlet velocity, we see the biggest differences and changes in our graph. We can recall that only the electrodes were doing work in this process. It reaches a maximum velocity of 27.89 μm/s in our 100 Hz. It then decreases to a value of 5.9856 × 10⁻²⁶ m/s in our 1000 Hz trial. It follows this trend because we determined the ACEO process produces the greatest results at lower frequencies. For our trials of 0.1–10 μm/s inlet velocity, we can observe a maximum value at our 100 Hz condition. They all then decrease back to a flat slope. It continues to be a flat graph for these trials because the inlet velocity keeps our fluid driving through our microchannel. For inlet velocities above 10 μm/s, the pressure-driven flow is too strong for the ACEO process to occur.

3.3.3. DC Electroosmosis

Figure 16 shows that the DCEO phenomena occurred inside the channel when DC voltage was applied on the electrodes. The fluid makes the circular motion in the microchannel that is similar to our results from our ACEO trials. The magnitude of the velocity is increased as the applied voltage increases as well. The results are congruent throughout each trial as well. We can also observe only the DCEO process occurring as there is no pressure-driven flow driving the fluid through our microchannel.

3.3.4. DC Graphs

Figure 17 shows the applied voltage vs. maximum velocity graph in the microchannel. The maximum velocity is in units of μm/s and the applied voltage is in units of volts (V). The maximum velocity was calculated inside the channel using Equation (8) (the Helmholtz–Smoluchowski velocity). Where $\zeta$ is the zeta potential, electric permittivity $(\epsilon ),$µ is the dynamics viscosity and Ex is the applied voltage. In Equation (8), zeta potential, electric permittivity and dynamics viscosity are constants, hence fluid motion increased when the applied voltage increased, which was observed in this study in Figure 17. The trend in our graph is linear. To increase our maximum fluid velocity, we had to increase our applied voltage; we can see this occur in Figure 17. At one volt, our fluid experienced a velocity of 4.13 × 10⁴ μm/s. At seven volts, our fluid experienced a velocity of 2.89 × 10⁵ μm/s. It also seems to increase at a constant rate, making our slope linear. Figure 17 shows that our maximum velocity will increase as we increase the voltage.

Figure 18 shows fluid conductivity vs. our maximum velocity. Conductivity is in units of S/m and our maximum velocity is in units of nm/s. This graph shows the trends for the applied DC current of 6 volts. At 0.1 S/m, we can observe a maximum velocity of 3.8767 × 10⁶ nm/s. The graph shows that our maximum velocity increases slowly with a lower conductivity. It then spikes at 0.3 S/m and gives us a maximum velocity of 3.8772 × 10⁶ nm/s. At 0.4 S/m, we have a maximum velocity of 3.87815 × 10⁶ nm/s. Our slope then flattens back out between 0.4 and 0.5 S/m. Our conductivity value of 0.5 S/m gives us a maximum velocity of 3.8784 × 10⁶ nm/s.

4. Discussion

Note that this work only examines COMSOL simulations with standard NS and Smoluchowski equations. That said, the ACEO is a method for transporting and mixing fluids within a microchannel using an alternating current electric field. The ACEO governing equation [18] demonstrates that higher electric fields lead to higher fluid velocities, which was confirmed through simulations. The tangential electric field points parallel to the electrode surface, allowing the fluid to flow throughout the channel driven by the electric field. The simulations showed that the flow rate increased from 0.358 μm/s at 10 Hz to 27.9 μm/s at 100 Hz. At 1000 and 10,000 Hz, a unique phenomenon was observed where the maximum fluid velocity occurred at the electrode surface and the electric field reduced the fluid motion in the center of the channel. Adding a pressure-driven flow improved the fluid velocity in all trials, with the 1000 and 10,000 Hz trials showing that the pressure-driven flow dominated the electric field. The conductivity slopes in Figure 11 followed a similar trend, with the 100 Hz trial showing a drastic increase in maximum velocity as conductivity increased. The 10 Hz trial had smaller maximum velocity values compared to the 100 Hz trial. The trendline for 1000 and 10,000 Hz remained constant throughout all trials.

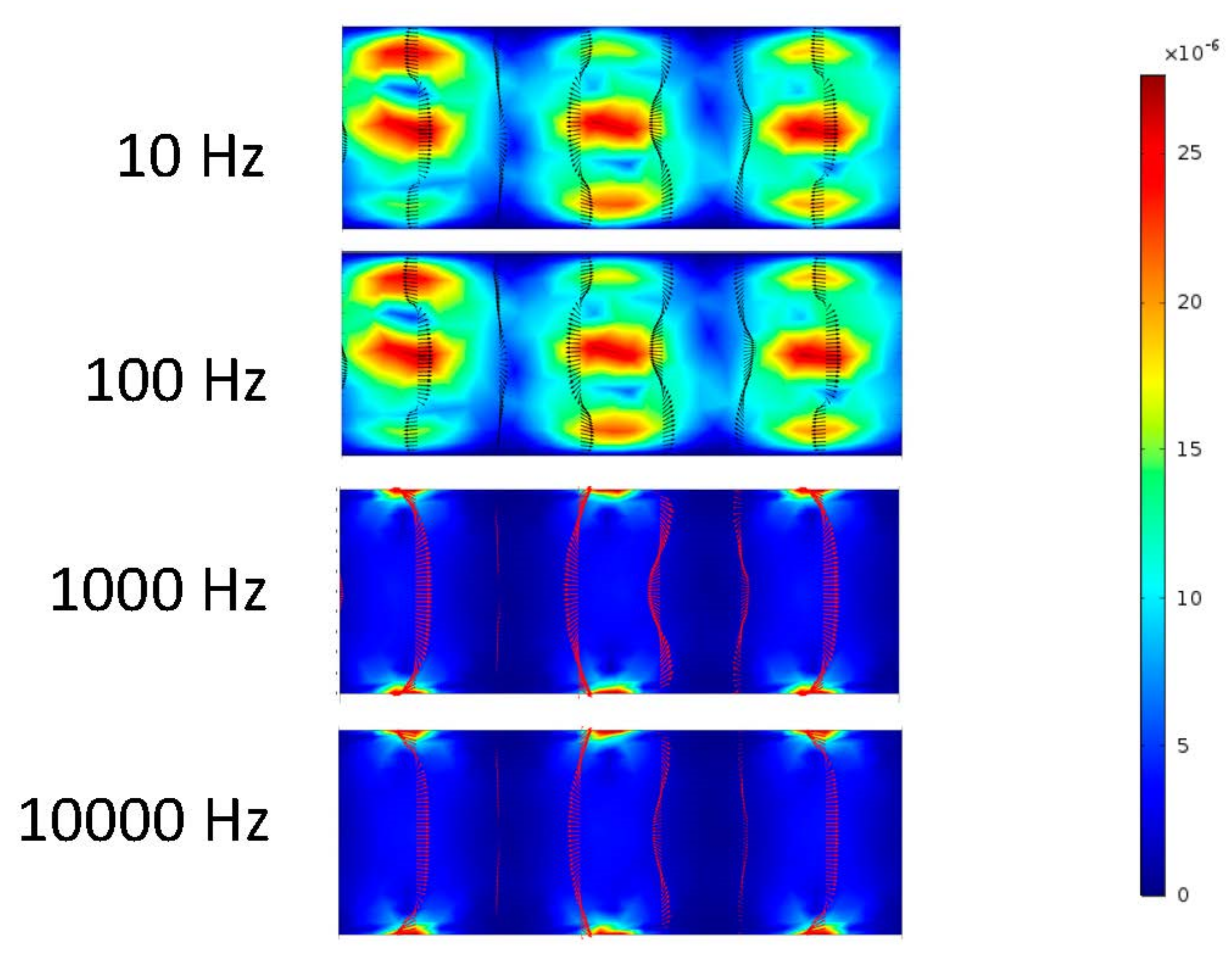
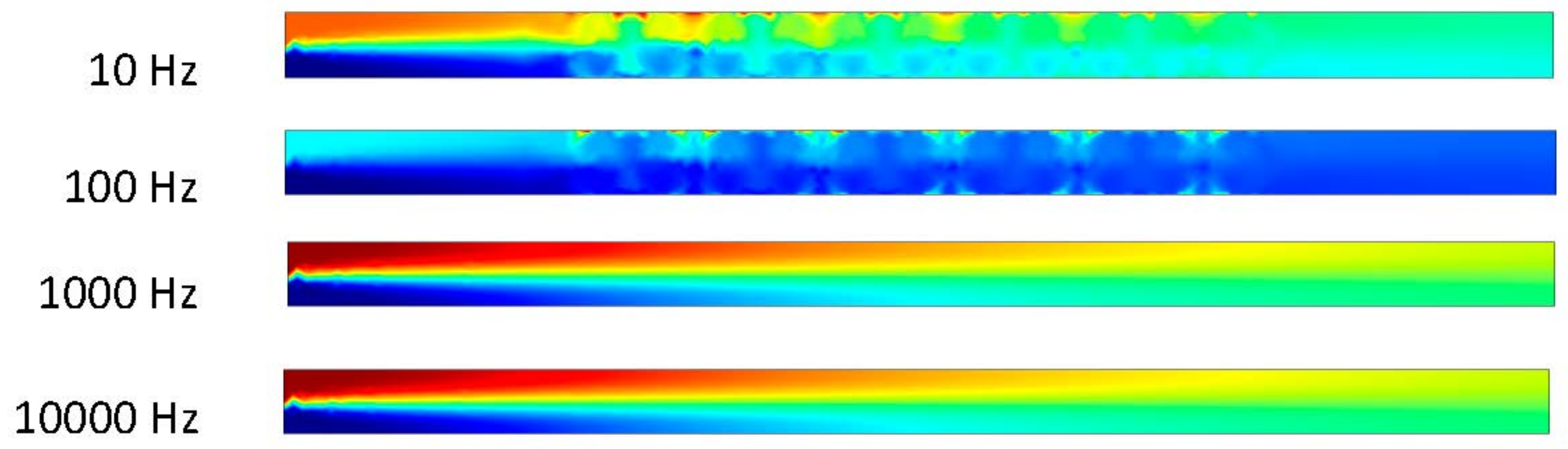
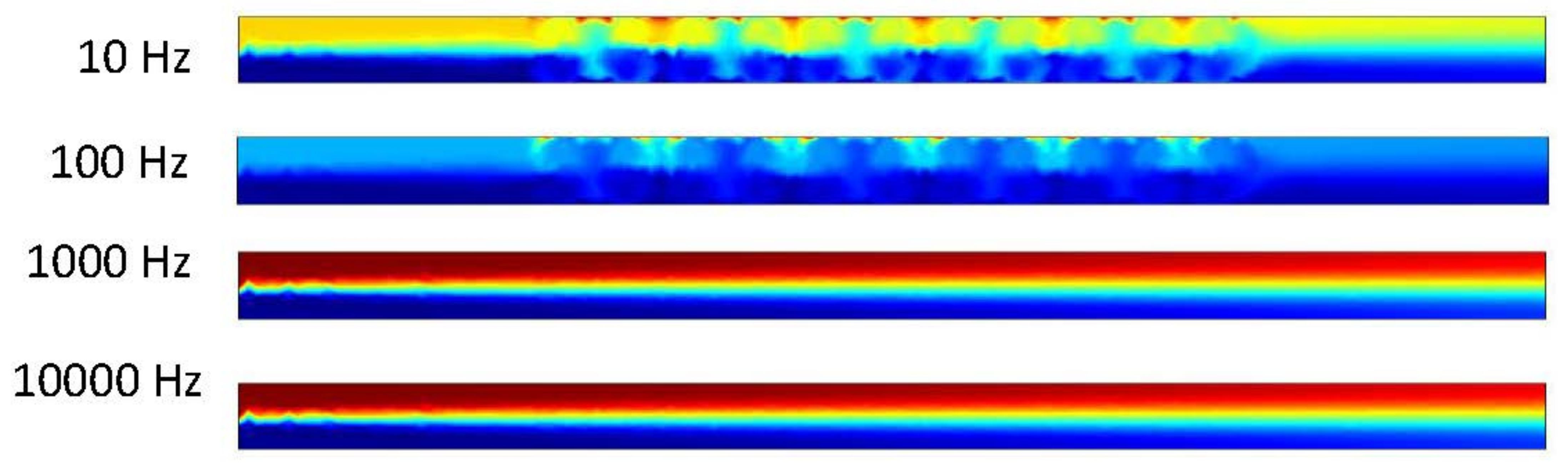
The trendline in Figure 15 for each trial was identical and showed a maximum velocity when 100 Hz was applied. This supports the idea that ACEO is effective at lower frequencies and is a cost-effective method for mixing fluids at these frequencies. Figure 9 shows that the two fluids remained separated without the help of either an electric-driven flow or pressure-driven flow. After 0.5 s, the electric-driven flow in the 10 and 100 Hz microchannels mixed the two fluids (Figure 10). At frequencies of 1000 and 10,000 Hz, however, the flow was too high to allow for mixing within the microchannel. From Figure 11 to 14, as the pressure-driven flow increased by 10, 50, and 100 μm/s in the trials, it was clear that mixing also increased. While the pressure-driven flow did mix the fluids slightly, the majority of the separation remained due to the pressure-driven flow alone, as the fluids generally reached the outlet before any mixing could occur. The electric-driven flow in the 10 and 100 Hz microchannels effectively mixed the fluid when an electric field was applied. In the microchannels subjected to 1000 and 10,000 Hz, however, the pressure-driven flow dominated the electric-driven flow. As the pressure-driven flow increased, the electric field improved the mixing in the lower frequency trials, allowing the separated fluids to mix more quickly. In the 1000 and 10,000 Hz trials, the increased pressure-driven flow pushed the two fluids past the electrodes before they could have any effect on the mixing.

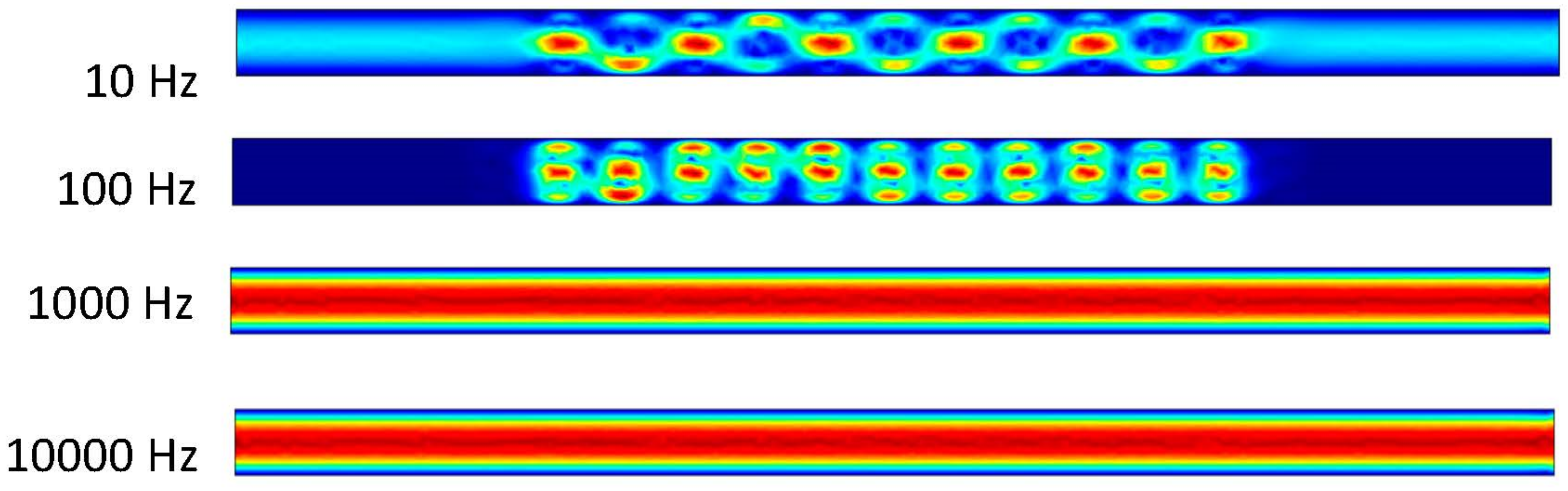
DCEO is a flow of fluid caused by an external electric field that directs the movement of ions. This flow can transport fluid efficiently as well. According to the DCEO simulations in Figure 16, the highest EOF (electroosmotic flow) occurs close to or at the electrode surface. According to the DC equation [8], increasing the tangential electric field proportionally increases the maximum velocity. In this equation, the only variable that changes is the tangential electric field. Therefore, as the voltage increases, the velocity of the EOF also increases, as demonstrated in Figure 16. 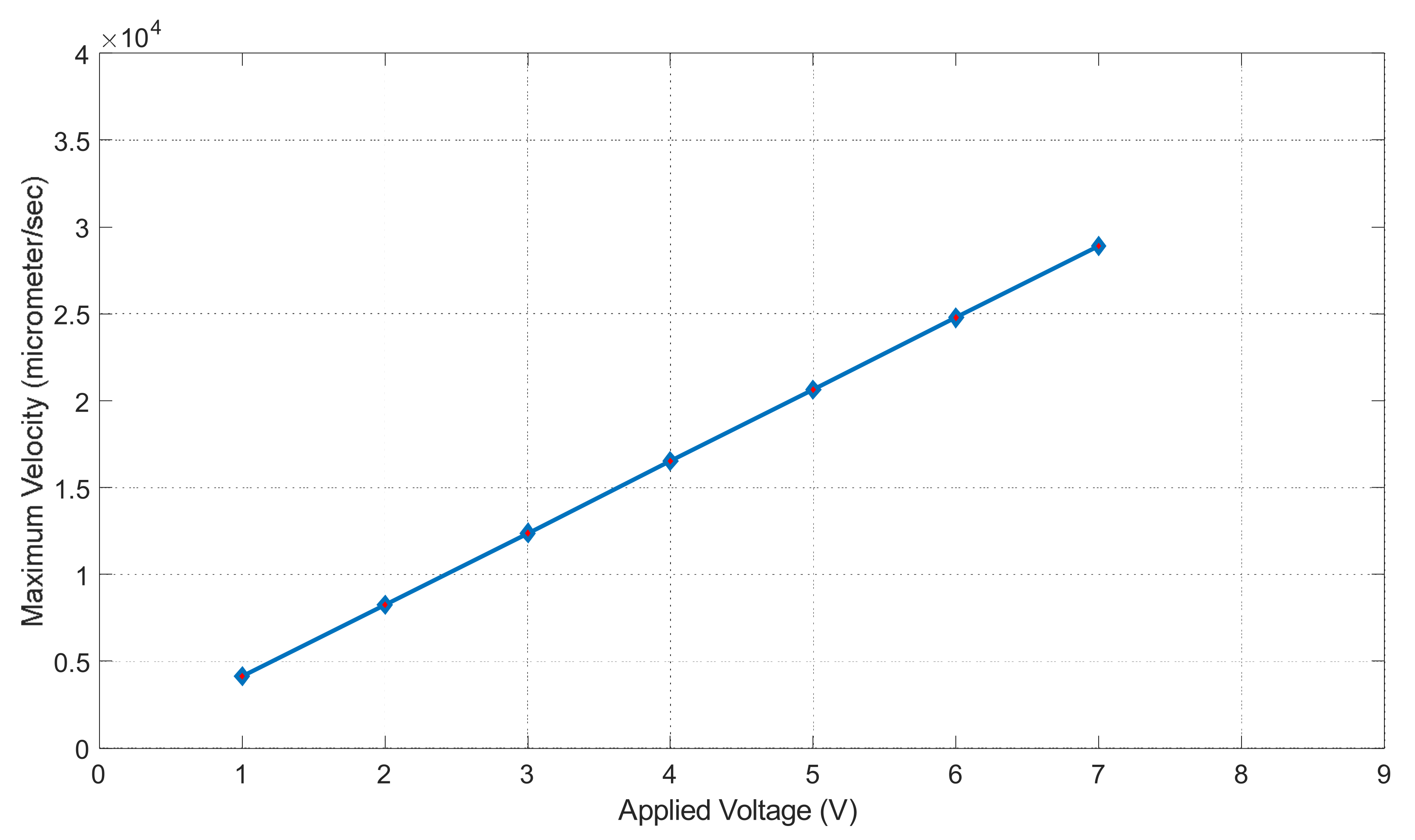Figure 17 shows that the maximum velocity increases linearly as the voltage increases. For instance, at a voltage of one volt, the fluid had a velocity of 4.13 × 104 μm/s, while at seven volts, it had a velocity of 2.89 × 105 μm/s. It can be seen that the electric-driven flow plays a crucial role in driving the fluid through the microchannel. 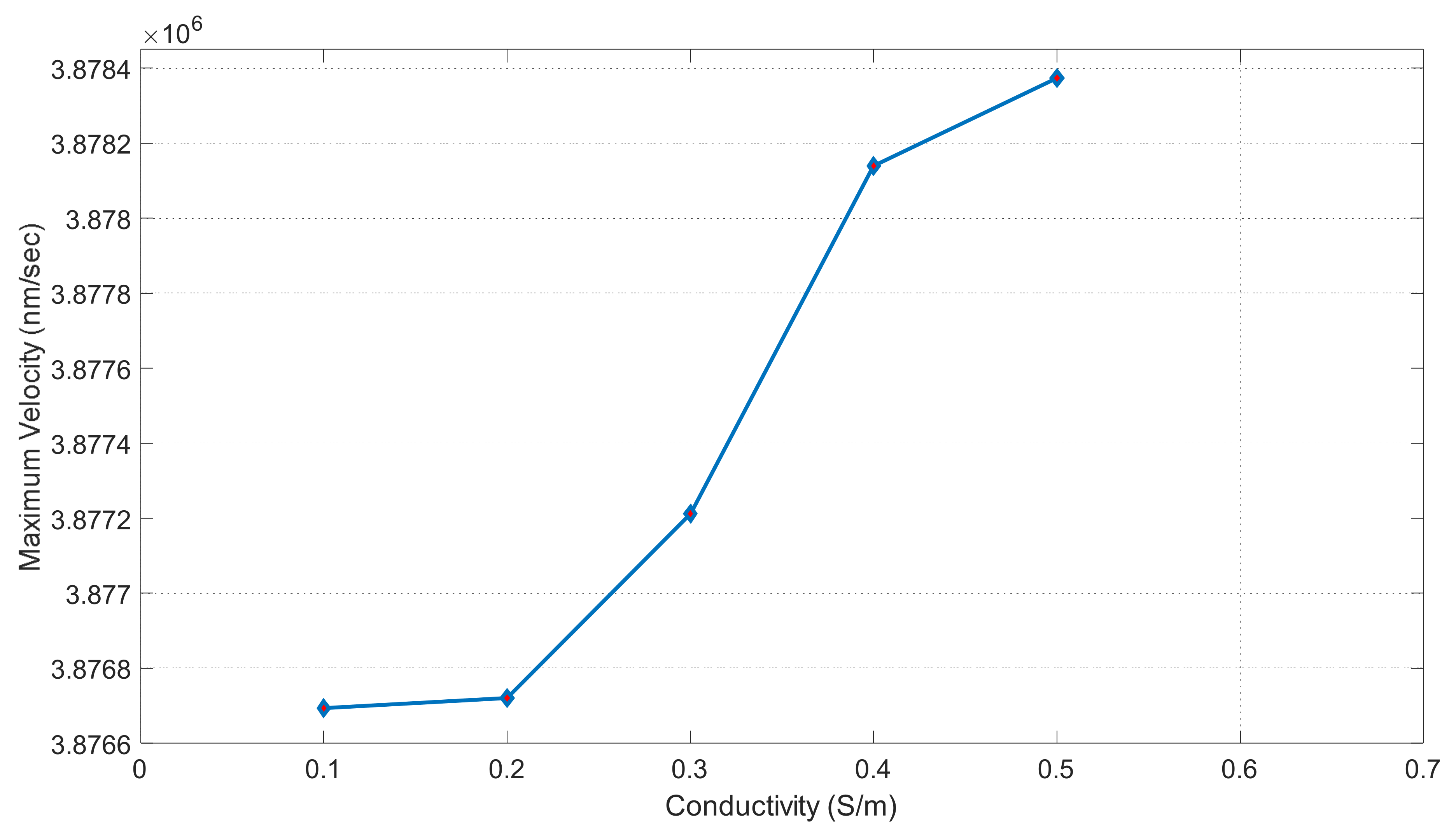Figure 18 demonstrates that the maximum velocity increases as the conductivity increases. The velocity increases exponentially between 0.3 and 0.4 S/m, which is a modest but still significant increase. Through experiments, various electroosmotic phenomena can be studied and applied.

The mixing demonstrated in the simulations showed that the frequency and duration of mixing is important. Data from passive mixing 2D simulations and 3D extrapolations published by Finlayson et al. in 2018 support that multiple device designs with predetermined mixing levels are possible and that they can be effective [47]. This can be augmented through active mixing as confirmed in magnetic particle mixing experiments demonstrated more than a decade ago by Wang et al. in 2008 [48]. Therein, they reported maximum efficiency through high operating frequencies and narrow microchannels for the purposes of their work that can also apply to lab-on-a-chip applications. Precision in both frequency and time as suggested by experiments of the work within this paper provide meaningful context and helpful parameters to consider.

Electroosmotic flow has been used considerably towards the optimization of lab-on-chip devices. Considerable optimization in terms of time has long been predicted, especially from theoretical work in the form of simulations from Bazant and Ben (2006) and Huang et al. (2010), which forecasted that fast 3D AC electroosmotic pumps were possible [33,49]. Other means were found that were effective from their simulation designs; for example, Lim et al. (2009) found means for the improvement of microflow via a T-type micromixer via both AC and DC to considerable effect [49]. Particularly with AC electroosmotic flow, they reported experimental results demonstrating primacy in amplitude and frequency, in addition to the constriction length towards mixing efficiency. They found that increasing the frequency reduced the mixing homogeneity and produced thinner fluid layers. An increased amplitude could be used to form uniformly distributed fluid plugs and improve the mixing efficiency. Altogether, tuning was possible towards optimal settings, which is a point shared by the simulation results in this paper. Further efficiency can be found in cost as demonstrated by Bashirzadeh et al. (2016), who demonstrated bio-compatible microchannel activity with pencil-based lead electrodes [45].

Microfluidics applications from our work can come in the form of boosting performance with chemical reactors, 2D and 3D printing, DNA analysis, drug delivery, point-of-care and analytical diagnostic devices, synthetic biology, and more. Specifically, in terms of disease diagnostics, enhanced microfluidics can help optimize single cell and DNA analysis in addition to general biomarker identification and detection. Towards drug discovery, our work could assist the screening of metabolites and real-time kinetic studies. In terms of synthetic biology uses, our device may assist with structural studies, protein quantification and engineering. Overall, the diverse applications of microfluidics in various fields demonstrate the great potential of these devices for advancing research, improving diagnostics, and enhancing performance in a range of industries. As such, continued development in microfluidic device design will likely have significant impacts on many areas of science and technology.

Overall, this study data exhibited a continuation in trends uncovered in ACEO in microchannels by prior researchers. Our simulations appear to agree, but also suggest how fluid velocity changes in terms of both frequency and time via ACEO. Dynamic flowrates and mixing states can be reasonably achieved in microscale via ACEO.

5. Conclusions

To summarize, simulations suggest that the design of the microchannel allows for efficient mixing and transportation of ionized fluid. This device can be easily created and tested under different experimental conditions using COMSOL. The advantages and disadvantages of AC and DC electroosmosis when used with these devices can be easily summarized. ACEO allows for higher fluid velocities and mixing within microchannels at lower frequencies, while DCEO has a maximum fluid velocity proportional to the applied voltage, which can be increased with a higher voltage. Both approaches can be tested cost-effectively for optimal fluid manipulation and this study provides a suitable foundation for further research on fluid behavior in a microchannel. Immediate applications can be found in medical diagnostic settings, for studying disease behavior at a microscale in lab-on-chip devices. In more general applications, it can be used for efficient and tunable pumping, depending on the specific context and need. The design of the microchannel in microfluidic devices allows for efficient mixing and transportation of ionized fluid, which can be created and tested under different experimental conditions using COMSOL. AC electroosmosis offers higher fluid velocity and mixing at low frequencies, while DC Electroosmosis has a fluid velocity proportional to the applied voltage, both of which can be tested cost-effectively for optimal fluid manipulation. This study provides a foundation for further research on fluid behavior in a microchannel with potential applications in medical diagnostic settings and efficient and tunable pumping.