Elastic–Plastic Material Deformation and Conveying Value of Twist-Free Turned Surfaces
Abstract
:1. Introduction
2. Materials and Methods
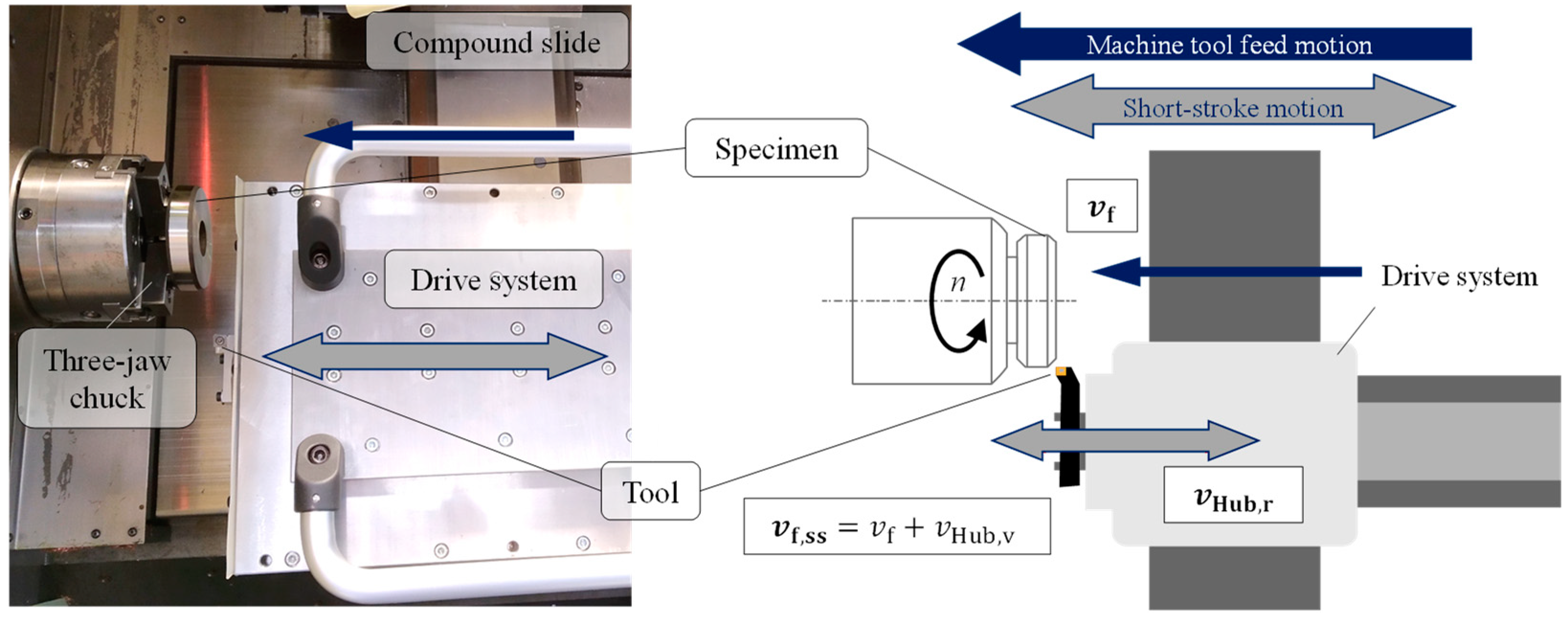
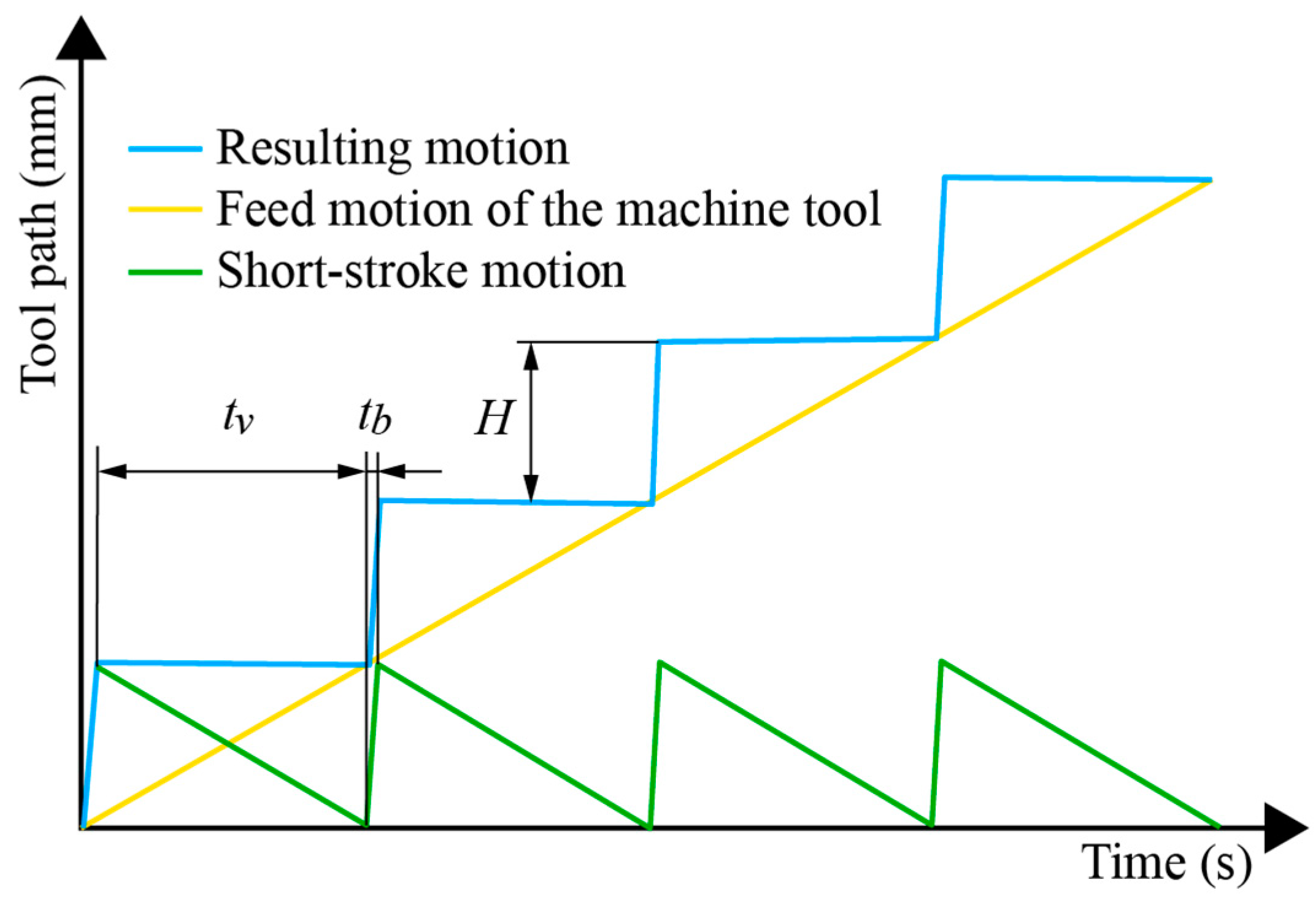
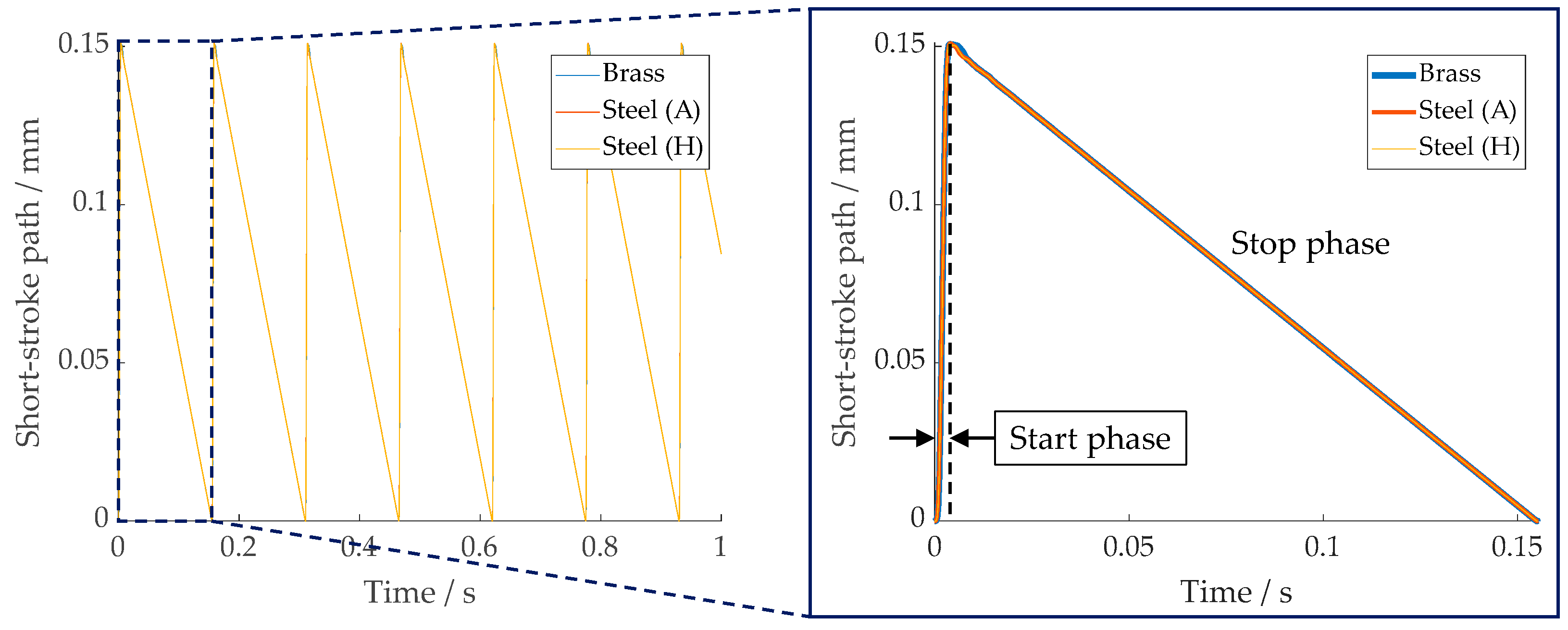
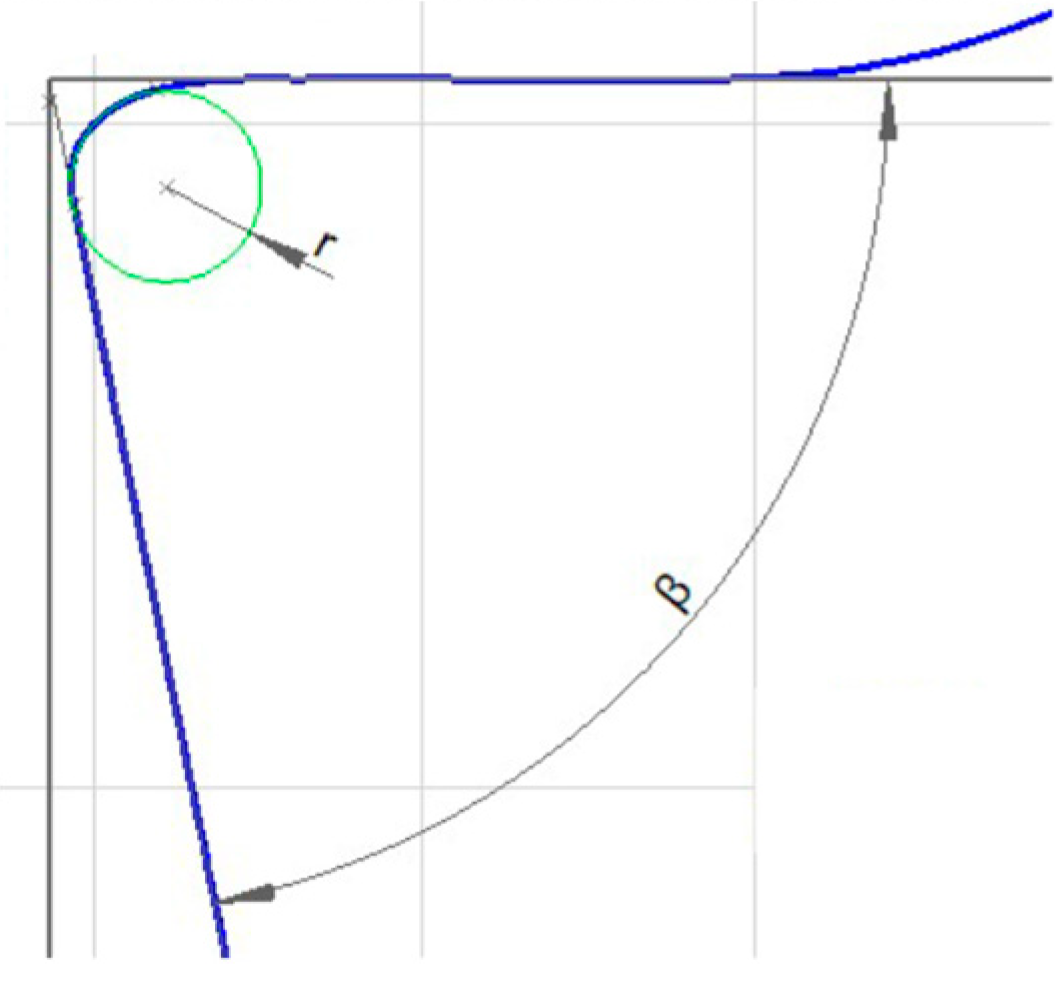
2.1. Start-Stop Turning Process
2.2. Resulting Twist-Free Surface Structure
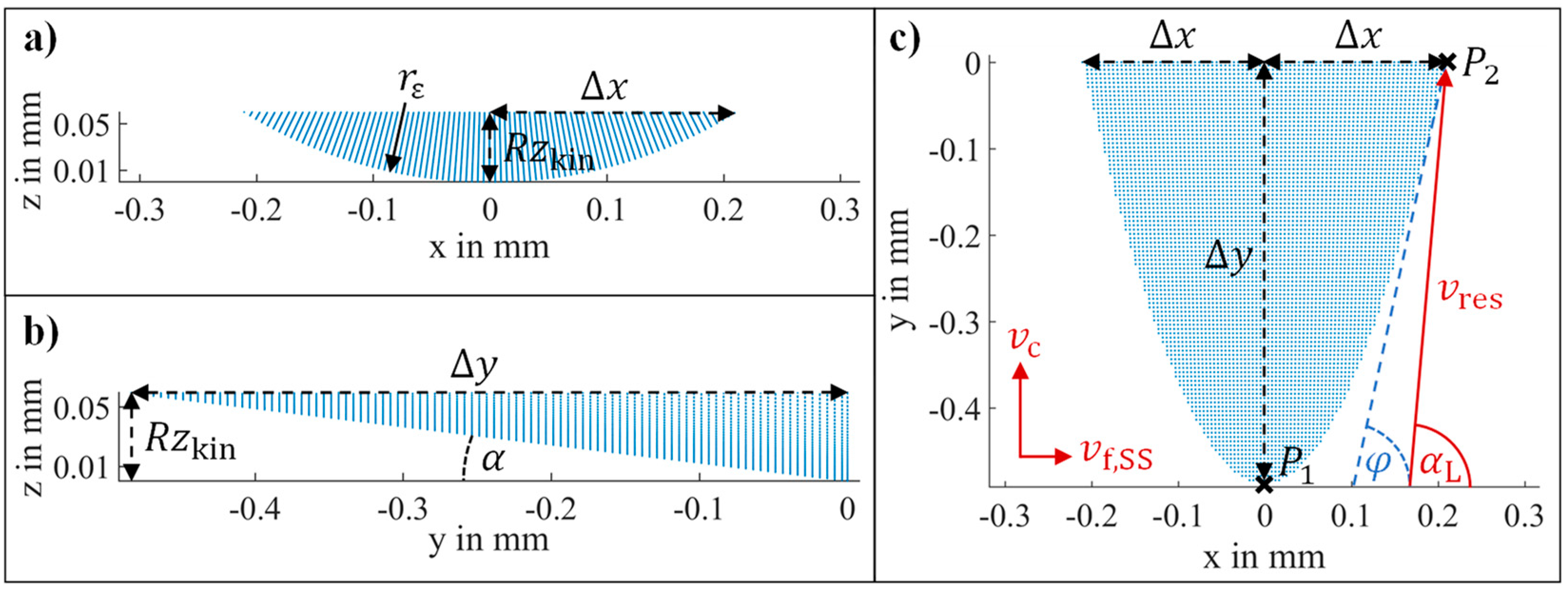
2.3. Kinematic Simulation
2.4. Experimental Procedure
- Single crystalline diamond (SCD) for machining of brass,
- Cubic boron nitride (CBN) for machining hardened steel,
- Coated cemented carbide (CCC) for machining of unhardened steel.
3. Results and Discussion
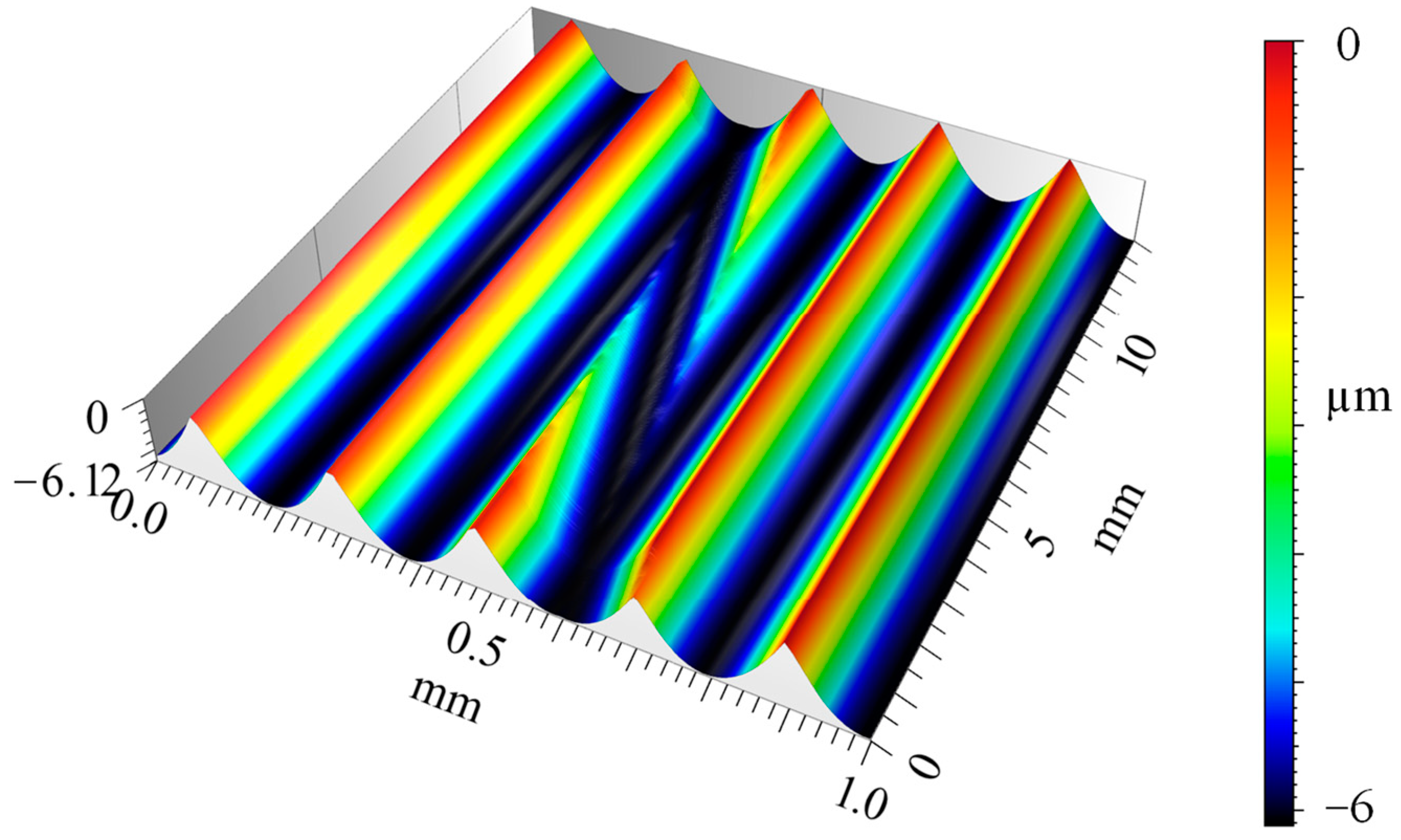
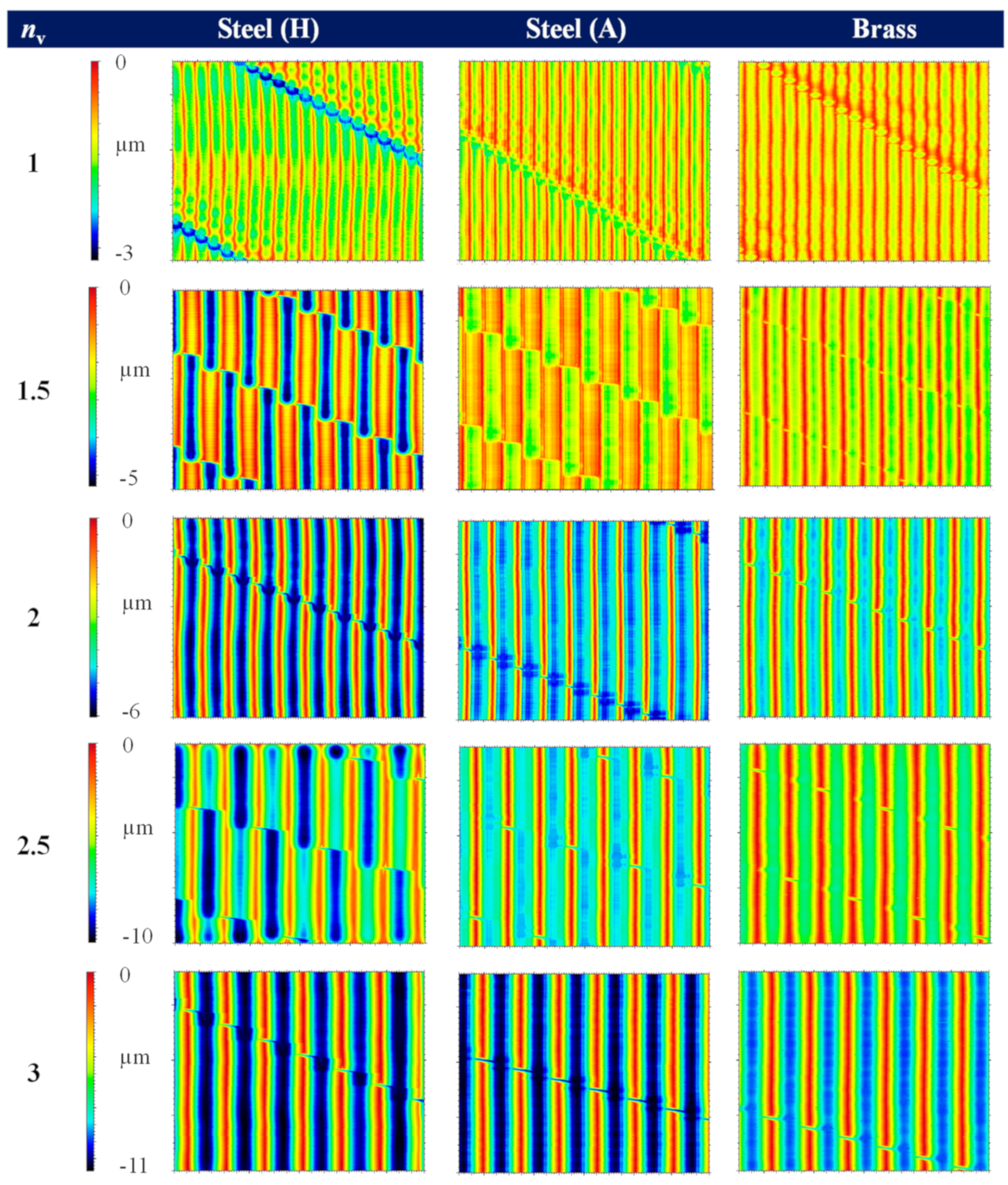
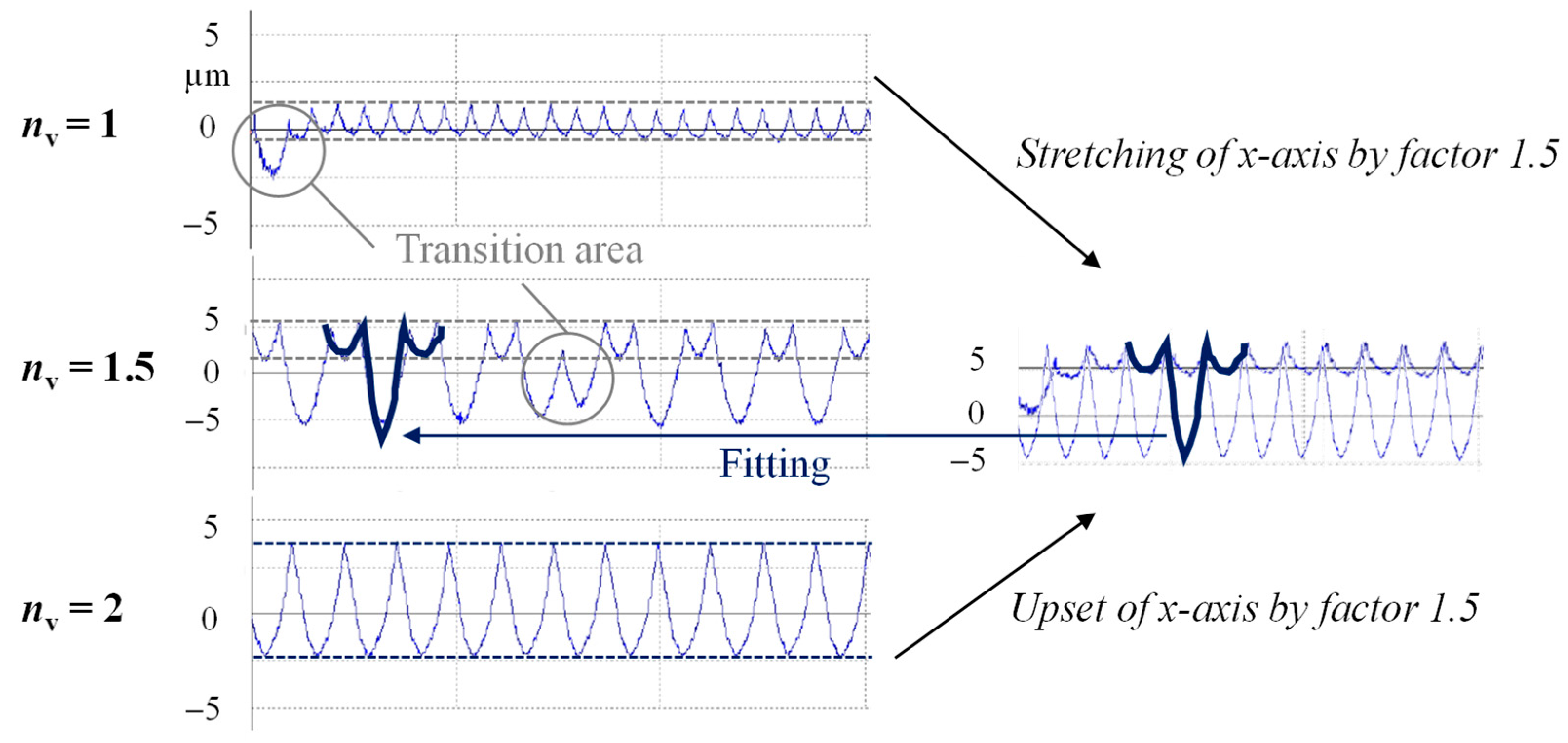
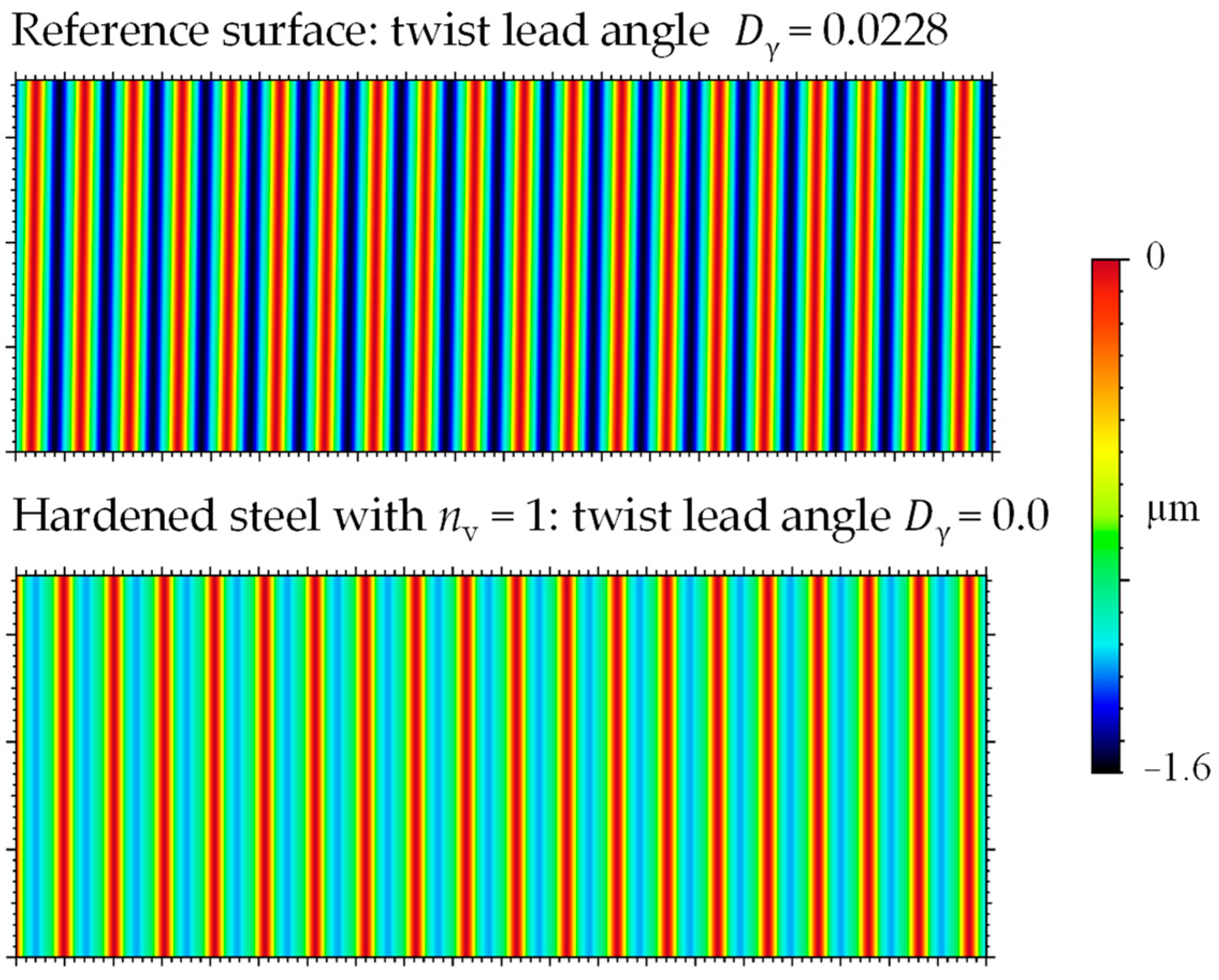
3.1. Surface Analysis
3.2. Functional Analysis
4. Summary and Conclusions
- (1)
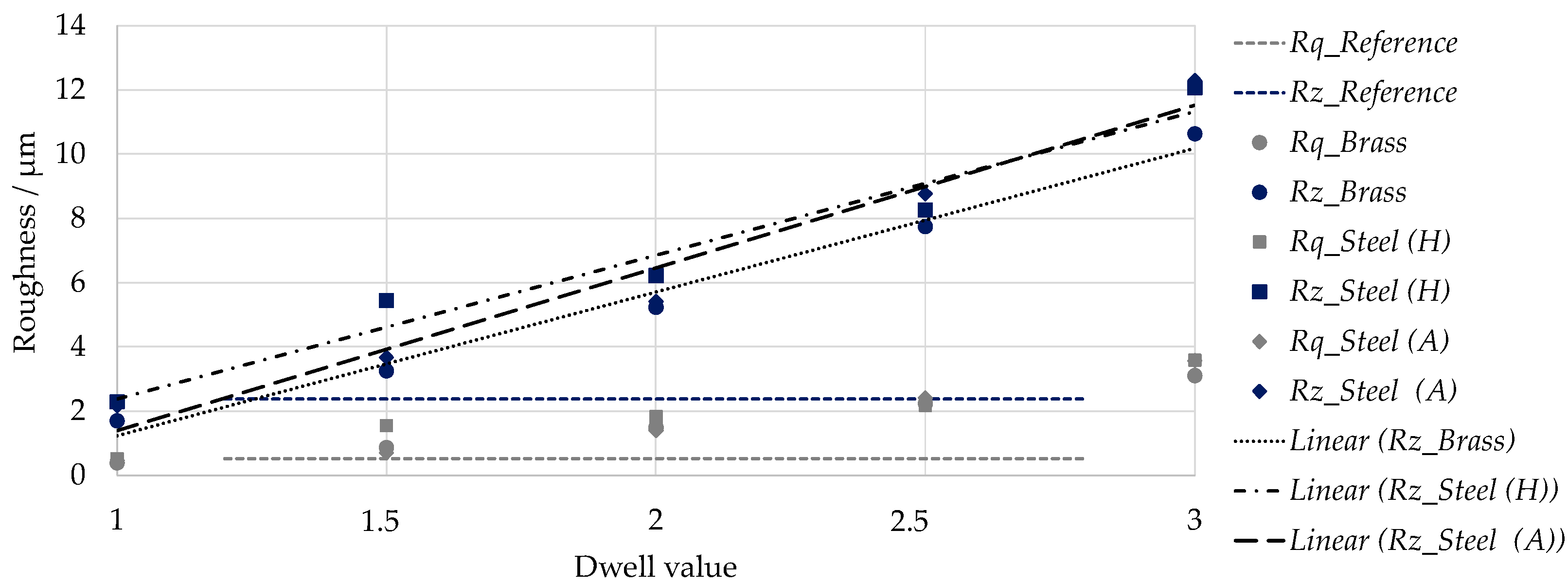
- The differences in comparison to the ideal kinematic surface simulations are a result of the elastic–plastic deformation effects that are dominant in the machining of hardened steel. For additional passes of the tool, the remaining thickness of the material is below the minimum undeformed chip thickness that leads to a ploughing effect.
- (2)
- The ploughing effect is less dominant in the machining of the unhardened steel as the spring back effect seems to be strongly reduced due to lower process forces.
- (3)
- For brass, such effects do not occur because of its low material hardness and the significantly smaller tool cutting-edge radius.
- (4)
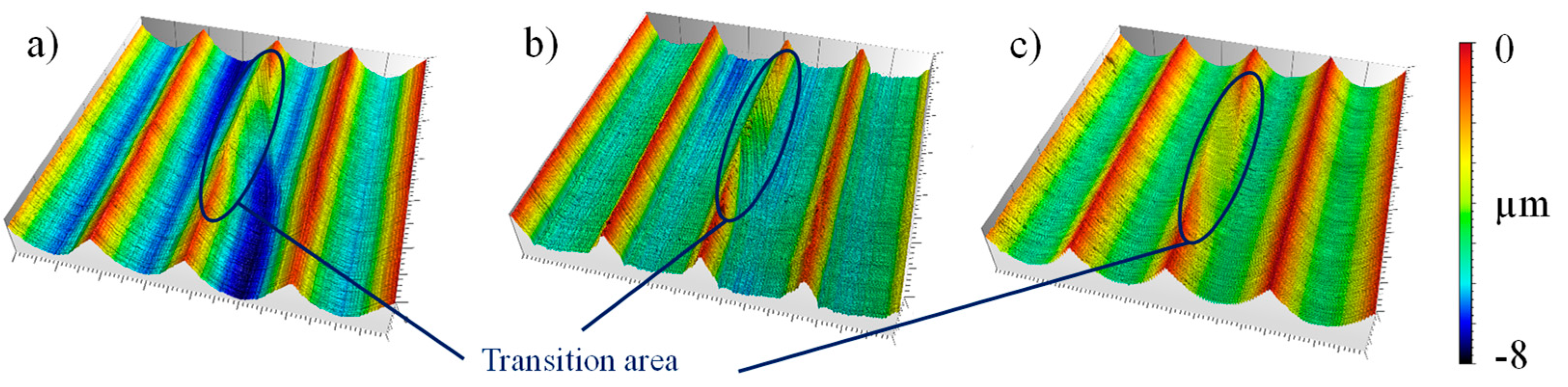
- The selection of an integer dwell value is recommended in order to achieve homogeneous twist-free surface structures without a depth difference in the circumferential direction. Additionally, a dwell value > 1 is suggested as a “smoothing” of the surface occurs for multiple passes, and the transition areas can be partially closed by the deformation of material during the SST of steel.
- (5)
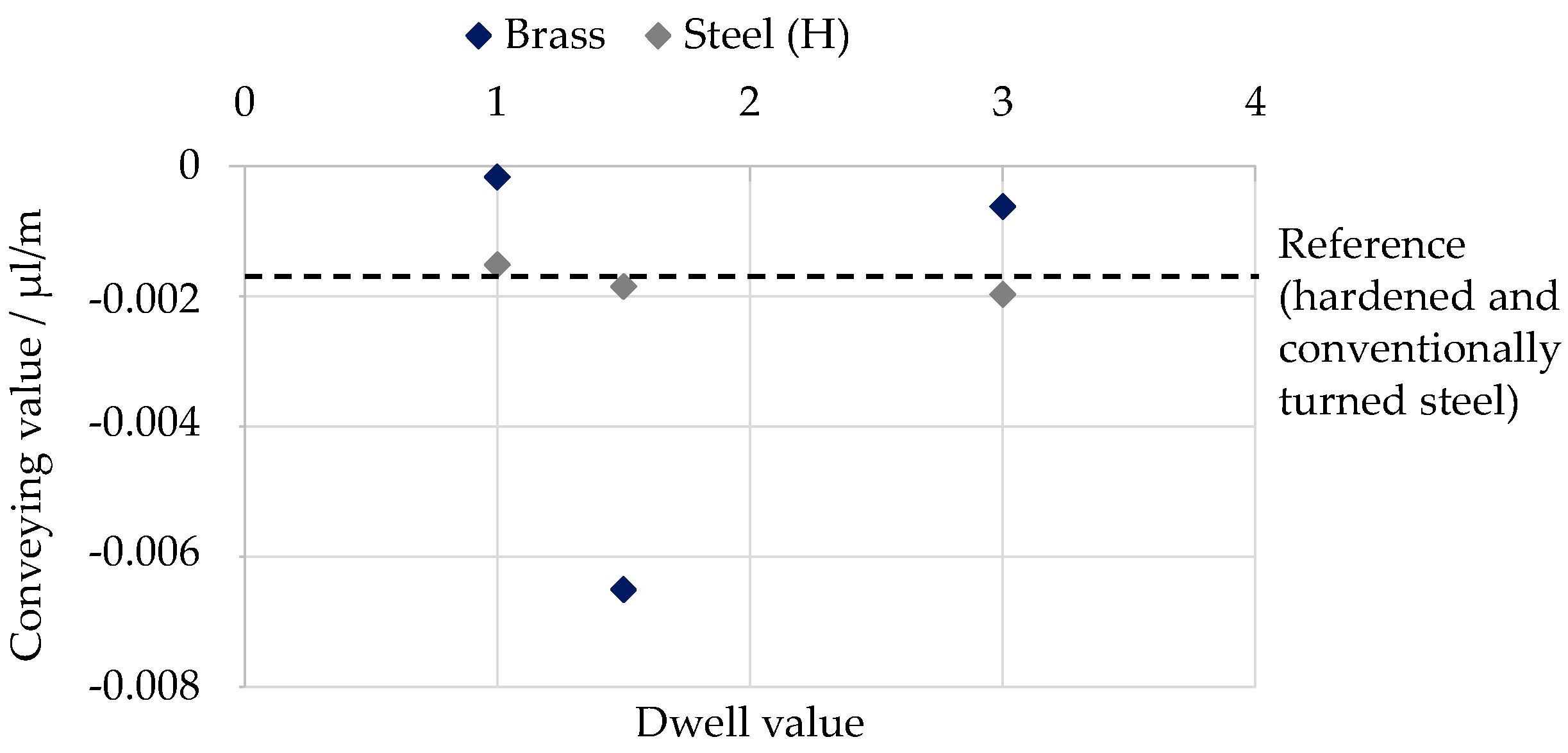
- The conveying value is independent of the periodical width for twist-free surfaces with periodical widths greater than or equal to the sealing lip width (100 µm–150 µm).
- (6)
- No reduction of the conveying value is achieved for the hardened steel specimens in comparison to the reference specimen with a twist structure.
- (7)
- The comparative investigations with a material exhibiting good machinability, such as brass, are only able to provide limited support, as, in particular, the determination of the conveying value is not robust enough, and, consequently, the meaningfulness of these results is not assured.
- (8)
- The SST method can enhance the economic efficiency of the machining of hardened steel by increasing the feed without affecting the conveying value. Additionally, it offers the potential to accomplish the finishing of, e.g., gear or cam shafts in one machining operation. Consequently, valuable machining time and costs can be saved by the application of this method.
5. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Depth of cut | µm | |
| CBN | Cubic boron nitride | |
| CCC | Coated cemented carbide | |
| Periodical width (according to MBN) | µm | |
| Periodical width (calculated) | µm | |
| Conveying cross-section (according to MBN) | µm2 | |
| Conveying cross-section (calculated) | µm2 | |
| Twist lead angle | 1° | |
| Machine tool feed | mm | |
| Short-stroke distance | mm | |
| MBN | Mercedes Benz Norm 31007-7 | |
| Rotational speed of the specimen | min−1 | |
| Dwell value—number of workpiece revolutions in the stop phase | - | |
| Cutting-edge radius | µm | |
| Corner radius | mm | |
| Rq | Square mean roughness | µm |
| Surface roughness depth | µm | |
| Kinematical surface roughness depth | µm | |
| Background noise from the ambient conditions | µm | |
| SCD | Single crystalline diamond | |
| SST | Start-stop turning | |
| Time spent in the start phase | s | |
| Time spent in the stop phase | s | |
| Cutting speed | m/min | |
| Feed velocity of the machine tool axis | m/min | |
| Feed velocity of the tool relative to the workpiece | m/min | |
| Short-stroke velocity in the negative direction of the machine tool feed motion/Back feed velocity | mm/min | |
| Short-stroke velocity in the positive direction of the machine tool feed motion | m/min | |
| Velocity of the tool in the start phase relative to the workpiece resulting from the superposition of and | m/min | |
| Clearance angle | 1° | |
| Transition angle of the tool-movement during the startphase | 1° | |
| Wedge angle | 1° | |
| Geometrical extension of the intersecting tool body in the direction of the x-axis | mm | |
| Geometrical extension of the intersecting tool body in the direction of the y-axis | mm | |
| ls | Gaussian profile filter (short-wave cut-off) | µm |
| Inclination angle of the tool body in the - plane | 1° |
References
- Baart, P.; Lugt, P.M.; Prakash, B. Review of the lubrication, sealing, and pumping mechanisms in oil- and grease-lubricated radial lip seals. Proc. I. Mech. E. Part. J. J. Eng. Tribol. 2008, 223, 347–358. [Google Scholar] [CrossRef]
- Baumann, M. Abdichtung drallbehafteter Dichtungsgegenlaufflächen–Messung, Analyse, Bewertung und Grenzen. Ph.D Thesis, Universität Stuttgart, Stuttgart, Germany, 15 February 2017. [Google Scholar]
- Schulz, M.; Baumann, M.; Bauer, F.; Haas, W. Influence of different shaft surface finishes on the tribological and functional behavior of radial shaft seals. In Fluid Power Networks-11th International Fluid Power Conference; Murrenhoff, H., Ed.; Publication Server RWTH Aachen University: Aachen, Germany, 2018; Volume 3, pp. 86–99. [Google Scholar]
- Kunstfeld, T.; Haas, W. Shaft surface manufacturing methods for rotary shaft lip seals. Seal. Technol. 2005, 7, 5–9. [Google Scholar] [CrossRef]
- Oliveira, J.F.G.; Silva, E.J.; Guo, C.; Hashimoto, F. Industrial challenges in grinding. CIRP Ann. Manuf. Technol. 2009, 58, 663–680. [Google Scholar] [CrossRef]
- Fleming, M. Werkzeugkonzepte für das Drehen von Getrieben mit PCBN. IDR 2005, 39, 23–28. [Google Scholar]
- Thielen, S.; Magyar, B.; Sauer, B.; Schneider, F.; Mayer, P.; Kirsch, B.; Müller, R.; Harbou, E.V.; Aurich, J.C. Functional investigation of zero lead radial shaft seal counter-surfaces turned with a special method. Tribol. Int. 2018, 118, 442–450. [Google Scholar] [CrossRef]
- Klocke, F.; Helbig, J.; Bertalan, C. Hartdrehen von Wellendichtflächen. VDI-Z Integr. Prod. 2004, 146, 37–40. [Google Scholar]
- Anonymous. Technisches Handbuch, 1st ed.; Freudenberg Sealing Technologies GmbH & Co. KG: Weinheim, Germany, 2015. [Google Scholar]
- Leichner, T.; Sauer, V.; Franke, B.; Aurich, J.C. Investigation of the tribological behaviour of radial shaft rings and soft turned shafts under the influence of abrasive particles. Prod. Eng. Res. Devel. 2011, 5, 531–538. [Google Scholar] [CrossRef]
- Schubert, A.; Zhang, R.; Steinert, P. Manufacturing of twist-free surfaces by hard turning. Procedia CIRP 2013, 7, 294–298. [Google Scholar] [CrossRef]
- Steinert, P.; Nestler, A.; Kühn, J.; Schubert, A. Efficient manufacturing of tribological surfaces by turning technologies with alternating movements. In Proceedings of the Conference on Competitive Manufacturing, Stellenbosch University, Stellenbosch, South Africa, 27–29 January 2016. [Google Scholar]
- Žůrek, F.; Junge, T.; Nestler, A.; Schaller, S.; Schubert, A. Dynamic properties of an air bearing drive system for manufacturing of twist-free surfaces by start-stop turning. Procedia CIRP 2021, 104, 1464–1469. [Google Scholar] [CrossRef]
- Junge, T.; Žůrek, F.; Nestler, A.; Schubert, A. Manufacturing of Twist-Free Hardened Surfaces by Start-Stop Turning Method. In Production at the Leading Edge of Technology Proceedings of the 11th Congress of the German Academic Association for Production Technology (WGP); Behrens, B.A., Brosius, A., Drossel, W.G., Hintze, W., Ihlenfeldt, S., Nyhuis, P., Eds.; Springer: Cham, Germany, 2022; pp. 203–211. [Google Scholar] [CrossRef]
- Börner, R.; Winkler, S.; Junge, T.; Titsch, C.; Schubert, A.; Drossel, W.G. Generation of functional surfaces by using a simulation tool for surface prediction and micro structuring of cold-working steel with ultrasonic vibration assisted face milling. J. Mater. Process. Technol. 2018, 255, 749–759. [Google Scholar] [CrossRef]
- Börner, R.; Penzel, M.; Junge, T.; Schubert, A. Design of Deterministic Microstructures as Substrate Pre-Treatment for CVD Diamond Coating. Surfaces 2019, 2, 497–519. [Google Scholar] [CrossRef] [Green Version]
- Burkhart, C.; Thielen, S.; Sauer, B. Online determination of reverse pumping values of radial shaft seals and their tribologically equivalent system. Tribol. Schmier. 2020, 67, 20–32. [Google Scholar] [CrossRef]
- Thielen, S.; Breuninger, P.; Hotz, H.; Burkhart, C.; Schollmayer, T.; Sauer, B.; Antonyuk, S.; Kirsch, B.; Aurich, J.C. Improving the tribological properties of radial shaft seal countersurfaces using experimental micro peening and classical shot peening processes. Tribol. Int. 2021, 155, 106764. [Google Scholar] [CrossRef]
- Foko Foko, F.; Burkhart, C.; Thielen, S.; Sauer, B. Analysis of the Sealing Capability of Radial Shaft Sealing Rings Using a Semi-Analytical Contact Model. Tribol. Online 2022, 17, 97–109. [Google Scholar] [CrossRef]

| SCD | CBN | CCC |
|---|---|---|
 |  |  |
 |  |  |
 |  |  |
| rb (Alicona): 4.9 µm rb (Keyence): 2.0 µm | rb (Alicona): 13.3 µm rb (Keyence): 8.5 µm | rb (Alicona): 30.0 µm rb (Keyence): 27.2 µm |
| Parameter | Value | Machine System |
|---|---|---|
| Feed | 0.1 mm | SPINNER PD 32 |
| Rotational speed | 597 min−1 | |
| Cutting speed | 150 m/min | |
| Depth of cut | 50 µm | |
| Back feed velocity | 59.7 mm/min | AeroLas System |
|
Dwell Value nv |
Short-Stroke Distance H |
Periodical Width DPtheor |
|---|---|---|
| 1 | 100 µm | 104 µm |
| 1.5 | 150 µm | 154 µm |
| 2 | 200 µm | 204 µm |
| 2.5 | 250 µm | 255 µm |
| 3 | 300 µm | 305 µm |
| Periodical Width (µm) | Conveying Cross-Section (µm2) | Rq (µm) | Rz (µm) | Conveying Value (µL/m) | ||
|---|---|---|---|---|---|---|
| Reference (R) | - | 0.1 | 92.0 | 0.52 | 2.38 | −0.0017 |
| Hardened (H) 1 | 1 | 0.104 | 84.9 | 0.46 | 2.28 | −0.0015 |
| H 2 | 1.5 | 0.310 * | 588.0 * | 0.70 | 5.44 | −0.0019 |
| H 3 | 2 | 0.205 | 658.0 | 1.39 | 6.21 | - |
| H 4 | 2.5 | 0.253 * | 926.0 * | 2.41 | 8.26 | - |
| H 5 | 3 | 0.308 | 1924.0 | 3.57 | 12.06 | −0.002 |
| Unhardened (A) 1 | 1 | 0.103 | 83.1 | 0.51 | 2.17 | - |
| A 2 | 1.5 | 0.308 * | 304.0 * | 1.54 | 3.67 | - |
| A 3 | 2 | 0.205 | 658.0 | 1.82 | 5.41 | - |
| A 4 | 2.5 | 0.255 | 1308.0 | 2.17 | 8.76 | - |
| A 5 | 3 | 0.305 | 2050.0 | 3.58 | 12.28 | - |
| Brass (B) 1 | 1 | 0.104 | 70.2 | 0.39 | 1.69 | −0.0002 |
| B 2 | 1.5 | 0.154 | 239.0 | 0.86 | 3.25 | −0.0065 |
| B 3 | 2 | 0.205 | 546.0 | 1.49 | 5.23 | - |
| B 4 | 2.5 | 0.255 | 1021.0 | 2.23 | 7.75 | - |
| B 5 | 3 | 0.305 | 1658.0 | 3.10 | 10.63 | −0.0006 |
| Periodical Width (µm) | Conveying Cross-Section (µm2) | Rq (µm) | Rz (µm) | Conveying Value (µL/m) | ||
|---|---|---|---|---|---|---|
| Simulation (S) 1 | - | 0.1 | 100.7 | 0.46 | 1.52 | - |
| S 2 | 1 | 0.104 | 110.2 | 0.48 | 1.61 | - |
| S 3 | 1.5 | 0.154 | 370.5 | 1.09 | 3.63 | - |
| S 4 | 2 | 0.204 | 808.8 | 1.86 | 6.08 | - |
| S 5 | 2.5 | 0.255 | 1413.1 | 2.69 | 8.72 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Börner, R.; Junge, T.; Subramanian, T.; Thielen, S.; Koch, O.; Schubert, A. Elastic–Plastic Material Deformation and Conveying Value of Twist-Free Turned Surfaces. Surfaces 2022, 5, 395-412. https://doi.org/10.3390/surfaces5030029
Börner R, Junge T, Subramanian T, Thielen S, Koch O, Schubert A. Elastic–Plastic Material Deformation and Conveying Value of Twist-Free Turned Surfaces. Surfaces. 2022; 5(3):395-412. https://doi.org/10.3390/surfaces5030029
Chicago/Turabian StyleBörner, Richard, Thomas Junge, Thirumanikandan Subramanian, Stefan Thielen, Oliver Koch, and Andreas Schubert. 2022. "Elastic–Plastic Material Deformation and Conveying Value of Twist-Free Turned Surfaces" Surfaces 5, no. 3: 395-412. https://doi.org/10.3390/surfaces5030029
APA StyleBörner, R., Junge, T., Subramanian, T., Thielen, S., Koch, O., & Schubert, A. (2022). Elastic–Plastic Material Deformation and Conveying Value of Twist-Free Turned Surfaces. Surfaces, 5(3), 395-412. https://doi.org/10.3390/surfaces5030029







