Finite Element Analyses of the Modified Strain Gradient Theory Based Kirchhoff Microplates
Abstract
1. Introduction
- (i)
- to introduce a variational formulation for microplates based on the Kirchhoff kinematics and the modified strain gradient theory,
- (ii)
- (iii)
- to further formulate 28- and 32-degree of freedom (DOF) rectangular micro-plate element formulations from 20- and 24-degree of freedom (DOF) rectangular micro-plate element formulations respectively,
- (iv)
- to assess the convergence of the derived element formulations and elaborate on the continuity requirements,
- (v)
- investigate the performance of the element through realistic MEMS switch geometries, and
- (vi)
- to contribute to the analysis of MEMS devices with various boundary conditions, particularly in the domain of RF-MEMS made of gold by proposing length scale parameters based on the proposed formulations.
2. Theory: Local and Nonlocal Kirchhoff Plate Theory
2.1. Variational Formulation of Nonlocal Elasticity
2.1.1. The Strain Gradient Theory
2.1.2. The Modified Strain Gradient Theory
2.2. Classical Kirchhoff Plate Theory
2.3. Modified Strain Gradient Theory for Kirchhoff Plates
3. The Microplate Finite Element Formulation
3.1. 12-Dof Adini-Clough-Melosh Element for Classical Kirchhoff Plates
3.2. 16-Dof Bogner-Fox-Schmit Element for Classical Kirchhoff Plates
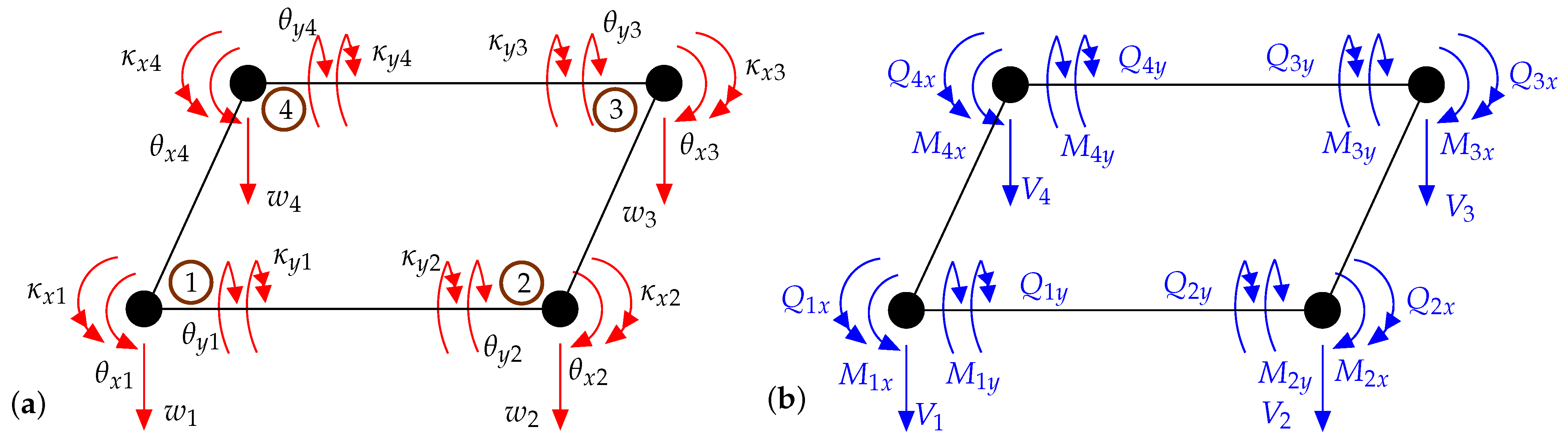
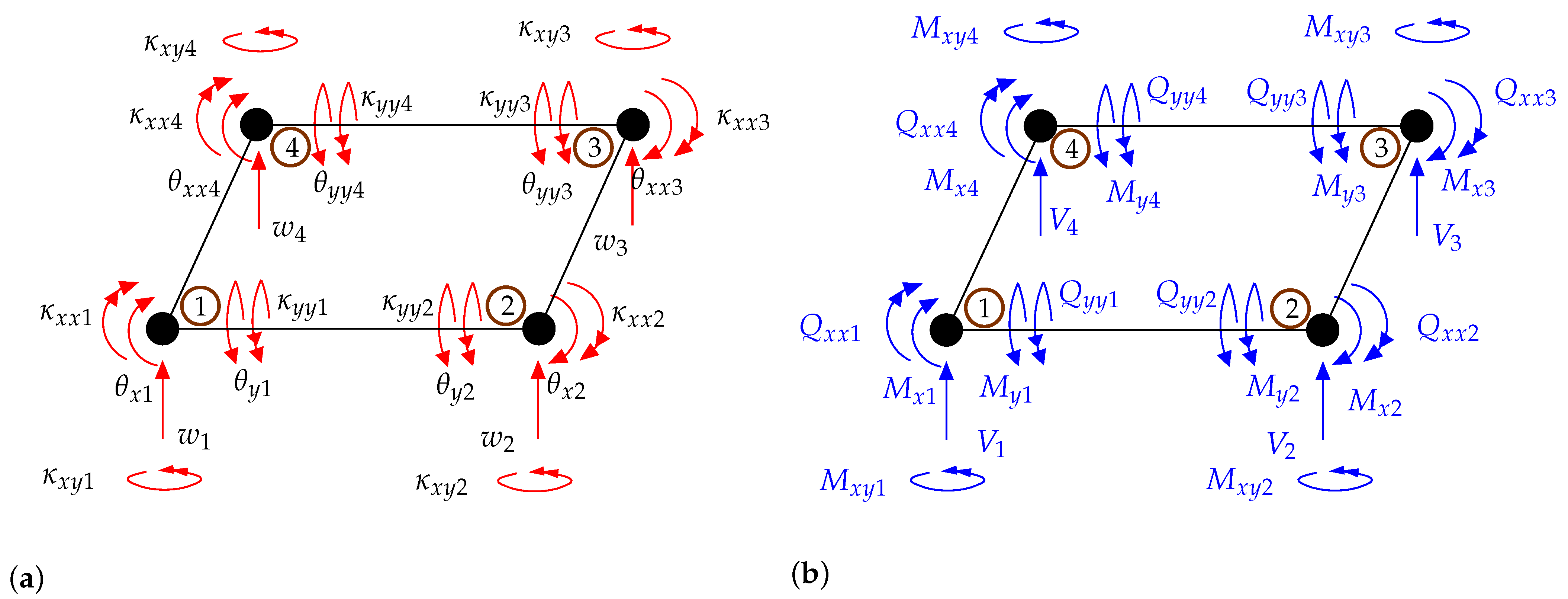
3.3. New 20-Dof Finite Element Formulation for Msgt-Based Kirchhoff Microplates
3.4. New 24-Dof Finite Element Formulation for Msgt-Based Kirchhoff Microplates
3.5. Conformity
4. Representative Numerical Examples
4.1. Comparison
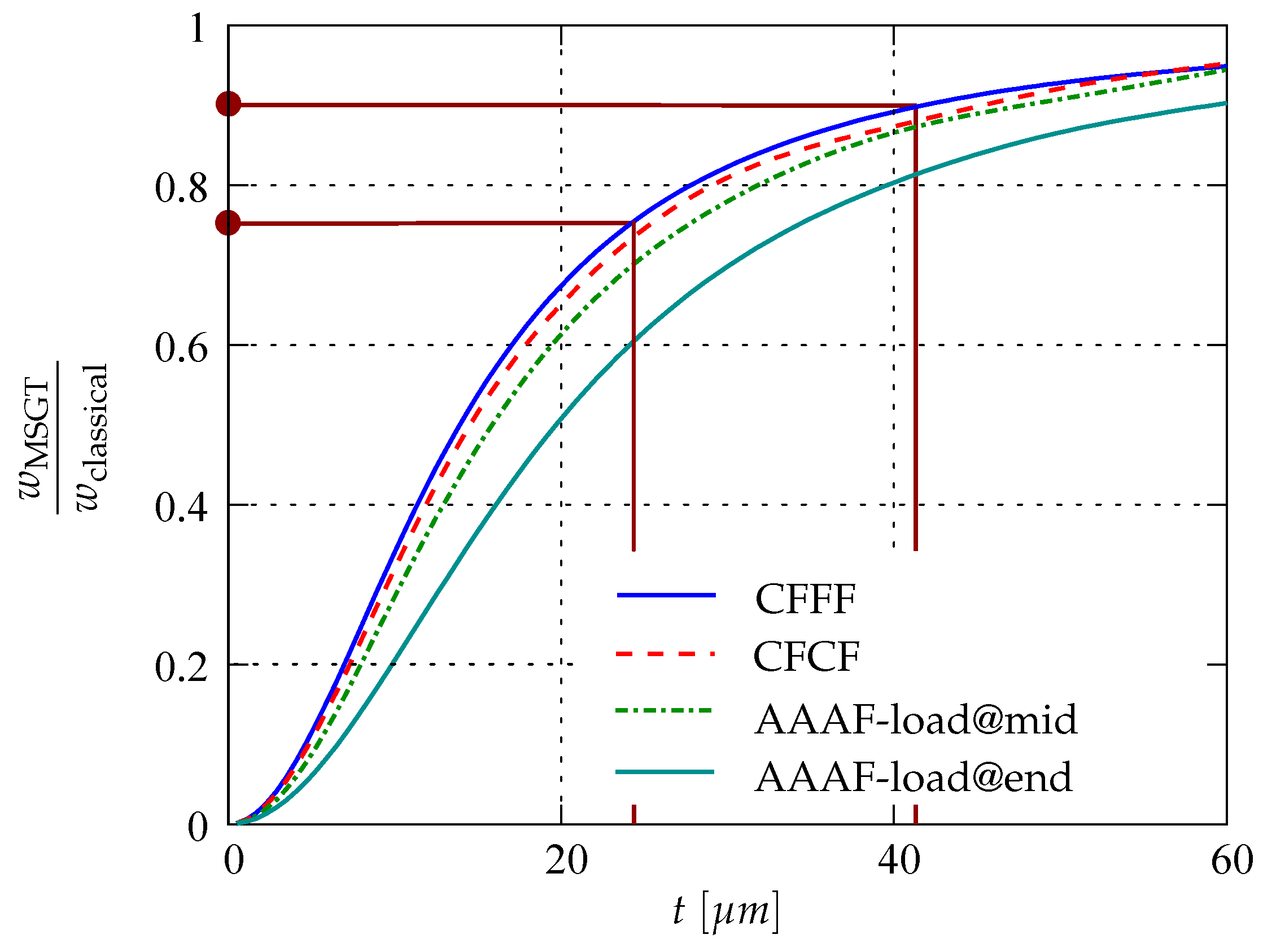
4.2. Length Scale Parameters for Gold Microplates
4.3. Assessment of Element Performance
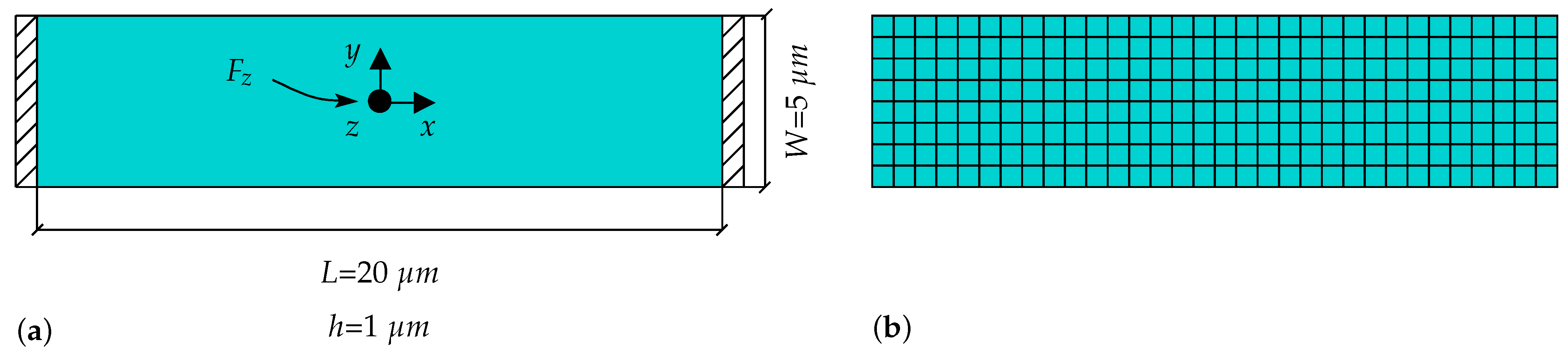
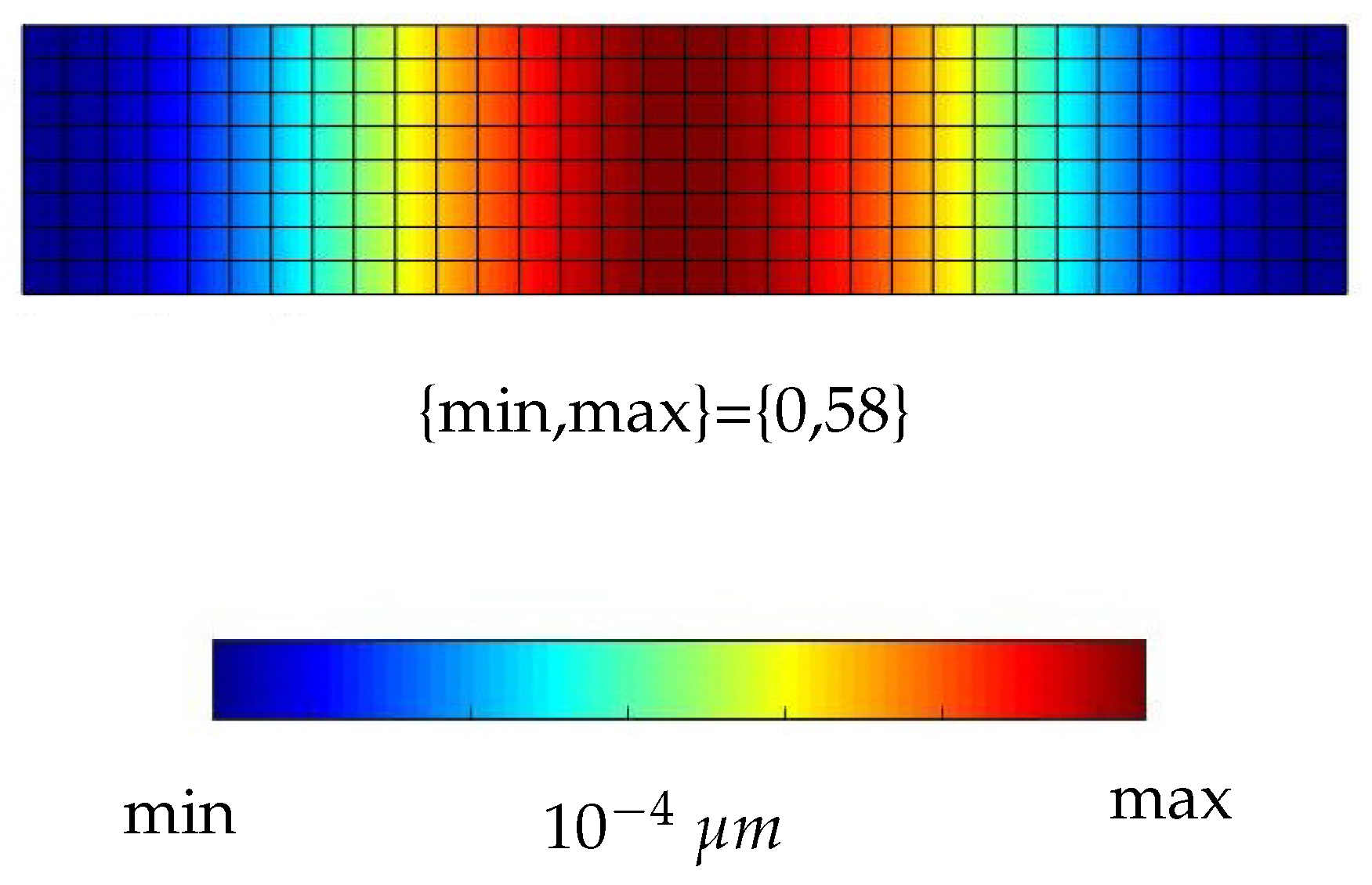
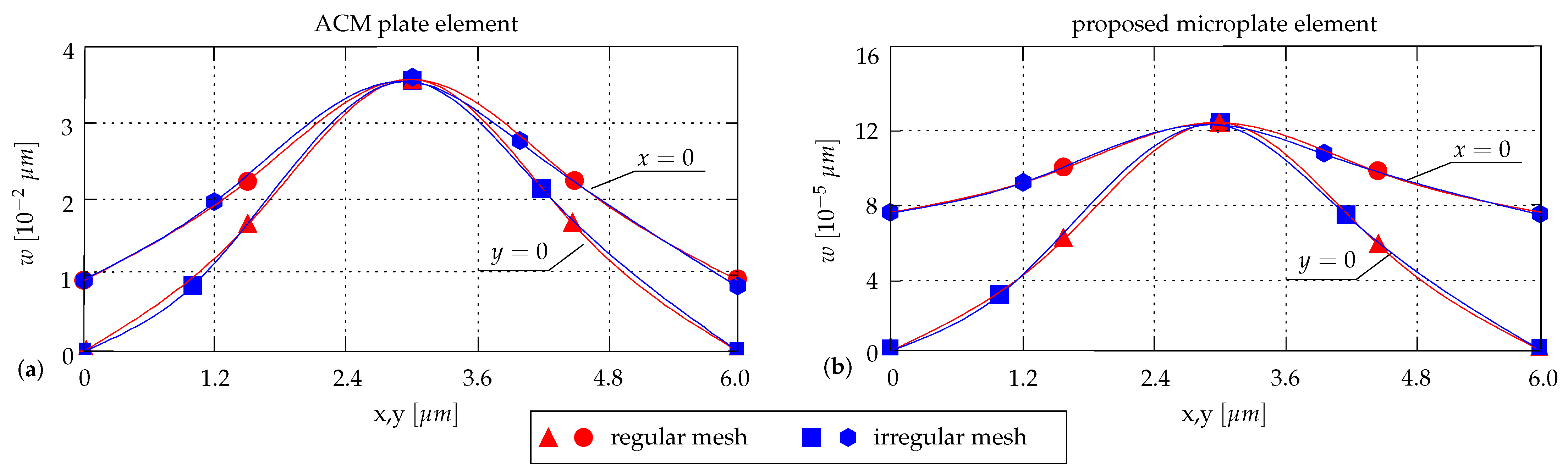
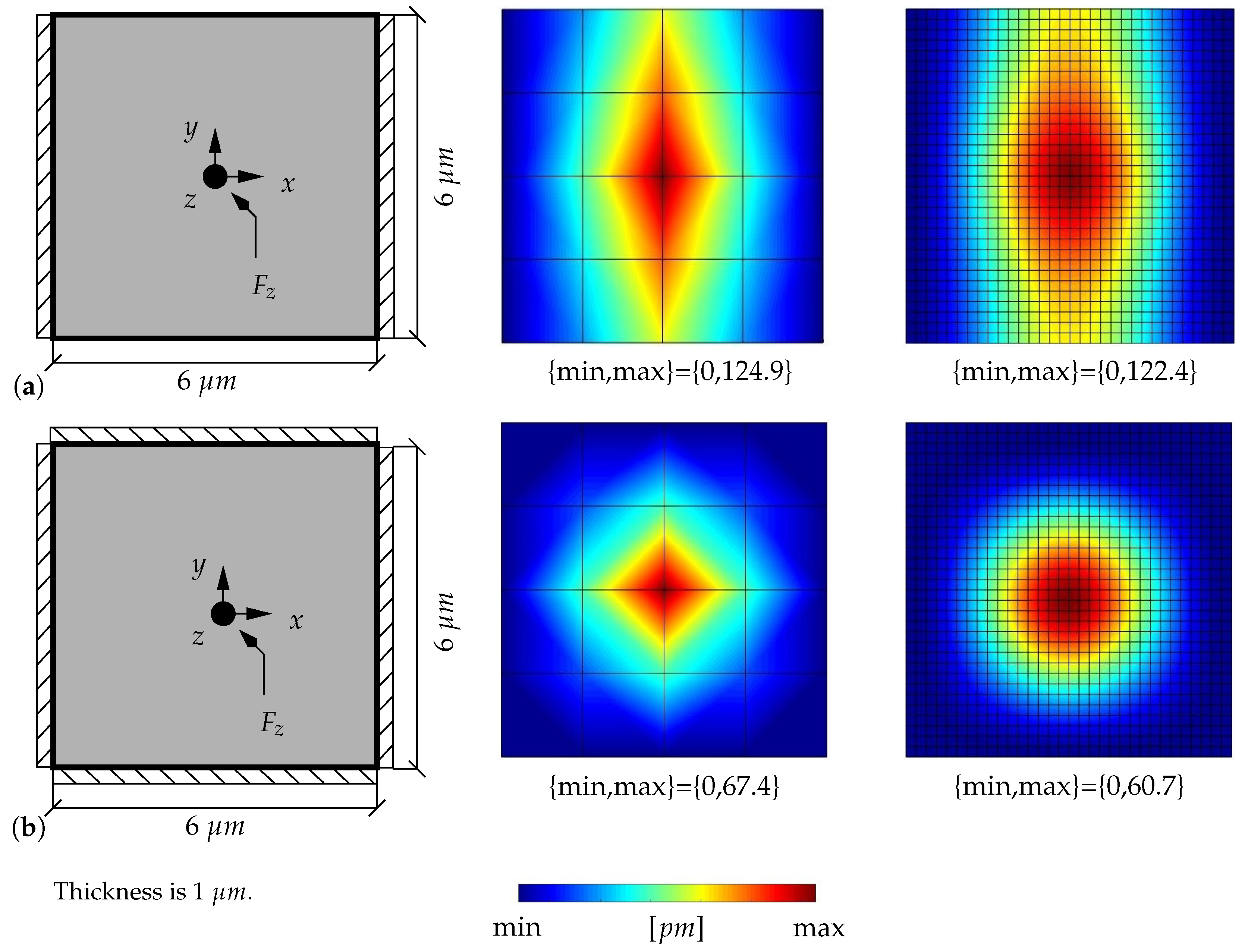
4.3.1. Microplate Response to Point Load
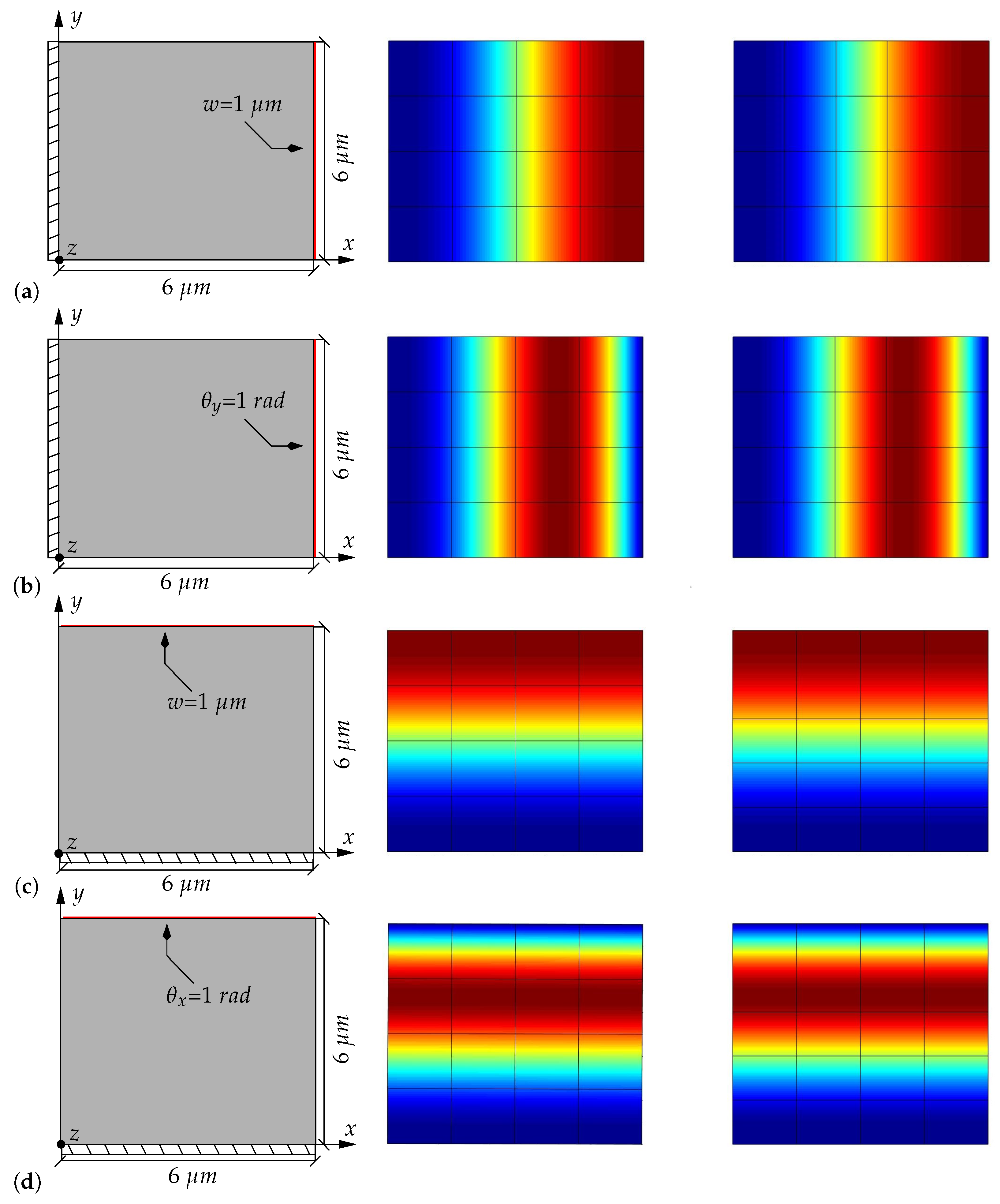
4.3.2. Microplate Response to Displacement and Rotation
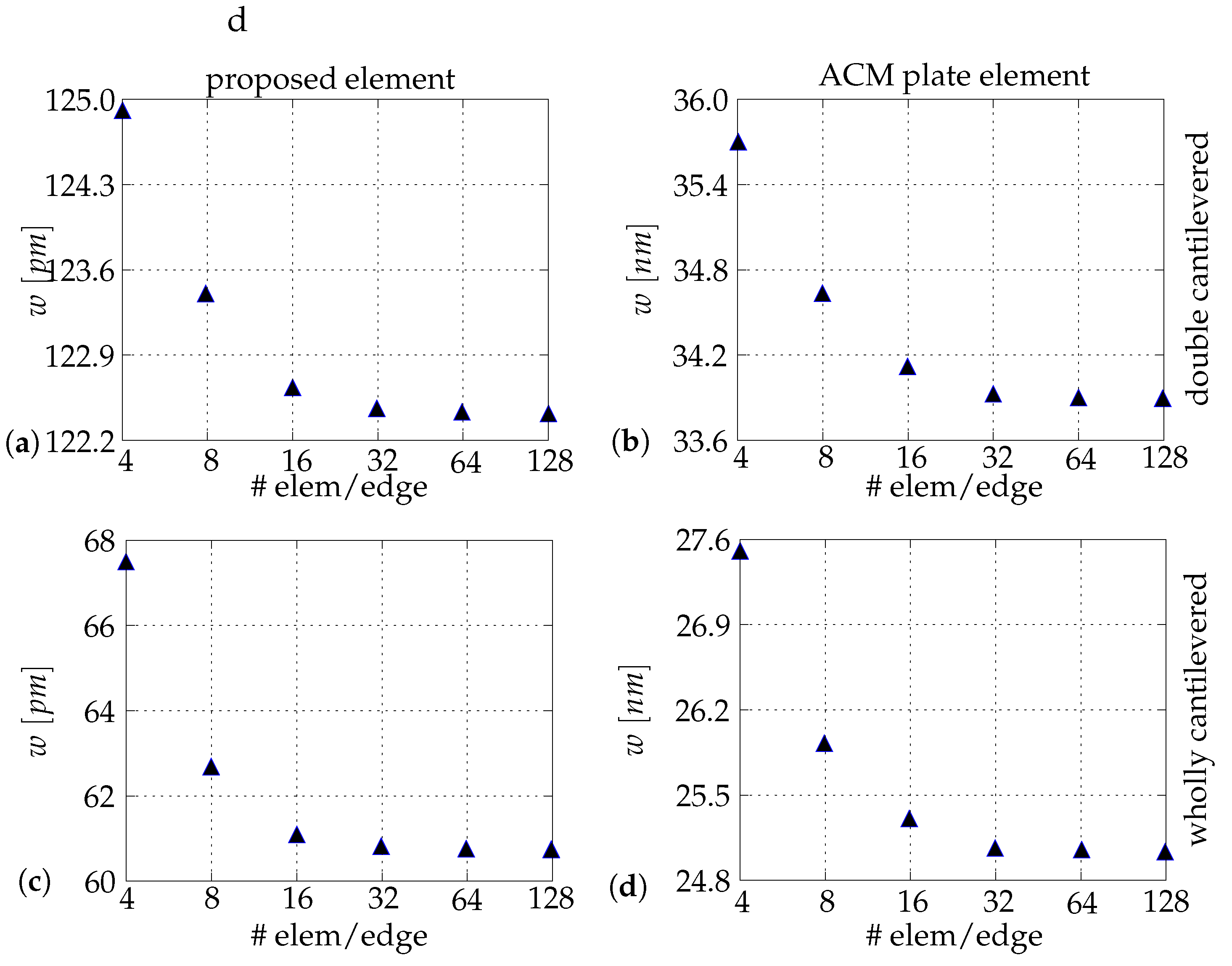
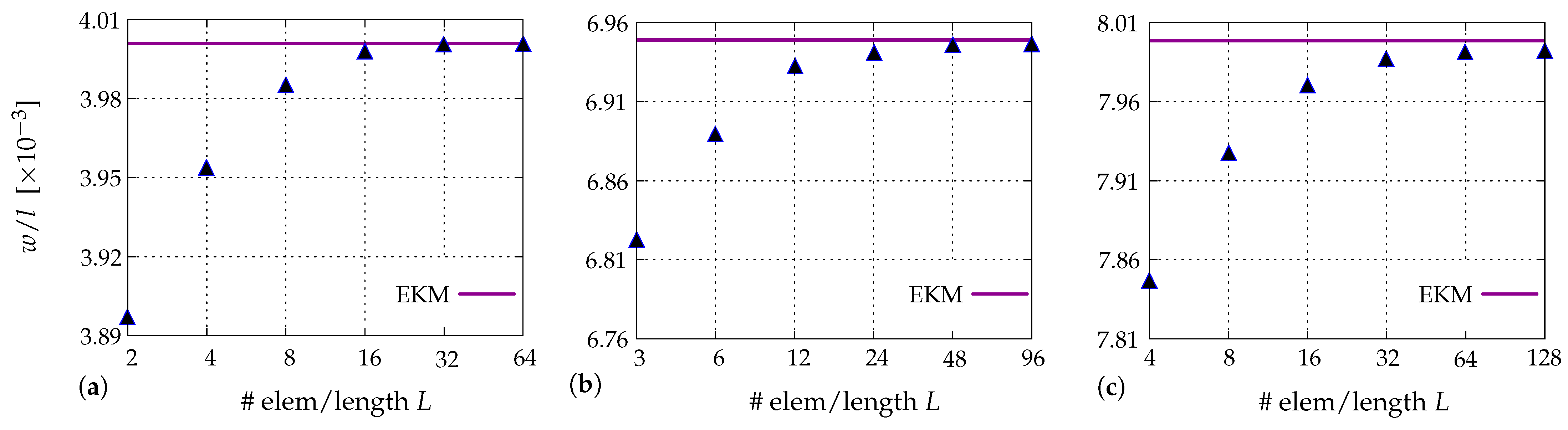
4.3.3. Mesh-Refinement and Convergence
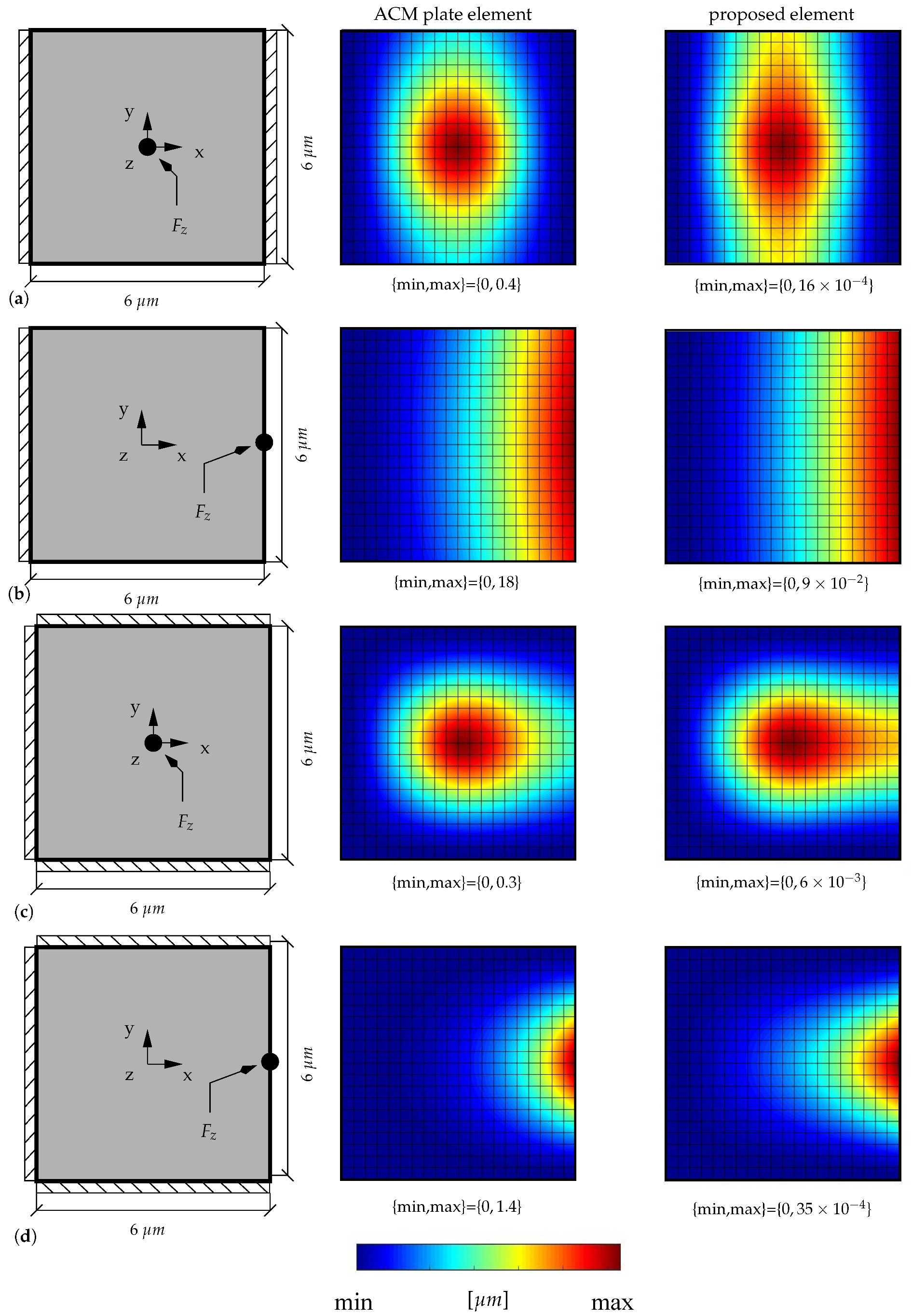
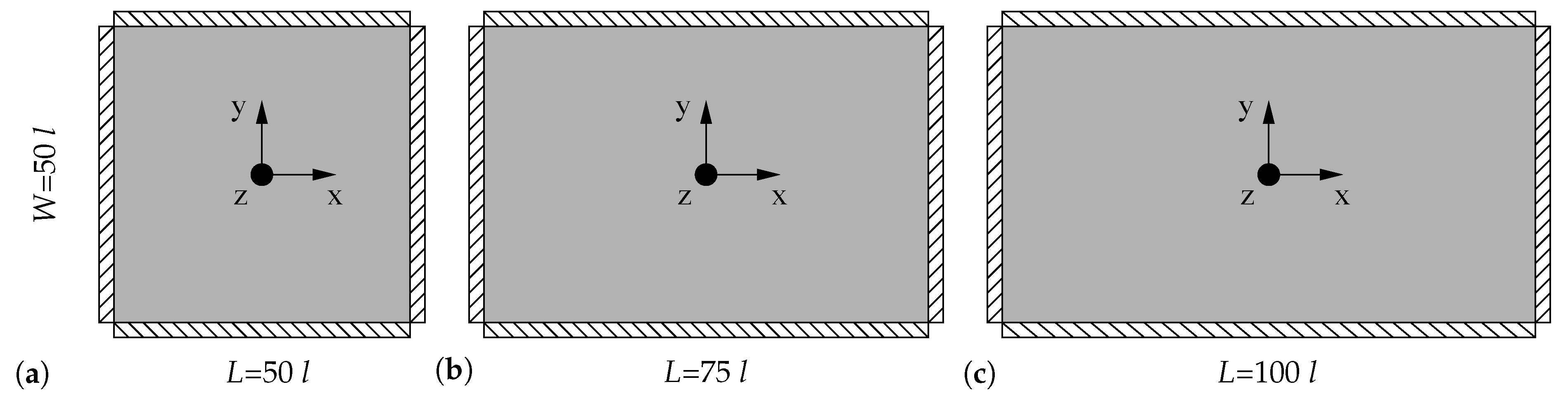
4.3.4. Square Microplate Subjected to Different Boundary Conditions
4.4. Benchmark Example: Rectangular Microplates Subjected to Evenly Distributed Load
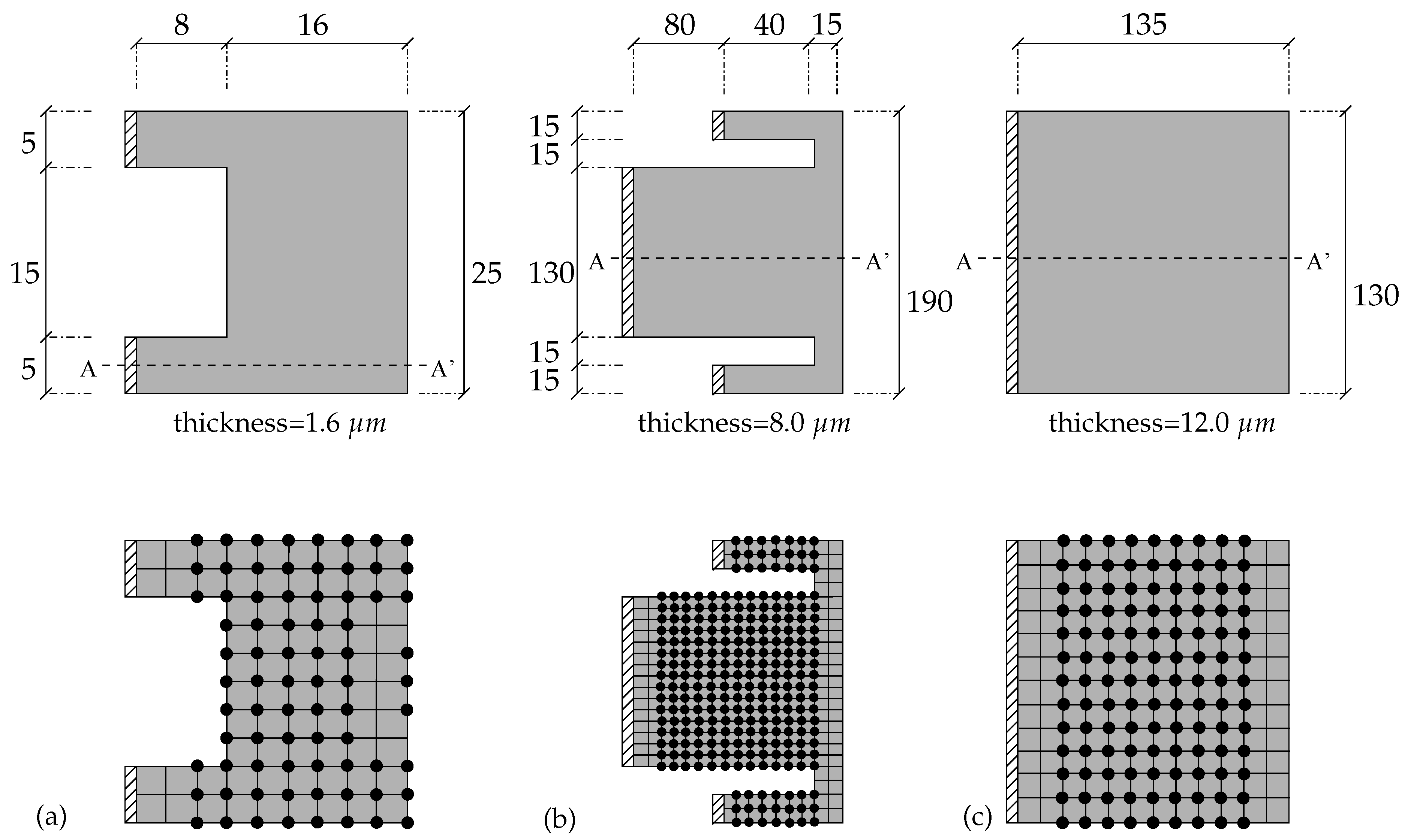
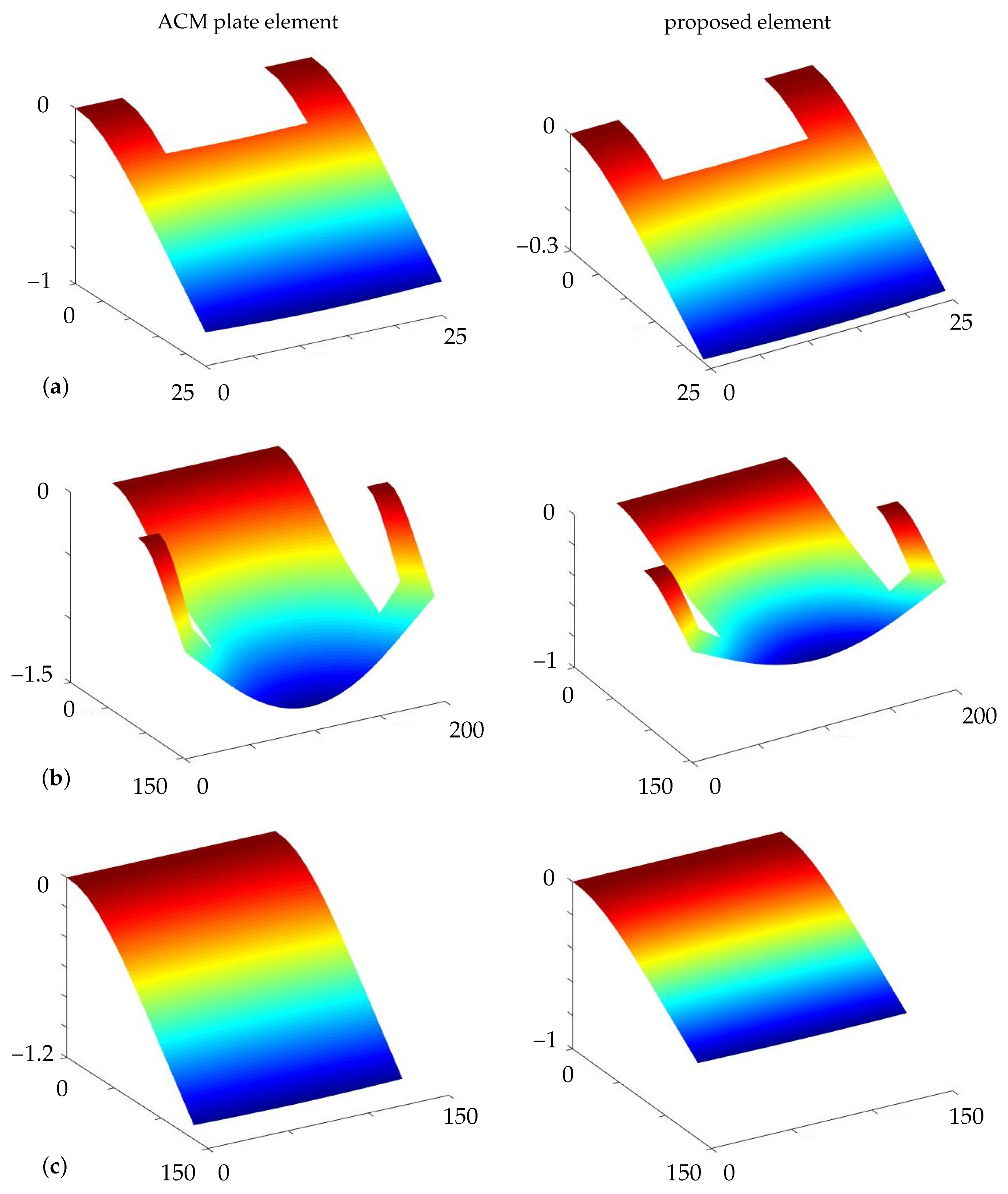
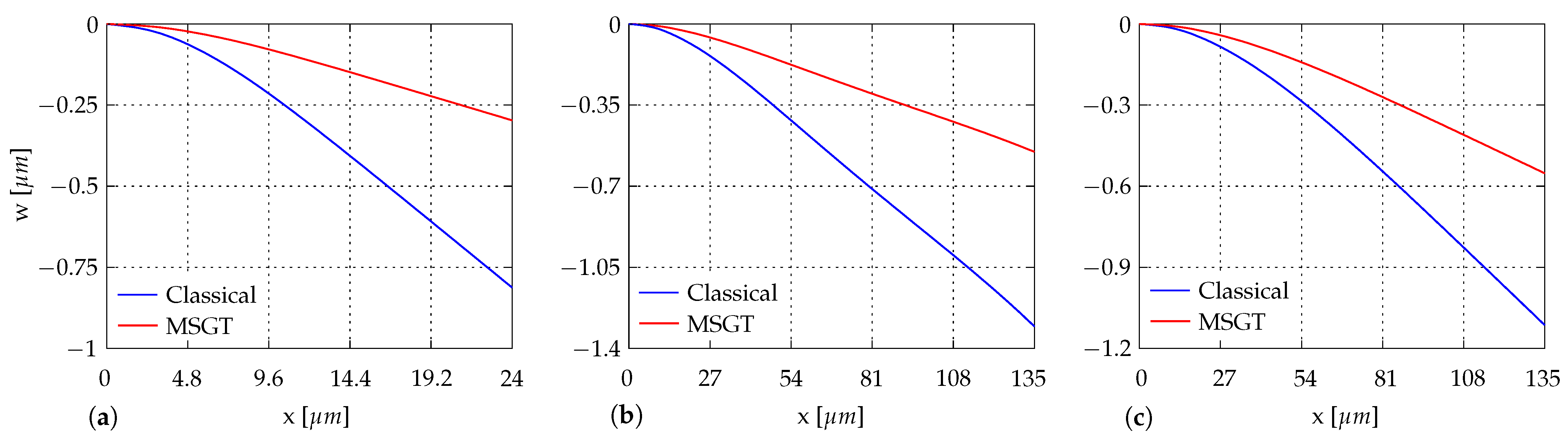
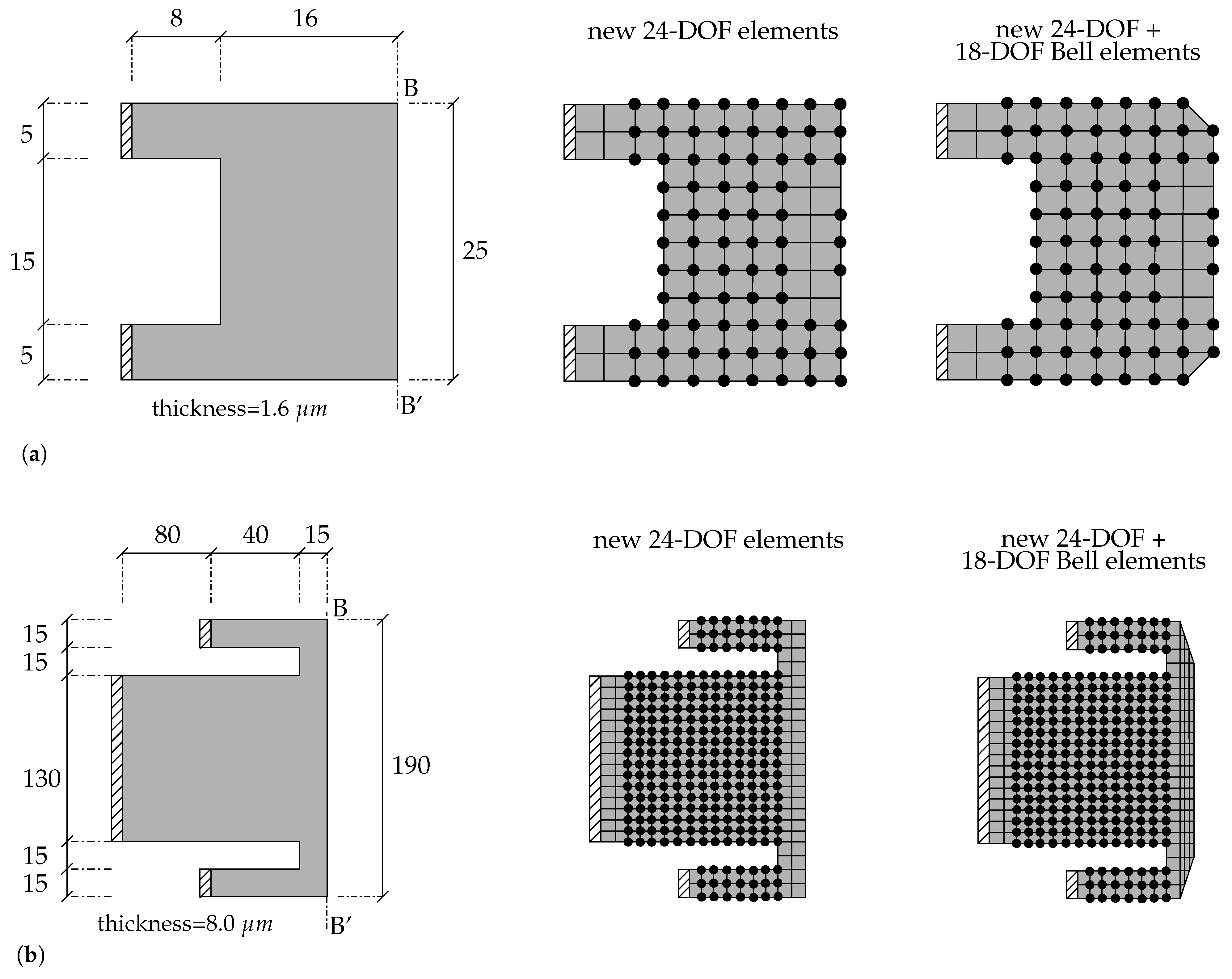
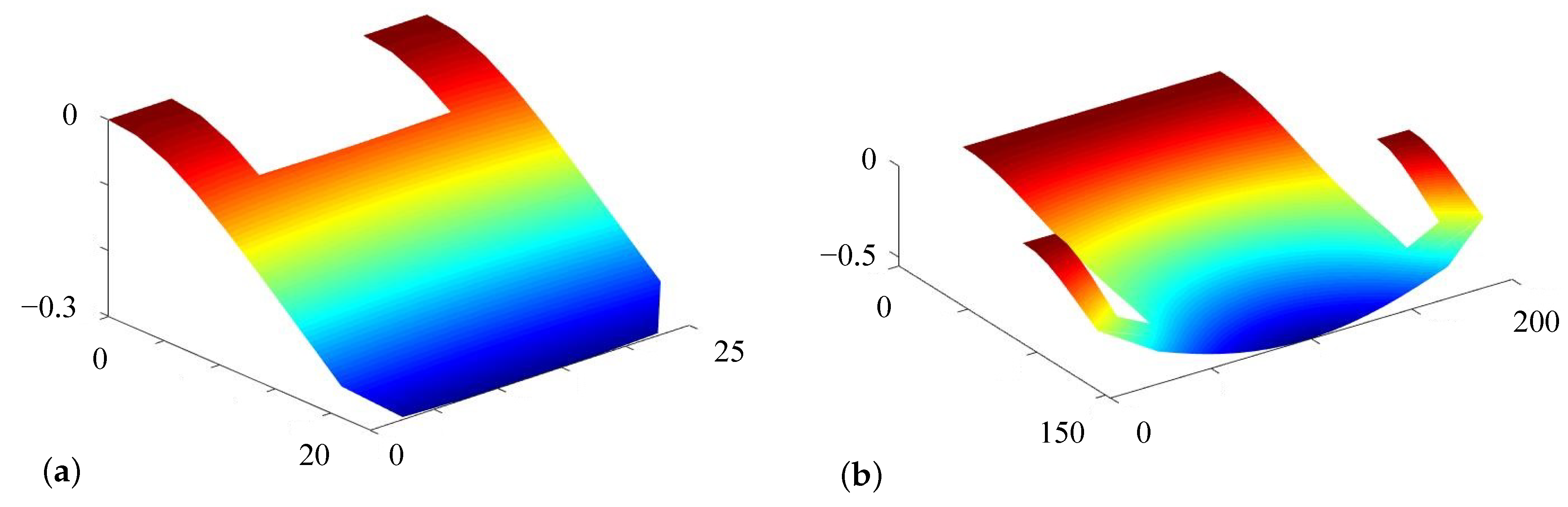
4.5. Analysis of Realistic Mems Switches with 20-Dof Elements
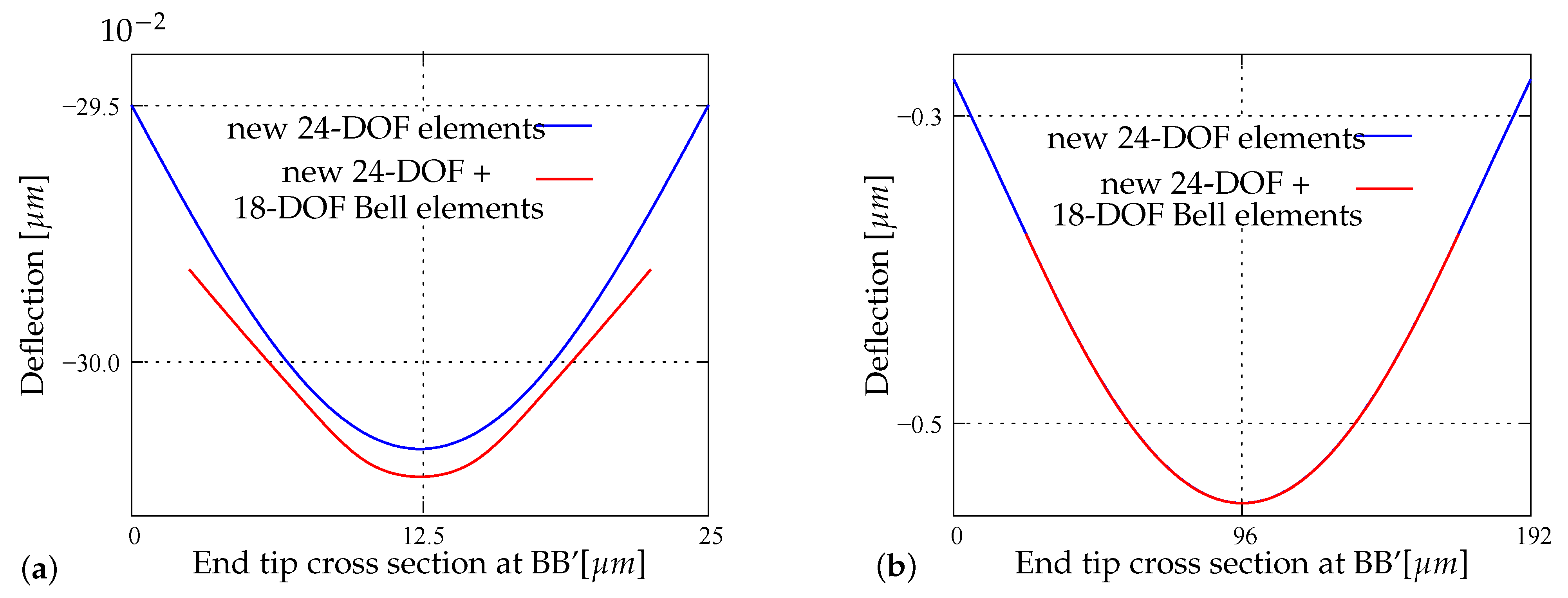
4.6. Analysis of Realistic Mems Switches with 24-Dof Elements
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A. Derivation of Euler-Lagrange Equations of Msgt-Based for Kirchhoff Microplates
Appendix B. Shape Functions for Acm Element Based on Classical Kirchhoff Plate Theory
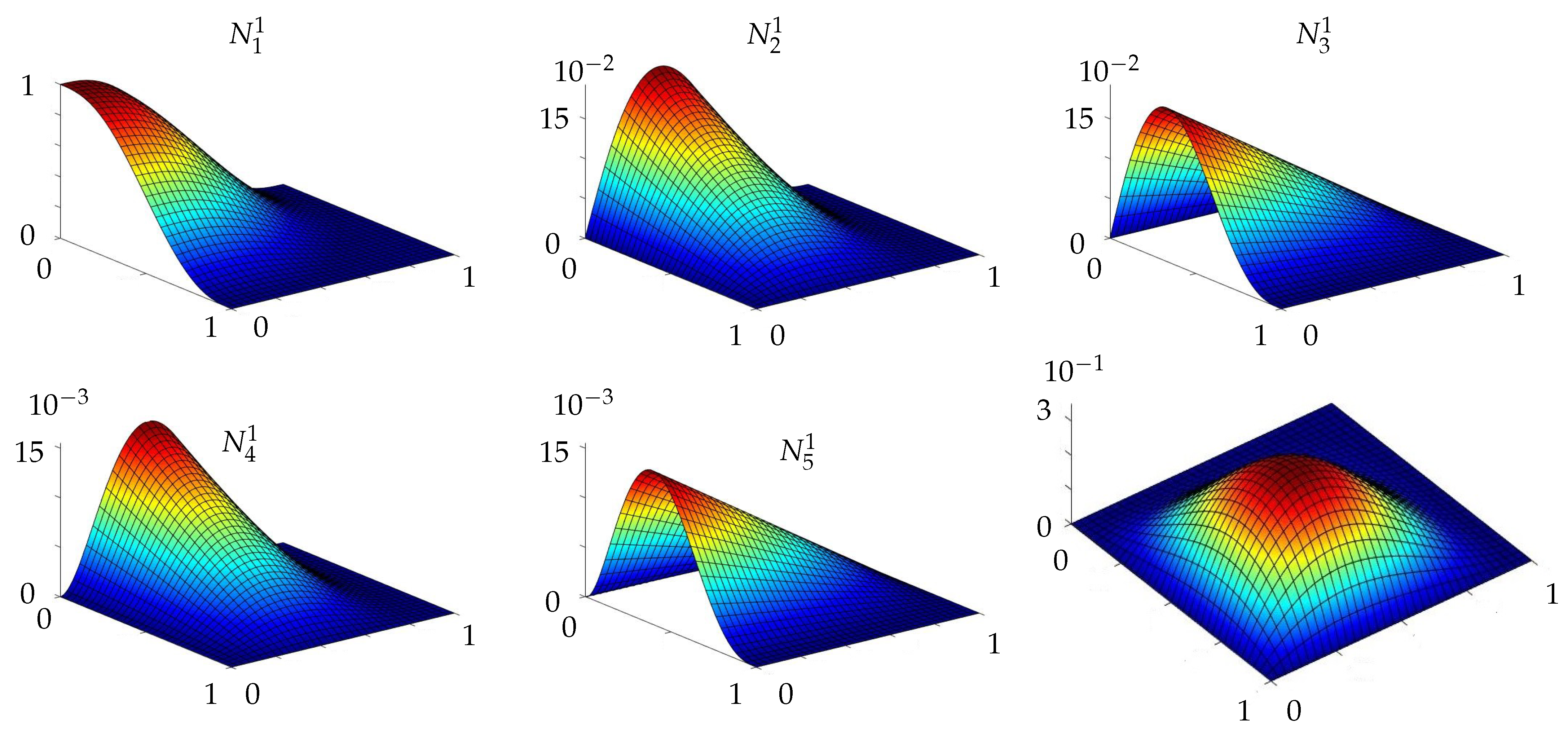
Appendix C. Shape Functions of the Proposed Element for Msgt-Based Kirchhoff Microplates
| - | + | ||||
| (A30) |
Appendix D. Strain-Displacement Matrices for Msgt-Based Kirchhoff Microplates
Appendix E. New 28-Dof Finite Element Formulation for Msgt-Based Kirchhoff-Love Microplates
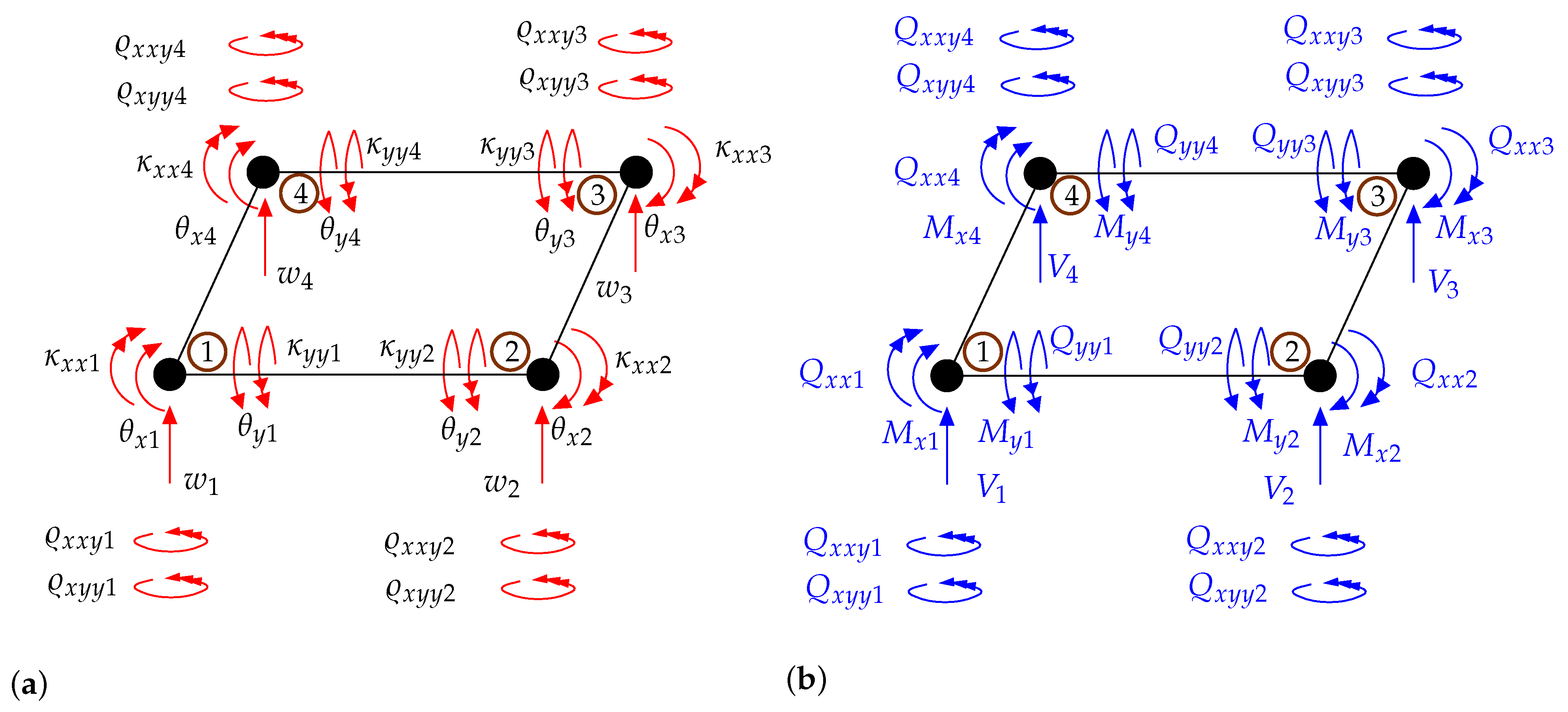
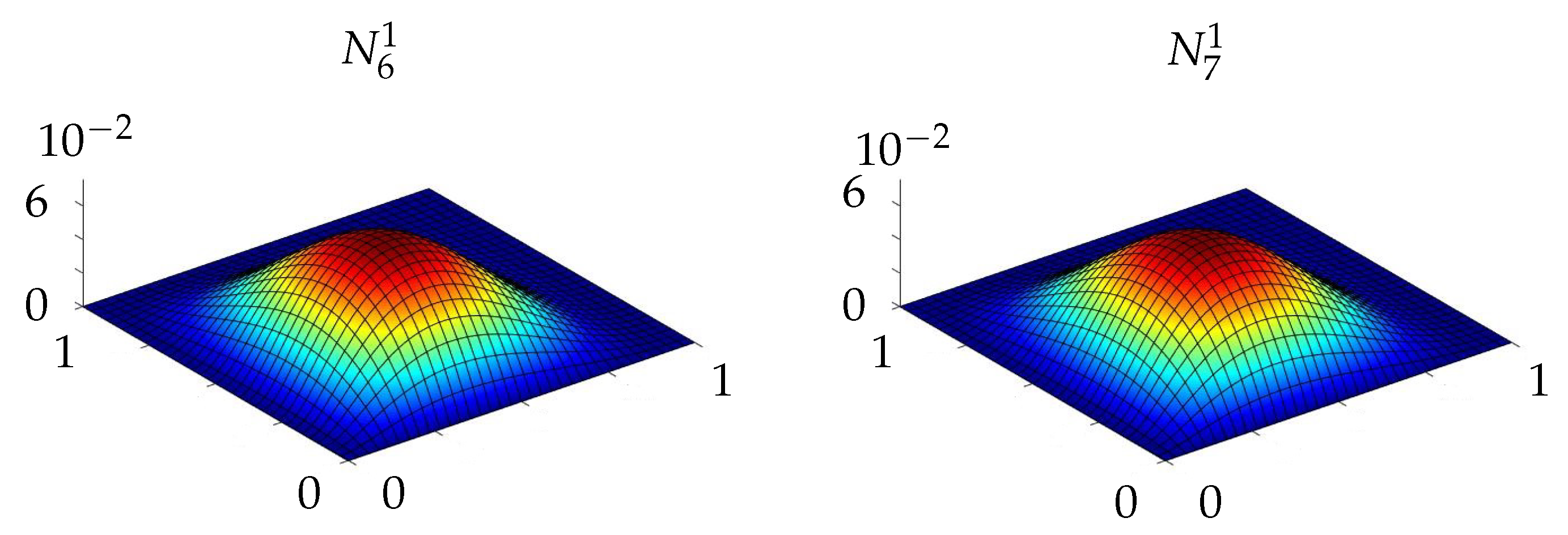
Appendix F. New 32-Dof Finite Element Formulation for Msgt-Based Kirchhoff-Love Microplates
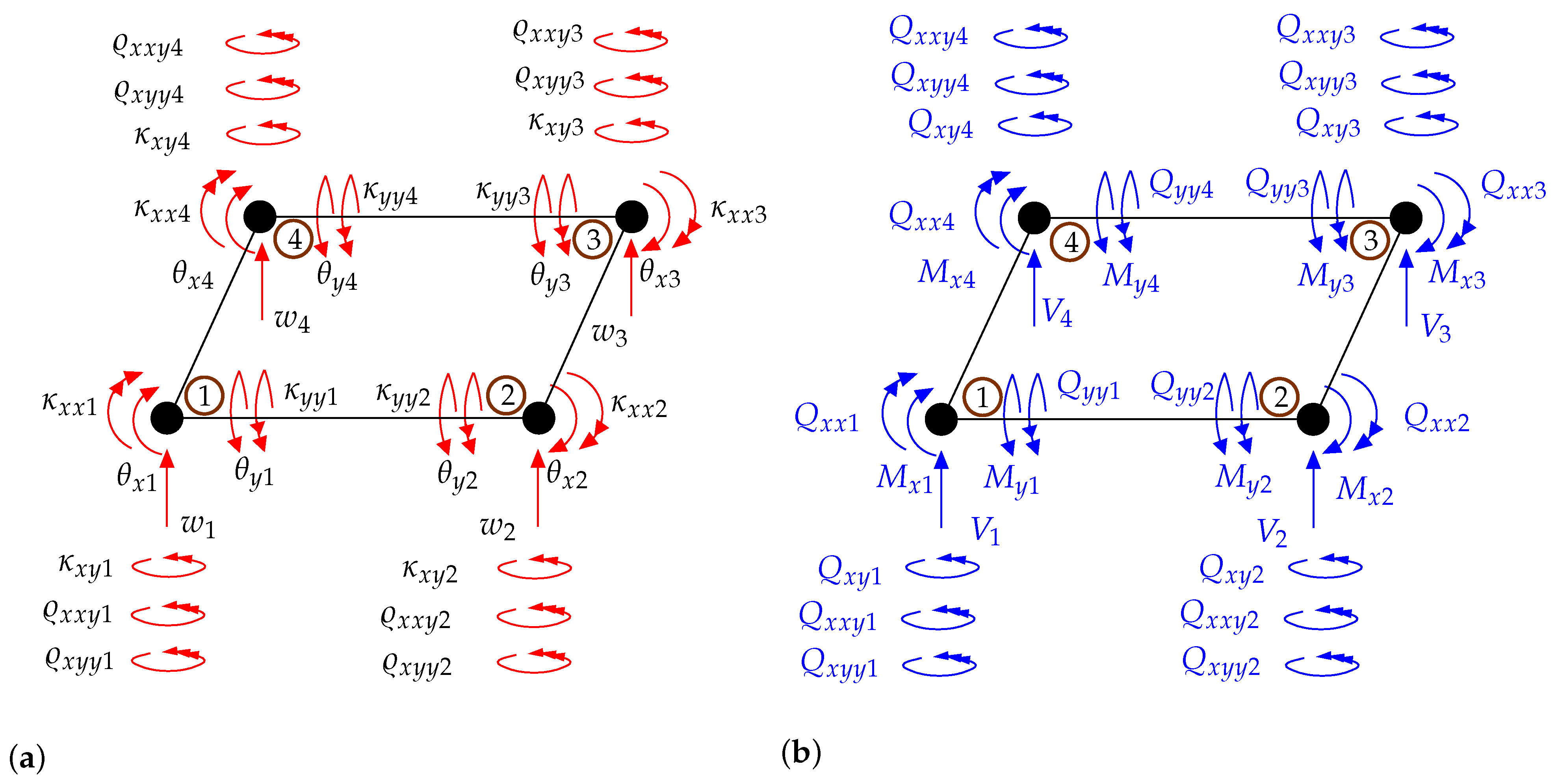
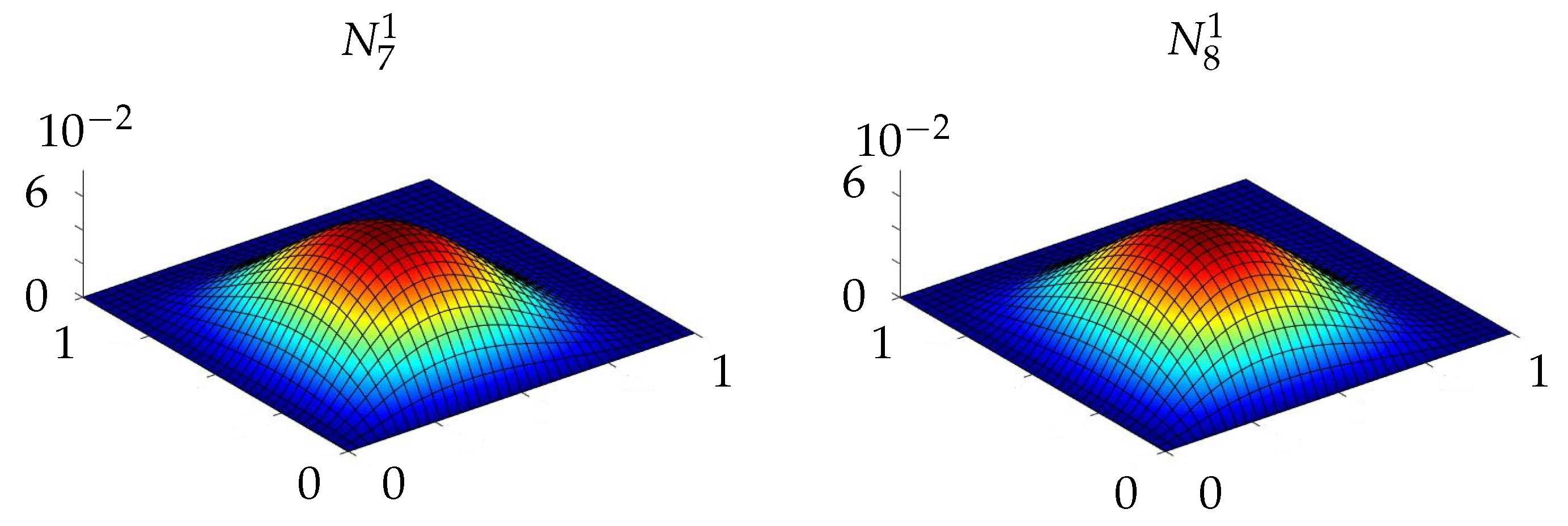
References
- Alper, S.; Akin, T. A single-crystal silicon symmetrical and decoupled MEMS gyroscope on an insulating substrate. J. Microelectromech. Syst. 2005, 14, 707–717. [Google Scholar] [CrossRef]
- Berry, C.; Wang, N.; Hashemi, M.; Unlu, M.; Jarrahi, M. Significant performance enhancement in photoconductive terahertz optoelectronics by incorporating plasmonic contact electrodes. Nat. Commun. 2013, 4, 1622. [Google Scholar] [CrossRef]
- Luo, L. Attitude angular measurement system based on MEMS accelerometer. In Proceedings of the 7th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Large Mirrors and Telescopes, Harbin, China, 26–29 April 2014. [Google Scholar]
- Mitcheson, P.; Yeatman, E.; Rao, G.; Holmes, A.; Green, T. Energy Harvesting From Human and Machine Motion for Wireless Electronic Devices. Proc. IEEE 2008, 96, 1457–1486. [Google Scholar] [CrossRef]
- Rebeiz, G.M. RF MEMS; Wiley-Blackwell: Hoboken, NJ, USA, 2003. [Google Scholar] [CrossRef]
- Unlu, M.; Hashemi, M.; Berry, C.W.; Li, S.; Yang, S.H.; Jarrahi, M. Switchable scattering meta-surfaces for broadband terahertz modulation. Nat. Sci. Rep. 2014, 4, 5708. [Google Scholar] [CrossRef]
- Bogue, R. Recent developments in MEMS sensors: A review of applications, markets and technologies. Sens. Rev. 2013, 33. [Google Scholar] [CrossRef]
- Divyananda, J.; Hod, S. Biomedical applications of mems and nems pressure transducers and sensors. Int. J. Innov. Res. Dev. 2013, 5, 1832. [Google Scholar]
- Karman, S.; Ibrahim, F.; Soin, N. A review of MEMS drug delivery in medical application. In Proceedings of the 3rd Kuala Lumpur International Conference on Biomedical Engineering 2006, Kuala Lumpur, Malaysi, 11–14 December 2006; Ibrahim, F., Osman, N.A.A., Usman, J., Kadri, N.A., Eds.; Springer: Berlin, Germany, 2007; pp. 312–315. [Google Scholar]
- Sahdom, A.S. Application of Micro Electro-Mechanical Sensors (MEMS) Devices with Wifi Connectivity and Cloud Data Solution for Industrial Noise and Vibration Measurements. J. Physics Conf. Ser. 2019, 1262, 012025. [Google Scholar] [CrossRef]
- Aero, E.; Kuvshinskii, E. Fundamental equations of the theory of elastic media with rotationally interacting particles. Fizika Tverdogo Tela 1960, 2, 1399–1409. [Google Scholar]
- Grioli, G. Elasticità asimmetrica. Ann. Mat. Pura Appl. 1960, 50, 389–417. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Tiersten, H.F. Effects of couple-stresses in linear elasticity. Arch. Ration. Mech. Anal. 1962, 11, 415–448. [Google Scholar] [CrossRef]
- Mindlin, R.D. Micro-structure in linear elasticity. Arch. Ration. Mech. Anal. 1964, 16, 51–78. [Google Scholar] [CrossRef]
- Mindlin, R.D. Second gradient of strain and surface-tension in linear elasticity. Int. J. Solids Struct. 1965, 1, 417–438. [Google Scholar] [CrossRef]
- Eringen, A. Simple microfluids. Int. J. Eng. Sci. 1964, 2, 205–217. [Google Scholar] [CrossRef]
- Eringen, A. Theory of micropolar continua. In Proceedings of the Ninth Midwestern Mechanics Conference, Madison, WI, USA, 16–18 August 1965. [Google Scholar]
- Eringen, A. Theory of micropolar elasticity. Fracture 1968, 1, 621–729. [Google Scholar]
- Koiter, W. Couple stresses in the theory of elasticity. Proc. K. Ned. Akad. Wet. 1964, 67, 17–44. [Google Scholar]
- Mindlin, R.D.; Eshel, N.N. On first strain-gradient theories in linear elasticity. Int. J. Solids Struct. 1968, 4, 109–124. [Google Scholar] [CrossRef]
- Nowacki, W. Theory of Micropolar Elasticity; Springer Science and Business Media: Berlin, Germany, 1970. [Google Scholar] [CrossRef]
- Toupin, R. Elastic materials with couple stress. Arch. Rational Mech. Anal 1962, 11, 385–414. [Google Scholar] [CrossRef]
- Eringen, A.C.; Suhubi, E. Nonlinear theory of simplemicroelastic solids: I. Int. J. Eng. Sci. 1964, 2, 189–203. [Google Scholar] [CrossRef]
- Suhubi, E.; Eringen, A.C. Nonlinear theory of simplemicroelastic solids: II. Int. J. Eng. Sci. 1964, 2, 389–404. [Google Scholar] [CrossRef]
- Fleck, N.A.; Hutchinson, J.W. A phenomenological theory for strain gradient effects in plasticity. J. Mech. Phys. Solids 1993, 41, 1825–1857. [Google Scholar] [CrossRef]
- Fleck, N.A.; Hutchinson, J.W. Strain gradient plasticity. Adv. Appl. Mech. 1997, 33, 296–358. [Google Scholar]
- Fleck, N.A.; Hutchinson, J.W. A reformulation of strain gradient plasticity. J. Mech. Phys. Solids 2001, 49, 2245–2271. [Google Scholar] [CrossRef]
- Lam, D.; Yang, F.; Chong, A.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.; Lam, D.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Akgöz, B.; Ömer, C. Strain gradient elasticity and modified couple stress models for buckling analysis of axially loaded micro-scaled beams. Int. J. Eng. Sci. 2011, 49, 1268–1280. [Google Scholar] [CrossRef]
- Akgöz, B.; Ömer, C. A microstructure-dependent sinusoidal plate model based on the strain gradient elasticity theory. Acta Mech. 2015, 226, 2277–2294. [Google Scholar] [CrossRef]
- Kandaz, M.; Dal, H. A comparative study of modified strain gradient theory and modified couple stress theory for gold microbeams. Arch. Appl. Mech. 2018, 88, 2051–2070. [Google Scholar] [CrossRef]
- Reddy, J. Nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates. Int. J. Eng. Sci. 2010, 48, 1507–1518. [Google Scholar] [CrossRef]
- Eringen, A.C. (Ed.) Nonlocal Continuum Field Theories; Springer Science and Business Media: Berlin, Germany, 2002. [Google Scholar] [CrossRef]
- Phadikar, J.; Pradhan, S. Variational formulation and finite element analysis for nonlocal elastic nanobeams and nanoplates. Comput. Mater. Sci. 2010, 49, 492–499. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, S.; Zhao, J.; Chen, X. A size-dependent Kirchhoff micro-plate model based on strain gradient elasticity theory. Eur. J. Mech. 2011, 30, 517–524. [Google Scholar] [CrossRef]
- Wang, B.; Huang, S.; Zhao, J.; Zhou, S. Reconsiderations on boundary conditions of Kirchhoff micro-plate model based on a strain gradient elasticity theory. Appl. Math. Model. 2016, 40, 7303–7317. [Google Scholar] [CrossRef]
- Balobanov, V.; Kiendl, J.; Khakalo, S.; Niiranen, J. Kirchhoff–Love shells within strain gradient elasticity: Weak and strong formulations and an H3-conforming isogeometric implementation. Comput. Methods Appl. Mech. Eng. 2019, 344, 837–857. [Google Scholar] [CrossRef]
- Khakalo, S.; Niiranen, J. Anisotropic strain gradient thermoelasticity for cellular structures: Plate models, homogenization and isogeometric analysis. J. Mech. Phys. Solids 2020, 134, 103728. [Google Scholar] [CrossRef]
- Niiranen, J.; Kiendl, J.; Niemi, A.H.; Reali, A. Isogeometric analysis for sixth-order boundary value problems of gradient-elastic Kirchhoff plates. Comput. Methods Appl. Mech. Eng. 2017, 316, 328–348. [Google Scholar] [CrossRef]
- Arefi, M.; Zenkour, A.M. Size-dependent electro-elastic analysis of a sandwich microbeam based on higher-order sinusoidal shear deformation theory and strain gradient theory. J. Intell. Mater. Syst. Struct. 2017, 29, 1394–1406. [Google Scholar] [CrossRef]
- Arefi, M.; Bidgoli, E.M.R.; Zenkour, A.M. Size-dependent free vibration and dynamic analyses of a sandwich microbeam based on higher-order sinusoidal shear deformation theory and strain gradient theory. Smart Struct. Syst. 2018, 22, 27–40. [Google Scholar]
- Arefi, M.; Zenkour, A.M. Vibration and bending analyses of magneto–electro–thermo-elastic sandwich microplates resting on viscoelastic foundation. Appl. Phys. A 2017, 123, 1–17. [Google Scholar] [CrossRef]
- Arefi, M.; Zenkour, A.M. Free vibration analysis of a three-layered microbeam based on strain gradient theory and three-unknown shear and normal deformation theory. Steel Compos. Struct. 2018, 26, 421–437. [Google Scholar]
- Sobhy, M.; Zenkour, A.M. A comprehensive study on the size-dependent hygrothermal analysis of exponentially graded microplates on elastic foundations. Mech. Adv. Mater. Struct. 2020, 27, 816–830. [Google Scholar] [CrossRef]
- Barati, M.R.; Faleh, N.M.; Zenkour, A.M. Dynamic response of nanobeams subjected to moving nanoparticles and hygro-thermal environments based on nonlocal strain gradient theory. Mech. Adv. Mater. Struct. 2019, 26, 1661–1669. [Google Scholar] [CrossRef]
- Movassagh, A.A.; Mahmoodi, M. A micro-scale modeling of Kirchhoff plate based on modified strain-gradient elasticity theory. Eur. J. Mech. 2013, 40, 50–59. [Google Scholar] [CrossRef]
- Sahmani, S.; Ansari, R. On the free vibration response of functionally graded higher-order shear deformable microplates based on the strain gradient elasticity theory. Compos. Struct. 2013, 95, 430–442. [Google Scholar] [CrossRef]
- Li, A.; Zhou, S.; Zhou, S.; Wang, B. A size-dependent model for bi-layered Kirchhoff micro-plate based on strain gradient elasticity theory. Compos. Struct. 2014, 113, 272–280. [Google Scholar] [CrossRef]
- Babu, B.; Patel, B. A new computationally efficient finite element formulation for nanoplates using second-order strain gradient Kirchhoff’s plate theory. Compos. Part Eng. 2019, 168, 302–311. [Google Scholar] [CrossRef]
- Babu, B.; Patel, B.P. An improved quadrilateral finite element for nonlinear second-order strain gradient elastic Kirchhoff plates. Meccanica 2020, 55, 139–159. [Google Scholar] [CrossRef]
- On the role of gradients in the localization of deformation and fracture. Int. J. Eng. Sci. 1992, 30, 1279–1299. [CrossRef]
- Aifantis, E.; Ru, C.Q. A simple approach to solve boundary-value problems in gradient elasticity. Acta Mechanica 1993, 101, 59–68. [Google Scholar]
- Beheshti, A. A finite element formulation for Kirchhoff plates in strain-gradient elasticity. Eur. J. Comput. Mech. 2019, 28, 123–146. [Google Scholar] [CrossRef]
- Bacciocchi, M.; Fantuzzi, N.; Ferreira, A. Conforming and nonconforming laminated finite element Kirchhoff nanoplates in bending using strain gradient theory. Comput. Struct. 2020, 239, 106322. [Google Scholar] [CrossRef]
- Bacciocchi, M.; Fantuzzi, N.; Ferreira, A. Static finite element analysis of thin laminated strain gradient nanoplates in hygro-thermal environment. Contin. Mech. Thermodyn. 2020, 1–24. [Google Scholar] [CrossRef]
- Adini, A.; Clough, R.W. Analysis of plate bending by the finite element method. NSF Rep. 1961, G, 7337. [Google Scholar]
- Melosh, R. Basis for derivation of matrices for the direct stiffness method. AIAA J. 1963, 1, 1631–1637. [Google Scholar] [CrossRef]
- Bogner, F.; Fox, R.; Schmit, L. The generation of interelement compatible stiffness and mass matrices by the use of interpolation formulas. In Proceedings of the Conference on Matrix Methods in Structural Mechanics, Wright-Patterson Air Force Base, Montgomery County, OH, USA; 1965; pp. 397–444. [Google Scholar]
- Espinosa, H.; Prorok, B.; Fischer, M. A methodology for determining mechanical properties of freestanding thin films and MEMS materials. J. Mech. Phys. Solids 2003, 51, 47–67. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L. (Eds.) The Finite Element Method, 5th ed.; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Dadgour, H.F.; Banerjee, K. Design and Analysis of Hybrid NEMS-CMOS Circuits for Ultra Low-Power Applications. In Proceedings of the 44th ACM/IEEE Design Automation Conference, San Diego, CA, USA, 4–8 June 2007; pp. 306–311. [Google Scholar]
- Moldovan, C.F.; Vitale, W.A.; Sharma, P.; Bernard, L.S.; Ionescu, A.M. Fabrication process and characterization of suspended graphene membranes for RF NEMS capacitive switches. Microelectron. Eng. 2015, 145, 5–8. [Google Scholar] [CrossRef]
- Unlu, M.; Jarrahi, M. Miniature multi-contact MEMS switch for broadband terahertz modulation. Opt. Express 2014, 22, 32245–32260. [Google Scholar] [CrossRef]
- Stefanini, R.; Chatras, M.; Blondy, P.; Rebeiz, G.M. Miniature MEMS Switches for RF Applications. J. Microelectromech. Syst. 2011, 20, 1324–1335. [Google Scholar] [CrossRef]
- Patel, C.; Rebeiz, G. RF MEMS metal-contact switches with mN-contact and restoring forces and low process sensitivity. IEEE Trans. Microw. Theory Tech. 2011, 59, 1230–1237. [Google Scholar] [CrossRef]
- Yu, W.; Zhou, K.; Wu, Z.; Yang, T. Analysis of NEMS Switch Using Changeable Space Domain. In Proceedings of the 2010 International Conference on Electrical and Control Engineering, Wuhan, China, 25–27 June 2010. [Google Scholar] [CrossRef]
- Soleymani, P.; Sadeghian, H.; Tahmasebi, A.; Rezazadeh, G. Pull-in instability investigation of circular micro pump subjected to nonlinear electrostatic force. Sens. Trans. 2006, 69, 622–628. [Google Scholar]
- Mohammadi, V.; Ansari, R.; Shojaei, M.F.; Gholami, R.; Sahmani, S. Size-dependent dynamic pull-in instability of hydrostatically and electrostatically actuated circular microplates. Nonlinear Dyn. 2013, 73, 1515–1526. [Google Scholar] [CrossRef]
- Shabani, R.; Sharafkhani, N.; Tariverdilo, S.; Rezazadeh, G. Dynamic analysis of an electrostatically actuated circular micro-plate interacting with compressible fluid. Acta Mechanica 2013, 224, 2025–2035. [Google Scholar] [CrossRef]
- Bell, K. A refined triangular plate bending finite element. Int. J. Numer. Methods Eng. 1969, 1, 101–122. [Google Scholar] [CrossRef]
- Gileva, L.; Shaydurova, V.; Dobronets, B. A family of triangular Hermite finite elements complementing the Bogner-Fox-Schmit rectangle. Russ. J. Numer. Anal. Math. Model. 2015, 30, 73–85. [Google Scholar] [CrossRef]
- Clough, R.; Felippa, C. A refined quadrilateral element for analysis of plate bending. In Proceedings of the 2nd Conference on Matrix Methods in Structural Mechanics, Wright-Patterson Air Force Base, Montgomery County, OH, USA, 15–17 October 1968. [Google Scholar]
- Kahrobaiyan, M.; Asghari, M.; Ahmadian, M. Strain gradient beam element. Finite Elem. Anal. Des. 2013, 68, 63–75. [Google Scholar] [CrossRef]
- Cirak, F.; Ortiz, M.; Schröder, P. Subdivision surfaces: A new paradigm for thin-shell finite-element analysis. Int. J. Numer. Methods Eng. 2000, 47, 2039–2072. [Google Scholar] [CrossRef]
- Cirak, F.; Ortiz, M. Fully C1-conforming subdivision elements for finite deformation thin-shell analysis. Int. J. Numer. Methods Eng. 2001, 51, 813–833. [Google Scholar] [CrossRef]
- Taylor, R.; Zienkiewicz, O.; Simo, J.; Chan, A. The patch test—A condition for assessing FEM converfence. Int. J. Num. Meth. Eng. 1986, 22, 39–62. [Google Scholar] [CrossRef]
- Okabe, M. Explicit interpolation formulas for the Bell triangle. Comput. Methods Appl. Mech. Eng. 1994, 117, 411–421. [Google Scholar] [CrossRef]



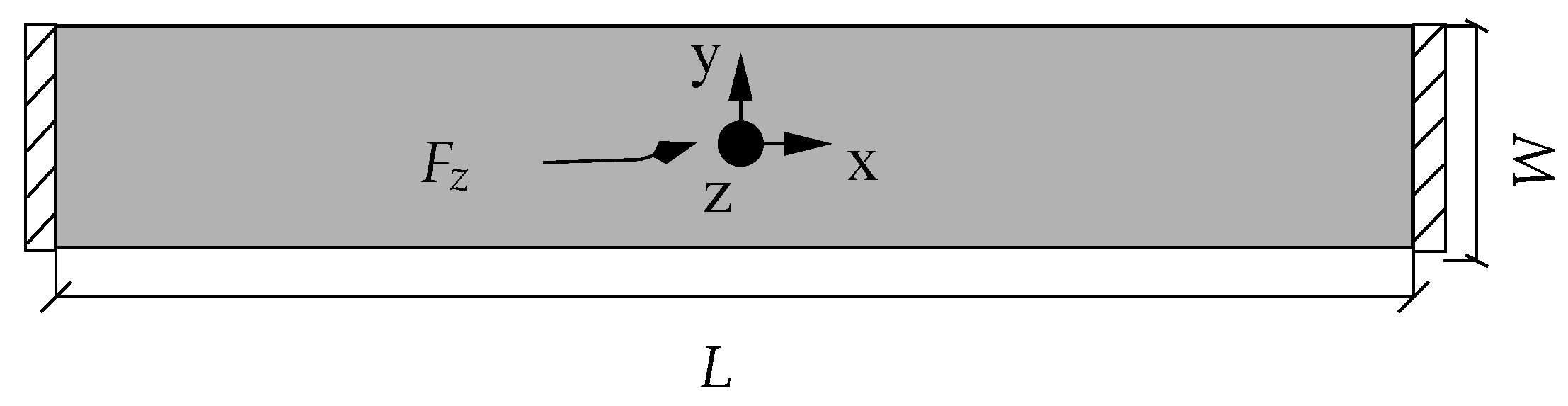




| Reference | Type | Specimen Tag No | Width, W [m] | Thickness, t [m] | Length, L [m] | Force, [] | Deflection, [m] |
|---|---|---|---|---|---|---|---|
| Espinosa et al. [60] | Double-cantilevered | 1 | 10* | 0.5 | 400* | 0.3 | 15 |
| Espinosa et al. [60] | Double-cantilevered | 2 | 10* | 1 | 400* | 0.3 | 9 |
| Gold | Epoxy | ||||
|---|---|---|---|---|---|
| Parameter | Value | Unit | Parameter | Value | Unit |
| E | 80 | [GPa] | E | [GPa] | |
| [–] | [–] | ||||
| [m] | [m] | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kandaz, M.; Dal, H. Finite Element Analyses of the Modified Strain Gradient Theory Based Kirchhoff Microplates. Surfaces 2021, 4, 115-156. https://doi.org/10.3390/surfaces4020014
Kandaz M, Dal H. Finite Element Analyses of the Modified Strain Gradient Theory Based Kirchhoff Microplates. Surfaces. 2021; 4(2):115-156. https://doi.org/10.3390/surfaces4020014
Chicago/Turabian StyleKandaz, Murat, and Hüsnü Dal. 2021. "Finite Element Analyses of the Modified Strain Gradient Theory Based Kirchhoff Microplates" Surfaces 4, no. 2: 115-156. https://doi.org/10.3390/surfaces4020014
APA StyleKandaz, M., & Dal, H. (2021). Finite Element Analyses of the Modified Strain Gradient Theory Based Kirchhoff Microplates. Surfaces, 4(2), 115-156. https://doi.org/10.3390/surfaces4020014






