Molecular Dynamics Modeling of Mechanical Properties of Polymer Nanocomposites Reinforced by C7N6 Nanosheet
Abstract
:1. Introduction
2. Simulation Methodology
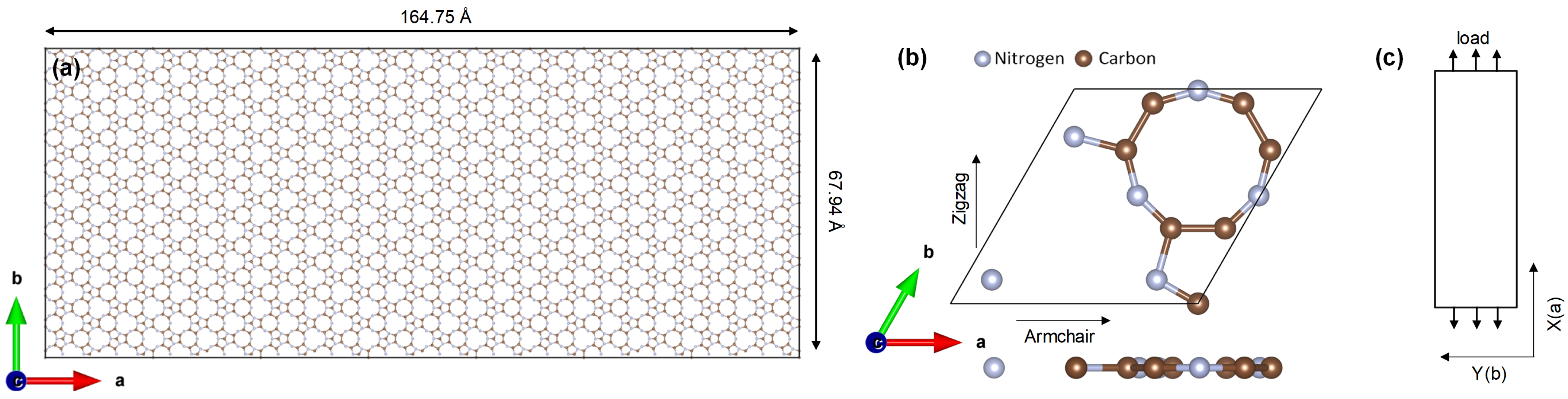
2.1. Potential and Uniaxial Tensile for Monolayer
2.2. Nanocomposite Mechanical Test
2.3. Cohesive Model for — Interface Investigation
3. Results and Discussion
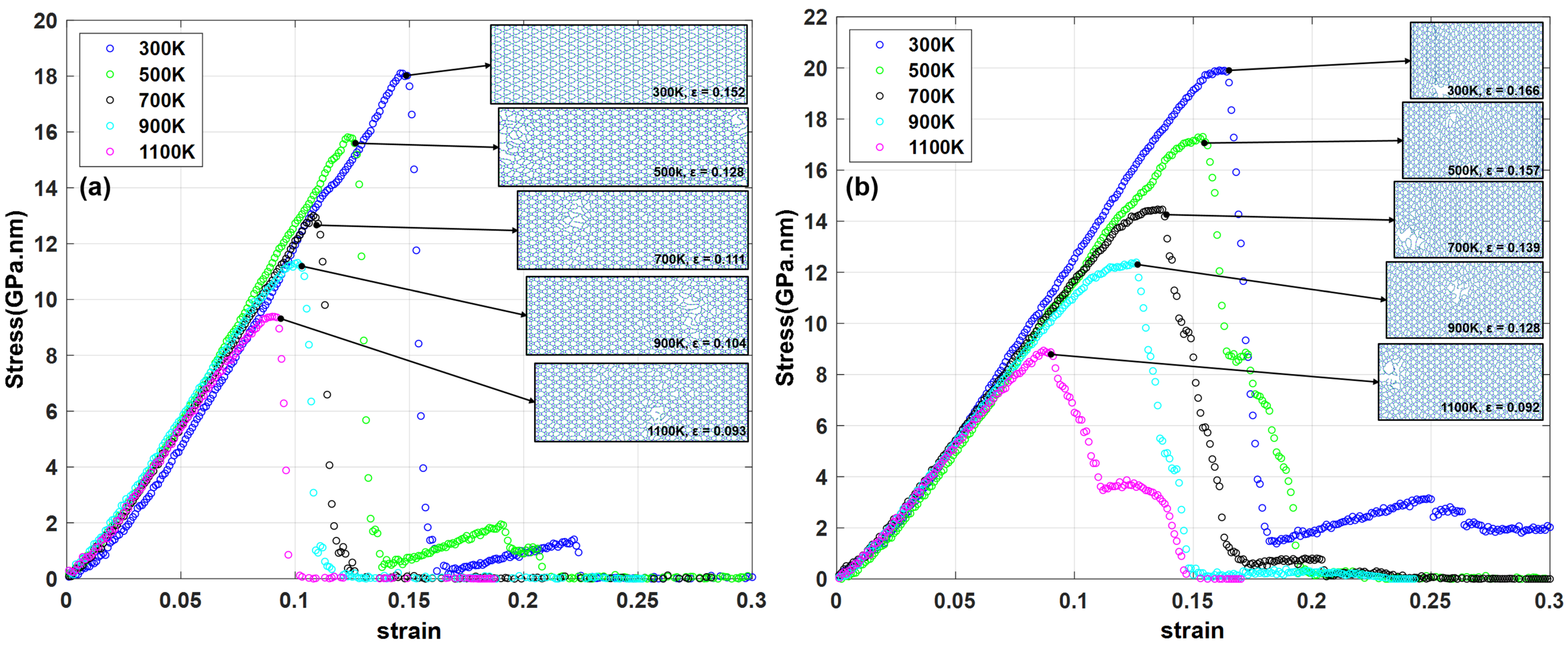
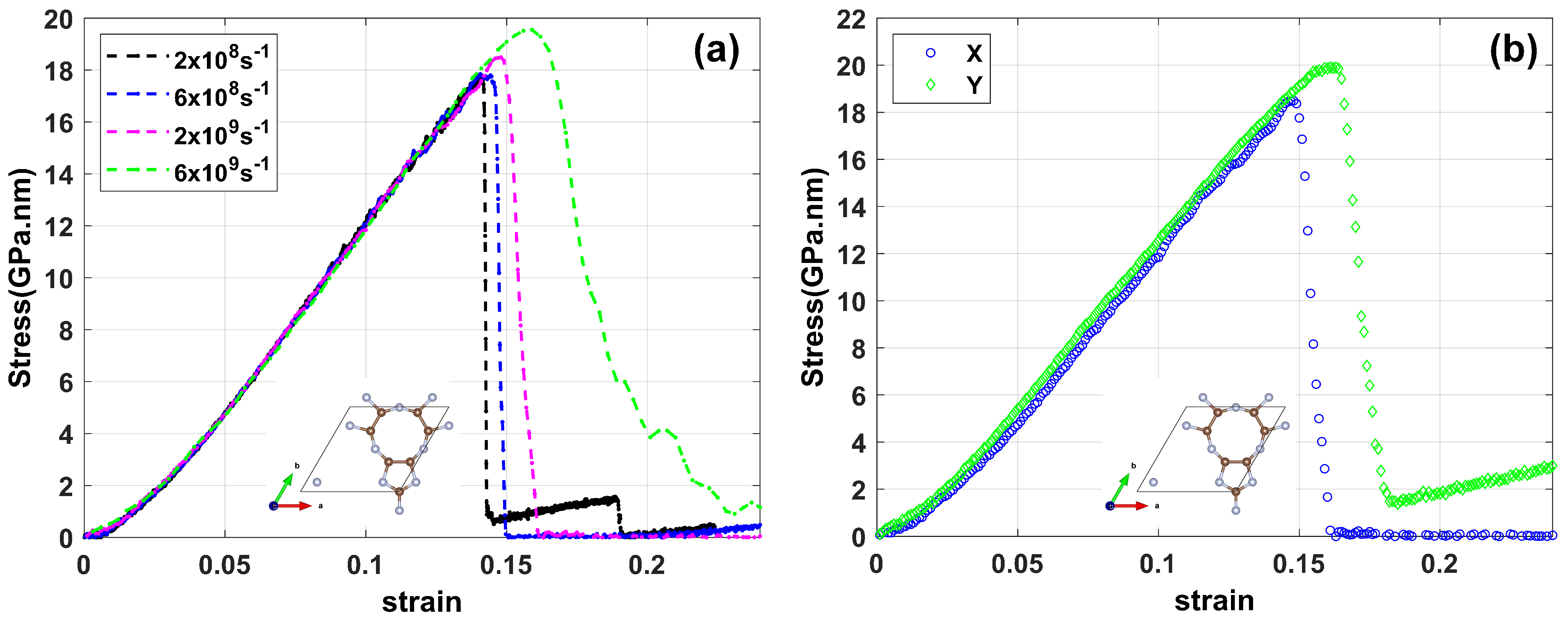
3.1. Mechanical Properties and Thermal Stability Test
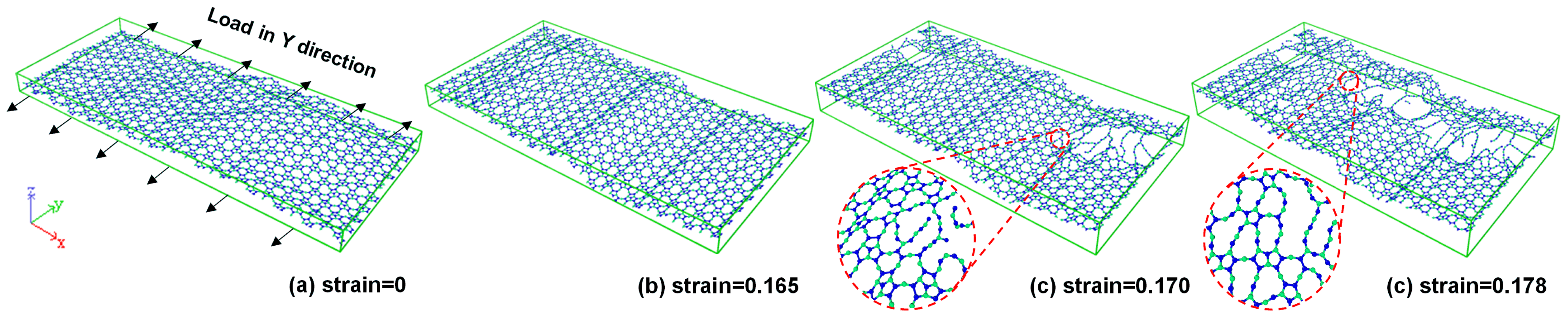
3.2. Fracture Analysis
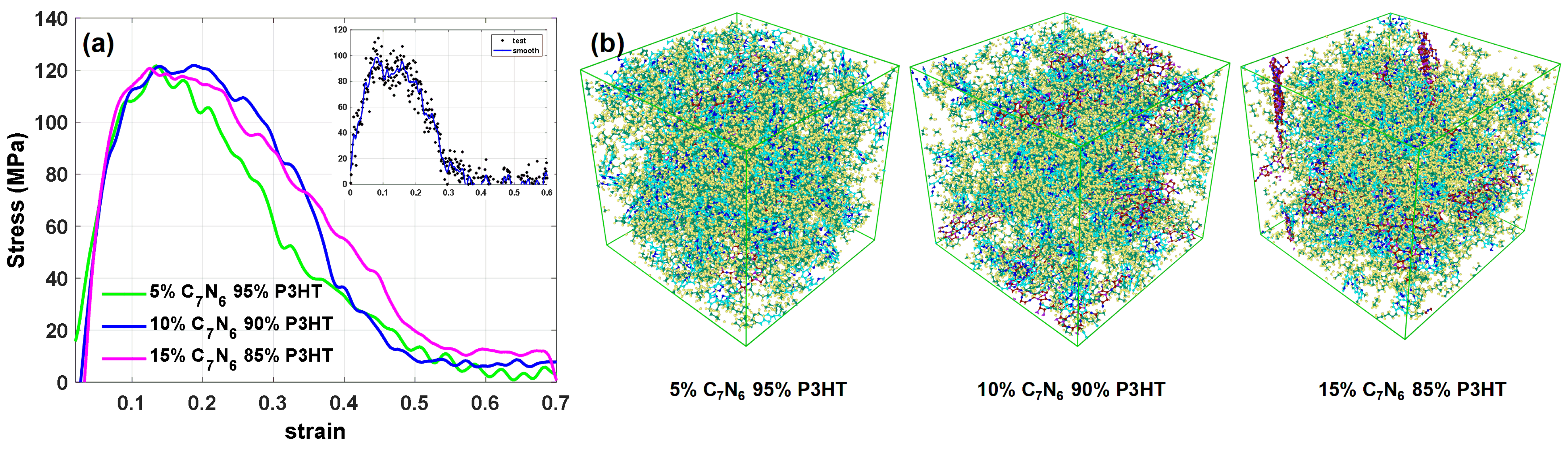
3.3. Composite Deformation
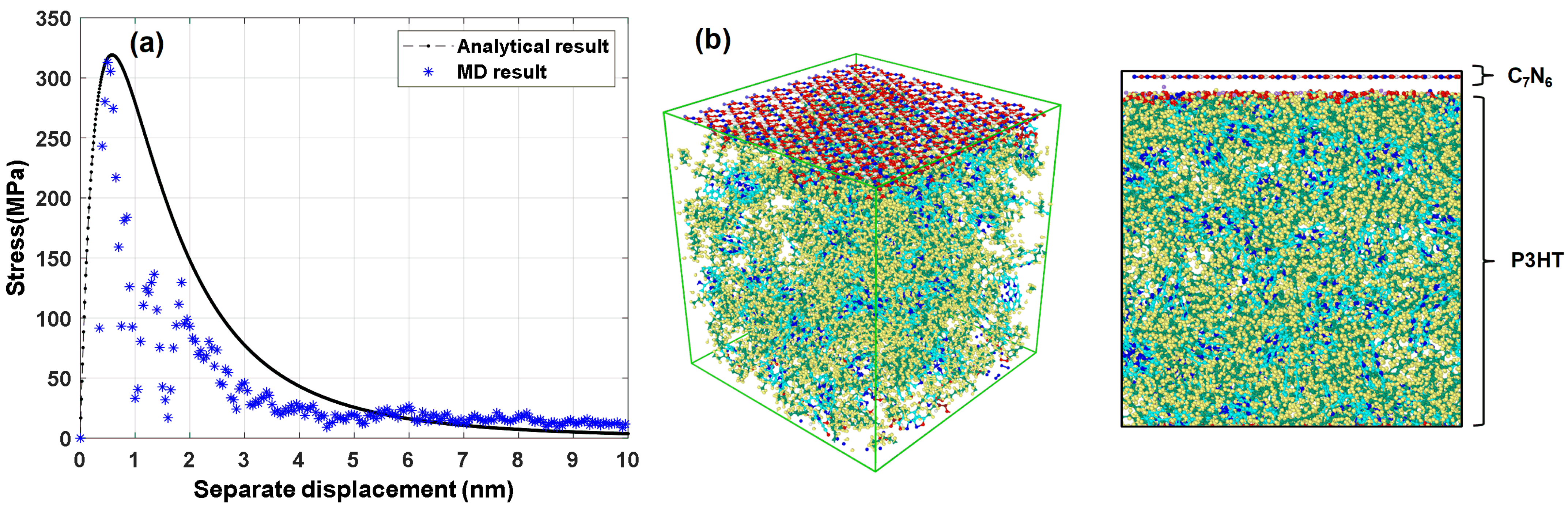
3.4. Interfacial Mechanical Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Atomic Structures in VASP POSCAR Format
Appendix B. Tersoff Potential to Simulate Mechanical Properties of C 7 N 6
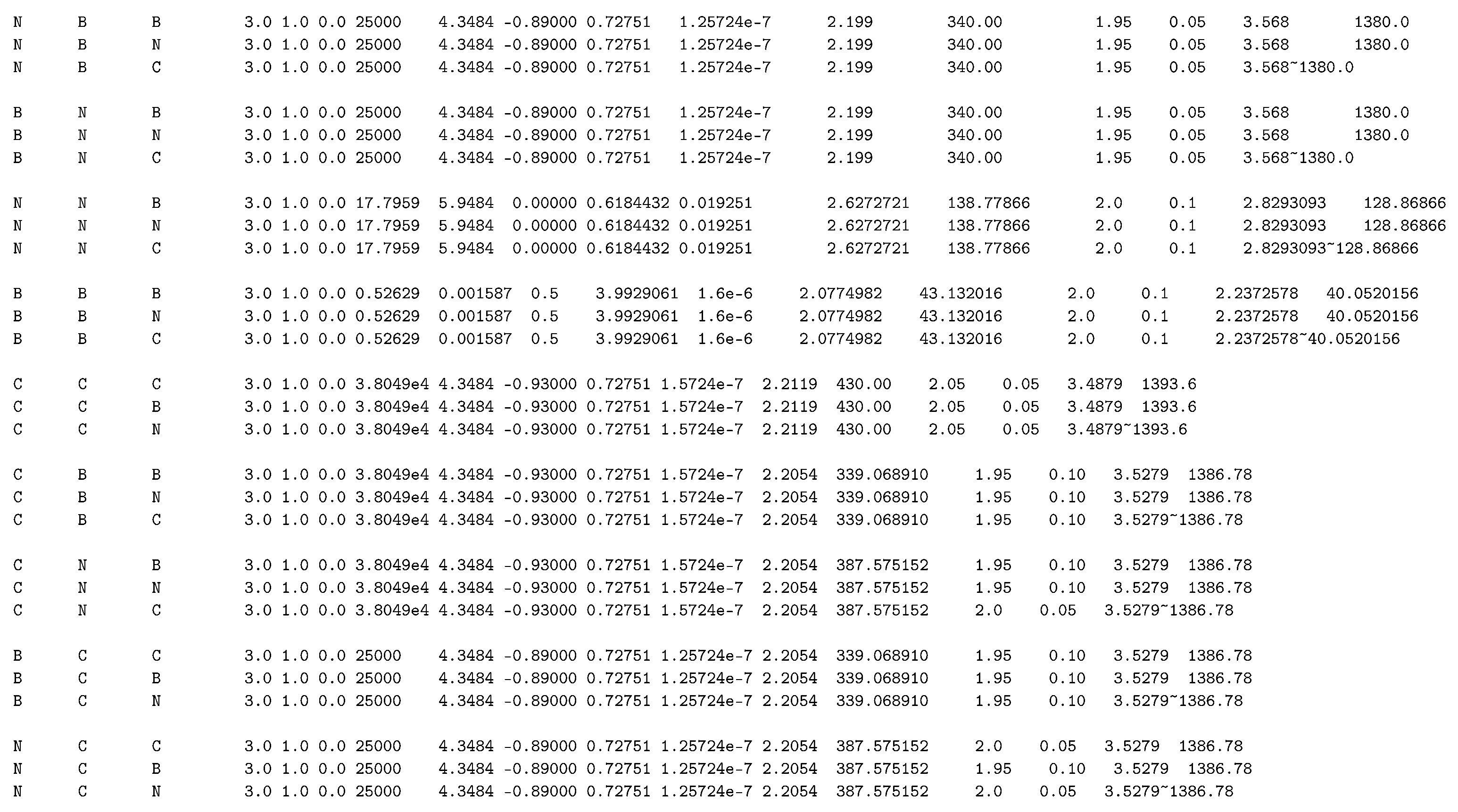
References
- Mortazavi, B. Ultrahigh thermal conductivity and strength in direct-gap semiconducting graphene-like bc6n: A first-principles and classical investigation. Carbon 2021, 182, 373–383. [Google Scholar] [CrossRef]
- Patnaik, S.; Sahoo, D.P.; Parida, K. Recent advances in anion doped g-c3n4 photocatalysts: A review. Carbon 2020, 172, 682–711. [Google Scholar] [CrossRef]
- An, M.; Li, L.; Hu, S.; Ding, Z.; Yu, X.; Demir, B.; Yang, N.; Ma, W.; Zhang, X. Mass difference and polarization lead to low thermal conductivity of graphene-like carbon nitride (c3n). Carbon 2020, 162, 202–208. [Google Scholar] [CrossRef]
- Neto, A.C.; Guinea, F.; Peres, N.M.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef] [Green Version]
- Mortazavi, B.; Shahrokhi, M.; Raeisi, M.; Zhuang, X.; Pereira, L.F.C.; Rabczuk, T. Outstanding strength, optical characteristics and thermal conductivity of graphene-like bc3 and bc6n semiconductors. Carbon 2019, 149, 733–742. [Google Scholar] [CrossRef] [Green Version]
- Shahil, K.M.; Balandin, A.A. Graphene–multilayer graphene nanocomposites as highly efficient thermal interface materials. Nano Lett. 2012, 12, 861–867. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Yang, S.; Li, W.; Ye, C.; Wang, G.; Tian, H.; Zhu, C.; He, P.; Ding, G.; Xie, X.; Liu, Y.; et al. C3n-a 2d crystalline, hole-free, tunable-narrow-bandgap semiconductor with ferromagnetic properties. Adv. Mater. 2017, 29, 1605625. [Google Scholar] [CrossRef]
- Rajabpour, A.; Bazrafshan, S.; Volz, S. Carbon-nitride 2d nanostructures: Thermal conductivity and interfacial thermal conductance with the silica substrate. Phys. Chem. Chem. Phys. 2019, 21, 2507–2512. [Google Scholar] [CrossRef]
- Mortazavi, B.; Shahrokhi, M.; Shapeev, A.V.; Rabczuk, T.; Zhuang, X. Prediction of c7n6 and c9n4: Stable and strong porous carbon-nitride nanosheets with attractive electronic and optical properties. J. Mater. Chem. C 2019, 7, 10908–10917. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Chen, Y.; Ma, C.; Lu, Z.; Zhang, H.; Mortazavi, B.; Hou, B.; Xu, K.; Mei, H.; Rabczuk, T.; et al. Monolayer c7n6: Room-temperature excitons with large binding energies and high thermal conductivities. Phys. Rev. Mater. 2020, 4, 064001. [Google Scholar] [CrossRef]
- Mortazavi, B. Ultra high stiffness and thermal conductivity of graphene like c3n. Carbon 2017, 118, 25–34. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Xiao, B.; Cheng, J.-B.; Li, Y.-C.; Li, Q.-Z.; Li, W.-Z.; Xu, X.-F.; Yu, X.-F. Carbon excess c3n: A potential candidate as li-ion battery material. ACS Appl. Mater. Interfaces 2018, 10, 37135–37141. [Google Scholar] [CrossRef] [PubMed]
- Thomas, A.; Fischer, A.; Goettmann, F.; Antonietti, M.; Müller, J.-O.; Schlögl, R.; Carlsson, J.M. Graphitic carbon nitride materials: Variation of structure and morphology and their use as metal-free catalysts. J. Mater. Chem. 2008, 18, 4893–4908. [Google Scholar] [CrossRef] [Green Version]
- Makaremi, M.; Grixti, S.; Butler, K.T.; Ozin, G.A.; Singh, C.V. Band engineering of carbon nitride monolayers by n-type, p-type, and isoelectronic doping for photocatalytic applications. ACS Appl. Mater. Interfaces 2018, 10, 11143–11151. [Google Scholar] [CrossRef]
- Zheng, Y.; Jiao, Y.; Chen, J.; Liu, J.; Liang, J.; Du, A.; Zhang, W.; Zhu, Z.; Smith, S.C.; Jaroniec, M.; et al. Nanoporous graphitic-c3n4@ carbon metal-free electrocatalysts for highly efficient oxygen reduction. J. Am. Chem. Soc. 2011, 133, 20116–20119. [Google Scholar] [CrossRef]
- Lyth, S.; Nabae, Y.; Islam, N.; Kuroki, S.; Kakimoto, M.; Miyata, S. Electrochemical oxygen reduction activity of carbon nitride supported on carbon black. J. Electrochem. Soc. 2010, 158, B194. [Google Scholar] [CrossRef]
- Lyth, S.M.; Nabae, Y.; Moriya, S.; Kuroki, S.; Kakimoto, M.-A.; Ozaki, J.-I.; Miyata, S. Carbon nitride as a nonprecious catalyst for electrochemical oxygen reduction. J. Phys. Chem. C 2009, 113, 20148–20151. [Google Scholar] [CrossRef]
- Hu, S.; Yong, Y.; Zhao, Z.; Gao, R.; Zhou, Q.; Kuang, Y. C7n6 monolayer as high capacity and reversible hydrogen storage media: A dft study. Int. J. Hydrogen Energy 2021, 46, 21994–22003. [Google Scholar] [CrossRef]
- Aoyama, Y.; Douhéret, O.; Leclère, P.; Moerman, D.; Mizukado, J.; Suda, H.; Lazzaroni, R.; Yoshida, Y. On the influence of the photo-oxidation of p3ht on the conductivity of photoactive film of p3ht: Pcbm bulk heterojunctions. Org. Electron. 2017, 43, 142–147. [Google Scholar] [CrossRef]
- Liao, W.-P.; Wu, J.-J. Efficient electron collection in hybrid polymer solar cells: In-situ-generated zno/poly (3-hexylthiophene) scaffolded by a tio2 nanorod array. J. Phys. Chem. Lett. 2013, 4, 1983–1988. [Google Scholar] [CrossRef]
- Thummalakunta, L.; Yong, C.H.; Ananthanarayanan, K.; Luther, J. P3ht based solution-processed pseudo bi-layer organic solar cell with enhanced performance. Org. Electron. 2012, 13, 2008–2016. [Google Scholar] [CrossRef]
- Savagatrup, S.; Printz, A.D.; Rodriquez, D.; Lipomi, D.J. Best of both worlds: Conjugated polymers exhibiting good photovoltaic behavior and high tensile elasticity. Macromolecules 2014, 47, 1981–1992. [Google Scholar] [CrossRef]
- Mueller, C. On the glass transition of polymer semiconductors and its impact on polymer solar cell stability. Chem. Mater. 2015, 27, 2740–2754. [Google Scholar] [CrossRef]
- Rogers, J.A.; Someya, T.; Huang, Y. Materials and mechanics for stretchable electronics. Science 2010, 327, 1603–1607. [Google Scholar] [CrossRef] [Green Version]
- Momma, K.; Izumi, F. Vesta 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Lindsay, L.; Broido, D. Optimized tersoff and brenner empirical potential parameters for lattice dynamics and phonon thermal transport in carbon nanotubes and graphene. Phys. Rev. B 2010, 81, 205441. [Google Scholar] [CrossRef] [Green Version]
- Kınacı, A.; Haskins, J.B.; Sevik, C.; Çağın, T. Thermal conductivity of bn-c nanostructures. Phys. Rev. B 2012, 86, 115410. [Google Scholar] [CrossRef] [Green Version]
- Lipomi, D.J.; Tee, B.C.-K.; Vosgueritchian, M.; Bao, Z. Stretchable organic solar cells. Adv. Mater. 2011, 23, 1771–1775. [Google Scholar] [CrossRef] [PubMed]
- Tromholt, T.; Madsen, M.V.; Krebs, F.C. Ultra high open circuit voltage (>1 v) of poly-3-hexylthiophene based organic solar cells with concentrated light. Appl. Phys. Lett. 2013, 102, 123904. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Nosé, S.; Klein, M. Constant pressure molecular dynamics for molecular systems. Mol. Phys. 1983, 50, 1055–1076. [Google Scholar] [CrossRef]
- Subramaniyan, A.K.; Sun, C. Continuum interpretation of virial stress in molecular simulations. Int. J. Solids Struct. 2008, 45, 4340–4346. [Google Scholar] [CrossRef] [Green Version]
- Plimpton, S. Units Command of Lammps Manual. 2021. Available online: https://docs.lammps.org/units.html (accessed on 30 July 2021).
- Plimpton, S.; Pollock, R.; Stevens, M. Particle-mesh ewald and rrespa for parallel molecular dynamics simulations. In PPSC; SIAM: Minneapolis, MN, USA, 1997. [Google Scholar]
- Sharma, S. Molecular Dynamics Simulation of Nanocomposites Using BIOVIA Materials Studio, Lammps and Gromacs; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Delhommelle, J.; Evans, D.J. Comparison of thermostatting mechanisms in nvt and npt simulations of decane under shear. J. Chem. Phys. 2001, 115, 43–49. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Z.; Lu, Z.; Yang, Z.; Sun, J.; Xie, F. A criterion for the normal properties of graphene/polymer interface. Comput. Mater. Sci. 2016, 120, 13–20. [Google Scholar] [CrossRef]
- Sun, H.; Mumby, S.J.; Maple, J.R.; Hagler, A.T. An ab initio cff93 all-atom force field for polycarbonates. J. Am. Chem. Soc. 1994, 116, 2978–2987. [Google Scholar] [CrossRef]
- Sun, H. Compass: An ab initio force-field optimized for condensed-phase applications overview with details on alkane and benzene compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Prosa, T.; Winokur, M.; Moulton, J.; Smith, P.; Heeger, A. X-ray structural studies of poly (3-alkylthiophenes): An example of an inverse comb. Macromolecules 1992, 25, 4364–4372. [Google Scholar] [CrossRef]
- Parnell, A.J.; Dunbar, A.D.; Pearson, A.J.; Staniec, P.A.; Dennison, A.J.; Hamamatsu, H.; Skoda, M.W.; Lidzey, D.G.; Jones, R.A. Depletion of pcbm at the cathode interface in p3ht/pcbm thin films as quantified via neutron reflectivity measurements. Adv. Mater. 2010, 22, 2444–2447. [Google Scholar] [CrossRef]
- Tan, H.; Jiang, L.; Huang, Y.; Liu, B.; Hwang, K. The effect of van der waals-based interface cohesive law on carbon nanotube-reinforced composite materials. Compos. Sci. Technol. 2007, 67, 2941–2946. [Google Scholar]
- Mortazavi, B.; Shojaei, F.; Shahrokhi, M.; Azizi, M.; Rabczuk, T.; Shapeev, A.V.; Zhuang, X. Nanoporous c3n4, c3n5 and c3n6 nanosheets; novel strong semiconductors with low thermal conductivities and appealing optical/electronic properties. Carbon 2020, 167, 40–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Shishir, M.I.R.; Elapolu, M.S.R.; Tabarraei, A. Investigation of fracture and mechanical properties of monolayer c3n using molecular dynamic simulations. Mech. Mater. 2021, 160, 103895. [Google Scholar] [CrossRef]
- Aldakheel, F.; Satari, R.; Wriggers, P. Feed-forward neural networks for failure mechanics problems. Appl. Sci. 2021, 11, 6483. [Google Scholar] [CrossRef]
- Aldakheel, F. A microscale model for concrete failure in poro-elasto-plastic media. Theor. Appl. Fract. Mech. 2020, 107, 102517. [Google Scholar] [CrossRef]
- Aldakheel, F. Mechanics of Nonlocal Dissipative Solids: Gradient Plasticity and Phase Field Modeling of Ductile Fracture; Institut für Mechanik (Bauwesen), Lehrstuhl I, Universität Stuttgart: Stuttgart, Germany, 2016. [Google Scholar] [CrossRef]

| Types | Mass (g/mol) | (Å) | (kcal/mol) | Mole Ratio | Comment | |
|---|---|---|---|---|---|---|
| c | 12.011 | 0.054 | 4.010 | 7/13 | generic carbon | |
| n | 14.007 | 0.096 | 3.830 | 1/13 | generic carbon | |
| n2 | 14.007 | 0.050 | 4.010 | 3/13 | generic nitrogen | |
| n3 | 14.007 | 0.015 | 3.720 | 2/13 | generic nitrogen | |
| P3HT | c3a | 12.011 | 0.068 | 3.915 | 6/25 | generic carbon |
| s2a | 32.064 | 0.125 | 4.047 | 1/25 | generic sulphur | |
| h1 | 1.008 | 0.032 | 2.878 | 14/25 | generic hydrogen | |
| c4 | 12.011 | 0.062 | 4.010 | 4/25 | generic carbon |
| Loading Direction | X | Y | ||
|---|---|---|---|---|
| Temperatures (K) | Stress | Strain | Stress | Strain |
| 300 | 18.101 | 0.146 | 19.908 | 0.161 |
| 500 | 15.815 | 0.123 | 17.306 | 0.152 |
| 700 | 12.997 | 0.108 | 14.465 | 0.135 |
| 900 | 11.317 | 0.101 | 12.391 | 0.126 |
| 1100 | 9.388 | 0.090 | 8.942 | 0.087 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Mortazavi, B.; Aldakheel, F. Molecular Dynamics Modeling of Mechanical Properties of Polymer Nanocomposites Reinforced by C7N6 Nanosheet. Surfaces 2021, 4, 240-254. https://doi.org/10.3390/surfaces4030019
Zhang Q, Mortazavi B, Aldakheel F. Molecular Dynamics Modeling of Mechanical Properties of Polymer Nanocomposites Reinforced by C7N6 Nanosheet. Surfaces. 2021; 4(3):240-254. https://doi.org/10.3390/surfaces4030019
Chicago/Turabian StyleZhang, Qinghua, Bohayra Mortazavi, and Fadi Aldakheel. 2021. "Molecular Dynamics Modeling of Mechanical Properties of Polymer Nanocomposites Reinforced by C7N6 Nanosheet" Surfaces 4, no. 3: 240-254. https://doi.org/10.3390/surfaces4030019
APA StyleZhang, Q., Mortazavi, B., & Aldakheel, F. (2021). Molecular Dynamics Modeling of Mechanical Properties of Polymer Nanocomposites Reinforced by C7N6 Nanosheet. Surfaces, 4(3), 240-254. https://doi.org/10.3390/surfaces4030019








