Controllable CaF2 Nanosized Stripe Arrays on Si(001) Studied by X-ray and Electron Diffraction
Abstract
1. Introduction
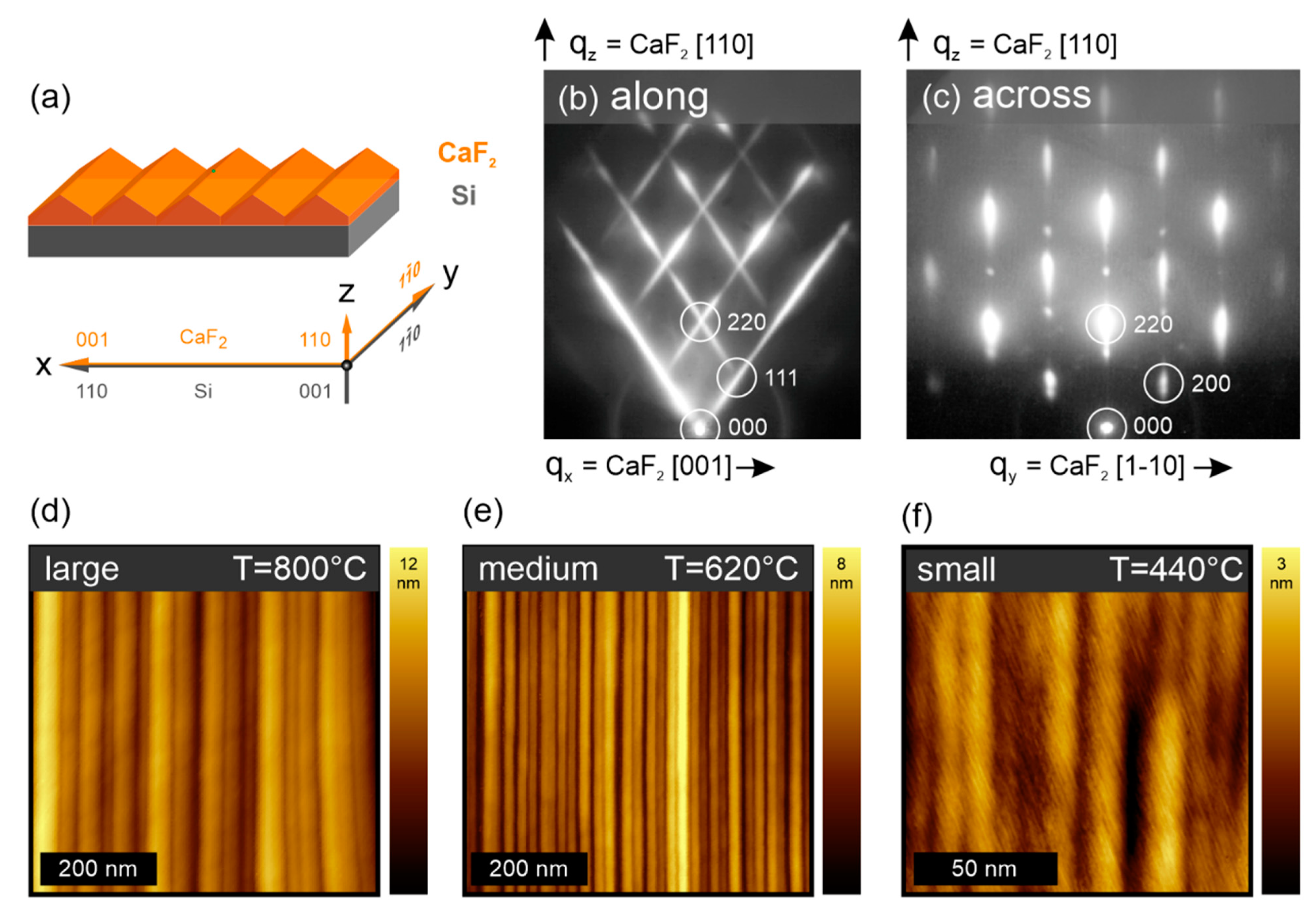
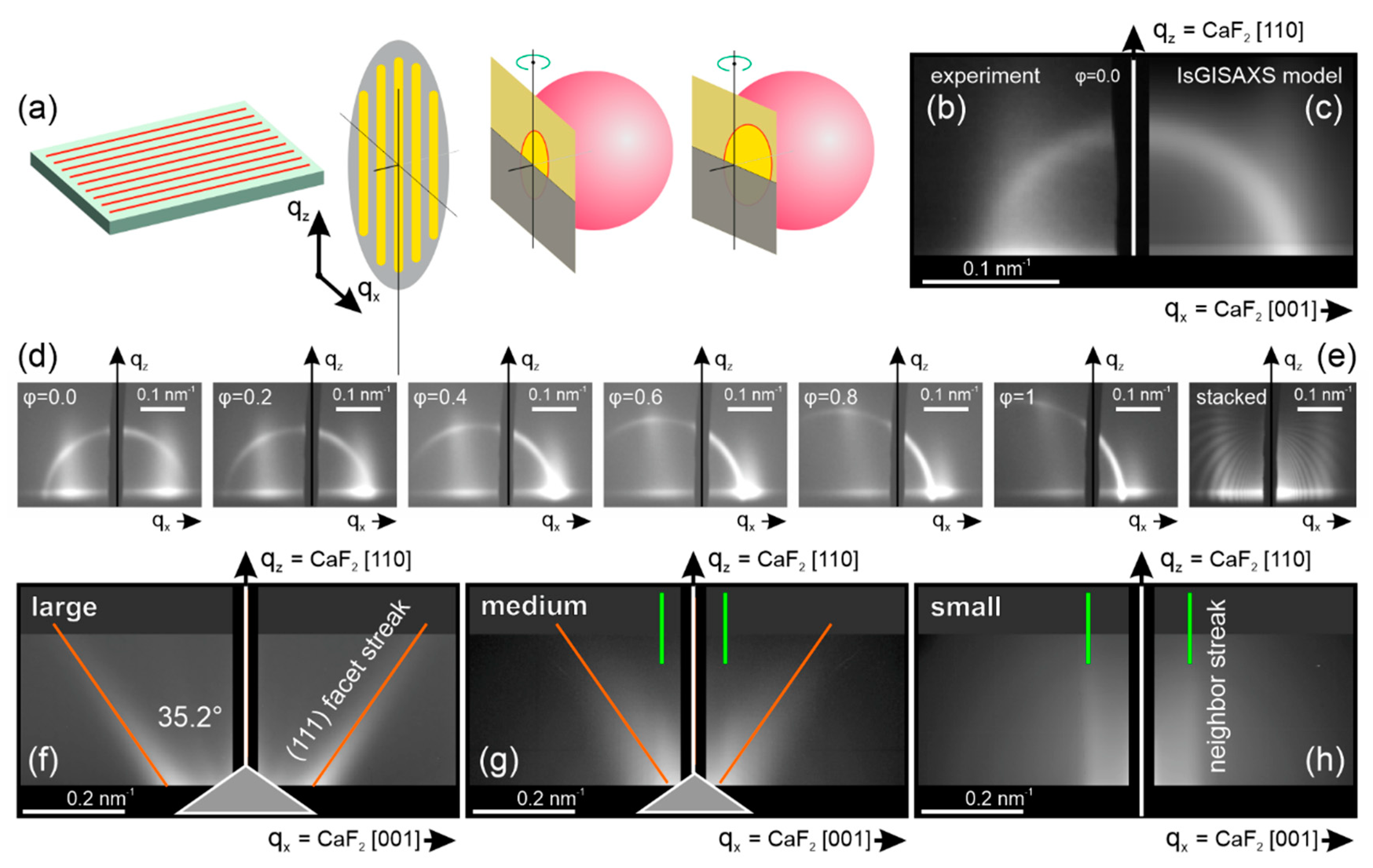
2. Materials and Methods
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tromp, R.M.; Reuter, M.C. Structure of the Si(111)-CaF2 Interface. Phys. Rev. Lett. 1988, 61, 1756–1759. [Google Scholar] [CrossRef] [PubMed]
- Zegenhagen, J.; Patel, J.R. CaF2/Si heteroepitaxy: Importance of stoichiometry, interface bonding, and lattice mismatch. Phys. Rev. B 1990, 41, 5315–5318. [Google Scholar] [CrossRef] [PubMed]
- Rieger, D.; Himpsel, F.J.; Karlsson, U.O.; McFeely, F.R.; Morar, J.F.; Yarmoff, J.A. Electronic structure of the CaF2/Si(111) interface. Phys. Rev. B 1986, 34, 7295–7306. [Google Scholar] [CrossRef] [PubMed]
- Sugiyama, M.; Oshima, M. MBE growth of fluorides. Microelectron. J. 1996, 27, 361–382. [Google Scholar] [CrossRef]
- Schowalter, L.J.; Fathauer, R.W. Growth and characterization of single crystal insulators on silicon. Crit. Rev. Solid State Mater. Sci. 1989, 15, 367–421. [Google Scholar] [CrossRef]
- Sokolov, N.S.; Suturin, S.M.; Krichevtsov, B.B.; Dubrovskii, V.G.; Gastev, S.V.; Sibirev, N.V.; Baranov, D.A.; Fedorov, V.V.; Sitnikova, A.A.; Nashchekin, A.V.; et al. Cobalt epitaxial nanoparticles on CaF2/Si(111): Growth process, morphology, crystal structure, and magnetic properties. Phys. Rev. B 2013, 87, 125407. [Google Scholar] [CrossRef]
- Baranov, D.A.; Krichevtsov, B.B.; Gastev, S.V.; Banschikov, A.G.; Fedorov, V.V.; Koshmak, K.V.; Suturin, S.M.; Sokolov, N.S. Magnetic anisotropy of cobalt nanoparticle 2D arrays grown on corrugated MnF2(110) and CaF2(110) surfaces. Appl. Surf. Sci. 2013, 267, 196–199. [Google Scholar] [CrossRef]
- Suturin, S.M.; Fedorov, V.V.; Korovin, A.M.; Sokolov, N.S.; Nashchekin, A.V.; Tabuchi, M. Epitaxial Ni nanoparticles on CaF2 (001), (110) and (111) surfaces studied by three-dimensional RHEED, GIXD and GISAXS reciprocal-space mapping techniques. J. Appl. Crystallogr. 2017, 50, 830–839. [Google Scholar] [CrossRef]
- Suturin, S.M.; Korovin, A.M.; Fedorov, V.V.; Valkovsky, G.A.; Tabuchi, M.; Sokolov, N.S. An advanced three-dimensional RHEED mapping approach to the diffraction study of Co/MnF2/CaF2/Si(001) epitaxial heterostructures. J. Appl. Crystallogr. 2016, 49, 1532–1543. [Google Scholar] [CrossRef]
- Suturin, S.M.; Fedorov, V.V.; Banshchikov, A.G.; Baranov, D.A.; Koshmak, K.V.; Torelli, P.; Fujii, J.; Panaccione, G.; Amemiya, K.; Sakamaki, M.; et al. Proximity effects and exchange bias in Co/MnF2(111) heterostructures studied by X-ray magnetic circular dichroism. J. Phys. Condens. Matter 2013, 25, 046002. [Google Scholar] [CrossRef]
- Banshchikov, A.G.; Golosovskii, I.V.; Krupin, A.V.; Koshmak, K.V.; Sokolov, N.S.; Chernenkov, Y.P.; Yagovkina, M.A.; Ulin, V.P.; Tabuchi, M. Epitaxial layers of nickel fluoride on Si(111): Growth and stabilization of the orthorhombic phase. Phys. Solid State 2015, 57, 1647–1652. [Google Scholar] [CrossRef]
- Rothman, A.; Dubrovskii, V.G.; Joselevich, E. Kinetics and mechanism of planar nanowire growth. Proc. Natl. Acad. Sci. USA 2020, 117, 152–160. [Google Scholar] [CrossRef]
- Weiss, N.O.; Duan, X. A guide for nanowire growth. Proc. Natl. Acad. Sci. USA 2013, 110, 15171–15172. [Google Scholar] [CrossRef]
- Ito, K.; Nakano, H.; Nakamura, Y. Formation of Silicon Quantum Dots Sheet on a Nonmetallic CaF2 Surface. Adv. Mater. Interfaces 2020, 7, 2001295. [Google Scholar] [CrossRef]
- Illarionov, Y.Y.; Vexler, M.I.; Fedorov, V.V.; Suturin, S.M.; Sokolov, N.S. Electrical and optical characterization of Au/CaF2/p-Si(111) tunnel-injection diodes. J. Appl. Phys. 2014, 115, 223706. [Google Scholar] [CrossRef]
- Vexler, M.I.; Sokolov, N.S.; Suturin, S.M.; Banshchikov, A.G.; Tyaginov, S.E.; Grasser, T. Electrical characterization and modeling of the Au/CaF2/nSi(111) structures with high-quality tunnel-thin fluoride layer. J. Appl. Phys. 2009, 105, 083716. [Google Scholar] [CrossRef]
- Illarionov, Y.Y.; Banshchikov, A.G.; Polyushkin, D.K.; Wachter, S.; Knobloch, T.; Thesberg, M.; Mennel, L.; Paur, M.; Stöger-Pollach, M.; Steiger-Thirsfeld, A.; et al. Ultrathin calcium fluoride insulators for two-dimensional field-effect transistors. Nat. Electron. 2019, 2, 230–235. [Google Scholar] [CrossRef]
- Sumiya, T.; Miura, T.; Fujinuma, H.; Tanaka, S. Surface reconstruction in CaF2/Si(001) investigated by scanning tunneling microscopy. Surf. Sci. 1997, 376, 192–204. [Google Scholar] [CrossRef]
- Loretto, D.; Ross, F.M.; Lucas, C.A. Quasi-one-dimensional CaF2 islands formed on Si(001) by molecular beam epitaxy. Appl. Phys. Lett. 1996, 68, 2363–2365. [Google Scholar] [CrossRef]
- Pasquali, L.; D’Addato, S.; Selvaggi, G.; Nannarone, S.; Sokolov, N.S.; Suturin, S.M.; Zogg, H. Formation of CaF2 nanostructures on Si(001). Nanotechnology 2001, 12, 403–408. [Google Scholar] [CrossRef]
- Sokolov, N.; Suturin, S.; Ulin, V.; Pasquali, L.; Selvaggi, G.; Nannarone, S. Initial stages of MBE growth and formation of CaF2/Si(001) high-temperature interface. Appl. Surf. Sci. 2004, 234, 480–486. [Google Scholar] [CrossRef]
- Pasquali, L.; Suturin, S.; Ulin, V.; Sokolov, N.; Selvaggi, G.; Giglia, A.; Mahne, N.; Pedio, M.; Nannarone, S. Calcium fluoride on Si(001): Adsorption mechanisms and epitaxial growth modes. Phys. Rev. B 2005, 72, 045448. [Google Scholar] [CrossRef]
- Suturin, S.M.; Sokolov, N.S.; Roy, J.; Zegenhagen, J. STM and LEED studies of CaF2 submonolayer coverage on Si(001). Surf. Sci. 2011, 605, 153–157. [Google Scholar] [CrossRef]
- Suturin, S.M.; Sokolov, N.S.; Banshchikov, A.G.; Kyutt, R.N.; Sakata, O.; Shimura, T.; Harada, J.; Tabuchi, M.; Takeda, Y. Initial Stages of High-Temperature CaF2/Si(001) Epitaxial Growth Studied by Surface X-Ray Diffraction. J. Nanosci. Nanotechnol. 2011, 11, 2990–2996. [Google Scholar] [CrossRef] [PubMed]
- Alzahrani, A.Z.; Usanmaz, D. Progressive changes in surface structure and electronic properties on Si(001) surface by CaF2 adsorption. J. Appl. Phys. 2011, 109, 123708. [Google Scholar] [CrossRef]
- Baskurt, M.; Kang, J.; Sahin, H. Octahedrally coordinated single layered CaF2: Robust insulating behaviour. Phys. Chem. Chem. Phys. 2020, 22, 2949–2954. [Google Scholar] [CrossRef]
- Suturin, S.M.; Fedorov, V.V.; Korovin, A.M.; Valkovskiy, G.A.; Konnikov, S.G.; Tabuchi, M.; Sokolov, N.S. A look inside epitaxial cobalt-on-fluorite nanoparticles with three-dimensional reciprocal space mapping using GIXD, RHEED and GISAXS. J. Appl. Crystallogr. 2013, 46, 874–881. [Google Scholar] [CrossRef]
- Chiaravalloti, F.; Dujardin, G.; Riedel, D. Atomic scale control of hexaphenyl molecules manipulation along functionalized ultra-thin insulating layer on the Si(100) surface at low temperature (9 K). J. Phys. Condens. Matter 2015, 27, 054006. [Google Scholar] [CrossRef]
- Duverger, E.; Boyer, A.-G.; Sauriat-Dorizon, H.; Sonnet, P.; Stephan, R.; Hanf, M.-C.; Riedel, D. Two-Dimensional Functionalized Ultrathin Semi-Insulating CaF2 Layer on the Si(100) Surface at a Low Temperature for Molecular Electronic Decoupling. ACS Appl. Mater. Interfaces 2020, 12. [Google Scholar] [CrossRef]
- Ramos, P.; Mankarious, M.; Pavanello, M.; Riedel, D. Probing charge transfer dynamics in a single iron tetraphenylporphyrin dyad adsorbed on an insulating surface. Nanoscale 2018, 10, 17603–17616. [Google Scholar] [CrossRef]
- Ishizaka, A.; Shiraki, Y. Low Temperature Surface Cleaning of Silicon and Its Application to Silicon MBE. J. Electrochem. Soc. 1986, 133, 666–671. [Google Scholar] [CrossRef]
- Rueda, D.R.; Martín-Fabiani, I.; Soccio, M.; Alayo, N.; Pérez-Murano, F.; Rebollar, E.; García-Gutiérrez, M.C.; Castillejo, M.; Ezquerra, T.A. Grazing-incidence small-angle X-ray scattering of soft and hard nanofabricated gratings. J. Appl. Crystallogr. 2012, 45, 1038–1045. [Google Scholar] [CrossRef]
- Wernecke, J.; Scholze, F.; Krumrey, M. Direct structural characterisation of line gratings with grazing incidence small-angle x-ray scattering. Rev. Sci. Instrum. 2012, 83, 103906. [Google Scholar] [CrossRef] [PubMed]
- Lazzari, R. IsGISAXS: A program for grazing-incidence small-angle X-ray scattering analysis of supported islands. J. Appl. Crystallogr. 2002, 35, 406–421. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suturin, S.M.; Fedorov, V.V.; Korovin, A.M.; Valkovskiy, G.A.; Tabuchi, M.; Sokolov, N.S. Controllable CaF2 Nanosized Stripe Arrays on Si(001) Studied by X-ray and Electron Diffraction. Surfaces 2021, 4, 97-105. https://doi.org/10.3390/surfaces4020012
Suturin SM, Fedorov VV, Korovin AM, Valkovskiy GA, Tabuchi M, Sokolov NS. Controllable CaF2 Nanosized Stripe Arrays on Si(001) Studied by X-ray and Electron Diffraction. Surfaces. 2021; 4(2):97-105. https://doi.org/10.3390/surfaces4020012
Chicago/Turabian StyleSuturin, Sergey M., Vladimir V. Fedorov, Alexander M. Korovin, Gleb A. Valkovskiy, Masao Tabuchi, and Nikolai S. Sokolov. 2021. "Controllable CaF2 Nanosized Stripe Arrays on Si(001) Studied by X-ray and Electron Diffraction" Surfaces 4, no. 2: 97-105. https://doi.org/10.3390/surfaces4020012
APA StyleSuturin, S. M., Fedorov, V. V., Korovin, A. M., Valkovskiy, G. A., Tabuchi, M., & Sokolov, N. S. (2021). Controllable CaF2 Nanosized Stripe Arrays on Si(001) Studied by X-ray and Electron Diffraction. Surfaces, 4(2), 97-105. https://doi.org/10.3390/surfaces4020012





