Molecular Dynamics Simulation Study of the Mechanical Properties of Nanocrystalline Body-Centered Cubic Iron
Abstract
:1. Introduction
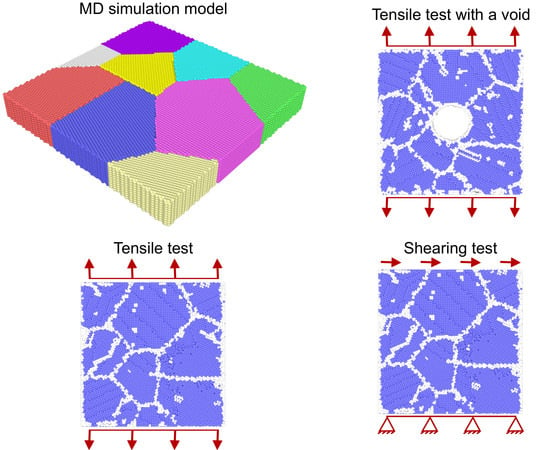
2. Molecular Dynamics Simulations
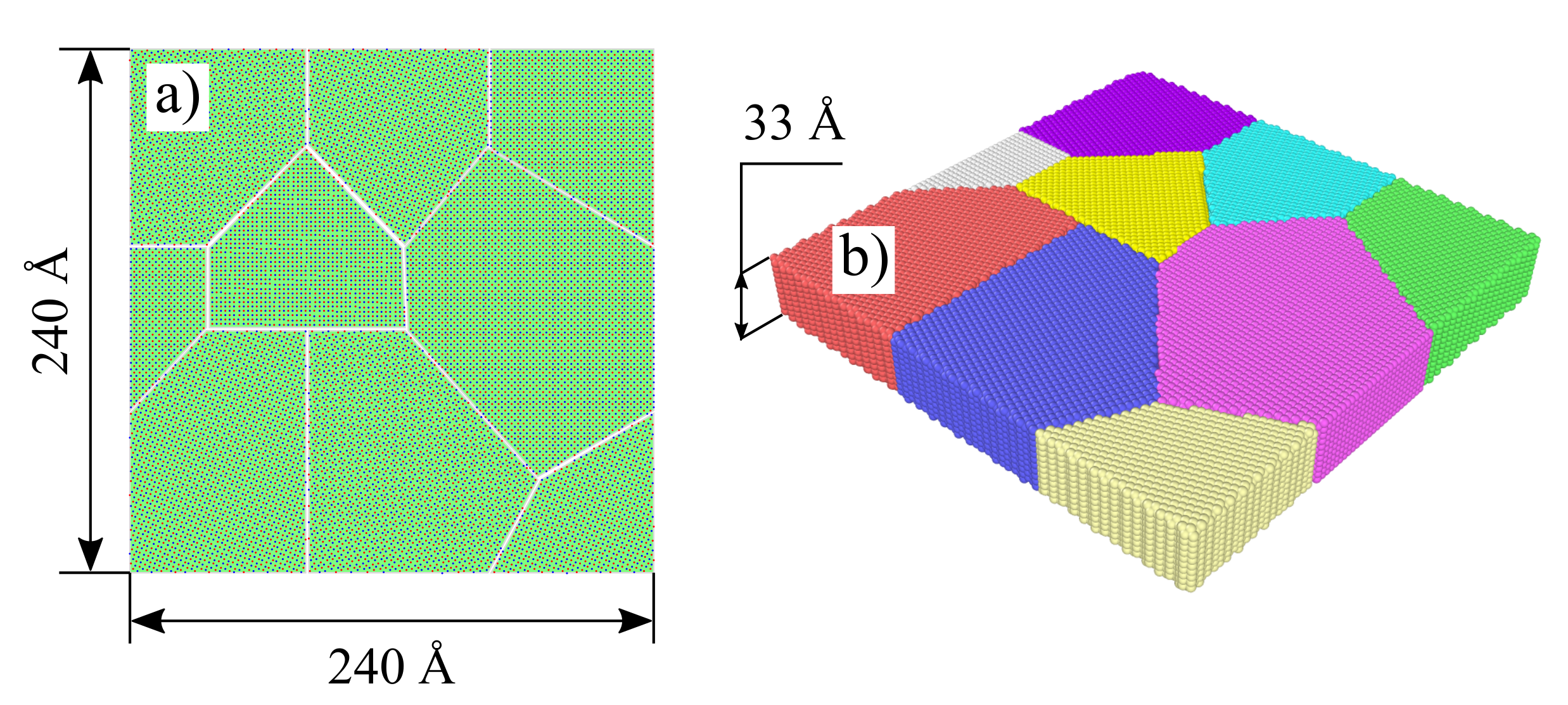
2.1. Model Generation
2.2. Simulation Details
3. Results and Discussion
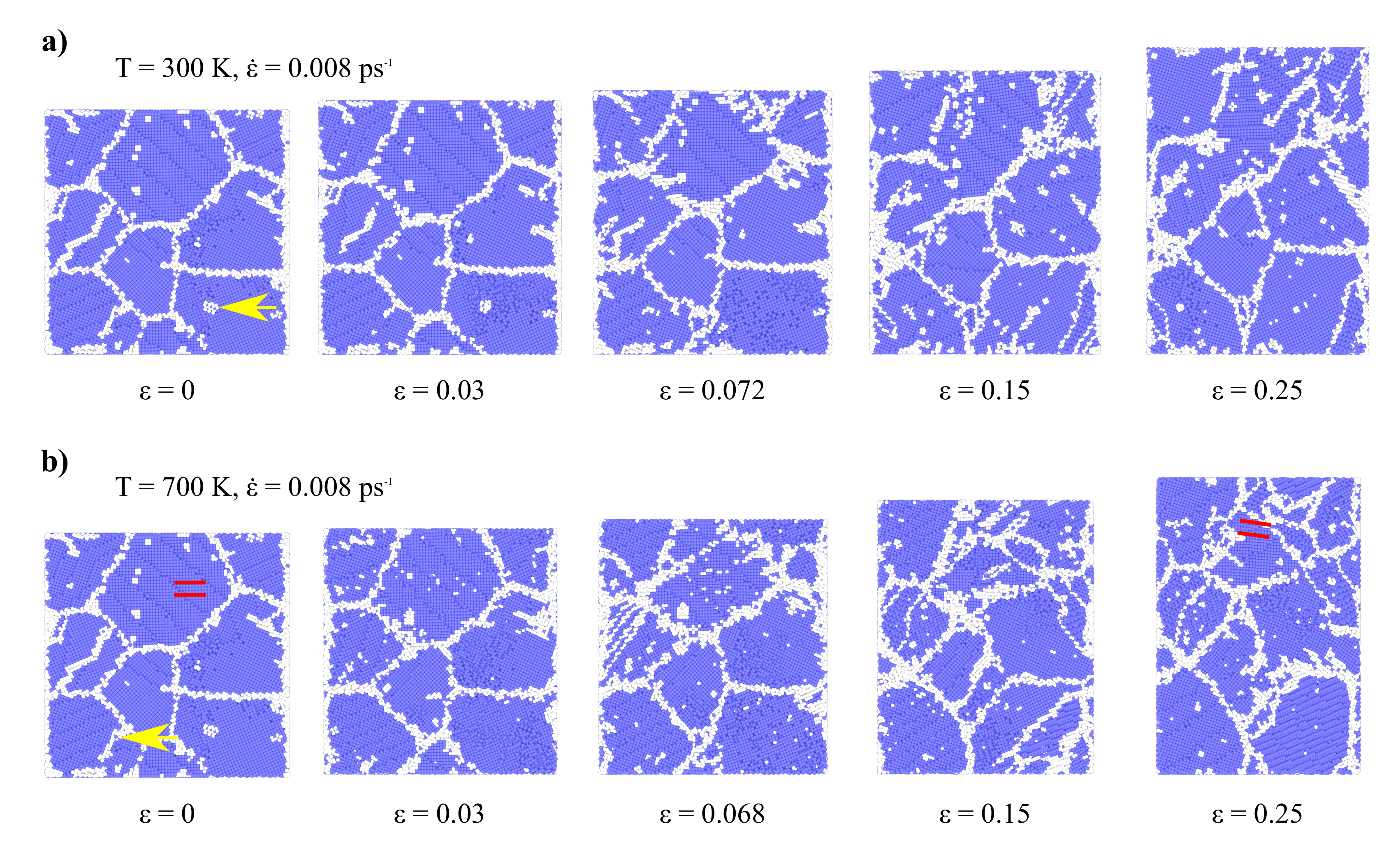
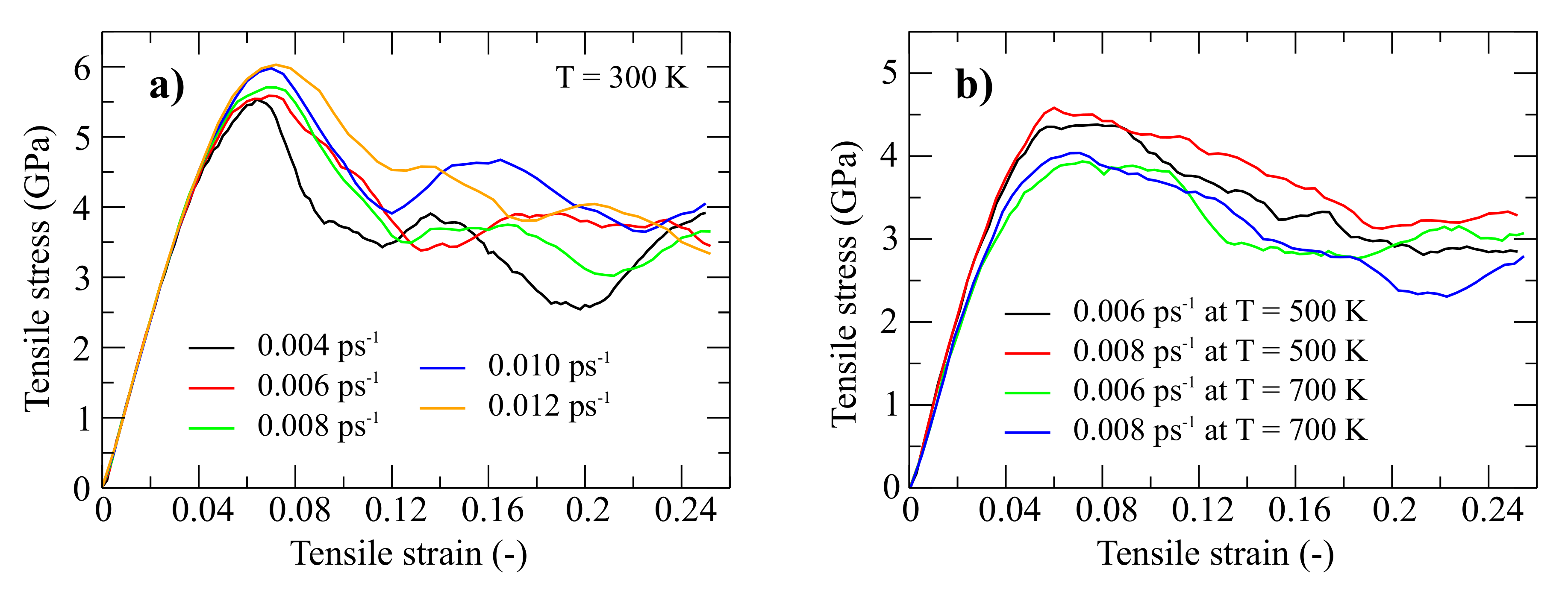
3.1. Tensile Test
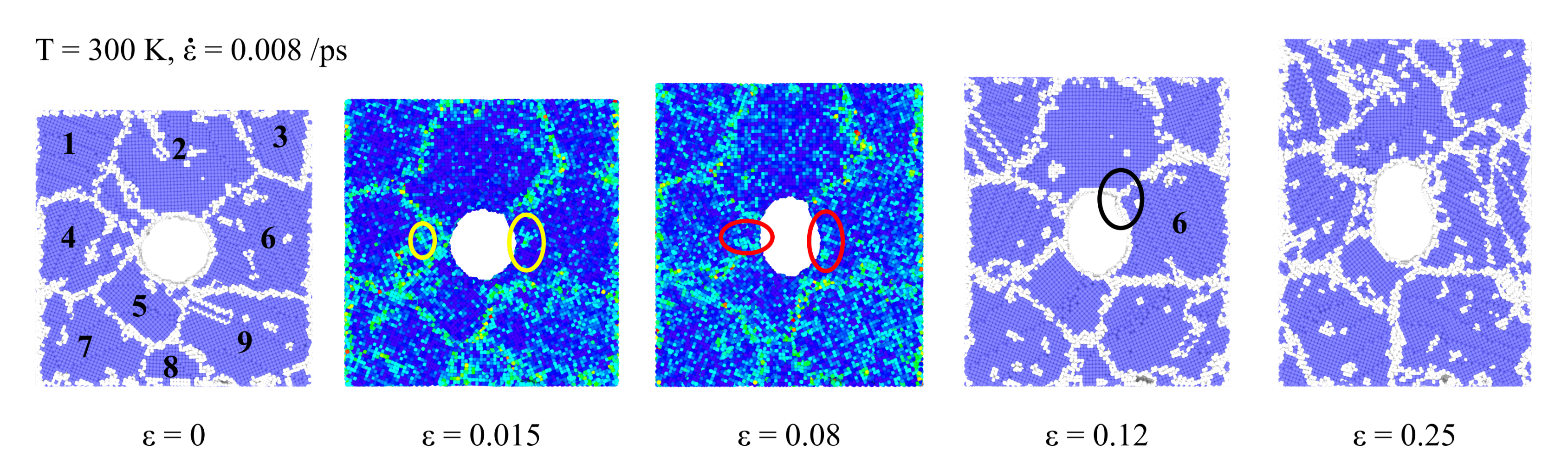
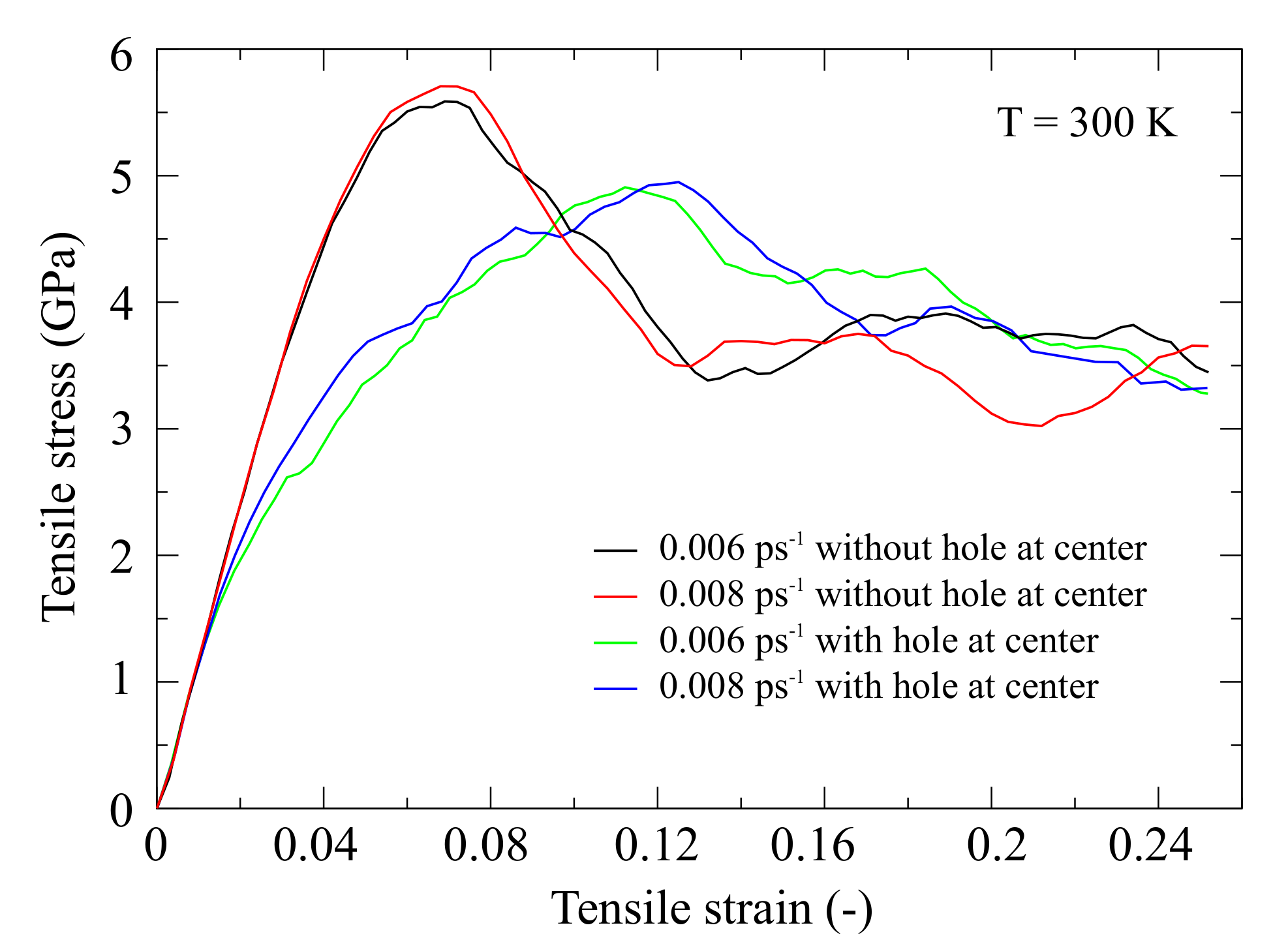
3.2. Specimen with Void
- Dislocations nucleate near the void;
- With additional deformation, dislocations initiated near void propagate to the specimen edges;
- Reduction of specimen stress resistance;
- Necking of specimen seen at higher strain values.
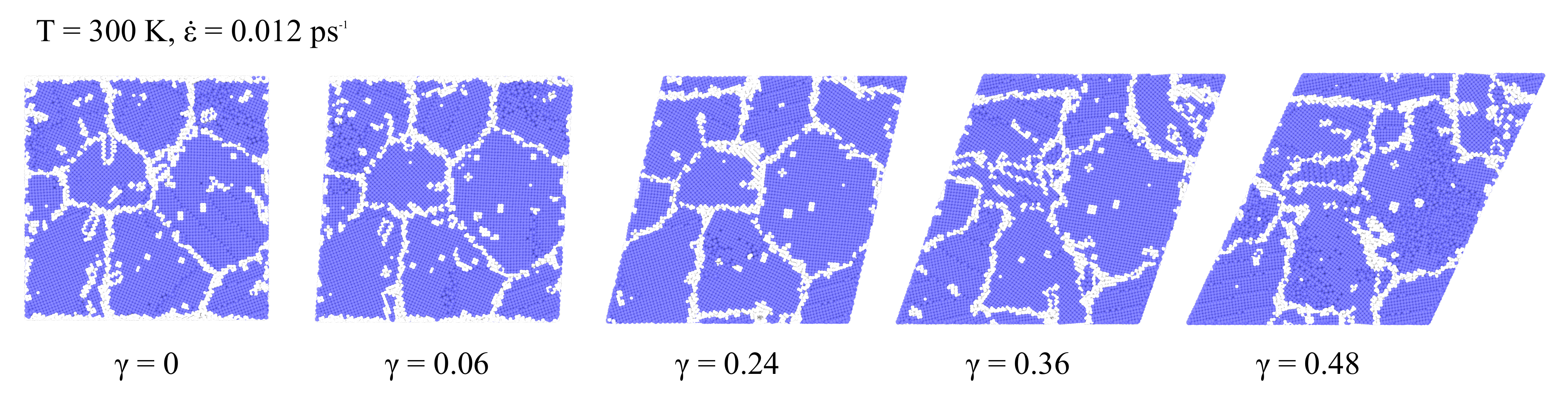
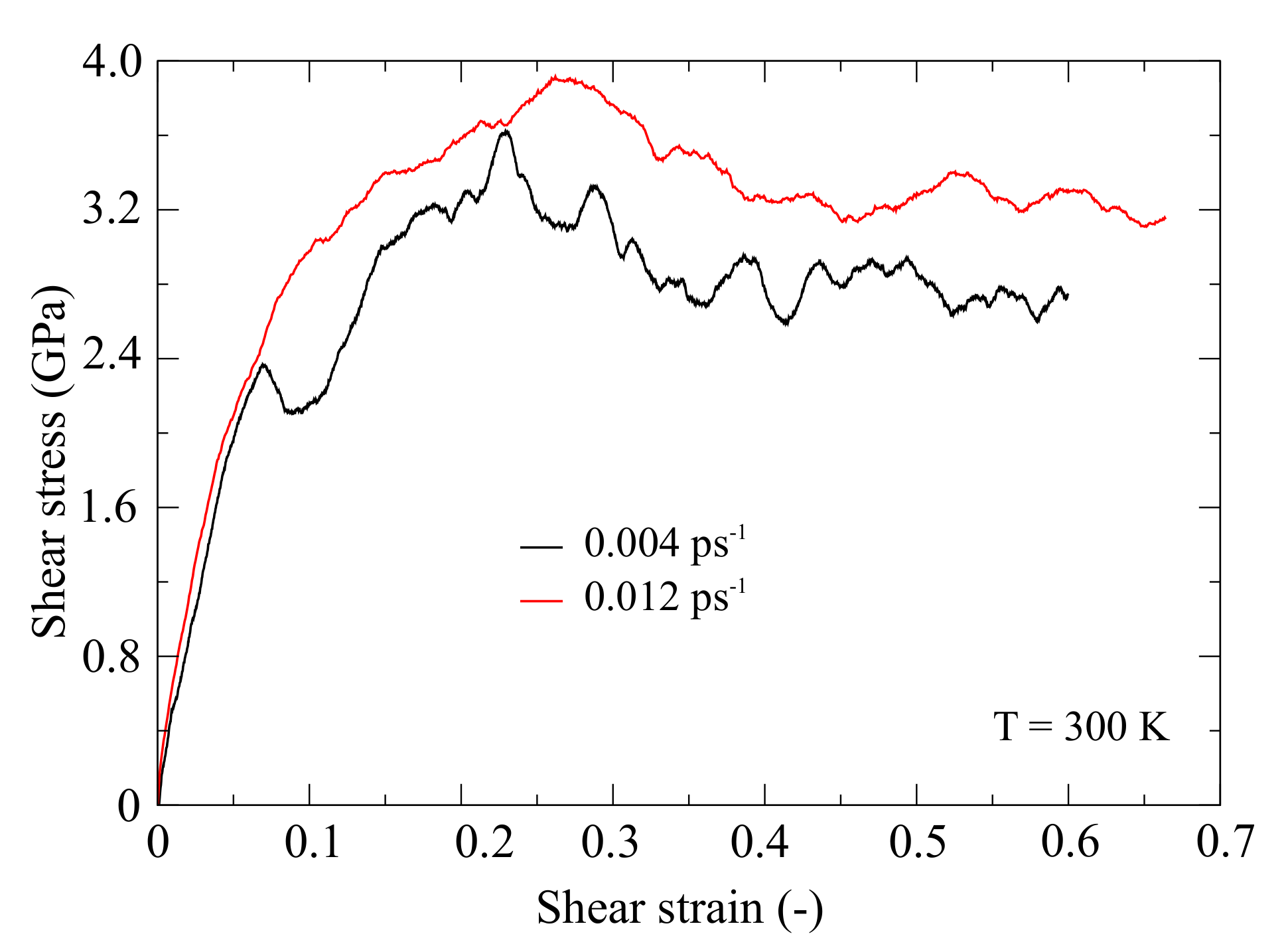
3.3. Shearing Test
4. Conclusions
- In the tensile test MD simulations, peak values of stress and average values of flow stress increase with strain rate, however, the strain rate does not affect the elasticity modulus. Moreover, an increase in temperature leads to a decrease in elasticity modulus, peak stress value and flow stress.
- When the model with the void at the center is under tension, stress concentrations in structure occur, which leads to dislocation pile up and grain boundary slips at lower strains. Furthermore, the model with the void reaches lower values of peak stresses as well as stress overshoot compared to the no void model. Furthermore, for different strain rate values, the stress flows of both models have approximately the same values.
- For high strain rates, in shear test simulations, the peak shear stress values, as well as flow stresses, were higher. However, the shearing modulus was not affected.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jeon, J.; Lee, B.J.; Chang, Y. Molecular dynamics simulation study of the effect of grain size on the deformation behaviour of nanocrystalline body-centered cubic iron. Scr. Mater. 2011, 64, 494–497. [Google Scholar] [CrossRef]
- Jia, D.; Ramesh, K.T.; Ma, E. Effects of nanocrystalline and ultrafine grain sizes on constitutive behavior and shear bands in iron. Acta Mater. 2003, 51, 3495–3509. [Google Scholar] [CrossRef]
- Kumar, K.; Van Swygenhoven, H.; Suresh, S. Mechanical behavior of nanocrystalline metals and alloys. Acta Mater. 2003, 51, 5743–5774. [Google Scholar] [CrossRef]
- Schiøtz, J.; Jacobsen, K. A Maximum in the Strength of Nanocrystalline Copper. Science 2003, 301, 1357–1359. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wei, Q.; Pan, Z.; Wu, X.; Schuster, B.; Kecskes, L.; Valiev, R. Microstructure and mechanical properties at different length scales and strain rates of nanocrystalline tantalum produced by high-pressure torsion. Acta Mater. 2011, 59, 2423–2436. [Google Scholar] [CrossRef] [Green Version]
- Valiev, R.; Islamgaliev, R.; Alexandrov, I.V. Bulk nanostructured materials from severe plastic deformation. Prog. Mater. Sci. 2000, 45, 103–189. [Google Scholar] [CrossRef]
- Hansen, N. Hall–Petch relation and boundary strengthening. Scr. Mater. 2004, 51, 801–806. [Google Scholar] [CrossRef]
- Siegel, R.W.; Thomas, G.J. Grain boundaries in nanophase materials. Ultramicroscopy 1992, 40, 376–384. [Google Scholar] [CrossRef]
- Van Swygenhoven, H.; Farkas, D.; Caro, A. Grain-boundary structures in polycrystalline metals at the nanoscale. Phys. Rev. B 2000, 62, 831–838. [Google Scholar] [CrossRef] [Green Version]
- Rajgarhia, R.; Spearot, D.; Saxena, A. Plastic deformation of nanocrystalline copper-antimony alloys. J. Mater. Res. 2010, 25, 411–421. [Google Scholar] [CrossRef]
- Vo, N.; Averback, R.; Bellon, P.; Caro, A. Yield strength in nanocrystalline Cu during high strain rate deformation. Scr. Mater. 2009, 61, 76–79. [Google Scholar] [CrossRef]
- Van Swygenhoven, H. Polycrystalline materials - Grain Boundaries and Dislocations. Science 2002, 296, 66–67. [Google Scholar] [CrossRef] [PubMed]
- Van Swygenhoven, H.; Spaczer, M.; Caro, A.; Farkas, D. Competing plastic deformation mechanisms in nanophase metals. Phys. Rev. B 1999, 60, 22–25. [Google Scholar] [CrossRef]
- Armstrong, R. The influence of polycrystal grain size on several mechanical properties of materials. Metall. Mater. Trans. 1970, 1, 1169–1176. [Google Scholar] [CrossRef]
- Armstrong, R.W.; Codd, I.; Douthwaite, R.M.; Petch, N.J. The plastic deformation of polycrystalline aggregates. Philos. Mag. 1962, 45–58. [Google Scholar] [CrossRef]
- Hugo, R.; Kung, H.; Weertman, J.; Mitra, R.; Knapp, J.; Follstaedt, D. In-situ TEM tensile testing of DC magnetron sputtered and pulsed laser deposited Ni thin films. Acta Mater. 2003, 51, 1937–1943. [Google Scholar] [CrossRef]
- Hasnaoui, A.; Van Swygenhoven, H.; Derlet, P. Cooperative processes during plastic deformation in nanocrystalline FCC metals a molecular dynamics simulation. Phys. Rev. B. 2002, 66. [Google Scholar] [CrossRef]
- Yamakov, V.; Wolf, D.; Phillpot, S.; Gleiter, H. Grain-boundary diffusion creep in nanocrystalline palladium by molecular-dynamics simulation. Acta Mater. 2002, 50, 61–73. [Google Scholar] [CrossRef]
- Mohammadzadeh, M.; Mohammadzadeh, R. Effect of grain size on apparent diffusivity in nanocrystal α-iron by atomistic simulation. Comput. Mater. Sci. 2017, 129, 239–246. [Google Scholar] [CrossRef]
- Mohammadzadeh, R.; Mohammadzadeh, M. Effect of grain boundary misorientation on the apparent diffusivity in nanocrystalline aluminum by atomistic simulation study. J. Appl. Phys. 2018, 124, 035102. [Google Scholar] [CrossRef]
- Yamakov, V.; Wolf, D.; Phillpot, S.; Mukherjee, A.; Gleiter, H. Deformation-mechanism map for nanocrystalline metals by molecular-dynamics simulation. Nat. Mater. 2004, 3, 43–47. [Google Scholar] [CrossRef] [PubMed]
- Mohammdzadeh, R. Analysis of plastic strain-enhanced diffusivity in nanocrystalline iron by atomistic simulation. J. Appl. Phys. 2019, 125, 135103. [Google Scholar] [CrossRef]
- Van Swygenhoven, H.; Weertman, J. Deformation in nanocrystalline metals. Mater. Today 2006, 9, 24–31. [Google Scholar] [CrossRef]
- Argon, A.; Yip, S. The strongest size. Philos. Mag. 2006, 86, 713–720. [Google Scholar] [CrossRef]
- Cassone, G.; Giaquinta, P.V.; Saija, F.; Saitta, A.M. Effect of electric field orientation on the mechanical and electrical properties of water ices: An Ab-initio study. J. Phys. Chem. B 2014, 118, 12717–12724. [Google Scholar] [CrossRef]
- Mortazavi, B.; Rahaman, O.; Makaremi, M.; Dianat, A.; Cuniberti, G.; Rabczuk, T. First-principles investigation of mechanical properties of silicene, germanene and stanene. Physica E 2017, 87, 228–232. [Google Scholar] [CrossRef] [Green Version]
- Gupta, P.; Yedla, N. Strain Rate and Temperature Effects on the Strength and Dissipative Mechanisms in Al-Cu50Zr50 Interface Model: Molecular Dynamics Simulation Study. Procedia Eng. 2017, 184, 631–636. [Google Scholar] [CrossRef]
- Rida, A.; Micoulaut, M.; Rouhaud, E.; Makke, A. Understanding the strain rate sensitivity of nanocrystalline copper using molecular dynamics simulations. Comput. Mater. Sci. 2019, 172. [Google Scholar] [CrossRef]
- Babicheva, R.; Dmitriev, S.; Zhang, Y.; Kok, S.; Zhou, K. Effect of Co Distribution on Plastic Deformation of Nanocrystalline Al-10.2 at.% Co Alloy. J. Nanomater. 2015, 2015, 1–8. [Google Scholar] [CrossRef]
- Inc., W.R. Mathematica, Version 12.1. Available online: https://www.wolfram.com/mathematica/ (accessed on 21 July 2020).
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Modell. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Mendelev, M.I.; Srolovitz, D.J.; Ackland, G.; Sun, D.; Asta, M. Development of new interatomic potentials appropriate for crystalline and liquid iron. Philos. Mag. 2003, 83, 3977–3994. [Google Scholar] [CrossRef]
- Stukowski, A.; Bulatov, V.; Arsenlis, A. Automated identification and indexing of dislocations in crystal interfaces. Model. Simul. Mater. Sci. 2012, 20, 085007. [Google Scholar] [CrossRef]
- Ghaffarian, H.; Karimi Taheri, A.; Kang, K.; Ryu, S. Molecular dynamics simulation study of the effect of temperature and grain size on the deformation behavior of polycrystalline cementite. Scr. Mater. 2014, 95. [Google Scholar] [CrossRef]
- Kadam, M.; Pawar, K.; Mantri, K. Effect of loading conditions on the stress concentration factor for a plate. IOSR J. Mech. Civil Eng. 2015, 3, 55–65. [Google Scholar]
- Potirniche, G.P.; Horstemeyer, M.; Wagner, G.; Gullett, P. A molecular dynamics study of void growth and coalescence in single crystal nickel. Int. J. Plast. 2006, 22, 257–278. [Google Scholar] [CrossRef]
- Jenkouk, V.; Patil, S.; Markert, B. Joining of tubes by gas detonation forming. J. Physics Conf. Ser. 2016, 734, 032101. [Google Scholar] [CrossRef]
- Patil, S.P.; Popli, M.; Jenkouk, V.; Markert, B. Numerical modelling of the gas detonation process of sheet metal forming. J. Physics Conf. Ser. 2016, 734, 032099. [Google Scholar] [CrossRef] [Green Version]
- Patil, S.; Prajapati, K.; Jenkouk, V.; Olivier, H.; Markert, B. Experimental and Numerical Studies of Sheet Metal Forming with Damage Using Gas Detonation Process. Metals 2017, 7, 556. [Google Scholar] [CrossRef] [Green Version]
- Patil, S.; Murkute, R.; Shirafkan, N.; Markert, B. Deformation of Stacked Metallic Sheets by Shock Wave Loading. Metals 2018, 8, 679. [Google Scholar] [CrossRef] [Green Version]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herman, J.; Govednik, M.; Patil, S.P.; Markert, B. Molecular Dynamics Simulation Study of the Mechanical Properties of Nanocrystalline Body-Centered Cubic Iron. Surfaces 2020, 3, 381-391. https://doi.org/10.3390/surfaces3030028
Herman J, Govednik M, Patil SP, Markert B. Molecular Dynamics Simulation Study of the Mechanical Properties of Nanocrystalline Body-Centered Cubic Iron. Surfaces. 2020; 3(3):381-391. https://doi.org/10.3390/surfaces3030028
Chicago/Turabian StyleHerman, Jan, Marko Govednik, Sandeep P. Patil, and Bernd Markert. 2020. "Molecular Dynamics Simulation Study of the Mechanical Properties of Nanocrystalline Body-Centered Cubic Iron" Surfaces 3, no. 3: 381-391. https://doi.org/10.3390/surfaces3030028
APA StyleHerman, J., Govednik, M., Patil, S. P., & Markert, B. (2020). Molecular Dynamics Simulation Study of the Mechanical Properties of Nanocrystalline Body-Centered Cubic Iron. Surfaces, 3(3), 381-391. https://doi.org/10.3390/surfaces3030028